Известия РАН. Теория и системы управления, 2023, № 2, стр. 44-59

Введение. В настоящее время в мире особое внимание уделяется тросовым группировкам космических аппаратов (КА), в которых благодаря существованию механических связей между КА (тросами) создаются условия для функционирования таких систем на орбите (при сохранении заданной геометрической конфигурации) в течение длительного времени практически без затрат топлива.

Первые проекты использования тросовых многоэлементных формирований на орбите появились почти полвека назад. Прежде всего этого были радиальные тросовые системы, в которых элементы располагались вдоль местной вертикали [1–3] на некотором расстоянии друг от друга. Была доказана устойчивость движения таких систем относительно вертикали в режиме гравитационной стабилизации и указаны много их полезных применений [1–6]. Позже появились публикации, где предлагались более сложные тросовые системы: многоугольные плоские и пространственные [7, 8]. Обеспечение согласованного полета по орбите тросовых группировок как многоэлементных систем КА, связанных легкими и гибкими связями, представляет собой сложную задачу, решение которой еще далеко от завершения.

Более глубокие и детальные исследования тросовых группировок КА начинают появляться в начале нашего века. Особое внимание специалистов привлекают тросовые группировки в виде “созвездий”, которые могут быть открытыми и замкнутыми (в виде кольца). Здесь можно отметить конфигурацию “ступица-спицы” (Hub-Spoke), динамика которой была исследована в [9, 10]. Система “ступица-спицы” имеет особенность с точки зрения управления, которая заключается в том, что большинство операций управления могут быть выполнены с помощью главного центрального КА. Большое количество исследований также было посвящено кольцевым конфигурациям, особенностью которых является отсутствие центрального КА и, следовательно, централизованного управления. Кольцевые конфигурации представляют собой замкнутую цепь, где все спутники соединены между собой. Особое внимание было уделено треугольной конфигурации [11–16], в частности методам управления ее движением. В [11] был проведен анализ равновесия и показана возможность полета треугольной группировки спутников в орбитальной плоскости. В [12] были разработаны законы управления движением вращающейся треугольной тросовой группировки, основанные на линеаризации и на использовании принципа обратной связи. В [13] решалась задача управления развертыванием вращающейся треугольной тросовой группировки с помощью контроля силы натяжения в тросах. Предполагалась возможность как выпуска тросов, так и их втягивания. В [14] была рассмотрена динамическая устойчивость вращающейся треугольной тросовой группировки вблизи точек либрации на этапах развертывания и при вращении в конечном состоянии. Теми же авторами были продолжены исследования треугольной конфигурации спутников с точки зрения влияние нелинейных эффектов на ее движение, где была показана связь между колебаниями троса и орбитальным движением системы [15]. В [16] для управления развертыванием треугольной группировки спутников с неизмеримыми скоростями разработали робастный контроллер с наблюдателями состояния, основанный на методе управления скользящим режимом (Sliding Mode Control – SMC). Анализ перечисленных работ показывает, что в них КА рассматривались как материальные точки, т.е. не учитывалось влияние их движения относительно центра масс на качество управления. Хотя естественно, что более полная постановка и решение рассматриваемой задачи управления движением треугольной группировки спутников (как и другими геометрическими конфигурациями тросовых систем) должны включать анализ их движения вокруг своих центров масс. Динамическая неустойчивость колебаний спутников относительно центров масс может привести к провисанию и ослаблению тросов и, как следствие, к потере управляемости в системе и структурной (с точки зрения геометрии) неустойчивости.

1. Описание задачи. В статье рассматривается формирование вращающейся тросовой группировки микроспутников в виде правильного треугольника. В исходном состоянии микроспутники жестко соединены между собой (в виде правильного треугольника), т.е. представляют собой твердое тело, которое вращается с некоторой ограниченной по модулю угловой скоростью, возникающей после отделения от ракеты-носителя или от базовой космической станции. После разделения микроспутников с некоторой относительной скоростью для формирования треугольной тросовой группировки используется комбинированный способ управления. Во-первых, осуществляется регулирование сил натяжения тросов, изменение которых должно соответствовать предлагаемой номинальной программе управления. Причем рассматриваются наиболее простые механизмы выпуска тросов, которые обеспечивают только торможение тросов, т.е. предполагается, что они не могут втягивать их обратно. Во-вторых, перевод системы во вращение обеспечивается двигателями малой тяги, установленными на каждом микроспутнике так, чтобы направление векторов сил тяги составляло постоянный угол с продольной осью спутника (продольная ось спутника – это линия, проходящая через его центр масс и точку крепления одного из тросов). Величина реактивных сил постоянна в течение формирования группировки и выбирается при построении номинальной программы управления.

Построение номинальной программы изменения сил натяжения тросов и выбор других параметров процесса формирования системы (скоростей разделения спутников, направления и величин сил малой тяги) осуществляется с использованием упрощенной модели движения, построенной с помощью уравнений Лагранжа. В математической модели в форме Лагранжа микроспутники рассматриваются как материальные точки, тросы представляют собой нерастяжимые идеальные механические связи и орбита центра масс всей системы не изменяется. Параметры номинальной программы и процесса развертывания системы выбираются исходя из выполнения конечных условий движения тросовой группировки с точки зрения приведения ее в заданное состояние, которое характеризуется размерами правильного треугольника и конечной величиной угловой скорости вращения системы относительно своего центра масс. В номинальном случае движение тросовой группировки осуществляется в плоскости орбиты центра масс системы. Для частного симметричного случая равных масс микроспутников получено аналитическое решение уравнений Лагранжа, которое может быть использовано для предварительного выбора параметров номинальной программы управления.

Для проверки возможности реализации номинальной программы управления построена более полная модель пространственного движения тросовой группировки, которая учитывает, в частности, растяжимость тросов, односторонность механических связей (тросов) между микроспутниками и движение спутников относительно центров масс. Эта модель предназначена для оценки влияния возмущений на процесс развертывания системы, при котором должны быть выполнены следующие базовые ограничения: сохраняться заданная треугольная конфигурация системы; выполняться ограничения на амплитуду угловых колебаний микроспутников относительно направления тросов; обеспечиваться необходимая точность приведения тросовой группировки в заданное конечное состояние. Таким образом, приведем основные возмущения, которые здесь учитываются в рамках этой модели: 1) возмущения угловой скорости вращения трех микроспутников как твердого тела после отделения от ракеты-носителя или от базовой космической станции; 2) возмущения, возникающие при разделении микроспутников; 3) возмущения, связанные с направлением действия сил малой тяги из-за колебаний микроспутников относительно своих центров масс; 4) наличие возможной малой статической и инерционной асимметрии микроспутников; 5) взаимное влияние угловых колебаний микроспутников и упругих колебаний тросов. Уравнения движения системы, соответствующие более полной модели, записываются в геоцентрической неподвижной системе координат. Причем характерной ее особенностью является использование кинематических уравнений углового движения спутников, в которых интегрируемыми переменными системы дифференциальных уравнений являются компоненты матрицы перехода от геоцентрической неподвижной к связанным со спутниками системам координат. Зная эту матрицу, нетрудно определить контролируемые углы между продольными осями спутников и направлениями тросов, которые соответствуют прямым, соединяющим точки крепления тросов смежных спутников. Здесь также необходимо отметить, что при использовании более полной модели уравнения движения центра масс и относительно центра масс системы не разделяются, т.е. интегрируются совместно. Причем это относится и к уравнениям движения микроспутников относительно своих центров масс, которые являются частью общей системы дифференциальных уравнений. Программная реализация процесса моделирования по более полным уравнениям движения основывается на применении матричных вычислений.

2. Математическая модель движения системы в форме Лагранжа. Для предварительного анализа движения системы, построения номинальной программы ее формирования и выбора параметров программы развертывания используются упрощенные уравнения плоского движения системы, в которых микроспутники рассматриваются как материальные точки, а тросы – нерастяжимые связи. Построение модели осуществляется в орбитальной подвижной системе координат $Cxyz$, начало которой находится в центре масс системы, ось $Cx$ направлена по радиус-вектору центра масс, а ось $Cy$ – по направлению движения в плоскости орбиты. Для вывода уравнений плоского движения системы применяются уравнения Лагранжа

где ${{T}_{c}}$ и $\Pi $ – кинетическая и потенциальная энергия системы, ${\mathbf{q}} = {{\left( {{{q}_{1}},{{q}_{2}},{{q}_{3}},{{q}_{4}}} \right)}^{{\text{T}}}}$ = ${{\left( {{{l}_{1}},{{l}_{2}},{{\theta }_{1}},{{\theta }_{2}}} \right)}^{{\text{T}}}}$ – вектор обобщенных координат, ${{l}_{1}},\;{{l}_{2}}$ – длины тросов, ${{\theta }_{1}},\;{{\theta }_{2}}$ – углы наклона тросов к местной вертикали, ${\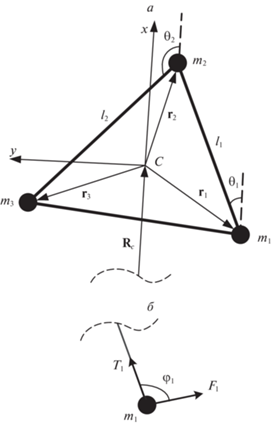mathbf{\dot {q}}}$ – соответствующий вектор обобщенных скоростей, ${\mathbf{Q}} = {{\left( {{{Q}_{{{{l}_{1}}}}},{{Q}_{{{{l}_{2}}}}},{{Q}_{{{{\theta }_{1}}}}},{{Q}_{{{{\theta }_{2}}}}}} \right)}^{{\text{T}}}}$ – вектор обобщенных непотенциальных сил. В вектор ${\mathbf{Q}}$ входят силы натяжения тросов и реактивные силы малой тяги, которые изменяются по заданной программе.

На рис. 1,а показаны обобщенные координаты ${{l}_{1}},{{l}_{2}},{{\theta }_{1}},{{\theta }_{2}}$ и нумерация микроспутников (материальных точек) ${{m}_{i}},i = \overline {1,3} $. Длина ${{l}_{3}}$ и угол ${{\theta }_{3}}$ для третьего троса вычисляются через обобщенные координаты из очевидных геометрических соотношений

Поскольку масса тросов не учитывается, то кинетическая и потенциальная энергии системы, входящие в уравнения (2.1), определяется следующим образом:

где ${{{\mathbf{R}}}_{c}}$ – радиус-вектор центра масс системы, ${{{\mathbf{r}}}_{i}}$ – радиусы-векторы микроспутников относительно центра масс системы (рис. 1).

Предполагая, что расстояние ${{{\mathbf{r}}}_{i}}$ много меньше, чем расстояние центра масс системы от притягивающего центра, выражение потенциальной энергии может быть аппроксимировано путем разложения его в биномиальный ряд и сохранения слагаемых до $O(1{\text{/}}R_{c}^{3})$. Тогда

где $m = {{m}_{1}} + {{m}_{2}} + {{m}_{3}}$, ${{\mu }_{i}} = {{{{m}_{i}}} \mathord{\left/ {\vphantom {{{{m}_{i}}} m}} \right. \kern-0em} m}$; $\omega = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu {R_{c}^{3}}}} \right. \kern-0em} {R_{c}^{3}}}} $ – орбитальная скорость центра масс системы, т.е. при использовании уравнений Лагранжа предполагается, что центр масс системы движется по круговой орбите.

Дифференцируя ${{T}_{c}},\;\Pi $ по обобщенным координатам и скоростям и подставляя полученные выражения в уравнения Лагранжа (2.1), получим [17]

При определении обобщенных сил ${{Q}_{{{{l}_{1}}}}},\;{{Q}_{{{{l}_{2}}}}},\;{{Q}_{{{{\theta }_{1}}}}},\;{{Q}_{{{{\theta }_{2}}}}}$ учитываются: 1) силы ${{T}_{i}},{\kern 1pt} {\kern 1pt} {\kern 1pt} i = \overline {1,\,3} $, создаваемые тормозными устройствами выпуска тросов и направленные вдоль каждого троса соответственно; 2) реактивные силы ${{F}_{{1,2,3}}}$, создаваемые двигателями малой тяги и составляющие углы ${{\varphi }_{{1,2,3}}}$ c направлениями тросов длиной ${{l}_{{1,2,3}}}$ (рис. 1,б). Обобщенные силы вычисляются из выражений

где $j = \overline {1,4} $.

3. Номинальная программа развертывания тросовой группировки. Предлагаемый закон управления силами натяжения имеет простой вид

где ${{L}_{d}}$ – конечная длина троса, ${{p}_{i}}{\text{,}}\;{{w}_{i}}$ – коэффициенты обратной связи, $T_{i}^{0} = {{m{{l}_{i}}{{{({{{\dot {\theta }}}_{i}} + \omega )}}^{2}}} \mathord{\left/ {\vphantom {{m{{l}_{i}}{{{({{{\dot {\theta }}}_{i}} + \omega )}}^{2}}} 9}} \right. \kern-0em} 9}$ – силы натяжения тросов, определенные в идеальном случае в предположении, что в процессе развертывания геометрическая конфигурация системы – это правильный треугольник. В выражении (3.1) слагаемые, зависящие от коэффициентов обратной связи, вводятся формально для обеспечения приведения системы в заданное конечное состояние, когда ${{l}_{i}} = {{L}_{d}}$, ${{\dot {l}}_{i}} = 0$, и система вращается с некоторой постоянной угловой скоростью ${{\omega }_{d}} = {{\dot {\theta }}_{i}} + \omega = {\text{const}}$, которая определяется моментом времени выключения двигателей ${{t}_{e}}$. В номинальном случае полагается, что модули сил ${{F}_{{1,2,3}}}$ и углы ${{\varphi }_{{1,2,3}}}$ равны: ${{F}_{{1,2,3}}} = F$ и ${{\varphi }_{{1,2,3}}} = \varphi $. Таким образом, реактивные силы изменяются по релейному закону

Покажем, что в частном случае ${{l}_{{\text{1}}}} = {{l}_{2}} = {{l}_{3}}$, ${{m}_{{\text{1}}}} = {{m}_{2}} = {{m}_{3}}$, который здесь принимается за номинальный, после выключения двигателей закон регулирования (3.1) при соответствующем выборе коэффициентов обратной связи обеспечивает асимптотическую устойчивость конечного состояния системы по переменным ${{l}_{i}} \to {{L}_{d}}$, ${\kern 1pt} {{\dot {l}}_{i}} \to 0$. Причем необходимо, чтобы в процессе развертывания ${{l}_{i}} < {{L}_{d}}$, ${{\dot {l}}_{i}} > 0$, т.е. переходный процесс был апериодическим, так как предполагается, что устройства выпуска троса работают только на торможение и не могут втягивать трос обратно. При этом угловая скорость вращения тросов ${{\dot {\theta }}_{i}} \to {{\dot {\theta }}_{d}}$, где ${{\dot {\theta }}_{d}}$ – некоторое ее постоянное значение, которое зависит от величины тяги $F$ и времени выключения двигателей ${{t}_{e}}$.

В данном частном случае уравнения для обобщенных координат ${{l}_{1}},\;{{\theta }_{1}}$ и ${{l}_{2}},\;{{\theta }_{2}}$, когда ${{F}_{{1,2,3}}} = 0$, тождественно совпадают и приводятся к линейной системе

где $\Delta l = l - {{L}_{d}}$, $l = {{l}_{{1,2,3}}}$, $\theta = {{\theta }_{{1,2,3}}}$, $p = {{p}_{{1,2,3}}}$, $w = {{w}_{{1,2,3}}}$.

Система уравнений (3.3)–(3.4) имеет решение

где произвольные постоянные ${{C}_{{1,2}}}$ определяются по значениям переменных в момент времени $t = {{t}_{e}}$.

Условия асимптотической устойчивости ${{l}_{i}} \to {{L}_{d}},$ ${{\dot {l}}_{i}} \to 0$ будут выполнены и переходный процесс будет апериодическим $\left( {{{l}_{i}} < {{L}_{d}},\,\,{{{\dot {l}}}_{i}} > 0} \right)$, если

В этом случае может быть найдено предельное значение угловой скорости

Понятно, что момент выключения двигателей ${{t}_{e}}$ должен быть выбран так, чтобы $l\left( {{{t}_{e}}} \right) < {{L}_{d}}$, и имелось еще время для завершения переходного процесса при развертывании системы.

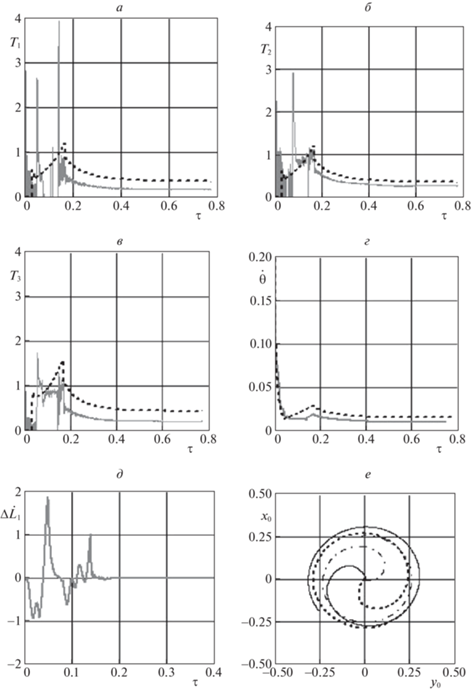
В качестве примера на рис. 2 представлены зависимости, характеризующие номинальную программу развертывания системы и соответствующие исходным данным, приведенным в табл. 1, где $\tau = \omega t$ – безразмерное время, где ω – угловая скорость движения центра масс системы на начальной круговой орбите. В номинальном случае длины тросов, силы натяжения, линейные и угловые скорости тросов изменяются по одинаковым законам, т.е. в каждый момент времени система представляет собой правильный треугольник, вращающийся в плоскости орбиты центра масс системы (рис. 2). Зависимости для длин, линейных и угловых скоростей тросов, построенные с помощью аналитических формул для $t > {{t}_{e}}$ (3.5)–(3.6), практически совпадают с зависимостями, полученными численным интегрированием уравнений (2.5)–(2.8). В качестве примера на рис. 2,г изображено предельное значение ${{\dot {\theta }}_{d}}$ (прямая линия), вычисленное по формуле (3.8), на рис. 2,д – траектории спутников относительно центра масс системы (0, 0) в процессе ее развертывания. Как будет показано ниже, приведенные аналитические оценки и численные результаты, полученные по уравнениям (2.5)–(2.8), подтвердились с помощью более полной модели движения тросовой группировки, записанной в геоцентрической системе координат и учитывающей движение спутников относительно своих центров масс.

В качестве двигателей малой тяги можно, например, использовать электрические двигатели, обладающие большой скоростью истечения рабочего тела (или удельным импульсом) и малым расходом массы. Так, например, при удельном импульсе ${{I}_{y}} = 20000$ м/с с тягой F = 1 Н массовый расход рабочего тела составит $F{\text{/}}{{I}_{y}} = 0.5 \times {{10}^{{ - 4}}}$ кг/с, что для исходных данных, приведенных в табл. 1, и для предлагаемой номинальной программы управления приведет к расходу массы для трех двигателей 0.023 кг. Поэтому изменением массы микроспутников при развертывании тросовой группировки в данном случае можно пренебречь.

4. Математическая модель движения тросовой группировки в геоцентрической неподвижной системе координат. Более полная модель движения системы записывается в геоцентрической системе координат $OXYZ$, где плоскость $OXY$ совпадает с плоскостью экватора, а ось $OX$ направлена в точку весеннего равноденствия. Уравнения движения центров масс микроспутников имеют вид

где ${{G}_{k}} = - \mu {{m}_{k}}{{R}_{k}}{\text{/}}R_{k}^{3},$ $k = \overline {1,3} $ – гравитационные силы, $\mu $ – гравитационный параметр Земли, ${{T}_{k}} = - T_{k}^{'}$ – силы натяжения тросов, ${{R}_{k}}$ – радиусы-векторы центров масс спутников, ${{F}_{k}}$ – реактивные силы малой тяги.

Силы натяжения тросов описывают одностороннюю механическую связь между спутниками и имеют вид

где ${{C}_{s}} = ES$ – жесткость тросов, $E$ – модуль упругости Юнга, $S$ – площадь поперечного сечения тросов, ${{L}_{k}}$ – недеформированные длины тросов, $\Delta {{r}_{k}},\,\,k = \overline {1,3} $, – радиусы-векторы, соединяющие точки крепления тросов, определяются следующим образом (рис. 3,а): где векторы ${{r}_{{12}}},\;{{r}_{{21}}},\;{{r}_{{23}}},\;{{r}_{{32}}},\;{{r}_{{13}}},\;{{r}_{{31}}}$ определяют положение точек крепления тросов относительно центров масс микроспутников.

Процесс выпуска троса моделируется с помощью динамических уравнений [18]

где коэффициент ${{m}_{e}}$ учитывает инерционность механизмов управления, U_k – управляющие силы. Принимается, что выпуск тросов длиной ${{L}_{k}}$ осуществляется с k-го микроспутника.

Управляющие силы вычисляются с использованием принципа обратной связи:

где номинальные значения ${{l}_{k}}$, ${{\dot {l}}_{k}}$ определяются интегрированием системы уравнений (2.5)–(2.8) или с помощью интерполяции из заранее составленных таблиц, ${{p}_{g}},{{w}_{g}}$ – коэффициенты обратной связи. Предполагается, что механизмы выпуска тросов осуществляют только торможение троса, поэтому если ${{\dot {L}}_{k}} \leqslant 0$ или ${{T}_{k}} \leqslant 0$, то выпуск тросов прекращается: ${{\dot {L}}_{k}} = {{\ddot {L}}_{k}} = 0$.

При определении углового движения микроспутников относительно своих центров масс используются классические динамическими уравнения Эйлера

где ${{\omega }_{k}}$ и J_k – вектор угловой скорости и тензор инерции k-го спутника, ${{M}_{k}}$ – вектор моментов от сил натяжения тросов. Предполагается, что микроспутники – это твердые тела, форма которых близка к сфере, и движение системы происходит на достаточно больших высотах. Поэтому гравитационные и аэродинамические моменты не учитываются. Тензоры инерции J_k спутников определяются в системах координат ${{с}_{k}}{{x}_{k}}{{y}_{k}}{{z}_{k}}$, связанных с главными центральными осями инерции спутников. На рис. 3,б в качестве примера показаны направления осей ${{с}_{1}}{{x}_{1}}$ и ${{с}_{1}}{{y}_{1}}$ для первого спутника.

Моменты ${{M}_{k}}$ представляют собой суммы

где ${{M}_{{12}}} = {{r}_{{12}}} \times {{T}_{1}}$, ${{M}_{{13}}} = {{r}_{{13}}} \times T_{3}^{'}$, ${{M}_{{21}}} = {{r}_{{21}}} \times T_{1}^{'}$, ${{M}_{{23}}} = {{r}_{{23}}} \times {{T}_{2}}$, ${{M}_{{31}}} = {{r}_{{31}}} \times {{T}_{3}}$, ${{M}_{{32}}} = {{r}_{{32}}} \times T_{2}^{'}$.

Направления реактивных сил ${{F}_{k}},\,\,k = \overline {1,3} \,,$ жестко связаны с корпусом микроспутников, лежат в плоскостях ${{с}_{k}}{{x}_{k}}{{y}_{k}}\,$и составляют углы ${{\varphi }_{k}}\,$(рис. 3,б) с осями ${{с}_{k}}{{x}_{k}}\,$. Предполагается, что направления реактивных сил проходят через центры масс спутников, поэтому соответствующие моменты не учитываются.

Кинематические уравнения записываются в форме уравнений Эйлера–Пуассона

где ${{e}_{{xk}}},\;{{e}_{{yk}}},\;{{e}_{{zk}}},$ $k = \overline {1,3} ,$ – орты систем координат ${{с}_{k}}{{x}_{k}}{{y}_{k}}{{z}_{k}}$.

В этом случае проекции единичных векторов ${{e}_{{xk}}},\;{{e}_{{yk}}},\;{{e}_{{zk}}}$ на оси неподвижной геоцентрической системы координат $OXYZ$ являются элементами матриц перехода от системы координат $OXYZ$ к системам координат ${{с}_{k}}{{x}_{k}}{{y}_{k}}{{z}_{k}}$. Эти матрицы имеют вид

При интегрировании уравнений (4.8) должны с заданной погрешностью выполняться условия ортогональности векторов ${{e}_{{xk}}},\;{{e}_{{yk}}},\;{{e}_{{zk}}}$ и $\left| {{{e}_{{xk}}}} \right| = \left| {{{e}_{{yk}}}} \right| = \left| {{{e}_{{zk}}}} \right| = 1$. Для этого можно использовать алгоритм коррекции, основанный на минимизации корректирующих добавок при изменении значений компонент векторов ${{e}_{{xk}}},\;{{e}_{{yk}}},\;{{e}_{{zk}}}$ [19].

При развертывании группировки и при ее движении по орбите после формирования конфигурации необходимо осуществлять контроль за угловым движением микроспутников, а именно за углами между характерными осями спутников ${{e}_{{xk}}}$ и направлениями тросов $\Delta {{r}_{k}},\;k = \overline {1,3} $. Эти углы определяются следующим образом (рис. 3,б):

где $\Delta r_{k}^{'} = - \Delta {{r}_{k}},$ $k = \overline {1,3} $. При отсутствии колебаний в идеальном случае имеем для правильного треугольника ${{\alpha }_{k}} = 0$, $\alpha _{k}^{{\left( {k - 1} \right)}} = \alpha _{1}^{{\left( 3 \right)}} = \pi {\text{/}}3$. В общем случае при наличии возмущений амплитуды колебаний пространственных углов (4.10) должны быть ограничены относительно своих невозмущенных значений.

5. Расчет процесса разделения микроспутников. В качестве примера рассматриваются три одинаковых микроспутника, причем в исходном состоянии до их разделения линии, соединяющие центры масс спутников, образуют правильный треугольник. После отделения группировки спутников, жестко связанных между собой, от ракеты-носителя или космической станции вся система вращается относительно своего центра масс с угловой скоростью ${{\omega }_{0}}$. Причем в общем случае группировка спутников как твердое тело совершает пространственное движение.

После разделения спутников векторы скоростей их центров масс и угловых скоростей вычисляются в соответствии с известными теоремами теоретической механики. Обозначим через ${{V}_{{r1}}}$ и ${{V}_{{r3}}}$ относительные скорости отделения спутников 1 и 3 от спутника 2. Тогда, используя закон сохранения импульса, определим скорости центров масс спутников ${{V}_{{1,2,3}}}$ после разделения

где ${{V}_{c}}$ – вектор скорости центра масс системы до разделения.

Для определения угловых скоростей спутников после разделения используется теорема об изменении кинетического момента твердого тела при ударном воздействии:

где $\Delta {{K}_{{1,2,3}}}$ – приращение кинетических моментов спутников, ${{S}_{{1,3}}}$ – ударные импульсы, действующие на спутники 1 и 3, причем $S_{{1,3}}^{'} = - {{S}_{{1,3}}}$. Импульсы ${{S}_{{1,3}}}$ определяются из выражений

Зная приращения $\Delta {{K}_{{1,2,3}}}$, нетрудно определить изменение угловых скоростей спутников после их разделения:

Следует отметить, если векторы импульсов ${{S}_{{1,3}}}$ проходят через центры масс микроспутников, то их угловые скорости не изменяются и равны угловым скоростям системы до разделения спутников. Если же, например, центры масс спутников смещены относительно геометрического центра сферы (статическая асимметрия), то угловые скорости спутников после их разделения изменяются. В общем случае влияние асимметрии спутников на их угловые колебания заключается в следующем: 1) в изменении начальных угловых скоростей их движения (5.4); 2) в изменении характера колебаний спутников относительно центров масс при развертывании тросовой системы и при ее последующем движении, которое описывается системой уравнений (4.6) и (4.8).

6. Численные результаты и их анализ. Исходные данные, принятые для численного моделирования движения тросовой группировки с использованием уравнений (4.1), (4.4), (4.6), (4.8), приводятся в табл. 2. В номинальном невозмущенном случае система до разделения спутников вращается в плоскости орбиты с некоторой ненулевой угловой скоростью (в численном примере ${{\omega }_{z}} = 0.1$ c^–1).

Простейший приближенный анализ движения тросовой группировки в виде правильного треугольника показывает, что углы ${{\varphi }_{{1,2,3}}}$, характеризующие направление действия сил тяги (предполагается, что они равны), должны удовлетворять неравенству $\pi {\text{/}}2 < {{\varphi }_{{1,2,3}}} < 5\pi {\text{/}}6$. Нарушение верхнего ограничения приводит к смене знака моментов от сил тяги относительно центра масс правильного треугольника, что ведет к невозможности перевода системы во вращение в заданном направлении (против часовой стрелки). Нарушение нижнего ограничения приводит к тому, что силы тяги не растягивают, а сжимают тросы (они становятся не натянутыми), что неизбежно ведет к изменению заданной геометрической конфигурации системы, к потере управляемости и, следовательно, к невозможности выполнить поставленную задачу по формированию треугольной тросовой группировки. Моделирование процесса развертывания системы по более полной модели (4.1) подтвердило приведенные утверждения. В частности, если ${{\varphi }_{{1,2,3}}} \approx \pi {\text{/}}2$, то движение системы становилось неустойчивым, причем это относится как к сохранению ее геометрической конфигурации, так и к движению спутников относительно своих центров масс. С другой стороны, уменьшение углов ${{\varphi }_{{1,2,3}}}$ в приведенном выше диапазоне приводит к более быстрому развертыванию системы (моменты от сил тяги увеличиваются). В связи с этим была выбрана некоторая компромиссная величина ${{\varphi }_{{1,2,3}}} = 100^\circ $ (табл. 1), при которой движение системы еще было устойчиво с точки зрения ее геометрии и углового движения спутников.

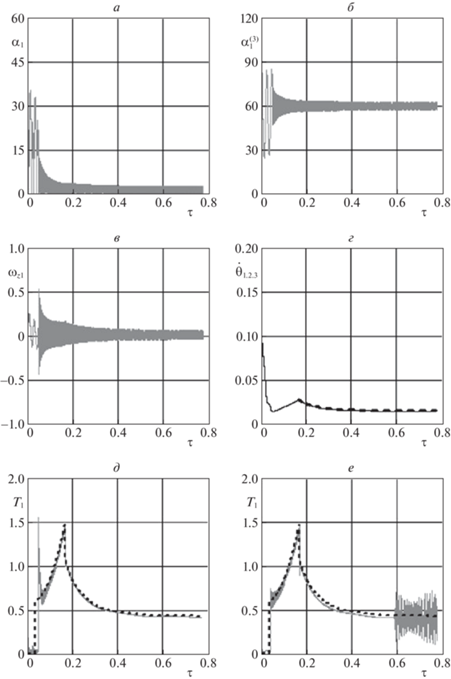
Рисунок 4 иллюстрирует изменение некоторых характерных параметров движения группировки при ее развертывании в номинальном плоском случае (начальная орбита – круговая). На рис. 4,а–в для примера показано изменение характеристик углового движения первого микроспутника: углов ${{\alpha }_{1}}$, $\alpha _{1}^{{\left( 3 \right)}}$ и угловой скорости ${{\omega }_{{z1}}}{\kern 1pt} {\kern 1pt} \left( {{{\omega }_{{y1}}} = {{\omega }_{{x1}}} = 0} \right)$. При этом угол $\alpha _{1}^{{\left( 3 \right)}}$ совершает колебания относительно значения $\pi {\text{/}}3$, амплитуда которых ограничена. Характеристики движения относительно центра масс других спутников изменяются аналогично. На рис. 4,г приводится график для угловых скоростей вращения тросов ${{\dot {\theta }}_{{1,2,3}}}$ длиной ${{l}_{{1,2,3}}}$ (жирной штриховой линией показано аналитическое решение (3.6)), определенных в соответствии с моделью (4.1), которые практически совпадают. Рисунок 4,д иллюстрирует изменение силы натяжения ${{T}_{1}}$, где штриховой линией показана сила натяжения, определенная по модели (2.5)–(2.8). По изменению силы натяжения ${{T}_{1}}$ можно определить характерные участки движения тросовой группировки при ее развертывании. На начальном небольшом по времени участке $\left( {0 \leqslant \tau < 0.05} \right)$ сила натяжения ведет себя сложным образом, что объясняется возмущением при включении реактивных двигателей (ступенчатое изменение тяги). Далее сила натяжения возрастает до момента выключения двигателей $\left( {\tau = 0.17} \right)$. Дальнейшее развертывание системы происходит только под действием центробежных сил до достижения всеми тросами заданной длины (0.5 км). Силы натяжения ${{T}_{{2,3}}}$ изменяются аналогично. В конечном итоге, тросовая группировка представляет собой почти правильный треугольник, который вращается с постоянной угловой скоростью, приблизительно равной 0.015 с^–1. При этом спутники совершают малые колебания относительно линий, характеризующих направления тросов (или направления действия сил натяжения). Конечное значение угловой скорости тросовой группировки можно изменить, смещая момент времени выключения реактивных двигателей. Значения коэффициентов обратной связи ${{p}_{g}},\;{{w}_{g}}$ (табл. 2) в уравнениях, записанных в геоцентрической системе координат, по сравнению с коэффициентами ${{p}_{{1,2,3}}},\;{{w}_{{1,2,3}}}$ (табл. 1) были изменены, так как в противном случае по окончанию выпуска троса, когда длина троса фиксируется, имеют место колебания сил натяжения тросов с увеличенной амплитудой (рис. 4,е).

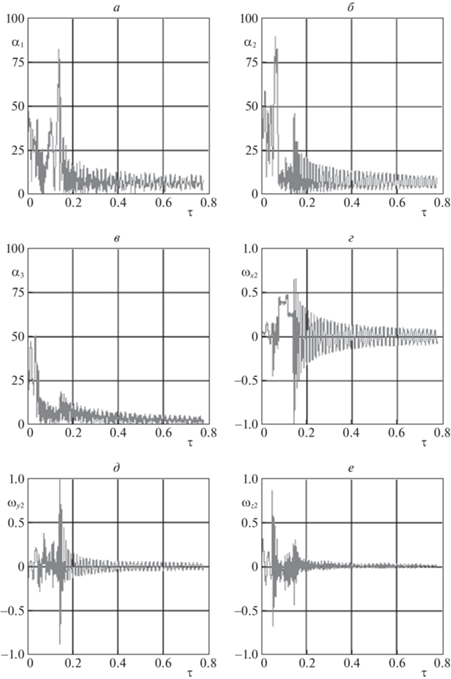
Далее, возмущенное движение тросовой группировки микроспутников иллюстрируется на рис. 5 и 6. Авторами специально был выбран один из наиболее сложных вариантов исходных данных для моделирования возмущенного движения группировки спутников. Рассматривались спутники с разными массами: ${{m}_{1}} = 8$ кг, ${{m}_{2}} = 10$ кг, ${{m}_{1}} = 12$ кг. До разделения спутников начальные угловые скорости системы составляли ${{\omega }_{x}} = {{\omega }_{z}} = 0.1$ с^–1, ${{\omega }_{y}} = - 0.1$ с^–1, т.е. угловые скорости по осям связанной системы координат ${{\omega }_{x}},\,\,{{\omega }_{y}}$ по модулю равны значению номинальной угловой скорости вращения ${{\omega }_{z}}$ системы (табл. 2). Имеет место также сложная статическая и динамическая асимметрия спутников: 1) центры масс спутников смещены по отношению к геометрическому центру сфер на величину ${{\Delta D} \mathord{\left/ {\vphantom {{\Delta D} D}} \right. \kern-0em} D} = 0.1$, где D – диаметр спутников, ΔD – величина смещения центра масс; 2) разность моментов инерции ${{\left| {{{J}_{{zk}}} - {{J}_{{yk}}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{J}_{{zk}}} - {{J}_{{yk}}}} \right|} {{{J}_{s}}}}} \right. \kern-0em} {{{J}_{s}}}} = 0.1$, где ${{J}_{s}}$ – момент инерции однородной сферы, ${{J}_{{yk}}},\;{{J}_{{zk}}}$ – моменты инерции спутников относительно систем координат ${{с}_{k}}{{x}_{k}}{{y}_{k}}{{z}_{k}}$. Наличие статической и динамической асимметрии приводит к соответствующему изменению начальных угловых скоростей спутников после разделения (5.4), так как направления импульсов не проходят через центры масс спутников и, кроме того, данная асимметрия влияет на последующее движение спутников относительно своих центров масс.

На рис. 5,а–в приводится изменение углов ${{\alpha }_{{1,2,3}}}$, характеризующих угловое движение спутников относительно направлений тросов длиной ${{l}_{{1,2,3}}}$, на рис. 5,г–е – в качестве примера изменение угловых скоростей ${{\omega }_{{x2}}},\;{{\omega }_{{y2}}},\;{{\omega }_{{z2}}}$ для спутника 2. Как следует из результатов, представленных на рис. 5, колебания углов ${{\alpha }_{{1,2,3}}}$ имеют ограниченный характер, т.е. действие рассматриваемых возмущений не приводит к неустойчивости углового движения спутников и проявляется в основном в начальных возмущениях из-за наличия статической асимметрии спутников. Изменение угловых скоростей ${{\omega }_{{x2}}},\;{{\omega }_{{y2}}},\;{{\omega }_{{z2}}}$ (рис. 5,г–е) показывает, что спутник 2 совершает сложное пространственное движение относительно направлений тросов. Это же имеет место для углов и угловых скоростей спутников 1 и 3, аналогичные зависимости для которых здесь не приводятся. Действие рассматриваемых возмущений изменяет силы натяжения тросов, величины которых по окончанию развертывания системы отличаются от номинальных значений (рис. 6,а–в), при этом конечная величина угловой скорости вращения системы уменьшается (рис. 6,г) по сравнению с невозмущенным случаем. В качестве примера на рис. 6,д показан переходный процесс по скорости $\Delta {{\dot {L}}_{1}} = {{\dot {L}}_{1}} - {{\dot {l}}_{1}}$ для троса длиной l₁. Изменение ошибок регулирования для других тросов аналогично. На рис. 6,е показаны траектории центров масс спутников, определенные по модели в геоцентрической системе координат и построенные относительно центра масс системы (0, 0). Таким образом, действие рассматриваемых возмущений не приводит к неустойчивости углового движения спутников и слабо влияет на конечное состояние тросовой группировки, которая после окончания развертывания имеет треугольную конфигурацию и вращается с постоянной угловой скоростью, а колебания спутников относительно направлений тросов ограничены.

Заключение. С помощью уравнений Лагранжа получена математическая модель движения рассматриваемой тросовой системы, с помощью которой построена номинальная программа формирования вращающейся группировки микроспутников треугольной конфигурации. В частном случае при отсутствии возмущений найдено аналитическое решение полученной системы уравнений, которое можно использовать для предварительных оценок при проектировании процесса формирования системы. Построена более полная модель движения тросовой группировки микроспутников в неподвижной геоцентрической системе координат, позволяющая оценить влияние на процесс развертывания растяжимости тросов, односторонности механических связей и угловых колебаний микроспутников относительно направлений тросов. Численные результаты моделирования движения тросовой группировки в геоцентрической системе координат подтвердили возможность использования предложенной программы управления для формирования вращающейся треугольной тросовой группировки микроспутников на орбите. Показано, что наличие малых возмущений в исходных данных и массово-инерционной асимметрии микроспутников не оказывает существенного влияния на процесс формирования тросовой группировки, в частности, амплитуды угловых колебаний спутников относительно направлений тросов остаются ограниченными.