Известия РАН. Теория и системы управления, 2023, № 2, стр. 73-84

Введение. Методики послеполетного восстановления вращательного движения космического аппарата (КА) по накопленной выборке измерений широко применяются в современной космонавтике. Они используются для решения таких задач, как определение фактической величины аэродинамического момента на низких околоземных орбитах [1, 2], оценка условий микрогравитации на борту КА [3–5], нахождение инерционных параметров КА [6, 7], исследование неуправляемого углового движения КА [8–10]. В процессе обработки измерительной информации обычно оцениваются кинематические (углы ориентации или кватернион), динамические (компоненты угловой скорости) и инерционные (коэффициенты инерции) параметры КА, а также другие параметры математической модели движения, характеризующие влияние внешней среды [11, 12]. В данной статье для послеполетного восстановления вращательного движения малого космического аппарата (МКА) BugSat-1 использовались элементы методики, разработанной авторами и опубликованной в [11].

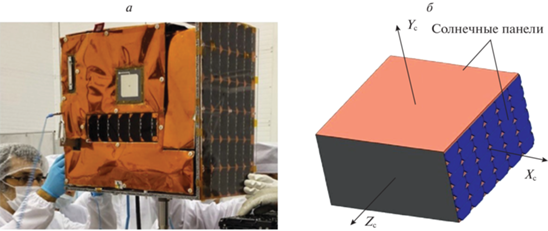
МКА BugSat-1 – технологический демонстратор, созданный аргентинской компанией Satellogic S.A. и предназначенный для отработки технологий дистанционного зондирования Земли (ДЗЗ). В этой миссии были проведены летные испытания бортовых систем, которые в последующем применялись при создании группировки спутников ДЗЗ Aleph-1. МКА был запущен 19 июня 2014 г. с космодрома “Ясный” на ракете-носителе “Днепр” и выведен на солнечно-синхронную орбиту с наклонением $91.3^\circ $, высотой апогея 612 км и высотой перигея 570 км. После завершения основной миссии по отработке технологий ДЗЗ МКА использовался как ретранслятор для любительской радиосвязи. Конструктивные характеристики МКА приведены в [13], масса составляет 22 кг, а габариты – 500 × 500 × 275 мм. Данные об инерционных характеристиках МКА отсутствуют. На рис. 1 представлен внешний вид МКА и расположение осей связанной системы координат.

1. Постановка задачи. Полетные данные МКА получены с помощью сервиса, предоставляющего открытые телеметрические данные SatNOGS [14]. Продолжительности рассматриваемых интервалов измерений вектора направления на Солнце ${{{\mathbf{S}}}_{{{\text{изм}}}}}({{t}_{i}})$ (выбраны на основании рекомендаций, приведенных в [11]) и количество измеренных векторов представлены в табл. 1.

Для записи уравнений движения МКА вокруг центра масс (точка $O{\kern 1pt} '$) (рис. 2), а также соотношений, используемых при обработке данных, вводятся три правые декартовые системы координат.

Связанная с МКА система координат (ССК) образована главными центральными осями инерции и имеет обозначение $O{\kern 1pt} '{{X}_{{\text{с}}}}{{Y}_{{\text{с}}}}{{Z}_{{\text{с}}}}$. Абсолютная геоцентрическая система координат (АСК) имеет обозначение $O{{X}_{{\text{a}}}}{{Y}_{{\text{a}}}}{{Z}_{{\text{a}}}}$ с началом в центре масс Земли (точка O). Ось ${{X}_{{\text{a}}}}$ направлена в точку весеннего равноденствия, ось ${{Z}_{{\text{a}}}}$ – в северный полюс мира, ось ${{Y}_{{\text{a}}}}$ дополняет систему до правой.

Орбитальная система координат (ОСК) имеет обозначение $O{\kern 1pt} '{{X}_{{\text{o}}}}{{Y}_{{\text{o}}}}{{Z}_{{\text{o}}}}$, ось ${{X}_{{\text{o}}}}$ направлена по радиус-вектору МКА, ось ${{Z}_{{\text{o}}}}$ перпендикулярна плоскости орбиты, ось ${{Y}_{{\text{o}}}}$ дополняет систему до правой, начало системы находится в центре масс МКА.

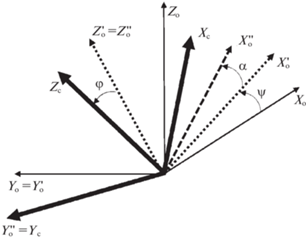
Положение ССК относительно ОСК (рис. 3) задается тремя последовательными поворотами на угол прецессии $\psi $ вокруг оси ${{Y}_{{\text{o}}}}$, угол нутации α вокруг новой оси $Z_{{\text{o}}}^{'}$ и на угол собственного вращения $\varphi $ вокруг новой оси $Y_{{\text{o}}}^{{''}}$.

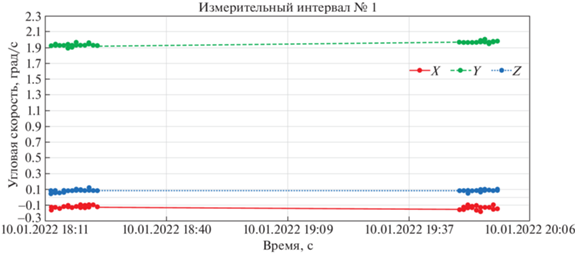
Телеметрические данные об угловой скорости вращения МКА показывают, что компоненты абсолютной угловой скорости мало изменяются на протяжении интервалов накопления измерений. Данный факт проиллюстрирован на примере интервала измерений № 1 (рис. 4).

Особенностью всех использованных телеметрических данных является то, что измерения присутствуют только на начало и конец интервала. Исходя из характера доступных измерений вектора угловой скорости ${\mathbf{\omega }}$, в работе сделано допущение, что компоненты вектора угловой скорости ${\mathbf{\omega }}$ не меняются на протяжении интервала формирования выборки измерительной информации. В связи с этим принимается, что уравнение для вектора угловой скорости МКА имеет вид

Кинематические уравнения запишем следующим образом [15]:

где ${{{\mathbf{\omega }}}_{o}} = {\mathbf{A}}({\mathbf{q}})\,{{[\begin{array}{*{20}{c}} 0&0&{\sqrt {{{{{\mu }_{e}}} \mathord{\left/ {\vphantom {{{{\mu }_{e}}} {{{{\mathbf{r}}}^{3}}}}} \right. \kern-0em} {{{{\mathbf{r}}}^{3}}}}} } \end{array}]}^{{\text{T}}}}$ – вектор орбитальной угловой скорости МКА, ${\mathbf{r}}$ – радиус-вектор МКА, вычисленный с использованием TLE-файлов (two line elements, двухстрочный набор элементов), q – кватернион ориентации МКА, ${\mathbf{A}}({\mathbf{q}})$ – матрица поворота из ОСК в ССК, которая имеет вид где E – единичная матрица.

В [11] авторами данной статьи описана методика идентификации бортовой математической модели наноспутника. В данной работе использованы элементы созданной методики – процедур идентификации параметров математической модели и оценки погрешностей.

Восстановление вращательного движения МКА происходит в результате минимизации следующей целевой функции:

где ${{{\mathbf{S}}}_{{{\text{изм}}}}}({{t}_{i}})$ – измеренный вектор направления на Солнце в момент времени ${{t}_{i}}$, ${{{\mathbf{S}}}_{{{\text{мод}}}}}({\mathbf{b}},{{t}_{i}})$ – смоделированный вектор направления на Солнце [16], N – число измеренных векторов ${{{\mathbf{S}}}_{{{\text{изм}}}}}({{t}_{i}})$ , b – вектор оцениваемых параметров, содержит кинематические и динамические параметры движения МКА и имеет следующий вид:

Движение центра масс МКА рассчитывалось по модели SGP4, учитывающей влияние 2-й и 4‑й зональных гармоник гравитационного поля Земли, в качестве начальных условий движения использовались данные наиболее близкого ко времени измерений TLE-файла МКА BugSat-1 [17].

Как будет показано ниже, вращение МКА происходит вокруг измеряемого вектора направления на Солнце. При таком вращении невозможно оценить три угла ориентации, поэтому в векторе оцениваемых параметров начальный угол $\varphi ({{t}_{0}})$ принимается равным нулю. Для удобства реализации численной процедуры минимизации (1.1) все расчеты производятся в кватернионах, затем кватернион переводится в углы для наглядности интерпретации.

Погрешности оцененных параметров определялись по следующей формуле [11]:

где ${{\sigma }_{J}} = \sqrt {{{J({\mathbf{\hat {b}}})} \mathord{\left/ {\vphantom {{J({\mathbf{\hat {b}}})} {\left( {3N - 5} \right)}}} \right. \kern-0em} {\left( {3N - 5} \right)}}} $ – среднеквадратическая погрешность [10], показывает, насколько математическая модель измерений близка к фактическим измерениям, ${\mathbf{\hat {b}}}$ – оценка вектора искомых параметров, полученная в результате минимизации функции (1.1). Погрешность ${{\sigma }_{J}}$ в данной работе можно наглядно представить через угол ${{\delta }_{S}}$ между единичными векторами ${{{\mathbf{S}}}_{{{\text{изм}}}}}({{t}_{i}})$ и ${{{\mathbf{S}}}_{{{\text{мод}}}}}({\mathbf{b}},{{t}_{i}})$ в трехмерном пространстве

2. Восстановление параметров углового движения. Идентификация вектора параметров углового движения МКА (1.2) проводилась с использованием процедуры идентификации [11]. Для минимизации функции (1.1) применялся метод дифференциальной эволюции (ДЭ) [18]. Для корректной работы метода ДЭ требуется настроить диапазоны поиска оцениваемых параметров табл. 2. Диапазоны для компонент вектора угловой скорости выбирались исходя из телеметрических данных с датчика угловой скорости, а для углов ориентации МКА – исходя из априорных телеметрических данных ${{{\mathbf{S}}}_{{{\text{изм}}}}}({{t}_{i}})$. Параметры алгоритма ДЭ, отвечающие за сходимость, выбраны исходя из рекомендованных значений [18], коэффициент $F = 0.5$, P = 0.9.

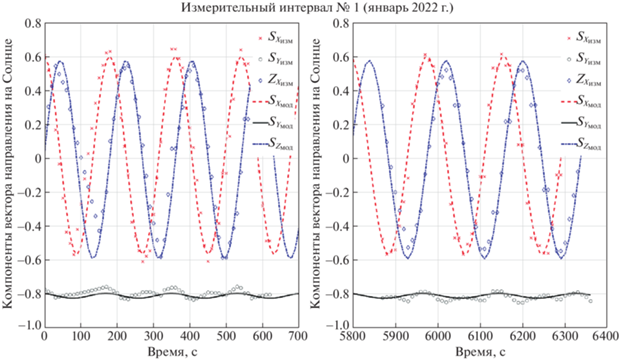
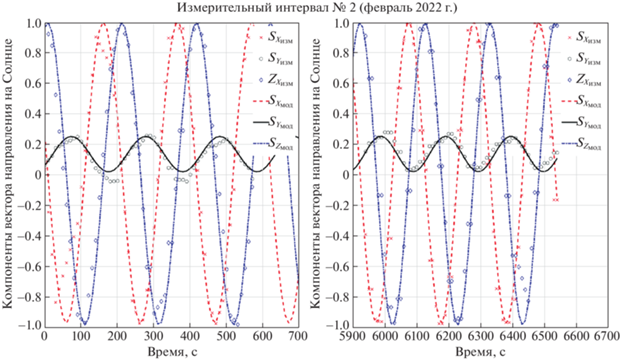
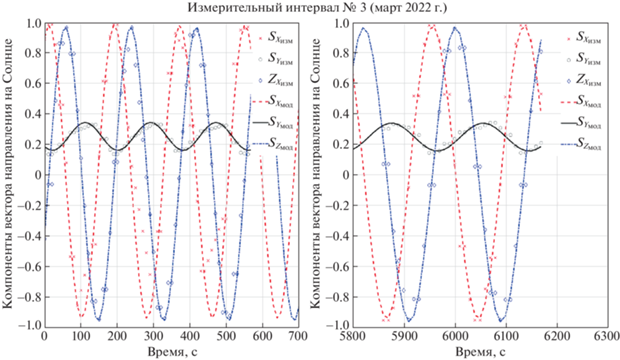
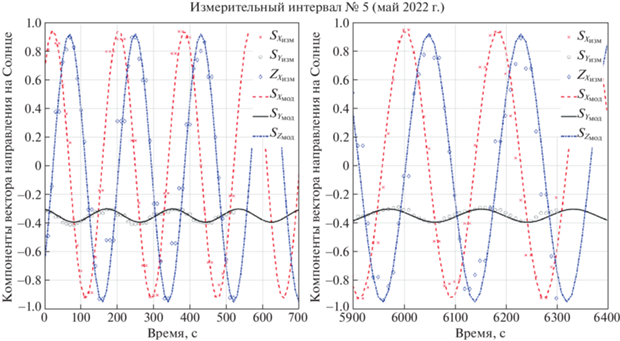
На рис. 5–9 приведены результаты выполненной обработки измерений вектора направления на Солнце (промежутки с отсутствующими измерениями вырезаны). Также следует отметить, что измерения приводились к постоянному шагу по времени с помощью линейной интерполяции. Это привело к несущественным погрешностям при обработке данных

Согласно рис. 5–9, был сделан вывод о достаточном согласовании математической модели вектора направления на Солнце и измерений. Результаты обработки данных представлены в табл. 3. Погрешности оценки параметров вычислены по формуле (1.3), угол рассогласования ${{\delta }_{S}}$ оценен по соотношению (1.4).

По оцененным параметрам углового движения МКА были построены вектор кинетического момента МКА в АСК на единичной сфере и вектор направления на Солнце для каждого интервала измерений. Направление вектора кинетического момента МКА на рассматриваемых интервалах времени, характеризующихся малыми изменениями значений угловых скоростей, принималось совпадающим с осью конуса прецессии в рамках принятой модели движения и вычислялось исходя из предположения, что ось ${{Y}_{{\text{с}}}}$ совершает равномерное вращение вокруг вектора кинетического момента. Взаимное расположение векторов представлено на рис. 10.

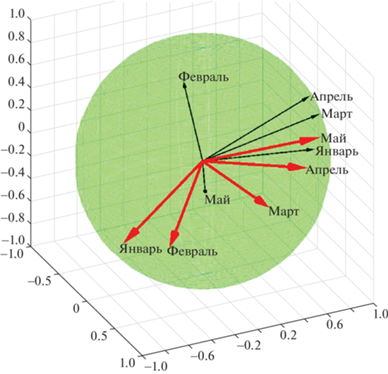
Согласно рис. 10, можно сделать вывод, что между измерительными интервалами МКА совершает переориентацию вектора кинетического момента.

Были построены годографы оси ${{Y}_{{\text{с}}}}$ МКА в ОСК для каждого измерительного интервала (рис. 11).

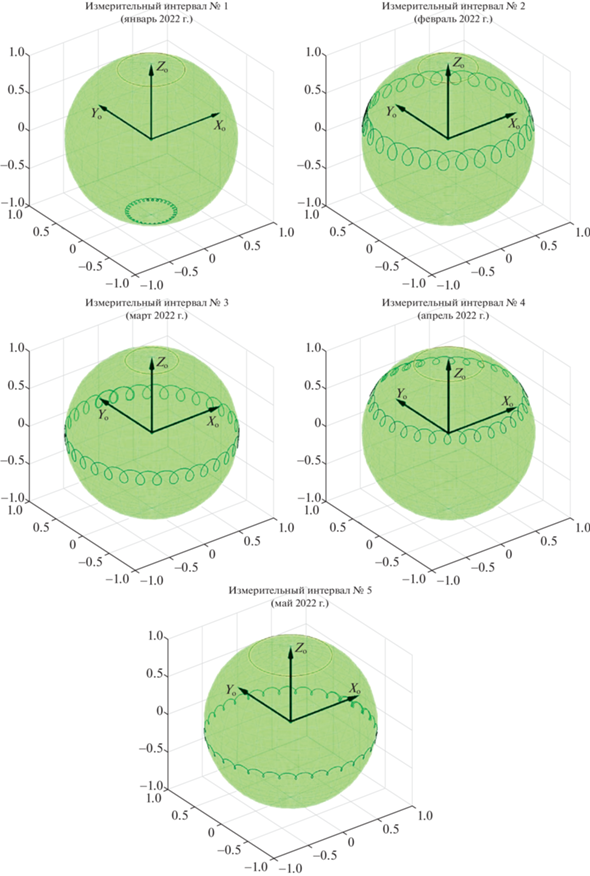
Из рис. 10 видно, что угловое движение МКА на рассматриваемых интервалах близко к случаю регулярной прецессии. Для оценки параметров прецессии была составлена расчетная схема (рис. 12).

На рис. 12 ${{\omega }_{{\text{п}}}} = \sqrt {\omega _{x}^{2} + \omega _{z}^{2}} $ – поперечная угловая скорость, $\dot {\psi }$ – скорость прецессии, $\dot {\varphi }$ – угловая скорость собственного вращения, ${\mathbf{K}}$ – вектор кинетического момента, ${{\alpha }_{{\text{к}}}}$ – угол полураствора конуса прецессии, который в принятой модели регулярной прецессии считается постоянным. Зная положение оси ${{Y}_{{\text{с}}}}$ в каждый момент времени, была оценена скорость прецессии и угол полураствора конуса прецессии. Согласно [19], из выражения ${{\dot {\varphi }} \mathord{\left/ {\vphantom {{\dot {\varphi }} {\left| {{{\omega }_{y}}} \right|}}} \right. \kern-0em} {\left| {{{\omega }_{y}}} \right|}} = \mu $ и геометрических соотношений рис. 11 получили формулу для оценки инерционного параметра МКА:

где $\mu = {{\left( {{{I}_{y}} - {{I}_{z}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{I}_{y}} - {{I}_{z}}} \right)} {{{I}_{x}}}}} \right. \kern-0em} {{{I}_{x}}}}$ – коэффициент инерции МКА, ${{\omega }_{{\text{п}}}}$ – поперечная угловая скорость. Также был вычислен угол между вектором кинетического момента МКА и вектором направления на Солнце ε. Исходя из погрешностей оценки вектора угловой скорости ${\mathbf{\omega }}$ и угла конуса прецессии ${{\alpha }_{{\text{к}}}}$ оценили математическое ожидание и среднеквадратическое отклонение параметра μ. Оценка проводилась на основе допущения о нормальном распределении параметра μ. Результаты расчетов представлены в табл. 4.

Полученные результаты позволили сделать вывод, что МКА находится в режиме одноосной солнечной ориентации. Положение вектора кинетического момента на рассматриваемых интервалах постоянно относительно Солнца. Угол между направлением на Солнце и осью ${{Y}_{{\text{с}}}}$ в период с февраля по март близок к 90°, что обеспечивает эффективное использование солнечных батарей.

Угол конуса прецессии изменялся в диапазоне от 1.97 до 9.5°, что предположительно связано с работой системы управления движением. Угловая скорость прецессии МКА на всех интервалах оставалась примерно постоянной – порядка 2, при этом в феврале 2022 г. наблюдалось снижение до 1.77 град/с.

Оценки коэффициента инерции МКА оставались в диапазоне от 0.235 до 0.377, усредненное значение коэффициента инерции на всех рассмотренных интервалах составило 0.298. Оценки коэффициента инерции отклонялись от усредненного значения не более чем на 13%. Погрешность оценки коэффициента инерции соответствует погрешностям, указанным в работах близкой тематики [8, 9].

Заключение. Показана возможность использования упрощенной математической модели углового движения МКА в задаче восстановления углового движения МКА. Восстановлено фактическое неуправляемое движение МКА BugSat-1 по выборкам данных об ориентации вектора направления на Солнце в связанной системе координат, извлеченных из телеметрии, которая находится в свободном доступе. Продемонстрирована возможность оценки инерционных характеристик МКА в условиях априорной неопределенности на основании выполненного анализа вращательного движения и привлечения аналитической модели регулярной прецессии. Погрешности оценки углов ориентации МКА BugSat-1 не превысили 10°, погрешность определения вектора угловой скорости не превышала 0.015 град/с, а разброс оценок коэффициента инерции составил 13%, что демонстрирует возможность косвенного контроля характера условий проведения космических экспериментов.