Известия РАН. Теория и системы управления, 2023, № 2, стр. 85-92

ИГРОВОЕ ВЗАИМОСВЯЗАННОЕ УПРАВЛЕНИЕ ГРУППОЙ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ В УСЛОВИЯХ ИНФОРМАЦИОННОГО ПРОТИВОДЕЙСТВИЯ

В. А. Болдинов^a, *, В. А. Бухалёв^b, А. А. Скрынников^a, c

^a Московский авиационный ин-т (национальный исследовательский ун-т)
Москва, Россия

^b Московский научно-исследовательский телевизионный ин-т
Москва, Россия

^c Государственный научно-исследовательский ин-т авиационных систем
Москва, Россия

^* E-mail: viktorboldinov@mail.ru

Поступила в редакцию 06.10.2022
После доработки 20.10.2022
Принята к публикации 05.12.2022

EDN: JDHTCO
DOI: 10.31857/S0002338823020063

Полный текст (PDF)

Аннотация

Рассматривается задача игрового управления группой беспилотных летательных аппаратов в условиях информационного противодействия со стороны группы неподвижных объектов. Получены два реккурентных информационно-управляющих алгоритма: алгоритм взаимосвязанного управления группой беспилотных летательных аппаратов и алгоритм управления постановщика помех, основанные на теории стохастических многошаговых игр и теории систем со случайной скачкоообразной структурой.

Введение. В [1] рассматривалась задача построения алгоритмов взаимосвязанного управления группой беспилотных летательных аппаратов (БПЛА) при наведении на группу объектов, часть из которых является ложными, создаваемыми с помощью имитационных помех и усиливаемыми маскирующими помехами, вызывающими перерывы информации.

Если система противодействия обладает способностью оценивать какие-то параметры процесса наведения, то она может активно влиять на управление им [2–4].

В этих условиях задача построения информационно-управляющих алгоритмов может быть сформулирована как антагонистическая дифференциальная или многошаговая стохастическая игра [3, 5–10]. Эта задача рассматривается в настоящей статье.

1. Постановка задачи. Группа БПЛА наводится на группу неподвижных объектов, прикрываемых имитационными и маскирующими помехами, в результате чего в информационных каналах систем БПЛА появляются сигналы от ложных объектов и возникают перерывы информации. Соседние БПЛА обмениваются информацией по двухсторонней линии связи для поддержания требуемой дистанции между ними. В системе управления каждого участника группы измеряются наблюдаемые координаты объектов и их некоторые различительные признаки. На основании измерений формируются необходимые оценки и сигналы управления БПЛА.

Управление БПЛА направлено на повышение точности наведения, управление системы противодействия – на ее снижение. При этом каждый из противников рассчитывает на наихудшее для себя поведение соперника.

Математически задача формулируется как антагонистическая многошаговая стохастическая игра, описываемая следующими уравнениями.

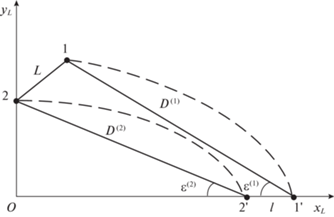
Схема наведения двух БПЛА (соседних участников группы) на два неподвижных объекта в вертикальной плоскости декартовой прямоугольной системы координат $(О,{{y}_{L}},{{x}_{L}})$ представлена на рис. 1. Здесь через L обозначена дистанция между соседними БПЛА (1 и 2), наводящихся на два неподвижных объекта (1' и 2'), которые отстоят друг от друга на расстоянии l. Дальности от БПЛА до объектов и углы пеленга объектов обозначены как D⁽¹⁾, D⁽²⁾ и ε⁽¹⁾, ε⁽²⁾ соответственно.

Рис. 1.

Траектории наведения двух БПЛА на два объекта

Наведение осуществляется по заданным траекториям, описываемым уравнениями (в непрерывной форме):

(1.1)

$\dot {\bar {\varepsilon }}(t) = \bar {\omega }(t),\quad \dot {\bar {\omega }}(t) = {{\tau }^{{ - 1}}}\left( t \right)\left( {1 - \nu } \right)\bar {\omega }(t),$

где $\bar {\varepsilon }(t)$, $\bar {\omega }(t)$ – требуемые угол и угловая скорость пеленга с заданными начальными и конечными условиями $\bar {\varepsilon }(0) = {{\bar {\varepsilon }}_{0}}$, $\bar {\varepsilon }({{t}_{n}}) = {{\bar {\varepsilon }}_{n}}$, $\bar {\omega }(0) = t_{n}^{{ - 1}}\nu ({{\bar {\varepsilon }}_{n}} - {{\bar {\varepsilon }}_{0}})$, $\bar {\omega }({{t}_{n}}) = 0$; $\nu $ – коэффиицент крутизны траектории, $\nu = {\text{const}}$, $\nu > 1$; ${{t}_{n}}$ – конечный момент времени наведения; $\tau = {{t}_{n}} - t$ – время, оставшееся до конца наведения.

Согласно выражению (1.1), заданная траектория – это кривая, описываемая формулами

(1.2)

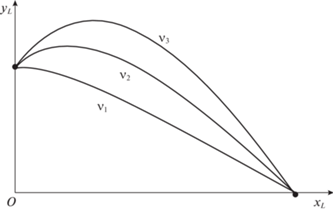
$\begin{gathered} \bar {\varepsilon }(t) = ({{{\bar {\varepsilon }}}_{0}} - {{{\bar {\varepsilon }}}_{n}}){{\left( {\frac{\tau }{{{{t}_{n}}}}} \right)}^{\nu }} + {{{\bar {\varepsilon }}}_{n}}, \\ \bar {\omega }(t) = \frac{\nu }{{{{t}_{n}}}}({{{\bar {\varepsilon }}}_{0}} - {{{\bar {\varepsilon }}}_{n}}){{\left( {\frac{\tau }{{{{t}_{n}}}}} \right)}^{{\nu - 1}}} \\ \end{gathered} $

и проходящая через две точки с углами наклона ${{\bar {\varepsilon }}_{0}}$ и ${{\bar {\varepsilon }}_{n}}$.

Форма кривой зависит от коэффициента крутизны ν. В частности, при $\nu = 1$ $\bar {\omega }(t)\,\, = \,\,t_{n}^{{ - 1}}({{\bar {\varepsilon }}_{n}} - {{\bar {\varepsilon }}_{0}})$ = = const, что соответствует движению с постоянной угловой скоростью по траектории, близкой к баллистической. Влияние $\nu $ на форму траектории показано на рис. 2.

Рис. 2.

Зависимость траектории от коэффициента крутизны ν

В общем случае заданные траектории обоих БПЛА не одинаковы: ${{\nu }^{{(1)}}} \ne {{\nu }^{{(2)}}}$, а требуемая дистанция ${{\bar {L}}_{{}}}$ между ними определяется, как следует из рис. 1, формулой

(1.3)

$\bar {L} = \sqrt {{{{({{{\bar {D}}}^{{(1)}}})}}^{2}} + {{{({{{\bar {D}}}^{{(2)}}})}}^{2}} - 2{{{\bar {D}}}^{{(1)}}}{{{\bar {D}}}^{{(2)}}}\cos ({{{\bar {\varepsilon }}}^{{\left( 1 \right)}}} - {{{\bar {\varepsilon }}}^{{\left( 2 \right)}}})} ,$

где ${{\bar {D}}^{{(1)}}}$, ${{\bar {D}}^{{(2)}}}$, ${{\bar {\varepsilon }}^{{(1)}}}$, ${{\bar {\varepsilon }}^{{(2)}}}$ – требуемые дальности и углы пеленга первого и второго БПЛА.

В каждом БПЛА измеряются пространственные координаты истинного объекта, условно именуемого “цель” (Ц), и ложного объекта, условно именуемого “помеха” (П). Динамика и измерение параметров объектов описываются следующими формулами и уравнениями в дискретной форме:

(1.4)

$\begin{gathered} D_{{k + 1}}^{j} = {{[{{D}^{j}} - \Delta t{v} + {{\xi }^{{{{D}^{j}}}}}]}_{k}},\quad D_{0}^{{\text{Ц}}} \ne D_{0}^{{\text{П}}}, \\ \varepsilon _{{k + 1}}^{j} = {{[{{\varepsilon }^{j}} + \Delta t{{\omega }^{j}}]}_{k}},\quad \varepsilon _{0}^{{\text{Ц}}} \ne \varepsilon _{0}^{{\text{П}}}, \\ \omega _{{k + 1}}^{j} = {{\left[ {{{\omega }^{j}} + \frac{{\Delta t}}{\tau }(2\omega + u + {{\xi }^{{{{\varepsilon }^{j}}}}})} \right]}_{k}},\quad \omega _{0}^{{\text{Ц}}} \ne \omega _{0}^{{\text{П}}},\quad j = {\text{Ц}},{\text{П;}} \\ \end{gathered} $

(1.5)

$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} _{k}^{i} = {{[{{D}^{j}} + {{\zeta }^{{{{D}^{j}}}}}]}_{k}}\left[ {1 - \delta ({{s}_{k}},3)} \right], \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } _{k}^{i} = {{[{{\varepsilon }^{j}} + {{\zeta }^{{{{\varepsilon }^{j}}}}}]}_{k}}\left[ {1 - \delta ({{s}_{k}},3)} \right],\quad i = 1,2,\quad j = {\text{Ц}},{\text{П;}} \\ \end{gathered} $

(1.6)

$\pi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{k}^{i}\,{\text{|}}\,{{r}_{k}}^{j}} \right),\quad i = 1,{\kern 1pt} 2,\quad j = {\text{Ц}},{\text{П}}{\text{.}}$

Здесь символом $\smile $ обозначены измерения соответствующих переменных; k – дискретный момент времени, $k = \overline {0,n} $ (индекс k у квадратных скобок ${{\left[ \bullet \right]}_{k}}$ относится ко всем переменным внутри этих скобок); $\Delta t = {{t}_{{k + 1}}} - t{}_{k}$; $j$ – индекс объекта: Ц, П; i – номер канала наблюдения, $i\, = \,1,2$; $D_{k}^{j}$ – дальности до Ц и до П; $\varepsilon _{k}^{j}$ – углы пеленга Ц и П; $\omega _{k}^{j}$ – угловые скорости пеленгов; ${{u}_{k}}$ – сигнал управления БПЛА; $\xi _{k}^{{{{D}^{j}}}}$, $\xi _{k}^{{{{\varepsilon }^{j}}}}$ – центрированные гауссовские дискретные белые шумы возмущений с дисперсиями соответственно ${{G}^{{{{D}^{j}}}}}$ и ${{G}^{{{{\varepsilon }^{j}}}}}$; $\zeta _{k}^{{{{D}^{j}}}}$, $\zeta _{k}^{{{{\varepsilon }^{j}}}}$ – центрированные гауссовские дискретные белые шумы ошибок измерения с дисперсиями соответственно ${{Q}^{{{{D}^{j}}}}}$ и ${{Q}^{{{{\varepsilon }^{j}}}}}{\text{/}}{{(\tau _{k}^{j})}^{2}}$; $\tau _{k}^{j} = D_{k}^{j}{\text{/}}{{{v}}_{k}}$ – время, оставшееся до конца наведения БПЛА соответственно на Ц и на П; ${{{v}}_{k}}$ – априорная оценка скорости сближения БПЛА с объектами (известная функция времени);

$\delta ({{s}_{k}},3) = \left\{ \begin{gathered} 1\quad {\text{при}}\quad {{s}_{k}} = 3, \hfill \\ 0\quad {\text{при}}\quad {{s}_{k}} \ne 3 \hfill \\ \end{gathered} \right.$

– символ Кронекера, описывает перерыв поступления информации, вызванный воздействием маскирующей помехи; ${{s}_{k}}$ – индекс структуры, ${{s}_{k}} = 1,2,3$; $\pi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{k}^{i}\,{\text{|}}\,r_{k}^{j}} \right)$ – условные вероятности правильных (при $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{k}^{i} = r_{k}^{j}$) и ошибочных (при $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{k}^{i} \ne r_{k}^{j}$) показаний индикатора $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{k}^{j}$ информационного различительного признака $r_{k}^{j}$ (известная функция времени) Ц и П ($j = {\text{Ц}},{\text{П}}$) в первом ($i = 1$) и втором ($i = 2$) каналах наблюдения.

Индекс структуры (помеховой ситуации) s_k – марковская цепь, заданная вероятностями переходов ${{q}_{k}}({{s}_{{k + 1}}}\,{\text{|}}\,{{s}_{k}})$ из состояния s_k в состояние ${{s}_{{k + 1}}}$ $\left( {{{s}_{k}},{{s}_{{k + 1}}} = \overline {1,3} } \right)$:

(1.7)

$\begin{gathered} {{q}_{k}}(2\,{\text{|}}\,1) = {{q}_{k}}(1\,{\text{|}}\,2) = 0,\quad {{q}_{k}}(1\,{\text{|}}\,3) = {{q}_{k}}(2\,{\text{|}}\,3) = {{d}_{k}} = {{d}^{{min}}},{{d}^{{max}}}, \\ {{q}_{k}}(3\,{\text{|}}\,1) = {{q}_{k}}(3\,{\text{|}}\,2) = {{g}_{k}} = {{g}^{{min}}},{{g}^{{max}}},\quad 0 < d,\quad g < 0.5. \\ \end{gathered} $

Множество возможных состояний структуры представлено в таблице 1.

Таблица 1.

Множество возможных состояний структуры

s	i = 1	i = 2
1	$j = {\text{Ц}}$	$j = {\text{П}}$
2	$j = {\text{П}}$	$j = {\text{Ц}}$
3	0	0

Как видно из таблицы, при s = 1 в первом информационном канале ($i = 1$) наблюдается цель, во втором – помеха; при $s = 2$ – в $i = 1$ – помеха, в $i = 2$ – цель; при $s = 3$ – перерыв информации.

Состояния структуры s_k фиксируются с ошибками индикаторами маскирующих помех, которые описываются условными вероятностями $\pi _{{k + 1}}^{\psi }\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{k}^{\psi }\,{\text{|}}\,{{s}_{k}}} \right)$ правильных (при $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{k}^{\psi } = {{s}_{k}}$) и ошибочных (при $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{k}^{\psi } \ne {{s}_{k}}$) показаний индикаторов, где ${{s}_{k}}$ – индекс структуры, ${{s}_{k}} = \overline {1,3} $; $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{k}^{\psi }$ – показания индикатора, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{k}^{\psi } = \overline {1,3} $; $\psi = {\text{Б}},{\text{П}}$; символ Б означает БПЛА, символ П – постановщик помехи (помеха).

Критерии оптимальности управлений описываются формулами

(1.8)

$J{\kern 1pt} * = \mathop {min}\limits_{{{u}_{{_{{\overline {0,n - 1} }}}}}} J;$

(1.9)

$J = \sum\limits_{k = 1}^n \,{\text{M}}\left[ {W_{k}^{u}\,{\text{|}}\,{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}_{{\overline {0,k - 1} }}},{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{{_{{\overline {0,k - 1} }}}}},{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }}_{{_{{\overline {0,k - 1} }}}}},\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{{_{{\overline {0,k - 1} }}}}^{{\text{Б}}}} \right];$

(1.10)

$W_{k}^{u} \triangleq {{\alpha }_{\varepsilon }}\tau _{k}^{{ - 2}}{{({{\varepsilon }_{k}} - {{\bar {\varepsilon }}_{k}})}^{2}} + {{\alpha }_{\omega }}{{({{\omega }_{k}} - {{\bar {\omega }}_{k}})}^{2}} + \beta u_{{k - 1}}^{2};$

(1.11)

${{J}^{{{\text{Б}}{\kern 1pt} *}}} = \mathop {min}\limits_{{{d}_{{\overline {0,n - 1} }}}} \mathop {max}\limits_{{{g}_{{\overline {0,n - 1} }}}} {{J}^{{\text{Б}}}};\quad {{J}^{{{\text{П}}{\kern 1pt} *}}} = \mathop {max}\limits_{{{g}_{{\overline {0,n - 1} }}}} \mathop {min}\limits_{{{d}_{{\overline {0,n - 1} }}}} {{J}^{{\text{П}}}};$

(1.12)

${{J}^{{\text{Б}}}} = \sum\limits_{k = 1}^n \,{\text{M}}[W_{k}^{{\text{Б}}}\left( {{{s}_{k}},{{d}_{{k - 1}}},{{g}_{{k - 1}}}} \right)\,{\text{|}}\,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }_{{\overline {0,k - 1} }}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }_{{\overline {0,k - 1} }}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }_{{\overline {0,k - 1} }}},\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{{\overline {0,k - 1} }}^{{\text{Б}}}];$

(1.13)

${{J}^{{\text{П}}}} = \sum\limits_{k = 1}^n \,{\text{M[}}W_{k}^{{\text{П}}}\left( {{{s}_{k}},{{d}_{{k - 1}}},{{g}_{{k - 1}}}} \right)\,{\text{|}}\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{{\overline {0,k - 1} }}^{{\text{П}}}{\text{]}}{\kern 1pt} {\kern 1pt} ;$

(1.14)

$W_{k}^{{\text{Б}}} = \delta ({{s}_{k}},3) + {{\lambda }^{{\text{Б}}}}{{d}_{{k - 1}}} - {{\mu }^{{\text{Б}}}}{{g}_{{k - 1}}};$

(1.15)

$W_{k}^{{\text{П}}} = \delta ({{s}_{k}},3) + {{\lambda }^{{\text{П}}}}{{d}_{{k - 1}}} - {{\mu }^{{\text{П}}}}{{g}_{{k - 1}}},$

где $J{\kern 1pt} *$, ${{J}^{{{\text{Б}}{\kern 1pt} *}}}$, ${{J}^{{{\text{П}}{\kern 1pt} *}}}$ – критерии оптимальности управлений; J, ${{J}^{{\text{Б}}}}$, ${{J}^{{\text{П}}}}$ – показатели эффективности; $W_{k}^{u}( \cdot )$, $W_{k}^{{\text{Б}}}( \cdot )$, $W_{k}^{{\text{П}}}( \cdot )$ – текущие функции потерь; ${{\alpha }_{\varepsilon }}$, ${{\alpha }_{\omega }}$, $\beta $, $\lambda $, $\mu $ – положительные константы – весовые коэффициенты, регулирующие распределение приоритетов между частными показателями в (1.8)–(1.15).

В начальный момент известны математические ожидания и ковариации фазовых координат процесса наведения, а также вероятности структуры $p_{0}^{{\text{Б}}}({{s}_{0}})$, $p_{0}^{{\text{П}}}({{s}_{0}})$. Весовые коэффициенты либо задаются, либо определяются путем параметрической оптимизации в процессе имитационного математического моделирования синтезированной системы.

Требуется найти оптимальные управления $u_{k}^{*}$, $d_{k}^{*}$, $g_{k}^{*}$ в классе детерминированных зависимостей от наблюдений ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }_{{\overline {0,k} }}}$, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }_{{\overline {0,k} }}}$, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }_{{\overline {0,k} }}}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{{\overline {0,k} }}^{{\text{Б}}}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{{\overline {0,k} }}^{{\text{П}}}$.

2. Информационно-управляющие алгоритмы. Оптимальные игровые алгоритмы управления линейными системами с марковской структурой рассмотрены в [3, 5, 8, 9]. Их особенностью по сравнению с системами с детерминированной структурой является многоканальность, обусловленная числом состояний структуры.

Как показано в [3], способом приближенной замены состояния структуры ${{s}_{k}}$ его оценкой ${{\hat {s}}_{k}}$ можно получить более простые одноканальные алгоритмы. Схема игрового управления БПЛА приведена на рис. 3.

Рис. 3.

Схема игрового управления БПЛА

2.1. Алгоритм игрока Б (БПЛА). 1. Закон управления БПЛА. Структурно-адаптивный одноканальный алгоритм, основанный на приближенной замене состояния структуры ${{s}_{k}}$ его оценкой $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{k}^{{\text{Б}}}$, согласно условиям задачи (1.1)–(1.15), имеет следующий вид:

(2.1)

$u_{k}^{*} = - {{[{{\tau }^{{ - 1}}}{{C}_{\varepsilon }}\left( {\hat {\varepsilon } - \bar {\varepsilon }} \right) + {{C}_{\omega }}\left( {\hat {\omega } - \bar {\omega }} \right) + (\nu + 1)\bar {\omega } + {{C}_{l}}(\hat {L} - \bar {L}) + {{C}_{{v}}}\left( {{\hat {v}} - {\bar {v}}} \right)]}_{k}},$

где ${v} \triangleq \dot {L}$, ${{{\hat {v}}}_{k}} = {{\dot {\hat {L}}}_{k}}$, ${{{\bar {v}}}_{k}} = {{\dot {\bar {L}}}_{k}}$, коэффициенты ${{C}_{L}}$, ${{C}_{\nu }}$ определяются путем параметрической оптимизации, а коэффициенты ${{C}_{\varepsilon }}$, ${{C}_{\omega }}$ находятся из уравнений

(2.2)

$\begin{array}{*{20}{l}} {}&{{{C}_{\varepsilon }}({{C}_{\varepsilon }} - {{C}_{\omega }} + 2) - {{\beta }^{{ - 1}}}{{\alpha }_{\varepsilon }} = 0,} \\ {}&{C_{\omega }^{2} - 3{{C}_{\omega }} - 2{{C}_{\varepsilon }} - {{\beta }^{{ - 1}}}{{\alpha }_{\omega }} = 0.} \end{array}$

2. Регулятор структуры (помеховых ситуаций). Применяя метод динамического программирования Беллмана [11 ] , обобщенный на класс систем со случайной скачкообразной структурой (ССС) [3, 5, 8], и критерий оптимальности ${{J}^{{{\text{Б}}{\kern 1pt} *}}}$ – (1.12), (1.14), получаем приближенно-оптимальный алгоритм регулятора:

(2.3)

$d_{k}^{*} = \left( {\begin{array}{*{20}{c}} {{{d}^{{min}}}}&{\;{\text{при}}\quad \hat {p}_{k}^{{\text{Б}}}(3) \leqslant {{{\tilde {\lambda }}}^{{\text{Б}}}},} \\ {{{d}^{{max}}}}&{\;{\text{при}}\quad \hat {p}_{k}^{{\text{Б}}}(3) > {{{\tilde {\lambda }}}^{{\text{Б}}}};} \end{array}} \right.$

(2.4)

${{\tilde {g}}_{k}} = \left( {\begin{array}{*{20}{c}} {{{g}^{{min}}}}&{\;{\text{при}}\quad \hat {p}_{k}^{{\text{Б}}}(3) \geqslant 1 - {{{\tilde {\mu }}}^{{\text{Б}}}},} \\ {{{g}^{{max}}}}&{\;{\text{при}}\quad \hat {p}_{k}^{{\text{Б}}}(3) < 1 - {{{\tilde {\mu }}}^{{\text{Б}}}};} \end{array}} \right.$

(2.5)

${{\tilde {\lambda }}^{{\text{Б}}}} = \frac{{{{\lambda }^{{\text{Б}}}}({{d}^{{max}}} + {{g}^{{max}}})}}{{1 + {{\lambda }^{{\text{Б}}}}({{d}^{{max}}} - {{d}^{{min}}}) + {{\mu }^{{\text{Б}}}}({{g}^{{max}}} - {{g}^{{min}}})}},\quad {{\tilde {\mu }}^{{\text{Б}}}} = \frac{{{{\mu }^{{\text{Б}}}}}}{{{{{\tilde {\lambda }}}^{{\text{Б}}}}}},$

где $d_{k}^{*}$ – оптимальное управление игорока ${\text{Б}}$; ${{\tilde {g}}_{k}}$ – предполагаемое игроком Б оптимальное управление игрока П, основанное на наблюдениях игрока Б; $\hat {p}_{k}^{{\text{Б}}}(1)$ – апостериорная вероятность состояния структуры ${{s}_{k}} = 1$, определяемая классификатором.

3. Фильтр. Структурно-адаптивный одноканальный фильтр с учетом условий задачи описывается следующими уравнениями:

(2.6)

$\begin{gathered} \hat {D}_{{k + 1}}^{j} = {{[{{{\tilde {D}}}^{j}} + (1 - \delta ({{{\hat {s}}}^{{\text{Б}}}},3)){{K}^{{{{D}^{j}}}}}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}^{{i({{{\hat {s}}}^{{\text{Б}}}})}}} - {{{\tilde {D}}}^{j}})]}_{{k + 1}}}, \\ \tilde {D}_{{k + 1}}^{j} = {{[{{{\hat {D}}}^{j}} - \Delta t{v}]}_{k}}; \\ \end{gathered} $

(2.7)

$\begin{gathered} \hat {\varepsilon }_{{k + 1}}^{j} = {{[{{{\tilde {\varepsilon }}}^{j}} + (1 - \delta ({{{\hat {s}}}^{{\text{Б}}}},3)){{K}^{{{{\varepsilon }^{j}}}}}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}^{{i({{{\hat {s}}}^{{\text{Б}}}})}}} - {{{\tilde {\varepsilon }}}^{j}})]}_{{k + 1}}}, \\ \tilde {\varepsilon }_{{k + 1}}^{j} = {{[{{{\hat {\varepsilon }}}^{j}} - \Delta t{{{\hat {\omega }}}^{j}}]}_{k}}; \\ \end{gathered} $

(2.8)

$\begin{gathered} \hat {\omega }_{{k + 1}}^{j} = {{[{{{\tilde {\omega }}}^{j}} + (1 - \delta ({{{\hat {s}}}^{{\text{Б}}}},3))({{K}^{{{{\omega }^{j}}}}} + {{K}^{{{{\varepsilon }^{j}}}}}{{\tau }^{{ - 1}}})({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}^{{i({{{\hat {s}}}^{{\text{Б}}}})}}} - {{{\tilde {\varepsilon }}}^{j}})]}_{{k + 1}}}, \\ \tilde {\omega }_{{k + 1}}^{j} = {{[{{{\hat {\omega }}}^{j}} + \Delta t{{\tau }^{{ - 1}}}(2{{{\hat {\omega }}}^{j}} + u{\kern 1pt} *)]}_{k}}; \\ \hat {D}_{0}^{j} = D_{0}^{j},\quad \hat {\varepsilon }_{0}^{j} = \varepsilon _{0}^{j},\quad \hat {\omega }_{0}^{j} = \omega _{0}^{j}, \\ i = 1,2,\quad \hat {s} = 1,2,3,\quad j = {\text{Ц}},{\text{П}}{\text{.}} \\ \end{gathered} $

${\text{При }}\,j = {\text{Ц:}}$

(2.9)

$i = \left( {\begin{array}{*{20}{c}} 1&{\;{\text{при}}\quad \hat {s}_{k}^{{\text{Б}}} = 1,} \\ 2&{\;{\text{при}}\quad \hat {s}_{k}^{{\text{Б}}} = 2,} \end{array}} \right.$

${\text{при}}\,{\text{ }}j = {\text{П:}}$

(2.10)

$i = \left( {\begin{array}{*{20}{c}} 1&{\;{\text{при}}\quad \hat {s}_{k}^{{\text{Б}}} = 2,} \\ 2&{\;{\text{при}}\quad \hat {s}_{k}^{{\text{Б}}} = 1,} \end{array}} \right.$

(2.11)

${{\hat {L}}_{k}} = {{\left[ {\sqrt {{{{({{{\hat {D}}}^{{({\text{Ц}}1)}}})}}^{2}} + {{{({{{\hat {D}}}^{{({\text{Ц}}2)}}})}}^{2}} - 2{{{\hat {D}}}^{{({\text{Ц}}1)}}}{{{\hat {D}}}^{{({\text{Ц}}2)}}}\cos ({{{\hat {\varepsilon }}}^{{\left( {{\text{Ц}}1} \right)}}} - {{{\hat {\varepsilon }}}^{{\left( {{\text{Ц}}2} \right)}}})} } \right]}_{k}}$.

Здесь символ $ \wedge $ обозначает, как обычно, апостериорные оценки координат цели, вычисляемые первым и вторым БПЛА.

4. Дисперсиометр. Алгоритм дисперсиометра состоит из формул для положительных постоянных “коэффициентов доверия” ${{K}^{{{{D}^{j}}}}}$, ${{K}^{{{{\varepsilon }^{j}}}}}$, ${{K}^{{{{\omega }^{j}}}}}$, получаемых в результате приближенного решения в установившемся режиме уравнений для ковариаций ошибок оценивания координат цели и помех [3]:

(2.12)

${{K}^{{{{D}^{j}}}}} = \Delta {{\omega }^{j}}\left( {\sqrt {1 + \frac{{{{G}^{{{{D}^{j}}}}}}}{{{{Q}^{{{{D}^{j}}}}}}}} - 1} \right),\quad {{K}^{{{{\varepsilon }^{j}}}}} = \sqrt {2{{K}^{{{{\omega }^{j}}}}}} ,\quad {{K}^{{{{\omega }^{j}}}}} = \sqrt {\frac{{{{G}^{{{{\omega }^{j}}}}}}}{{{{Q}^{{{{\omega }^{j}}}}}}}} ,\quad j = {\text{Ц}},{\text{П}}{\text{.}}$

5. Классификатор структуры. Алгоритм классификатора, согласно [3], c учетом условий задачи описывается следующими уравнениями:

(2.13)

$\hat {p}_{k}^{{\text{Б}}}({{s}_{k}}) = \frac{{\vartheta _{k}^{{\text{Б}}}({{s}_{k}})}}{{\sum\limits_{{{s}_{k}}} \vartheta _{k}^{{\text{Б}}}({{s}_{k}})}},\quad \hat {p}_{0}^{{\text{Б}}}({{s}_{0}}) = \left\{ \begin{gathered} 0.5\quad {\text{при}}\quad {{s}_{0}} = 1,2, \hfill \\ 0\quad {\text{при}}\quad {{s}_{0}} = 3; \hfill \\ \end{gathered} \right.$

(2.14)

$\begin{gathered} \vartheta _{k}^{{\text{Б}}}(1) = {{\left[ {\left. {{{{\tilde {p}}}^{{\text{Б}}}}(1){\kern 1pt} {{\pi }^{r}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }}^{1}}\,{\text{|}}\,{{r}^{{\text{Ц}}}}} \right){{\pi }^{r}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }}^{2}}\,{\text{|}}\,{{r}^{{\text{П}}}}} \right){\kern 1pt} {{\pi }^{{\text{Б}}}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}^{{\text{Б}}}}\,{\text{|}}\,1} \right){\kern 1pt} {{e}^{{ - \Delta (1)}}}} \right)} \right]}_{k}}, \\ \vartheta _{k}^{{\text{Б}}}(2) = {{\left[ {\left. {{{{\tilde {p}}}^{{\text{Б}}}}(2){\kern 1pt} {{\pi }^{r}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }}^{1}}\,{\text{|}}\,{{r}^{{\text{П}}}}} \right){{\pi }^{r}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }}^{2}}\,{\text{|}}\,{{r}^{{\text{Ц}}}}} \right){{\pi }^{{\text{Б}}}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}^{{\text{Б}}}}\,{\text{|}}\,2} \right){{e}^{{ - \Delta (2)}}}} \right)} \right]}_{k}}, \\ \vartheta _{k}^{{\text{Б}}}(3) = \tilde {p}_{k}^{{\text{Б}}}(3){{\pi }^{{\text{Б}}}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}^{{\text{Б}}}}\,{\text{|}}\,3} \right); \\ \end{gathered} $

(2.15)

$\begin{gathered} {{\Delta }_{k}}(1) = \frac{1}{2}{{\left[ {{{{\left[ {{{K}^{D}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}^{1}} - {{{\hat {D}}}^{{\text{Ц}}}}} \right)} \right]}}^{2}} + {{{\left[ {{{K}^{\varepsilon }}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}^{1}} - {{{\hat {\varepsilon }}}^{{\text{Ц}}}}} \right)} \right]}}^{2}} + {{{\left[ {{{K}^{D}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}^{2}} - {{{\hat {D}}}^{{\text{П}}}}} \right)} \right]}}^{2}} + {{{\left[ {{{K}^{\varepsilon }}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}^{2}} - {{{\hat {\varepsilon }}}^{{\text{П}}}}} \right)} \right]}}^{2}}} \right]}_{k}}, \\ {{\Delta }_{k}}(2) = \frac{1}{2}{{\left[ {{{{\left[ {{{K}^{D}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}^{1}} - {{{\hat {D}}}^{{\text{П}}}}} \right)} \right]}}^{2}} + {{{\left[ {{{K}^{\varepsilon }}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}^{1}} - {{{\hat {\varepsilon }}}^{{\text{П}}}}} \right)} \right]}}^{2}} + {{{\left[ {{{K}^{D}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}^{2}} - {{{\hat {D}}}^{{\text{Ц}}}}} \right)} \right]}}^{2}} + {{{\left[ {{{K}^{\varepsilon }}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}^{2}} - {{{\hat {\varepsilon }}}^{{\text{Ц}}}}} \right)} \right]}}^{2}}} \right]}_{k}}, \\ {{\Delta }_{k}}(3) = 0; \\ \end{gathered} $

(2.16)

$\begin{gathered} \tilde {p}_{{k + 1}}^{{\text{Б}}}(1) = \left[ {\hat {p}(1) + d{\kern 1pt} *{\kern 1pt} \hat {p}(3)} \right]_{k}^{{\text{Б}}}, \\ \tilde {p}_{{k + 1}}^{{\text{Б}}}(2) = \left[ {\hat {p}(2) + d{\kern 1pt} *{\kern 1pt} \hat {p}(3)} \right]_{k}^{{\text{Б}}}, \\ \tilde {p}_{{k + 1}}^{{\text{Б}}}(3) = \left[ {\tilde {g}(\hat {p}(1) + \hat {p}(2)) + \left( {1 - 2d{\kern 1pt} *} \right)\hat {p}(3)} \right]_{k}^{{\text{Б}}}. \\ \end{gathered} $

6. Идентификатор структуры:

(2.17)

$\hat {s}_{k}^{{\text{Б}}} = arg\mathop {max}\limits_{{{s}_{k}}} \hat {p}_{k}^{{\text{Б}}}({{s}_{k}}),\quad {{s}_{k}} = 1,2,3.$

В целом, алгоритм игрока Б описывается замкнутой системой уравнений (2.1)–(2.17) с входными сигналами $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} _{k}^{{ij}}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } _{k}^{{ij}}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{k}^{i}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} _{k}^{{\text{Б}}}$ и выходными сигналами $u_{k}^{*}$, $d_{k}^{*}$, $\hat {D}_{k}^{j}$, $\hat {\varepsilon }_{k}^{j}$, $\hat {\omega }_{k}^{j}$, $\hat {p}_{k}^{{\text{Б}}}({{s}_{k}})$, $\hat {s}_{k}^{{\text{Б}}}$, $i = 1,{\kern 1pt} 2$; $j = {\text{Ц}},{\kern 1pt} {\text{П}}$.

2.2. Алгоритм игрока П. Алгоритм состоит из регулятора, классификатора и идентификатора, описываемых уравнениями соответственно (2.3)–(2.5), (2.13)–(2.16) и (2.17), в которых надо заменить $d_{k}^{*} \to {{\tilde {d}}_{k}}$, ${{\tilde {g}}_{k}} \to g{\kern 1pt} *$, ${{\tilde {\lambda }}^{{\text{Б}}}} \to {{\tilde {\lambda }}^{{\text{П}}}}$, ${{\tilde {\mu }}^{{\text{Б}}}} \to {{\tilde {\mu }}^{{\text{П}}}}$, $\hat {p}_{k}^{{\text{Б}}}({{s}_{k}}) \to \hat {p}_{k}^{{\text{П}}}({{s}_{k}})$, $\tilde {p}_{k}^{{\text{Б}}}({{s}_{k}}) \to \tilde {p}_{k}^{{\text{П}}}({{s}_{k}})$, $\hat {s}_{k}^{{\text{Б}}} \to \hat {s}_{k}^{{\text{П}}}$.

1. Регулятор структуры:

(2.18)

$\begin{gathered} {{{\tilde {d}}}_{k}} = \left\{ \begin{gathered} {{d}^{{min}}}\quad {\text{при}}\quad \hat {p}_{k}^{{\text{П}}}(3) \leqslant {{{\tilde {\lambda }}}^{{\text{П}}}}, \hfill \\ {{d}^{{max}}}\quad {\text{при}}\quad \hat {p}_{k}^{{\text{П}}}(3) > {{{\tilde {\lambda }}}^{{\text{П}}}}, \hfill \\ \end{gathered} \right.\quad g_{k}^{*} = \left\{ \begin{gathered} {{g}^{{min}}}\quad {\text{при}}\quad \hat {p}_{k}^{{\text{П}}}(3) \geqslant 1 - {{{\tilde {\mu }}}^{{\text{П}}}}, \hfill \\ {{g}^{{max}}}\quad {\text{при}}\quad \hat {p}_{k}^{{\text{П}}}(3) < 1 - {{{\tilde {\mu }}}^{{\text{П}}}}, \hfill \\ \end{gathered} \right. \\ {{{\tilde {\lambda }}}^{{\text{П}}}} = \frac{{{{\lambda }^{{\text{П}}}}({{d}^{{max}}} + {{g}^{{max}}})}}{{1 + {{\lambda }^{{\text{П}}}}({{d}^{{max}}} - {{d}^{{min}}}) + {{\mu }^{{\text{П}}}}({{g}^{{max}}} - {{g}^{{min}}})}},\quad {{{\tilde {\mu }}}^{{\text{П}}}} = \frac{{{{\mu }^{{\text{П}}}}}}{{{{{\tilde {\lambda }}}^{{\text{П}}}}}}, \\ \end{gathered} $

где $g{\kern 1pt} *$ и $\tilde {d}$ – соответственно оптимальное управление игрока П и предполагаемое им оптимальное управление игрока Б, основанные на наблюдениях игрока П; $\hat {p}_{k}^{{\text{П}}}(1)$ – апостериорная вероятность состояния структуры ${{s}_{k}} = 1$.

2. Классификатор структуры:

(2.19)

$\begin{gathered} \hat {p}_{k}^{{\text{П}}}({{s}_{k}}) = \frac{{\vartheta _{k}^{{\text{П}}}({{s}_{k}})}}{{\sum\limits_{{{s}_{k}}} \vartheta _{k}^{{\text{П}}}({{s}_{k}})}},\quad \hat {p}_{0}^{{\text{П}}}({{s}_{0}}) = \left\{ \begin{gathered} 0.5\quad {\text{при}}\quad {{s}_{0}} = 1,2, \hfill \\ 0\quad {\text{при}}\quad {{s}_{0}} = 3, \hfill \\ \end{gathered} \right. \\ \vartheta _{k}^{{\text{П}}}(1) = \tilde {p}_{k}^{{\text{П}}}({{s}_{k}}){\kern 1pt} {{\pi }^{{\text{П}}}}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}^{{\text{П}}}}\,{\text{|}}\,{{s}_{k}}),\quad {{s}_{k}} = \overline {1,3} ; \\ \end{gathered} $

(2.20)

$\begin{gathered} {{{\tilde {p}}}_{{k + 1}}}(1) = [\hat {p}(1) + \tilde {d}{\kern 1pt} \hat {p}(3)]_{k}^{{\text{П}}}, \\ {{{\tilde {p}}}_{{k + 1}}}(2) = [\hat {p}(2) + \tilde {d}{\kern 1pt} \hat {p}(3)]_{k}^{{\text{П}}}, \\ {{{\tilde {p}}}_{{k + 1}}}(3) = [g{\kern 1pt} {\text{*}}\left( {\hat {p}(1) + \hat {p}(2)} \right) + (1 - 2\tilde {d})\hat {p}(3)]_{k}^{{\text{П}}}. \\ \end{gathered} $

3. Идентификатор структуры:

(2.21)

$\hat {s}_{k}^{{\text{П}}} = arg\mathop {max}\limits_{{{s}_{k}}} \hat {p}_{k}^{{\text{П}}}({{s}_{k}}).$

Заключение. Представлены взаимосвязанные информационно-управляющие алгоритмы соседних участников группы БПЛА, наводящихся на группу неподвижных объектов по заданным траекториям. Часть объектов является истинными целями, часть – ложными целями, создаваемыми с помощью имитационных помех. Коме того, противодействие осуществляется путем постановки маскирующих помех, прерывающих поступление информации в системе управления БПЛА.

Задача построения алгоритмов поставлена и решена как антагонистическая стохастическая многошаговая игра в чистых стратегиях в системах ССС [8] двух противников (игроков) Б и П, управляющих процессом наведения. Игрок Б оптимизирует свое управление по минимаксному критерию, а игрок П – по максиминному критерию, основываясь каждый на показаниях своих измерителей и индикаторов.

Алгоритмы игроков основаны на теории систем ССС. Алгоритм игрока Б осуществляет распознавание помеховых ситуаций, оценивание координат объектов и соседних участников группы БПЛА и управление БПЛА для выполнения требуемых точности наведения и дистанции между соседними БПЛА.

Алгоритм игрока П осуществляет распознавание и управление перерывами информации, ухудшая тем самым точность наведения и соблюдение требуемой дистанции между соседними БПЛА.

Рассмотренная задача представляет собой игру с неполной информацией, ненулевой суммой и без седловой точки вследствие неодинаковой информированности игроков о состоянии игры.

Список литературы

Болдинов В.А., Бухалëв В.А., Скрынников А.А. Система взаимосвязанного управления группой беспилотных летательных аппаратов в условиях информационного противодействия // Изв. РАН. ТиСУ. 2022. № 6. С. 11–19.
Баханов Л.Е., Давыдов А.Н., Корниенко В.Н. и др. Системы управления вооружением истребителей. Основы интеллекта многофункционального самолета / Под ред. Е.А. Федосова. М.: Машиностроение, 2005.
Евдокименков В.Н., Красильщиков М.Н., Оркин С.Д. Управление смешанными группами пилотируемых и беспилотных летательных аппаратов в условиях единого информационно-управляющего поля. М.: Изд. МАИ, 2015.
Бухалëв В.А. Распознавание, оценивание и управление в системах со случайной скачкообразной структурой. М.: Наука, 1996.
Piers B.D., Sworder D.D. Bayes and Minimax Controllers for a Linear Systems for Stochastic Jump Parameters // IEEE Trans. AC-16. 1971. № 4. P. 677–685.
Айзекс Р. Дифференциальные игры. М.: Мир, 1967.
Бухалëв В.А., Скрынников А.А., Болдинов В.А. Игровое управление системами со случайной скачкообразной структурой. М.: Физматлит, 2021.
Moon J.A Sufficient Condition for Linear-Quadratic Stochastic Zero-Sum Differential Games for Markov Jump Systems // IEEE Trans. Autom. Control. 2019. V. 64. № 4. P. 1619–1626.
Оуэн Г. Теория игр. М.: Вузовская книга, 2007.
Беллман Р. Динамическое программирование. М.: Изд-во иностр. лит., 1960.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал