Известия РАН. Теория и системы управления, 2023, № 2, стр. 108-122
СРАВНЕНИЕ ПАРАЛЛЕЛЬНЫХ РЕАЛИЗАЦИЙ МЕТОДА ВЕТВЕЙ И ГРАНИЦ ДЛЯ СИСТЕМ С ОБЩЕЙ ПАМЯТЬЮ
А. Ю. Горчаков a, *, М. А. Посыпкин a, **
a ФИЦ ИУ РАН
Москва, Россия
* E-mail: agorchakov@frccsc.ru
** E-mail: mposypkin@frccsc.ru
Поступила в редакцию 20.10.2022
После доработки 22.11.2022
Принята к публикации 05.12.2022
- EDN: JDULMW
- DOI: 10.31857/S0002338823020099
Аннотация
Рассматривается четыре параллельных алгоритма, реализующих метод ветвей и границ для решения задач поиска глобального минимума. Алгоритмы предназначены для вычислительных систем с общей памятью. Метод ветвей и границ базируется на двух основных операциях – ветвление и отсев. Для реализации операции отсева используется интервальная арифметика, которая для вещественных интервалов определяет операции, аналогичные обычным арифметическим. Основное отличие алгоритмов заключается в различной реализации хранения списка подзадач. В процессе тестирования на представительном наборе тестовых задач исследованы быстродействие алгоритмов, масштабируемость и устойчивость к аномалиям поиска.
0. Введение. Рассматривается задача оптимизации
состоящая в поиске минимума целевой функции $f(x):{{\mathbb{R}}^{n}} \to \mathbb{R}$ на допустимом множестве (множестве допустимых решений) $X \subseteq {{\mathbb{R}}^{n}}$. Точки множества X в дальнейшем будем называть допустимыми решениями. Точка $x{\kern 1pt} * \in X$ является глобальным решением задачи (0.1), если для каждого $x \in X$ имеет место неравенствоДля приближенного решения задачи достаточно найти хотя бы одну точку, принадлежащую множеству ε-решений этой задачи:
(0.3)
$X_{*}^{\varepsilon } = \{ x \in X:f(x) \geqslant f(x{\kern 1pt} *) + \varepsilon \} ,\quad \varepsilon > 0,$Методы поиска глобального минимума условно делятся на два типа – с доказательством и без доказательства оптимальности. К первой группе относятся различные варианты метода ветвей и границ (МВГ) [2], например метод неравномерных покрытий [3]. Вторая группа методов основана на различных стратегиях случайного поиска – методы Монте-Карло [4, 5], мультистарта [6–8], популяционные алгоритмы [9].
Современные методы оптимизации сложно представить без применения парараллельных вычислений. Для систем с общей памятью применяются технологии распараллеливания OpenMP, векторизации AVX2/AVX512 и реже – message passing interface (MPI). Распараллеливание методов случайного поиска в большинстве случаев заключается в запуске множества вычислительных потоков и операции редукции в конце вычислений. Особую актуальность имеет распараллеливание детерминированных методов, так как численное доказательство оптимальности найденных решений, как правило, требует очень существенных вычислений. Реализация одного из наиболее распространенных методов решения задач глобальной оптимизации – МВГ в параллельном варианте осложняется необходимостью, во-первых, регулярно обновлять рекордное значение, во-вторых, обращаться к дереву ветвления, чья структура заранее не известна и строится в процессе решения.
В процессе работы параллельного МВГ наблюдаются поисковые аномалии [10], т.е. ситуации, когда общее число итераций изменяется от запуска к запуску. Этот эффект обусловлен различным упорядочиванием операций ветвления и, как следствие, различной скоростью обновления рекорда, что в свою очередь может приводить к изменению числа произведенных итераций алгоритма. Недетерминированная природа динамической балансировки нагрузки между потоками параллельного приложения, применяемой в параллельной реализации МВГ, является дополнительной причиной существенных колебаний времени решения одной и той же задачи при разных запусках. Существенные колебания времени работы параллельных реализаций МВГ делают затруднительным применение таких традиционных инструментов анализа эффективности параллельных вычислений, как ускорение и масштабируемость. Необходимо проводить многократные повторные запуски на одних и тех же входных данных и анализировать разбос времени решения, исследовать статистические характеристики результатов изменения времени работы параллельного алгоритма.
В данной работе мы провели сравнительное тестирование четырех различных параллельных реализаций МВГ – двух версий parallel AMIGO (PAMIGO) [11] (global-PAMIGO и local-PAMIGO) и двух авторских реализаций BnB-Brf и BnB-Atomic. Тестирование проводилось на наборе тестовых задач [12], из 150 задач по объективным критериям было выбрано подмножество из 7 задач. На этом подмножестве задач было показано отсутствие масштабируемости у global-PAMIGO – предел 8 ядер процессора, и у алгоритмов local-PAMIGO и BnB-Brf – предел 32 ядра.
1. Общая схема МВГ. Настоящая схема является базовой алгоритмической схемой многих методов глобальной оптимизации. Считается, что МВГ был впервые предложен в работе [13] для задач частично-целочисленного линейного программирования. В дальнейшем эта схема использовалась при решении многих задач. МВГ оперирует подзадачами. Подзадачей называется задача вида
где $\hat {X} \subseteq X$ – подмножество исходного допустимого множества. Поскольку подзадача полностью определяется своим допустимым подмножеством $\hat {X}$, то в дальнейшем будем использовать его для обозначения подзадач (“подзадача $\hat {X}$”).МВГ основан на двух основных операциях – ветвление и отсев. Операция ветвления заключается в декомпозиции подзадачи на несколько подзадач таким образом, что совокупность множеств допустимых решений подзадач содержит множество допустимых решений исходной подзадачи. Для подзадачи, задаваемой (1.1), определим операцию ветвления split следующим образом:
(1.2)
$\begin{gathered} split({{{\hat {X}}}_{0}}) = \{ {{{\hat {X}}}_{1}}, \ldots ,{{{\hat {X}}}_{k}}\} , \\ {{{\hat {X}}}_{0}} = {{{\hat {X}}}_{1}} \cup \ldots \cup {{{\hat {X}}}_{k}}. \\ \end{gathered} $Операция ветвления разбивает подзадачу ${{\hat {X}}_{0}}$ на k подзадач ${{\hat {X}}_{1}}, \ldots ,{{\hat {X}}_{k}}$. Следующее утверждение, которое мы оставляем без доказательства ввиду его очевидности, играет ключевую роль в обосновании корректности метода ветвей и границ.
Утверждение. Пусть
где ${{\hat {X}}_{i}}$, $i = \overline {0,k} $ удовлетворяют соотношению (1.2). Тогда $f_{0}^{*} = \mathop {\min }\nolimits_{i = \overline {1,k} } f_{i}^{*}$.В процессе работы МВГ сохраняется “лучшее” найденное на данный момент решение xr, так называемое рекордное решение и рекородное значение ${{z}^{r}} = f({{x}^{r}})$. Рекордные решение и значение периодически обновляются с помощью функции update_record$(x)$. Данная функция, псевдокод которой представлен в листинге 1, сравнивает значение целевой функции в некоторой допустимой точке x с рекордным.
Листинг 1. Функция модификации рекорда
| 1 | Funtionupdate_record (x, z) | |||
| Input:$x$ – допустимая точка | ||||
| Input:$z$ – значение функции в этой точке ($z = f(x)$) | ||||
| 2 | if $z < {{f}^{r}}$then | |||
| 3 | ${{x}^{r}}: = x$ | |||
| 4 | ${{f}^{r}}: = z$ | |||
| 5 | end | |||
| 6 | end | |||
Если значение целевой функции, вычисленное в точке x, меньше рекордного значения, то производится замена точки xr на x и значения f r на $z$.
Рекордное значение используется для сокращения перебора с помощью правила отсева подзадач, реализуемого функцией discard(Y) (листинг 2).
Листинг 2. Функция отсева
| 1 | Functiondiscard (Y) | |||||
| Input:Y – подзадача | ||||||
| 2 | if get_bound(Y) $ \leqslant $${{f}^{r}} - \varepsilon $then | |||||
| 3 | return false | |||||
| 4 | else | |||||
| 5 | returntrue | |||||
| 6 | end | |||||
| 7 | end | |||||
Эта функция сравнивает $get\_bound(Y)$ – нижнюю оценку значения целевой функции в подзадаче Y и величину ${{f}^{r}} - \varepsilon $. На основании этого сравнения формируется возвращаемое логическое значение. Если discard($Y$) = true, то подзадача исключается из дальнейшего рассмотрения. В противном случае – подвергается дальнейшему ветвлению. Нижняя оценка значения целевой функции вычисляется с помощью библиотеки интервальной арифметики [12].
Функция обработки подзадач process, представленная в листинге 3, получает на вход подзадачу Y и генерирует по ней список новых (“дочерних”) подзадач $\mathcal{Y}$ с помощью функции split() (строка 4).
Листинг 3. Функция обработки подзадач
| 1 | Function Process($Y$, $\mathcal{L}$) | |||||||||
| Input:$Y$ – подзадача для ветвления | ||||||||||
| Input: $\mathcal{L}$ – список подзадач | ||||||||||
| 2 | ifdiscard($Y$) = false then | |||||||||
| 3 | $\mathcal{Y}$ = split($Y$) | |||||||||
| 4 | $z{\kern 1pt} *: = \infty $ | |||||||||
| 5 | $y{\kern 1pt} *: = (0, \ldots ,0)$ | |||||||||
| 6 | for $\hat {Y} \in Y$do | |||||||||
| 7 | $y = $get_trial_point($\hat {Y}$) | |||||||||
| 8 | $z = f(y)$ | |||||||||
| 9 | if $z < z{\kern 1pt} *$then | |||||||||
| 10 | $z{\kern 1pt} *: = z$ | |||||||||
| 11 | $y{\kern 1pt} *: = y$ | |||||||||
| 12 | end | |||||||||
| 13 | end | |||||||||
| 14 | if $z{\kern 1pt} * \ne \infty $then | |||||||||
| 15 | update_record ($y{\kern 1pt} *$, $z{\kern 1pt} *$) | |||||||||
| 16 | end | |||||||||
| 17 | for $\hat {Y} \in \mathcal{Y}$do | |||||||||
| 18 | if discard($Y$) = falsethen | |||||||||
| 19 | $\mathcal{L}$ := $\mathcal{L} \cup \hat {Y}$ | |||||||||
| 20 | end | |||||||||
| 21 | end | |||||||||
| 22 | end | |||||||||
| 23 | end | |||||||||
В наиболее распространенном случае подзадача разбивается на две. Возможны и другие варианты.
Для каждой подзадачи из списка с помощью функции get_trial_point находится новая допустимая точка, в которой вычисляется значение целевой функции (строки 8, 9). Из всех найденных решений выбирается решение y*, соответствующее минимальному значению целевой функции z*. Это решение используется для обновления рекордного решения и значения в строке 15. В цикле в строках 18–22 для каждой подзадачи из списка $\mathcal{Y}$ вычисляется нижняя граница. В случае, когда эта граница не превосходит ${{f}^{r}} - \varepsilon $, подзадача добавляется к общему списку подзадач $\mathcal{L}$.
Функция BnB (листинг 4) выполняет основной цикл метода ветвей и границ.
Листинг 4. Базовая функция МВГ
| 1 | Function BnB ($\mathcal{L}$, ${{N}_{{{\text{max}}}}}$): | ||||
| Input:$\mathcal{L}$, ${{x}_{r}}$ | |||||
| 2 | while$\mathcal{L} \ne \emptyset $and${{N}_{{{\text{max}}}}} > 0$do | ||||
| 3 | select $\hat {X}$ from $\mathcal{L}$ | ||||
| 4 | $\mathcal{L}: = \mathcal{L}{{\backslash }}\hat {X}$ | ||||
| 5 | Process$(\hat {X},\mathcal{L})$ | ||||
| 6 | ${{N}_{{{\text{max}}}}}: = N{\text{max}} - 1$ | ||||
| 7 | end | ||||
| 8 | end | ||||
В процессе ее работы модифицируется список $\mathcal{L}$ текущих подзадач, которые не были отсеяны и еще не подверглись ветвлению. Этот список передается в функцию в качестве входного параметра. На каждом шаге одна из подзадач извлекается из списка и обрабатывается функцией process, в результате работы которой изменяется список $\mathcal{L}$. Работа алгоритма прекращается, если исчерпан список подзадач $\mathcal{L}$ или превышено ограничение на максимальное число итераций Nmax.
Последовательная программа для решения задачи МВГ представляет собой вызов функции BnB со списком, состоящим только из одного элемента – исходной задачи. Параметр Nmax задается таким образом, чтобы обеспечить завершение программы в любом случае за разумное время.
Список $\mathcal{L}$ может быть реализован различными способами. Классические варианты реализации перечислены далее. Структура last-in-first-out (LIFO) соответствует “ветвлению в глубину”, так как на каждом шаге из списка извлекается одна из подзадач, сгенерированных на предыдущем этапе. Организация списка по принципу first-in-first-out (FIFO), наоборот, соответствует “ветвлению в ширину”. При таком подходе для обработки всегда выбирается подзадача, которая расположена в дереве ближе всего к его корню. Тем самым достигается последовательное раскрытие уровней дерева ветвления.
Третьим классическим подходом является использование упорядоченного списка, в котором порядок подзадач определяется их нижней оценкой. На очередном шаге для ветвления всегда выбирается подзадача с наименьшей нижней оценкой, находящаяся в начале списка. При таком подходе нижняя оценка подзадачи, соответствующей началу списка, дает нижнюю оценку для оптимального решения исходной задачи. Таким образом, на каждом шаге легко определяется интервал, которому принадлежит значение оптимального решения. Правым и левым концами этого интервала являются значения рекордного решения и нижней оценки подзадачи из вершины упорядоченного списка соответственно. Достоинством этого подхода также является возможность быстрого сокращения списка за счет удаления подзадач, удовлетворяющих правилу отсева, с конца списка.
2. Варианты параллельной реализации МВГ. В работе в качестве вычислительной платформы рассматривается многопроцессорная система с общей памятью, являющаяся на данный момент наиболее распространенной архитектурой параллельных вычислительных систем. В этой модели вычислительные ядра имеют доступ к единому адресному пространству. Каждое ядро может выполнять команды чтения и записи данных по любому адресу оперативной памяти. Для обеспечения корректности работы программы необходимы механизмы синхронизации доступа к памяти с разных вычислительных ядер.
Для изучения были выбраны алгоритмы Global-PAMIGO и Local-PAMIGO [11] и две авторские реализации МВГ – BnB-Brf и BnB-Atomic.
2.1. Global-PAMIGO. Алгоритм global-PAMIGO, предложенный в работе [11], предполагает наличие единого списка подзадач $\mathcal{L}$ для всех потоков. Подробно работа алгоритма представлена на листинге 5.
Листинг 5. Алгоритм global-PAMIGO
| 1 | Functionglobal-PAMIGO (L): | ||||||||||
| 2 | while true do | ||||||||||
| 3 | critical | ||||||||||
| 4 | $n{{t}_{{idle}}}: = n{{t}_{{idle}}} + 1$ | ||||||||||
| 5 | wait ($\mathcal{L} \ne \emptyset $or$n{{t}_{{idle}}} = n{{t}_{{{\text{max}}}}}$or$N = {{N}_{{{\text{max}}}}}$) | ||||||||||
| 6 | if $N = {{N}_{{{\text{max}}}}}$or$(\mathcal{L} = \emptyset $and$n{{t}_{{idle}}} = n{{t}_{{{\text{max}}}}})$then | ||||||||||
| 7 | notify_all | ||||||||||
| 8 | break | ||||||||||
| 9 | else | ||||||||||
| 10 | select $\hat {X}$ from $\mathcal{L}$ | ||||||||||
| 11 | $\mathcal{L}: = \mathcal{L}{{\backslash }}\hat {X}$ | ||||||||||
| 12 | $n{{t}_{{idle}}}: = n{{t}_{{idle}}} - 1$ | ||||||||||
| 13 | end | ||||||||||
| 14 | end | ||||||||||
| 15 | Process$(\hat {X},\mathcal{L})$ | ||||||||||
| 16 | $N: = N + 1$ | ||||||||||
| 17 | end | ||||||||||
| 18 | end | ||||||||||
Основной цикл while выполняется всеми потоками одновременно. В критической секции (строки 3–13) ведется подсчет числа участвующих в работе потоков (глобальная переменная $nt - idle$). Далее поток переходит в состояние ожидания до момента выполнения хотя бы одного из трех условий – общий список подзадач не пуст, число итераций стало равным максимальному, число шагов метода достигло максимально допустимого значения.
Ожидание реализуется с помощью механизма условных переменных. При срабатывании условной переменной проверяется указанный предикат. Если его значение – true, то функция wait завершается. В противном случае ожидание возобновляется. Во время ожидания на условной переменной поток не находится в критической секции, позволяя тем самым другим потокам ее выполнять. После завершения ожидания критическая секция возобновляется.
В алгоритме global-AMIGO при выходе из ожидания выполняется проверка условия достижения максимального числа итераций. Если оно верно, то все потоки оповещаются с использованием вызова notify_all условной переменной и цикл разрывается. Отметим, что при разрыве цикла завершается также и критическая секция. Те же действия производятся в случае, когда список подзадач пуст и все потоки находятся в состоянии idle, т.е. или выполняют вызов wait или уже закончили выполнять основной цикл.
Алгоритм global-PAMIGO прост в реализации. Его главным недостатком является наличие общего списка подзадач, обрабатываемого всеми потоками параллельного приложения, что приводит к существенным потерям производительности при большом их числе за счет частой синхронизации.
2.2. Local-PAMIGO. Основным недостатком алгорима global-PAMIGO является наличие единого для всех потоков списка подзадач, что приводит к деградации производительности при большом числе потоков. В алгоритме local-PAMIGO, также предложенном в работе [11], данный недостаток преодолевается за счет использования локального списка каждым из потоков параллельного приложения. Действия, выполняемые каждым потоком, представлены на листинге 6.
Листинг 6. Алгоритм local-PAMIGO
| 1 | Functionlocal-PAMIGO ($\mathcal{L}$): | |||||||||
| 2 | while$L \ne \emptyset $do | |||||||||
| 3 | if $N = {{N}_{{{\text{max}}}}}$then | |||||||||
| 4 | break | |||||||||
| 5 | end | |||||||||
| 6 | if $nt < n{{t}_{{{\text{max}}}}}$then | |||||||||
| 7 | critical | |||||||||
| 8 | $\mathcal{L}{\kern 1pt} ' = {\text{odd}}\;{\text{elements}}\;{\text{of}}\;\mathcal{L}$ | |||||||||
| 9 | $\mathcal{L}: = \mathcal{L}{{\backslash }}\mathcal{L}{\kern 1pt} '$ | |||||||||
| 10 | launchlocal-PAMIGO($\mathcal{L}{\kern 1pt} '$) | |||||||||
| 11 | $nt: = nt + 1$ | |||||||||
| 12 | end | |||||||||
| 13 | end | |||||||||
| 14 | select $\hat {X}$ from $\mathcal{L}$ | |||||||||
| 15 | $\mathcal{L}: = \mathcal{L}{{\backslash }}\hat {X}$ | |||||||||
| 16 | Process$(\hat {X},\mathcal{L})$ | |||||||||
| 17 | $N: = N + 1$ | |||||||||
| 18 | end | |||||||||
| 19 | end | |||||||||
На каждой итерации основного цикла поток сравнивает текущее значение запущенных потоков nt с максимальным $n{{t}_{{{\text{max}}}}}$. Если запущено меньше потоков, чем указано в $n{{t}_{{{\text{max}}}}}$, то выполняется запуск еще одного потока, которому передается половина подзадач текущего (берутся подзадачи с нечетными номерами в списке). Максимальное число потоков выбирается большим или равным числу вычислительных ядер с тем, чтобы обеспечить максимальную загрузку ресурсов процессора.
2.3. BnB-Brf. Данный вариант распараллеливания ориентирован на выполнение в среде OpenMP [14]. Особенностью среды OpenMP является поддержка директивного распараллеливания циклов. Директива OpenMP omp for приводит к распределению итераций цикла for, которому она предшествует, между параллельными потоками приложения. Основной цикл метода ветвей и границ не может быть непосредственно распараллелен, так как на каждой итерации модифицируется общий список подзадач. В алгоритме BnB-Brf, представленном на листинге 7, указанная проблема преодолевается с помощью разделения списков, из которых происходит чтение подзадач и списков, в которые вновь сгенерированные подзадачи записываются.
Листинг 7. Алгоритм BnB-Brf
| 1 | FunctionBnBBrf ($\mathcal{L}$): | |||||||||||||
| 2 | $i: = 1$ | |||||||||||||
| 3 | while $\mathcal{L} \ne \emptyset $do | |||||||||||||
| 4 | select $\hat {X}$ from $\mathcal{L}$ | |||||||||||||
| 5 | $\mathcal{L}: = \mathcal{L}{{\backslash }}\hat {X}$ | |||||||||||||
| 6 | ${{\mathcal{L}}_{i}}: = {{\mathcal{L}}_{i}} \cup \hat {X}$ | |||||||||||||
| 7 | $i = (i\bmod nt) + 1$ | |||||||||||||
| 8 | end | |||||||||||||
| 9 | while$\exists i \in \overline {1,nt} :{\kern 1pt} {{\mathcal{L}}_{i}} \ne \emptyset $do | |||||||||||||
| 10 | parallel | |||||||||||||
| 11 | for$j = \overline {1,nt} $do | |||||||||||||
| 12 | par forall $\hat {X} \in {{\mathcal{L}}_{j}}$do | |||||||||||||
| 13 | $cur: = GetThreadNumber()$ | |||||||||||||
| 14 | Process$(\hat {X},{{\hat {L}}_{{cur}}})$ | |||||||||||||
| 15 | end | |||||||||||||
| 16 | end | |||||||||||||
| 17 | end | |||||||||||||
| 18 | for$j = \overline {1,nt} $do | |||||||||||||
| 19 | $swap({{L}_{j}}: = {{\hat {\mathcal{L}}}_{j}})$ | |||||||||||||
| 20 | ${{\hat {\mathcal{L}}}_{j}}: = \emptyset $ | |||||||||||||
| 21 | end | |||||||||||||
| 22 | end | |||||||||||||
| 23 | end | |||||||||||||
Рассмотрим детально работу алгоритма, представленного на листинге 7. Предполагается, что число параллельных потоков, одновременно выполняемых на параллельных участках, составляет nt. В цикле в строках 3–8 производится инициализация списков ${{\mathcal{L}}_{i}}$ таким образом, чтобы обеспечить равномерное распределение подзадач по спискам. Списки ${{\mathcal{L}}_{i}}$, $i = \overline {1,nt} $, содержат подзадачи, предназначенные для считывания и последующей обработки.
Основной цикл в строках 9–22 выполняет итерации метода ветвей и границ до тех пор, пока совокупность списков $\{ {{\mathcal{L}}_{i}}\} $ содержит хотя бы одну подзадачу. В теле цикла параллельный участок в строках 10–17 приводит к созданию nt потоков. Далее в цикле в строках 11–16 производится обход всех списков совокупности $\{ {{\mathcal{L}}_{i}}\} $. Параллельный цикл в строках 12–15 производит стандартную операцию МВГ, изымая из списка очередную подзадачу, выполняя ветвление и помещая результат в список ${{\hat {\mathcal{L}}}_{{cur}}}$, соответствующий номеру потока. Таким образом, потоки не конфликтуют, поскольку запись идет в различные списки. Они отличаются от тех, из которых производится чтение. После завершения параллельного участка, перед началом очередной итерации цикла, выполняется копирование списков $\{ {{\hat {\mathcal{L}}}_{i}}\} $ в $\{ {{\mathcal{L}}_{i}}\} $ с помощью цикла в строках 18–21. Фактическое копирование заменяется обменом указателей на соответствующие адреса памяти.
2.4. BnB-Atomic. В алгоритме BnB-Atomic, представленном на листинге 2.4, каждый поток либо запускает два новых потока, распределяя между ними подзадачи, либо выполняет шаги последовательного алгоритма.
Функция BnBAtomic имеет три параметра: L – список подзадач, $procs$ – выделяемый ресурс по числу потоков, $steps$ – максимальный ресурс по числу шагов. Предполагается, что число потоков, созданных при выполнении функции BnBAtomic, не превысит значения $procs$, а число шагов – значения $steps$.
Листинг 8. Алгоритм BnB-Atomic
| 1 | FunctionBnBAtomic($\mathcal{L}$, $procs$, $steps$): | |||||||||
| 2 | if$procs = 1$then | |||||||||
| 3 | BnB($\mathcal{L}$, steps) | |||||||||
| 4 | else | |||||||||
| 5 | while$steps > 0$do | |||||||||
| 6 | if$steps \leqslant steps\_limit$then | |||||||||
| 7 | BnB($\mathcal{L}$, $steps$) | |||||||||
| 8 | else | |||||||||
| 9 | $step{{s}_{1}} = \left\lfloor {steps{\text{/}}2} \right\rfloor $ | |||||||||
| 10 | $step{{s}_{2}} = steps - spep{{s}_{1}}$ | |||||||||
| 11 | ${{\mathcal{L}}_{1}} = {\text{odd}}\;{\text{elements}}\;{\text{of}}\;\mathcal{L}$ | |||||||||
| 12 | ${{\mathcal{L}}_{2}} = {\text{even}}\;{\text{elements}}\;{\text{of}}\;\mathcal{L}$ | |||||||||
| 13 | launchBnBAtomc(${{\mathcal{L}}_{1}}$, $proc{{s}_{1}}$, $step{{s}_{1}}$) | |||||||||
| 14 | aunchBnBAtomc(${{\mathcal{L}}_{2}}$, $proc{{s}_{2}}$, $step{{s}_{2}}$) | |||||||||
| 15 | $steps = steps - step{{s}_{1}} - step{{s}_{2}}$ | |||||||||
| 16 | $\mathcal{L}: = {{\mathcal{L}}_{1}} \cup {{\mathcal{L}}_{2}}$ | |||||||||
| 17 | end | |||||||||
| 18 | end | |||||||||
| 19 | end | |||||||||
| 20 | end | |||||||||
Последовательный вариант алгоритма используется в двух случаях: когда число выделенных потоков составляет в точности 1 (проверка в строках 2–4) и когда количество выделенного ресурса шагов не превосходит пороговой величины steps_limit (проверка в строках 6–8). Значение steps_limit выбирается таким образом, чтобы суммарное время выполнения соответствующего числа шагов было существенно больше времени создания потока и тем самым делало целесообразным его создание.
Создание потоков выполняется в строках 9–16. Ресурс максимального числа потоков, шагов и множество подзадач текущего потока делятся в равных долях между создаваемыми в строках 13, 14 потоками. После завершения их работы выделенный ресурс числа шагов $steps$ уменьшается на сумму количеств шагов $step{{s}_{1}} + step{{s}_{2}}$, выполненных каждым потоком. Множества подзадач, полученные в результате выполнения потоков, объединяются в строке 16.
3. Методика сравнения эффективности алгоритмов. При сравнении эффективности параллельных алгоритмов ветвей и границ необходимо учитывать, что число итераций алгоритмов может варьироваться в широких пределах из-за так называемых поисковых аномалий. Причина поисковых аномалий заключается в том, что скорость обновления рекорда может оказывать очень существенное влияние на эффективность отсева подзадач и, как следствие, число итераций алгоритма. Из-за разницы в относительной скорости работы потоков параллельного приложения число итераций может очень существенно варьироваться от запуска к запуску. Поэтому для обеспечения качества сравнения параллельных вариантов МВГ необходимо проведение достаточно большого числа экспериментов. Ниже приводится методика определения достаточного числа экспериментов исходя из статистического анализа их результатов. Для полноценного сравнения эксперименты производятся на разных задачах глобальной оптимизации, так как разные задачи приводят к разным деревьям ветвлений, обуславливающих различное поведение параллельных алгоритмов ветвей и границ. При этом задачи должны обладать достаточной вычислительной сложностью, в противном случае распараллеливание нецелесообразно.
Для сравнения разработанных алгоритмов использовался набор из 150 задач глобальной оптимизации [12]. Тестовые задачи отбирались следующим образом:
1) каждая m-я задача решалась K раз с помощью a-го алгоритма, $a = \overline {1,4} $, с неизвестным значением минимума и максимальным количеством вычислительных ядер процессора;
2) вычислялось среднее количество шагов для каждой задачи:
3) задачи отбирались так, чтобы значение ${{N}_{{\overline m }}}$ удовлетворяло ограничениям:
Эффективность работы алгоритмов сравнивалась по следующим метрикам: $T$ – время решения задачи, $N$ – количество шагов алгоритма, $tps = T{\text{/}}N$ – среднее время решения одного шага (time per subproblem).
Критерии сравнения: среднее значение метрик, масштабируемость – способность алгоритма увеличивать свою производительность при добавлении аппаратных ресурсов, стабильность работы алгоритма.
Среднее значение метрик рассчитывалось как сумма всех чисел деленная на их количество:
Масштабируемость алгоритмов оценивалась через ускорение:
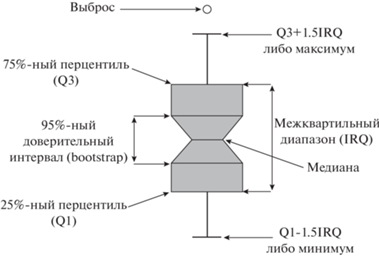
где ${{T}_{{\overline {ma1} }}}$ – среднее время решения задачи в последовательном режиме (на одном ядре процессора), ${{T}_{{\overline {man} }}}$ – в параллельном режиме (на $n$ ядрах процессора).Стабильность работы алгоритма сравнивалась с помощью статистических характеристик, указываемых на диаграмме данных (matplotlib.pyplot.boxplot). Элементы диаграммы показаны на рис. 1. На диаграмме отображается медиана, 95%-ный доверительный интервал, вычисленный с использованием техники bootstrap, 25%-ный и 75%-ный перцентили, усы (whiskers), показывающие максимум или минимум данных и возможные выбросы.
4. Численный эксперимент. Работа выполнялась с помощью инфраструктуры Центра коллективного пользования “Высокопроизводительные вычисления и большие данные” (ЦКП “Информатика”) ФИЦ ИУ РАН (Москва) [20]. Эксперименты проводились на двухпроцессорном сервере Kunpeng 920, 64 ядра, 2.6 ГГц, 256 Гб RAM. В первой серии экспериментов каждый из четырех методов был запущен 10 раз для набора из 150 функций [12] с неизвестным значением минимума на 128 ядрах сервера. Кроме этого, были заданы следующие параметры запуска алгоритмов для всех серий экспериментов:
1) $\epsilon {{ = 10}^{{ - 2}}}$,
2) ${{N}_{{{\text{max}}}}}{{ = 10}^{8}}$ – максимальное количество подзадач,
3) $procs$ = $\left\{ \begin{gathered} 1\quad ncores = 1, \hfill \\ 32ncores\quad ncores > 1 \hfill \\ \end{gathered} \right.$
– выделяемый ресурс по числу потоков для алгоритма BnB-Atomic, где $ncores$ – количество ядер, на которых запускается алгоритм,
4. $steps\_limit = 1000$ – пороговое значение перехода к последовательному варианту для алгоритма BnB-Atomic.
Для дальнейших экспериментов были выбраны задачи, для которых среднее количество подзадач лежало в пределах от ${{N}_{{{\text{min}}}}} = {{10}^{7}}$ до ${{N}_{{{\text{max}}}}} = {{10}^{8}}$. Данный критерий отбора позволил нам исключить из тестирования задачи, не решающиеся ни одним алгоритмом ($Trid10$ и $Trid6$) и задачи, решающиеся за небольшое количество шагов. Cписок выбранных задач приведен в табл. 1. Необходимо отметить и в дальнейшем это будет показано, что в этот список попали задачи, которые решались менее чем за 107 шагов одним алгоритмом и не решались за 108 шагов другим алгоритмом.
Таблица 1.
Список задач, выбранных для тестирования
| Задача | Количество шагов |
|---|---|
| Biggs EXP6 | 64 610 645 |
| Colville | 13 016 908 |
| Deckkers-Aarts | 37 967 225 |
| Langerman-5 | 10 057 600 |
| Mishra 8 | 12 516 309 |
| Powell Singular 2 8s | 30 053 649 |
| Schwefel 2.36 | 16 995 852 |
Во второй серии экспериментов для выбранных функций было задано известное значение минимума. Количество ядер, как и в первой серии экспериментов, равно 128. В табл. 2 приведены минимальное и максимальное количество решенных подзадач для каждой функции.
Таблица 2.
Минимум и максимум количества шагов для различных задач
| Количество шагов | ||
|---|---|---|
| Задача | минимальное | максимальное |
| Biggs EXP6 | 1 | 1 |
| Colville | 224 561 | 224 561 |
| Deckkers-Aarts | 36 893 793 | 36 893 793 |
| Langerman-5 | 2871 | 2871 |
| Mishra 8 | 1 | 1 |
| Powell Singular 2 8s | 1 | 1 |
| Schwefel 2.36 | 15 599 251 | 15 599 251 |
Как мы и ожидали, для известного значения глобального минимума при каждом запуске любой из четырех алгоритмов порождает одинаковое количество подзадач. Сравнивая табл. 1 и 2, можно увидеть, что для тестовых функций $Deckkers{\text{ - }}Aarts$ и $Schwefel2.36$ знание значения глобального минимума не приводит к существенному ускорению решения задачи. В табл. 3 приведено среднее время решения задач $Deckkers{\text{ - }}Aarts$ и $Schwefel2.36$ и относительная погрешность его оценки.
Таблица 3.
Время решения задачи и относительная погрешность оценки
| Задача | Алгоритм | Время, с | Относительная погрешность оценки, % |
|---|---|---|---|
| Deckkers-Aarts | BnB Aatomic | 4.5 | 1.0 |
| Deckkers-Aarts | BnB-Brf | 12.2 | 2.3 |
| Deckkers-Aarts | Global-PAMIGO | 113.2 | 1.2 |
| Deckkers-Aarts | Local-PAMICO | 14.6 | 2.1 |
| Schwefel 2.36 | BnB-Aatomic | 2.1 | 1.2 |
| Schwefel 2.36 | BnB-Brf | 5.0 | 1.3 |
| Schwefel 2.36 | Global-PAMIGO | 46.8 | 1.6 |
| Schwefel 2.36 | Local-PAMICO | 6.1 | 1.1 |
Алгоритмы BnB-Brf и local-PAMIGO имеют примерно равную эффективность, алгоритм BnB-Atomic работает более чем в 2 раза быстрее, а global-PAMIGO показывает результаты, худшие на порядок.
В третьей серии экспериментов мы запустили решение двух задач: $Deckkers{\text{ - }}Aarts$ и $Schwefel2.36$ для различного количества ядер с известным значением минимума. Алгоритмы BnB-Brf, global-PAMIGO и local-PAMIGO запускались для [1, 2, 4, 8, 16, 32, 64, 128] ядер, а BnB-Atomic – [1, 32, 64, 128] ядер. Так как алгоритм BnB-Atomic может быть запущен либо в однопоточном режиме, либо с использованием всех ядер процессора, для запуска на [32, 64] ядрах мы использовали технологию отключения отдельных ядер. Отключение ядра производилось с помощью команд:
$ echo 0 | sudo tee /sys/devices/system/cpu/cpu<N>/online,
$ dmesg,
где N – номер ядра. Для 64 ядер включенными оставались четные ядра, для 32 – каждое четвертое.
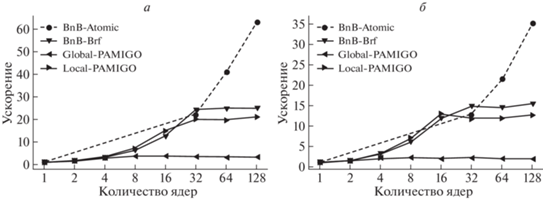
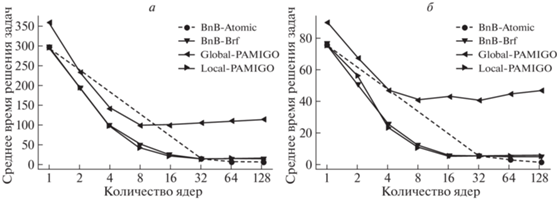
Результаты запусков представлены на рис. 2. Как можно увидеть, ускорение зависит от задачи и для трех алгоритмов при достижении определенного количества ядер стабилизируется. Для алгоритмов BnB-Brf и local-PAMIGO стабилизация наступает при количестве ядер 32, а алгоритм global-PAMIGO стабилизируется уже на 8 ядрах. На рис. 3 приведено среднее время решения задач $Deckkers - Aarts$ и $Schwefel2.36$ в этой же серии экспериментов.
Как видно из графика, алгоритм global-PAMIGO в однопоточном режиме работает немного медленнее остальных. Но тем не менее, для задачи $Deckkers - Aarts$ до 4–8 ядер его производительность существенно не ухудшается по сравнению с остальными алгоритмами. Поэтому если тестировать его на “персональных” компьютерах, то эффект стабилизации заметить будет невозможно.
В четвертой серии экспериментов запуск алгоритмов осуществлялся при неизвестном значении минимума на 128 ядрах, при этом каждая задача запускалась 40 раз (табл. 4).
Таблица 4.
Количество решенных задач
| Задача/Алгоритм | BnB-Atomic | BnB-Brf | Global-PAMIGO | Local-PAMIGO |
|---|---|---|---|---|
| Biggs EXP6 | 40 | 40 | 0 | 18 |
| Colville | 40 | 40 | 25 | 40 |
| Deckkers-Aarts | 40 | 40 | 40 | 40 |
| Langerman-5 | 40 | 40 | 28 | 40 |
| Mishra 8 | 40 | 40 | 22 | 40 |
| Powell Singular 2 8s | 40 | 40 | 1 | 40 |
| Schwefel 2.36 | 40 | 40 | 40 | 40 |
Из таблицы видно, что BnB-Atomic и BnB-Brf решают все выбранные нами задачи, local-PAMIGO решает 6 задач, а для задачи $BiggsEXP6$ терпит неудачу в 22 запусках из 40. Global-PAMIGO решает только 2 ранее рассмотренные задачи. Исключив неудачные запуски, посмотрим на количество шагов сделанных во время решения задачи при каждом запуске. В табл. 5 приведено среднее количество шагов.
Таблица 5.
Среднее количество шагов в успешных запусках
| Задача/Алгоритм | BnB-Atomic | BnB-Brf | Global-PAMIGO | Local-PAMIGO |
|---|---|---|---|---|
| Biggs EXP6 | 55 060 988 | 21 054 960 | 49 661 882 | |
| Colville | 1 282 078 | 235 925 | 20 620 662 | 740 605 |
| Deckkers-Aarts | 37 333 173 | 36 894 781 | 40 356 543 | 37 165 043 |
| Langerman-5 | 58 965 | 8688 | 13 743 657 | 40 966 |
| Mishra 8 | 1.130 | 578 | 5 359 005 | 17 137 |
| Powell Singular 2 8s | 9 747 155 | 746 139 | 13 114 293 | 12 740 698 |
| Schwefel 2.36 | 16 235 180 | 15 599 421 | 19 957 545 | 16 013 319 |
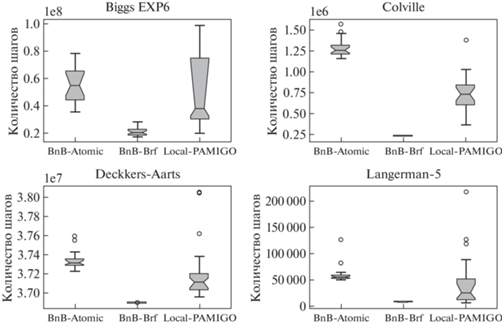
Согласно таблице, алгоритм global-PAMIGO на всех задачах проигрывает остальным алгоритмам, причем на задачах, кроме $Deckkers - Aarts$ и $Schwefel2.36$, этот проигрыш составляет несколько порядков. Учитывая стабилизацию ускорения данного алгоритма на 8 процессах, применение данного алгоритма для решения задач нецелесообразно. Лучшим алгоритмом по критерию количества шагов является BnB-Brf, но более высокое время одного шага (табл. 6), связанное со стабилизацией ускорения на 32 процессах, не позволяют ему доминировать над алгоритмом BnB-Atomic. Кроме средних значений, приводим также характеристики распределения количества шагов для первых четырех задач (рис. 4). Распределения для остальных задач имеют аналогичный характер. Можно увидеть, что алгоритм BnB-Brf не только эффективен по среднему количеству шагов, но и более стабилен.
Таблица 6.
Среднее время шага в успешных запусках (микросекунды)
| Задача/Алгоритм | BnB-Atomic | BnB-Brf | Global-PAMIGO | Local-PAMIGO |
|---|---|---|---|---|
| Biggs EXP6 | 0.72 | 0.89 | 0.68 | |
| Colville | 1.23 | 0.96 | 3.12 | 0.69 |
| Deckkers-Aarts | 0.12 | 0.32 | 3.01 | 0.38 |
| Langerman-5 | 5.55 | 11.31 | 3.09 | 6.70 |
| Mishra 8 | 85.54 | 33.48 | 16.51 | 16.35 |
| Powell Singular 2 8s | 0.74 | 0.76 | 3.34 | 0.70 |
| Schwefel 2.36 | 0.13 | 0.32 | 3.03 | 0.38 |
Далее посмотрим итоговый критерий – среднее время решения задач. В табл. 7 указана величина неточности измерений среднего времени решения задачи для каждого алгоритма. Первое, что мы можем увидеть – точность измерения времени решения подзадач позволяет нам сравнивать алгоритмы друг с другом. Второе, алгоритм BnB-Atomic становится более стабилен по времени решения задач, чем алгоритм BnB-Brf.
Таблица 7.
Неточность измерения среднего времени шага в успешных запусках (проценты)
| Задача/Алгоритм | BnB-Atomic | BnB-Brf | Global-PAMIGO | Local-PAMIGO |
|---|---|---|---|---|
| Biggs EXP6 | 0.24 | 5.51 | 0.77 | |
| Colville | 2.04 | 3.66 | 0.96 | 3.43 |
| Deckkers-Aarts | 0.51 | 0.51 | 0.50 | 0.46 |
| Langerman-5 | 3.47 | 18.41 | 1.66 | 16.73 |
| Mishra 8 | 6.73 | 7.85 | 56.99 | 29.47 |
| Powell Singular 2 8s | 1.07 | 2.95 | 0.56 | |
| Schwefel 2.36 | 1.30 | 0.42 | 0.80 | 0.46 |
В табл. 8 приводится среднее время решения задач в успешных запусках. За счет результативного распараллеливания алгоритм BnB-Atomic работает лучше всех на задачах $Deckkers - Aarts$ и $Schwefel2.36$. Для задач $BiggsEXP6$, $Colville$, $Langerman - 5$ и $PowellSingular28s$ эффективней оказывается алгоритм BnB-Brf из-за более рациональной стратегии поиска. И только для задачи $Mishra8$ алгоритмы BnB-Brf и local-PAMIGO оказываются сравнимы по производительности. Алгоритм global-PAMIGO, стабилизируясь на 8 ядрах, показывает худшие результаты.
Таблица 8.
Среднее время решения задачи в успешных запусках (секунды)
| Задача/Алгоритм | BnB-Atomic | BnB-Brf | Global-PAMIGO | Local-PAMIGO |
|---|---|---|---|---|
| Biggs EXP6 | 39.53 | 18.89 | 33.69 | |
| Colville | 1.57 | 0.23 | 64.33 | 0.50 |
| Deckkers-Aarts | 4.60 | 11.72 | 121.32 | 14.05 |
| Langerman-5 | 0.32 | 0.10 | 41.98 | 0.16 |
| Mishra 8 | 0.07 | 0.02 | 16.67 | 0.03 |
| Powell Singular 2 8s | 7.114 | 0.57 | 43.86 | 8.92 |
| Schwefel 2.36 | 2.07 | 4.98 | 60.50 | 6.16 |
Заключение. Сравнительный анализ алгоритмов показал, что наиболее эффективными по времени решения задач являются алгоритмы BnB-Brf и BnB-Atomic. Исследование масштабируемости продемонстрировало, что при увеличении аппаратных ресурсов (в диапазоне от 1 до 128 ядер) только алгоритм BnB-Atomic увеличивает свою производительность. Для остальных алгоритмов обнаружено, что, начиная с некоторого количества ядер, происходит стабилизация ускорения, т.е. добавление аппаратных ресурсов не приводит к ускорению решения задач. У global-PAMIGO порог стабилизации ускорения равен 8 ядрам, у BnB-Brf и local-PAMIGO порог равен 32 ядрам. Рассматривая данный эффект, необходимо отметить, что для работы алгоритмов аппаратными ресурсами являются не только ядра процессора, но и компоненты процессора, отвечающие за конкурентный доступ к оперативной памяти. Архитектура использованного сервера Kunpeng 920, состоящего из двух процессоров, в каждом из которых содержится по два суперкластера из 8 четырехъядерных кластеров, позволила нам показать это.
Кроме среднего времени решения задач и масштабируемости, мы исследовали стабильность работы алгоритмов по количеству шагов, среднему времени шага и времени решения задач. Стабильность работы алгоритмов по количеству шагов обеспечивается устойчивостью алгоритма к аномалиям поиска, а стабильность по среднему времени шага – устойчивым конкурентным доступом к общей памяти. Пример алгоритма BnB-Brf стабильного и эффективного по количеству шагов, но менее стабильного по среднему времени шага показывает нам, что рациональная поисковая стратегия, не учитывающая в полной мере архитектуру процессора, в результате может привести к замедлению работы параллельного алгоритма.
Одним из важнейших параметров рассматриваемых алгоритмов является степень ветвления подзадач. В работе не исследовали влияние этого параметра на масштабируемость алгоритмов и время решения задач. Также было бы интересно посмотреть на зависимость эффективности алгоритмов от архитектуры используемых серверов. Результаты данных исследований будут проведены в последующей публикации авторов.
Список литературы
Евтушенко Ю.Г. Численный метод поиска глобального экстремума функций (перебор на неравномерной сетке) // ЖВМ и МФ. 1971. Т. 11. № 6. С. 1390–1403.
Lawler E.L., Wood D.E. Branch-and-Bound Methods: A survey // Operations research. 1966. V. 14. № 4. P. 699–719.
Евтушенко Ю.Г., Посыпкин М.А. Применение метода неравномерных покрытий для глобальной оптимизации частично целочисленных нелинейных задач // ЖВМ и МФ. 2011. Т. 51. № 8. С. 1376–1389.
Karnopp D.C. Random Search Techniques for Optimization Problems // Automatica. 1963. V. 1. № 2–3. P. 111–121.
Solis F.J., Wets R.J.B. Minimization by Random Search Techniques // Mathematics of Operations Research. 1981. V. 6. № 1. P. 19–30.
Marte R., Lozano J.A., Mendiburu A. et al. Multi-start Methods // Handbook of Heuristics. Cham: Springer, 2018. P. 155–175.
Marte R., Aceves R., LeГin M.T at al. Intelligent Multi-start Methods // Handbook of Heuristics. Cham: Springer, 2019. P. 221–243.
Амирханова Г.А., Горчаков А.Ю., Дуйсенбаева А.Ж., Посыпкин М.А. Метод мультистарта с детерминированным механизмом рестарта // Вестн. С.-Петербургского ун-та. Прикладная математика. Информатика. Процессы управления. 2020. Т. 16. № 2. С. 100–111.
Зайцев А.А., Курейчик В.В., Полупанов А.А. Обзор эволюционных методов оптимизации на основе роевого интеллекта // Изв. Южного федерального ун-та. Технические науки. 2010. Т 113. № 12. С. 7–12.
Crainic T.G., Le Cun B., Roucairol C. Parallel Branch-and-bound Algorithms // Parallel Combinatorial Optimization. New Jersey: John Wiley & Sons, Inc., 2006. P. 1–28.
Casado L.G., Martinez J.A., García I. et al. Branch-and-bound Interval Global Optimization on Shared Memory Multiprocessors // Optimization Methods & Software. 2008. V. 23. № 5. P. 689–701.
Posypkin M., Usov A. Implementation and Verification of Global Optimization Benchmark Problems // Open Engineering. 2017. V 7. № 1. P. 470–478.
Land A.H., Doig A.G. An Automatic Method of Solving Discrete Programming Problems // Econometrica. 1960. V. 28. № 3. C. 497–520.
Van Der Pas R., Stotzer E., Terboven C. Using OpenMP-The Next Step: Affinity, Accelerators, Tasking, and SIMD. London: MIT Press, 2017.
Rabinovich S.G., Rabinovich M. Evaluating Measurement Accuracy. N.Y.: Springer, 2010.
Dekking F.M., Kraaikamp C., Lopuhaí H.P. et al. A Modern Introduction to Probability and Statistics: Understanding why and how. London: Springer, 2005.
Efron B., Tibshirani R. J. A An Introduction to the Bootstrap. Boca Raton: CRC press, 1994.
Helwig N.E. Bootstrap Confidence Intervals // Twin:University of Minnesota, 2017.
Virtanen P.,Gommers R., Oliphant T.E. et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python // Nature methods. 2020. V. 17. № 3. C. 261–272.
Положение о ЦКП “Информатика”. 2020. URL: http://www.frccsc.ru/ ckp (onlineНѕ accessed: 2020-07-23).
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления