Известия РАН. Теория и системы управления, 2023, № 2, стр. 123-139
ЗАДАЧА УПРАВЛЕНИЯ ПАРОГЕНЕРАТОРОМ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ ПРИ ОГРАНИЧЕНИЯХ НА ФАЗОВЫЕ ПЕРЕМЕННЫЕ И УПРАВЛЕНИЯ
С. И. Гулюкина a, *, В. А. Уткин a, **
a ИПУ РАН
Россия, Москва
* E-mail: gulyukina.s.i@mail.ru
** E-mail: vicutkin@ipu.ru
Поступила в редакцию 08.09.2022
После доработки 17.09.2022
Принята к публикации 05.12.2022
- EDN: JEBMEQ
- DOI: 10.31857/S0002338823020105
Аннотация
Рассматривается задача управления парогенератором с учетом ограничений на фазовые переменные и управление при воздействии внешних неконтролируемых возмущений. Для синтеза закона управления применяется блочный подход с формированием линейных локальных связей с насыщением, что позволяет учесть ограничения на фазовые переменные и управление при выборе параметров обратной связи. В условиях неполной информации о векторе состояния и при воздействии внешних возмущений синтезирован наблюдатель состояний и возмущений, позволяющий получить оценки неизвестных сигналов с заданной точностью. Эффективность предложенных алгоритмов подтверждена результатами численного моделирования.
Введение. На крупных современных теплоэнергетических объектах распространена схема выработки электроэнергии и тепла, основанная на генерации водяного пара при сжигании угля или природного газа и последующей его подачи на паротурбинные установки. В данной схеме достигаются лучшие по сравнению с другими установками технологические характеристики, в том числе энергоэффективность, особенно для энергетических объектов большой мощности. Математические модели, описывающие теплоэнергетические объекты, являются многомерными и многосвязными, с большим количеством физических параметров, не подлежащих прямым измерениям [1–3]. Необходимость учета в подобных моделях нелинейностей обусловливается тепловыми, механическими и электрическими ограничениями при наличии общего ограничения на суммарную мощность протекающих процессов. Учет данных ограничений становится обязательным в связи с всеобщим требованием минимизации потерь энергетических ресурсов при одновременной интенсификации технологических процессов энергетических объектов.
Известные алгоритмы управления энергетическими объектами часто основаны на методах линеаризации исходной нелинейной системы [4, 5]. Следует отметить, что применительно к линеаризованным моделям удается обеспечить работоспособность системы управления только в окрестности рабочей точки. В отличие от линеаризованных моделей, методы линеаризации нелинейных моделей по обратной связи, разработанные в рамках блочного подхода [6, 7] и алгоритмов обратного обхода интеграторов (back-stepping control) [8, 9], обеспечивают глобальную сходимость замкнутой системы. Часто в задачах управления применяются также методы робастного управления [10–12], в частности, робастность и инвариантность к внешним возмущениям обеспечиваются при использовании методов теории скользящих режимов [13–16]. Для получения оценок, недоступных для измерения компонент вектора состояния, а также модельных неопределенностей и внешних возмущений, весьма эффективными являются наблюдатели состояний с разрывными управлениями и глубокими обратными связями [17–19].
В настоящее время вопросы, связанные с учетом ограничений на фазовые переменные и управления, недостаточно изучены в теории управления. В последнее время появился ряд исследований по учету ограничений на фазовые переменные и управления [20–22], в которых с использованием блочного подхода синтезируются локальные обратные связи и собственно управления в виде функций с насыщением, что позволяет уже на стадии синтеза обратной связи учитывать указанные ограничения.
В работе ставится задача синтеза робастной системы управления парогенератором при действии на объект управления внешних несогласованных ограниченных по модулю возмущений. Цель управления в форме обратной связи состоит в поддержании давления перед задвижкой, регулирующей подачу пара в турбину, на заданном уровне с учетом ограничений на фазовые переменные и управление. Для решения поставленной задачи предлагается применить блочный подход с использованием в качестве локальных обратных связей линейных функций с насыщением (sat-функций).
Работа организована следующим образом. В разд. 1 приводится математическая модель объекта управления и формализуется постановка задачи. Раздел 2 посвящен синтезу обратной связи с учетом ограничений на фазовые переменные и управление в предположении, что вектор состояния модели объекта управления и внешние возмущения доступны для измерения. Для информационного обеспечения предложенных алгоритмов управления при неполном комплекте датчиков в разд. 3 разрабатывается наблюдатель состояний и возмущений. В разд. 4 приводятся результаты численного моделирования в среде MATLAB–Simulink, демонстрирующие работоспособность предложенных алгоритмов.
1. Математическая модель объекта управления. Постановка задачи. Рассматриваемая система представлена котлом-парогенератором, использующимся в паровых турбинах. Данный вид парогенератора широко применяется в технологических операциях различных производств. Принципиальная схема котла приведена на рис. 1.
Промышленный парогенератор состоит из металлического бойлера с водой. Посредством теплового потока ${{D}_{Q}}(t)$ нагревательный прибор внутри устройства доводит воду до кипения, которая затем переходит в состояние пара. Перегретый пар поднимается к задвижке, находящейся в положении q(t), перед которой создается высокое давление ${{P}_{T}}(t)$. Управляющим воздействием в системе является подача топлива в топку печи, пропорциональная расходу топлива ${{u}_{1}}(t)$.
Модель процессов в котле описывается системой из трех дифференциальных уравнений [1–3]:
(1.1)
$\begin{gathered} {{C}_{n}}{{{\dot {P}}}_{T}}(t) = {{k}_{s}}\sqrt {{{P}_{D}}(t) - {{P}_{T}}(t)} - {{k}_{\mu }}{{P}_{T}}(t)q(t), \\ {{С}_{b}}{{{\dot {P}}}_{D}}(t) = {{k}_{m}}{{D}_{Q}}(t) - {{k}_{s}}\sqrt {{{P}_{D}}(t) - {{P}_{T}}(t)} , \\ {{T}_{b}}{{{\dot {D}}}_{Q}}(t) = - {{D}_{Q}}(t) + {{u}_{1}}(t){\text{,}} \\ \end{gathered} $Предполагается, что подача топлива в печь обеспечивается устройством подачи топлива с двигателем постоянного тока (ДПТ). Поведение ДПТ описывается системой уравнений второго порядка [23]:
(1.2)
$\begin{gathered} \dot {\omega }(t) = {{a}_{{21}}}({{a}_{{22}}}{{I}_{{\text{я}}}}(t) - {{m}_{L}}(t)), \\ {{{\dot {I}}}_{{\text{я}}}}(t) = {{a}_{{32}}}({{u}_{2}}(t) - {{a}_{{22}}}\omega (t) - {{a}_{{31}}}{{I}_{{\text{я}}}}(t)), \\ \end{gathered} $Полагая, что скорость подачи топлива в печь пропорциональна частоте вращения ДПТ ${{u}_{1}}(t) = m{\kern 1pt} \omega {\kern 1pt} {\kern 1pt} (t),$ $m = {\text{const}} > 0$, запишем системы (1.1) и (1.2) следующим образом:
(1.3)
$\begin{gathered} {{{\dot {e}}}_{1}}(t) = - {{a}_{1}}q(t){{e}_{1}}(t) + {{a}_{2}}{{x}_{2}}(t) - {{\eta }_{1}}(t), \\ {{{\dot {x}}}_{2}}(t) = \frac{{\text{1}}}{{2{{x}_{2}}(t)}}{\text{[}}{{a}_{1}}q(t){{e}_{{\text{1}}}}(t) + {{a}_{3}}{{x}_{3}}(t) + {{\eta }_{1}}] - {{\eta }_{2}}, \\ {{{\dot {x}}}_{3}}(t) = - b{{x}_{3}}(t) + bm{{x}_{4}}(t), \\ \end{gathered} $(1.4)
$\begin{gathered} {{{\dot {x}}}_{4}}(t) = {{a}_{{21}}}[{{a}_{{22}}}{{x}_{5}}(t) - {{m}_{L}}], \\ {{{\dot {x}}}_{5}}(t) = {{a}_{{32}}}[{{u}_{2}}(t) - {{a}_{{22}}}{{x}_{4}}(t) - {{a}_{{31}}}{{x}_{5}}(t)]. \\ \end{gathered} $Здесь ${{e}_{1}}(t) = {{P}_{T}}(t) - {{P}_{{Td}}}(t)$, ${{P}_{{Td}}}(t)$ – желаемое давление перед задвижкой, x2(t) = $\sqrt {{{P}_{D}}(t) - {{P}_{T}}(t)} $, ${{x}_{3}} = {{D}_{Q}}(t)$, ${{x}_{4}} = \omega \,(t)$, ${{x}_{5}} = {{I}_{{\text{я}}}}(t)$, ${{\eta }_{1}}(t) = {{a}_{1}}q(t){{P}_{{Td}}}$, ${{\eta }_{2}}(t) = {{k}_{s}}({{C}_{b}} + {{C}_{n}}){\text{/}}(2{{C}_{b}}{{C}_{n}}) = {\text{const}}$, ${{a}_{1}} = {{k}_{\mu }}{\text{/}}{{С}_{n}}$, ${{a}_{2}} = {{k}_{s}}{\text{/}}{{С}_{n}}$, $\,{{a}_{3}} = {{k}_{m}}{\text{/}}{{С}_{b}}$, $b = 1{\text{/}}{{T}_{b}}$ и ${{a}_{{ij}}} = {\text{const}} > 0$ – параметры ДПТ.
Ставится задача слежения за заданным значением давления перед задвижкой ${{P}_{{Td}}} = {\text{const}}$ с заданной точностью
(1.5)
$\left| {{{e}_{{\text{1}}}}(t)} \right| = \left| {{{P}_{T}}(t) - {{P}_{{Td}}}} \right| \leqslant {{{{\Delta }}}_{{\text{1}}}} = {\text{const}}$1) для измерения доступны давление перед задвижкой ${{P}_{T}}(t)$ и, следовательно, e1(t) = = ${{P}_{T}}(t) - {{P}_{{Td}}}$, давление в парогенераторе ${{P}_{D}}(t)$ и, следовательно, ${{x}_{2}}(t) = \sqrt {{{P}_{D}}(t) - {{P}_{T}}(t)} $, а также ток якоря ДПТ ${{x}_{{\text{5}}}}$(t);
2) возмущения ${{\eta }_{1}}{\text{(}}t{\text{)}},{{\eta }_{2}}$ и положение задвижки q(t) полагаются неизвестными и удовлетворяют следующим ограничениям:
(1.6)
$\begin{gathered} q(t) \in [{{q}_{{\min }}},1]{\text{,}}\quad \left| {{{q}^{{{\text{(i)}}}}}{\text{(}}t{\text{)}}} \right| \leqslant {{Q}_{i}},\quad i = \overline {1,4} \Rightarrow {{\eta }_{1}}(t) \in [{{N}_{{{\text{11}}}}},{{N}_{{12}}}],\quad {{\eta }_{{\text{2}}}} \leqslant {{N}_{2}}; \\ {{Q}_{i}},{{q}_{{\min }}},{{N}_{{11}}},{{N}_{{12}}},{{{\bar {N}}}_{1}},{{N}_{2}} = {\text{const}} > 0. \\ \end{gathered} $Тот факт, что положение выпускной задвижки полагается неизвестным и рассматривается в качестве внешнего возмущения, означает автономный режим работы парогенератора. Такая ситуация часто встречается при групповом использовании парогенераторов, работающих на общий паропровод;
3) на переменные системы наложены физические ограничения
(1.7)
$\begin{gathered} \left| {{{e}_{{\text{1}}}}} \right| \in {{E}_{1}},\quad {{x}_{2}}(t) \in ({{X}_{{21}}},{{X}_{{22}}}],\quad {{x}_{i}}(t) \in [0,{{X}_{i}}],\quad i = \overline {3,4} ; \\ \left| {{{x}_{5}}{\text{(}}t)} \right| \leqslant {{X}_{{\text{5}}}},\quad {{u}_{1}}{\text{(}}t) \in [0,{{U}_{1}}],\quad \left| {{{u}_{2}}{\text{(}}t)} \right| \leqslant {{U}_{2}}; \\ {{E}_{1}},{{X}_{{21}}},{{X}_{{22}}},{{X}_{i}},{{X}_{5}},{{U}_{1}},{{U}_{2}} = {\text{const}} > 0. \\ \end{gathered} $В разд. 2 решается задача синтеза обратной связи в задаче регулирования относительно выходной переменной (1.5) в условиях полной параметрической и сигнальной определенности с учетом ограничений (1.6)–(1.7).
2. Синтез обратной связи. Представим решение в общем виде в рамках блочного подхода в условиях полной информации о компонентах вектора состояния и возмущениях. Далее используется следующее определение.
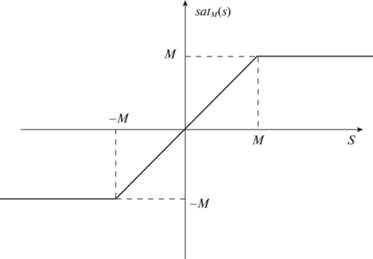
Определение. Для $M = {\text{const}} > {\text{0}}$ и аргумента функции $s$ имеем
Ниже приведена поэтапная процедура синтеза обратной связи в решении задачи регулирования (1.5) в предположениях (1.6)–(1.7).
Этап 1.
1. В первом уравнении системы (1.3) в качестве фиктивного управляющего воздействия рассматривается разность давлений на выходе из котла и перед задвижкой x2.
2. Введем невырожденную замену переменных, учитывающую ограничения (1.7):
где ${{s}_{{\text{2}}}}(t) = - {{k}_{1}}{{e}_{1}}(t) + {{\eta }_{1}}(t)$. Как видим, решение задачи стабилизации переменной ${{e}_{2}}(t) \to 0$ при выборе амплитуды $0 < {{M}_{2}} \leqslant {{a}_{2}}{{X}_{2}}$ обеспечивает заданные ограничения ${{x}_{2}} \in [0,{{X}_{2}}]$ (1.7). После подстановки (2.1) первое уравнение системы (1.3) преобразуется к виду(2.2)
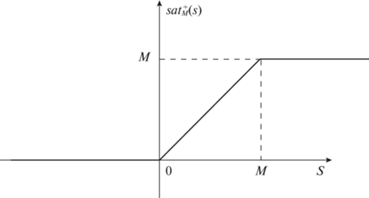
${{\dot {e}}_{1}}(t) = - {{a}_{{\text{1}}}}q(t{\text{)}}{{e}_{1}}(t) + {{e}_{2}}(t) + sat_{{{{M}_{2}}}}^{ + }({{s}_{2}}(t)) - {{\eta }_{1}}(t).$3. При попадании переменной ${{s}_{{\text{2}}}}(t)$ в линейную зону $0 < {{s}_{{\text{2}}}}(t) < {{M}_{{\text{2}}}}$ первая система (1.3) описывается уравнением
где выбор параметра ${{k}_{1}} = {\text{const}} \geqslant 0$ определяет сходимость состояния данной подсистемы в некоторую окрестность нуля, определяемую выражением $\left| {{{e}_{1}}(t)} \right| \leqslant {{{{\Delta }}}_{2}}{\text{/}}({{a}_{{\text{1}}}}{{q}_{{\min }}} + {{k}_{1}})$ в предположении, что выполнено неравенство $\left| {{{e}_{2}}(t)} \right| \leqslant {{{{\Delta }}}_{2}} = {\text{const}}$, обеспечиваемое на втором этапе процедуры.4. Условия попадания в линейную зону определяются выбором амплитуды M2 и коэффициента усиления k1, исходя из обеспечения соотношения ${{s}_{2}}(t){{\dot {s}}_{2}}(t)$ < 0 в нелинейной зоне ${{s}_{2}}(t) \in ( - \infty ,{\text{0}}) \cup ({{M}_{2}},\infty )$.
Запишем дифференциальное уравнение относительно переменной ${{s}_{{\text{2}}}}(t)$:
(2.4)
${{\dot {s}}_{2}}(t) = {{f}_{1}}(t) - {{k}_{1}}[sat_{{{{M}_{2}}}}^{ + }({{s}_{2}}(t)) + {{\varphi }_{1}}(t)],$5. Ставится задача выбора коэффициента k1 и амплитуды M2 функции с насыщением $sat_{{{{M}_{2}}}}^{ + }({{s}_{2}})$.
Положим далее $\left| {{{f}_{1}}(t)} \right| \leqslant {{F}_{1}} = {{\bar {N}}_{1}}$, $ - {{\varphi }_{1}}(t) \in {\text{[}}{{\Phi }_{{11}}},{{\Phi }_{{12}}}]$, ${{F}_{1}},{{\Phi }_{{11}}},{{\Phi }_{{12}}} = {\text{const}} > {\text{0}}$.
При ${{s}_{2}}(t) \in ({{M}_{{\text{2}}}},\infty )$ и, следовательно, $sat_{{{{M}_{2}}}}^{ + }({{s}_{2}}(t)) = {{M}_{{\text{2}}}}$ должно выполняться неравенство ${{\dot {s}}_{2}}(t) = {{f}_{1}}(t) - {{k}_{1}}[{{M}_{2}} + {{\varphi }_{1}}(t)] < {\text{0}}$, откуда следует неравенство на выбор амплитуды ${{M}_{{\text{2}}}} > {{\Phi }_{{12}}} + {{F}_{1}}{\text{/}}{{k}_{1}}$.
При ${{s}_{2}}(t) \in ( - \infty ,{\text{0}})$ и, следовательно, $sat_{{{{M}_{2}}}}^{ + }({{s}_{2}}(t)) = 0$ должно выполняться неравенство ${{\dot {s}}_{2}}(t) = {{f}_{1}}(t) - {{k}_{1}}{{\varphi }_{1}}(t)$ > 0. В силу ${{\varphi }_{1}}(t) < {\text{0}}$ найдется такой коэффициент ${{k}_{1}} > 0$, что условие ${{\dot {s}}_{2}}(t) < 0$ справедливо: ${{k}_{1}} > {{F}_{{\text{1}}}}{\text{/}}{{\Phi }_{{{\text{11}}}}}$.
Этап 2.
1. Обеспечим попадание переменной ${{e}_{{\text{2}}}}(t)$ из (2.1) в заданную окрестность нуля $\left| {{{e}_{{\text{2}}}}(t)} \right| \leqslant {{{{\Delta }}}_{2}}$. Другими словами, решим задачу стабилизации с заданной точностью системы вида
(2.5)
${{\dot {e}}_{2}}(t) = \frac{{{{a}_{{\text{2}}}}}}{{2{{x}_{2}}(t)}}{\text{[}}{{a}_{1}}q(t){{e}_{{\text{1}}}}(t) + {{a}_{3}}{{x}_{3}}(t) + {{\eta }_{1}}(t)] - {{a}_{{\text{2}}}}{{\eta }_{2}} - \frac{{\text{d}}}{{{\text{dt}}}}[sat_{{{{M}_{2}}}}^{ + }({{s}_{2}}(t))],$2. Рассматривая переменную ${{x}_{3}}(t)$ в системе (2.5) в качестве фиктивного управления, введем замену переменной:
гдеВыбор амплитуды из соотношения $0 < {{M}_{3}} \leqslant {{a}_{3}}{{X}_{3}}$ в результате решения задачи стабилизации переменной ${{e}_{3}}(t)$ обеспечивает ограничение ${{x}_{3}}(t) \in [0,{{X}_{3}}]$.
3. После подстановки (2.6) в (2.5) имеем
(2.7)
${{\dot {e}}_{2}}(t) = \frac{{{{a}_{{\text{2}}}}}}{{2{{x}_{2}}(t)}}[{{a}_{1}}q(t){{e}_{{\text{1}}}}(t) + {{e}_{3}}(t) + sat_{{{{M}_{3}}}}^{ + }\left( {{{s}_{3}}(t)} \right) + {{\eta }_{1}}(t)] - {{a}_{{\text{2}}}}{{\eta }_{2}} - \frac{{\text{d}}}{{{\text{dt}}}}[sat_{{{{M}_{2}}}}^{ + }\left( {{{s}_{2}}(t)} \right)].$4. При попадании в линейную зону система (2.7) описывается уравнением вида
(2.8)
${{\dot {e}}_{2}}(t) = \frac{{{{a}_{{\text{2}}}}}}{{2{{x}_{2}}(t)}}( - {{k}_{2}}{{e}_{{\text{2}}}}(t) + {{e}_{3}}(t)).$Таким образом, решена задача стабилизации переменной ${{e}_{{\text{2}}}}(t)$ в окрестности нуля $\left| {{{e}_{{\text{2}}}}(t)} \right| \leqslant {{{{\Delta }}}_{2}} = {{{{\Delta }}}_{3}}{\text{/}}{{k}_{{\text{2}}}}$ в предположении, что на следующем этапе будет обеспечено соотношение $\left| {{{e}_{{\text{3}}}}(t)} \right| \leqslant {{{{\Delta }}}_{3}}$.
5. Выбор амплитуды и коэффициента усиления функции $sat_{{{{M}_{3}}}}^{ + }\left( {{{s}_{3}}(t)} \right)$ с целью обеспечения попадания переменной ${{s}_{3}}(t)$ в линейную зону определяется аналогично первому этапу.
Запишем уравнение, описывающее поведение переменной ${{s}_{3}}(t)$:
(2.9)
${{\dot {s}}_{{\text{3}}}}(t) = {{f}_{2}}(t) - \frac{{{{k}_{{\text{2}}}}{{a}_{{\text{2}}}}}}{{2{{x}_{2}}(t)}}[sat_{{{{M}_{3}}}}^{ + }({{s}_{3}}(t)) + {{\varphi }_{2}}(t)],$Положим далее $\left| {{{f}_{2}}(t)} \right| \leqslant {{F}_{2}},$ $ - {{\varphi }_{2}}(t) \in {\text{[}}{{\Phi }_{{21}}},{{\Phi }_{{22}}}],$ ${{F}_{2}},{{\Phi }_{{21}}},{{\Phi }_{{22}}} = {\text{const}} > {\text{0}}$.
По аналогии с первым этапом выбор ${{M}_{{\text{3}}}} > {{\Phi }_{{22}}} + 2{{X}_{{22}}}{{F}_{2}}{\text{/}}({{k}_{2}}{{a}_{{\text{2}}}})$ и ${{k}_{2}} > 2{{X}_{{22}}}{{F}_{{\text{2}}}}{\text{/}}({{a}_{2}}{{\Phi }_{{{\text{21}}}}})$ гарантирует попадание переменной ${{s}_{3}}(t)$ в линейную зону ${{s}_{3}}(t) \in {\text{[0,}}\,{{M}_{{\text{3}}}}{\text{]}}$.
Этап 3.
1. Обеспечим попадание переменной ${{e}_{{\text{3}}}}(t)$ из (2.6) в заданную окрестность нуля $\left| {{{e}_{{\text{3}}}}(t)} \right| \leqslant {{{{\Delta }}}_{3}}$, т.е. решим задачу стабилизации с заданной точностью системы вида
(2.10)
${{\dot {e}}_{3}}(t) = {{a}_{{\text{3}}}}b( - {{x}_{3}}(t) + m{{x}_{4}}(t)) - \frac{{\text{d}}}{{{\text{dt}}}}[sat_{{{{M}_{3}}}}^{ + }\left( {{{s}_{3}}(t)} \right){\text{]}}{\text{.}}$2. Рассматриваем переменную ${{x}_{4}}(t)$ в системе (2.10) в качестве фиктивного управления, введем замену переменной
гдеВыбор амплитуды из соотношения $0 < {{M}_{4}} \leqslant m{{X}_{4}}$ в результате решения задачи стабилизации переменной ${{e}_{4}}(t)$ обеспечивает ограничение ${{x}_{4}}(t) \in [0,{{X}_{4}}]$.
3. После подстановки (2.11) в (2.10) имеем
(2.12)
${{\dot {e}}_{3}}(t) = {{a}_{{\text{3}}}}b[ - {{x}_{3}}(t) + {{e}_{4}}(t) + sat_{{{{M}_{4}}}}^{ + }\left( {{{s}_{4}}(t)} \right)] - \frac{{\text{d}}}{{{\text{dt}}}}[sat_{{{{M}_{3}}}}^{ + }\left( {{{s}_{3}}(t)} \right)].$4. При функционировании в линейной зоне система (2.12) стабилизируется с заданной точностью
(2.13)
${{\dot {e}}_{3}}(t) = {{a}_{{\text{3}}}}b( - {{k}_{{\text{3}}}}{{e}_{3}}(t) + {{e}_{4}}(t)).$Действительно, $\left| {{{e}_{{\text{3}}}}(t)} \right| \leqslant {{{{\Delta }}}_{3}} = {{{{\Delta }}}_{4}}{\text{/}}{{k}_{{\text{3}}}}$ в предположении, что $\left| {{{e}_{4}}{\text{(}}t{\text{)}}} \right| \leqslant {{\Delta }_{4}} = {\text{const}}$ будет обеспечено на следующем этапе.
5. Выбор амплитуды и коэффициента усиления функции $sat_{{{{M}_{4}}}}^{ + }\left( {{{s}_{4}}(t)} \right)$ с целью попадания переменной ${{s}_{4}}(t)$ в линейную зону определяется аналогично первому этапу.
Запишем уравнение, описывающее поведение переменной ${{s}_{4}}(t)$
(2.14)
${{\dot {s}}_{{\text{4}}}}(t) = {{f}_{3}}(t) - {{k}_{3}}{{a}_{{\text{3}}}}bsat_{{{{M}_{4}}}}^{ + }\left( {{{s}_{4}}(t)} \right) + {{\varphi }_{3}}(t)),$Положим далее $\left| {{{f}_{3}}(t)} \right| \leqslant {{F}_{3}},$ $ - {{\varphi }_{3}}(t) \in {\text{[}}{{\Phi }_{{31}}},{{\Phi }_{{32}}}],$ ${{F}_{3}},{{\Phi }_{{31}}},{{\Phi }_{{32}}} = {\text{const}} > {\text{0}}$.
Выбор ${{M}_{{\text{4}}}} > {{\Phi }_{{32}}} + {{F}_{3}}{\text{/}}({{k}_{3}}{{a}_{3}}b)$ и ${{k}_{3}} > {{F}_{{\text{3}}}}{\text{/}}({{a}_{3}}b{{\Phi }_{{{\text{31}}}}})$ по аналогии с первым этапом гарантирует попадание переменной ${{s}_{4}}(t)$ в линейную зону ${{s}_{4}}(t) \in {\text{[0,}}\,{{M}_{{\text{4}}}}{\text{]}}$.
Этап 4.
1. Рассматривается динамическое уравнение относительно переменной системы ${{e}_{{\text{4}}}}(t)$ из (2.11) вида
(2.15)
${{\dot {e}}_{{\text{4}}}}(t) = m{{a}_{{21}}}({{a}_{{22}}}{{x}_{5}}(t) - {{m}_{L}}) - \frac{{\text{d}}}{{{\text{dt}}}}sat_{{{{M}_{4}}}}^{ + }({{s}_{4}}(t)).$2. В выражении (2.15) в качестве фиктивного управления выступает ток якоря ${{x}_{{\text{5}}}}(t)$, положим его равным
гдеВыбор амплитуды из соотношения $\left| {{{M}_{5}}} \right| \leqslant {{a}_{{{\text{22}}}}}{{X}_{5}}$ в результате решения задачи стабилизации переменной ${{e}_{5}}(t)$ обеспечивает ограничение $\left| {{{x}_{5}}} \right| \leqslant {{X}_{5}}$.
3. После подстановки (2.16) в (2.15) имеем
(2.17)
${{\dot {e}}_{{\text{4}}}}(t) = m{{a}_{{21}}}[{{e}_{5}}(t) + sa{{t}_{{{{M}_{5}}}}}({{s}_{5}}(t)) - {{m}_{L}}] - \frac{{\text{d}}}{{{\text{dt}}}}sat_{{{{M}_{4}}}}^{ + }({{s}_{4}}(t)).$4. При функционировании в линейной зоне система (2.17) стабилизируется с заданной точностью
где выбор параметра ${{k}_{{\text{4}}}} > 0$ определяет сходимость переменной данной подсистемы в заданную окрестность нуля, определяемую выражением $\left| {{{e}_{4}}(t)} \right| \leqslant {{{{\Delta }}}_{5}}{\text{/}}{{k}_{4}}$ в предположении, что выполняется условие $\left| {{{e}_{5}}(t)} \right| \leqslant {{{{\Delta }}}_{5}} = {\text{const}}$, обеспечивающееся на последнем этапе процедуры.5. Выбор амплитуды ${{M}_{{\text{5}}}} > 0$ из (2.16), обеспечивающей попадание переменной e4 в окрестность нуля, определяется на основе второго метода Ляпунова: $V = 0.5s_{5}^{2}(t)$.
Запишем производную функции ${{s}_{5}}(t)$ в виде
(2.19)
${{\dot {s}}_{5}}(t) = {{f}_{4}}(t) - {{k}_{4}}m{{a}_{{21}}}(sa{{t}_{{{{M}_{5}}}}}({{s}_{5}}(t)) + {{\varphi }_{4}}(t)),$Требование $\dot {V} = {{s}_{5}}(t){\text{[}}{{f}_{4}}(t) - {{k}_{4}}m{{a}_{{21}}}sa{{t}_{{{{M}_{5}}}}}({{s}_{5}}(t)) + {{\varphi }_{4}}(t))] < 0$ вне линейной зоны $\left| {{{s}_{{\text{5}}}}(t)} \right| \geqslant {{M}_{5}}$ дает производную функции Ляпунова вида $\dot {V} = {{s}_{5}}(t){\text{[}}{{f}_{4}}(t) - {{k}_{4}}m{{a}_{{21}}}{\text{sig}}{{{\text{n}}}_{{{{M}_{5}}}}}({{s}_{5}}(t)) + {{\varphi }_{4}}(t))] < 0$, откуда следует выражение для выбора амплитуды ${{M}_{{\text{5}}}} > {{\Phi }_{4}} + {{F}_{4}}{\text{/}}({{k}_{4}}m{{a}_{{21}}})$, где $\left| {{{f}_{4}}(t)} \right| \leqslant {{F}_{4}} = {\text{const}}$, $\left| {{{\varphi }_{4}}(t)} \right| \leqslant {{\Phi }_{4}}$ = const.
Этап 5.
Решается задача стабилизации переменой (2.16), описываемой уравнением
(2.20)
${{\dot {e}}_{5}}(t) = {{a}_{{22}}}{{a}_{{32}}}\left\{ {{{u}_{2}}(t) - \frac{{{{a}_{{22}}}}}{m}[{{e}_{4}}(t) + sat_{{{{M}_{4}}}}^{ + }({{s}_{4}}(t)] - \frac{{{{a}_{{31}}}}}{{{{a}_{{22}}}}}[{{e}_{5}}(t) + sa{{t}_{{{{M}_{5}}}}}({{s}_{5}}(t)]} \right\} - \frac{{\text{d}}}{{{\text{dt}}}}sa{{t}_{{{{M}_{5}}}}}({{s}_{5}}(t)).$Выберем управление в виде разрывной функции ввиду физических соображений:
При условии выполнения условия существования скользящего режима
Для наглядности выпишем уравнения движения замкнутой системы (1.3), (1.4) в новых переменных ${{e}_{i}}(t) = 0,$ $i = \overline {1,5} $, задаваемых уравнениями (1.5), (2.1), (2.6), (2.11), (2.16) при попадании компонент вектора в новых переменных в линейные зоны соответствующих sat-функций и возникновении скользящего режима по плоскости ${{e}_{5}}(t) = 0$, согласно уравнениям (2.3), (2.8), (2.13), (2.18):
(2.22)
$\begin{gathered} {{{\dot {e}}}_{1}}(t) = - ({{a}_{{\text{1}}}}q(t) + {{k}_{1}}){{e}_{1}}(t) + {{e}_{2}}(t),\quad {{{\dot {e}}}_{2}}(t) = \frac{{{{a}_{{\text{2}}}}}}{{2{{x}_{2}}(t)}}( - {{k}_{2}}{{e}_{{\text{2}}}}(t) + {{e}_{3}}(t)), \\ {{{\dot {e}}}_{3}}(t) = {{a}_{{\text{3}}}}b( - {{k}_{{\text{3}}}}{{e}_{3}}(t) + {{e}_{4}}(t)),\quad {{{\dot {e}}}_{{\text{4}}}}(t) = m{{a}_{{21}}}( - {{k}_{4}}{{e}_{4}}(t) + {{e}_{5}}(t)),\quad {{e}_{5}}(t) = 0. \\ \end{gathered} $В системе (2.22) осуществляется декомпозиция снизу вверх общего движения на последовательно сходящиеся в ноль подсистемы первого порядка: ${{е}_{5}}(t) = 0 \Rightarrow {{e}_{{\text{4}}}}(t) \to 0$ ⇒ ${{e}_{{\text{3}}}}(t) \to 0$ ⇒ ⇒ ${{e}_{{\text{2}}}}(t) \to 0 \Rightarrow {{e}_{1}}(t) \to 0$, что и решает поставленную задачу регулирования выходной переменной.
В следующем разделе решается задача оценивания компонент вектора состояния и возмущений в системе (1.3), (1.4) с использованием каскадного метода синтеза наблюдателя в рамках методов систем с глубокими обратными связями и скользящими режимами.
3. Наблюдатель вектора состояния и внешних возмущений. 3.1. Наблюдатель вектора состояния и возмущений. Относительно модели объекта управления (1.3), (1.4) предполагается, что для измерения доступны переменные ${{e}_{1}}(t)$, ${{x}_{{\text{2}}}}(t)$ и ${{x}_{{\text{5}}}}(t)$, построим наблюдатель вида
(3.1)
$\begin{gathered} {{{\dot {z}}}_{1}}(t) = {{a}_{2}}{{z}_{2}}(t) + {{\varepsilon }_{1}}(t){{l}_{1}}, \\ {{{\dot {z}}}_{2}}(t) = \frac{{\text{1}}}{{2{{x}_{2}}(t)}}{{a}_{3}}{{z}_{3}}(t) + {{\varepsilon }_{2}}(t){{l}_{2}}, \\ {{{\dot {z}}}_{3}}(t) = - b{{z}_{3}}(t) + bm{{z}_{4}}(t) + {{\upsilon }_{3}}({\text{t}}), \\ {{{\dot {z}}}_{4}}(t) = {{a}_{{21}}}{{a}_{{22}}}{{x}_{5}}(t) + {{\upsilon }_{4}}(t), \\ {{{\dot {z}}}_{5}}(t) = {{a}_{{32}}}({{u}_{2}}(t) - {{a}_{{22}}}{{z}_{4}}(t) - {{a}_{{31}}}{{x}_{5}}(t)) + {{\upsilon }_{5}}(t), \\ \end{gathered} $Запишем систему в невязках ${{\varepsilon }_{i}}(t) = {{x}_{i}}(t) - {{z}_{i}}(t),$ $i = \overline {1,5} $, с учетом (1.3)–(1.4) и (3.1):
(3.2)
$\begin{gathered} {{{\dot {\varepsilon }}}_{1}}(t) = {{a}_{2}}{{\varepsilon }_{2}}(t) - \eta _{1}^{*}(t) - {{l}_{1}}{{\varepsilon }_{1}}(t), \\ {{{\dot {\varepsilon }}}_{2}}(t) = \frac{{\text{1}}}{{2{{x}_{2}}(t)}}{\text{[}}{{a}_{3}}{{\varepsilon }_{3}}(t) + \eta _{1}^{*}(t)] - {{\eta }_{2}}(t) - {{l}_{2}}{{\varepsilon }_{2}}(t), \\ {{{\dot {\varepsilon }}}_{3}}(t) = - b{{\varepsilon }_{3}}(t) + bm{{\varepsilon }_{4}}(t) - {{\upsilon }_{3}}(t), \\ {{{\dot {\varepsilon }}}_{4}}(t) = - {{a}_{{{\text{21}}}}}{{m}_{L}} - {{\upsilon }_{4}}(t), \\ {{{\dot {\varepsilon }}}_{5}}(t) = - {{a}_{{32}}}{{a}_{{22}}}{{\varepsilon }_{4}}(t) - {{\upsilon }_{5}}(t), \\ \end{gathered} $Дальнейший анализ и синтез наблюдателя вектора состояния и возмущений (3.1) основывается на следующем результате.
Лемма [21]. Пусть дана система $\dot {\varepsilon }(t) = - l\varepsilon (t) + \eta (t)$, $l,N,\bar {N} = {\text{const}} > 0$, $\left| {\eta (t)} \right| \leqslant N,$ $\left| {\dot {\eta }(t)} \right| \leqslant \bar {N}$. Тогда через конечный промежуток времени ${{t}_{{\text{1}}}} \geqslant 0$ справедливы оценки:
Ниже представлена поэтапная процедура каскадного синтеза наблюдателя состояния и возмущений применительно к системе (1.3) и (1.4) на основе теории скользящих режимов и глубоких обратных связей.
1. Выбором корректирующего воздействия в последней подсистеме (3.2) в виде ${{\upsilon }_{5}}(t)\, = \,M{\text{sign}}({{\varepsilon }_{5}}(t))$ (M = ${\text{const}}\, > \,\left| {{{a}_{{32}}}{{a}_{{22}}}{{\varepsilon }_{4}}(t)} \right|$) обеспечивается скользящий режим по прямой ${{\varepsilon }_{5}}(t)$ = 0. При этом среднее значение разрывного сигнала равно ${{\upsilon }_{{5eq}}}(t) = - {{a}_{{32}}}{{a}_{{22}}}{{\varepsilon }_{4}}(t)$.
2. Из последнего выражения имеем ${{\varepsilon }_{{\text{4}}}}(t) = - {{\upsilon }_{{5eq}}}(t){\text{/}}({{a}_{{32}}}{{a}_{{22}}})$, с учетом которой построим корректирующее воздействие для четвертой подсистемы (3.2) в виде ${{\upsilon }_{4}} = {{l}_{{\text{4}}}}( - {{\upsilon }_{{5eq}}}(t){\text{/}}({{a}_{{32}}}{{a}_{{22}}})) = {{l}_{4}}{{\varepsilon }_{4}},$ ${{l}_{4}} = {\text{const}} > 0$. После подстановки корректирующего воздействия четвертая подсистема примет вид ${{\dot {\varepsilon }}_{4}}(t) = - {{l}_{4}}{{\varepsilon }_{4}}(t) - {{a}_{{21}}}{{m}_{L}}$. В предположении $\left| {{{m}_{L}}} \right| \leqslant {{M}_{L}}{\text{,}}$ $\left| {{{{\dot {m}}}_{L}}} \right| \leqslant {{\bar {M}}_{L}},$ ${{M}_{L}},{{\bar {M}}_{L}} = {\text{const}}$, согласно лемме, обеспечивается стабилизация переменной ${{\varepsilon }_{4}}$ с заданной точностью $\left| {{{\varepsilon }_{4}}(t)} \right| \leqslant {{a}_{{{\text{21}}}}}{{M}_{L}}{\text{/}}{{l}_{{\text{4}}}} = {{{{\Delta }}}_{4}},$ ${\text{lim}}{{{{\Delta }}}_{4}} = 0$ при ${{l}_{{\text{4}}}} \to \infty $, т.е. получаем оценку переменной ${{x}_{4}}(t)$: ${{\varepsilon }_{4}}(t) \to 0 \Rightarrow {{z}_{4}}(t) \approx {{x}_{4}}(t)$. Кроме того, из соотношения леммы $\left| { - {{l}_{4}}{{\varepsilon }_{4}}(t) - {{a}_{{21}}}{{m}_{L}}} \right| \leqslant {{a}_{{{\text{21}}}}}{{\bar {M}}_{L}}{\text{/}}{{l}_{4}} = {{{{\bar {\Delta }}}}_{4}}{\text{,}}$ $\lim {{{{\bar {\Delta }}}}_{4}} = 0$ при ${{l}_{{\text{4}}}} \to \infty $ получаем оценку момента сопротивления с заданной точностью:
Отметим что, согласно лемме, при ${{m}_{L}} = {\text{const,}}$ ${{\dot {m}}_{L}} = 0 \Rightarrow {{{{\bar {\Delta }}}}_{4}} \to 0$ оценка момента нагрузки сходится к истинному значению асимптотически:
3. Используя исходную модель объекта управления (1.1), синтезируем вспомогательный автономный наблюдатель первого порядка состояния:
4. Рассмотрим вторую подсистему (3.2), которая при ${{\varepsilon }_{3}}(t) = 0$ примет вид
(3.3)
${{\dot {\varepsilon }}_{2}}(t) = \frac{{\text{1}}}{{2{{x}_{2}}(t)}}\eta _{1}^{*}(t) - {{\eta }_{2}}(t) - {{l}_{2}}{{\varepsilon }_{2}}(t).$Система (3.3) в обозначениях леммы записывается как
В предположении $\left| {\eta {\kern 1pt} *(t)} \right| \leqslant N{\kern 1pt} *,$ $\left| {\dot {\eta }{\kern 1pt} *(t)} \right| \leqslant \bar {N}{\kern 1pt} *;$ $N{\kern 1pt} *,{{\bar {N}}^{ \cdot }} = {\text{const}} > 0$ справедливы соотношения из леммы: существует такой коэффициент ${{l}_{{\text{2}}}} > 0$, что $\left| {{{\varepsilon }_{2}}(t)} \right| \leqslant {{{{\Delta }}}_{{\text{2}}}} = N{\kern 1pt} *{\text{/}}{{l}_{2}}$, $\left| {\dot {\varepsilon }(t)} \right| \leqslant {{{{\bar {\Delta }}}}_{{\text{2}}}} = \bar {N}{\kern 1pt} {\text{*/}}{{l}_{2}}$, ${{\Delta }_{2}},\;{{\bar {\Delta }}_{2}}$ – наперед заданные числа, $ - {{l}_{{\text{2}}}}{{\varepsilon }_{2}}(t) + \eta {\kern 1pt} *(t) = {{\bar {\delta }}_{2}}({\text{t}}) \leqslant {{{{\bar {\Delta }}}}_{2}}$ и, следовательно, переменная l2ε2(t) = = $\eta {\kern 1pt} {\text{*}}(t) + {{\bar {\delta }}_{2}}(t)$ служит оценкой возмущения с наперед заданной точностью.
5. С учетом ${{\varepsilon }_{2}}(t) \to 0$ первое уравнение системы (3.2) примет вид ${{\dot {\varepsilon }}_{1}}(t) = - \eta _{1}^{*}(t) - {{l}_{1}}{{\varepsilon }_{1}}(t)$, где в предположении ${\text{|}}\eta _{1}^{*}(t){\text{|}} \leqslant N_{1}^{*},$ ${\text{|}}\dot {\eta }_{1}^{*}(t){\text{|}} \leqslant \bar {N}_{1}^{*};$ $N_{1}^{*},\bar {N}_{1}^{*} = {\text{const}} > 0$ выбором коэффициента ${{l}_{1}} > {\text{0}}$ обеспечивается стабилизация $\left| {{{\varepsilon }_{1}}(t)} \right| \leqslant N_{1}^{*}{\text{/}}{{l}_{1}} = {{{{\Delta }}}_{1}}$, при ${{l}_{1}} \to \infty \Rightarrow {{\Delta }}{{\,}_{1}} \to 0 \Rightarrow {{z}_{1}}(t) \to {{e}_{1}}(t)$. Согласно лемме, с учетом $\left| {{{{\dot {\varepsilon }}}_{1}}(t)} \right| \leqslant \bar {N}_{1}^{*}{\text{/}}{{l}_{1}} = {{{{\bar {\Delta }}}}_{1}}$ также может быть получена оценка внешнего возмущения с заданной точностью ${{l}_{{\text{1}}}}{{\varepsilon }_{1}}(t) = - \eta _{1}^{*}(t) + {{\bar {\delta }}_{1}}(t){\text{,}}$ ${{\bar {\delta }}_{1}}(t) \leqslant {{\bar {\Delta }}_{1}}$.
В результате синтеза наблюдателя вектора состояния и возмущений (3.1) имеются оценки с заданной точностью переменных вектора состояния системы (1.3), (1.4) ${{z}_{i}}(t) \to x{}_{i}(t),$ $i = \overline {1,5} $, причем вместо оценок переменных ${{z}_{1}}(t) \approx {{e}_{1}}(t)$ и ${{z}_{2}}(t) \approx {{x}_{2}}(t)$ можно использовать доступные для измерения переменные ${{e}_{1}}(t)$ и ${{x}_{2}}(t)$.
Кроме того, имеем оценки внешних возмущений с заданной точностью:
момента сопротивления на валу ДПТ на втором этапе: ${{m}_{L}} \approx - {{\upsilon }_{4}}{\text{/}}{{a}_{{21}}}$;
на четвертом этапе процедуры получена оценка возмущения: η*(t): ${{l}_{{\text{2}}}}{{\varepsilon }_{2}}(t) = - \eta {\text{*}}(t) + {{\bar {\delta }}_{2}}(t)$, ${{l}_{{\text{2}}}}{{\varepsilon }_{2}}(t) \approx \eta {\kern 1pt} {\text{*}}(t)$;
на пятом этапе процедуры найдена оценка возмущения $\eta _{1}^{*}(t{\text{)}}$: ${{l}_{{\text{1}}}}{{\varepsilon }_{1}}(t) = - \eta _{1}^{*}(t) + {{\bar {\delta }}_{1}}(t)$, ${{l}_{{\text{1}}}}{{\varepsilon }_{1}}(t) \approx - \eta _{1}^{*}(t)$;
из выражения $\eta {\kern 1pt} * = \eta _{1}^{*}(t){\text{/(}}2{{x}_{2}}(t){\text{)}} - {{\eta }_{2}}(t)$ четвертого этапа находится возмущение
3.2. Синтез наблюдателя-дифференциатора. Как следует из разд. 2, для формирования управления (2.21) требуется информация о положении задвижки $q(t)$ и ее четырех первых производных. Оценка положения задвижки найдена выше. Для получения оценок ее первых четырех производных построим дополнительный наблюдатель-дифференциатор.
Изложим кратко процедуру синтеза наблюдателя-дифференциатора.
1. Построим фильтр с устойчивой собственной динамикой:
(3.4)
${{\dot {\xi }}_{i}}(t) = {{\xi }_{{i + 1}}}(t) + q(t),\quad i = \overline {1,4} ,\quad {{\dot {\xi }}_{5}}(t) = {{c}^{T}}\xi (t) + q(t),$2. Представим систему (3.4) в каноническом виде
(3.5)
${{\dot {\bar {\xi }}}_{i}}(t) = {{\bar {\xi }}_{{i + 1}}}(t),\quad i = \overline {1,4} ,\quad {{\dot {\bar {\xi }}}_{5}}(t) = {{c}^{T}}\xi (t) + {{\bar {\xi }}_{6}}{\text{(t),}}$(3.6)
$\begin{gathered} {{{\bar {\xi }}}_{1}}(t) = {{\xi }_{1}}(t), \\ {{{\bar {\xi }}}_{2}}(t) = {{\xi }_{2}}(t) + q(t), \\ {{{\bar {\xi }}}_{3}}(t) = {{\xi }_{3}}(t) + q(t) + \dot {q}(t), \\ {{{\bar {\xi }}}_{4}}(t) = {{\xi }_{4}}(t) + q(t) + \dot {q}(t) + \ddot {q}(t), \\ {{{\bar {\xi }}}_{5}}(t) = {{\xi }_{5}}(t) + q(t) + \dot {q}(t) + \ddot {q}(t) + \dddot q(t), \\ {{{\bar {\xi }}}_{6}}(t) = {{c}^{T}}\xi + q(t) + \dot {q}(t) + \ddot {q}(t) + \dddot q(t) + {{q}^{{(4)}}}(t). \\ \end{gathered} $3. Построим наблюдатель вектора состояния ${{\bar {\xi }}^{T}}(t) = ({{\bar {\xi }}_{1}}(t),...,{{\bar {\xi }}_{5}}(t))$ и сигнала ${{\bar {\xi }}_{6}}(t)$ применительно к системе (3.5):
(3.7)
${{\dot {\hat {\xi }}}_{i}}(t) = {{\hat {\xi }}_{{i + 1}}}(t) + {{{v}}_{i}},\quad i = \overline {1,4} ,\quad {{\dot {\hat {\xi }}}_{5}}(t) = {{c}^{T}}\hat {\xi }(t) + {{{v}}_{5}},\quad {{\hat {\xi }}^{T}}(t) = ({{\hat {\xi }}_{1}}(t),...,{{\hat {\xi }}_{5}}(t)).$4. Запишем уравнения (3.6) и (3.7) в невязках ${{\bar {\varepsilon }}_{{\text{i}}}}(t) = {{\bar {\xi }}_{i}}(t) - {{\hat {\xi }}_{i}}(t)$:
(3.8)
${{\dot {\bar {\varepsilon }}}_{{\text{i}}}}(t) = {{\bar {\varepsilon }}_{{i + 1}}}(t) - {{{v}}_{i}},\quad i = \overline {1,4} ,\quad {{\dot {\bar {\varepsilon }}}_{{\text{5}}}}(t) = {{c}^{T}}\bar {\varepsilon }(t) + {{\bar {\xi }}_{6}}(t) - {{{v}}_{5}},\quad {{\bar {\varepsilon }}^{T}}(t) = ({{\bar {\varepsilon }}_{1}}(t),...,{{\bar {\varepsilon }}_{5}}(t)).$5. В работах [24, 25] показано, что выбор корректирующих воздействий в наблюдателе (3.7) в классе линейных функций с насыщением по иерархическому принципу
Действительно, в предположениях $\left| {{{{\bar {\varepsilon }}}_{i}}(t)} \right| \leqslant {{E}_{i}}{\text{,}}$ $\left| {{{{\dot {\bar {\varepsilon }}}}_{i}}(t)} \right| \leqslant {{E}_{i}}{\text{,}}$ ${{\bar {E}}_{i}} = {\text{const}}$ и $\left| {\bar {\xi }(t)} \right| \leqslant {{E}_{{\text{6}}}} = {\text{const}}$ опишем схематично процедуру стабилизации системы (3.8).
1. В первой подсистеме ${{\dot {\bar {\varepsilon }}}_{1}}({\text{t}}) = {{\bar {\varepsilon }}_{2}}(t) - {{L}_{1}}sat({{l}_{1}}{{\bar {\varepsilon }}_{1}}(t))$ при выборе амплитуды ${{L}_{1}} > \left| {{{{\bar {\varepsilon }}}_{{\text{2}}}}(t)} \right|$ переменная ${{\bar {\varepsilon }}_{1}}(t)$ за конечное время оказывается в линейной зоне и имеет место: ${{\dot {\bar {\varepsilon }}}_{1}}({\text{t}}) = {{\bar {\varepsilon }}_{2}}(t) - {{l}_{1}}{{\bar {\varepsilon }}_{1}}(t)$. Согласно лемме, выполняются соотношения $\left| {{{{\bar {\varepsilon }}}_{1}}(t)} \right| \leqslant {{E}_{2}}{\text{/}}{{l}_{1}}$, $\left| {{{{\bar {\varepsilon }}}_{2}}(t) - {{l}_{1}}{{{\bar {\varepsilon }}}_{1}}(t)} \right| \leqslant {{\bar {E}}_{2}}{\text{/}}{{l}_{1}}$ и с ростом коэффициента усиления стабилизируется с заданной точностью переменная ${{\bar {\varepsilon }}_{1}}(t) \approx 0$. В итоге имеем оценку с заданной точностью переменной ${{\bar {\varepsilon }}_{2}}(t) \approx {{l}_{1}}{{\bar {\varepsilon }}_{1}}(t)$.
Опишем первый пункт логической схемой:
2. В дальнейшем на последующих этапах $i = \overline {{\text{2,4}}} $ синтезируем корректирующие воздействия по следующей логической схеме:
3. Рассматривается система ${{\dot {\bar {\varepsilon }}}_{{\text{5}}}}(t) = {{c}^{T}}\bar {\varepsilon }(t) + {{\bar {\xi }}_{6}}(t) - {{L}_{5}}{\text{sat}}({{l}_{5}}{{\bar {\varepsilon }}_{5}}(t)$ и с учетом ${{\bar {\varepsilon }}_{i}}(t) \approx 0$ выбором ${{L}_{6}} > \left| {{{{\bar {\xi }}}_{6}}(t)} \right|$ обеспечивается соотношение ${{\bar {\xi }}_{6}}(t) \approx {{l}_{5}}{{\bar {\varepsilon }}_{5}}(t)$.
С использованием полученных оценок вектора состояния $\bar {\xi }(t)$ и сигнала ${{\bar {\xi }}_{6}}(t)$ находим первые четыре производные сигнала $q(t)$, решая последовательно сверху вниз систему уравнений (3.6).
Таким образом, для формирования управления (2.21) вместо недоступных для измерения компонент вектора состояния и возмущений в системе (1.3), (1.4) следует использовать полученные в данном разделе оценки.
4. Численное моделирование. Результаты численного моделирования проводились в системе MATLAB–Simulink. При моделировании системы (1.4)–(1.5), наблюдателя (3.1) и управления (2.21) были выбраны параметры из табл. 1.
Таблица 1.
Параметры модели объекта управления и обратной связи
| Модель парогенератора: ${{k}_{s}} = 2.41,\,{{k}_{\mu }} = 0.25,\,{{C}_{n}} = 2.78,\,{{C}_{b}} = 27.767,\,{{k}_{m}} = 0.2,\,{{T}_{b}} = 150,\,\,m = {\text{3, }}q = {\text{0}}{\text{.6}}$ Модель ДПТ: ${{a}_{{21}}} = 0.5,\,\,{{a}_{{22}}} = 1.8,\,\,{{a}_{{31}}} = 0.02,\,\,{{a}_{{32}}} = 20,{{m}_{L}} = 10$ |
| Начальные условия ОУ: ${{P}_{T}}(0) = 18,{{P}_{D}}(0) = 19.27,{{D}_{Q}}(0) = 13.5,\omega (0) = 450,{{I}_{{\text{я}}}} = 0.05$ |
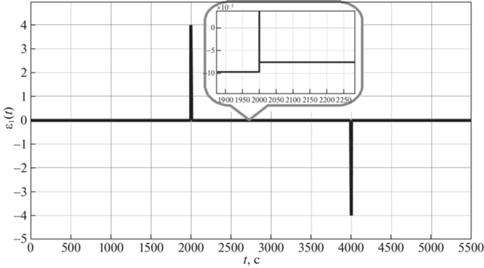
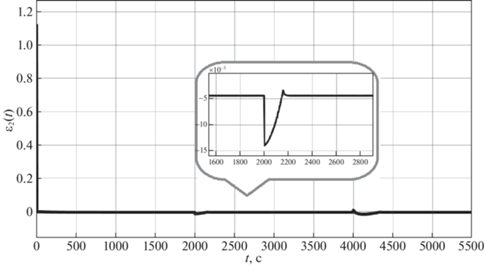
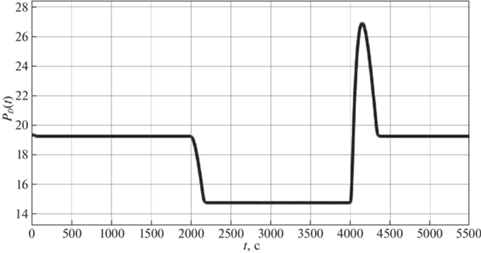
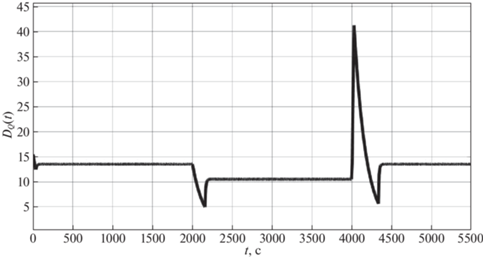
| Сценарий моделирования: ${{P}_{{Td}}}(t) = 18$ при $t \in [0,\,{{{\text{t}}}_{{\text{1}}}}) \cup {\text{[}}{{{\text{t}}}_{{\text{2}}}}{\text{,}}\infty {\text{]}}$, ${{P}_{{Td}}}(t) = 14$ при $t \in [{{t}_{1}}{\text{, }}{{{\text{t}}}_{{\text{2}}}}),\,{{t}_{1}} = 2000$, t2 = 4000 |
| Параметры наблюдателя: ${{z}_{i}}(0) = 0,\,\,\,i = \overline {1,4} $, ${{l}_{1}} = 100,{{l}_{2}} = 10,{{l}_{3}} = 0.1,{{l}_{4}} = 1,$$M = 1000$ |
| Параметры контроллера: ${{k}_{1}}\, = \,0.1,{{k}_{2}}\, = \,{\text{1}},{{k}_{3}}\, = \,{\text{50,}}\,\,{{k}_{4}}\, = \,{\text{1000,}}$${{M}_{2}} = {\text{10,}}\,\,{{M}_{3}} = {\text{30,}}$${{M}_{4}} = {\text{1000,}}$M5 = 30, ${{M}_{6}}\, = \,{\text{220}}$ |
| Физические ограничения на фазовые переменные: ${{P}_{D}} \in [0,30],{{D}_{Q}} \in {\text{[}}0,150],\omega \in [0,9000],\,\,\left| {{{I}_{{\text{я}}}}} \right| < 20,\,\,\left| {{{u}_{2}}} \right| \leqslant 220$ |
Предполагается, что в объекте для измерения доступны давление пара перед задвижкой ${{P}_{T}}(t)$, давление пара на выходе из котла – парогенератора PD и ток якоря ${{I}_{{\text{я}}}}$. Для получения полной информации о фазовых переменных объекта управления и о действующих на него внешних возмущениях был построен наблюдатель состояния (3.1), дающий оценки неизвестных сигналов с заданной точностью.
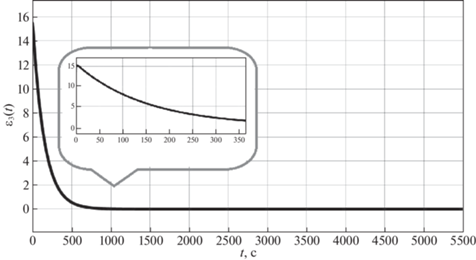
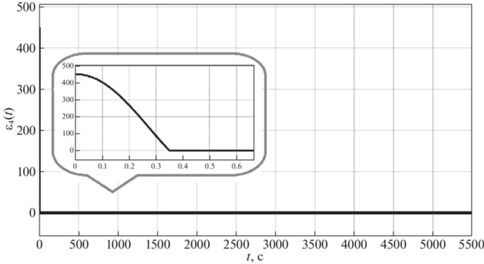
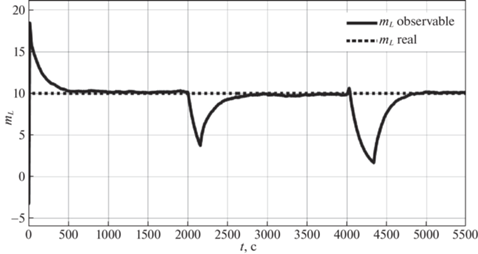
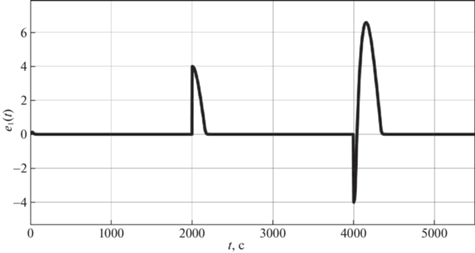
На рис. 4–8 представлены ошибки наблюдения ${{\varepsilon }_{i}} = {{x}_{i}} - {{z}_{i}},$ $i = \overline {1,5} $. На рис. 9 приведен график зависимости момента нагрузки ${{m}_{L}}{\text{(}}t{\text{)}}$ на валу ДПТ от времени, пунктирной линией обозначено истинное значение момента нагрузки из таблицы, непрерывной линией – значение, полученное с помощью наблюдателя (3.1).
На рис. 10 изображен график отклонения давления пара перед задвижкой от желаемого значения, а на рис. 11 – график давления пара на выходе из котла – парогенератора в зависимости от времени.
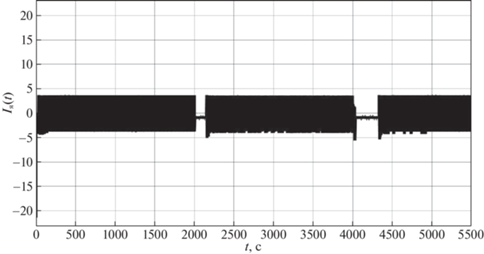
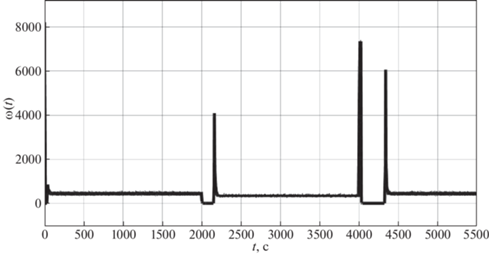
На рис. 12–15 представлены графики теплового потока печи ${{D}_{Q}}(t)$, угловой частоты вращения вала двигателя $\omega \,(t)$, тока якоря ${{I}_{{\text{я}}}}(t)$ и напряжения якоря ${{u}_{2}}(t)$ в зависимости от времени соответственно.
Заключение. Предложены алгоритмы синтеза обратной связи применительно к решению поддержанию заданного давления перед выпускной задвижкой в парогенераторе в условиях действия внешних возмущений и неполной информации о векторе состояния модели объекта управления. Существенным отличием данной работы от известных результатов решения аналогичной задачи [4, 7, 9, 11] является учет технологических ограничений на компоненты вектора состояния и управления на стадии разработки алгоритмов управления.
Использование блочного подхода позволило, с одной стороны, осуществить линеаризацию по обратной связи нелинейной модели парогенератора, а с другой стороны, обеспечить заданные ограничения на фазовые переменные и управление за счет использования в качестве локальных обратных связей линейных функций с насыщением. Для информационного обеспечения предложенных алгоритмов управления разработан комбинированный наблюдатель состояний и возмущений на основе методов систем с глубокими обратными связями и скользящими режимами, позволяющий получить оценки компонент вектора состояний и возмущений с заданной точностью.
Работоспособность предложенного алгоритма подтверждена как аналитически, так и с помощью моделирования в среде MATLAB–Simulink.
Список литературы
De Mello F.P. Boiler Models for System Performance Studies // IEEE Transaction on Power Systems. 1991. № 1. V. 6. P. 66–74.
De Mello F.P. Dynamic Models for Fossil Fueled Steam Units in Power System Studies // IEEE Transaction on Power Systems. 1991. № 2. V. 6. P. 753–761.
Johan Astrom K., D Bell R. Drum Boiler Dynamics // Automatica. 2000. № 36. P. 363–378.
Labibi B., Marquez H.J., Chen T. Decentralized Robust PI Controller Design for an Industrial Utility Boiler // Process Control. 2009. V. 19. P. 216–230.
Utkin A.V., Utkin V.A., Krasnov S.A. Synthesis of a Control System for a Waste Heat Boiler with Forced Circulation under Restrictions on Control Actions. Mathematics. 2022. V. 10. P. 1–24. https://doi.org/10.3390/ math10142397
Уткин В.А. Инвариантность и автономность в системах с разделяемыми движениями // АиТ. 2001. № 11. С. 73–94.
Utkin A.V. Synthesis of a Control System for a Steam Turbine // Automation and Remote Control. 2018. V. 79. № 12. P. 2185–2201.
Krstic M., Kokotovic P.V., Kanellakopoulos I. Nonlinear and Adaptive Control Design, 1st Edition. USA: John Wiley Sons, Inc, 1995.
Bolek W., Sasiadek J., Wisniewski T. Adaptive Backstepping Control of a Power Plant Station Model // IFAC 15-th Triennial World Congress. Barselona, Spain, 2002. P. 1650–1655.
Краснова С.А., Сиротина Т.Г., Уткин В.А. Структурный подход к робастному управлению // АиТ. 2011. № 8. С. 65–95.
Zheng K., Bentsman J., Taft C. W. Full Operating Range Robust Hybrid Control of a Coal-Fired Boiler/Turbine Unit // Dynamic Systems, Measurement, and Control. 2008. № 4. V. 130. P. 1–14.
Уткин В.А., Уткин А.В. Задача слежения в линейных системах с параметрическими неопределенностями при неустойчивой нулевой динамике // АиТ. 2014. № 9. С. 62–81.
Loukianov A.G., Dominguez J. Rivera, Sastillo-Toledo B. Robust Sliding Mode Regulation of Nonlinear Systems // Automatica. 2018. V. 89. P. 241–246.
Loukianov A.G. Robust Block Decomposition Sliding Mode Control Design // Mathematical Problems in Engineering. 2002. V. 74. P. 349–365.
Loukianov A.G., Dominguez J.R., Sastillo-Toledo B. Robust Sliding Mode Regulation of Nonlinear Systems // Automatica. 2018. V. 89. P. 241–246.
Краснова С.А., Уткин В.А., Уткин А.В. Блочный подход к анализу и синтезу инвариантных нелинейных систем слежения // АиТ. 2017. № 12. С. 26–53.
Уткин В.А. Метод разделения движений в задачах наблюдения // АиТ. 1990. № 3. С. 27–37.
Khalil H.K., Praly L. High-Gain Observers in Nonlinear Feedback Control // Int. J. Robust and Nonlinear Control. 2014. V. 24. № 6. P. 993–1015.
Маликов А.И. Синтез наблюдателей состояния и неизвестных входов для нелинейных липшицевых систем с неопределенными возмущениями // АиТ. 2018. № 3. С. 21–43.
Campo E., Monroy J., Abundis H., Chemori A., Creuze V., Torres J. A Nonlinear Controller Based on Saturation Functions with Variable Parameters to Stabilize an AUV // Int. J. Nav. 2019. V. 11. P. 211–224.
Гулюкина С.И., Уткин В.А. Управление реактором с непрерывным перемешиванием в условиях неопределенности и с учетом ограничений на фазовые переменные и управления // Проблемы управления. 2021. № 5. С. 48–59.
Antipov A., Krasnova S, Utkin V. Methods of Ensuring Invariance with Respect to External Disturbances: Overview and New Advances. Mathematics. 2021. V. 9. P. 1–20. https://doi.org/10.3390/ math9233140
Кочетов С.А., Уткин В.А. Вихревые алгоритмы в задаче управления двигателем постоянного тока // Проблемы управления. 2014. № 5. С. 20–27.
Краснов Д.В., Уткин А.В. Синтез многофункциональной системы слежения в условиях неопределенности // УБС. 2017. Вып. 69. С. 29–49.
Кокунько Ю.Г., Краснова С.А., Уткин В.А. Каскадный синтез дифференциаторов с кусочно-линейными корректирующими воздействиями // АиТ. 2021. № 7. С. 37–68.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления