Известия РАН. Теория и системы управления, 2023, № 2, стр. 3-25

Введение. Кратко напомним основные этапы исследования на экстремум [1] полинома $p(x)$, где $x = ({{x}_{1}},...,{{x}_{n}}) \in {{\mathbb{R}}^{n}}$, для определенности – на минимум (аналогичные рассуждения могут быть перенесены и на степенные ряды, а тем самым – на аналитические функции). Пусть уже найдена некоторая стационарная точка x⁽⁰⁾, для которой $p{\kern 1pt} '({{x}^{{(0)}}}) = {{0}_{{(n)}}} = (0,...,0) \in {{\mathbb{R}}^{n}}$, где $p{\kern 1pt} '({{x}^{{(0)}}})$ – вектор производных. Следующим этапом является проверка достаточного условия минимума. Для этого исследуется квадратичная форма φ(h) = $\langle p{\kern 1pt} '{\kern 1pt} '({{x}^{{(0)}}})h,h\rangle $, где $h \in {{\mathbb{R}}^{n}}$, $p{\kern 1pt} '{\kern 1pt} '({{x}^{{(0)}}})$ – квадратная матрица вторых производных порядка n, $\left\langle {x,y} \right\rangle = {{x}_{1}}{{y}_{1}} + ... + {{x}_{n}}{{y}_{n}}$ – скалярное произведение векторов $x,y \in {{\mathbb{R}}^{n}}$. Тогда если эта форма положительно определена, т.е. φ(h) > 0 для всех $h \ne {{0}_{{(n)}}}$ (фактически означает, что полином p(x) будет сильно выпуклым в окрестности x⁽⁰⁾), то x⁽⁰⁾ – точка локального минимума полинома p(x). Если $\exists {{h}^{{(0)}}} \in {{\mathbb{R}}^{n}}$: $\varphi ({{h}^{{(0)}}}) < 0$, то x⁽⁰⁾ не является точкой локального минимума. А если $\varphi (h) \geqslant 0$ для всех $h \ne {{0}_{{(n)}}}$ и одновременно $\exists {{h}^{{(0)}}} \in {{\mathbb{R}}^{n}}$: ${{h}^{{(0)}}} \ne {{0}_{{(n)}}}$, $\varphi ({{h}^{{(0)}}}) = 0$, то “требуются более тонкие методы исследования”, которые, как правило, не приводятся. Таким образом, уже в случае несильной выпуклости p(x) в окрестности x⁽⁰⁾ предлагаемые схемы “не работают”. Между тем возможны случаи с $\varphi (h) \equiv 0$, когда $p{\kern 1pt} '{\kern 1pt} '({{x}^{{(0)}}})$ – нулевая матрица, и для этих случаев также описаны как необходимые, так и достаточные условия минимума [2–4]. Если $\varphi (h) \equiv 0,$ можно лишь утверждать об отсутствии у полинома квадратичной формы (т.е. однородной формы степени 2), но при этом могут существовать какие-то другие пригодные для исследований формы, т.е. требуется обобщение понятия главной формы полинома. Для этого рассмотрим “многогранник Ньютона” [5] полинома p(x). Под обобщением понятия главной формы полинома будем понимать сумму членов полинома, соответствующих какой-нибудь грани этого многогранника. Следует отметить, что многогранники Ньютона являются инструментом для исследования широкого класса задач, например [5–8]. В частности, теория многогранников Ньютона связывает геометрию многогранников с алгебраической геометрией [8]. В разд. 5 приведены конкретные примеры задач, в которых может быть применена предложенная методика: нахождение равновесных состояний сложной системы частиц (например, молекул), использование метода наименьших квадратов для определения неизвестных параметров по набору значений параметрической функции, идентификация параметров динамических систем.

1. Носитель полинома. Многогранник Ньютона. Для дальнейшего потребуются некоторые обозначения для вектора $k \in \mathbb{Z}_{ \geqslant }^{n}$, где ${{\mathbb{Z}}_{ \geqslant }} = \mathbb{N} \cup \{ 0\} $, полинома p(x) и множества $N \subseteq \mathbb{Z}_{ \geqslant }^{n}$: x^k = = $x_{1}^{{{{k}_{1}}}}x_{2}^{{{{k}_{2}}}} \cdot \cdot \cdot x_{n}^{{{{k}_{n}}}}$; $coef(p,k) = a$ – коэффициент при члене (мономе) ax^k полинома p(x); N_p = = $\{ k \in \mathbb{Z}_{ \geqslant }^{n}\,{\text{|}}\,coef(p,k) \ne 0\} $ – носитель полинома p(x),

– N-укорочение полинома p(x).

Пример 1. Пусть n = 2, $x = ({{x}_{1}},{{x}_{2}})$, $k = (4,{\text{ }}5) \in \mathbb{Z}_{ \geqslant }^{2}$,

Тогда

Под выпуклой комбинацией точек ${{x}^{{(1)}}},...,{{x}^{{(m)}}} \in {{\mathbb{R}}^{n}}$ понимаем сумму вида ${{\lambda }_{1}}{{x}^{{(1)}}}$ + … + ${{\lambda }_{m}}{{x}^{{(m)}}}$, где ${{\lambda }_{1}},...,{{\lambda }_{m}} \geqslant 0$, ${{\lambda }_{1}} + ... + {{\lambda }_{m}} = 1$, и для любого множества $Y \subseteq {{\mathbb{R}}^{n}}$ под его выпуклой оболочкой CoY – множество всех выпуклых комбинаций его точек. Под выпуклым многогранником (или, для краткости, просто многогранником) имеем в виду выпуклую оболочку непустого конечного множества точек ${{x}^{{(1)}}},...,{{x}^{{(m)}}} \in {{\mathbb{R}}^{n}}$, под многогранником Ньютона полинома 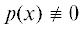– CoN_p.

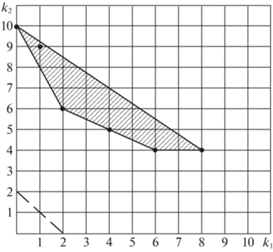
Пример 2. Многогранником Ньютона для полинома p(x) из примера 1 является множество

(см. заштрихованную область на рисунке).

Нам понадобятся следующие обозначения для произвольного множества $Y \subseteq {{\mathbb{R}}^{n}}$ [1]: affY – аффинная оболочка множества Y, LinY – несущее подпространство Y (${\text{Lin }}Y = {\text{aff }}Y - y$, где y – произвольная точка из Y), ${\text{dim }}Y = $$\dim {\text{aff }}Y = \dim {\text{Lin }}Y$– размерность Y, intY – совокупность всех внутренних точек множества $Y,$ riY – совокупность всех относительно внутренних точек множества Y.

Пусть $X \subset {{\mathbb{R}}^{n}}$ – непустое конечное множество, $Y = {\text{Co }}X$– выпуклый многогранник. Его выпуклое подмножество $C \subseteq Y$ называется гранью Y, если $\forall {{y}^{{(1)}}},{{y}^{{(2)}}} \in Y$, $\forall \alpha \in (0,{\text{ 1)}}$, в случае $\alpha {{y}^{{(1)}}} + (1 - \alpha ){{y}^{{(2)}}} \in С$ выполняется ${{y}^{{(1)}}},{{y}^{{(2)}}} \in C$. Подмножества $\emptyset $ и Y являются гранями Y. Они называются несобственными гранями, а все остальные – собственными. Точка $y \in Y$ – угловая (крайняя) точка многогранника Y, если {y} – грань. Множество угловых точек многогранника Y обозначим через extY. Нетрудно видеть, что ${\text{ext }}Y \subseteq X.$ Любая непустая грань $C \subseteq Y$ многогранника Y = CoX в свою очередь является многогранником, и при этом C = ${\text{Co(}}X \cap С)$. В дальнейшем нас будут интересовать так называемые главные квазиоднородные формы полинома p(x), являющиеся суммами его членов, которые соответствуют какой-нибудь собственной грани многогранника Ньютона CoN_p. Таким образом, каждой собственной грани C многогранника CoN_p отвечает главная квазиоднородная форма ${{p}_{{C \cap {{N}_{p}}}}}(x)$. Кроме того, если размерность CoN_p меньше n (т.е. при ${\text{int Co }}{{N}_{p}} = \emptyset $), то считаем полином p(x) одной из своих главных квазиоднородных форм. В этом случае также выполняется равенство $p(x) = {{p}_{{C \cap {{N}_{p}}}}}(x)$, но уже для несобственной грани C = CoN_p.

Пример 3. У многогранника CoN_p из примера 2 (рисунок 1) восемь собственных граней: четыре угловых точки: (2, 6), (6, 4), (0, 10), (8,4) и четыре ребра – прямолинейные отрезки, соединяющие пары угловых точек:

Следовательно, у полинома $p(x)$ из примера 1 имеется восемь квазиоднородных форм:

Заметим, что приведенное определение квазиоднородной формы дает возможность в простейших случаях (при n = 2 и иногда при n = 3) визуально выделять все квазиоднородные формы полинома. Следующее утверждение позволяет определять их аналитически.

Утверждение 1. Пусть $Y \subseteq {{\mathbb{R}}^{n}}$ – выпуклый многогранник. Тогда для любой его собственной грани C найдется вектор $A \in {{\mathbb{R}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $, такой, что $C = {\text{Arg}}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle $. Обратно: для любого вектора $A \in {{\mathbb{R}}^{n}}$ множество ${\text{Arg}}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle $ является гранью Y, а в случае $Y \ne {\text{Arg}}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle $ (если $\exists x{\kern 1pt} * \in Y$: $\left\langle {A,x{\kern 1pt} *} \right\rangle > \mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle $) – собственной гранью.

Замечание 1. Пусть мы находимся в условиях утверждения 1 и дополнительно выполняется ${\text{ext}}Y \subset {{\mathbb{Q}}^{n}}$ ($\mathbb{Q}$ – множество всех рациональных чисел). Тогда в утверждении 1 условие $A \in {{\mathbb{R}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ можно заменить на $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $. При этом для любого полинома 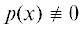верно ${\text{ext Co }}{{N}_{p}} \subseteq {{N}_{p}} \subset \mathbb{Z}_{ \geqslant }^{n}$.

Доказательство утверждения 1 и замечания 1 приведено в разд. 4 (см. утверждения 17, 18, 20).

В соответствии с утверждением 1 дадим иное (но эквивалентное предыдущему) определение главной квазиоднородной формы полинома.

Назовем полином φ(x) A-квазиоднородной формой, где $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $, если 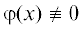, и $\exists B \in \mathbb{Z}$: $\forall k \in {{N}_{\varphi }}$ $\left\langle {A,k} \right\rangle = B$; считаем φ(x) квазиоднородной формой, если $\exists A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $, что $\varphi (x)$ является A‑квазиоднородной формой. Для полиномов p(x), q(x) пишем, что $q \preccurlyeq p$, если а) ${{N}_{q}} \subseteq {{N}_{p}}$, б) $\forall k \in {{N}_{q}}$ $coef(q,k) = coef(p,k)$. Для полиномов p(x), q(x) и вектора $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ говорим, что φ(x) – главная A-квазиоднородная форма полинома p(x), если 1) 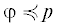; 2) ${{N}_{\varphi }} = {\text{Arg}}\mathop {\min }\limits_{k \in {{N}_{p}}} \left\langle {A,k} \right\rangle $. Полином φ(x) назовем главной квазиоднородной формой полинома p(x), если он является главной A-квазиоднородной формой этого полинома для некоторого $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $.

Утверждение 2. Пусть X – непустое конечное множество из ${{\mathbb{R}}^{n}}$, $A \in {{\mathbb{R}}^{n}}$, ${{X}_{A}} = {\text{Arg}}\mathop {\min }\limits_{x \in X} \left\langle {A,x} \right\rangle $, а ${{C}_{A}} = {\text{Arg}}\mathop {\min }\limits_{x \in {\text{Co }}X} \left\langle {A,x} \right\rangle $. Тогда ${{X}_{A}} = X \cap {{C}_{A}}$.

Доказательство. Заметим, что значение линейной функции на выпуклой комбинации конечного числа точек не превосходит минимального значения этой функции на множестве этих точек, откуда

Но тогда, очевидно, выполняется включение ${{X}_{A}} \supseteq X \cap {{C}_{A}}$. Покажем обратное включение. Пусть $x \in {{X}_{A}}$. Тогда $x \in X$, и в силу (1.1) $x \in {{C}_{A}}$, откуда $x \in X \cap {{C}_{A}}$. Утверждение 2 доказано.

Используя утверждения 1, 2, покажем эквивалентность двух определений. Пусть φ(x) – главная квазиоднородная форма полинома p(x) в соответствии со вторым определением. Тогда существует $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} ,$ для которого φ(x) является главной A-квазиоднородной формой полинома p(x), и при этом $\varphi = {{p}_{{{{N}_{\varphi }}}}}$, где N_φ = ${\text{Arg}}\mathop {\min }\limits_{k \in {{N}_{p}}} \left\langle {A,k} \right\rangle $. Пусть C_A = ${\text{Arg}}\mathop {\min }\limits_{k \in {\text{Co }}{{N}_{p}}} \left\langle {A,k} \right\rangle .$ Тогда, в силу утверждения 2, ${{N}_{\varphi }}{\text{ = }}{{C}_{A}} \cap {{N}_{p}}$, откуда $\varphi = {{p}_{{{{N}_{\varphi }}}}} = {{p}_{{{{C}_{A}} \cap {{N}_{p}}}}}$, где, в силу утверждения 1, C_A – грань CoN_p. Очевидно, что C_A может совпадать с CoN_p, т.е. являться несобственной гранью, только в случае ${\text{int Co }}{{N}_{p}} = \emptyset $.

Допустим, что φ(x) – главная квазиоднородная форма полинома p(x) в соответствии с первым определением. Тогда $\varphi (x) = {{p}_{{C \cap {{N}_{p}}}}}(x)$ для некоторой грани C многогранника CoN_p. Возможны варианты: а) C – собственная грань многогранника CoN_p; б) ${\text{int Co }}{{N}_{p}} = \emptyset $, $C = {\text{Co }}{{N}_{p}}$ (тогда C – несобственная грань ${\text{Co }}{{N}_{p}}$), $\varphi (x) = {{p}_{{C \cap {{N}_{p}}}}}(x) = p(x)$. В случае а), в силу утверждения 1, а также замечания 1, существует $A \in {{\mathbb{Z}}^{n}}{{\backslash }}{{0}_{{(n)}}}$, при котором C = ${\text{Arg}}\mathop {\min }\limits_{k \in {\text{Co }}{{N}_{p}}} \left\langle {A,k} \right\rangle $. Тогда, в силу утверждения 2, ${\text{Arg}}\mathop {\min }\limits_{k \in {{N}_{p}}} \left\langle {A,k} \right\rangle = C \cap {{N}_{p}}$. Таким образом, $\varphi (x) = {{p}_{{C \cap {{N}_{p}}}}}(x)$ является главной A-квазиоднородной формой полинома p(x). В случае б) размерность подпространства $L = H - {{k}^{{(0)}}}$, где $H = {\text{aff Co }}{{N}_{p}}$, k⁽⁰⁾ – произвольный элемент из N_p, меньше n, а следовательно, найдется вектор $e \in {{\mathbb{R}}^{n}},$ отличный от нулевого и ортогональный к L. Таким образом, $\left\langle {e,k} \right\rangle = 0$, $\forall k \in L$, откуда $\langle e,k - {{k}^{{(0)}}}\rangle = 0$, $\forall k \in H \supseteq {\text{Co}}{{N}_{p}} \supseteq {{N}_{p}}$, т.е.

а следовательно, ${{N}_{p}} = {\text{Arg}}\mathop {\min }\limits_{k \in {{N}_{p}}} \left\langle {e,k} \right\rangle $. Заметим, что системе (1.2) соответствует система линейных однородных уравнений с целыми коэффициентами. Тогда ее решение можно искать в поле рациональных чисел, т.е. считать, что координаты вектора $e \ne {{0}_{{(n)}}}$, удовлетворяющего (1.2), будут рациональными числами. Но домножив e на подходящее натуральное число λ > 0, получим, что $A = \lambda e \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $. При этом ${{N}_{p}} = {\text{Arg}}\mathop {\min }\limits_{k \in {{N}_{p}}} \left\langle {e,k} \right\rangle $, т.е. p(x) является главной A-квазиоднородной формой полинома p(x).

Замечание 2. Как будет показано в разд. 3, второе определение квазиоднородных форм позволяет строить алгоритмы их конструктивного выделения для полиномов с произвольным количеством переменных n.

Пример 4. У полинома p(x) из примера 1 выражение $x_{1}^{2}x_{2}^{6}$ – главная (1, 1)-квазиоднородная форма; $x_{1}^{6}x_{2}^{4}$ – главная (1, 3)-квазиоднородная форма; $x_{2}^{{10}}$ – главная (3, 1)-квазиоднородная форма; $ - 0.1x_{1}^{8}x_{2}^{4}$ – главная (–1, 1)-квазиоднородная форма; $x_{1}^{2}x_{2}^{6} + x_{2}^{{10}}$ – главная (2, 1)-квазиоднородная форма; $x_{1}^{2}x_{2}^{6} - 2x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4}$ – главная (1, 2)-квазиоднородная форма; $x_{1}^{6}x_{2}^{4} - 0.1x_{1}^{8}x_{2}^{4}$ – главная (0, 1)-квазиоднородная форма; $x_{2}^{{10}} - 0.1x_{1}^{8}x_{2}^{4}$ – главная (–3, –4)-квазиоднородная форма.

Замечание 3. Одна и та же квазиоднородная форма может быть главной A-квазиоднородной формой полинома при различных $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $. Например, $x_{2}^{{10}}$ является главной A-квазиоднородной формой полинома p(x) из примера 1 при $A = (3,{\text{1)}}$, а также при $A \in \{ (4,{\text{1), }}(0, - 1{\text{), }}( - 1, - 3{\text{)}}$, (1, 0)}.

Покажем теперь, каким образом квазиоднородные формы можно использовать для рассмотренной ранее задачи исследования полинома на наличие экстремума. Нам понадобятся дополнительные определения. Пусть функция f(x) определена на всем пространстве ${{\mathbb{R}}^{n}}$. Скажем, что f(x) существенно зависит от переменной x_i, если существуют две точки из ${{\mathbb{R}}^{n}}$, отличающиеся только по i-й координате, с различными значениями функции f(x) в этих точках. Функция f(x) – неотрицательная, если 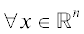$f(x) \geqslant 0,$ функция f(x) – невырожденная в слабом (сильном) смысле, если ${{x}_{{{{i}_{1}}}}} \ne 0$, …, ${{x}_{{{{i}_{r}}}}} \ne 0$ ($x_{{{{i}_{1}}}}^{2} + ... + x_{{{{i}_{r}}}}^{2} \ne 0$) $ \Rightarrow f(x) \ne 0$, где ${{x}_{{{{i}_{1}}}}},...,{{x}_{{{{i}_{r}}}}}$ – набор переменных, от которых существенно зависит f(x). Очевидно, что из невырожденности в сильном смысле следует невырожденность в слабом смысле.

Пример 5. Функции (полиномы) ${{x}_{1}}$, $x_{1}^{2}$, ${{x}_{1}}x_{2}^{3}$, ${{x}_{1}}{{x}_{2}}{{x}_{3}}$, ${{g}_{1}}({{x}_{1}},{{x}_{2}}) = x_{1}^{2} + {{({{x}_{2}} - {{x}_{1}})}^{2}}$, ${{g}_{2}}({{x}_{1}},{{x}_{2}}) = x_{1}^{4} + x_{1}^{2}{{({{x}_{2}} - {{x}_{1}})}^{2}}$, ${{g}_{3}}({{x}_{1}},{{x}_{2}},{{x}_{3}}) = x_{1}^{2} + {{(x_{2}^{3} - x_{1}^{2})}^{2}} + {{(x_{3}^{3} - x_{1}^{3} - x_{2}^{5})}^{2}}$ являются невырожденными в слабом смысле. Функции $x_{1}^{2}$, ${{g}_{1}}({{x}_{1}},{{x}_{2}})$, ${{g}_{2}}({{x}_{1}},{{x}_{2}})$, ${{g}_{3}}({{x}_{1}},{{x}_{2}},{{x}_{3}})$ – неотрицательные. Функция $x_{1}^{2}$ существенно зависит только от переменной x₁, а функция ${{g}_{3}}({{x}_{1}},{{x}_{2}},{{x}_{3}})$ – от переменных ${{x}_{1}},{{x}_{2}},{{x}_{3}}$. Кроме того, функции $x_{1}^{2}$, ${{g}_{1}}({{x}_{1}},{{x}_{2}})$, ${{g}_{3}}({{x}_{1}},{{x}_{2}},{{x}_{3}})$ являются невырожденными в сильном смысле (очевидно, что ${{g}_{1}}({{x}_{1}},{{x}_{2}}) = 0 \Rightarrow {{x}_{1}} = 0$, ${{x}_{2}} = 0$,${{g}_{3}}({{x}_{1}},{{x}_{2}},{{x}_{3}}) = 0 \Rightarrow {{x}_{1}} = 0,$ ${{x}_{2}} = 0,$ ${{x}_{3}} = 0$).

Поскольку в дальнейшем исследование неотрицательности и невырожденности будет проводиться только для полиномов, используем следующие простые утверждения.

Утверждение 3. Пусть p(x) – полином. Тогда для того, чтобы он существенно зависел от переменной x_i, где $i = \overline {1,n} $, необходимо и достаточно, чтобы $\exists k \in {{N}_{p}}$: ${{k}_{i}} > 0$.

Утверждение 4. Пусть p(x) – полином, существенно зависящий от переменной x_i, где $i = \overline {1,n} $. Тогда для любого полинома полином $q(x)p(x)$ также существенно зависит от x_i.

Утверждение 5. Пусть $p(x),\;q(x)$ – неотрицательные полиномы, невырожденные в слабом смысле. Тогда полиномы $p(x) + q(x)$, $p(x)q(x)$ также являются неотрицательными и невырожденными в слабом смысле.

Теорема [3, с. 209]. Пусть p(x) – полином, $p({{0}_{{(n)}}}) = 0$, $p{\kern 1pt} '({{0}_{{(n)}}}) = {{0}_{{(n)}}}$, и $\forall A \in {{\mathbb{N}}^{n}}$ ($\mathbb{N}$ – натуральный ряд) все главные A-квазиоднородные формы полинома p(x) являются неотрицательными и невырожденными в слабом смысле. Тогда 0_(n) – точка локального минимума p(x).

Лемма 1 [3, с. 210]. Пусть 0_(n) – точка локального минимума полинома $p(x)$,$p({{0}_{{(n)}}}) = 0$, $p{\kern 1pt} '({{0}_{{(n)}}}) = {{0}_{{(n)}}}$. Тогда $\forall A \in {{\mathbb{N}}^{n}}$ все главные A-квазиоднородные формы p(x) неотрицательны.

Замечание 4. Следует отметить, что в утверждениях теоремы и леммы 1 рассматриваются A‑квазиоднородные формы полинома p(x) не для любого вектора$A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $, а лишь для $A \in {{\mathbb{N}}^{n}}$ (в двухмерном случае это соответствует множеству граней “юго-западной” части многогранника Ньютона). Между тем во многих других задачах могут понадобиться A-квазиоднородные формы полинома p(x) для всех векторов $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $, например, при исследовании полинома на знакоопределенность в положительном ортанте (см. [9], а также приведенные там ссылки на предыдущие работы автора).

Замечание 5. В [2] описаны практически реализуемые алгоритмы выделения всех форм полинома p(x), являющихся его главными A-квазиоднородными формами хотя бы при одном $A \in {{\mathbb{N}}^{n}}$, что облегчает возможность применения теоремы и леммы 1. Краткое описание этих алгоритмов приведено в разд. 3, а также некоторые модификации этих алгоритмов для случая, когда ищутся все формы полинома p(x), представляющие собой его главные A-квазиоднородные формы при всех возможных $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $.

Замечание 6. В случае $A \in {{\mathbb{N}}^{n}}$ можно ставить задачу о нахождении совокупности главных A-квазиоднородных форм не только для полинома, но и для степенного ряда, который будет результатом разложения аналитической функции по степеням переменных в окрестности стационарной точки, поскольку в этом случае их число конечно и потребуется конечное число “первых” членов из этого разложения. При этом теорема и лемма 1 остаются в силе и для степенного ряда p(x) [4].

Замечание 7. Пусть выполняются условия теоремы, и при этом ${\text{int Co }}{{N}_{p}} = \emptyset .$ Тогда возможен случай, когда для некоторого $A \in {{\mathbb{N}}^{n}}$ главной A-квазиоднородной формой полинома p(x) является сам этот полином. Тогда неотрицательность p(x) (как одной из главных квазиоднородных форм) уже означает, что 0_(n) – точка локального (и даже глобального) минимума этого полинома (т.е. утверждение теоремы становится тривиальным). Между тем даже в случае ${\text{int Co }}{{N}_{p}} = \emptyset $ далеко не всегда существует вектор $A \in {{\mathbb{N}}^{n}}$, такой, что величина 〈A, k〉 будет постоянной при всех $k \in {{N}_{p}}$.

Проиллюстрируем, как работают приведенные утверждения для полиномов с тем же носителем, что и для полинома $p({{x}_{1}},{{x}_{2}})$ из примера 1.

Пример 6. Пусть ${{p}_{1}}({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 1.98x_{1}^{4}x_{2}^{5} + $ $x_{1}^{6}x_{2}^{4} + x_{2}^{{10}} - 10{{x}_{1}}x_{2}^{9} - 0.1x_{1}^{8}x_{2}^{4}$. Тогда (см. пример 4) главными A-квазиоднородными формами этого полинома при некоторых $A \in {{\mathbb{N}}^{2}}$ являются: а) $\varphi ({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 1.98x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4} = $ $x_{1}^{2}x_{2}^{4}[0.99{{({{x}_{2}} - x_{1}^{2})}^{2}} + 0.01(x_{2}^{2} + x_{1}^{4})]$ – главная (1, 2)-квазиоднородная форма, неотрицательная и невырожденная в слабом смысле (если ${{x}_{1}} \ne 0$, ${{x}_{2}} \ne 0$, то $\varphi ({{x}_{1}},{{x}_{2}}) > 0$); б) $x_{2}^{{10}}$ ($A = (3,{\text{1)}}$), $x_{1}^{2}x_{2}^{6} + x_{2}^{{10}}$ ($A = (2,{\text{1)}}$), $x_{1}^{2}x_{2}^{6}$ ($A = (1,{\text{1)}}$), $x_{1}^{6}x_{2}^{4}$ ($A = (1,{\text{3)}}$) – неотрицательные невырожденные в слабом смысле главные A-квазиоднородные формы (при указанных $A \in {{\mathbb{N}}^{2}}$). Пользуясь методами из разд. 3 (см. замечание 5), нетрудно показать, что оставшиеся две главные квазиоднородные формы $x_{1}^{6}x_{2}^{4} - 0.1x_{1}^{8}x_{2}^{4}$,$x_{2}^{{10}} - 0.1x_{1}^{8}x_{2}^{4}$ (см. пример 4) не являются главными A-квазиоднородными формами полинома ${{p}_{1}}({{x}_{1}},{{x}_{2}})$ ни при каких $A \in {{\mathbb{N}}^{2}}$. В силу теоремы, 0₍₂₎ – точка локального минимума полинома ${{p}_{1}}({{x}_{1}},{{x}_{2}})$.

Пусть ${{p}_{2}}({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - $ $2.01x_{1}^{4}x_{2}^{5}$ $ + \,\,x_{1}^{6}x_{2}^{4} + x_{2}^{{10}} - 10{{x}_{1}}x_{2}^{9} - 0.1x_{1}^{8}x_{2}^{4}$. Тогда главная квазиоднородная форма $\eta ({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - $ $2.01x_{1}^{4}x_{2}^{5}$ $ + \,\,x_{1}^{6}x_{2}^{4}$ полинома ${{p}_{2}}({{x}_{1}},{{x}_{2}})$ не является неотрицательной ($\eta (1,{\text{ }}1) = - 0.01$), а следовательно, согласно леммы 1, 0₍₂₎ не будет точкой локального минимума. $~$

Пусть $p({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 2x_{1}^{4}x_{2}^{5} + $ $x_{1}^{6}x_{2}^{4} + x_{2}^{{10}} - 10{{x}_{1}}x_{2}^{9} - 0.1x_{1}^{8}x_{2}^{4}$ – полином из примера 1. Тогда $\forall A \in {{\mathbb{N}}^{2}}$ все главные A-квазиоднородные формы этого полинома неотрицательны, т.е. условия леммы 1 выполняются. Однако главная (1, 2) – квазиоднородная форма $x_{1}^{2}x_{2}^{6} - 2x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4} = x_{1}^{2}x_{2}^{4}{{({{x}_{2}} - x_{1}^{2})}^{2}}$ не является невырожденной в слабом смысле, поскольку принимает значение 0, например, при ${{x}_{1}} = 1$, ${{x}_{2}} = 1$. Поэтому теорема в этом случае “не работает”, т.е. требуются более “тонкие” исследования, которые будут приведены далее (см. разд. 2).

Из формулировок теоремы и леммы 1 следует, что для выяснения, будет ли некоторая стационарная точка 0_(n) полинома (или степенного ряда; см. замечание 6) p(x) точкой локального минимума, возникает необходимость исследования полиномов, представляющих собой главные квазиоднородные формы этого полинома при всех возможных $A \in {{\mathbb{N}}^{n}}$, во-первых, на неотрицательность, а во-вторых, на невырожденность в слабом смысле. В связи с этим желательно иметь возможность такого исследования для как можно большего числа случаев.

Самым простым и весьма многочисленным будет случай, когда главные квазиоднородные формы полинома являются мономами, соответствующими угловым точкам многогранника Ньютона CoN_p. Чтобы исследовать этот простейший случай, потребуются некоторые определения и обозначения. Запишем для любого конечного множества $Y \subseteq {{\mathbb{R}}^{n}}$ через $\Psi (Y)$ множество угловых точек многогранника CoY, т.е. $\Psi (Y) = {\text{ext Co }}Y$. Тогда $\Psi ({{N}_{p}})$ – множество угловых точек многогранника Ньютона CoN_p. Кроме того, понадобится дополнительное утверждение, позволяющее сузить множество исследуемых точек из $\Psi ({{N}_{p}}).$ Введем сначала некоторые обозначения. Пусть $ \leqslant $ – отношение Парето на ${{\mathbb{R}}^{n}}$:$\forall a,b \in {{\mathbb{R}}^{n}}$ $a \leqslant b \Leftrightarrow \left[ {{{a}_{i}} \leqslant {{b}_{i}},i = \overline {1,n} } \right]$.

Пусть $Y \subseteq {{\mathbb{R}}^{n}}$; $P(Y) = \left\{ {y{\kern 1pt} * \in Y\left| {\forall y \in Y{\text{ }}\left[ {y \leqslant y{\kern 1pt} *\,\; \Rightarrow \,y = y{\kern 1pt} *} \right]} \right.} \right\}$ – множество парето-оптимальных точек из Y. Обозначим $\Omega ({{N}_{p}}) = \Psi ({{N}_{p}}) \cap P({{N}_{p}})$. Справедливо следующее простое утверждение.

Утверждение 6. Пусть $Y \subseteq {{\mathbb{R}}^{n}},$ $A \in {{\mathbb{R}}^{n}},$ ${{A}_{i}} > 0,$ $i = \overline {1,n} $. Тогда ${\text{Arg}}\mathop {\min }\limits_{y \in y} \left\langle {A,y} \right\rangle \subseteq P(Y).$

Используя утверждение 6, а также то, что минимум линейной функции на многограннике достигается в его угловых точках [11], получаем, что справедливо утверждение.

Утверждение 7. Пусть p(x) – полином, ${{N}_{p}} \ne \emptyset $. Тогда $\forall A \in {{\mathbb{N}}^{n}}$, для любой главной A-квазиоднородной формы $\varphi (x)$ полинома p(x) вида ${{N}_{\varphi }} = \{ k\} $ верно $k \in \Omega ({{N}_{p}})$.

Кроме того, можно показать, что справедливо следующее утверждение.

Утверждение 8. Пусть p(x) – полином, ${{N}_{p}} \ne \emptyset $. Тогда $\forall k \in \Omega ({{N}_{p}})$ найдется вектор $A \in {{\mathbb{N}}^{n}}$, такой, что для главной A-квазиоднородной формы φ(x) полинома p(x) выполняется ${{N}_{\varphi }} = \{ k\} $.

Замечание 8. Для доказательства утверждения 8 можно воспользоваться утверждением о строгом разделении (за исключением общей точки) двух выпуклых замкнутых многогранных конусов, имеющих единственную общую точку 0_(n), которая является также единственной угловой точкой для каждого из них.

Таким образом, на первом этапе проверки выполнения условий теоремы или леммы 1 проверяем неотрицательность каждого монома ax^k (его невырожденность в слабом смысле очевидным образом выполняется) полинома $p(x)$, где $k \in \Omega ({{N}_{p}})$, $a = coef(p,k),$которая в этом случае осуществляется тривиальным образом. Действительно, для неотрицательности ax^k, где $a \ne 0$, необходимо и достаточно, чтобы выполнялись два условия: 1) a > 0, 2) каждая компонента вектора k является четной (в том числе равной нулю).

Таким образом, можно дополнить лемму 1.

Лемма 2. Пусть 0_(n) – точка локального минимума полинома p(x), $p({{0}_{{(n)}}}) = 0$, $p{\kern 1pt} '({{0}_{{(n)}}}) = {{0}_{{(n)}}}$. Тогда $\forall k \in \Omega ({{N}_{p}})\,\;coef(p,k) > 0$, и каждая компонента вектора k будет четной (в том числе равной нулю).

Понятно, что уже простое применение леммы 2 может выявить многие случаи, когда исследуемая стационарная точка не является точкой локального минимума полинома. Следующим по сложности будет случай, когда главная квазиоднородная форма соответствует грани многогранника Ньютона размерности 1 (т.е. является отрезком прямой). Нам понадобится следующее простое утверждение.

Утверждение 9. Пусть $Y \subset {{\mathbb{R}}^{n}}$ – многогранник, C – его грань. Тогда множество угловых точек C – совокупность угловых точек многогранника Y, принадлежащих C, т.е. ${\text{ext }}C = C \cap {\text{ext }}Y$.

Доказательство. Включение $C \cap {\text{ext }}Y \subseteq {\text{ext }}C$ очевидно (см. определение угловой точки многогранника). Докажем обратное включение. Пусть $y \in {\text{ext }}C$, тогда y ∈ C. Покажем, что $y \in {\text{ext }}Y$. Пусть ${{y}^{{(1)}}},{{y}^{{(2)}}} \in Y$, $a \in (0,{\text{ }}1),\,\,a{{y}^{{(1)}}} + (1 - a){{y}^{{(2)}}} = y$. Докажем, что ${{y}^{{(1)}}} = {{y}^{{(2)}}} = y$. Используя то, что C – грань Y, получаем ${{y}^{{(1)}}},{{y}^{{(2)}}} \in C$, откуда и следует доказываемое равенство, поскольку $y \in {\text{ext }}C$. Утверждение 9 доказано.

Следствие 1. Пусть X – конечное множество из ${{\mathbb{R}}^{n}}$, C – грань многогранника CoX. Тогда ${\text{ext }}C \subseteq C \cap X$. Действительно, используя то, что ${\text{ext}}\,{\text{Co }}X \subseteq X$, из утверждения 9 имеем: ${\text{ext }}C = C \cap {\text{ext Co }}X \subseteq C \cap X$. В частности, если – полином, C – грань многогранника CoN_p, то ${\text{ext }}C \subseteq C \cap {{N}_{p}}$. При этом для главной квазиоднородной формы $\varphi (x) = {{p}_{{C \cap {{N}_{p}}}}}(x)$ полинома p(x) выполняется $C = {\text{Co (}}C \cap {{N}_{p}}) = {\text{Co }}{{N}_{\varphi }}$.

Весьма распространенным будет также случай, когда главная квазиоднородная форма полинома p(x), являющаяся главной A-квазиоднородной формой этого полинома при некотором $A \in {{\mathbb{N}}^{n}}$, соответствует грани размерности 1 (т.е. отрезку прямой, соединяющей две угловые точки этой грани) и при этом ее носитель состоит из двух точек. Тогда, в силу следствия 1, они обязательно будут угловыми точками этой грани, а в силу утверждения 9 – угловыми точками многогранника Ньютона CoN_p, и при этом, в силу утверждения 6, принадлежат P(N_p), а тем самым принадлежат $\Omega ({{N}_{p}})$. Если необходимые условия из леммы 2 выполняются, то главные квазиоднородные формы для этого случая будут невырожденными в слабом смысле и неотрицательными, поэтому удовлетворяют условиям и теоремы, и леммы 1.

Рассмотрим теперь случай, когда грань размерности 1 состоит из более чем двух точек. Нам понадобятся некоторые обозначения и утверждения. Пусть X – множество из ${{\mathbb{R}}^{n}}$,${{g}_{i}}(x),\;i = \overline {1,k} $, – функции, определенные на X. Введем множества

Обозначим ${\text{lex Arg}}[X,{{g}_{1}},...,{{g}_{k}}] = {{X}_{k}}$ (возможно, что ${{X}_{k}} = \emptyset $, если в рассматриваемой последовательности равенств хотя бы один inf не достигается).

Утверждение 10. Пусть X – конечное непустое множество из ${{\mathbb{R}}^{n}}$, $A \in {{\mathbb{R}}^{n}}$, X_A = = ${\text{lexArg}}[X,\langle A,x\rangle ,{{x}_{1}},...,{{x}_{n}}]$. Тогда X_A состоит из единственной точки ${{x}^{A}} \in \Psi (X) = {\text{ext}}\,{\text{Co }}X$.

Доказательство. Единственность очевидна. Покажем, что ${{x}^{A}} \in \Psi (X)$. Обозначим ${{B}_{A}} = \langle A,{{x}^{A}}\rangle $. Проведем для простоты доказательство для n = 2 (обобщение на общий случай очевидно). Пусть ${{x}^{A}} \in {{X}_{A}}$, $\alpha \in (0,{\text{ }}1)$, $u,v \in {\text{Co }}X$, ${{x}^{A}} = \alpha u + (1 - \alpha )v$. Покажем, что $u = v = {{x}^{A}}$. В силу (1.1) имеем ${{B}_{A}} \leqslant \langle A,u\rangle $, ${{B}_{A}} \leqslant \langle A,{v}\rangle $, откуда при ${{B}_{A}} = \langle A,{{x}^{A}}\rangle = \alpha \langle A,u\rangle + (1 - \alpha )\langle A,v\rangle $, $\alpha \in (0,{\text{ }}1)$ получаем $\langle A,u\rangle = {{B}_{A}}$, $\langle A,v\rangle = {{B}_{A}}$. Далее, используя то, что что значение линейной функции (в частности, функции $\langle A,x\rangle $ или x₁) на выпуклой комбинации конечного числа точек не может быть меньше минимального значения этой функции на множестве этих точек, находим равенство $\min \{ {{x}_{1}}\,{\text{|}}\,x \in X,\langle A,x\rangle = {{B}_{A}}\} = $ $\min \{ {{x}_{1}}\,{\text{|}}\,x \in {\text{Co }}X,\langle A,x\rangle = {{B}_{A}}\} $ (легко доказывается от противного). Следовательно, $x_{1}^{A} \leqslant {{u}_{1}}$, $x_{1}^{A} \leqslant {{v}_{1}}$, откуда при $x_{1}^{A} = a{{u}_{1}} + (1 - a){{v}_{1}}$, $a \in (0,{\text{ }}1)$ получаем $x_{1}^{A} = {{u}_{1}}$, $x_{1}^{A} = {{v}_{1}}$. Совершенно аналогично находим, что $x_{2}^{A} = {{u}_{2}}$, $x_{2}^{A} = {{v}_{2}}$. Утверждение 10 доказано.

Замечание 9. Утверждение 10 остается в силе и при X_A = ${\text{lexArg}}[X,\langle A,x\rangle ,{{( - 1)}^{{{{i}_{1}}}}}{{x}_{1}},...,{{( - 1)}^{{{{i}_{n}}}}}{{x}_{n}}]$, где ${{i}_{1}},...,{{i}_{n}} \in \{ 0,{\text{ }}1\} $. В случае $A = {{0}_{{(n)}}}$ имеем ${\text{lexArg}}[X,\langle A,x\rangle ,{{( - 1)}^{{{{i}_{1}}}}}{{x}_{1}},...,{{( - 1)}^{{{{i}_{n}}}}}{{x}_{n}}]$ = lexArg[X, ${{( - 1)}^{{{{i}_{1}}}}}{{x}_{1}},...,{{( - 1)}^{{{{i}_{n}}}}}{{x}_{n}}]$.

Пусть C – грань CoN_p размерности 1 (отрезок прямой), ${{N}_{p}} \cap C = \{ {{k}^{{(1)}}},...,{{k}^{{(r)}}}\} $, где $r \geqslant 3$. Приведем рассуждения об исследовании на неотрицательность и невырожденность в слабом смысле для полинома ${{p}_{{{{N}_{p}} \cap C}}}(x)$ в этом случае (предполагая, что необходимые условия из леммы 2 выполняются). Пусть для простоты обозначений {k⁽¹⁾} = lex${\text{Arg}}[{{N}_{p}} \cap C,{{x}_{1}},...,{{x}_{n}}]$, {k^(r)} = ${\text{lexArg}}[{{N}_{p}} \cap C, - {{x}_{1}}$, ..., –x_n]. Тогда, в силу утверждения 10, а также замечания 9, ${{k}^{{(1)}}},{{k}^{{(r)}}}$  – угловые точки многогранника CoN_p. Обозначим

(НОД – наибольший общий делитель целых чисел; нулевые компоненты при вычислении НОД не учитываем, например ${\text{НОД}}(4,0,6,0,0) = {\text{НОД}}(4,6) = 2$). Пусть α_i – числа, такие, что ${{k}^{{(i)}}} = {{k}^{{(1)}}} + {{\alpha }_{i}}e$, $i = \overline {1,r} $. Такие числа найдутся, поскольку точки ${{k}^{{(1)}}},...,{{k}^{{(r)}}}$ лежат на одной прямой. В силу выбора ${{k}^{{(1)}}},{{k}^{{(r)}}}$ эти числа неотрицательны (${{\alpha }_{1}} = 0$, а остальные положительны). Кроме того, используя (1.3), нетрудно показать, что эти числа целые, т.е. ${{\alpha }_{i}} \in \mathbb{Z},$ $i = \overline {1,r} $. Но тогда где

Согласно сделанному предположению о выполнении условий леммы 2, верно $coef(p,{{k}^{{(1)}}}) > 0$, ${{k}^{{(1)}}}\, \in \,{{(2{{\mathbb{Z}}_{ \geqslant }})}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $, откуда, $\forall x\, \in \,{{(\mathbb{R}{{\backslash }}\{ 0\} )}^{n}}$ ${{x}^{{{{k}^{{(1)}}}}}} > 0$. Заметим далее, что (поскольку ${\text{НОД}}(\left| {{{е}_{1}}} \right|,...,\left| {{{e}_{n}}} \right|)$ = 1) найдется номер $i = \overline {1,n} $, такой, что e_i – нечетно. Следовательно, при $x \in {{\mathbb{R}}^{n}}$ переменная u = x^e может принимать любые действительные значения. Но тогда для рассматриваемого случая выполняются следующие простые условия:

1) полином ${{p}_{{{{N}_{p}} \cap C}}}(x)$ является неотрицательным тогда и только тогда, когда многочлен g(u) неотрицателен;

2) полином ${{p}_{{{{N}_{p}} \cap C}}}(x)$ является неотрицательным и невырожденным в слабом смысле тогда и только тогда, когда у многочлена g(u) отсутствуют действительные корни.

Докажем второе условие. Необходимость этого условия очевидна. Для доказательства достаточности заметим, что $g(0) = coef(p,{{k}^{{(1)}}}) > 0$. В случае отсутствия действительных корней у g(u) выполняется $\forall u \in \mathbb{R}$ $\,\,g(u) > 0,$ откуда с учетом того, что $\forall x \in {{(\mathbb{R}{{\backslash }}\{ 0\} )}^{n}}$ $\,\,{{x}^{{{{k}^{{(1)}}}}}} > 0,$ получаем неотрицательность и невырожденность в слабом смысле полинома ${{p}_{{{{N}_{p}} \cap C}}}(x) = {{x}^{{{{k}^{{(1)}}}}}}g({{x}^{e}})$.

Заметим, что существуют online программы нахождения действительных корней многочлена от одной переменной.

Допустим, что C – грань CoN_p размерности 2 (многогранник на плоскости), ${{N}_{p}}\, \cap \,C\, = \,\{ {{k}^{{(1)}}},...,{{k}^{{(r)}}}\} $, где $r \geqslant 3$. Приведем рассуждения об исследовании на неотрицательность и невырожденность в слабом смысле для полинома ${{p}_{{{{N}_{p}} \cap C}}}(x)$ в этом случае. Пусть для простоты обозначений $\{ {{k}^{{(1)}}}\} = {\text{lex Arg}}[{{N}_{p}} \cap C,{{x}_{1}},...,{{x}_{n}}]$. Тогда, в силу утверждения 10, а также замечания 9, k⁽¹⁾ – угловая точка многогранника CoN_p. Далее для простоты обозначений ${{k}^{{(2)}}},{{k}^{{(3)}}}$ – смежные с k⁽¹⁾ угловые точки (т.е. $[{{k}^{{(1)}}},{{k}^{{(2)}}}]$, $[{{k}^{{(1)}}},{{k}^{{(3)}}}]$ – грани размерности 1 многогранника CoN_p), так что грань C является подмножеством множества

т.е. выпуклого конуса, сдвинутого на вектор k⁽¹⁾. Тогда, действуя в поле рациональных чисел $\mathbb{Q}$, получаем, что найдутся рациональные неотрицательные числа α_i, β_i, такие, что

Рассмотрим многочлен

где

Многочлен $h(u,v)$ зависит от двух переменных и имеет рациональные неотрицательные показатели степени. В связи с этим его в общем случае можно рассматривать только при неотрицательных $u,\;v$. Тем самым был сделан неэквивалентный переход с возможной потерей решений. Чтобы сделать переход эквивалентным, следует рассматривать 2ⁿ полиномов вида ${{p}_{{{{N}_{p}} \cap C}}}({{( - 1)}^{{{{i}_{1}}}}}{{x}_{1}},...,{{( - 1)}^{{{{i}_{n}}}}}{{x}_{n}})$, где ${{i}_{1}},...,{{i}_{n}} \in \{ 0,{\text{ }}1\} $ (некоторые из этих полиномов могут совпадать) при неотрицательных значениях переменных ${{x}_{1}},...,{{x}_{n}}$. Но тогда и соответствующие им полиномы вида $h(u,v)$ будут рассматриваться при неотрицательных $u,\;v$. В работе [9] предлагаются некоторые алгоритмы исследования многочленов вида $h(u,v)$ на неотрицательность и строгую положительность в положительном ортанте, т.е. при положительных $u,\;v$. Если все полученные таким образом многочлены вида $h(u,v)$ строго положительны в положительном ортанте, то полином ${{p}_{{{{N}_{p}} \cap C}}}(x)$ является неотрицательным и невырожденным в слабом смысле и наоборот.

Замечание 10. В случае, когда C – грань CoN_p размерности 2, в качестве точки k⁽¹⁾ можно взять любую точку из ${\text{ext }}C = C \cap \Omega ({{N}_{p}})$, а в качестве k⁽²⁾, k⁽³⁾ – две возможные (из геометрических соображений понятно, что других в этом случае не будет) точки $k \in {\text{ext}}\,C$, удовлетворяющие условию $0.5(k + {{k}^{{(1)}}}) \notin {\text{ri}}\,C$. Это условие легко проверяется решением соответствующей задачи линейного программирования (ЗЛП) (см. утверждение 3.8 [2]). Выделение всех элементов множества $\Omega ({{N}_{p}})$ – достаточно простая вычислительная задача, сводящаяся к решению конечного числа ЗЛП [2].

Аналогично рассматриваются грани C многогранника CoN_p размерности 3, 4 и т.д. Соответственно грань размерности 3 приводит к необходимости исследования на неотрицательность и строгую положительность в положительном ортанте 2ⁿ многочленов с рациональными показателями степени, зависящих от трех переменных и т.д. Отметим, что в случае размерности 3 среди показателей степеней в многочленах могут оказаться и отрицательные числа, но это не имеет значения для методов из [9].

Пример 7. Ранее в предыдущих примерах рассматривались главные (1, 2)-квазиоднородные формы полиномов вида: $\psi ({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 2x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4}$, $\varphi ({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 1.98x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4},$ $\eta ({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 2.01x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4}$, которые соответствуют граням размерности 1, состоящим из более чем двух членов. Тогда для каждой из этих форм $\phi \in \{ \psi ,\varphi ,\eta \} $ (они отличаются только коэффициентами при своих членах) имеем: ${{N}_{\phi }} = \{ {{k}^{{(1)}}} = (2,{\text{ }}6),$ ${{k}^{{(2)}}} = (4,{\text{ }}5),$ ${{k}^{{(3)}}} = (6,{\text{ }}4)\} $,

${{k}^{{(1)}}} = {{k}^{{(1)}}} + 0 \cdot e = (2,{\text{ }}6)$, ${{k}^{{(2)}}} = {{k}^{{(1)}}} + 1 \cdot e = (4,{\text{ }}5)$, ${{k}^{{(3)}}} = {{k}^{{(1)}}} + 2 \cdot e = (6,{\text{ 4}})$. Поставим теперь в соответствие каждой форме ϕ свою функцию вида ${{g}_{\phi }}(u)$ (согласно (1.4)):

Очевидно, что ${{g}_{\psi }}(u)$ – неотрицательный многочлен, но у него имеется действительный корень, равный 1. Следовательно, форма $\psi ({{x}_{1}},{{x}_{2}})$ не является невырожденной в слабом смысле. Поэтому для полинома $p({{x}_{1}},{{x}_{2}})$ из примера 1, для которого $\psi ({{x}_{1}},{{x}_{2}})$ – главная (1, 2)-квазиоднородная форма, теорема “не работает”, т.е. требуются более тонкие исследования, которые и будут приведены далее (см. пример 9). Соответственно ${{g}_{\varphi }}(u)$ не имеет действительных корней, следовательно, форма $\varphi ({{x}_{1}},{{x}_{2}})$ является неотрицательной и невырожденной в слабом смысле. У многочлена ${{g}_{\eta }}(u)$ имеются отрицательные значения, например ${{g}_{\eta }}( - 1) = - 0.01$, следовательно, форма $\eta ({{x}_{1}},{{x}_{2}})$ не будет неотрицательной.

2. Разложение полинома на сумму A-квазиоднородных форм. Приложение к необходимым и достаточным условиям минимума полинома и степенного ряда. Для любого полинома 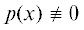, для любого $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ можно разложить этот полином на сумму A-квазиоднородных форм вида

где ; $\forall k \in {{N}_{{{{\varphi }_{i}}}}}$ $\left\langle {A,k} \right\rangle = {{B}_{i}} \in \mathbb{Z}$, $i = \overline {1,r} $, $r \in \mathbb{N}$, и при этом ${{B}_{1}} < {{B}_{2}} < ... < {{B}_{r}}$. Если, кроме того, $A \in {{\mathbb{N}}^{n}}$, $p({{0}_{{(n)}}})\, = \,0$, то ${{B}_{i}} \in \mathbb{N},$ $i = \overline {1,r} $. Обозначим для любого полинома p(x) H_p = $\{ x \in {{\mathbb{R}}^{n}}\,{\text{|}}\,p(x)$ = 0}.

Для многочлена $q(t) = {{b}_{1}}{{t}^{{{{k}_{1}}}}} + {{b}_{2}}{{t}^{{{{k}_{2}}}}} + ... + {{b}_{l}}{{t}^{{{{k}_{l}}}}}$, где ${{b}_{1}},...,{{b}_{l}} \in \mathbb{R}{{\backslash }}\{ 0\} $, ${{k}_{1}},...,{{k}_{l}} \in \mathbb{N},$ $1 \leqslant {{k}_{1}} < ... < {{k}_{l}}$, зависящего от переменной $t \in \mathbb{R}$, кратко запишем (выделяя главный член в этом многочлене) $q(t) = {{b}_{1}}{{t}^{{{{k}_{1}}}}} + o({{t}^{{{{k}_{1}}}}})$. Аналогичную запись можно использовать и в случае l = 1, а также, если требуется выделить в q(t) первые несколько главных членов. Используем следующие простые факты относительно многочленов.

Пусть $k \in \mathbb{Z}_{ \geqslant }^{n}{{\backslash }}\{ {{0}_{{(n)}}}\} $, $p(x) = {{x}^{k}}$ – моном, $A = ({{A}_{1}},...,{{A}_{n}}) \in {{\mathbb{N}}^{n}}$, $\left\langle {A,k} \right\rangle = B \in \mathbb{N}$, ${{a}_{i}} \ne 0$, q_i(t) = = ${{a}_{i}}{{t}^{{{{A}_{i}}}}} + o({{t}^{{{{A}_{i}}}}})$ – многочлены от переменной $t \in \mathbb{R}$, $i = \overline {1,n} $, $a = ({{a}_{1}},...,{{a}_{n}}) \in {{\mathbb{R}}^{n}}$. Тогда $p({{q}_{1}}(t),...,{{q}_{n}}(t)) = {{a}^{k}}{{t}^{B}} + o({{t}^{B}})$.

Пусть $A = ({{A}_{1}},...,{{A}_{n}}) \in {{\mathbb{N}}^{n}}$, 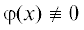– полином, являющийся A-квазиоднородной полиномиальной формой, $\forall k \in {{N}_{\varphi }}$ $\left\langle {A,k} \right\rangle = B \in \mathbb{N},$ $a = ({{a}_{1}},...,{{a}_{n}}) \in {{\mathbb{R}}^{n}}$ $i = \overline {1,n} $. Тогда $\varphi ({{a}_{1}}{{t}^{{{{A}_{1}}}}},...,{{a}_{n}}{{t}^{{{{A}_{n}}}}}) = \varphi (a){{t}^{B}}$. Если ${{q}_{i}}(t) = {{a}_{i}}{{t}^{{{{A}_{i}}}}} + o({{t}^{{{{A}_{i}}}}})$ – многочлены от переменной $t \in \mathbb{R}$, ${{a}_{i}} \ne 0,$ $i = \overline {1,n} ,$ $\varphi (a) \ne 0$, то $\varphi ({{q}_{1}}(t),...,{{q}_{n}}(t)) = \varphi (a){{t}^{B}} + o({{t}^{B}}).$

Лемму 1 можно усилить.

Лемма 3. Пусть 0_(n) – точка локального минимума полинома $p(x),\,\,p({{0}_{{(n)}}}) = 0$, $p{\kern 1pt} '({{0}_{{(n)}}}) = {{0}_{{(n)}}}$. Тогда $\forall A \in {{\mathbb{N}}^{n}}$, для разложения (2.1) выполняется $\forall i \in \{ 1,...,r\} $, $\forall x \in {{H}_{{{{\varphi }_{1}}}}} \cap ... \cap {{H}_{{{{\varphi }_{{i - 1}}}}}}$ ${{\varphi }_{i}}(x) \geqslant 0$ (в частности, при i = 1 имеем $\forall x \in {{\mathbb{R}}^{n}}$ ${{\varphi }_{1}}(x) \geqslant 0$).

Доказательство. Предположим, что для разложения (2.1) при некотором $A \in {{\mathbb{N}}^{n}}$ для некоторых $i \in \{ 1,...,r\} $, $x{\kern 1pt} * = (x_{1}^{*},...,x_{n}^{*}) \in {{H}_{{{{\varphi }_{1}}}}} \cap ... \cap {{H}_{{{{\varphi }_{{i - 1}}}}}}$ верно ${{\varphi }_{i}}(x{\kern 1pt} *) < 0$. Обозначим x*(t) = = $(x_{1}^{*}{{t}^{{{{A}_{1}}}}},...,x_{n}^{*}{{t}^{{{{A}_{n}}}}})$, где $t \in \mathbb{R}$. Тогда

где ${{\varphi }_{i}}(x{\text{*}}) < 0$, а это противоречит тому, что 0_(n) – точка локального минимума полинома p(x). Лемма 3 доказана.

Для дальнейшего понадобятся некоторые простые утверждения.

Утверждение 11. Пусть ${{q}_{1}}(t)$, ${{q}_{2}}(t)$ – два многочлена от переменной $t \in \mathbb{R}$ и выполняется ${{q}_{i}}(t) = {{a}_{i}}{{t}^{{{{\alpha }_{i}}}}} + o({{t}^{{{{\alpha }_{i}}}}})$, где ${{a}_{i}} > 0,$ ${{\alpha }_{i}} \in \mathbb{N}$, i = 1, 2. Тогда найдутся ${{a}_{0}} > 0$, ${{\alpha }_{0}} \in \mathbb{N}$, такие, что ${{q}_{1}}(t) + {{q}_{2}}(t) = {{a}_{0}}{{t}^{{{{\alpha }_{0}}}}} + o({{t}^{{{{\alpha }_{0}}}}})$.

Замечание 11. Утверждение 11 остается справедливым для произвольного количества многочленов, а также в случае, если некоторые из них (но не все) тождественно нулевые.

Утверждение 12. Пусть p(x) – неотрицательный полином, $p({{0}_{{(n)}}}) = 0$, 0_(n) – точка локального минимума p(x), q_i(t) – многочлены от переменной $t \in \mathbb{R}$ и верно ${{q}_{i}}(t) = {{a}_{i}}{{t}^{{{{\alpha }_{i}}}}} + o({{t}^{{{{\alpha }_{i}}}}})$, где ${{a}_{i}} \ne 0$, ${{\alpha }_{i}} \in \mathbb{N}$, $i = \overline {1,n} $. Тогда либо $p({{q}_{1}}(t),...,{{q}_{n}}(t)) \equiv 0$, либо найдутся ${{a}_{0}} > 0$, ${{\alpha }_{0}} \in \mathbb{N}$, такие, что $p({{q}_{1}}(t),...,{{q}_{n}}(t)) = {{a}_{0}}{{t}^{{{{\alpha }_{0}}}}} + o({{t}^{{{{\alpha }_{0}}}}})$.

Утверждение 13 (первое усиление теоремы 1). Пусть p(x) – полином, $p({{0}_{{(n)}}}) = 0$, $p{\kern 1pt} '({{0}_{{(n)}}}) = {{0}_{{(n)}}}$, $\forall A \in {{\mathbb{N}}^{n}}$ все главные A-квазиоднородные формы p(x) неотрицательны (т.е. выполняются необходимые условия минимума из леммы 1). Пусть, кроме того, для любого $A \in {{\mathbb{N}}^{n}}$ для разложения (2.1) справедливо, что главная A-квазиоднородная форма ${{\varphi }_{1}}(x)$ полинома p(x) либо является невырожденной в слабом смысле (т.е. ${{H}_{{{{\varphi }_{1}}}}} \cap {{\left[ {\mathbb{R}{{\backslash }}\left\{ 0 \right\}} \right]}^{n}} = \emptyset $), либо $\forall x \in {{H}_{{{{\varphi }_{1}}}}} \cap {{\left[ {\mathbb{R}{{\backslash }}\left\{ 0 \right\}} \right]}^{n}}$ ${{\varphi }_{2}}(x) > 0$. Тогда 0_(n) – точка локального минимума p(x).

Доказательство. Предположим противное. Тогда в силу леммы 7 из [3, с. 208] найдутся многочлены ${{q}_{i}}(t)$ от переменной $t \in \mathbb{R}$, такие, что ${{q}_{i}}(0) = 0$, $i = 1, \ldots ,n$,

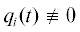где ${{a}_{0}} < 0$, ${{\alpha }_{0}} \in \mathbb{N}$. Не теряя общности рассуждений, можно считать, что , $i = \overline {1,n} $ (так как в случае, если для некоторого ${{i}_{0}} \in \{ 1, \ldots ,n\} $ справедливо ${{q}_{{{{i}_{0}}}}}(t) \equiv 0$, положив ${{q}_{{{{i}_{0}}}}}(t) = {{t}^{{{{\alpha }_{0}} + 1}}}$, снова получаем (2.2)). Пусть

Рассмотрим разложение (2.1) относительно $A = ({{A}_{1}}, \ldots {{A}_{n}})$. Возможны случаи:

а) ${{\varphi }_{1}}(a) > 0$, и тогда $p\left( {{{q}_{1}}\left( t \right),~ \ldots ~,~{{q}_{n}}\left( t \right)} \right) = {{\varphi }_{1}}\left( a \right){{t}^{{{{B}_{1}}}}} + o({{t}^{{{{B}_{1}}}}})$, что в силу ${{a}_{0}} < 0$, ${{\alpha }_{0}} \in \mathbb{N}$ противоречит (2.2);

б) ${{\varphi }_{1}}(a)\, = \,0$, и тогда $a \in {{H}_{{{{\varphi }_{1}}}}} \cap {{\left[ {\mathbb{R}{{\backslash }}\left\{ 0 \right\}} \right]}^{n}}$, а следовательно, по условиям доказываемого утверждения $~{{\varphi }_{2}}\left( a \right) > 0$ и $~{{\varphi }_{1}}\left( x \right) \geqslant 0$ при всех $x \in {{\mathbb{R}}^{n}}$. При этом $p({{q}_{1}}(t),~ \ldots ,~{{q}_{n}}(t))$ = φ₁(q₁(t), ..., q_n(t)) + + ${{\varphi }_{2}}(a){{t}^{{{{B}_{2}}}}} + o({{t}^{{{{B}_{2}}}}})$, что в силу утверждений 11, 12, а также замечания 11 противоречит (2.2), поскольку ${{a}_{0}} < 0$, ${{\alpha }_{0}} \in \mathbb{N}$. Утверждение 13 доказано.

Возможно также дальнейшее уточнение достаточного условия минимума.

Утверждение 14 (второе усиление теоремы 1). Пусть выполняются условия утверждения 13, и для любого $A \in {{\mathbb{N}}^{n}}$ для разложения (2.1) справедливо, что для некоторого $j \in \{ 2, \ldots ,r\} $ A-квазиоднородные формы ${{\varphi }_{1}}(x), \ldots ,{{\varphi }_{{j - 1}}}(x)$ являются неотрицательными. При этом либо ${{H}_{{{{\varphi }_{1}}}}}\, \cap \, \ldots \, \cap \,{{H}_{{{{\varphi }_{{j - 1}}}}}}\, \cap \,{{\left[ {\mathbb{R}{{\backslash }}\{ 0\} } \right]}^{n}}\, = \,\emptyset $, либо $\forall x \in {{H}_{{{{\varphi }_{1}}}}} \cap \ldots \cap {{H}_{{{{\varphi }_{{j - 1}}}}}} \cap {{\left[ {\mathbb{R}{{\backslash }}\left\{ 0 \right\}} \right]}^{n}}$ $\,\,{{\varphi }_{j}}(x) > 0$. Тогда 0_(n) – точка локального минимума p(x).

Доказательство. Предположим противное. Тогда, в силу леммы 7 из [3, с. 208], найдутся многочлены q_i(t) от переменной $t \in \mathbb{R}$, такие, что ${{q}_{i}}(0) = 0$, $i = \overline {1,n} $, и выполняется (2.2), где ${{a}_{0}} < 0$, ${{\alpha }_{0}} \in \mathbb{N}$. Как и при доказательстве утверждения 13, не теряя общности рассуждений, можно считать, что 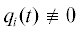, $i = \overline {1,n} $, и верно (2.3). Рассмотрим разложение (2.1) относительно $A = ({{A}_{1}}, \ldots {{A}_{n}})$. Из условий доказываемого утверждения получаем, что ${{\varphi }_{1}}(a) \geqslant 0, \ldots ,{{\varphi }_{{j - 1}}}(a) \geqslant 0$ и в случае ${{\varphi }_{1}}(a) = 0, \ldots ,{{\varphi }_{{j - 1}}}(a) = 0$ обязательно выполняется ${{\varphi }_{j}}(a) > 0$. Таким образом, возможны случаи:

а) ${{\varphi }_{1}}(a) > 0$, и тогда $p({{q}_{1}}(t), \ldots ,{{q}_{n}}(t)) = {{\varphi }_{1}}(a){{t}^{{{{B}_{1}}}}} + o({{t}^{{{{B}_{1}}}}})$, что противоречит (2.2);

б) для некоторого ${{j}_{1}} \in \{ 2, \ldots ,j\} $ справедливо, что ${{\varphi }_{1}}(a) = 0, \ldots ,{{\varphi }_{{{{j}_{1}} - 1}}}(a) = 0,{{\varphi }_{{{{j}_{1}}}}}(a) > 0$, и при этом $p\left( {{{q}_{1}}\left( t \right),~ \ldots ~,~{{q}_{n}}\left( t \right)} \right) = $ ${{\varphi }_{1}}\left( {{{q}_{1}}\left( t \right),~ \ldots ~,~{{q}_{n}}\left( t \right)} \right) + \cdots + $ ${{\varphi }_{{{{j}_{1}} - 1}}}\left( {{{q}_{1}}\left( t \right),~ \ldots ~,~{{q}_{n}}\left( t \right)} \right) + {{\varphi }_{{{{j}_{1}}}}}\left( a \right){{t}^{{{{B}_{{{{j}_{1}}}}}}}} + o({{t}^{{{{B}_{{{{j}_{1}}}}}}}})$ что, согласно утверждений 11, 12, а также замечания 11, противоречит (2.2). Утверждение 14 доказано.

Утверждение 15 (третье усиление теоремы 1). Условие неотрицательности ${{\varphi }_{1}}(x), \ldots ,{{\varphi }_{{j - 1}}}(x)$ в утверждении 14 можно заменить на условие: 0_(n) – точка локального минимума полиномов ${{\varphi }_{1}}(x)$, ${{\varphi }_{1}}(x) + {{\varphi }_{2}}(x)$, …, ${{\varphi }_{1}}(x) + \cdots + {{\varphi }_{{j - 1}}}(x)$.

Действительно, если для некоторого ${{j}_{1}} \in \{ 2, \ldots ,j - 1\} $ выполняется ${{\varphi }_{1}}(a) = 0$, …, ${{\varphi }_{{{{j}_{1}} - 1}}}(a) = 0$ (где  a удовлетворяет (2.3)), то ${{\varphi }_{{{{j}_{1}}}}}(a) \geqslant 0$, а при ${{\varphi }_{1}}(a) = 0,$ …, ${{\varphi }_{{j - 1}}}(a) = 0$ справедливо ${{\varphi }_{j}}(a) > 0$,   (поскольку для a(t) = $({{a}_{1}}{{t}^{{{{A}_{1}}}}},\,\,...,\,\,{{a}_{n}}{{t}^{{{{A}_{n}}}}})$, где $t \in \mathbb{R}$, имеем ${{\varphi }_{1}}(a(t)) + \ldots + {{\varphi }_{{{{j}_{1}} - 1}}}(a(t)) = {{t}^{{{{B}_{{{{j}_{1}}}}}}}}{{\varphi }_{1}} + ... + {{t}^{{{{B}_{{{{j}_{1}}}}}}}}{{\varphi }_{{{{j}_{1}} - 1}}}(a))$). Таким образом, рассмотрение случаев а), б) при доказательстве этого утверждения является аналогичным, как и при доказательстве утверждения 14.

Замечание 12. Лемму 3, а также утверждения 13–15 можно перенести и на степенные ряды. Тогда разложение (2.1) становится бесконечным и условие $\forall i \in \{ 1, \ldots ,r\} $ в лемме 3 следует заменить на $\forall i \in \mathbb{N}$. Утверждение 13 переносится без изменений, а утверждения 14, 15 – с заменой $j \in \{ 2, \ldots ,r\} $ на $j \in \mathbb{N}$, $j \geqslant 2$.

3. Некоторые практически реализуемые процедуры, используемые для проверки выполнения необходимых и достаточных условий минимума. Для практического применения полученных результатов понадобится также решение следующих задач.

1. Необходим практически реализуемый алгоритм выделения всех главных A-квазиоднородных форм полинома, где $A \in {{\mathbb{N}}^{n}}$ (а при решении некоторых других задач [9] – для $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $).

2. В случае использования разложения вида (2.1) следует также иметь практически реализуемый алгоритм нахождения всех возможных разложений при $A \in {{\mathbb{N}}^{n}}$.

Ранее уже говорилось, что при n = 2 все главные квазиоднородные формы полинома p(x) можно выделять визуально (основываясь на первом определении квазиоднородных форм полинома), пользуясь изображением CoN_p. Но уже при n = 3 такое выделение становится проблематичным и поэтому требуются аналитические методы, базирующиеся на втором определении главных квазиоднородных форм полинома. В [2] было предложено несколько практически реализуемых алгоритмов, основанных на многократном решении соответствующих ЗЛП. Приведем простейший (базовый) метод. Для любого непустого множества U кратко обозначим, что ${{2}^{U}} = \{ V\,{\text{|}}\,V \subseteq U\} $ – совокупность всех подмножеств U. В указанном методе перебираем все непустые подмножества $N \subset {{N}_{p}}$ (т.е. $N \in {{2}^{{{{N}_{p}}}}}{{\backslash }}\{ \emptyset ,{{N}_{p}}\} $ и рассматриваем нетривиальный случай, когда $N \ne {{N}_{p}}$). Тогда для проверки, является ли p_N(x) главной квазиоднородной формой полинома p(x), достаточно убедиться, существует ли целочисленное решение системы равенств и неравенств (относительно неизвестного вектора $e \in {{\mathbb{Z}}^{n}}$):

(если |N| = 1, то равенства в (3.1) отсутствуют), где k⁽⁰⁾ – произвольный элемент из множества N. Если имеется целочисленное решение e = A системы (3.1), то $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ (при $e = {{0}_{{(n)}}}$ не выполняются неравенства в (3.1)) и p_N(x) – главная A-квазиоднородная форма полинома p(x). В противном случае p_N(x) не является главной квазиоднородной формой полинома p(x). Это непосредственно следует из определения главной квазиоднородной формы полинома. Для нахождения целочисленного решения системы (3.1) можно рассмотреть задачу $\mathop {\max }\limits_{i = \overline {1,n} } \left| {{{e}_{i}}} \right| \to min$ с ограничениями (3.1) или эквивалентную ей ЗЛП (добавляем новую переменную u):

Нетрудно видеть, что ЗЛП (3.2) разрешима тогда и только тогда, когда система (3.1) имеет хотя бы одно решение. Для решения ЗЛП (3.2) полезно воспользоваться симплекс-методом, поскольку любое решение, полученное этим методом, будет угловой точкой выпуклого полиэдрального множества, заданного системой линейных равенств и неравенств с целыми коэффициентами. Следовательно, компоненты этого решения – рациональные числа. Заметим далее, что если e – решение системы (3.1), то $\forall \lambda \geqslant 1$ $\lambda e$ также является решением этой системы. Но тогда, взяв любое рациональное решение e системы (3.1), полученное, например, решением ЗЛП (3.2), и умножив его на наименьшее общее кратное знаменателей ненулевых компонент этого решения, получаем целочисленное решение системы (3.1). Нетрудно видеть [10, с. 35], что если ЗЛП (3.2) имеет решение, то в его допустимом множестве обязательно найдется угловая точка, являющаяся одним из решений этой ЗЛП (поскольку ранг системы неравенств [10, с. 7] в (3.2) равен числу переменных, т.е. n + 1), из которой легко получить целочисленное решение системы (3.1). Таким образом, система (3.1) совместна тогда и только тогда, когда она имеет хотя бы одно целочисленное решение.

Поскольку для исследования полиномов и степенных рядов на локальный минимум требуются A-квазиоднородные формы не для всех$A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $, а лишь для $A \in {{\mathbb{N}}^{n}}$, то в этом случае требуется уточнение метода. Тогда следует добавить к системе (3.1) неравенства

и для нахождения целочисленного решения системы (3.1), (3.3) рассматривать ЗЛП при условиях (3.1), (3.3). При этом объединенная система (3.1), (3.3) совместна тогда и только тогда, когда она имеет какое-нибудь целочисленное решение (рассуждение такое же, как и в случае системы (3.1)).

Следует, однако, отметить, что в случае, когда величина |N_p| достаточно большая, количество элементов в ${{2}^{{{{N}_{p}}}}}$ является крайне большим, что делает невозможным применение метода. В связи с этим в [2] приводятся различные способы сокращения необходимого количества ЗЛП (а также количества ограничений в них), решение которых дает решение поставленной задачи выделения всех главных A-квазиоднородных форм полинома для $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ или для$A \in {{\mathbb{N}}^{n}}$. Показано, что вместо $N \in {{2}^{{{{N}_{p}}}}}{{\backslash }}\{ \emptyset \} $ достаточно ограничиться рассмотрением $N \in {{2}^{{\Psi ({{N}_{p}})}}}{{\backslash }}\{ \emptyset \} $, где Ψ(N_p) = = ${\text{extCo}}{{N}_{p}}$ – в случае $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $, а при $A \in {{\mathbb{N}}^{n}}$ – расмотрением $N \in {{2}^{{\Omega ({{N}_{p}})}}}{{\backslash }}\{ \emptyset \} $, где Ω(N_p) = = $\Psi ({{N}_{p}})\, \cap \,P({{N}_{p}})$. В [2] предложены также и другие методы сокращения.

Аналогичный подход может использоваться и для последовательного нахождения полиномов ${{\varphi }_{1}}(x), \ldots ,{{\varphi }_{r}}(x)$ в разложении (2.1) для заданного полинома p(x) после нахождения полинома ${{\varphi }_{1}}(x)$, являющегося главной A-квазиоднородной формой p(x) для некоторого $A \in {{\mathbb{N}}^{n}}$. При этом следует учитывать возможную неоднозначность выбора $A \in {{\mathbb{N}}^{n}}$ для одной и той же главной квазиоднородной формы ${{\varphi }_{1}}(x)$ полинома p(x) (см. пример в замечании 3). В некоторых случаях, описанных в разд. 4, такая неоднозначность не влияет на однозначность разложения (2.1) при любом выборе $A \in {{\mathbb{N}}^{n}}$, при котором ${{\varphi }_{1}}(x)$ будет главной A-квазиоднородной формой p(x). Если же такой однозначности нет, можно и в этом случае применить прием из [2]. Снова опишем простейший метод, который можно затем аналогичным образом модифицировать (в целях сокращения числа решаемых ЗЛП).

В простейшем варианте метода для нахождения ${{\varphi }_{2}}(x)$ в разложении (2.1) (после того, как был получен полином ${{\varphi }_{1}}(x)$, являющийся главной A-квазиоднородной формой полинома p(x) для некоторого$A \in {{\mathbb{N}}^{n}}$) рассматриваем для всех $N \in {{2}^{{{{N}_{P}}\backslash {{N}_{{{{\varphi }_{1}}}}}}}}{{\backslash }}\{ \emptyset \} $ систему линейных равенств и неравенств:

где k⁽⁰⁾, k⁽¹⁾ – произвольные элементы из множеств ${{N}_{{{{\varphi }_{1}}}}}$, N соответственно (при $\left| {{{N}_{{{{\varphi }_{1}}}}}} \right| = 1$ равенства $\left\langle {e,k} \right\rangle = \langle e,{{k}^{{(0)}}}\rangle $, $k \in {{N}_{{{{\varphi }_{1}}}}}{{\backslash }}\{ {{k}^{{(0)}}}\} $, отсутствуют и при |N| = 1 равенства $\left\langle {e,k{\kern 1pt} '} \right\rangle = \langle e,{{k}^{{(1)}}}\rangle $, $k{\kern 1pt} ' \in N{{\backslash }}\{ {{k}^{{(1)}}}\} $, отсутствуют). Тогда если имеется целочисленное решение e = A системы (3.5), то $A \in {{\mathbb{N}}^{n}}$ и ${{\varphi }_{2}}(x) = {{p}_{N}}(x)$ – следующая после ${{\varphi }_{1}}(x)$ A-квазиоднородная форма полинома p(x) в разложении (2.1). В противном случае p_N(x) не может ни при каком $A \in {{\mathbb{N}}^{n}}$ (при котором ${{\varphi }_{1}}(x)$ является главной A-квазиоднородной формой полинома p(x)) быть следующей после ${{\varphi }_{1}}(x)$ A-квазиоднородной формой полинома p(x) в разложении (2.1). Для нахождения какого-нибудь решения системы (3.5) рассматриваем ЗЛП (3.4), (3.5). При этом как и в случае системы (3.1) система (3.5) совместна тогда и только тогда, когда она имеет какое-нибудь целочисленное решение (рассуждения аналогичны). Кроме того, для уменьшения числа вариантов и здесь можно применить сходные приемы, используемые в [2] для выделения всех главных квазиоднородных форм полинома. После нахождения второго члена в разложении (2.1) аналогичным образом можем подбирать все возможные полиномы, которые при некоторых $A \in {{\mathbb{N}}^{n}}$ являются третьими членами в разложении (2.1) и т.д.

Замечание 13. Приведенные рассуждения можно перенести и на степенные ряды. При этом следует воспользоваться тем, что если для некоторого $A \in {{\mathbb{N}}^{n}}$ полином φ_A(x) будет главной A-квазиоднородной формой степенного ряда p(x), то ${{N}_{{{{\varphi }_{A}}}}} \subseteq P({{N}_{p}})$, а, следовательно, во всех приведенных рассуждениях можно заменить N_p на множество P(N_p), которое для степенных рядов конечно (см. утверждение 2 из [4]). Используя эти же соображения, получаем, что в системе (3.5) условие $\tilde {k} \in {{N}_{p}}{{\backslash }}(N \cup {{N}_{{{{\varphi }_{1}}}}})$ можно заменить на $\tilde {k} \in P\left( {{{N}_{p}}{{\backslash }}(N \cup {{N}_{{{{\varphi }_{1}}}}})} \right)$.

4. Некоторые случаи, когда разложение полинома на сумму A-квазиоднородных форм (2.1) оказывается единственным при выбранной главной форме φ₁(x). В предыдущем разделе был описан некоторый универсальный подход для получения разложения вида (2.1) для произвольного полинома p(x). Этот подход является весьма громоздким и требующим решения большого количества ЗЛП вида (3.5). Между тем возможны случаи, когда разложение (2.1) будет единственным при выбранной главной форме φ₁(x), т.е. не зависящим от выбора $A \in {{\mathbb{N}}^{n}}$, такого, что φ₁(x) – главная A-квазиоднородная форма полинома p(x). Тогда проверка выполнения условий леммы 3 и утверждений 13–15 значительно упрощается. В настоящем разделе показывается, что такая единственность имеет место, когда ${\text{Co}}{{N}_{{{{\varphi }_{1}}}}}$ – грань многогранника CoN_p, размерность которой ровно на 1 меньше размерности CoN_p.

Нам понадобятся некоторые вспомогательные утверждения о выпуклых многогранниках. Ранее было введено определение выпуклого многогранника как выпуклой оболочки некоторого конечного множества точек из ${{\mathbb{R}}^{n}}$. Существует эквивалентное определение выпуклого многогранника, как ограниченного множества, являющегося пересечением конечного числа замкнутых полупространств [11]. Таким образом, выпуклый многогранник $Y \subset {{\mathbb{R}}^{n}}$, определенный ранее как выпуклая оболочка конечного множества точек из ${{\mathbb{R}}^{n}}$, всегда может быть представлен в виде

где ${{a}^{{(i)}}} \in {{\mathbb{R}}^{n}}$, ${{a}^{{(i)}}} \ne {{0}_{{(n)}}}$, ${{b}_{i}} \in \mathbb{R}$, $i = \overline {1,r} $. С другой стороны, любое непустое множество $Y \subset {{\mathbb{R}}^{n}}$, представимое в виде (4.1), будет выпуклым многогранником тогда и только тогда, когда множество Y является ограниченным. При этом если $Y$ – ограниченное непустое множество, представимое в виде (4.1), то ${\text{ext }}Y \ne \emptyset $, множество extY конечно и $Y = {\text{Co ext }}Y$ [11]. Обозначим $\left\| x \right\| = {{(x_{1}^{2} + ... + x_{n}^{2})}^{{1/2}}}$, ${{B}^{\delta }}(u) = \{ x \in {{\mathbb{R}}^{n}}\,{\text{|}}\,{\text{ }}\left\| {x - u} \right\| \leqslant \delta \} $, где $\delta > 0$, $x,u \in {{\mathbb{R}}^{n}}$.

Нам понадобятся некоторые утверждения.

Утверждение 16. Пусть $Y = \left\{ {x \in {{\mathbb{R}}^{n}}\,{\text{|}}\,\langle {{a}^{{(i)}}},x\rangle \leqslant {{b}_{i}},i = \overline {1,r} } \right\} \ne \emptyset $ – выпуклый многогранник, C – его собственная грань, H = affC, $\forall x \in {{\mathbb{R}}^{n}}$ $I(x) = \left\{ {i \in \{ 1, \ldots ,r\} \,{\text{|}}\,\left\langle {{{a}^{{(i)}}},x} \right\rangle = {{b}_{i}}} \right\},$ $I(C) = {{ \cap }_{{x \in C}}}I(x)$. Тогда: а) $I(C) \ne \emptyset $; б) $C = \left\{ {x \in Y\,{\text{|}}\,\langle {{a}^{{(i)}}},x\rangle = {{b}_{i}},i \in I(C)} \right\}$; в) H = $\left\{ {x \in {{\mathbb{R}}^{n}}\,{\text{|}}\,\langle {{a}^{{(i)}}},x\rangle = {{b}_{i}},i \in I(C)} \right\}$; г) C = = $Y \cap H = Y \cap {\text{aff}}C$.

Доказательство а). Предположим, что $I(C) = \emptyset $. Тогда $\forall i \in \{ 1, \ldots r\} $ $\exists x(i) \in C{\text{:}}$ $\langle {{a}^{{(i)}}},x(i)\rangle < {{b}_{i}}$. Следовательно, для

выполняется $\langle {{a}^{{(i)}}},x{\kern 1pt} *\rangle < {{b}_{i}}$, $i = \overline {1,r} $, откуда $x{\kern 1pt} * \in C \cap \operatorname{int} Y$. Из этого условия, используя то, что C – грань Y, нетрудно показать, что C = Y (действительно, в этом случае любая точка $y \in Y$ будет одной из угловых точек отрезка, содержащегося в Y, внутренней точкой которого является $x{\kern 1pt} * \in C$ и по определению грани будет принадлежать C), а это противоречит исходным условиям.

Доказательство б). Обозначим $C{\kern 1pt} '\, = \,\{ x\, \in \,Y\,{\text{|}}\,\langle {{a}^{{(i)}}},x\rangle = {{b}_{i}},i \in I(C)\} $, H  '  =  $\{ x \in {{\mathbb{R}}^{n}}\,{\text{|}}\,\langle {{a}^{{(i)}}},x\rangle = $ $ = {{b}_{i}},i \in I(C)\} $. Заметим, что  $\exists v(C) \in C:I(v(C)) = I(C)$, $\langle {{a}^{{(i)}}},v(C)\rangle < {{b}_{i}}$, $i \in \{ 1,...,r\} {{\backslash }}I(C)$ ($v(C)$ получается по аналогии с x*), следовательно, найдется число $\delta > 0,$ такое, что $\forall x \in {{B}^{\delta }}(v(C))$ $I(x) \subseteq I(v(C)) = I(C)$, откуда $C{\kern 1pt} '\; \cap {{B}^{\delta }}(v(C)) = H{\kern 1pt} '\; \cap {{B}^{\delta }}(v(C))$. Но тогда ${\text{aff }}C{\kern 1pt} ' = H{\kern 1pt} '$, $v(C) \in {\text{ri }}C{\kern 1pt} '$. Пусть ${\text{ext }}C{\kern 1pt} ' = \{ v(1), \ldots ,v({{k}_{1}})\} $. Поскольку $v(C) \in {\text{ri}}C{\kern 1pt} '$, в силу утверждения 3.3 из [2], найдутся ${{\alpha }_{1}}, \ldots ,{{\alpha }_{{{{k}_{1}}}}} \in \mathbb{R}$ такие, что ${{\alpha }_{1}} > 0, \ldots ,{{\alpha }_{{{{k}_{1}}}}} > 0,$

откуда, используя то, что C – грань, получаем ${\text{ext }}C{\kern 1pt} ' \subseteq C$. Но тогда ввиду того, что ${\text{Co ext }}C{\kern 1pt} ' = C{\kern 1pt} '$ [11], используя выпуклость C, получаем $C{\kern 1pt} ' \subseteq C$. Обратное включение очевидно (см. определение $I(C)$).

Доказательство в). Следует из б) и равенства ${\text{aff }}C{\kern 1pt} ' = H{\kern 1pt} '$.

Доказательство г). Следует из б), в). Утверждение 16 доказано.

Утверждение 17. Пусть $Y = \left\{ {x \in {{\mathbb{R}}^{n}}\,{\text{|}}\,\left\langle {{{a}^{{(i)}}},x} \right\rangle \leqslant {{b}_{i}},i = \overline {1,r} } \right\} \ne \emptyset $ – выпуклый многогранник, C – его собственная грань, $\forall x \in {{\mathbb{R}}^{n}}$ $I(x) = \left\{ {i \in \{ 1, \ldots ,r\} \,{\text{|}}\,\left\langle {{{a}^{{(i)}}},x} \right\rangle = {{b}_{i}}} \right\}$,

Тогда $I(C) \ne \emptyset $, $A \ne {{0}_{{(n)}}},{\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle = C$.

Доказательство. Достаточно доказать, что $\forall x \in C{\text{ }}\left\langle {A,x} \right\rangle = b$; $\forall x \in Y$ $\left[ {\left\langle {A,x} \right\rangle = b \Rightarrow x \in C} \right]$. Пусть x ∈ C. Тогда $\langle {{a}^{{(i)}}},x\rangle = {{b}_{i}}$, $i \in I(C)$, следовательно, $\left\langle {A,x} \right\rangle = b$. Пусть x ∈ Y, $\left\langle {A,x} \right\rangle = b$. Покажем, что x ∈ C. Из того, что

используя неравенства $\langle {{a}^{{(i)}}},x\rangle \leqslant {{b}_{i}}$, $i = \overline {1,r} $, имеем $\langle {{a}^{{(i)}}},x\rangle = {{b}_{i}}$, $i \in I(C)$. Следовательно, $x \in \left\{ {x{\kern 1pt} ' \in Y\left| {\langle {{a}^{{(i)}}},x{\kern 1pt} '\rangle = {{b}_{i}},i \in I(C)} \right.} \right\} = C$ (см. утверждение 16б)). Утверждение 17 доказано.

Замечание 14. Очевидно, что если ${{a}^{{(i)}}} \in {{\mathbb{Q}}^{n}}$, $i = \overline {1,r} $, то

Утверждение 18. Пусть $Y \subset {{\mathbb{R}}^{n}}$ – выпуклый многогранник, $A \in {{\mathbb{R}}^{n}}$, $C = {\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle $. Тогда C – грань Y.

Доказательство. Выпуклость C очевидна. Предположим, что ${{y}^{{(1)}}},{{y}^{{(2)}}} \in Y,$ $\alpha \in (0,{\text{ }}1),$ $\alpha {{y}^{{(1)}}} + (1 - \alpha ){{y}^{{(2)}}} \in C$. Покажем, что ${{y}^{{(1)}}},{{y}^{{(2)}}} \in C$. Пусть $B = \mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle $. Из $\alpha {{y}^{{(1)}}} + (1 - \alpha ){{y}^{{(2)}}} \in C$ следует, что $\langle A,\alpha {{y}^{{(1)}}} + (1 - \alpha ){{y}^{{(2)}}}\rangle = B$, откуда $\alpha \langle A,{{y}^{{(1)}}}\rangle + (1 - \alpha )\langle A,{{y}^{{(2)}}}\rangle = B$. Из последнего равенства с учетом того, что $\left\langle {A,{{y}^{{(1)}}}} \right\rangle \geqslant B$, $\left\langle {A,{{y}^{{(2)}}}} \right\rangle \geqslant B,$ $\alpha \in (0,{\text{ }}1)$, получаем $\left\langle {A,{{y}^{{(1)}}}} \right\rangle = B$, $\left\langle {A,{{y}^{{(2)}}}} \right\rangle = B$, т.е. ${{y}^{{(1)}}},{{y}^{{(2)}}} \in C.$ Утверждение 18 доказано.

Утверждение 19. Пусть $X \subset {{\mathbb{Z}}^{n}}$ – непустое конечное множество. Тогда CoX можно представить в виде ${\text{Co }}X = \left\{ {x \in {{\mathbb{R}}^{n}}\,{\text{|}}\,\langle {{a}^{{(i)}}},x\rangle \leqslant {{b}_{i}},i = \overline {1,r} } \right\}$, где ${{a}^{{(i)}}} \in {{\mathbb{Q}}^{n}}$, ${{b}_{i}} \in \mathbb{Q}$, $i = \overline {1,r} $.

Для доказательства утверждения 19 достаточно воспользоваться теоремой 46 из [12], доказательство которой содержит в себе алгоритм для представления многогранных множеств в виде пересечения конечного числа замкнутых подпространств, а также замечанием 2 из [12, с. 69]. Утверждение 19 является также следствием того, что ${{a}^{{(i)}}},{{b}_{i}},i = \overline {1,r} $, – решения соответствующих систем линейных уравнений с коэффициентами из поля рациональных чисел $\mathbb{Q}$, а поэтому их компоненты тоже могут быть найдены в поле $\mathbb{Q}$.

Следствием утверждений 17, 19, и замечания 14 будет следующее утверждение.

Утверждение 20. Пусть $X \subset {{\mathbb{Z}}^{n}}$ – непустое конечное множество. Тогда для любой собственной грани C многогранника CoX найдется вектор $A \in {{\mathbb{Q}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ (а следовательно, и $A \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $), такой, что $C = {\text{Arg}}\mathop {\min }\limits_{x \in {\text{Co }}X} \left\langle {A,x} \right\rangle $.

Множество K называется выпуклым конусом, если оно выпукло и вместе с каждой точкой x ∈ K содержит все точки λx при $\lambda > 0.$ Нетрудно видеть, что если $x,y \in K$, то $x + y \in K$. Действительно, поскольку K – выпуклое множество, то $0.5x + 0.5y \in K$, откуда $x + y = 2(0.5x + 0.5) \in K$.

Существует эквивалентное определение: K называется выпуклым конусом, если для любых $x,y \in K$, $\lambda > 0$ выполняется $\lambda x \in K$, $x + y \in K$. Достаточно показать, что из второго определения следует выпуклость K. Действительно, $\forall x,y \in K$, $\forall \lambda \in (0,{\text{ }}1)$ справедливо $\lambda x \in K$, $(1 - \lambda )y \in K \Rightarrow \lambda x + (1 - \lambda )y \in K$.

Утверждение 21. Пусть $Y \subset {{\mathbb{R}}^{n}}$ – выпуклый многогранник, C – его собственная грань. Тогда $K(C) = \left\{ {A \in {{\mathbb{R}}^{n}}\,{\text{|}}\,C = {\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle } \right\}$ – непустой выпуклый конус, при этом ${{0}_{{(n)}}} \notin K(C)$.

Доказательство. В силу утверждения 17, $K(C) \ne \emptyset $. Очевидно, что ${{0}_{{(n)}}} \notin K(C)$, поскольку $C \ne Y$. Пусть $A,\tilde {A} \in K(C)$, т.е.

Тогда $\forall \lambda > 0$ $C = {\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle = {\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {\lambda A,x} \right\rangle $, т.е. $\lambda A \in K(C)$. Покажем, что C = = ${\text{Arg}}\mathop {\min }\limits_{x \in Y} \langle A + \tilde {A},x\rangle $, т.е. $A + \tilde {A} \in K(C)$. Заметим, что в силу (4.2) выполняется

откуда $\forall x \in C$, $\forall y \in Y$ $\left\langle {A + \tilde {A},x} \right\rangle = {{b}_{A}} + {{b}_{{\tilde {A}}}} \leqslant \left\langle {A + \tilde {A},y} \right\rangle $. Следовательно,

Предположим, что ${\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {A + \tilde {A},x} \right\rangle \backslash C \ne \emptyset $. Тогда, в силу (4.3), $\exists y \in Y$: $\left\langle {A + \tilde {A},y} \right\rangle $ = = $\mathop {\min }\limits_{x \in Y} \left\langle {A + \tilde {A},x} \right\rangle = {{b}_{A}} + {{b}_{{\tilde {A}}}}$, $y \notin C$. Из условий $y \in Y$, $y \notin C$, в силу (4.2), получаем $\left\langle {A,y} \right\rangle > {{b}_{A}}$, $\left\langle {\tilde {A},y} \right\rangle > {{b}_{{\tilde {A}}}}$. Но ${{b}_{A}} + {{b}_{{\tilde {A}}}} = \left\langle {A + \tilde {A},y} \right\rangle = \left\langle {A,y} \right\rangle + \left\langle {\tilde {A},y} \right\rangle > {{b}_{A}} + {{b}_{{\tilde {A}}}}$, т.е. пришли к противоречию. Утверждение 21 доказано.

Введенный в утверждении 21 конус K(C) будем использовать и для любого полинома 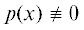, предполагая, что выпуклым многогранником $Y$ в определении K(C) является CoN_p.

Назовем вектор $A = ({{A}_{1}},...,{{A}_{n}}) \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ нормированным, если ${\text{НОД}}({\text{|}}{{A}_{1}}{\text{|}},...,{\text{|}}{{A}_{n}}{\text{|}}) = 1$ (как и ранее, нулевые компоненты при вычислении НОД не учитываем, например, ${\text{НОД}}(4,0,6,0,0)$ = НОД(4, 6) = 2). Любой вектор $A = ({{A}_{1}},...,{{A}_{n}}) \in {{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ тривиальным образом приводится к нормированному (делением на натуральное число, равное ${\text{НОД}}({\text{|}}{{A}_{1}}{\text{|}},...,{\text{|}}{{A}_{n}}{\text{|}})$). Множество всех нормированных векторов из ${{\mathbb{Z}}^{n}}{{\backslash }}\{ {{0}_{{(n)}}}\} $ обозначим через $\mathbb{Z}_{0}^{n}$. Соответственно $\mathbb{N}_{0}^{n} = {{\mathbb{N}}^{n}} \cap \mathbb{Z}_{0}^{n}$.

Следствие 2. Из утверждения 21 следует, что для полинома 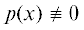, для любой собственной грани C многогранника CoN_p квазиоднородная форма $\varphi (x) = {{p}_{{C \cap {{N}_{p}}}}}(x)$ является главной A-квазиоднородной формой полинома p(x) для любого вектора $A \in K(C) \cap {{\mathbb{Z}}^{n}}$, где K(C) = $\{ A \in {{\mathbb{R}}^{n}}\,{\text{|}}\,C = {\text{Arg}}\mathop {\min }\limits_{x \in {\text{Co }}{{N}_{p}}} \langle A,x\rangle \} $. При этом, в силу утверждений 20, 21, $K(C) \cap {{\mathbb{Z}}^{n}} \ne \emptyset $, ${{0}_{{(n)}}} \notin K(C) \cap {{\mathbb{Z}}^{n}}$. Очевидно, что если $\varphi (x) = {{p}_{{C \cap {{N}_{p}}}}}(x)$ – главная A-квазиоднородная форма полинома $p(x)$ для некоторого вектора $A \in K(C) \cap {{\mathbb{Z}}^{n}}$, то $\varphi (x)$ – также главная λA-квазиоднородная форма полинома p(x) для любого $\lambda > 0,$ такого, что $\lambda A \in {{\mathbb{Z}}^{n}}$. Поэтому при выборе для некоторой квазиоднородной формы $\varphi (x) = {{p}_{{C \cap {{N}_{p}}}}}(x)$ соответствующего ей вектора $A \in K(C) \cap {{\mathbb{Z}}^{n}}$ достаточно ограничиться рассмотрением нормированных векторов. Однако простые примеры (см. пример 8) показывают, что множество $K(C) \cap \mathbb{Z}_{0}^{n}$ может оказаться бесконечным. Поэтому нахождение всех главных квазиоднородных форм путем перебора и выбора подходящих векторов $A \in K(C) \cap \mathbb{Z}_{0}^{n}$ является в общем случае невыполнимой задачей. В связи с этим в разд. 3 использовался другой подход, основанный на переборе подходящих подмножеств множества N_p, а множество таких подмножеств, очевидно конечно.

Следствие 3. С учетом следствия 2 в условиях теоремы, а также утверждений 13–15 можно условие $\forall A \in {{\mathbb{N}}^{n}}$ заменить на $\forall A \in \mathbb{N}_{0}^{n}$.

Пример 8. В примере 1 моном $x_{2}^{{10}}$ – главная A-квазиоднородная форма полинома $p({{x}_{1}},{{x}_{2}})$ для всех векторов (очевидно, нормированных) $A = (n, - 1)$, где $n \in \mathbb{N}$.

Перейдем теперь к рассмотрению случаев, когда разложение (2.1) является единственным для любого $A \in {{\mathbb{N}}^{n}}$ такого, что ${{\varphi }_{1}}(x)$ – главная A-квазиоднородная форма полинома p(x). При этом получение разложения (2.1) (необходимого для проверки условий леммы 3 и утверждений 13–15) для заданной главной квазиоднородной формы ${{\varphi }_{1}}(x)$ будет очень простой задачей, поскольку легко находится по любому подходящему $A \in {{\mathbb{N}}^{n}}$. Предварительно докажем некоторые утверждения.

Утверждение 22. Пусть $Y \subset {{\mathbb{R}}^{n}}$ – выпуклый многогранник, C – его собственная грань, $\operatorname{int} Y \ne \emptyset $, $H = {\text{aff }}C$, $\dim H = n - 1$. Тогда найдется вектор $e \in {{\mathbb{R}}^{n}}$, такой, что $e \ne {{0}_{{(n)}}},$ $K(C) = \left\{ {A \in {{\mathbb{R}}^{n}}\,{\text{|}}\,C = {\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle } \right\} = \left\{ {\lambda e\left| {\lambda > 0} \right.} \right\}$.

Доказательство. Пусть $L = H - {{x}^{0}} = {\text{Lin }}C$ – линейное подпространство, где x⁰ – произвольная точка из C. Покажем, что найдется ненулевой вектор $e \in {{\mathbb{R}}^{n}}$, такой, что

Заметим, что $\dim L = \dim H = n - 1 \Rightarrow \exists e \in {{\mathbb{R}}^{n}}$: $e \ne {{0}_{{(n)}}}$, $e \bot L \Rightarrow \forall x \in L$ $\left\langle {e,x} \right\rangle = 0$. Но тогда $\forall x \in C \subseteq H = L + {{x}^{0}}$ $\,\,\,x - {{x}^{0}} \in L \Rightarrow \left\langle {e,x - {{x}^{0}}} \right\rangle = 0 \Rightarrow \left\langle {e,x} \right\rangle = \left\langle {e,{{x}^{0}}} \right\rangle $.

Покажем также, что

Используя утверждение 16 г), а также то, что $e \bot L$, $\dim L = n - 1$, имеем

Пусть теперь $x{\kern 1pt} * \in \operatorname{int} Y$. Тогда $\exists \delta > 0$: $B(x{\kern 1pt} *,\delta ) \subseteq Y$. Докажем, что $\left\langle {e,x{\kern 1pt} *} \right\rangle \ne \left\langle {e,{{x}^{0}}} \right\rangle $. Заметим, что $x{\kern 1pt} * \notin C$. Если предположить противное, то в силу того, что $C$ – грань и $x{\kern 1pt} * \in C$, получим $B(x{\kern 1pt} *,\delta ) \subseteq C$, откуда $\dim H = n$, что противоречит условиям. Таким образом, $x{\kern 1pt} * \notin C$, следовательно, в силу (4.5) $\left\langle {e,x{\kern 1pt} *} \right\rangle \ne \left\langle {e,{{x}^{0}}} \right\rangle $ и для определенности $\left\langle {e,{{x}^{0}}} \right\rangle < \left\langle {e,x{\kern 1pt} *} \right\rangle $ (иначе вместо e будем рассматривать –e). Если предположить, что для некоторого другого $\tilde {x} \in \operatorname{int} Y$ не выполняется $\langle e,{{x}^{0}}\rangle \, < \,\left\langle {e,\tilde {x}} \right\rangle $, то либо $\langle e,{{x}^{0}}\rangle \, = \,\left\langle {e,\tilde {x}} \right\rangle $ (что в силу (4.5) противоречит утверждению $\tilde {x} \in \operatorname{int} Y \Rightarrow \tilde {x} \notin C$), либо $\left\langle {e,{{x}^{0}}} \right\rangle > \left\langle {e,\tilde {x}} \right\rangle $. Тогда в силу очевидной выпуклости intY получим, что для некоторых $\alpha \in (0,{\text{ }}1)$, x^α = = $\alpha \tilde {x} + (1 - \alpha )x{\kern 1pt} * \in \operatorname{int} Y$ верно $\left\langle {e,{{x}^{0}}} \right\rangle = \left\langle {e,{{x}^{\alpha }}} \right\rangle $, что, согласно (4.5), противоречит утверждению ${{x}^{\alpha }} \in \operatorname{int} Y \Rightarrow {{x}^{\alpha }} \notin C$. Таким образом, (4.4) выполняется.

Из (4.4), (4.5) следует, что $C = {\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {e,x} \right\rangle $, откуда $e \in K(C)$. Осталось показать, что если $e{\kern 1pt} * \in K(C)$, то для некоторого λ > 0   $e{\kern 1pt} * = \lambda e$. Из условия $e{\kern 1pt} * \in K(C)$ получаем (см. утверждение 21), что

откуда $\forall x \in C$ $\,\,\,\left\langle {e{\kern 1pt} *,x - {{x}^{0}}} \right\rangle = 0$, где ${{x}^{0}} \in C.$ Но тогда и для любой аффинной комбинации [11] $x$ точек из $C$ снова выполняется это равенство. Тем самым $\forall x \in H$ $\left\langle {e{\kern 1pt} *,x - {{x}^{0}}} \right\rangle = 0$, откуда $\forall x \in L$ $\left\langle {e{\kern 1pt} *,x} \right\rangle = 0$. Следовательно, $e{\kern 1pt} * \bot L$ и, согласно $e \bot L$, $\dim L = \dim H = n - 1$, найдется число $\lambda \ne 0$: $e{\kern 1pt} * = \lambda e$. При этом из (4.4), (4.6) следует, что $\lambda > 0$. Утверждение 22 доказано.

Применяя утверждения 20, 22, находим, что справедливо следующее утверждение.

Утверждение 23. Пусть $X \subset {{\mathbb{Z}}^{n}}$ – конечное непустое множество, C – собственная грань многогранника Y = CoX, $\operatorname{int} Y \ne \emptyset $, $H = {\text{aff }}C$, $\dim H = n - 1$. Тогда $\exists e \in \mathbb{Z}_{0}^{n}$: K(C) = $\left\{ {A \in {{\mathbb{R}}^{n}}\,{\text{|}}\,C = {\text{Arg }}\mathop {\min }\limits_{x \in Y} \left\langle {A,x} \right\rangle } \right\} = \{ \lambda e\,{\text{|}}\,\lambda > 0\} $.

Следствие 4. Таким образом, если выполняются условия $\operatorname{int} {\text{Co }}{{N}_{p}} \ne \emptyset $, $\dim H = n - 1$, где $H = {\text{aff Co }}{{N}_{{{{\varphi }_{1}}}}}$, то, в силу утверждения 23, разложение (2.1) является единственным для любого $A \in {{\mathbb{N}}^{n}}$, такого, что ${{\varphi }_{1}}(x)$ – главная A-квазиоднородная форма полинома p(x) (т.е. при ${{N}_{{{{\varphi }_{1}}}}} = {\text{Arg }}\mathop {\min }\limits_{x \in {{N}_{p}}} \left\langle {A,x} \right\rangle $) и получение этого разложения (необходимого для проверки условий леммы 3 и утверждений 13–15) является тривиальной задачей. Оно легко находится по указанному вектору $A \in {{\mathbb{N}}^{n}}$. Действительно, в силу утверждения 2 ${{N}_{{{{\varphi }_{1}}}}}$ = ${\text{Arg }}\mathop {\min }\limits_{x \in {{N}_{p}}} \left\langle {A,x} \right\rangle = {{C}_{1}} \cap {{N}_{p}}$, где C₁ = = ${\text{Arg}}\mathop {\min }\limits_{x \in {\text{Co }}{{N}_{p}}} \left\langle {A,x} \right\rangle $ – грань многогранника CoN_p (см. утверждение 1) и при этом ${\text{Co}}{{N}_{{{{\varphi }_{1}}}}} = {\text{Co(}}{{C}_{1}} \cap {{N}_{p}}) = {{C}_{1}}$, а следовательно, $A \in K({{C}_{1}})$, где в силу утверждения 23 K(C₁) = = $\{ A \in {{\mathbb{R}}^{n}}\,{\text{|}}\,{{C}_{1}} = {\text{Arg }}\mathop {\min }\limits_{x \in {\text{Co }}{{N}_{p}}} \left\langle {A,x} \right\rangle \} $ – одномерный конус, т.е. $K({{C}_{1}}) = \left\{ {\lambda A\,{\text{|}}\,\lambda > 0} \right\}.$ Понятно, что при выборе вместо A любого другого вектора из $K({{C}_{1}}) \cap {{\mathbb{N}}^{n}}$ разложение вида (2.1) не меняется.

Рассмотрим также случай, когда для некоторого $A \in {{\mathbb{N}}^{n}}$ для соответствующего этому A разложению (2.1) выполняется ${{N}_{{{{\varphi }_{1}}}}} = {{N}_{p}} \cap {{C}_{1}}$ , где C₁ – грань многогранника CoN_p, размерность которой ровно на 1 меньше размерности CoN_p, и при этом $\operatorname{int} {\text{Co }}{{N}_{p}} = \emptyset $, ${{C}_{1}} = {\text{Co }}{{N}_{{{{\varphi }_{1}}}}}$ (см. следствие 1). Если $\operatorname{int} {\text{Co }}{{N}_{p}} = \emptyset $, то $\dim {\text{Co }}{{N}_{p}} = n - k$, где $k \geqslant 1$. Тогда найдется совокупность линейно независимых векторов ${{e}^{{(1)}}},...,{{e}^{{(k)}}} \in {{\mathbb{Q}}^{n}}$ (учитываем, что эти векторы являются решениями системы линейных однородных уравнений с целыми коэффициентами, а следовательно, решения этой системы можно искать в поле $\mathbb{Q}$), ортогональных линейному подпространству L = = ${\text{aff Co }}{{N}_{p}} - {{y}^{{(1)}}}$, где ${{y}^{{(1)}}}$ – произвольная точка из N_p. Пусть ${{N}_{p}} = \{ {{y}^{{(1)}}},...,{{y}^{{(l)}}}\} $ и для простоты обозначений ${{N}_{{{{\varphi }_{1}}}}} = \{ {{y}^{{(1)}}},...,{{y}^{{({{l}_{{1)}}}}}}\} $. Рассмотрим систему линейных однородных уравнений (относительно вектора $e \in {{\mathbb{R}}^{n}}$):

Множество решений этой системы соответствует множеству векторов, лежащих в L и ортогональных линейному подпространству ${{L}_{1}} = {{H}_{1}} - {{y}^{{(1)}}} \subset L$, где ${{H}_{1}} = {\text{aff }}{{C}_{1}}$, размерности $n - k - 1$ (любой ненулевой вектор e, удовлетворяющий (4.7), ортогонален L₁ и дополняет базис в L₁ до базиса в L), т.е. является линейным подпространством размерности 1, а следовательно, имеет вид $\{ \lambda {{e}^{{(0)}}}\,{\text{|}}\,\lambda \in \mathbb{R}\} $, где ${{e}^{{(0)}}} \in \mathbb{Z}_{0}^{n}$ (снова учитываем, что коэффициенты системы (4.6) являются целыми или рациональными числами). Пусть для e⁽⁰⁾, кроме того, выполняется ${{N}_{{{{\varphi }_{1}}}}} = {\text{Arg }}\mathop {\min }\limits_{x \in {{N}_{p}}} \left\langle {{{e}^{{(0)}}},x} \right\rangle $. Если это не так, то меняем e⁽⁰⁾ на –e⁽⁰⁾ (см. замечание 15). Тогда любой вектор $A \in {{\mathbb{N}}^{n}}$, для которого φ₁(x) – главная A-квазиоднородная форма полинома p(x), удовлетворяет равенству

где ${{\lambda }_{0}} > 0$, ${{\lambda }_{1}},...,{{\lambda }_{k}} \in \mathbb{R}$. При любом выборе $A \in {{\mathbb{N}}^{n}}$ по формуле (4.8) разложение (2.1) остается неизменным. Таким образом, и в этом случае получение разложения (2.1) является тривиальной задачей.

Замечание 15. Приведем обоснование того, что либо для $e = {{e}^{{(0)}}}$, либо для $e = - {{e}^{{(0)}}}$ выполняется

Поскольку e в любом из этих случаев – решение системы (4.7), то 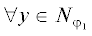$\left\langle {e,y} \right\rangle = \left\langle {e,{{y}^{{(1)}}}} \right\rangle ,$ откуда

Заметим, что

Действительно, используя то, что ${{H}_{1}} \cap {\text{Co }}{{N}_{p}} = {{C}_{1}}$ (см. утверждение 16г)), из левой части (4.11) получаем

Согласно (4.11), имеем

Теперь для доказательства (4.9) в силу (4.10), (4.12) осталось показать, что $\forall y \in {{N}_{p}}{{\backslash }}{{N}_{{{{\varphi }_{1}}}}}$. Выражение $\left\langle {e,y - {{y}^{{(1)}}}} \right\rangle $ отлично от нуля (следует из (4.12)) и имеет один знак. Действительно, предположив, что нашлись $y,\tilde {y} \in {{N}_{p}}{{\backslash }}{{N}_{{{{\varphi }_{1}}}}}$, для которых $\left\langle {e,y - {{y}^{{(1)}}}} \right\rangle $, $\left\langle {e,\tilde {y} - {{y}^{{(1)}}}} \right\rangle $ имеют разные знаки, получаем, что для некоторого $\alpha \in (0,{\text{ }}1)$ для ${{y}^{\alpha }} = \alpha y + (1 - \alpha )\tilde {y}$ выполняется ${{y}^{\alpha }} \in {\text{Co }}{{N}_{p}}$, $\left\langle {e,{{y}^{\alpha }} - {{y}^{{(1)}}}} \right\rangle = \alpha \left\langle {e,y - {{y}^{{(1)}}}} \right\rangle + (1 - \alpha )\left\langle {e,\tilde {y} - {{y}^{{(1)}}}} \right\rangle $ = 0, откуда в силу (4.11) 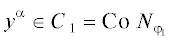. Но тогда, используя то, что C₁ – грань, получаем $y,\tilde {y} \in {{C}_{1}}$, а это противоречит (4.10).

Пример 9. Ранее в примере 1 рассматривался полином $p({{x}_{1}},{{x}_{2}})$ = $x_{1}^{2}x_{2}^{6}$ – $2x_{1}^{4}x_{2}^{5}$ + + $x_{1}^{6}x_{2}^{4} + x_{2}^{{10}} - 10{{x}_{1}}x_{2}^{9} - 0.1x_{1}^{8}x_{2}^{4}$ с

у которого (см. рисунок) $\psi ({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 2x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4}$ – главная (1, 2)-квазиоднородная полиномиальной форма. Поскольку полином $\psi ({{x}_{1}},{{x}_{2}})$ не является невырожденным в слабом смысле (см. пример 7), то в этом случае теорема и лемма 1 “не работают”, т.е. требуются более тонкие исследования. 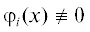Рассмотрим разложение вида (2.1) для полинома $p({{x}_{1}},{{x}_{2}})$ на сумму (1, 2)-квазиоднородных форм вида где A = (1, 2), , $\forall k \in {{N}_{{{{\varphi }_{i}}}}}$ $\left\langle {A,k} \right\rangle = {{B}_{i}}$, $i = \overline {1,r} $, при этом ${{B}_{1}} < {{B}_{2}} < \cdots < {{B}_{r}}$. В нашем случае r = 4, ${{\varphi }_{1}}({{x}_{1}},{{x}_{2}}) = \psi ({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 2x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4}$, B₁ = 14, ${{\varphi }_{2}}({{x}_{1}},{{x}_{2}}) = - 0.1x_{1}^{8}x_{2}^{4}$, B₂ = 16, ${{\varphi }_{3}}({{x}_{1}},{{x}_{2}}) = - 10{{x}_{1}}x_{2}^{9}$, ${{B}_{3}} = 19$, ${{\varphi }_{4}}({{x}_{1}},{{x}_{2}}) = x_{2}^{{10}}$, B₄ = 20. Заметим, что

Например, при $(1,{\text{ }}1) \in {{H}_{{{{\varphi }_{1}}}}}$ верно ${{\varphi }_{2}}(1,{\text{ }}1) = - 0.1 < 0$. Следовательно, условия леммы 3 не выполняются при i = 2, т.е. (0, 0) не является точкой локального минимума полинома $p({{x}_{1}},{{x}_{2}})$. Рассмотрим теперь полином ${{p}_{3}}({{x}_{1}},{{x}_{2}})$, отличающийся от $p({{x}_{1}},{{x}_{2}})$ только одним членом: вместо монома $ - 0.1x_{1}^{8}x_{2}^{4}$ у ${{p}_{3}}({{x}_{1}},{{x}_{2}})$ присутствует моном $0.1x_{1}^{8}x_{2}^{4}$, т.е. в разложении вида (2.1) в случае $A = (1,{\text{ }}2)$ для полинома ${{p}_{3}}({{x}_{1}},{{x}_{2}})$ справедливо ${{\varphi }_{2}}({{x}_{1}},{{x}_{2}}) = 0.1x_{1}^{8}x_{2}^{4}$. Как уже отмечалось в примере 6, пользуясь методами из разд. 3, нетрудно показать, что у полинома ${{p}_{3}}({{x}_{1}},{{x}_{2}})$ (так же, как у полинома $p({{x}_{1}},{{x}_{2}})$ из примеров 1, 6) всего имеются пять квазиоднородных форм, которые при некоторых $A \in {{\mathbb{N}}^{2}}$ являются главными A-квазиоднородными формами этого полинома: $\psi ({{x}_{1}},{{x}_{2}}) = x_{1}^{2}x_{2}^{6} - 2x_{1}^{4}x_{2}^{5} + x_{1}^{6}x_{2}^{4}$ (A = (1, 2)), $x_{2}^{{10}}$ ($A = (3,{\text{ 1)}}$), $x_{1}^{2}x_{2}^{6} + x_{2}^{{10}}$ (A = (2, 1)), $x_{1}^{2}x_{2}^{6}$ (A = (1, 1)), $x_{1}^{6}x_{2}^{4}$ (A = (1, 3)). При этом последние четыре формы будут неотрицательными и невырожденными в слабом смысле. Заметим, что в этом примере $\operatorname{int} {\text{Co }}{{N}_{p}} \ne \emptyset $, что дает возможность использовать следствие 4 (см. также следствие 3). Таким образом, осталось рассмотреть случай разложения (2.1) для A = (1, 2). Тогда

и

Следовательно, в силу утверждения 13 точка (0, 0) является точкой локального минимума полинома ${{p}_{3}}({{x}_{1}},{{x}_{2}})$.

5. Примеры задач, в которых возможно использование предложенных методов. Пример 10 (нахождение равновесных состояний сложной системы). Рассмотрим систему из n молекул (частиц, тел и т.д.). Между каждыми двумя молекулами действует сила отталкивания и сила притяжения. Требуется определить равновесные (т.е. устойчивые) состояния для этой системы. Известно, что потенциал (Леннарда-Джонса) взаимодействия двух молекул i, j определяется формулой

где r_ij – расстояние между ними, $C_{{ij}}^{{(6)}},\;C_{{ij}}^{{(12)}}$ – постоянные величины, первый член в правой части соответствует силе отталкивания, а второй – силе притяжения. Будем для простоты считать, что общий потенциал взаимодействия $n$ молекул выражается формулой (простой учет всех попарных взаимодействий) где $x = ({{x}_{1}},{{x}_{2}},{{x}_{3}},...,{{x}_{{3n - 2}}},{{x}_{{3n - 1}}},{{x}_{{3n}}}) \in {{\mathbb{R}}^{{3n}}}$, $({{x}_{{3i - 2}}},{{x}_{{3i - 1}}},{{x}_{{3i}}})$ – координаты i-й молекулы, r_ij = = $\sqrt {{{{({{x}_{{3i - 2}}} - {{x}_{{3j - 2}}})}}^{2}} + {{{({{x}_{{3i - 1}}} - {{x}_{{3j - 1}}})}}^{2}} + {{{({{x}_{{3i}}} - {{x}_{{3j}}})}}^{2}}} $ (рассмотрение общего потенциала конфигурации молекул при более общих предположениях несколько усложнит вид функции Φ(x), но не потребует новых идей). Тогда устойчивым состояниям рассматриваемой системы соответствуют точки локального минимума функции Φ(x). При этом функция Φ(x) является аналитической, т.е. раскладывается в степенной ряд в окрестности любой точки с ${{r}_{{ij}}} \ne 0$ при всех i < j (это условие естественным образом выполняется). Поскольку функция Φ(x) будет бесконечно гладкой, то для нахождения точек локального минимума можно применять любой градиентный метод, например метод сопряженных градиентов. Стартуя из некоторой выбранной точки, сходимся к одной из стационарных точек, т.е. с градиентом функции Φ(x), равным нулю. Применяя предложенную в настоящей работе методику, определяем, является ли найденная точка точкой локального минимума или нет. Помещая первую молекулу в начало координат, количество переменных можно сократить на три. В случае трех молекул можно расположить их на координатной плоскости, первую – в начале координат, а вторую – на одной из осей. Таким образом, в случае трех молекул понадобятся только три переменные. Соответственно, в случае четырех молекул понадобятся шесть переменных, в случае пяти – 10 переменных и т.д.

Пример 11 (использование метода наименьших квадратов для определения неизвестных параметров по набору значений параметрической функции). Пусть $\varphi ({{c}_{1}},...,{{c}_{l}},t)$ – некоторая заданная полиномиальная или аналитическая функция переменной $t \in \mathbb{R}$, зависящая от параметров ${{c}_{1}},...,{{c}_{l}} \in \mathbb{R}$, например,

Пусть, далее, каким-то образом определены значения функции

где $c = ({{c}_{1}},...,{{c}_{{lr}}}) \in {{\mathbb{R}}^{{lr}}}$, на некоторой конечной сетке значений: $t \in T = \left\{ {{{t}_{1}},...,{{t}_{q}}} \right\}$, т.е. заданы числа ${{F}_{i}} = \Phi (c,{{t}_{i}})$, $i = 1,...,q$. Требуется найти неизвестные значения $c = ({{c}_{1}},...,{{c}_{{lr}}})$. Такая задача часто возникает при обработке и анализе результатов физических экспериментов. Для решения указанной задачи можно воспользоваться методом наименьших квадратов. Составляется функция и ищется ее минимум по $c = ({{c}_{1}},...,{{c}_{{lr}}})$. Поскольку нахождение глобального минимума – крайне сложная задача (особенно для большого числа переменных), то применяем какой-нибудь градиентный метод минимизации (с учетом того, что целевая функция является сколь угодно гладкой), например методом сопряженных градиентов. Стартуем из какой-нибудь начальной точки, обычно выбираемой исходя из содержательной части задачи. В результате спускаемся к некоторой стационарной точке $\bar {c}$, для которой $\Gamma {\kern 1pt} '(\bar {с}) = {{0}_{{(lr)}}}$. Далее, применяя предложенную в настоящей работе методику, определяем, является ли $\bar {c}$ точкой локального минимума или нет. Если $\bar {c}$ – точка локального минимума и значение $\Gamma (\bar {с})$ близко к 0, то считаем, что $\bar {c}$ – приемлемое решение задачи. В противном случае стартуем из некоторой другой начальной точки и т.д.

Пример 12 (идентификация параметров динамических систем). В работе [13] рассматривается один из возможных способов решения задачи оценки неизвестных параметров динамических моделей, описываемых дифференциально-алгебраическими уравнениями. Оценка параметров производится по результатам наблюдений за поведением математической модели. Их значения находятся в результате минимизации критерия, описывающего суммарное квадратическое отклонение значений координат вектора состояния от полученных при измерениях точных значений в различные моменты времени. Таким образом, в [13] рассматривается целевая функция

при ограничениях: где $f(t,x,\theta )$ − известная непрерывно-дифференцируемая вектор-функция, $t \in [{{t}_{0}},{{t}_{e}}]$ – время функционирования системы, $\theta \in \Theta $ − вектор неизвестных параметров системы, $\Theta \subseteq {{\mathbb{R}}^{p}}$ − множество возможных значений параметров, $x \in {{\mathbb{R}}^{n}}$ − вектор состояния системы, ${{x}^{{(0)}}} \in {{\mathbb{R}}^{n}}$ − вектор начального состояния. На промежутке времени $[{{t}_{0}},{{t}_{e}}]$ известны наблюдения $\hat {x}(t)$ за вектором состояния системы в моменты времени $t = {{t}_{j}} \in [{{t}_{0}},{{t}_{e}}]$, $j = 1,...,T$. При фиксированном векторе параметров θ можно найти решение x(θ, t) системы дифференциальных уравнений. Требуется определить оценку вектора неизвестных параметров θ, при которой x(θ, t) наилучшим образом согласуется с наблюдениями, т.е. обеспечивается минимальное значение целевой функции E(θ). Для решения задачи оптимизации предлагается использовать градиентные методы оптимизации, применяемые в процедурах машинного обучения: метод стохастического градиентного спуска, классический метод моментов, ускоренный градиентный метод Нестерова, метод адаптивного градиента, метод скользящего среднего, метод адаптивной оценки моментов, модификация метода адаптивной оценки, ускоренный по Нестерову метод адаптивной оценки. В результате применения этих методов спускаемся к некоторой стационарной точке $\bar {\theta }$, для которой $E{\kern 1pt} '(\bar {\theta }) = {{0}_{{(p)}}}$. Часто оказывается, что решение системы дифференциальных уравнений $x(\theta ,t)$ является при каждом фиксированном $t \in [{{t}_{0}},{{t}_{e}}]$ либо полиномиальной, либо аналитической функцией по параметрам θ (достаточно, чтобы это выполнялось в окрестности точки $\bar {\theta }$). В этом случае, применяя предложенную в работе методику, определяем, будет ли $\bar {\theta }$ точкой локального минимума или нет. Например, работе [14] рассматривается математическая модель, описывающая необратимую реакцию первого порядка, в которой измеряются концентрации ${{x}_{1}},{{x}_{2}}$ компонент веществ, а θ₁, θ₂ − коэффициенты скоростей реакций соответственно:

В этом примере целевая функция имеет вид

т.е. является аналитической в окрестности любой точки $\theta = ({{\theta }_{1}},{{\theta }_{2}})$, в которой ${{\theta }_{1}} \ne {{\theta }_{2}}$. В найденном в [14] решении это условие выполняется.

Заключение. Предложены необходимые и достаточные условия локального экстремума для полиномов и степенных рядов, основанные на использовании многогранника Ньютона, а также разложения полинома (степенного ряда) на сумму квазиоднородных полиномиальных форм. При небольшом количестве переменных эти условия могут быть проверены с помощью практически реализуемых алгоритмов, главные идеи которых также приведены в работе. Применение предложенной методики иллюстрируется на примерах в следующих задачах: нахождения равновесных состояний сложной системы частиц (молекул), определения неизвестных параметров по набору значений параметрической функции методом наименьших квадратов, идентификации параметров динамических систем.