Известия РАН. Теория и системы управления, 2023, № 3, стр. 57-75
ОПТИМИЗАЦИЯ ФУНКЦИОНАЛА РИСКА ДЛЯ УПРАВЛЕНИЯ СОСТАВОМ И СТРУКТУРОЙ РАЗНОРОДНОЙ ГРУППИРОВКИ СЕНСОРОВ ОБНАРУЖЕНИЯ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
В. А. Дюков a, А. М. Казанцев b, *, И. Ю. Макушев c, М. С. Путилин a, А. В. Тимошенко d
a Национальный исследовательский ун-т “МИЭТ”
Москва, Россия
b АО “Радиотехнический институт имени академика А.Л. Минца”
Москва, Россия
c ПАО “МАК “Вымпел”,
Москва, Россия
d МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: kazantsev.andrei@gmail.com
Поступила в редакцию 27.06.2022
После доработки 08.08.2022
Принята к публикации 05.12.2022
- EDN: JEZOLY
- DOI: 10.31857/S0002338823020075
Аннотация
Неуклонный рост массовости и динамики применения воздушных средств в ходе различных конфликтов обуславливает необходимость постановки и решения задач построения систем их обнаружения, близких к реальности. Следует отметить, что в настоящее время вектор приоритетов в развитии сенсоров обнаружения изменяется с решения задач по повышению их характеристик на оптимизацию и адаптивность в их управлении. В качестве объекта рассматривается разнородная группировка сенсоров, решающая задачи обнаружения подвижного воздушного объекта. Предметом служит методология построения моделей управления разнородными сенсорами обнаружения. На основе анализа антагонистического взаимодействия разнородной группировки и воздушных объектов, процессов их функционирования предложен геометрический подход к решению задачи обнаружения подвижного объекта, в котором используется адаптированный и усовершенствованный функционал риска как один из возможных показателей для дальнейшего синтеза алгоритмов управления. С помощью имитационного моделирования приведено обоснование практической эффективности применения данного функционала и представлено сравнение с другими показателями эффективности.
Введение. Задача обнаружения подвижного объекта (ПО) в конфликтной среде (равно как и похожая на нее задача о нахождении оптимальной траектории ПО в конфликтной среде) изучается достаточно давно [1–11]. Под конфликтной средой, согласно [2], понимается совокупность объектов (они называются конфликтующими), сближение с которыми для управляемого объекта нежелательно в ходе выполнения им основной задачи. Как правило, ПО представляет собой воздушную цель, которая должна достигнуть контрольной точки $\left( {{{x}_{{0~}}},{{y}_{0}},~{{z}_{0}}} \right)$ либо пересечь определенную область пространства V0. Цель ПО – таким образом изменять траекторию движения и свои физические параметры (например, скорость), чтобы свести к минимуму воздействие, оказываемое со стороны сенсоров конфликтующей стороны. Цель конфликтующей стороны (сенсоров обнаружения) прямо противоположна – подобрать собственные физические параметры и так изменить свою траекторию движения, чтобы максимизировать воздействие, оказываемое на ПО.
Данная задача решена аналитически для случая пассивной радиолокации в двумерном пространстве вариационным методом для одного сенсора [1]; в случае нескольких сенсоров используется численный счет [3], основанный на алгоритме Дейкстры [12]. В [2] для тех же целей применялся метод конформных отображений, при этом был произведен учет возможных ограничений на траекторию и величину скорости ПО. Также существует возможность решать поставленную задачу с ограничениями на длину траектории методами дискретной оптимизации [4], причем как в случае пассивной, так и в случае активной радиолокации.
Существует ряд исследований (например, [11, 13]), в которых задача выбора оптимальной траектории ПО в конфликтной среде решена с помощью вероятности обнаружения подвижного объекта. В качестве альтернативы вероятности обнаружения для управления сенсором и/или ПО в ряде исследований применяется функционал риска.
В некоторых работах рассмотрена задача с нечетким положением сенсоров обнаружения. Так, в [6] приводится статистический критерий для вариационной задачи о построении оптимальной траектории движения ПО в трехмерном пространстве. Точные координаты наблюдателя полагаются неизвестными, при этом они распределены в пространстве в соответствии с некоторым априори заданным вероятностным распределением. При решении задачи управления сенсорами обнаружения относительно небольшое число работ (например, [5, 14]) затрагивают вопрос об учете особенностей рельефа, над которым совершает движение ПО.
В случае непосредственного использования представленных выше подходов в процессе управления составом и структурой разнородной группировкой сенсоров обнаружения в конфликтной среде возникают следующие трудности:
процесс взаимодействия противоборствующих сторон (ПО и сенсоров обнаружения) рассматривается как плоскостная задача, причем моделирование взаимодействия проводится в двумерном пространстве с учетом эквидистантного движения ПО (на постоянной высоте над рельефом), в то время как функционирование и сенсоров обнаружения, и ПО осуществляется в трехмерном пространстве;
ресурс сенсоров обнаружения и ПО (число и тип сенсоров, зоны их размещения, дальности полета воздушных сенсоров и др.) статичен в каждый момент времени, не рассматриваются закономерности изменения параметров и характеристик обоих сторон в динамике противоборства, обусловленные как влиянием дестабилизирующих факторов на сенсоры, так и влиянием перегрузок и других физических ограничений на характеристики ПО.
Целью настоящей работы является формализация показателя эффективности управления разнородной группировкой на основе эвристических методов, который учитывал бы физические особенности и принципы работы сенсоров обнаружения. При этом данный показатель должен обеспечивать эффективное управление составом и структурой разнородной группировкой сенсоров в конфликтной среде на заданном рельефе в трехмерном пространстве.
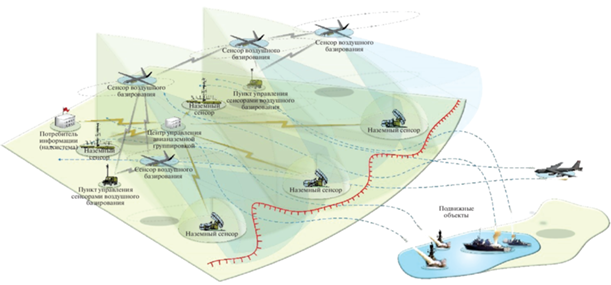
1. Постановка задачи. Рассматривается разнородная группировка сенсоров, решающая задачи радиолокационного обнаружения ПО, которые проникают в зону ее ответственности (рис. 1). Группировка состоит из сенсоров наземного базирования, включающая радиолокационные станции (РЛС), которые работают на принципах активной радиолокации и сенсоров воздушного базирования – беспилотных летательных аппаратов (БПЛА) с РЛС бокового обзора.
Целью рассматриваемой группировки является своевременное обнаружение ПО для последующей выдачи сигнала оповещения потребителю информации (надсистеме). При этом ПО имеют противоположную цель, заключающуюся в незаметном проникновении и прохождении рабочей зоны разнородной группировки сенсоров [1, 2]. Необходимо отметить, что сенсоры указанной группировки и ПО функционируют в трехмерном пространстве с учетом особенностей рельефа местности.
Противоборство между конфликтующими сторонами происходит следующим образом. Будем полагать, что атакующая сторона имеет информацию о местоположении наземных сенсоров, но не обладает информацией о местоположении сенсоров воздушного базирования и их количестве. Полет ПО осуществляется по оптимальным траекториям из начальной (случайной по одной из координат, но фиксированной по двум другим) в конечную (заданную) точки, при этом все ПО начинают свое движение одновременно. Конфликтующая сторона не обладает информацией о том, в каком количестве и с какого направления движутся ПО, но она может изменять векторы параметров наземных сенсоров (например, выбирать мощность и рабочий диапазон РЛС), а также выбирать траекторию движения БПЛА таким образом, чтобы их зоны патрулирования обеспечивали прикрытие наиболее проблемных зон с точки зрения возможности необнаружения ПО.
ПО считается обнаруженным сенсором воздушного базирования в том случае, если он попал в сектор обзора бортовой РЛС БПЛА либо находился в секторе обзора наземной РЛС в течение времени, превышающего некий заданный порог. Критерием эффективности группировки сенсоров обнаружения будем считать процент обнаруженных ПО.
Таким образом, необходимо разработать научно-методический аппарат управления составом и структурой разнородной группировкой сенсоров обнаружения с адаптивной пространственно-разнесенной структурой на основе показателя, учитывающего физические особенности активной радиолокации.
2. Анализ научно-методического аппарата управления группировкой средств. Как показывают результаты исследований, прямая задача – задача обнаружения ПО, равно как и обратная – задача о нахождении оптимальной траектории ПО в конфликтной среде, может быть решена различными способами.
В ряде работ задача выбора оптимальной траектории ПО решена с использованием вероятности обнаружения подвижного объекта. Так, в исследовании [11] задача решена кинематически в реальном времени. В качестве ПО выбран малозаметный БПЛА и предложены различные сценарии и алгоритмы, основанные на алгоритме A-star [15]. A-star представляет собой алгоритм поиска по первому наилучшему совпадению на графе, который находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), и является развитием алгоритма Дейкстры [12]. Указанный алгоритм успешно применяется для решения различных задач [16]. Среди прочих алгоритмов поиска A-star отличается доказанной допустимостью и оптимальностью, а также полнотой. Для системы с одним сенсором, если известны вероятность обнаружения и вероятность ложной тревоги, вероятность обнаружения ПО связана только с расстоянием от ПО до сенсора:
(2.1)
${{P}_{t}} = \frac{1}{{1 + {{{\left( {\frac{{{{c}_{2}}\rho _{i}^{4}}}{\sigma }} \right)}}^{{{{c}_{1}}}}}}},$Отметим, что при решении задач управления воздушными средствами довольно успешно используются методы теории управления. Например, в [17] воздушная дуэль между БПЛА и ПО противника рассматривается с позиции игровой задачи. В работе получен алгоритм гарантирующего управления траекторией беспилотного перехватчика на этапе его сближения с маневрирующей воздушной целью, пригодный для потенциальной бортовой реализации, в серии вычислительных экспериментов доказана его эффективность. Задача решается с использованием матричных методов, а также методов численного моделирования. К недостаткам данного исследования можно отнести предположение о том, что любому из конфликтующих ПО доступна информация о его собственном текущем состоянии (положении, скорости), а также о положении и скорости ПО противника. Данное предположение существенно ограничивает потенциальную применимость алгоритма.
В [18] описаны архитектура и алгоритмы интеллектуальной системы управления ударно-разведывательной группы БПЛА, представлен метод планирования предполетной миссии, основанный на триангуляции Делоне, а также алгоритмы распознавания тактических ситуаций и принятия решений. В качестве примера рассмотрен алгоритм управления групповым полетом БПЛА типа “ведущий-ведомый”, базирующийся на пропорциональном интегродифференциальном регуляторе. Показано, что представленный вариант реализации системы управления ведомого БПЛА обеспечивает выдерживание заданной конфигурации строя даже при многократном маневрировании ведущего БПЛА по скорости и курсу. Заметим, что задача решена в двумерном пространстве. В трехмерном случае используемый метод может перестать соответствовать физической реальности. Так, например, вследствие наличия рельефа местности и вектора характеристик источников угрозы, отличного от двумерного, изменятся области потенциальной угрозы, и решение, полученное с помощью простейшего трехмерного обобщения метода Делоне, станет неэффективным.
Отметим также, что алгоритмы, базирующиеся на решении игровых задач по противоборству сторон в конфликтной среде, применимы для задач поражения ПО и практически бесполезны в задачах обнаружения ПО, где в качестве показателя должна быть задействована вероятность обнаружения или же какой-либо альтернативный показатель. Это происходит из-за того, что в задачах обнаружения отсутствует непосредственный контакт между ПО конфликтующих сторон, а противодействие зачастую происходит в условиях недостатка информации о состоянии и стратегии противника.
Альтернативой вероятности обнаружения, важным показателем для управления сенсором и/или ПО, является функционал риска. Согласно определению, данному в [2] для задач пассивной радиолокации, риск – это величина, пропорциональная интегральному уровню принятого наблюдателем сигнала, излученного подвижным объектом и прошедшего через среду распространения за время движения объекта по маршруту. Различают такие понятия, как полный и мгновенный риск. Полный риск определяет риск для ПО быть обнаруженным за время всего движения объекта до контрольной точки, мгновенный – в данный момент времени.
В зависимости от метода решения может использоваться как функционал, так и функция риска. Здесь и далее без ограничения общности и памятуя о том, что изначально задача обнаружения подвижного объекта в конфликтной среде решалась методами вариационного исчисления, будем говорить о функционале риска. Отметим, что риск коррелирует с вероятностью обнаружения ПО, но не сводится к вероятности в классическом смысле, поскольку не выполняется условие нормировки.
Формула риска, как правило, задается эвристически исходя из определенных физических соображений. В ряде исследований используется так называемая степенная модель, в которой риск r за единицу времени (или за единицу траектории) пропорционален уровню интенсивности сигнала ${{I}_{i}}$, принимаемого на входе i-го сенсора. Данный риск зависит как от скорости ПО ${v}$, так и от расстояния $\rho $ от ПО до сенсора обнаружения:
Необходимо отметить, что физическая интерпретация сигнала может быть различной в зависимости от источника сигнала и рассматриваемого поля [3]. Например, для гидроакустического поля $m = 1,$ $n = 2$ (2.2). Это соответствует изменению уровня интенсивности излучаемого сигнала пропорционально квадрату скорости объекта и распространению сигнала в среде по сферическому закону.
При этом во многих моделях риск аддитивен: полный риск R за единицу времени для данного ПО равен сумме рисков обнаружения для различных сенсоров:
Другими словами, в качестве полного риска может выступать интегральный уровень сигнала, принятый системой из N наземных сенсоров за все время движения. Для этого нужно проинтегрировать полученное значение “мгновенного” риска либо по всему времени движения ПО до контрольной точки, либо по всей траектории движения:
где $r(t),$ $r(s)$ – “мгновенный” риск обнаружения ПО сенсором в момент времени $t$ и участке траектории s соответственно; $T$ – общее время движения ПО; $L$ – общая длина траектории движения ПО.Такой способ задания функционала риска является популярным, но отнюдь не единственным. В [1, 2] используется функционал риска следующего вида ($n = 2$):
(2.6)
$R = \mathop \smallint \limits_0^T \frac{{{{{({{{\dot {x}}}^{2}} + {{{\dot {y}}}^{2}})}}^{m}}}}{{{{x}^{2}} + {{y}^{2}}}}dt,$В [3] риск для N сенсоров задан с учетом их местоположения:
(2.7)
$R = \mathop \smallint \limits_0^T \mathop \sum \limits_{i = 1}^N \frac{{{{{({{{\dot {x}}}^{2}} + {{{\dot {y}}}^{2}})}}^{m}}}}{{{{{({{{\left( {x\left( t \right) - {{a}_{i}}} \right)}}^{2}} + {{{\left( {y\left( t \right) - {{b}_{i}}} \right)}}^{2}})}}^{{n/2}}}}}dt,$В [4] применяют следующий функционал риска для N сенсоров:
(2.8)
$R = \mathop \smallint \limits_A^B \mathop \sum \limits_{i = 1}^N \frac{{{{\sigma }_{i}}}}{{{{\rho }_{i}}^{2}}}ds,$Ключевым недостатком риска в выражениях (2.6)–(2.8) является отсутствие учета в функционале риска технических характеристик сенсоров обнаружения. Как правило, в качестве наземного сенсора выступает РЛС с вполне определенным вектором параметров, в который входит дальность действия, рабочий диапазон частот, форма диаграммы направленности и т.п. [19, 20]. Именно эти параметры определяют эффективность работы наземного сенсора по обнаружению ПО. Более того, ПО обладает таким важным параметром, как эффективная площадь рассеяния. Функционал риска в формуле (2.4)–(2.7) не учитывает ЭПР, а в формуле (2.8) учитывает ЭПР, но не учитывает вектор параметров наземного сенсора. Кроме того, как функционалы (2.4)–(2.7), так и функционал (2.8) справедлив лишь для решения плоскостных задач.
Существует ряд попыток рассмотреть задачу с нечетким положением сенсоров обнаружения. Так, в [6] рассматривается статистический критерий для вариационной задачи о построении оптимальной траектории движения ПО в трехмерном пространстве. Точные координаты наблюдателя полагаются неизвестными, распределенными в пространстве в соответствии с некоторым априори заданным вероятностным распределением. В качестве функционала риска вариационной задачи принимается математическое ожидание интегрального функционала потерь детерминированной задачи, зависящего от некоторого случайного параметра, который задается формулами (2.2)–(2.4). Недостаток у приведенной работы все тот же – отсутствует учет вектора параметров сенсора обнаружения.
Некоторые исследования проводятся в предположении, что распределение риска в пространстве задано и известно подвижному объекту. В [7] представлена стратегия движения ПО в области вероятностной угрозы, карта которой известна заранее. Оптимальные траектории находятся с помощью деревьев решений. Риски сенсоров обнаружения задаются в виде гауссовой функции плотности вероятностного распределения:
(2.9)
${{f}_{i}}\left( {x,y} \right) = \left\{ {\frac{1}{{2\pi \sqrt {\det \left( {{{K}_{i}}} \right)} }}} \right\}\exp \left[ { - \frac{1}{2}{{{\left( {X - {{\mu }_{i}}} \right)}}^{{\text{T}}}}{{K}_{i}}^{{ - 1}}\left( {X - {{\mu }_{i}}} \right)} \right],$(2.10)
$X = \left[ {\begin{array}{*{20}{c}} x \\ y \end{array}} \right],\quad {{\mu }_{i}} = \left[ {\begin{array}{*{20}{c}} {{{\mu }_{i}}\left( x \right)} \\ {{{\mu }_{i}}\left( y \right)} \end{array}} \right],\quad {{K}_{i}} = \left[ {\begin{array}{*{20}{c}} {{{\sigma }_{i}}{{{\left( x \right)}}^{2}}}&0 \\ 0&{{{\sigma }_{i}}{{{\left( y \right)}}^{2}}} \end{array}} \right],$Зачастую при расчете оптимальной траектории движения объектов в конфликтной среде используются методы динамического программирования. Так, в [8] рассматривается двумерная задача поиска оптимальных траекторий ПО в конфликтной среде. Функционал риска экспоненциально убывает с расстоянием от источника, что удобно для построения математической модели, но не имеет внятной интерпретации с точки зрения физического смысла:
(2.11)
$R\left( {{{\rho }_{i}}} \right) = K{{e}^{{ - \alpha {{\rho }_{i}}}}},\quad {{\rho }_{i}} = \sqrt {{{{\left( {x - {{x}_{i}}} \right)}}^{2}} + {{{\left( {y - {{y}_{i}}} \right)}}^{2}}} ,$Весьма перспективными для управления составом и структурой разнородной группировкой сенсоров на заданном рельефе в конфликтной среде являются генетические алгоритмы. В [9] используется генетический алгоритм поиска оптимальной траектории ПО на плоскости, учитывающего особенности рельефа. В этом случае применяется следующий функционал риска:
(2.12)
$r\left( {x,y} \right) = \mathop \sum \limits_{i = 1}^n \frac{{{{Г}_{i}}}}{{\sqrt {{{{\left( {x - {{x}_{i}}} \right)}}^{2}} + {{{\left( {y - {{y}_{i}}} \right)}}^{2}}} }},$В [10] решена детерминированная трехмерная задача определения оптимальной траектории ПО в конфликтной среде с переменной ЭПР. Эффективная поверхность рассеяния подвижного объекта описывается эллипсоидом c площадью поверхности ${{S}_{i}}$ и константой ${{\sigma }_{i}}$, представляющей технические параметры сенсора (дальность обнаружения, мощность, рабочий диапазон). Для i-го сенсора обнаружения риск имеет вид
(2.13)
${{r}_{i}} = \frac{{RS{{C}_{i}}}}{{{{{\left\| {{{\rho }_{i}}} \right\|}}^{2}}}} = \frac{{{{\sigma }_{i}}{{S}_{i}}}}{{{{{\left\| {{{\rho }_{i}}} \right\|}}^{2}}}},$Полный риск можно найти при использовании методического аппарата, представленного в (2.3), (2.5) и (2.13), в которых приведены как аналитические, так и численные методы решения: аналитически получено решение в квадратурах с помощью вариационного метода (метода множителей Лагранжа) для случая одного сенсора. Численно задача решается для нескольких сенсоров обнаружения с помощью методов дискретной оптимизации. Технические параметры сенсора обнаружения представлены отдельной константой. В качестве недостатков данной работы можно отметить зависимость найденного решения от параметра ЭПР (формы эллипсоида) и недостаточный учет других характеристик РЛС, а также пренебрежение физическими особенностями движения ПО.
Таким образом, главным недостатком большей части описанных работ является модельное двумерное рассмотрение, что во многом обусловлено вычислительными особенностями – добавление еще одной координаты создает существенные трудности в численных решениях; в некоторых аналитических решениях переход к пространству с большей размерностью становится непреодолимой проблемой. Вместе с тем все современные ПО обладают в трехмерном пространстве высокими маневренными характеристиками. Возможность изменять высоту в широком диапазоне приводит к тому, что для ряда практически важных задач, требующих высокой точности либо учета изменения положения объектов в реальном времени, двумерное рассмотрение оказывается неприменимым. При данных обстоятельствах возникает необходимость разработки показателя эффективности, который нивелировал бы вышеуказанные ограничения.
3. Формализация показателя управления разнородной группировкой средств обнаружения. Рассмотрим вопрос построения показателя эффективности управления разнородной группировкой средств обнаружения. В качестве основных исходных данных примем:
методологию функционала риска для оптимального размещения сенсоров обнаружения и динамического управления ими;
степенную модель риска – формула (2.2), для которого должен выполняться принцип суперпозиции (2.3); формула полного риска должна иметь вид (2.4);
риск должен быть универсальным показателем, характеризующим эффективность группировки в целом, при этом он должен иметь смысл вероятностной меры, т.е. коррелировать с вероятностью обнаружения ПО.
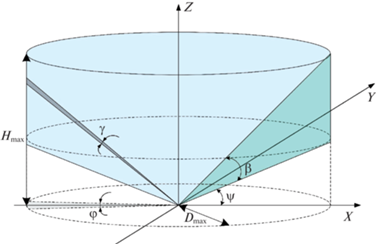
Для того, чтобы учесть в функционале риска физические принципы работы наземных сенсоров, рассмотрим принцип функционирования РЛС кругового обзора. В высокоточных наземных сенсорах кругового обзора реализуется в основном последовательный обзор пространства узким лучом, сканирующим каждую его точку пространства в пределах своей рабочей зоны с определенным периодом $T$. Вероятность попадания ПО в луч в одной точке, принадлежащей пространству зоны обнаружения сенсора, определяется следующим образом:
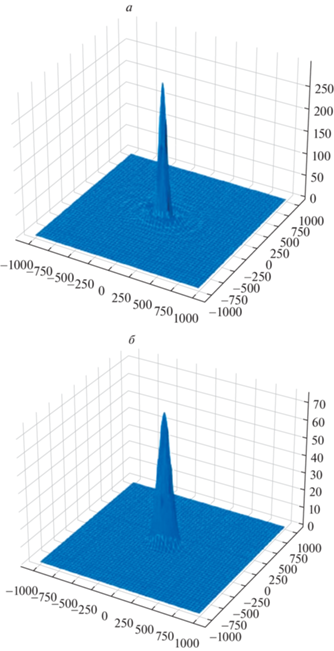
где $\gamma $ и $\varphi $ – ширина сканирующего луча в азимутальной и угломестной плоскостях, $\beta $ – ширина сектора сканирования луча в угломестной плоскости (рис. 2).При этом вероятность обнаружения ПО на дальности, не превышающей заданную в технических характеристиках сенсора, будет равна $P \approx 1$, в остальных случаях $P \approx 0$. Отметим, что многие РЛС состоят из системы фазированных антенных решеток (ФАР), причем совокупная диаграмма направленности системы ФАР может иметь различный вид [21] (рис. 3). Отметим, что, во-первых, диаграмма направленности, как правило, обладает аксиальной симметрией. Во-вторых, сканирование воздушного пространства – это периодический процесс, поэтому представляется возможным провести усреднение движения сканирующего луча по пространству.
Рис. 3.
Трехмерное моделирование диаграммы направленности РЛС: а – ${{\sin }^{2}}x$, б – ${{\cos }^{2}}x$
Для наземных РЛС с большой дальностью обнаружения объем сканирующего луча гораздо меньше объема зоны обнаружения, что позволяет представить средство обнаружения в виде пространственно-распределенного тела его рабочей зоны, в пределах которого обнаружение ПО с заданными характеристиками производится с вероятностью не ниже заданной. Для средства кругового обзора данное тело получается вращением фигуры – образующей конуса – относительно вертикали, описывающей зону обзора пространства в вертикальной плоскости. При этом конус позволяет менять угол места, радиус наземного средства, а также координаты его расположения и дальность обнаружения.
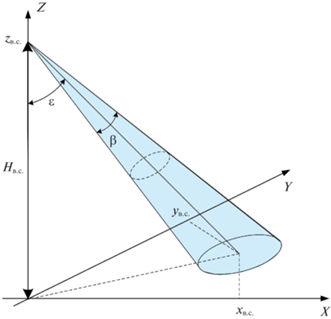
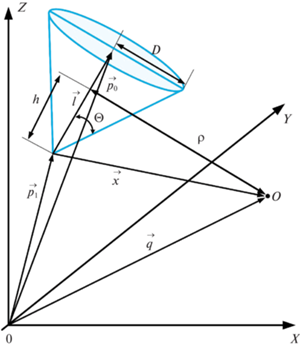
Модель воздушного сенсора аналогично задается фигурой, представленной на рис. 4 в виде конуса. Исходными данными являются координаты начального местоположения сенсора $({{x}_{{{\text{в}}{\text{.с}}}}},{{y}_{{{\text{в}}{\text{.с}}}}},{{z}_{{{\text{в}}{\text{.с}}}}})$, высота его полета ${{H}_{{{\text{в}}{\text{.с}}}}}$, ширина сектора зоны обнаружения $\beta $, угол наклона $\varepsilon $.
Таким образом, вектор параметров сенсоров обнаружения фактически задает геометрические параметры полученного конуса, т.е. вопрос обнаружения ПО в некотором смысле сводится к геометрической задаче.
Определим аналитическое выражение критерия обнаружения ПО для наземного сенсора. Пусть ПО пролетает зону обнаружения системы мониторинга за время $\tau $, зависящее от скорости его движения и выбранной траектории. Наземный сенсор производит последовательное сканирование пространства лучом; он обнаруживает цель с вероятностью $P = 1$ при условии, что ПО находится в зоне обнаружения сенсора и $T < \tau $. Вероятность обнаружения ПО можно представить как функцию от дискретного времени с равномерным законом распределения. В таком случае вероятность обнаружения ПО сенсором будет равна
Процесс пространственного размещения сенсоров решается как задача оптимизации на основе максимизации вероятности обнаружения в зоне ответственности разнородной группировки. В качестве исходных данных используются число, типы и характеристики сенсоров. Данная задача решается в два этапа: на первом этапе осуществляется расстановка сенсоров наземного базирования, а на втором – выбор районов барражирования сенсоров воздушного базирования.
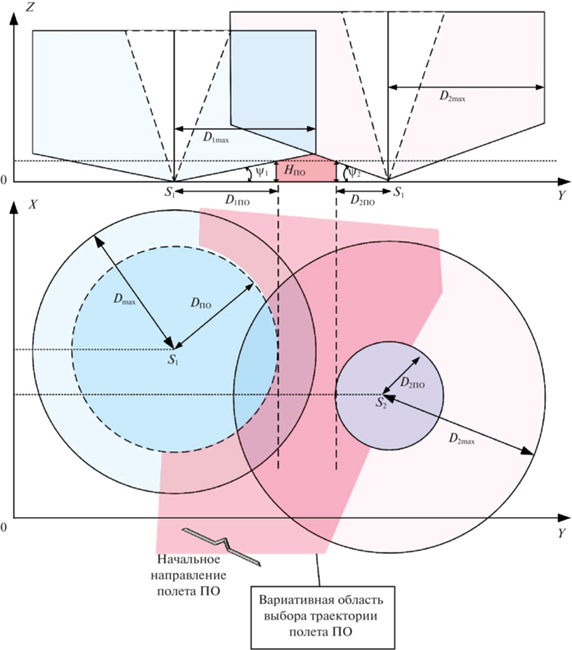
Средства наземного базирования размещаются по принципу максимального охвата зоны, подконтрольной группировке, как с учетом тактико-технических характеристик сенсоров на конкретном рельефе местности, так и с учетом характерных высот зон обнаружения. Оптимальное размещение сенсоров воздушного базирования направлено на компенсацию недостатков в зоне обнаружения наземных сенсоров, прежде всего на высотах полета ПО ${{H}_{{{\text{ПО}}}}}$(рис. 5). ПО выбирает свою траекторию таким образом, чтобы в процессе полета не попадать в зоны обзора наземных сенсоров обнаружения.
Модель наземного сенсора (рис. 2) позволяет задать пространственное распределение зоны обнаружения, которое описывается фигурой вращения, определяемой следующим образом:
где $\psi $ – угол между горизонтальной плоскостью и поверхностью конуса при расположении вершины в начале координат, позволяющий учитывать характеристики сенсоров, такие, как угол нижней границы зоны обнаружения.В искомое выражение, очевидно, должны входить координаты расположения сенсора обнаружения. Имеем
Представленная выше формула позволяет определить, находится ли рассматриваемая точка пространства внутри конуса, на его поверхности или же располагается вне конуса:
Отметим, что в знаменатель получаемого выражения необходимо добавить малое слагаемое $\delta $ – так называемое регуляризационное слагаемое. Данное малое положительное слагаемое необходимо вводить, чтобы избавиться от бесконечно большого риска на вертикальной оси, проходящей через сенсор. Возникновение бесконечного риска на оси может приводить к нежелательным последствиям при численном счете.
В результате для функционала риска наземного сенсора было получено следующее выражение:
(3.1)
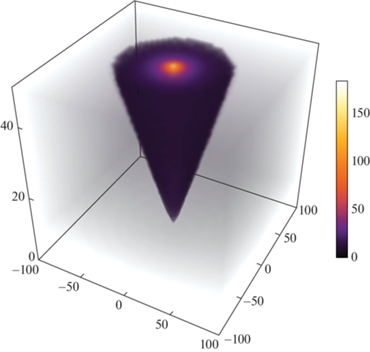
${{r}_{i}}\left( {x,y,z} \right) = {{\sigma }_{i}}\frac{{z - {{z}_{i}}}}{{\sqrt {{{{\left( {x - {{x}_{i}}} \right)}}^{2}} + {{{(y - {{y}_{i}})}}^{2}} + \delta } }}\frac{1}{{{\text{tg}}\left( {{{\psi }_{i}}} \right)}}H({{z}_{i}} - {{z}^{{{\text{max}}}}})H(\sqrt {x_{i}^{2} + y_{i}^{2} + z_{i}^{2}} - {{r}^{{{\text{max}}}}}),$Рис. 6.
Пример конуса, ограниченного плоскостью сверху и сферой по боковой поверхности, ${{r}^{{\max }}} = 300$ км, ${{z}^{{\max }}} = 100$ км. Масштаб по горизонтальной и по вертикальной осям различен
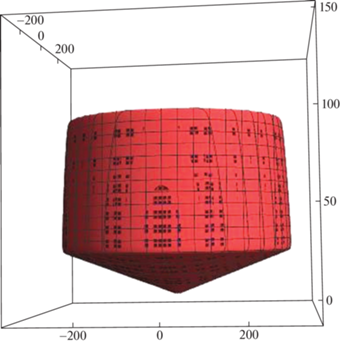
С помощью функции Хевисайда $H(z - \sqrt {{{x}^{2}} + {{y}^{2}}~} {\text{tg}}\left( {{{\psi }_{i}}} \right))$ можно вырезать “мертвую” воронку в центральной части конуса, так как излишняя детализация почти не влияет на результаты, ${{\sigma }_{i}}$ – множитель, отвечающий за вектор характеристик i-го наземного средства. При исправном средстве ${{\sigma }_{i}} = 1$, в случае технических неисправностей ${{\sigma }_{i}} < 1$, при полном выходе сенсора из строя ${{\sigma }_{i}} = 0$. Другими словами, множитель ${{\sigma }_{i}}$ напрямую связан с возможными отказами в работе сенсоров обнаружения: при возникновении неисправностей зона обнаружения i-го сенсора сужается вплоть до полного выхода сенсора из строя, а дальность обнаружения – пропорционально; ${{\psi }_{i}}$ – угол между линией горизонта и нижней границей зоны обнаружения i-го наземного сенсора.
Для группировки N наземных сенсоров в силу принципа суперпозиции функционал риска может быть представлен в виде
(3.2)
$R\left( {x,y,z} \right) = \mathop \sum \limits_i^N {{\sigma }_{i}}\frac{{z - {{z}_{i}}}}{{\sqrt {{{{(x - {{x}_{i}})}}^{2}} + {{{(y - {{y}_{i}})}}^{2}} + \delta } {\text{tg}}\left( {{{{{\psi }}}_{i}}} \right)}}H({{z}_{i}} - z_{i}^{{{\text{max}}}})~H(\sqrt {x_{i}^{2} + y_{i}^{2} + z_{i}^{2}} - {{r}_{i}}^{{{\text{max}}}}),$Введенный функционал риска имеет следующий смысл: чем больше данный функционал, тем выше вероятность того, что ПО, находящийся в данной точке пространства, будет обнаружен группировкой сенсоров обнаружения. Важно отметить, что риск не пропорционален интегральному уровню принятого наблюдателем сигнала, излученного воздушным объектом и прошедшего через среду распространения за время движения объекта по маршруту, как это было в степенной модели (2.2). Таким образом, необходимо определить минимум функции $R\left( {x,y,z} \right)$. Окрестности точки минимума и определяют местоположение зоны обнаружения и самого сенсора воздушного базирования. Добавление еще одной зоны обнаружения изменяет значение функции риска $R$, что требует ее пересчета с учетом особенностей вновь добавленной зоны, которые заключаются, кроме отличий по форме и ее направленностью на земную поверхность (рис. 4), в геометрической интерпретации при повороте конуса.
Отметим, что в случае воздушного сенсора функционал риска (3.1) несколько видоизменится за счет естественного поворота системы координат, в которой описывается конус. Пересчет функции риска выражается путем введения дополнительного слагаемого, учитывающего особенности сенсора воздушного базирования. Отличия от выражения (2.2) в случае воздушного расположения сенсора заключаются в изменении определения параметров $h$ и $\rho $ (рис. 7), характеризующих расстояние между оцениваемой точкой и зоной обзора сенсора воздушного базирования.
Для оценки значения функции риска в точке О (рис. 7) исходными данными являются векторы $\left( {{{{\vec {p}}}_{1}},\;{{{\vec {p}}}_{1}},\;\vec {q}} \right)$, соответствующие зоне обзора сенсора и точке О. Выразим из них величины $h$ и $\rho $, входящие в функцию риска (3.3):
(3.4)
$h = \left| {P{{r}_{{\vec {l}}}}\vec {x}} \right| = \left| {\frac{{\vec {l}{\text{\;}}\vec {x}}}{{\vec {l}{\text{\;}}\vec {l}{\text{\;}}}}\vec {l}{\text{\;}}} \right|,$(3.5)
$\rho = \left| {\vec {x} - P{{r}_{{\vec {l}}}}\vec {x}} \right| = \left| {\vec {x} - \frac{{\vec {l}{\text{\;}}\vec {x}}}{{\vec {l}{\text{\;}}\vec {l}{\text{\;}}}}\vec {l}} \right|,$Подставляя уравнения (3.3)–(3.6) в функционал риска (3.1), получаем выражение для функционала риска, обусловленное j-м сенсором воздушного базирования:
(3.7)
${{r}_{j}}(\vec {l}{\text{\;}},\vec {x}) = {{\sigma }_{i}}\frac{{\left| {\frac{{\vec {l}{\text{\;}}\vec {x}}}{{\vec {l}{\text{\;}}\vec {l}{\text{\;}}}}\vec {l}{\text{\;}}} \right|}}{{\left| {\vec {x} - \frac{{\vec {l}{\text{\;}}\vec {x}}}{{\vec {l}{\text{\;}}\vec {l}{\text{\;}}}}\vec {l}} \right|}}\frac{D}{{\left| {\vec {l}} \right|}}H.$В выражении (3.7) H – множитель, аналогичный по смыслу функциям Хевисайда из (3.2). Данный множитель ограничивает конус по высоте. Обобщая (3.2) и (3.7) для множества сенсоров N – наземного и M – воздушного базирования функционал риска может быть представлен как
(3.8)
$R = \mathop \sum \limits_i^N {{\sigma }_{i}}\frac{{z - {{z}_{i}}}}{{\sqrt {{{{(x - {{x}_{i}})}}^{2}} + {{{(y - {{y}_{i}})}}^{2}} + \delta } {\text{tg}}\left( {{{\psi }_{i}}} \right)}} + \mathop \sum \limits_j^M {{r}_{j}}(\vec {l}{\text{\;}},\vec {x}).$Использование полученного функционала риска (3.8) обеспечивает решение задач обоснования и выбора оптимальных мест дислокации сенсоров воздушного базирования, связанных с рисками пропуска ПО и разработки дальнейших стратегий по их перемещению в условиях неизменной или сокращающейся неопределенности.
Представленный функционал риска может быть проиллюстрирован следующим образом. На рис. 8 показан функционал риска одиночного наземного сенсора, рассчитанный с помощью формулы (3.1). Величина риска изображена цветом: чем светлее цвет, тем выше мгновенный риск в данной точке. Самый высокий риск ожидаемо располагается на оси сенсора. Вне зоны обнаружения сенсора (вне конуса) риск равен нулю.
На рис. 9 приведен суммарный функционал риска для двух наземных сенсоров с заданными координатами. Наблюдается аддитивный эффект – риск увеличился в области между сенсорами, также можно проследить выполнение принципа суперпозиции (2.3).
Рис. 9.
Суммарный функционал риска для двух наземных сенсоров (сечение плоскостью $y = 0$, центры сенсоров расположены в точках $x = 50,$ $y = 0,$ $z = 0$ и $x = 500,$ $y = 0,$ $z = 0$)
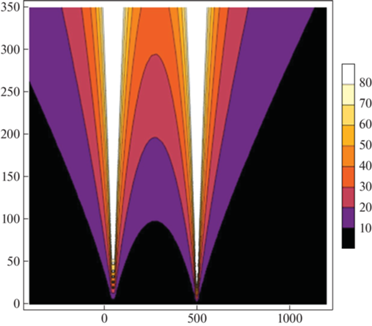
4. Результаты математического моделирования. Эффективность применения функционала риска (3.8) при управлении разнородной группировкой сенсоров обнаружения была подтверждена имитационным моделированием задачи обнаружения ПО и сравнением результатов с другими показателями эффективности. В качестве исходных данных рассматривались:
1. Трехмерное пространство размерами 200 × 200 × 5 км, с шагом дискретной сетки по оси ОХ – 0.3 км, по оси OY – 0.3 и 0.1 км по оси OZ соответственно, шаг по времени был равен 1 с.
2. Разнородная группировка средств обнаружения состоит из 5 наземных сенсоров кругового обзора и пяти воздушных сенсоров (БПЛА), которые перемещаются по полю боя с постоянной скоростью 120 км/ч на высоте 5 км над заданным рельефом. Рельеф представляет собой карту высот z над плоскостью (x, y), для моделирования которого использовались открытые базы данных NASA [22].
3. Группа ПО представляет собой 20 маловысотных объектов, перемещающихся в пространстве из произвольной начальной (по координатам $x$ и $z$) точки с фиксированной y-координатой (${{y}_{{{\text{нач}}}}} = 200$) в произвольную конечную (по координатам$x$ и $z$) точку с y-координатой (${{y}_{{{\text{конеч}}}}} = 0$) со скоростью 1200 км/ч с учетом кинематических физических ограничений на возможные траектории движения. Перемещение ПО осуществляется при помощи алгоритма A-star (рис. 10), который основывается на выборе траектории полета с минимальной “стоимостью”. В качестве “стоимости” в данном случае выступает полный риск.
Рис. 10.
Трехмерные шаблоны алгоритма выбора следующей точки для разных направлений движения ПО: 1 – предыдущая точка, 2 – текущая точка, 3 – следующие
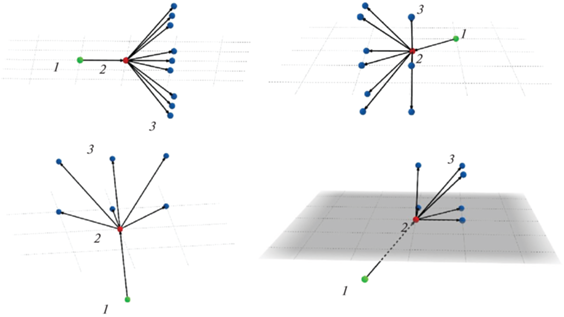
Моделирование траекторий движения двух ПО в обход наземных сенсоров рассмотрены на рис. 11. Очевидно, для ПО достаточно облетать зону обнаружения наземных сенсоров (конусы РЛС), чтобы не быть обнаруженными. Сравнивая результаты с рисунка 9, можно сделать вывод, что даже между двумя наземными сенсорами имеется область с чрезвычайно малым риском. Следовательно, ПО при достаточно низкой высоте полета и достаточно большом пространстве взаимодействия может облететь любые наземные расстановки наземных сенсоров кругового обзора, поэтому для их обнаружения целесообразно использовать подвижные сенсоры (например, БПЛА).
Рис. 11.
Траектории ПО с заданными начальными, конечными точками и высотой полета, построенные в обход наземных сенсоров (сенсоры расположены в точках $x = 0,$ $y = 0,$ $z = 0$ и $x = 200,$ $y = 0,$ $z = - 30$)
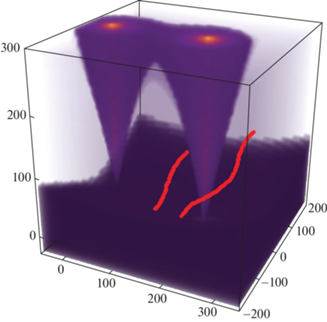
На рис. 12 показано, как группа крылатых ракет с заданными начальными и конечными точками может облететь одиночный наземный сенсор.
Рис. 12.
Траектории группы ПО с заданными начальными и конечными точками и заданной высотой полета, построенные в обход наземного сенсора
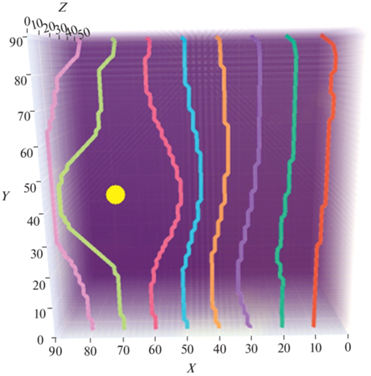
4. Функционал риска R для каждой точки поля пространства с координатами $(x,y,z)$ определяет вещественное число N. Набор таких вещественных чисел {N} для всех точек трехмерного пространства также называется полем риска. Данный способ задания поля риска широко принят в литературе [1–11]. Чем больше число N, тем выше вероятность того, что ПО, оказавшись в точке $(x,y,z)$ в данный момент времени, будет обнаружена. Отметим, что информация о поле риска {N} крайне важна для сенсоров обнаружения для управления составом и структурой группировки в режиме реального времени, так как с помощью данного поля риска можно предсказать наиболее вероятные траектории полета ПО и вовремя “закрыть” проблемные, например с помощью подвижных сенсоров – БПЛА.
5. Алгоритмически возможны различные способы перемещения БПЛА при заданном поле риска, рассмотрение данных способов также выходит за рамки настоящего исследования [23].
6. Начальная расстановка сенсоров основана на внемодельных соображениях – текущей оперативно-тактической обстановке, условиях рельефа и т.д.
Вследствие малой продолжительности конфликтного взаимодействия (время взаимодействия ПО и разнородной группировки меньше времени передислокации и развертывания подвижных наземных сенсоров обнаружения) все наземные средства являются условно неподвижными. После расстановки наземных сенсоров (задания их координат в пространстве) рассчитывается функционал риска во всех точках пространства (поле риска), исходя из которого происходит размещение БПЛА на начальных позициях – минимумы этого поля закрываются воздушными средствами обнаружения.
Необходимо отметить, что из-за неподвижности наземных сенсоров поле риска во времени в результате действия только наземных сенсоров не изменяется, однако при перемещении БПЛА или выхода из строя одного или нескольких сенсоров обнаружения поле риска изменится. Следовательно, необходимо пересчитывать для каждого подобного случая изменения обстановки.
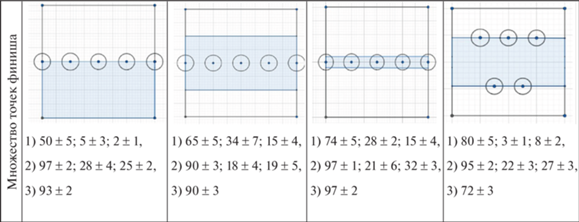
Результаты имитационного моделирования приведены на рис. 13, где схематично изображена расстановка наземных сенсоров и зона полета БПЛА (серый прямоугольник). В качестве стратегий движения воздушных сенсоров рассматривались следующие стратегии:
1) патрулирование: БПЛА проводит поиск и обнаружение ПО вдоль заданной границы зоны полета;
2) барражирование: БПЛА осуществляет поиск и обнаружение ПО вокруг минимума функционала риска в заданной области пространства;
3) адаптивная: БПЛА реализует поиск и обнаружение ПО на каждом шаге траектории своего движения, пересчитывая поле риска $\left\{ N \right\}$ и учитывая как взаимодействие БПЛА с наземными сенсорами обнаружения, так и взаимодействие воздушных сенсоров между собой.
В качестве функционалов риска выбраны (2.7) (при n = 1), (2.11) и (3.8).
Результаты моделирования представлены на одном и том же рельефе, при этом для каждой фиксированной стратегии и фиксированного функционала риска проводилось 20 запусков модели со случайными точками вылета ПО противника.
Процент обнаруженных ПО при моделировании функционала риска в виде (3.8), как показано на рис. 13, существенно выше, чем при использовании степенной модели (2.7) или экспоненциально спадающего функционала (2.11). Во многом это связано с тем, что глобальные минимумы поля риска для каждого функционала оказываются разными. Данное обстоятельство влияет на начальное расположение БПЛА и, как следствие, на эффективность работы стратегий. Необходимо отметить, что адаптивная стратегия непосредственно связана с функционалом риска (3.8), поэтому имитационное моделирование стратегии (3) для других функционалов не проводилось. В результате для различных расстановок наземных сенсоров и для разных зон полета БПЛА применение функционала риска (3.8) привело к высоким показателям эффективности: ни в одной стратегии средний процент обнаруженных ПО не был ниже 50%, при этом для каждой расстановки наземных сенсоров можно подобрать такую стратегию движения, при которой эффективность обнаружения по заданному критерию будет выше 90%.
Результаты моделирования позволяют сделать следующие выводы. Построение разнородной группировки сенсоров обнаружения в условиях антагонистического взаимодействия с ПО противника необходимо выполнять на основе анализа возможных стратегий и действий противостоящей стороны, что позволит повысить адаптивность группировки в условиях информационной неопределенности. Предложенная модель сенсоров как наземного, так и воздушного базирования дала возможность формализовать функционал риска, позволяющий сформировать управляющие воздействия в разнородной группировке сенсоров обнаружения с целью повышения качества ее функционирования. При этом на его основе можно определить такое управление разнородной группировкой сенсоров, что задача обнаружения ПО будет выполнена даже при массовом одновременном налете ПО из случайных начальных точек.
Заключение. Необходимость своевременного и высокоточного обнаружения любых ПО разнородной группировкой сенсоров обнаружения диктуется скоротечностью развития самого конфликта, при этом заблаговременное обнаружение ПО повышает вероятность оперативного принятия решений вышестоящей системой. Одним из вариантов повышения эффективности обнаружения ПО является оптимальность в управлении имеющимися ресурсами группировки в зоне ее ответственности. Повышение качества управления может быть достигнуто за счет оценки и анализа характеристик как отдельных сенсоров, так и всей группировки в динамике ее функционирования и выбора показателей, на основании которых синтезируется управляющее воздействие.
Предложенная модель сенсора обнаружения в виде пространственно-распределенного тела его рабочей зоны, в пределах которого обнаружение объектов локации производится с вероятностью не ниже заданной, определяет вектор параметров данного средства в виде параметров геометрической фигуры (конуса), что в свою очередь снижает вычислительные нагрузки средств автоматизации.
Проведенный анализ показателей эффективности управления разнородной группировкой сенсоров обнаружения позволил обосновать применение функционала риска как критерия выбора оптимальных траекторий полета ПО. Адаптированный вариант данного функционала использовался при обосновании и выборе решений по размещению сенсоров воздушного базирования, связанных с рисками пропуска ПО, и разработке дальнейших стратегий по их перемещению в условиях неизменной или сокращающейся неопределенности.
Применение показателя функционала риска дает возможность:
разработать алгоритмы управления структурой и составом разнородной группировки как решения задачи адаптации процесса обнаружения ПО в различных режимах ее работы;
совершенствовать модели сенсоров обнаружения, заключающиеся в расширении классов используемых сенсоров – не только по пространственному признаку, но и по физическим принципам, положенным в основу их работы, а также по режимам работы (кругового обзора, секторного обзора и т.п.);
увеличить в модели сенсоров количество варьируемых параметров и характеристик разнородной группировки.
Дальнейшими направлениями исследований являются:
расширение дестабилизирующих воздействий на разнородную группировку со стороны объектов локации, строящиеся на принципе: разведка, выбор оптимального дестабилизирующего (деструктивного) воздействия, реализация воздействия на группировку;
совершенствование функционала риска за счет добавления в него составляющих, которые позволяют повысить адекватность оценки стратегий, проникающих в зону ответственности группировки ПО, и стратегий ее реакций на проникновения;
оптимизация вычислительных процессов и совершенствование алгоритмов взаимодействия разнородной группировкой сенсоров с ПО.
Список литературы
Галяев А.А., Маслов Е.П., Рубинович Е.Я. Об одной задаче управления движением объекта в конфликтной среде // Изв. РАН. ТиСУ. 2009. № 3. С. 134–140.
Галяев А.А., Маслов Е.П. Оптимизация закона уклонения подвижного объекта от обнаружения при наличии ограничений // АиТ. 2012. № 6. С. 73–88.
Абрамянц Т.Г., Маслов Е.П., Яхно В.П. Уклонение подвижного объекта от обнаружения группой наблюдателей // Проблемы управления. 2010. № 5. С. 73–79.
Zabarankin M., Uryasev S., Pardalos P. Optimal Risk Path Algorithms // Cooperative Control and Optimization. Applied Optimization. 2002. V. 66. P. 273–298.
Петров М.Ю. Построение маршрута полета летательного аппарата на малых высотах // Изв. РАН. ТиСУ. 2019. № 3. С. 140–146.
Шайкин М.Е. О статистическом функционале риска в задаче управления движением объекта в конфликтной среде // Изв. РАН. ТиСУ. 2011. № 1. С. 22–31.
Dogan A., Ugur Z. Unmanned Aerial Vehicle Dynamic-Target Pursuit by Using Probabilistic Threat Exposure Map // AIIA Guidance, Dynamics and Control. 2006. V. 29. № 4. P. 944–954.
Воронин А.Н., Зиатдинов Ю.К., Пермяков А.Ю., Варламов И.Д. Синтез компромиссно-оптимальных траекторий мобильных объектов в конфликтной среде // Сучасні інформаційні технології у сфері безпеки та оборони. 2015. № 1 (22). С. 40–49.
Kumar G.N., Dadarya S., Verandani A., Sarkar A.K., Talole S.E. Cruise Missile Mission Planning Using Genetic Algorithm // Proc. Intern. Conf. on Modern Research in Aerospace Engineering. Noida, NCR-Delhi, 2018. P. 353–362.
Zabarankin M., Uryasev S., Murphey R. Aircraft Routing Under the Risk of Detection // Naval Research Logistics. 2006. V. 53. P. 728–747.
Zhang Z., Wu J., Dai J., He C. A Novel Real-Time Penetration Path Planning Algorithm for Stealth UAV in 3D Complex Dynamic Environment // IEEE Access. 2020. V. 8. P. 122757–122771.
Dijkstra E. A Note of Two Problems in Connection with Graphs // Numerische Mathematik. 1959. V. 1. P. 269–271.
Jong-Jin S., Hyochoong B. UAV Path Planning under Dynamic Threats Using an Improved PSO Algorithm // Intern. Aerospace Engineering. 2020. V. 10. P. 1–17.
Miller B., Stepanyan K., Miller A., Andreev M. 3D Path Planning in a Threat Environment // Proc. IEEE Conf. on Decision and Control and European Control Conf. Orlando, FL, USA, 2011. P. 6864–6869.
Ежов Г.В. Алгоритмы нахождения пути, их сравнение и визуализация на базе движка Unity // Молодой ученый. 2020. № 50 (340). С. 15–24.
Hart P.E., Nilsson N.J., Raphael B.A. Formal Basis for the Heuristic Determination of Minimum Cost Paths // IEEE Transactions on Systems Science and Cybernetics SSC4. 1968. V. 4. № 2. P. 100–107.
Евдокименков В.Н., Красильщиков М.Н., Ляпин Н.А. Гарантирующее управление траекторией̆ беспилотного летательного аппарата при сближении с маневрирующей воздушной целью // Изв. РАН. ТиСУ. 2018. № 5. С. 40–53. https://doi.org/10.31857/S000233880002851-5
Евдокименков В.Н., Красильщиков М.Н., Себряков Г.Г. Распределенная интеллектуальная система управления группой беспилотных летательных аппаратов: архитектура и программно-математическое обеспечение // Системы управления, связи и безопасности. 2019. № 3. С. 1–13. https://doi.org/10.24411/2410-9916-2019-10301
Справочник офицера воздушно-космической обороны / Под общ. ред. С.К. Бурмистрова. Тверь: BA ВКО, 2006. 564 с.
Тяпкин В.Н., Фомин А.Н., Гарин Е.Н. и др. Основы построения радиолокационных станций радиотехнических войск: учебник / Под общ. ред. В.Н. Тяпкина. Красноярск: Сибирск. федер. ун-т, 2016. 536 с.
Пантенков Д.Г., Гусаков Н.В. Компьютерное моделирование активной фазированной антенной решетки// Космическая техника и технологии. 2013. № 1. С. 34–39.
https://earthexplorer.usgs.gov/
Valavanis K.P., Vachtsevanos G.J. Handbook of Unmanned Aerial Vehicles. Dordrecht: Springer, 2015.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления