Известия РАН. Теория и системы управления, 2023, № 3, стр. 38-56
МЕТОДЫ И МОДЕЛИ УПРАВЛЕНИЯ РЕСУРСАМИ ПРОЕКТА В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
О. А. Косоруков a, *, Д. В. Лемтюжникова b, c, **, А. В. Мищенко d, ***
a МГУ им. М.В. Ломоносова
Москва, Россия
b ИПУ им. В.А. Трапезникова РАН
Москва, Россия
c МАИ (национальный исследовательский ун-т)
Москва, Россия
d Технологический ун-т им. дважды Героя Советского Союза, летчика-космонавта А.А. Леонова
Королев, Моск. обл., Россия
* E-mail: kosorukovoa@mail.ru
** E-mail: darabbt@gmail.com
*** E-mail: alnex4957@rambler.ru
Поступила в редакцию 23.09.2022
После доработки 05.10.2022
Принята к публикации 05.12.2022
- EDN: JEPAKF
- DOI: 10.31857/S0002338823020117
Аннотация
Рассматриваются методы оптимизации расписаний выполнения работ проекта для критерия минимизации средневзвешенного времени их выполнения. В том случае, когда длительности работ заданы детерминировано, предложен точный и приближенный метод решения задачи выбора оптимального расписания. Если возможны изменения длительности работ, создан аналитический инструментарий оценки устойчивости расписаний как для ситуации интервального задания длительностей работ, так и для ситуации изменения длительнстей работ при возможных возмущениях внешней среды. В том случае, если длительности работ заданы стохастически, предлагается механизм оценки эффективности расписания по двум критериям и предложена процедура количественной оценки риска расписания.
Введение. При оценке эффективности проекта необходимо учитывать такой показатель, как продолжительность инвестиционной фазы проекта. Этот показатель, в частности, отвечает на вопрос: за какое время может быть создано то или иное предприятие, производящее конечную продукцию или оказывающее определенные услуги потребителю, реализация которых обеспечивает окупаемость проекта по созданию предприятия. При формировании календарного плана выполнения работ проекта большое значение имеет оценка жизненного цикла выпускаемой продукции или оказываемых услуг, так как соотношение продолжительности инвестиционной фазы проекта и жизненного цикла выпускаемой продукции существенным образом влияет на его окупаемость. В статье рассмотрены методы и модели оптимизации инвестиционной фазы проекта, позволяющие формировать наиболее рациональные решения при формировании календарного плана выполнения работ проекта.
Общая постановка этих задач заключается в том, чтобы упорядочить во времени выполнение определенных действий при соблюдении ряда условий. Каждое действие состоит из элементарных операций, называемых работами (заявками или заданиями), которые могут быть либо подготовлены заранее, либо поступать динамически. Организация выполнения работ осуществляется таким образом, чтобы минимизировать один из следующих показателей: время выполнения всех работ, среднее взвешенное время завершения работ, объем незавершенной обработки заявок за определенный период, потери времени на ожидание обработки заявок. Моделирование распределения ограниченных ресурсов часто сводится к решению линейных и нелинейных задач дискретной оптимизации, большинство которых относится к NP-трудным, которые характеризуются экспоненциальным ростом объема вычислений при увеличении размерности задачи [1]. Это обстоятельство, а также то, что находить оптимальное решение часто приходится в условиях неточной исходной информации, определяет актуальность разработки эффективных методов управления ограниченными ресурсами. В предлагаемой статье основное внимание будет уделено оптимизации управления проектом при изменяющихся длительностях работ. Несмотря на то, что на текущий момент времени созданы многочисленные методы и модели оптимизации управления ресурсами проектов, тем не менее, при решении проблемы минимизации инвестиционной фазы проекта в условиях неопределенности и риска существует определенный дефицит соответствующего количественного инструментария. При этом именно инвестиционная фаза как наиболее трудоемкая и капиталоемкая играет существенную роль в успехе всего проекта. Ошибки планирования на этом периоде, вызванные неучтенным риском, могут привести к значительным потерям. Рассмотрена детерминированная модель теории расписаний, предполагающая использование нескладируемых ресурсов с учетом матричного задания времени выполнения операций исполнителями и предложен метод ветвей и границ получения оптимального решения. Получены методы оценки устойчивости расписаний при выполнении непрерываемых работ проекта при различных способах задания изменения их длительности. В ситуации, когда длительности работ заданы как случайные величины, предложена двухкритериальная модель оценки эффективности расписания. Модели оптимального управления ограниченными ресурсами рассматривались в ряде публикаций отечественных и зарубежных авторов. Например, оптимизационные задачи оценки эффективности производственных программ в условиях неопределенности исследуются в [2, 3]. Методы оценки устойчивости расписаний при изменении параметров задачи анализируются в [4, 5]. Динамические и статические модели и методы управления ограниченными ресурсами на транспорте рассмотрены в [6–8]. Точные и приближенные алгоритмы построения оптимальных расписаний для планирования работы многопроцессорной вычислительной техники представлены в [9–11]. Модели и методы управления ограниченными ресурсами, которые сводятся к решению минимаксных задач, приведены в [12–18].
1. Постановка задачи и метод решения. Рассмотрим, ситуацию выполнения $n$ работ проекта с использованием нескладируемых ресурсов, объем которых задан вектором $b = ({{b}_{1}}, \ldots ,~{{b}_{n}}$). Технологическая последовательность выполнения работ задана ориентированным ациклическим графом $G\left( {m,n} \right)$, где $m$ – дуги орграфа, $n$ – вершины орграфа, соответствующие работам проекта. Для выполнения работы i необходимы нескладируемые ресурсы в объеме ${{\bar {a}}_{i}} = \left( {{{a}_{{i1}}}, \ldots ,~{{a}_{{im}}}} \right)$, $i = \overline {1,n} $. Длительности работ заданы вектором $t = \left( {{{t}_{1}},{{t}_{2}}, \ldots ,~{{t}_{n}}} \right)$. Необходимо сформировать оптимальное расписание выполнения работ проекта, не нарушающего технологических ограничений на последовательность выполнения работ, заданных орграфом $G\left( {m,n} \right)$, и ограничение на объем используемых нескладируемых ресурсов в каждый момент времени выполнения работ проекта. В качестве критерия эффективности расписания будем применять средневзвешенное время завершения всех работ проекта, т.е. в оптимальном расписании необходимо минимизировать:
Здесь ${{\tau }_{i}}$ – время завершения работы $i$; ${{\alpha }_{i}}$ – весовой коэффициент, определяющий, насколько важно скорейшее завершение работы $i,~~i = \overline {1,n} {\text{\;}}$. Далее будем предполагать, что работы проекта не прерываемы, т.е. если ресурсы выделены некоторой работе $K$, то они должны быть ею использованы до полного ее выполнения.
1.1. Метод ветвей и границ. В представленной выше формулировке задача принадлежит к классу NP-трудных задач целочисленной оптимизации, для решения которых применяется подход, получивший название “метод ветвей и границ”. Ниже предлагается описание метода ветвей и границ для данной задачи.
Шаг 1. Вычисляется нижняя оценка оптимального расписания с помощью критерия (1.1). При этом предполагается, что ресурсные ограничения отсутствуют и работы выполняются в последовательности, заданной орграфом $G\left( {m,n} \right)$. Таким образом, определяется момент окончания работы ${{\tau }_{i}}$:
(1.2)
$\tau _{i}^{{\text{н}}} = \mathop {\max }\limits_{l = ~\overline {1,{{L}_{i}}} } \left\{ {\mathop \sum \limits_{g \in K_{i}^{l}} {{t}_{g}}} \right\} + {{t}_{i}}.~$Здесь $~\tau _{i}^{{\text{н}}}$ – нижняя оценка момента окончания работы $i$; $K_{i}^{l}$ – множество работ предшественников для работы i в пути с номером $l$, ${{L}_{i}}$ – число путей, в которые входит работа $i$; ${{t}_{i}}$ – продолжительность работы i.
Вычислив все величины $\tau _{i}^{{\text{н}}}$, $i = \overline {1,n} $, найдем величину нижней оценки эффективности оптимального расписания ${{T}_{{\text{н}}}}$:
Шаг 2. Рассчитывается верхняя оценка значения целевой функции на оптимальном решении. Для этого формируется некоторое допустимое расписание (c учетом последовательности выполнения работ, заданных орграфом $G\left( {m,n} \right),~$ и ресурсных ограничений). Соответствующие моменты завершения работ обозначим через $\tau _{i}^{{\text{в}}},~~i = \overline {1,n,} $ и вычислим значение верхней оценки оптимального расписания ${{T}_{{\text{в}}}}$:
Если ${{T}_{{\text{в}}}} = {{T}_{{\text{н}}}}$, то оптимальное решение определено, оно сформировано на шаге 2. Если ${{T}_{{\text{в}}}} > {{T}_{{\text{н}}}}$, переходим к шагу 3.
Шаг 3. На этом шаге определяются так называемые текущие нижние оценки. Это вычисление происходит каждый раз при формировании очередного расписания после завершения одной из работ проекта в момент $\tau $ по следующей формуле:
(1.5)
$T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right) = ~\mathop \sum \limits_{i \in R\left( \tau \right)} {{\tau }_{i}}{{\alpha }_{i}} + {{T}_{{\text{н}}}}\left( {N{{\backslash }}R\left( \tau \right)} \right).$Здесь $N$ – множество всех работ проекта; $R\left( \tau \right)$ – множество работ, выполненных к моменту времени $\tau $; ${{\tau }_{i}}$ – моменты завершения работ из множества $R\left( \tau \right)$; ${{T}_{{\text{н}}}}\left( {N{{\backslash }}R\left( \tau \right)} \right)$ – нижняя оценка на множестве работ, заданных графом $G\left( {m,n} \right),~$с учетом того, что работы множества $R\left( \tau \right)$ завершены полностью и, значит, их длительности равны нулю. Некоторые работы выполнены частично и, следовательно, их длительности должны быть скорректированы при расчетах ${{T}_{{\text{н}}}}\left( {N{{\backslash }}R\left( \tau \right)} \right)$. Таким образом, первое слагаемое в формуле (1.5) – значение целевой функции (1.1) для выполненных работ, а вторая часть формулы (1.5) – нижняя оценка целевой функции (1.1) для невыполненных работ формируемого расписания.
Если получили, что $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right) \geqslant {{T}_{{\text{в}}}}$, то прерывается формирование текущего расписания и переход на формирование другого расписания. Если $T_{{\text{н}}}^{{{\text{тек}}}}\left( r \right) < {{T}_{{\text{в}}}}$, то осуществляется выбор очередной невыполненной работы и выделяются необходимые ресурсы для ее выполнения. Далее вычисляется очередной момент ${{\tau }^{1}} > \tau $, связанный с окончанием одной из работ, определяется $T_{{\text{н}}}^{{{\text{тек}}}}\left( {{{\tau }_{1}}} \right)$ по формуле (1.5). В зависимости от результата формируемое расписание либо отбраковывается, либо его формирование продолжается. Эта итеративная процедура вычисления $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right)$ приведет таким образом либо к ситуации отбраковки расписания, либо к ситуации, когда все работы будут выполнены, и получим сформированное расписание, у которого значение целевой функции (1.1) $T{\kern 1pt} *$ будет меньше ${{T}_{{\text{в}}}}$. Во втором случае корректируем значение ${{T}_{{\text{в}}}}$, полагая, что ${{T}_{{\text{в}}}} = T{\kern 1pt} *$. Таким образом мы сократили интервал (${{T}_{{\text{н}}}},\;{{T}_{{\text{в}}}}$). Если при этом ${{T}_{{\text{н}}}}$ стало равно ${{T}_{{\text{в}}}}$, то последнее сформированное расписание будет оптимальным.
Если ${{T}_{{\text{н}}}} < {{T}_{{\text{в}}}}$, то переходим к анализу очередного варианта формирования расписания с вычислением текущих нижних оценок. Вычислительная процедура получения оптимального решения завершится, когда будет сформировано решение, значение целевой функции на которой равно ${{T}_{{\text{н}}}}$. Если это не произойдет и будут проанализированы все допустимые расписания, то в качестве оптимального выбирается то, которое соответствует последнему (минимальному) значению ${{T}_{{\text{в}}}}$.
Переборный характер предлагаемого метода и, возможно, большой объем вычислений с учетом того, что исследуемая задача является NP – трудной, приводит к необходимости использовать приближенную схему, основанную на идеологии метода ветвей и границ.
Особенность так называемого усеченного метода ветвей и границ позволяет сократить количество анализируемых расписаний за счет того, что анализ допустимых расписаний осуществляется до тех пор, пока не будет выполняться неравенство:
Здесь $\Delta $ – требуемая близость верхней и нижней оценок. Также может применяться оценка относительной близости ${{T}_{{\text{в}}}}$ и ${{T}_{{\text{н}}}}$, такая, как
$K$ – это относительная точность полученного приближенного решения в процентах.1.2. Пример использования метода ветвей и границ. Рассмотрим этот пример для следующего перечня работ, последовательности выполнения которых заданы графом $G\left( {m,n} \right)$ (рис. 1).
Будем полагать, что для выполнения каждой работы требуется один исполнитель, а всего исполнителей два. Длительности работы заданы по правилу ${{t}_{i}} = i,$ т.е. $t = \left( {1,~2,~3,~4,~5,~6,~7} \right)$. Весовые коэффициенты ${{\alpha }_{i}}$ равны: ${{\alpha }_{1}} = 1;$ ${{\alpha }_{2}} = 2$; ${{\alpha }_{3}} = 3$; ${{\alpha }_{4}} = 4$; ${{\alpha }_{5}} = 5$; ${{\alpha }_{6}} = 6$; ${{\alpha }_{7}} = 7$.
Шаг 1. Вычисляем ${{T}_{{\text{н}}}}$ с помощью алгоритма, предложенного в методе ветвей и границ. Используя формулы (1.2) и (1.3), получим:
Таким образом ${{Т}_{{\text{н}}}} = 170$.
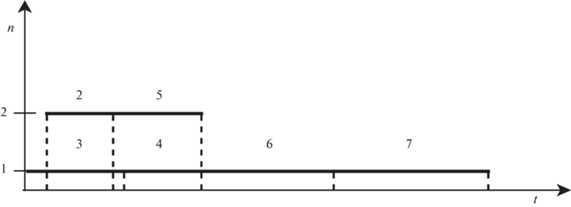
Шаг 2. Для вычисления $~{{Т}_{{\text{в}}}}$ сформируем следующее допустимое расписание для заданных длительностей работ.
Горизонтальная ось – время; вертикальная ось – номера исполнителей 1 и 2. Согласно диаграмме Ганта (рис. 2), получим расписание: ${{\tau }_{1}} = 1$; ${{\tau }_{2}} = 3$; ${{\tau }_{3}} = 4$; ${{\tau }_{4}} = 8$; ${{\tau }_{5}} = 8$; ${{\tau }_{6}} = 14$; ${{\tau }_{7}} = 21$. Следовательно, значение целевой функции на этом расписании, а значит, и значение верхней оценки равны:
С учетом того, что ${{Т}_{{\text{в}}}} > {{Т}_{{\text{н}}}}$ , переходим к шагу 3.
Шаг 3. Начинаем формировать очередное расписание с вычислением $Т_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right)$ с использованием формулы (1.5). Вначале, как и в первом пояснении, выполняем работу 1, а затем ставим на выполнение работы 3 и 4 (рис. 3):
Рис. 3.
Фрагмент диаграммы Ганта для вычисления $Т_{{\text{н}}}^{{{\text{тек}}}}\left( {\tau = 4} \right)$
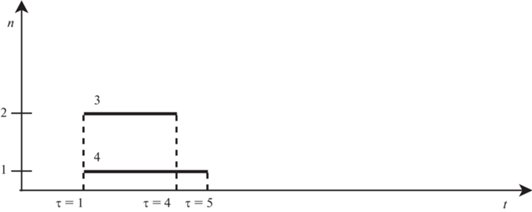
Так как $Т_{{\text{н}}}^{{{\text{тек}}}} < {{Т}_{{\text{в}}}}$ = 324, то продолжаем формировать расписание (рис. 4):
Рис. 4.
Фрагмент диаграммы Ганта для вычисления $Т_{{\text{н}}}^{{{\text{тек}}}}\left( {\tau = 5} \right)$
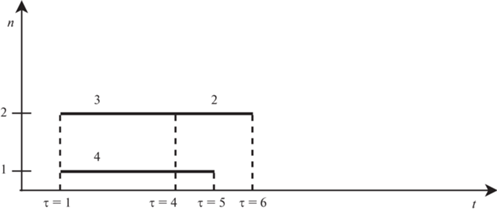
С учетом того, что $Т_{{\text{н}}}^{{{\text{тек}}}}\left( {\tau = 5} \right) < {{Т}_{{\text{в}}}}$, продолжаем формировать расписание (рис. 5):
Рис. 5.
Фрагмент диаграммы Ганта для вычисления $Т_{{\text{н}}}^{{{\text{тек}}}}\left( {\tau = 6} \right)$
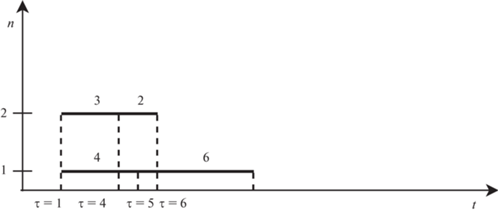
Поскольку $Т_{{\text{н}}}^{{{\text{тек}}}}\left( {\tau = 6} \right) < {{Т}_{{\text{в}}}}$, продолжаем формировать расписание (рис. 6):
Рис. 6.
Фрагмент диаграммы Ганта для вычисления $Т_{{\text{н}}}^{{{\text{тек}}}}\left( {\tau = 11} \right)$
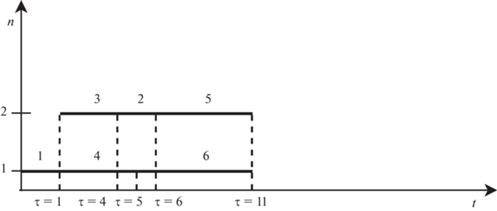
С учетом того, что в момент $\tau = 11$ ставится на выполнение работа 7 и момент ее завершения равен 18, получаем новое расписание (рис. 7), значение целевой функции Т на котором равно:
Рис. 7.
Диаграмма Ганта для второго расписания, значение целевой функции на котором $Т = \mathop \sum \limits_{i = 1}^n {{\tau }_{i}}{{\alpha }_{i}} = 287$
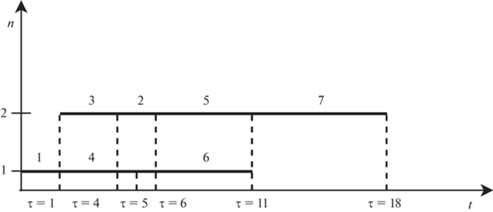
При условии, что значение целевой функции на втором расписании лучше, чем на первом, присваиваем ${{T}_{{\text{в}}}}$ значение 287, т.е. ${{T}_{{\text{в}}}}$ = 287.
Далее вычисления по оптимизации расписания выполнения работ проводятся, согласно описанию, приведенного выше, метода ветвей и границ.
2. Управление работами проекта с учетом интервального задания их длительностей. Рассмотрим ситуацию оптимизации расписания выполнения работ по критерию (1.1) в условиях, когда длительности работ заданы интервально. Это означает, что продолжительность работы $i$ может принимать любое значение из интервала $[t_{i}^{1},t_{i}^{2}]$, т.е. ${{t}_{i}} \in [t_{i}^{1},t_{i}^{2}]$. Необходимо в этой ситуации определить оптимальные расписания выполнения работ для всех значений продолжительностей работ, т.е.
Здесь $t = \left( {{{t}_{1}},~ \ldots ,~{{t}_{n}}} \right).$ Отметим, что для ситуации критерия быстродействия эта модель была рассмотрена в [4].
2.1. Метод формирования области устойчивости оптимального расписания. Для решения поставленной задачи рассмотрим списковую форму представления расписания выполнения работ.
Определение 1. Расписанием выполнения работ R в списковой форме называется совокупность подмножества работ ${{M}_{1}},~ \ldots ,~{{M}_{L}}~\left( {L \leqslant n} \right)$ и совокупность подмножеств работ ${{m}_{1}},~ \ldots ,~{{m}_{L}}~\left( {L~ \leqslant n} \right),$ обладающих следующими свойствами:
1) $\bigcup\nolimits_{i = 1}^L {{{M}_{i}} = N} ,$ где N – множество всех работ,
2) ${{m}_{i}} \subseteq {{M}_{i}},$ $i = \overline {1,n} ,$
3) ${{m}_{k}} \cap {{m}_{e}} = \emptyset $, где $\emptyset $ – пустое множество, $k = \overline {1,n} $, $l = \overline {1,n} $, $k~ \ne l$,
4) $\bigcup\nolimits_{i = 1}^L {{{m}_{i}} = N} $.
Выполнение работ по расписанию R заключается в том, что вначале выполняются работы множества ${{M}_{1}}$ до тех пор, пока не будут выполнены все работы множества ${{m}_{1}}$, затем выполняются работы множества ${{M}_{2}}$, пока не завершится выполнение работ множества ${{m}_{2}},$ и т.д. до тех пор, пока не будет завершено выполнение работ множества ${{m}_{L}}.$ При этом формирование множеств $\{ {{M}_{i}}\} ,\;\left\{ {{{m}_{i}}} \right\}$, $i = \overline {1,L} $, происходит таким образом, чтобы при выполнении работ, согласно расписанию в списковой форме, не нарушались ограничения, накладываемые графом $G\left( {m,n} \right),$ и ограничения на потребляемые ресурсы в любой момент времени $\tau \in \left( {0,~{{Т}_{r}}} \right)$. Такое расписание будем называть допустимым. Если на некотором допустимом расписании достигается минимум целевой функции (1.1), то это расписание будет оптимальным. В этом определении $(0,~{{Т}_{r}})$ – временной интервал, на котором выполняются работы множества N. Как видно из определения расписания в списковой форме, изменение множества выполняемых работ не привязано к какому-либо моменту времени, а связано с завершением выполнения некоторого подмножества работ mi, $i = \overline {1,L} $. Таким образом момент завершения работы i равен продолжительности этой работы плюс сумма продолжительностей некоторого подмножества работ из множества N.
С учетом этого, а также формулы (1.2) значение целевой функции (1.1) при длительности работ ${{t}_{j}}$ для расписания $r$ может быть представлено следующим образом:
(2.1)
${{F}_{r}} = ~\mathop \sum \limits_{i = 1}^n {{\alpha }_{i}}\mathop \sum \limits_{j = 1}^n a_{{jr}}^{i}{{t}_{j}},\quad ~r = \overline {1,\tilde {R}~} .~$Здесь $a_{{jr}}^{{i~}} \in {{Z}^{ + }}$, где ${{Z}^{ + }} = \left\{ {0,1} \right\}$ – множество, состоящее из 0 и 1; $\tilde {R}$ – число допустимых расписаний. Представление целевой функции (1.1) на расписании r по формуле (2.1) связано с тем, что момент завершения работы i может быть представлен, как сумма длительностей некоторого подмножества работ из множества N.
Если длительности работ меняются на интервале $[t_{i}^{1},t_{i}^{2}]$, то значение целевой функции ${{F}_{r}}$ будет меняться на интервале $[F_{r}^{1},F_{r}^{2}]$, где $F_{r}^{1}$ – значение целевой функции (2.1) при длительностях работ ${{t}_{i}} = {{t}_{{i1}}}$, а $F_{r}^{2}$ – значение целевой функции (2.1) при длительностях работ ${{t}_{i}} = {{t}_{{i2}}}$.
Таким образом, сравнивая два допустимых расписания p и q, возможны две ситуации:
1) $[F_{p}^{1},~F_{p}^{2}] \cap [F_{q}^{1},~F_{q}^{2}] = \emptyset $.
И в этом случае одно из расписаний p или q дает лучшее значение целевой функции (2.1) для всех длительностей работ ti ∈ [$t_{i}^{1}$, $t_{i}^{2}$], i = $\overline {1,n} $. Здесь $\emptyset $ – пустое множество.
2) $[F_{p}^{1},~F_{p}^{2}] \cap [F_{q}^{1},~F_{q}^{2}] \ne \emptyset $.
В этой ситуации многомерный параллелепипед
на котором меняются длительности работ, может быть разбит на два многогранника, на одном из которых будет лучше расписание Rp, а на другом – Rq.Аналитическое задание этих многогранников осуществляется следующим образом.
Для расписания Rp:
(2.3)
$\sum\limits_{i = 1}^n {{{\alpha }_{i}}} \mathop \sum \limits_{j = 1}^n a_{{jp}}^{i}{{t}_{j}} \leqslant \sum\limits_{i = 1}^n {{{\alpha }_{i}}} \mathop \sum \limits_{j = 1}^n a_{{jq}}^{i}{{t}_{j}}.$Для расписания Rq:
Если длительности работ ${{t}_{i}}$ будут таковы, что
Таким образом, на основе предыдущего анализа можно сделать следующее заключение.
Утверждение 1. Если длительности работ ${{t}_{i}} \in [t_{i}^{1},t_{i}^{2}]$ заданы интервально, то многомерный параллелепипед
может быть разбит на множество многогранников ${{Q}_{1}}, \ldots ,~{{Q}_{k}}$ таким образом, что:1) $\bigcup\nolimits_{j = 1}^k {{{Q}_{j}} = P} $,
2) если длительность работ меняется на множестве Qj, то оптимальным остается некоторое расписание Rj, заданное в списковой форме для всех значений длительностей $t = ~({{t}_{1}}, \ldots ~,{{t}_{n}}),$ таких, что $t \in {{Q}_{j}}$.
Таким образом, многогранник Qj можно назвать областью устойчивости для оптимального расписания Rj в списковой форме.
2.2. Пример формирования области устойчивости оптимального расписания. Рассмотрим пример формирования области устойчивости расписаний для ситуации интервального задания длительности работ.
Пусть есть три работы проекта, выполняемых двумя исполнителями, длительность которых задана интервально:
Рассмотрим два расписания R1 и R2 в списковой форме:
Будем считать ${{\alpha }_{1}} = 1$; ${{\alpha }_{2}} = 2$; ${{\alpha }_{3}} = 3$.
Вычислим соответственно значения левой и правой границ целевой функции на первом и втором расписании.
Для первого расписания левая граница целевой функции $F_{1}^{1}$ равна:
Правая граница значения целевой функции $F_{1}^{1}$ на первом расписании равна:
Таким образом, значение целевой функции $F_{1}^{1}~$на первом расписании меняется на интервале [7; 35 ] , т.е. ${{F}_{1}} \in \left[ {7;35} \right]$.
Рассчитаем соответственно левую и правую границу целевой функции (2.1) на втором расписании:
Поскольку значение целевой функции на любом допустимом расписании может быть представлено по формуле (2.1) для любых значений ${{t}_{{i~}}} \in [t_{i}^{1},t_{i}^{2}]$, получим
С учетом формулы (2.2) и (2.3) область изменения длительностей работ оптимального расписания R1 задается следующей системой неравенств:
(2.4)
$\begin{gathered} 1 \leqslant {{t}_{i}} \leqslant 5,\quad i = 1,2,3, \\ 3{{t}_{3}} + 3{{t}_{2}} + {{t}_{{1{\text{\;}}}}} \leqslant {\text{\;}}5{{t}_{3}} + 2{{t}_{2}} + {{t}_{1}}. \\ \end{gathered} $Неравенство (2.4) можно переписать как
Соответственно область изменения длительности работ, на которой оптимальным будет решение R2, задается следующей системой неравенств:
3. Управление работами проекта с учетом внешних возмущений. Планирование выполнения работ проекта может охватывать длительный временной период (от года и больше), что в свою очередь приводит к тому, что точно оценить продолжительность выполняемых работ проекта часто невозможно. Это происходит, в частности, в силу изменяющейся внешней среды, которая влияет на продолжительность выполняемых работ. Такое влияние внешней среды на процесс реализации проекта еще называют возмущением.
Видами таких возмущающих воздействий может быть: изменяющиеся природно-климатические условия, дефицит трудовых ресурсов, изменение курса национальной валюты по отношению к иностранным валютам, затраты на обучение специалистов и т.д. Влияние перечисленных факторов приводит к отклонению длительностей работ от их прогнозируемых значений.
В общем случае длительность работы в этом случае может применяться по закону:
(3.1)
${{t}_{i}}\left( {{{\varepsilon }_{1}}, \ldots ,~{{\varepsilon }_{k}}} \right) = {{t}_{i}} + ~\mathop \sum \limits_{i = 1}^n {{\varphi }_{i}}\left( {{{\varepsilon }_{1}}, \ldots ,~{{\varepsilon }_{k}}} \right).$Здесь ${{\varphi }_{i}}\left( {{{\varepsilon }_{1}}, \ldots ,~{{\varepsilon }_{k}}} \right)$ – некоторая неубывающая функция от переменных ${{\varepsilon }_{1}}, \ldots ,~{{\varepsilon }_{k}}$; ${{\varepsilon }_{i}}$ – величина возмущающего воздействия i-го вида.
Рассмотрим частный случай использования формулы (3.1), полагая, что длительность работы i, $i = \overline {1,n} $, зависит линейно только от одного вида возмущений, т.е.
(3.2)
${{t}_{i}}\left( \varepsilon \right) = {{t}_{i}} + {{k}_{i}}\varepsilon ,\quad i = \overline {1,n} .$Здесь ${{t}_{i}}\left( {~\varepsilon } \right)$ – длительность работы i при уровне возмущения $\varepsilon $; ${{k}_{i}}$ – положительная константа; ${{t}_{i}}$ – длительность работы i без учета внешнего возмущения.
Согласно формулы (2.1), продолжительность расписания r с учетом возмущения $\varepsilon $ равна:
(3.3)
${{F}_{r}}(\varepsilon ) = \sum\limits_{I = 1}^n {{{\alpha }_{i}}\sum\limits_{j = 1}^n {a_{{jr}}^{i}({{t}_{j}} + {{k}_{j}}\varepsilon )\sum\limits_{i = 1}^n {{{\alpha }_{i}}\sum\limits_{j = 1}^n {a_{{jr}}^{i}{{t}_{j}} + \varepsilon \sum\limits_{i = 1}^n {{{\alpha }_{i}}\sum\limits_{j = 1}^n {{{k}_{j}}a_{{jr}}^{i},\quad r = \overline {1,R} } ,} } } } } $Очевидно, что если расписание R – оптимально при отсутствии внешнего возмущения и
(3.4)
$\mathop \sum \limits_{i = 1}^n {{\alpha }_{i}}\mathop \sum \limits_{j = 1}^n {{k}_{j}}a_{{jp}}^{i} = \mathop {\min }\limits_{p = \overline {1,R} } \left\{ {\mathop \sum \limits_{i = 1}^n {{\alpha }_{i}}\mathop \sum \limits_{j = 1}^n {{k}_{j}}a_{{jp}}^{i}} \right\},$В ситуации, если соотношение (3.4) не выполняется, т.е. существует расписание $l$, для которого
Это означает, что целевая функция (1.1) на расписании l растет медленнее, чем на расписании p, и, следовательно, учитывая линейность этих функций, существует такое ${{\varepsilon }_{е}}$, что будет выполняться неравенство
Тогда, при уровне возмущения $\varepsilon \geqslant {{\varepsilon }_{е}}$ предпочтительнее будет расписание $l~$ с точки зрения критерия (1.1).
Учитывая приведенный анализ, а также конечность числа допустимых расписаний, можно сформулировать следующее утверждение.
Утверждение 2. Если длительность работ меняется по формуле (3.2) и критерием оптимальности является средневзвешенное время завершения всех работ (формула (1.1)), то любой интервал изменения возмущений $\varepsilon \in \left( {0,~\omega } \right)$ может быть разбит на конечное число отрезков таким образом, что при любом изменении $\varepsilon $ в границах одного отрезка оптимальное расписание сохраняется.
Рассмотрим ситуацию, когда увеличение длительности работ от величины внешнего возмущения $\varepsilon $ носит более общий характер, например:
где ${{\varphi }_{i}}\left( \varepsilon \right)$ является дифференцируемой функцией по $\varepsilon $ иУсловие конечности разбиения на интервалы отрезка изменения возмущения $\varepsilon \in \left( {0,~\omega } \right)$ может не соблюдаться, так как в этом случае переход на любое оптимальное решение возможен при различных значениях ε, являющихся решением уравнений:
Здесь R – количество допустимых расписаний, которое является следствием того, что нелинейное уравнение может иметь более одного решения.
В силу нелинейности функций ${{F}_{k}}\left( \varepsilon \right)~$ и ${{F}_{j}}\left( \varepsilon \right)$ число переходов c одного оптимального решения на другое на любом ограниченном интервале $\left( {0,~\omega } \right)$ изменения $\varepsilon $ может быть достаточно большими. Если же $\omega \to \infty $, то и число переходов от одного оптимального расписания к другому может быть сколько угодно большим.
4. Оценка эффективности расписаний выполнения работ проекта с учетом риска. Рассмотрим ситуацию, когда длительности работ проекта заданы как случайная величина с известным законом распределения, т.е. $t_{i}^{1} - {{P}_{1}}$, …, $t_{i}^{m} - ~{{P}_{m}}$, ${{P}_{j}} \geqslant 0:$
В этой ситуации в качестве продолжительности работ может быть выбрано математическое ожидание продолжительностей работ. В этом случае формула, по которой вычисляется значение целевой функции (1.1) на расписании (аналог формулы (2.1)) r, будет следующей:
(4.1)
${{F}_{r}} = \mathop \sum \limits_{i = 1}^n {{\alpha }_{i}}\mathop \sum \limits_{j = 1}^n a_{{jr}}^{i}{{\bar {t}}_{j}},$Таким образом, формула (4.1) задает средневзвешенное время завершения работ для расписания r в условиях, когда длительности работ заданы как случайные величины.
4.1. Метод оценки эффективности расписания с учетом риска. С учетом изменчивости длительностей выполняемых работ еще одной характеристикой расписания является его риск, который количественно может быть оценен как суммарная дисперсия значения целевой функции (4.1) при различных реализациях случайной величины ${{t}_{i}}$ по формуле:
(4.2)
${{\omega }_{r}} = \mathop \sum \limits_{i = 1}^n \sigma _{i}^{2}{{d}_{i}} + 2\mathop \sum \limits_{i = 1}^n \mathop \sum \limits_{j > i} co{{v}_{{ij}}}{{d}_{i}}{{d}_{j}}.$Здесь ${{\omega }_{r}}$ – риск календарного плана r, $\sigma _{i}^{2}$ – дисперсия продолжительности работы i; $co{{v}_{{ij}}}$ – ковариация продолжительностей работ i и j, ${{d}_{i}}$ – доля работы i в величине целевой функции (4.1),
(4.3)
${{d}_{i}} = \frac{{{{\alpha }_{i}}\sum\limits_{j = 1}^n {a_{{jr}}^{i}{{{\bar {t}}}_{j}}} }}{{\sum\limits_{i = 1}^n {{{\alpha }_{i}}\sum\limits_{j = 1}^n {a_{{jr}}^{i}{{{\bar {t}}}_{j}}} } }},\quad i = \overline {1,n} .$Таким образом, в ситуации задания длительности работ как случайных величин эффективность расписания оценивается по двум критериям: 1) математическое ожидание средневзвешенного времени завершения работ данного расписания (формула (4.1)) и 2) количественная оценка риска расписания (формула (4.3)).
4.2. Пример оценки эффективности расписания с учетом риска. Рассмотрим пример двухкритериальной оценки расписания.
Пусть есть проект, состоящий из трех работ. Работы могут выполняться в любой последовательности, и их длительности заданы как случайные величины, имеющие следующие распределения вероятностей (табл. 1):
Таблица 1.
Длительности работ
| Вероятность | Работа | ||
|---|---|---|---|
| первая | вторая | третья | |
| $\frac{1}{2}$ | 0.9 | 2.2 | 3.2 |
| $\frac{1}{3}$ | 1.3 | 2.1 | 3 |
| $\frac{1}{6}$ | 1.1 | 1.9 | 2.8 |
Будем полагать, что работы выполняются двумя исполнителями и для этого каждой работе нужен один исполнитель. Величины весовых коэффициентов равны ${{\alpha }_{1}} = 1,$ ${{\alpha }_{2}} = 2,$ ${{\alpha }_{3}} = 3$. Рассчитаем математические ожидания длительностей работ:
Рассмотрим следующее расписание (рис. 8).
Таким образом, математическое ожидание средневзвешенного времени завершения работ равно:
Для оценки риска календарного плана рассчитаем di, i = 1, 2, 3:
Используя таблицу, вычислим $\sigma _{1}^{2},~~\sigma _{2}^{2},~~\sigma _{3}^{2}$ и $co{{v}_{{12}}},\;~co{{v}_{{22}}},~\;co{{v}_{{23}}}$:
Оценим риск календарного плана, изображенного на рис. 8 с использованием формулы (2.1):
Здесь количественная оценка риска – это дисперсия значения целевой функции (2.1) на расписании, изображенном на рис. 8.
5. Методы управления работами проекта в условиях различной производительности исполнителей. Рассмотрим ситуацию минимизации средневзвешенного времени выполнения работ проекта (критерий (1.1)) в условиях, когда работа может быть сделана несколькими исполнителями, при различной производительности каждого. Множество исполнителей определяется перед началом выполнения работы и не меняется до ее полного завершения. Иными словами, задана матрица (${{t}_{{ij}}}$) $i = \overline {1,n} $; $j = \overline {1,m} ,$ и элемент ${{t}_{{ij}}}$ этой матрицы есть время, за которое исполнитель j выполнит работу i.
В том случае если работу i выполняет подмножество исполнителей ${{M}_{i}}\dot { \subseteq }M$ (M – множество всех исполнителей), то ее длительность ${{t}_{i}}\left( {{{M}_{i}}} \right)~$равна
Если работа i выполняется исполнителями ${{M}_{i}}\dot { \subseteq }M$, $i = \overline {1,n} $, то минимальное время завершения работы $t_{i}^{{\text{н}}}$ можно вычислить как
(5.1)
$\tau _{i}^{{\text{н}}} = \mathop {\min }\limits_{j = \overline {1,{{\mathcal{L}}_{i}}} } {{S}_{j}} + {{t}_{j}}({{M}_{i}}),$Таким образом, для того чтобы оценить значение целевой функции (1.1) на каждом расписании выполнения работ в ситуации различных производительностей исполнителей, необходимо не только задать последовательность выполнения работ, но и определить состав исполнителей для каждой работы.
5.1. Метод ветвей и границ для случая различных производительностей исполнителей. Рассмотрим метод ветвей и границ для определения оптимального расписания по критерию (1.1) поставленной задачи.
Шаг 1. Вычислим нижнюю оценку оптимального значения целевой функции. Пусть технологическая последовательность выполнения работ проекта задается циклическим ориентированным графом G. Оценим минимально возможную длительность работы i:
Далее определим время завершения $\tau _{i}^{{\text{н}}}$ каждой работы по формуле (5.1) при условии, что длительность каждой работы минимальна, т.е. задана выражением (5.2), и вычислим значение целевой функции (1.1) в предложенных условиях. Это значение выберем в качестве нижней оценки ${{T}_{{\text{н}}}}$.
Шаг 2. Расчет верхней оценки оптимального значения целевой функции ${{T}_{{\text{в}}}}$ осуществляется путем формирования какого-либо допустимого расписания и вычисления целевой функции (1.1) на этом расписании.
Шаг 3. Если ${{T}_{{\text{в}}}} = {{T}_{{\text{н}}}}$, то оптимальное решение найдено. Если ${{T}_{{\text{в}}}} > {{T}_{{\text{н}}}}$, то происходит переход на анализ очередного расписания с определением текущих нижних оценок в момент времени $\tau $, связанных с окончанием одной из работ:
(5.3)
$T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right) = \sum\limits_{i \in N(\tau )}^{} {{{\alpha }_{i}}{{\tau }_{i}} + {{T}_{{\text{н}}}}(N{{\backslash }}N(\tau )).} $Здесь $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right)$ – текущая нижняя оценка целевой функции на формируемом расписании, $N\left( \tau \right)$ – множество работ, завершенных к моменту времени $\tau $, ${{T}_{н}}~(N{{\backslash }}N\left( \tau \right)$) – нижняя оценка целевой функции (1.1) на множестве работ $N{{\backslash }}N\left( \tau \right)$, незавершенных к моменту времени $\tau $.
Если $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right) \geqslant {{T}_{{\text{в}}}}$, то отбраковываем формируемое расписание, если $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right) < {{T}_{{\text{в}}}}$, то вычисляем минимальное ${{\tau }_{1}} > \tau $. Когда произойдет очередное завершение работы формируемого расписания, вычисляем очередное значение $T_{{\text{н}}}^{{{\text{тек}}}}\left( {{{\tau }_{1}}} \right)$ и сравниваем его с ${{T}_{{\text{в}}}}$. Продолжая описанную итерационную процедуру вычисления $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right)$, мы либо отбракуем формируемое расписание, либо получим новое расписание, значение целевой функции на котором $Т{\kern 1pt} *$ будет меньше ${{T}_{{\text{в}}}}$. В этом случае полагаем ${{T}_{{\text{в}}}} = Т{\kern 1pt} *$ и сравниваем новое значение ${{T}_{{\text{в}}}}~$ с $~{{T}_{{\text{н}}}}$. Если ${{T}_{{\text{в}}}} = {{T}_{{\text{н}}}}$, то оптимальное решение построено. Если ${{T}_{{\text{в}}}} > {{T}_{{\text{н}}}}$, то происходит переход на анализ очередного расписания.
Метод ветвей и границ прекращает свою работу, когда произойдет одно из событий.
1. При очередной корректировке ${{T}_{{\text{в}}}}$ получим, что ${{T}_{{\text{в}}}} = {{T}_{{\text{н}}}}$. Оптимальным решением будет то, которое соответствует этому ${{T}_{{\text{в}}}}$.
2. Все варианты формирования допустимых расписаний проанализированы, и последнее значение ${{T}_{{\text{в}}}} > {{T}_{{\text{н}}}}$.
В этом случае оптимальное решение то, которое соответствует последнему (минимальному) значению ${{T}_{{\text{в}}}}$.
5.2. Пример использования метода ветвей и границ. Пусть при формировании оптимального расписания задан ориентированный граф (рис. 9), определяющий технологическую последовательность выполнения работ проекта. Далее будем полагать, что для выполнения каждой работы необходим один исполнитель, а всего исполнителей два. Производительность каждого исполнителя на каждой работе задана матрицей T = $({{t}_{{ij}}})$, $i = \overline {1,7} $; j = 1, 2:
Рис 9.
Ориентированный граф $G\left( {m,n} \right)$, определяющий последовательность выполнения работ проекта
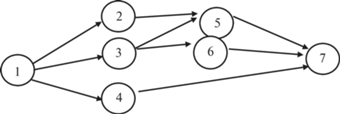
Вычислим минимально возможное время выполнения каждой работы. Очевидно, что это время будет получено в условиях выполнения каждой работы двумя исполнителями:
Рассчитаем минимально возможные моменты завершения работ $\tau _{i}^{{{\text{min}}}},~\;i = \overline {1,7} $, при условии, что их длительности равны $t_{i}^{{{\text{min}}}},\;i = \overline {1,7} $:
Далее будем полагать, что в целевой функции (1.1) весовые коэффициенты заданы следующим образом: ${{\alpha }_{1}} = 1$; ${{\alpha }_{2}} = 2$; ${{\alpha }_{3}} = 3$; ${{\alpha }_{4}} = 4$; ${{\alpha }_{5}} = 5$; $~{{\alpha }_{6}} = 6$; ${{\alpha }_{7}} = 7$.
В этих условиях вычислим нижнюю оценку оптимального значения целевой функции ${{T}_{{\text{н}}}}$ для рассматриваемой задачи:
Перейдем к вычислению верхней оценки $~{{T}_{{\text{в}}}}$. Для этого сформулируем некоторое допустимое расписание и вычислим на нем значение целевой функции (1.1). Это расписание изобразим с помощью следующей диаграммы Ганта (рис. 10).
Рис. 10.
Диаграмма Ганта выполнения работ проекта с учетом различной производительности исполнителей
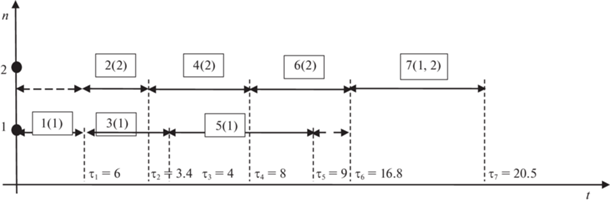
На диаграмме Ганта (рис. 10) предполагается, что все работы проекта, за исключением седьмой, выполняет один исполнитель (в скобках указан номер исполнителя). Седьмую работу выполняют оба исполнителя, и в этом случае ее продолжительность равна 3.9 единицы времени. С учетом сформированного расписания вычислим значение целевой функции (1.1), которое и будет верхней оценкой:
Исходя из того, что ${{T}_{{\text{в}}}} > {{T}_{{\text{н}}}}$, переходим к формированию очередного допустимого расписания с вычислением $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right)$ в момент $\tau $, связанного с завершением какой-либо работы проекта по формуле (4.6). При формировании второго расписания поставим на выполнение после завершения первой, вторую и четвертую работы (рис. 11).
Рассчитаем $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right)$ для момента завершения второй работы (${{{{\tau }}}_{2}}$ = 3.4):
С учетом того, что ${{T}_{в}} > T_{н}^{{{\text{тек}}}}\left( {\tau = 3.4} \right)$, продолжаем формировать второе расписание и после завершения второй работы поставим на выполнение третью работу (рис. 12).
Рис. 12.
Фрагмент второго формируемого расписания после выполнения первой, второй, четвертой и третьей работ
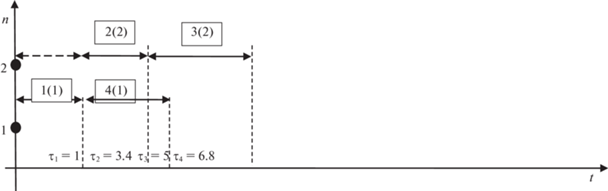
Вычислим $T_{{\text{н}}}^{{{\text{тек}}}}\left( \tau \right)$ для момента завершения четвертой работы, т.е. момента ${{{{\tau }}}_{3}}$ = 5:
Учитывая, что ${{T}_{{\text{в}}}} > T_{{\text{н}}}^{{{\text{тек}}}}$ $\left( {{{{{\tau }}}_{3}} = 5} \right)$, продолжаем формировать текущее расписание и в момент времени ${{{{\tau }}}_{3}} = 5$, т.е. когда закончено выполнение четвертой работы, поставим на выполнение пятую работу (рис. 13).
Рис. 13.
Фрагмент формирования второго расписания после выполнения первой, второй, четвертой, третьей и пятой работ
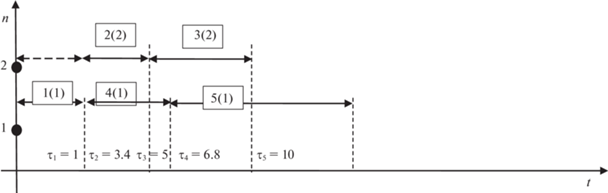
В момент времени ${{{{\tau }}}_{4}}$ = 6.8 закончится выполнение третьей работы, поэтому вычисляем $T_{{\text{н}}}^{{{\text{тек}}}}({{{{\tau }}}_{4}})$:
С учетом того, что ${{T}_{в}} > T_{{\text{н}}}^{{{\text{тек}}}}\left( {{{{{\tau }}}_{4}}} \right)$, продолжаем формирование текущего расписания и в момент времени ${{{{\tau }}}_{4}} = 6.8,$ когда пятая работа не завершена, ставим на выполнение шестую работу (рис. 14). В момент времени ${{{{\tau }}}_{5}}$ = 10 произошло завершение пятой работы, поэтому вычисляем значение $T_{{\text{н}}}^{{{\text{тек}}}}\left( {{{{{\tau }}}_{5}}} \right)$:
Рис. 14.
Фрагмент формирования второго расписания после выполнения первой, второй, четвертой, третьей, пятой и шестой работ
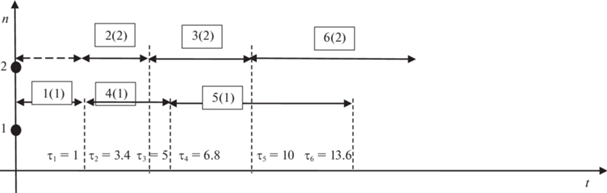
После завершения шестой работы в момент времени ${{{{\tau }}}_{6}}$ = 13.6 седьмая работа может быть выполнена двумя исполнителями и ее продолжительность будет равна
Следовательно, значение целевой функции T* на формируемом расписании вычислим как
Учитывая, что ${{T}_{{\text{в}}}} > Т{\kern 1pt} *$, новое значение ${{T}_{{\text{в}}}} = 313.8$ и переходим к анализу других вариантов формирования расписаний.
Заключение. Рассмотрены методы оптимизации расписаний выполнения работ проекта для критерия минимизации средневзвешенного времени их выполнения. В том случае, когда длительности работ заданы детерминировано, предложен точный и приближенный метод решения задачи выбора оптимального расписания. Если возможны изменения длительности работ, предложен аналитический инструментарий оценки устойчивости расписаний как для ситуации интервального задания длительностей работ, так и для ситуации изменения длительностей работ при возможных возмущениях внешней среды. В том случае если длительности работ заданы стохастически, предлагается механизм оценки эффективности расписания по двум критериям и предложена процедура количественной оценки риска расписания. В разд. 5 статьи исследована ситуация возможности выполнения каждой работы несколькими исполнителями и предложен метод оптимизации расписаний выполнения работ для этого случая.
Список литературы
Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982.
Мищенко А.В., Халиков М.А. Распределение ограниченных ресурсов в задаче оптимизации производственной деятельности предприятия // Изв. АН СССР. Техн. кибернетика. 1991. № 6.
Мищенко А.В., Пилюгина А.В. Динамические модели управления научно-производственными системами // Вестн. МГТУ им. Баумана. Сер. Приборостроение. 2019. № 2.
Мищенко А.В., Сушков Б.Г. Задача оптимального распределения ресурсов на сетевой модели при линейных ограничениях на время выполнения работ // ЖВМ и МФ. 1980. Т. 10. № 5.
Мищенко А.В., Когаловский В.М. Проблемы устойчивости задач производственного планирования в машиностроении // Экономика и мат. методы. 1992. № 3.
Мищенко А.В. Устойчивость решений в задаче перераспределения транспортных средств в случае экстренного закрытия движения на участке метрополитена // Изв. АН СССР. Техн. кибернетика. 1990. № 3.
Мищенко А.В. Задача распределения транспортных средств по автобусным маршрутам при неточно заданной матрице корреспонденций пассажиропотока // Изв. АН СССР. Техн. кибернетика. 1992. № 2.
Катюхина О.А., Мищенко А.В. Динамические модели управления транспортными ресурсами на примере организации работы автобусного парка // Аудит и финансовый анализ. 2016. № 2. С. 156–167.
Косоруков Е.О., Фуругян М.Г. Некоторые алгоритмы распределения ресурсов в многопроцессорных системах // Вестн. МГУ. Сер. 15. Вычисл. математика и кибернетика. 2009. № 4. С. 34–37.
Фуругян М.Г. Планирование вычислений в многопроцессорных АСУ реального времени с дополнительным ресурсом // АиТ. 2015. № 3.
Косоруков Е.О., Фуругян М.Г. Алгоритмы распределения ресурсов в многопроцессорных системах с нефиксированными параметрами // Некоторые алгоритмы планирования вычислений и организации контроля в системах реального времени. М.: ВЦ РАН, 2011. С. 40–51.
Mironov A.A., Tsurkov V.I. Transport-type Problems with a minimax Criterion // AиT. 1995. № 12. C. 109–118.
Миронов А.А., Цурков В.И. Наследственно-минимаксные матрицы в моделях транспортного типа // Изв. РАН. ТиСУ. 1998. № 6. С. 104–121.
Mironov A.A., Levkina T.A., Tsurkov V.I. Minimax Estimations of Expectates of Arc Weights in Integer Networks with Fixed Node Degrees // Applied and Computational Mathematics. 2009. T. 8. № 2. C. 216–226.
Mironov A.A., Tsurkov V.I. Class of Distribution Problems with Minimax Criterion // Doklady Akademii Nauk. 1994. V. 336. № 1. P. 35–38.
Tizik A.P., Tsurkov V.I. Iterative Functional Modification Method for Solving a Transportation Problem // Automation and Remote Control. 2012. V. 73. № 1. P. 134–143.
Mironov A.A., Tsurkov V.I. Hereditarily Minimax Matrices in Models of Transportation Type // J. Computer and Systems Sciences International. 1998. V. 37. № 6. P. 927–944.
Mironov A.A., Tsurkov V.I. Minimax in Transportation Models with Integral Constraints. 1 // J. Computer and Systems Sciences International. 2003. V. 42. № 4. P. 562–574.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления