Известия РАН. Теория и системы управления, 2023, № 4, стр. 25-49

Введение. Термин “машина Дубинса” в настоящее время используется для обозначения управляемого объекта, который передвигается на двумерной плоскости с постоянной по величине линейной скоростью и заданными ограничениями на мгновенную угловую скорость поворота.

К классическим работам, где рассматривался подобный объект, помимо статьи [1], следует отнести публикации [2, 3]. Количество работ, связанных с машиной Дубинса, огромно. Многие из них указаны в списке литературы к статье [4]. В [5, 6] описаны содержательные задачи, где применяется модель “машина Дубинса” и ее различные модификации/обобщения.

Отметим некоторые работы, выполненные в последние годы. В [7] исследуется задача перехвата машиной Дубинса за наименьшее время объекта, движение которого задано заранее. В [8] изучается весьма общая постановка задач управления с двумя геометрическими координатами и двумерным управлением. В качестве одного из частных случаев применения полученных результатов рассматривается задача быстродействия для машины Дубинса. В [9] предложен вариант алгоритмического построения оптимальных программных траекторий машины Дубинса в задаче быстродействия. Численное построение трехмерного множества достижимости для машины Дубинса при наличии движущихся препятствий на плоскости геометрических координат рассмотрено в [10]. Некоторые задачи управления гибридной системой, составленной с использованием машины Дубинса, исследованы в [11].

Настоящая работа посвящена исследованию трехмерного множества достижимости для машины Дубинса. Не теряя общности, величину линейной скорости объекта считаем равной единице, а начальное фазовое состояние полагаем нулевым. Под множеством достижимости G(t_f) понимаем совокупность всех трехмерных фазовых состояний $x,y,\varphi $ ($x,y$ – координаты геометрического положения, φ – угол направления вектора скорости), в каждое из которых можно перевести объект в заданный момент времени t_f. Двумерное сечение множества G(t_f) по угловой координате φ обозначим G_φ(t_f) и назовем φ-сечением.

Каноническим считаем случай, когда скалярное управление u (имеющее смысл мгновенной угловой скорости поворота) стеснено ограничением $\left| u \right|{\text{\;}} \leqslant {\text{\;}}1$. Задачи с несимметричными ограничениями $u \in \left[ {{{u}_{1}},{{u}_{2}}} \right]$, где ${{u}_{1}} < 0$, ${{u}_{2}} > 0$, также рассматриваются в литературе (см., например, [12]).

В качестве практического примера несимметричных ограничений можно указать координированное движение (см., например, [13, с. 60, 61; 14, с. 764]) самолета в горизонтальной плоскости с постоянной величиной линейной скорости. Повороты при этом осуществляются изменением угла крена. Для модельного кинематического описания используется кинематика машины Дубинса. Нарушение симметрии ограничений по крену (в том числе за счет неправильной работы исполнительных механизмов) приводит к рассмотрению несимметричного случая.

Работа является продолжением статьи [15]. Показано, что исследование φ-сечений для произвольного несимметричного случая сводится к исследованию φ-сечений в каноническом случае. А именно установлено аффинное взаимно-однозначное соответствие между φ-сечениями множества достижимости для произвольного несимметричного случая и φ-сечениями для канонического случая. Аналитическое описание φ-сечений для канонического случая приведено в [4, 16].

Кратко опишем содержание статьи. В разд. 1 приводится постановка задачи о нахождении множества достижимости для машины Дубинса с несимметричными ограничениями ${{u}_{1}} < 0$, ${{u}_{2}} > 0$ на управление. Множество достижимости G(t_f) представляется в виде совокупности его сечений по угловой координате φ. Описание φ-сечений для общего случая требуется осуществить посредством сведения к рассмотрению φ-сечений в каноническом случае.

Исследование опирается на принцип максимума Л.С. Понтрягина [17], которому удовлетворяют движения и управления, ведущие на границу множества достижимости. В качестве несложного следствия принципа максимума в разд. 2 получаем, что при описании границы можно ограничиться кусочно-постоянными управлениями с конечным числом переключений и со значениями в трехэлементном множестве $\left\{ {{{u}_{1}},0,{{u}_{2}}} \right\}$. В разд. 3 формулируются и доказываются утверждения о свойствах движений и управлений, удовлетворяющих принципу максимума. Показано, что при построении границы множества достижимости достаточно взять шесть типов управлений с не более чем двумя переключениями. Этот результат распространяется на точки из внутренности множества достижимости при подходящем сужении ограничений на управление. В разд. 4 при зафиксированном значении угловой координаты $\varphi \geqslant 0$ дается описание движений, которые порождаются управлениями из разд. 3. Получаемые в момент t_f   точки образуют непрерывную замкнутую кривую ${{\mathcal{A}}_{\varphi }}\left( {{{t}_{f}}} \right)$ на плоскости геометрических координат. Эта кривая содержит все точки границы рассматриваемого φ-сечения, но часть ее, вообще говоря, проходит и во внутренности φ-сечения. Важное свойство состоит в том, что кривая ${{\mathcal{A}}_{\varphi }}\left( {{{t}_{f}}} \right)$ симметрична относительно оси X некоторой вспомогательной прямоугольной системы координат X, Y (зависящей от φ).

Раздел 5 является центральным в статье. В нем при ${{\varphi }} \geqslant 0$ устанавливается соответствие между кривой ${{\mathcal{A}}_{\varphi }}({{t}_{f}})$ и некоторой кривой $\mathcal{A}_{\varphi }^{{\text{c}}}(t_{f}^{{\text{c}}})$, рассматриваемой для канонического случая. Момент $t_{f}^{{\text{c}}}$ задается определенной формулой и отличается от момента t_f. На базе этого соответствия выводится аналогичное соотношение между φ-сечениями G_φ(t_f) и $G_{\varphi }^{{\text{c}}}(t_{f}^{{\text{c}}})$ для исходного и канонического случаев во вспомогательной системе координат. В разд. 6 для значений ${{\varphi }} < 0$ описание φ‑сечений получаем, опираясь на случай ${{\varphi }} > 0$.

Рассматриваемые в статье шесть типов управления совпадают в каноническом случае с шестью вариантами, указанными в работе [1] для задачи быстродействия. В связи с этим подчеркнем, что в нашей статье речь идет об описании границы множества достижимости в заданный момент t_f. С логической точки зрения совокупность программных управлений, решающих задачу быстродействия, вообще говоря, является недостаточной для полного построения границы множества достижимости в момент.

1. Постановка задачи. Пусть движение управляемого объекта на плоскости описывается системой дифференциальных уравнений

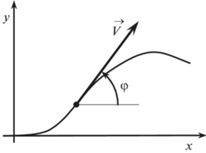
Здесь  x, y – координаты геометрического положения, φ – угол наклона вектора скорости (рис. 1), отсчитываемый против часовой стрелки от положительного направления оси x. Величина скорости равна единице. Допустимыми управлениями u(·) считаем измеримые функции времени, удовлетворяющие ограничению ${{u}_{1}} \leqslant u\left( t \right) \leqslant {{u}_{2}}$. Значения угла φ рассматриваются на промежутке $\left( { - \infty ,\infty } \right)$. Фазовый вектор ${{\left( {x,y,\varphi } \right)}^{{\text{T}}}}$ системы (1.1) обозначим через z.

Зафиксируем ${{z}_{0}}$ – фазовое состояние системы (1.1) в начальный момент времени t₀. Множество достижимости G(t_f) в момент времени ${{t}_{f}} > {{t}_{0}}$ есть совокупность всех точек z трехмерного фазового пространства, в каждую из которых возможен перевод системы (1.1) в момент t_f  при помощи некоторого допустимого управления на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ из начальной точки ${{z}_{0}}$.

Обозначим через G_φ(t_f) двумерное φ-сечение множества G(t_f). Отметим, что если некоторая точка ${{\left( {x,y} \right)}^{{\text{T}}}}$ принадлежит $\partial {{G}_{\varphi }}\left( {{{t}_{f}}} \right)$, то точка ${{\left( {x,y,\varphi } \right)}^{{\text{T}}}}$ принадлежит $\partial G\left( {{{t}_{f}}} \right)$. Обратное, вообще говоря, неверно. Здесь символ $\partial $ означает границу множества.

При изучении множеств достижимости, не ограничивая общности, полагаем ${{t}_{0}} = 0$ и ${{z}_{0}} = {{\left( {0,{\text{\;}}0,{\text{\;}}0} \right)}^{{\text{T}}}}$. Систему (1.1) в частном случае симметричных ограничений ${{u}_{1}} = - 1$, ${{u}_{2}} = 1$ будем называть канонической. Соответствующее ей множество достижимости обозначим через $G_{{}}^{{\text{c}}}(t_{f}^{{}})$.

Цель статьи – показать и обосновать способ получения φ-сечений множества достижимости G(t_f) исходной системы (1.1) для произвольных $\varphi \in \left[ {{{t}_{f}}{{u}_{1}},{{t}_{f}}{{u}_{2}}} \right]$ на основе φ-сечений множества достижимости канонической системы.

2. Принцип максимума Понтрягина. Из общих результатов математической теории управления [18] следует, что множество достижимости G(t_f) замкнуто и ограничено. Известно также, что управления, которые ведут на границу множества достижимости, удовлетворяют принципу максимума Понтрягина (ПМП). Запишем соотношения принципа максимума для системы (1.1).

Пусть u*(·) – некоторое допустимое управление, ${{\left( {x{\text{*}}\left( \cdot \right),y{\text{*}}\left( \cdot \right),\varphi {\text{*}}\left( \cdot \right)} \right)}^{{\text{T}}}}$ – соответствующее движение системы (1.1) на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$. Дифференциальные уравнения сопряженной системы записываются в виде

ПМП означает, что существует ненулевое решение ${{(\psi _{1}^{{\text{*}}}\left( \cdot \right),\psi _{2}^{{\text{*}}}\left( \cdot \right),\psi _{3}^{{\text{*}}}\left( \cdot \right))}^{{\text{T}}}}$ системы (2.1), для которого почти всюду (п.в.) на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ выполнено равенство

Таким образом, условие максимума имеет вид

Предполагая, что $u{\text{*}}\left( \cdot \right)$ удовлетворяет (2.2), сформулируем несколько простых свойств. Отметим, что функции $\psi _{1}^{{\text{*}}}\left( \cdot \right)$ и $\psi _{2}^{{\text{*}}}\left( \cdot \right)$ есть константы. Обозначим их $\psi _{1}^{{\text{*}}}$ и $\psi _{2}^{{\text{*}}}$. Если $\psi _{1}^{{\text{*}}} = 0$ и $\psi _{2}^{{\text{*}}} = 0$, то $\psi _{3}^{{\text{*}}}\left( t \right) = {\text{const\;}} \ne 0$ на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$. Следовательно, в этом случае либо п.в. $u{\text{*}}\left( t \right) = {{u}_{2}}$, либо п.в. $u{\text{*}}\left( t \right) = {{u}_{1}}$.

Пусть теперь хотя бы одно из чисел $\psi _{1}^{{\text{*}}}$, $\psi _{2}^{{\text{*}}}$ не равно нулю. Опираясь на (1.1) и (2.1), можно записать выражение $\psi _{3}^{{\text{*}}}\left( t \right) = \psi _{1}^{{\text{*}}}y{\text{*}}\left( t \right) - \psi _{2}^{{\text{*}}}x{\text{*}}\left( t \right) + C.$ Отсюда следует, что $\psi _{3}^{{\text{*}}}\left( t \right) = 0$ тогда и только тогда, когда точка ${{\left( {x{\text{*}}\left( t \right),y{\text{*}}\left( t \right)} \right)}^{{\text{T}}}}$ геометрического положения в момент t удовлетворяет уравнению прямой:

Прямая переключения (2.3) не является универсальной: при смене движения, удовлетворяющего ПМП, изменяется, вообще говоря, и прямая переключения.

В силу соотношения (2.2), если $\psi _{3}^{{\text{*}}}\left( t \right) > 0$ ($\psi _{3}^{{\text{*}}}\left( t \right) < 0$) на некотором промежутке времени, то $u{\text{*}}\left( t \right) = {{u}_{2}}$ ($u{\text{*}}\left( t \right) = {{u}_{1}}$) п.в. на этом промежутке. Соответствующее движение в проекции на плоскость x, y при этом идет по дуге окружности радиуса 1/u₂ против часовой стрелки в полуплоскости $\psi _{1}^{{\text{*}}}y - \psi _{2}^{{\text{*}}}x + C > 0$ (по дуге окружности радиуса $ - 1{\text{/}}{{u}_{1}}$ по часовой стрелке в полуплоскости $\psi _{1}^{{\text{*}}}y - \psi _{2}^{{\text{*}}}x + C < 0$). Условимся называть левым (правым) циклом участок движения длительностью $2\pi {\text{/}}{{u}_{2}}$ (соответственно длительностью $ - 2\pi {\text{/}}{{u}_{1}}$), на котором п.в. $u{\text{*}}\left( t \right) = {{u}_{2}}$ ($u{\text{*}}\left( t \right) = {{u}_{1}}$). Траектория движения на таком участке в проекции на плоскость x, y представляет собой окружность.

Если $\psi _{3}^{{\text{*}}}\left( t \right) = 0$ на некотором промежутке времени, то на этом промежутке движение ${{\left( {x{\text{*}}\left( t \right),y{\text{*}}\left( t \right)} \right)}^{{\text{T}}}}$ идет по прямой переключения. Стало быть, $\varphi {\text{*}}\left( t \right) = {\text{const\;}}$. Поэтому $u{\text{*}}\left( t \right) = 0$ п.в. на этом промежутке.

На рис. 2 показаны движения системы (1.1), удовлетворяющие ПМП. Здесь и на последующих поясняющих рисунках для определенности полагаем ${{u}_{2}} > - {{u}_{1}}$. Траектория на рис. 2, а имеет три момента переключения и последовательность управлений ${{u}_{2}},{{u}_{1}},{{u}_{2}},{{u}_{1}}$. На рис. 2, б показана траектория с шестью моментами переключения с последовательностью управлений u₂, 0, ${{u}_{1}},0,{{u}_{2}},0,{{u}_{1}};~$ существуют левый и правый циклы.

Возможны лишь следующие три варианта взаимного расположения траектории движения ${{\left( {x{\text{*}}\left( t \right),y{\text{*}}\left( t \right)} \right)}^{{\text{T}}}}$ и прямой переключения.

1. Траектория пересекает прямую (2.3) в некоторый момент под ненулевым углом (рис. 2, а). Тогда траектория представляет собой набор дуг окружностей с одинаковым угловым раствором между соседними точками пересечения прямой переключения. Функция $\psi _{3}^{{\text{*}}}\left( \cdot \right)$ меняет знак на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ конечное число раз.

2. Траектория касается прямой (2.3) в некоторый момент (рис. 2, б). Тогда траектория представляет собой набор дуг окружностей и прямолинейных участков. Прямолинейные участки лежат на прямой (2.3), дуги окружностей касаются этой прямой. При этом любой полный участок в виде дуги окружности, не являющийся крайним, представляет собой один или несколько подряд идущих циклов. Функция $\psi _{3}^{{\text{*}}}\left( \cdot \right)$ на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ либо не меняет знак, либо меняет его конечное число раз.

3. Траектория не пересекается с прямой (2.3). В этом случае функция $\psi _{3}^{{\text{*}}}\left( \cdot \right)$ имеет один и тот же знак на всем промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ и траектория является дугой окружности.

Таким образом, если выполнено условие максимума (2.2), то функция $\psi _{3}^{{\text{*}}}\left( \cdot \right)$ на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ может менять знак лишь конечное число раз. Поэтому в качестве управления $u{\text{*}}\left( \cdot \right)$, порождающего движение z*(·) и удовлетворяющего ПМП, можно взять кусочно-постоянное управление со значениями ${{u}_{1}},0,{{u}_{2}}$ и конечным числом переключений на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$. Для определенности будем считать такое управление кусочно-непрерывным справа. Момент t_f  не включаем в число моментов переключения.

Изложенное выше позволяет сформулировать следующие два утверждения.

Утверждение 1. Пусть движение $z{\text{*}}\left( \cdot \right)$ системы (1.1) на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ порождается допустимым измеримым управлением и при этом выполнен ПМП. Тогда движение $z{\text{*}}\left( \cdot \right)$ может быть реализовано при помощи кусочно-постоянного управления с конечным числом переключений и со значениями в трехэлементном множестве $\left\{ {{{u}_{1}},0,{{u}_{2}}} \right\}$.

Утверждение 2. Пусть движение $z{\text{*}}\left( \cdot \right)$ системы (1.1) на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ порождается кусочно-постоянным управлением $u{\text{*}}\left( \cdot \right)$ и при этом выполнен ПМП. Тогда:

а) точки геометрического положения системы (1.1) на плоскости x, y в моменты переключения управления $u{\text{*}}\left( \cdot \right)$ лежат на прямой переключения (2.3);

б) если на движении $z{\text{*}}\left( \cdot \right)$ нет участков с нулевым управлением, нет циклов и число переключений управления $u{\text{*}}\left( \cdot \right)$ больше двух, то приращение угла между соседними моментами переключения одинаково по модулю;

в) если на движении $z{\text{*}}\left( \cdot \right)$ нет участков с нулевым управлением, есть хотя бы один цикл и число переключений управления $u{\text{*}}\left( \cdot \right)$ больше одного, то все точки геометрического положения в моменты переключения совпадают;

г) если на движении $z{\text{*}}\left( \cdot \right)$ есть участок с нулевым управлением, то любой участок движения между соседними моментами переключения, на котором реализуется постоянное управление u₁ или ${{u}_{2}}$, представляет собой один или несколько подряд идущих циклов.

3. Свойства движений, удовлетворяющих ПМП. В основной части данного раздела будут доказаны несколько лемм и опирающаяся на них теорема 1 о числе и характере переключений управлений, ведущих на границу множества G(t_f). В соответствии с утверждением 1 рассматриваем кусочно-постоянные управления $u\left( t \right) \in \left\{ {{{u}_{1}},0,{{u}_{2}}} \right\}$ c конечным числом моментов переключения. Таких управлений достаточно для построения границы множества достижимости. В леммах 1–3 исследуются движения без участков с нулевым управлением. В лемме 4 анализируется случай с участком нулевого управления. Итоговый результат сформулирован в теореме 1. Аналогом теоремы 1, но для управлений, ведущих в произвольную точку множества G(t_f), является теорема 2. Для обозначения внутренности множества будем использовать символ int.

Лемма 1. Пусть движение $z\left( \cdot \right)$ на некотором промежутке $\left[ {{\text{\;}}\overline {{{t}_{~}}} ,{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right]$ порождается кусочно-постоянным управлением u(·) с двумя моментами переключения t₁ и t₂, где ${\text{\;}}\overline {{{t}_{~}}} < {{t}_{1}} < {{t}_{2}} < \widehat {{{t}_{~}}}.{\text{\;}}$ При этом управление последовательно принимает значения u₁, ${{u}_{2}}$, u₁ (соответственно u₂, u₁, u₂). Предположим, что $\varphi \left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right) = \varphi \left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)$. Тогда на том же промежутке времени существует управление $\widetilde {u~}\left( \cdot \right)$ с некоторыми двумя моментами переключения $\widetilde {{{t}_{1}}}$ и $\widetilde {{{t}_{2}}}$, где ${\text{\;}}\overline {{{t}_{~}}} < \widetilde {{{t}_{1}}} < \widetilde {{{t}_{2}}} < \widehat {{{t}_{~}}}$, которое осуществляет перевод из точки $~\widetilde {z~}\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right) = z~\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right)~$ в точку $~\widetilde {z~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right) = z~\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)~$ и последовательно принимает значения ${{u}_{2}}$, u₁, ${{u}_{2}}$ (соответственно u₁, u₂, u₁).

Доказательство. Пусть управление $u\left( \cdot \right)$ последовательно принимает значения u₁, ${{u}_{2}}$, ${{u}_{1}}$. Положим $~\widetilde {{{t}_{1}}} = {\text{\;}}\overline {{{t}_{~}}} - ({\text{\;}}\widehat {{{t}_{~}}} - {{t}_{2}}){\text{\;}}{{u}_{1}}{\text{/}}{{u}_{2}}$, $~\widetilde {{{t}_{2}}} = \widehat {{{t}_{~}}} + {\text{(}}{{t}_{1}} - {\text{\;}}\overline {{{t}_{~}}} {\text{)}}{{u}_{1}}{\text{/}}{{u}_{2}}$. Очевидно, что $~\overline {{{t}_{~}}} < \widetilde {{{t}_{1}}}$ и $\widetilde {{{t}_{2}}} < \widehat {{{t}_{~}}}$. Кроме того,

Равенство $\varphi (\bar {t})\, = \,\varphi (\hat {t})$ запишем в виде $~{{u}_{1}}({{t}_{1}}\,\, - \,\,\bar {t}{\text{\;}})\,\, + \,\,{{u}_{2}}({{t}_{2}}\,\, - \,\,{{t}_{1}})\,\, + \,\,{{u}_{1}}(\hat {t}\,\, - \,\,{{t}_{2}})\,\, = \,\,0.$ Отсюда $\hat {t}\, - \,{\text{\;}}\bar {t}{\text{\;}}$ = = ${\text{\;}}({{t}_{2}}\, - \,{{t}_{1}})({{u}_{1}}\, - \,{{u}_{2}}){\text{/}}{{u}_{1}}.{\text{\;}}$ Подставляя в (3.1) полученное выражение для ${\text{\;}}\widehat {{{t}_{~}}} - {\text{\;}}\overline {{{t}_{~}}} $, имеем

Учитывая (3.2), получаем ${\text{\;}}\overline {{{t}_{~}}} < \widetilde {{{t}_{1}}} < \widetilde {{{t}_{2}}} < \widehat {{{t}_{~}}}$.

Зададим управление $~\widetilde {u~}\left( \cdot \right)$ на промежутке $\left[ {{\text{\;}}\overline {{{t}_{~}}} ,{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right]$ двумя моментами переключения $~\widetilde {{{t}_{1}}}$, $\widetilde {{{t}_{2}}}{\text{\;}}$ и значениями $~{{u}_{2}}$, ${{u}_{1}}$, ${{u}_{{2{\text{\;}}}}}$ на трех участках постоянства. Рассмотрим соответствующее движение $~\widetilde {z~}\left( \cdot \right) = {{\left( {\widetilde {x~}\left( \cdot \right),{\text{\;}}\widetilde {y~}\left( \cdot \right),{\text{\;}}\widetilde {\varphi ~}\left( \cdot \right)} \right)}^{{\text{T}}}}$, выходящее в момент $~\overline {{{t}_{~}}} {\text{\;}}$ из точки $~\widetilde {z~}\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right) = z\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right)$. Покажем, что $~z\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right) = \widetilde {z~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)$.

Из определения моментов $~\widetilde {{{t}_{1}}}$, $\widetilde {{{t}_{2}}}~$ и соотношения (3.2) имеем

Стало быть,

Складывая левые и правые части этих равенств, получаем $\varphi \left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right) - \varphi \left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right) = \widetilde {\varphi ~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right) - \widetilde {\varphi ~}\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right).$ Отсюда с учетом условия $\widetilde {\varphi ~}\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right) = \varphi \left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right)$ приходим к равенству $\widetilde {\varphi ~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right) = \varphi \left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)$. Подставляя это равенство вместе с равенством $\varphi \left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right) = \varphi \left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)$ в первое и третье соотношения из (3.3), имеем

Проинтегрируем первое уравнение системы (1.1) в силу управления u(·) на $\left[ {{\text{\;}}\overline {{{t}_{~}}} ,{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right]$:

Интегрируя в силу управления $~\widetilde {u~}\left( \cdot \right)$, имеем

С учетом (3.4) получаем $~\widetilde {x~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right){\text{\;}} = {\text{\;}}x~\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)$. Непосредственным интегрированием также устанавливается равенство $~\widetilde {y~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right){\text{\;}} = {\text{\;}}y~\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)$.

Случай, когда исходное управление последовательно принимает значения ${{u}_{2}}$, ${{u}_{1}}$, ${{u}_{2}}$, рассматривается аналогично. Следует лишь поменять местами символы ${{u}_{1}}$ и ${{u}_{2}}$. Лемма 1 доказана.

Лемма 2. Пусть движение $z\left( \cdot \right)$ на промежутке $[{{t}_{0}},{{t}_{f}}]$ порождается кусочно-постоянным управлением u(·) со значениями ${{u}_{1}},{{u}_{2}}$ и двумя моментами переключения ${{t}_{1}}$, ${{t}_{2}}$, причем ${{t}_{0}}\, < \,{{t}_{1}}\, < \,{{t}_{2}}\, < \,{{t}_{f}}$. Предположим, что

Тогда $z\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$.

Доказательство. Условие (3.5) содержательно означает, что сумма приращений угла φ на первом и третьем участках постоянства управления, взятая по модулю, больше модуля приращения угла на среднем участке. Не теряя общности, примем следующую последовательность значений управления $u\left( \cdot \right)$: ${{u}_{1}},{{u}_{2}},{{u}_{1}}$. Тогда условие (3.5) запишется в виде

Предположим от противного, что $z\left( {{{t}_{f}}} \right) \in \partial G\left( {{{t}_{f}}} \right)$. Тогда любое управление, ведущее в эту точку, удовлетворяет ПМП.

1. Рассмотрим случай, когда точки ${{\left( {x\left( {{{t}_{1}}} \right),y\left( {{{t}_{1}}} \right)} \right)}^{{\text{T}}}}$ и ${{\left( {x\left( {{{t}_{2}}} \right),y\left( {{{t}_{2}}} \right)} \right)}^{{\text{T}}}}$ геометрического положения на плоскости x, y в моменты переключения ${{t}_{1}}$ и ${{t}_{2}}$ не совпадают. В силу утверждения 2в получаем, что движение $z\left( \cdot \right)$ на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ не имеет циклов.

Выберем моменты ${\text{\;}}\overline {{{t}_{~}}} \in \left( {{{t}_{0}},{\text{\;}}{{t}_{1}}} \right)$ и ${\text{\;}}\widehat {{{t}_{~}}} \in \left( {{{t}_{2}},{\text{\;}}{{t}_{f}}} \right)$ так, чтобы выполнялось равенство

Возможность выбора $~\overline {{{t}_{~}}} ~$ и $~\widehat {{{t}_{~}}}~$ с обеспечением (3.7) следует из монотонного изменения угла φ в зависимости от общей длины двух крайних промежутков с управлением u₁. Можно взять, например,

В самом деле, неравенство $\varphi \left( {{{t}_{0}}} \right) - \varphi \left( {{{t}_{f}}} \right) > 0$ справедливо в силу условия (3.5), а неравенство $\varphi \left( {{{t}_{2}}} \right) - \varphi \left( {{{t}_{1}}} \right) > 0$ выполнено, так как на интервале $\left[ {{{t}_{1}},{{t}_{2}}} \right)$ действует управление u₂. Поэтому $q \in \left( {0,1} \right)$ и, стало быть, $\overline {{{t}_{~}}} \in \,\,\left( {{{t}_{0}},{\text{\;}}{{t}_{1}}} \right)$, $\widehat {{{t}_{~}}} \in \left( {{{t}_{2}},{\text{\;}}{{t}_{f}}} \right)$. Для введенных таким образом моментов $~\overline {{{t}_{~}}} {\text{\;}}$ и ${\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}$ имеем

Подстановкой этих равенств в соотношение (3.7) убеждаемся в его выполнении. Соотношение (3.7) означает, что $\varphi \left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right) = \varphi \left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)$.

Опираясь на лемму 1, рассмотрим на промежутке $~\left[ {{\text{\;}}\overline {{{t}_{~}}} ,{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right]$ движение, выходящее из точки $~z\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right)$, приходящее в точку $~z\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)~$ и использующее последовательно управления ${{u}_{2}}$, ${{u}_{1}}$, ${{u}_{{2{\text{\;}}}}}$ с двумя моментами переключения $~\widetilde {{{t}_{1}}}~$, $~\widetilde {{{t}_{2}}}~$.

Наряду с исходным движением $~z\left( \cdot \right)$, порождаемым управлением u(·), введем вспомогательное движение $~\widetilde {z~}\left( \cdot \right) = {{\left( {{\text{\;}}\widetilde {x~}\left( \cdot \right),{\text{\;}}\widetilde {y~}\left( \cdot \right),{\text{\;}}\widetilde {\varphi ~}\left( \cdot \right){\text{\;}}} \right)}^{{\text{T}}}}$, выходящее из начальной точки $~\widetilde {z~}\left( {{{t}_{0}}} \right) = z\left( {{{t}_{0}}} \right){\text{\;}}$ в силу управления:

Управление $~\widetilde {u~}\left( \cdot \right){\text{\;}}$ отличается от исходного управления $~u\left( \cdot \right){\text{\;}}$ только на промежутке $~\left[ {{\text{\;}}\overline {{{t}_{~}}} ,{\text{\;}}\widehat {t{\text{\;}}}{\text{\;}}} \right)$. При этом $~\widetilde {z~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right) = z\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)$. Стало быть, $~\widetilde {z~}\left( {{{t}_{f}}} \right) = z\left( {{{t}_{f}}} \right)$. Следовательно, $~\widetilde {z~}\left( {{{t}_{f}}} \right) \in \partial G\left( {{{t}_{f}}} \right)$. Поэтому управление $~\widetilde {u~}\left( \cdot \right)~$ удовлетворяет ПМП.

Движение $~\widetilde {z~}\left( \cdot \right)$ не имеет циклов на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$. Это следует из определения управления $~\widetilde {u~}\left( \cdot \right)$ и отсутствия циклов на движении z(·). В силу утверждения 2б получаем, что приращение угла φ по модулю между любыми соседними моментами переключения управления $~\widetilde {u~}\left( \cdot \right)$ является постоянным вдоль данного движения.

Однако это не так. Возьмем подряд идущие моменты переключения $\overline {{{t}_{~}}} $, $\widetilde {{{t}_{1}}}$, $\widetilde {{{t}_{2}}}$, $\widehat {{{t}_{~}}}$ на вспомогательном движении. Для него приращение угла между соседними моментами переключения также постоянно по модулю. Обозначим такую величину через $~{{\Delta }}\widetilde {\varphi ~}$. Тогда $~\widetilde {\varphi ~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right){\text{\;}}$ можно выразить через $~\widetilde {\varphi ~}\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right){\text{\;}}$ с учетом последовательности значений управления $~\widetilde {u~}\left( \cdot \right){\text{\;}}$ на промежутке $~\left[ {{\text{\;}}\overline {{{t}_{~}}} ,{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right)~$:

Поскольку $~{{\Delta }}\widetilde {\varphi ~} \ne 0$, то $~\widetilde {\varphi ~}\left( {{\text{\;}}\widehat {{{t}_{~}}}{\text{\;}}} \right) \ne \widetilde {\varphi ~}\left( {{\text{\;}}\overline {{{t}_{~}}} {\text{\;}}} \right)$. Получили противоречие.

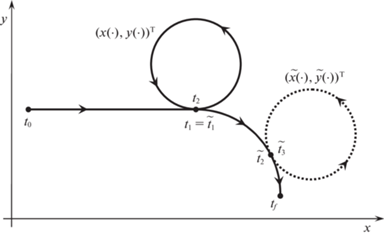
Стало быть, $~z\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right){\text{\;}}$ в случае $~{{\left( {x\left( {{{t}_{1}}} \right),y\left( {{{t}_{1}}} \right)} \right)}^{{\text{T}}}} \ne {{\left( {x\left( {{{t}_{2}}} \right),y\left( {{{t}_{2}}} \right)} \right)}^{{\text{T}}}}$. Траектории исходного и вспомогательного движений для этого случая показаны схематично на рис. 3.

2. Пусть теперь $~{{\left( {x\left( {{{t}_{1}}} \right),y\left( {{{t}_{1}}} \right)} \right)}^{{\text{T}}}} = {{\left( {x\left( {{{t}_{2}}} \right),y\left( {{{t}_{2}}} \right)} \right)}^{{\text{T}}}}$. В таком случае движение на промежутке $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ представляет собой один или несколько подряд идущих циклов с управлением u₂. При этом в силу (3.6) суммарный накопленный угол на первом и третьем участках по модулю превышает 2π, т.е.

Данный факт позволяет задать вспомогательное движение $~\widetilde {z~}\left( \cdot \right){\text{\;}}$ на промежутке [t₀, t_f] (выходящее из точки $~\widetilde {z~}\left( {{{t}_{0}}} \right) = z\left( {{{t}_{0}}} \right){\text{\;}}$ и приходящее в точку $~\widetilde {z~}\left( {{{t}_{f}}} \right) = z\left( {{{t}_{f}}} \right)$) посредством управления $~\widetilde {u~}\left( \cdot \right){\text{\;}}$:

с тремя моментами переключения:

Можно убедиться с использованием (3.8), что ${{t}_{0}} < \widetilde {{{t}_{1}}} < \widetilde {{{t}_{2}}} < \widetilde {{{t}_{3}}} < {{t}_{f}}$ и $\widetilde {z~}\left( {{{t}_{f}}} \right) = z\left( {{{t}_{f}}} \right)$.

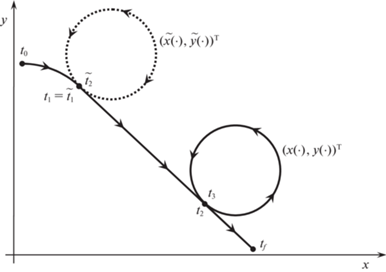
Формирование вспомогательного движения для случая ${{\left( {x\left( {{{t}_{1}}} \right),y\left( {{{t}_{1}}} \right)} \right)}^{{\text{T}}}} = {{\left( {x\left( {{{t}_{2}}} \right),y\left( {{{t}_{2}}} \right)} \right)}^{{\text{T}}}}$ иллюстрируется на рис. 4. Здесь на промежутке $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ исходное движение ${{\left( {x\left( \cdot \right),y\left( \cdot \right)} \right)}^{{\text{T}}}}$ (сплошная линия) имеет цикл в силу управления ${{u}_{2}}$. Геометрические положения в моменты t₁ и t₂ совпадают. Траектория вспомогательного движения ${{\left( {{\text{\;}}\widetilde {x~}\left( \cdot \right),\widetilde {y~}\left( \cdot \right){\text{\;}}} \right)}^{{\text{T}}}}$ отмечена точечной линией. Моменты переключения $\widetilde {{{t}_{2}}}$, $\widetilde {{{t}_{3}}}$ взяты так, чтобы выполнялись равенства $\widetilde {{{t}_{3}}} - \widetilde {{{t}_{2}}} = - 2\pi {\text{/}}{{u}_{1}}$ и ${{t}_{f}} - \widetilde {{{t}_{3}}} = \pi {\text{/}}{{u}_{2}}$. Поэтому вспомогательное движение на участке $\left[ {\widetilde {{{t}_{3}}},{{t}_{f}}} \right]$ представляет собой полуокружность, а на участке $\left[ {\widetilde {{{t}_{2}}},\widetilde {{{t}_{3}}}} \right]$ является целой окружностью (т.е. образует цикл). Геометрические положения на вспомогательном движении в моменты $\widetilde {{{t}_{1}}}$ и t_f совпадают. Также совпадают положения в моменты $\widetilde {{{t}_{2}}}$ и $\widetilde {{{t}_{3}}}$.

Для вспомогательного движения имеем $\left( {\widetilde {{{t}_{2}}} - \widetilde {{{t}_{1}}}} \right){{u}_{2}} = \left( {{{t}_{2}} - {{t}_{1}}} \right){{u}_{2}} - \pi $. Исходное движение на промежутке $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ представляет собой один или несколько подряд идущих циклов с управлением u₂. Поэтому выражение $\left( {{{t}_{2}} - {{t}_{1}}} \right){{u}_{2}}$ кратно 2π. Стало быть, величина $\left( {\widetilde {{{t}_{2}}} - \widetilde {{{t}_{1}}}} \right){{u}_{2}}$ не является кратной 2π. Отсюда следует, что геометрические положения вспомогательного движения в моменты $\widetilde {{{t}_{1}}}$, $\widetilde {{{t}_{2}}}$ не совпадают. С учетом утверждения 2в получаем, что вспомогательное движение в силу управления $\widetilde {u~}\left( \cdot \right)$ не удовлетворяет ПМП. Поэтому $z\left( {{{t}_{f}}} \right) = \widetilde {z~}\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$ в случае, когда точки геометрического положения исходного движения в моменты переключения t₁ и t₂ совпадают. Лемма 2 доказана.

Лемма 3. Пусть движение z(·) на промежутке [t₀, t_f] порождается кусочно-постоянным управлением u(·) со значениями u₁, u₂ и тремя моментами переключения ${{t}_{1}},{{t}_{2}},{{t}_{3}}$, причем ${{t}_{0}} < {{t}_{1}} < {{t}_{2}} < {{t}_{3}} < {{t}_{f}}$. Тогда $z\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$.

Доказательство. Из двух средних промежутков $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ и $\left[ {{{t}_{2}},{{t}_{3}}} \right]$ рассматриваемого движения возьмем тот, на котором изменение угла φ, взятое по модулю, меньше. Если изменение углов по модулю совпадает, то берем любой промежуток.

Предположим, что выбран промежуток $\left[ {{{t}_{2}},{{t}_{3}}} \right]$. Тогда $\left| {\varphi \left( {{{t}_{3}}} \right) - \varphi \left( {{{t}_{2}}} \right)} \right| \leqslant \left| {\varphi \left( {{{t}_{2}}} \right) - \varphi \left( {{{t}_{1}}} \right)} \right|$. Дополнительно учитывая, что на промежутках $\left[ {{{t}_{1}},{{t}_{2}}} \right)$ и $\left[ {{{t}_{3}},{{t}_{f}}} \right]$ управления совпадают, получаем

Отсюда следует, что на $\left[ {{{t}_{1}},{{t}_{f}}} \right]$ движение z(·) удовлетворяет условиям леммы 2 и, следовательно, $z\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$.

Если выбран промежуток $\left[ {{{t}_{1}},{{t}_{2}}} \right]$, то условия леммы 2 выполнены для движения z(·) на промежутке $\left[ {{{t}_{0}},{{t}_{3}}} \right]$. Поэтому $z\left( {{{t}_{3}}} \right) \in {\text{int}}G\left( {{{t}_{3}}} \right)$ и, стало быть, $z\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$. Лемма 3 доказана.

Лемма 4. Пусть движение z(·) на промежутке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ порождается кусочно-постоянным управлением u(·) со значениями в множестве $\left\{ {{{u}_{1}},0,{{u}_{2}}} \right\}$ и двумя моментами переключения. Предположим, что участок с нулевым управлением один и является одним из двух крайних участков постоянства управления. Тогда $z\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$.

Доказательство. Пусть для определенности управление u(·) принимает последовательно значения $0,{{u}_{2}},{{u}_{1}}$. Предположим от противного, что $z\left( {{{t}_{f}}} \right) \in \partial G\left( {{{t}_{f}}} \right)$. Тогда управление u(·) удовлетворяет ПМП.

В силу утверждения 2г движение z(·) на промежутке $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ представляет собой один или несколько подряд идущих циклов (рис. 5). Поэтому ${{\left( {x\left( {{{t}_{1}}} \right),y\left( {{{t}_{1}}} \right)} \right)}^{{\text{T}}}} = {{\left( {x\left( {{{t}_{2}}} \right),y\left( {{{t}_{2}}} \right)} \right)}^{{\text{T}}}}$.

Рассмотрим вспомогательное движение $\widetilde {z~}\left( \cdot \right)$, выходящее в момент t₀ из точки $z\left( {{{t}_{0}}} \right)$ и задаваемое управлением:

Здесь $\widetilde {{{t}_{1}}} = {{t}_{1}} + \varepsilon $, $\widetilde {{{t}_{2}}} = {{t}_{2}} + \varepsilon $, где величина ε взята из диапазона $\left( {0,{\text{min}}\left\{ {{{t}_{f}} - {{t}_{2}},{\text{\;}}2\pi {\text{/}}{{u}_{2}}} \right\}} \right)$.

Движения $\widetilde {z~}\left( \cdot \right)$ и z(·) совпадают на промежутке $\left[ {\widetilde {{{t}_{2}}},{{t}_{f}}} \right]$. Следовательно, $\widetilde {z~}\left( {{{t}_{f}}} \right) = z\left( {{{t}_{f}}} \right)$. Поэтому $\widetilde {z~}\left( {{{t}_{f}}} \right) \in \partial G\left( {{{t}_{f}}} \right)$. Стало быть, управление $\widetilde {u~}\left( \cdot \right)$ удовлетворяет ПМП. Однако движение $\widetilde {z~}\left( \cdot \right)$ на промежутке $\left[ {{{t}_{1}},\widetilde {{{t}_{1}}}} \right]$ не имеет циклов, что противоречит утверждению 2г.

Таким образом, $z\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$. Лемма 4 доказана.

Сформулируем основную теорему о характере управлений, ведущих на границу множества достижимости.

Теорема 1. В каждую точку границы множества достижимости G(t_f) системы (1.1) можно перейти в момент t_f при помощи кусочно-постоянного управления с не более чем двумя переключениями и со значениями в трехэлементном множестве $\left\{ {{{u}_{1}},0,{{u}_{2}}} \right\}$. При этом в случае двух переключений можно ограничиться шестью вариантами последовательности управлений:

Доказательство. В любую точку границы множества достижимости ведет управление, удовлетворяющее ПМП. В силу утверждения 1 его можно считать кусочно-постоянным с конечным числом переключений и со значениями в трехэлементном множестве $\left\{ {{{u}_{1}},0,{{u}_{2}}} \right\}$.

Предположим от противного, что на границе множества достижимости G(t_f) есть точка ${\text{\;}}\widehat {{{z}_{{\text{\;}}}}}$, перевод в которую возможен лишь при помощи управления с тремя или более переключениями. Если таких управлений несколько, то возьмем управление ${{u}^{{\diamondsuit }}}\left( \cdot \right)$ с наименьшим числом переключений. Порождаемое им движение обозначим ${{z}^{{\diamondsuit }}}\left( \cdot \right)$.

Рассмотрим движение ${{z}^{{\diamondsuit }}}\left( \cdot \right)$ на четырех последних участках постоянства управления. Среди них может быть не более двух участков с нулевым управлением. При этом возможны следующие четыре случая.

1. Нет участков с нулевым управлением. Тогда ${{z}^{{\diamondsuit }}}\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$ в силу леммы 3. Это противоречит тому, что ${{z}^{{\diamondsuit }}}\left( {{{t}_{f}}} \right) = \hat {z} \in \partial G\left( {{{t}_{f}}} \right)$.

2. Участок с нулевым управлением один. В этом случае можно выделить три подряд идущих участка так, чтобы участок с нулевым управлением был расположен в начале или в конце такой тройки. Опираясь на лемму 4, имеем ${{z}^{{\diamondsuit }}}({{t}_{f}})\, \in \,{\text{int}}G({{t}_{f}})$, что противоречит соотношению $~{{z}^{{\diamondsuit }}}({{t}_{f}})\, = \,\hat {z}\, \in \,\partial G({{t}_{f}})$.

3. Участков с нулевым управлением два, и они расположены по краям. Здесь аналогично предыдущему случаю при помощи леммы 4 устанавливаем, что $~{{z}^{{\diamondsuit }}}\left( {{{t}_{f}}} \right) \in {\text{int}}G\left( {{{t}_{f}}} \right)$, и получаем противоречие.

4. Участков с нулевым управлением два (из четырех), и между ними расположен только один участок с ненулевым управлением. Управление ${{u}^{{\diamondsuit }}}\left( \cdot \right)$ удовлетворяет ПМП. Поэтому в силу утверждения 2г средний участок с ненулевым управлением, лежащий между участками с нулевым управлением, представляет собой один или несколько подряд идущих циклов. Переносим все циклы со среднего участка в начальную точку первого прямолинейного участка либо в конечную точку второго прямолинейного участка. Склеивая во времени прямолинейные участки, получаем вспомогательное движение $\widetilde {z~}\left( \cdot \right)$, ведущее в ту же точку в момент времени t_f, что и исходное движение ${{z}^{{\diamondsuit }}}\left( \cdot \right)$. При этом вспомогательное движение имеет на одно переключение меньше, чем исходное. Это противоречит сделанному предположению о выборе управления ${{u}^{{\diamondsuit }}}\left( \cdot \right)$ с наименьшим числом переключений.

В качестве пояснения на рис. 6 показан пример движения с тремя моментами переключения ${{t}_{1}},{{t}_{2}},{{t}_{3}}$ и последовательностью управлений ${\text{\;}}{{u}_{1}},0,{{u}_{2}},0{\text{\;}}$. На третьем участке (от момента ${{t}_{2}}$ до момента ${{t}_{3}}$) реализуется один или несколько циклов с управлением u₂. При формировании вспомогательного движения циклы со среднего участка исходного движения перенесены в начальную точку первого прямолинейного участка. Получаем на вспомогательном движении два момента переключения ${{\tilde {t}}_{1}} = {{t}_{1}}$, ${{\tilde {t}}_{2}} = {{t}_{1}} + \left( {{{t}_{3}} - {{t}_{2}}} \right)$ и последовательность управлений ${{u}_{1}},{{u}_{2}},0$.

Таким образом, в любую точку на границе множества достижимости G(t_f) можно перейти при помощи кусочно-постоянного управления с не более чем двумя переключениями.

Перейдем к вопросу о виде последовательности управлений. Кроме указанных в формулировке теоремы 1 вариантов U1–U6 управлений с двумя переключениями, логически возможны еще шесть вариантов:

Управления вида 7)–10) не могут приводить на границу множества достижимости в силу леммы 4.

Рассмотрим варианты 11), 12). Здесь для каждого движения можно уменьшить число переключений на единицу аналогично тому, как это сделано для случая 4. Получим управление с одним переключением, ведущее в ту же точку на границе. Теорема 1 доказана.

С учетом лемм 1 и 2 можно уточнить результат теоремы 1 в зависимости от знака угла φ для рассматриваемой точки $z = {{\left( {x,y,\varphi } \right)}^{{\text{T}}}}$ на границе множества $G\left( {{{t}_{f}}} \right)$.

Замечание 1. Если $\varphi > 0$, то в перечне (3.9) из шести типов управлений можно оставить лишь четыре: U1, U2, U3, U6. В случае $\varphi < 0$ в перечне (3.9) можно ограничиться четырьмя типами: U2, U3, U4, U5. Если $\varphi = 0$, то в перечне (3.9) можно оставить типы U2, U3, U5, U6; при этом управления типов U5 и U6 порождают одну и ту же совокупность точек.

Доказательство. Пусть $\varphi = 0$. Любое управление типа U1 ведет в точку с $~\varphi \left( {{{t}_{f}}} \right) > 0$. Для управлений типа U4 имеем $\varphi \left( {{{t}_{f}}} \right) < 0$. Поэтому типы U1, U4 исключаем. В силу леммы 1 управления U5 и U6 порождают одну и ту же совокупность точек при ${\text{\;}}\overline {t{\text{\;}}} = {{t}_{0}}{\text{\;}}$ и ${\text{\;}}\widehat {t{\text{\;}}} = {{t}_{f}}$.

Пусть $\varphi > 0$. Управления типа U4 исключаем по аналогии со случаем $\varphi = 0$. Управления типа U5 также исключаем, поскольку в силу леммы 2 такие управления ведут во внутренность множества достижимости.

Случай $\varphi < 0$ разбирается аналогично. Здесь также получаем четыре варианта управлений: U2, U3, U4, U5. Замечание 1 доказано.

Опираясь на теорему 1, сформулируем теорему об управлениях, ведущих в произвольную точку множества достижимости $G\left( {{{t}_{f}}} \right)$.

Теорема 2. Пусть даны некоторые непрерывные строго возрастающие функции ${{f}_{1}}\left( \alpha \right)$ и ${{f}_{2}}\left( \alpha \right)$, определенные на [0, 1] со значениями ${{f}_{1}}\left( 0 \right) = {{f}_{2}}\left( 0 \right) = 0$, ${{f}_{1}}\left( 1 \right) = {{f}_{2}}\left( 1 \right) = 1$ в крайних точках. Тогда для любой точки $z = {{\left( {x,y,\varphi } \right)}^{{\text{T}}}} \in G\left( {{{t}_{f}}} \right)$ найдется такое ${{\alpha }^{\flat }} \in \left( {0,1} \right]$, что в точку z можно перейти в момент t_f  при помощи кусочно-постоянного управления с не более чем двумя переключениями и со значениями в трехэлементном множестве $\left\{ {u_{1}^{\flat },0,u_{2}^{\flat }} \right\}$, где $u_{1}^{\flat } = {{f}_{1}}({{\alpha }^{\flat }}){{u}_{1}}$ и $u_{2}^{\flat } = {{f}_{2}}({{\alpha }^{\flat }}){{u}_{2}}$. При этом в случае двух переключений можно ограничиться шестью вариантами последовательности управлений:

Доказательство. Обозначим через $G\left( {{{t}_{f}},\alpha } \right)$ при $\alpha \in \left[ {0,1} \right]$ множество достижимости управляемой системы, аналогичной системе (1.1) с тем лишь отличием, что управление u стеснено ограничением $u \in \left[ {{{u}_{1}}\left( \alpha \right),{{u}_{2}}\left( \alpha \right)} \right]$, где ${{u}_{1}}\left( \alpha \right) = {{f}_{1}}\left( \alpha \right){{u}_{1}}$, ${{u}_{2}}\left( \alpha \right) = {{f}_{2}}\left( \alpha \right){{u}_{2}}$. Если α = 0, то единственным допустимым управлением является управление $u\left( t \right) \equiv 0$ и множество $G\left( {{{t}_{f}},\alpha = 0} \right)$ состоит из одной точки. Если α = 1, то множество $G\left( {{{t}_{f}},\alpha = 1} \right)$ совпадает с G(t_f).

Пусть $z = {{\left( {x,y,\varphi } \right)}^{{\text{T}}}} \in \partial G\left( {{{t}_{f}}} \right)$. Тогда нужный результат следует из теоремы 1 при ${{\alpha }^{\flat }}$ = 1. В частности, на границу множества G(t_f) ведет управление, тождественно равное нулю. Действительно, в этом случае движение приходит в точку ${\text{\;}}z\left( {{{t}_{f}}} \right) = {{\left( {{{t}_{f}},0,{\text{\;}}0} \right)}^{{\text{T}}}}{\text{\;}}$ с максимально возможным значением первой координаты.

Пусть теперь $~z \in {\text{int}}G\left( {{{t}_{f}}} \right)$. Обозначим символом ${{\alpha }^{\flat }}$ наименьшее $\alpha \in \left[ {0,1} \right]$, при котором $z \in G\left( {{{t}_{f}},\alpha } \right)$. Такое ${{\alpha }^{\flat }}$ существует в силу непрерывности функций  f₁ и  f₂, непрерывной зависимости множества G(t_f) в метрике Хаусдорфа от параметров u₁ и u₂, а также в силу замкнутости множества достижимости. Непрерывность множества достижимости по параметрам u₁, u₂ вытекает из некоторого весьма общего свойства дифференциальных включений, описанного в [19] (гл. 4, теорема 5.4 (п. b) и следствие 5.5).

Отметим, что $~{{\alpha }^{\flat }} > 0$. Действительно, при ${{\alpha }^{\flat }} = 0$ мы имели бы $~z \in G({{t}_{f}},{{\alpha }^{\flat }} = 0)$. Это невозможно, поскольку, как отмечено выше, одноточечное множество $G({{t}_{f}},{{\alpha }^{\flat }} = 0)$ принадлежит $\partial G\left( {{{t}_{f}}} \right)$, в то время как $z \in {\text{int}}G\left( {{{t}_{f}}} \right)$.

Возьмем последовательность $\left\{ {{{\alpha }_{i}}} \right\}$ положительных чисел, сходящуюся к ${{\alpha }^{\flat }}$ снизу. Имеем ${\text{\;}}z \notin G\left( {{{t}_{f}},{{\alpha }_{i}}} \right)$. Пусть z_i – точка на границе множества $G\left( {{{t}_{f}},{{\alpha }_{i}}} \right)$, ближайшая к точке z. Покажем, что последовательность {z_i} сходится к точке z.

Учитывая монотонное возрастание функций ${{f}_{1}}\left( \alpha \right)$ и ${{f}_{2}}\left( \alpha \right)$, получаем монотонное возрастание (по включению) множеств $~G\left( {{{t}_{f}},{{\alpha }_{i}}} \right)~$ с увеличением номера i. В силу непрерывности изменения множества $G\left( {{{t}_{f}},\alpha } \right)$ по параметру α в метрике Хаусдорфа, имеем $h(G({{t}_{f}},{{\alpha }^{\flat }}),G({{t}_{f}},{{\alpha }_{i}}))\, \to \,0$ при $i \to \infty $. Здесь h – хаусдорфово расстояние. Поскольку евклидово расстояние $r\left( {z,G\left( {{{t}_{f}},{{\alpha }_{i}}} \right)} \right)$ от точки z до множества $G\left( {{{t}_{f}},{{\alpha }_{i}}} \right)$ не превышает $h(G({{t}_{f}},{{\alpha }_{i}}),G({{t}_{f}},{{\alpha }^{\flat }}))$, получаем $r(z,G({{t}_{f}},{{\alpha }_{i}}))\, = \,r(z,{{z}_{i}})\, \to \,0$ при $i \to \infty $.

Так как ${{z}_{i}} \in \partial G\left( {{{t}_{f}},{{\alpha }_{i}}} \right)$, то в силу теоремы 1 (рассматривая в ней ограничения ${{u}_{1}}\left( {{{\alpha }_{i}}} \right)$, ${{u}_{2}}\left( {{{\alpha }_{i}}} \right)$ на управление u) в точку z_i можно попасть при помощи управления с не более чем двумя переключениями со значениями в трехэлементном множестве $\left\{ {{{u}_{1}}\left( {{{\alpha }_{i}}} \right),0,{\text{\;}}{{u}_{2}}\left( {{{\alpha }_{i}}} \right)} \right\}$, где ${{u}_{1}}\left( {{{\alpha }_{i}}} \right) = {{f}_{1}}\left( {{{\alpha }_{i}}} \right){{u}_{1}}$ и ${{u}_{2}}\left( {{{\alpha }_{i}}} \right) = {{f}_{2}}\left( {{{\alpha }_{i}}} \right){{u}_{2}}$. При этом в случае двух переключений можно ограничиться управлениями вида

Из последовательности {α_i} выделим подпоследовательность {α_j} с одним и тем же числом переключений при каждом j. При этом на одном и том же по порядку следования во времени интервале постоянства управления (их не более трех) реализуется либо управление с одинаковым знаком, либо нулевое управление.

Длины участков постоянства управления ограничены. Поэтому из последовательности {α_j} можно выделить подпоследовательность {α_k}, для которой соответствующие длины промежутков постоянства управления имеют предел (возможно, равный нулю). Предельные значения этих длин определяют некоторое допустимое управление с не более чем двумя переключениями, которое ведет в точку z. Структура этого управления удовлетворяет свойствам, указанным в формулировке теоремы. Теорема 2 доказана.

Теорему 2 можно уточнить по аналогии с теоремой 1, учитывая знак угла φ для рассматриваемой точки $z = {{\left( {x,y,\varphi } \right)}^{{\text{T}}}}$ в множестве достижимости $G\left( {{{t}_{f}}} \right)$.

Замечание 2. Если φ > 0, то в перечне (3.10) управлений с двумя переключениями из шести типов можно оставить лишь четыре: ${\text{U}}{{1}^{\flat }}$, ${\text{U}}{{2}^{\flat }}$, ${\text{U}}{{3}^{\flat }}$, ${\text{U}}{{6}^{\flat }}$. В случае $\varphi < 0$ в перечне (3.10) можно ограничиться четырьмя типами: ${\text{U}}{{2}^{\flat }}$, ${\text{U}}{{3}^{\flat }}$, ${\text{U}}{{4}^{\flat }}$, ${\text{U}}{{5}^{\flat }}$. Если $\varphi = 0$, то в перечне (3.10) можно оставить типы ${\text{U}}{{2}^{\flat }}$, ${\text{U}}{{3}^{\flat }}$, ${\text{U}}{{5}^{\flat }}$, ${\text{U}}{{6}^{\flat }}$; при этом управления типов ${\text{U}}{{5}^{\flat }}$ и ${\text{U}}{{6}^{\flat }}$ порождают одну и ту же совокупность точек.

Доказательство. Если $z = {{\left( {x,y,\varphi } \right)}^{{\text{T}}}} \in \partial G\left( {{{t}_{f}}} \right)$, то доказательство сформулированного замечания следует из замечания 1 при ${{\alpha }^{\flat }} = 1$.

Предположим, что $z \in {\text{int}}G\left( {{{t}_{f}}} \right)$.

Пусть φ = 0. Этот случай анализируется так же, как и в замечании 1, с заменой типов U1, U4, U5, U6 на типы ${\text{U}}{{1}^{\flat }}$, ${\text{U}}{{4}^{\flat }}$, ${\text{U}}{{5}^{\flat }}$, ${\text{U}}{{6}^{\flat }}$.

Пусть $\varphi > 0$. При доказательстве теоремы 2 была рассмотрена последовательность {α_i}, для которой точки z_i были выбраны на $\partial G\left( {{{t}_{f}},{{\alpha }_{i}}} \right)$. Поскольку $\varphi > 0$, то, начиная с некоторого номера $\overline {i{\text{\;}}} $, имеем ${{\varphi }_{i}} > 0$. Для точек z_i, где ${\text{\;}}i > \overline {i{\text{\;}}} $, в качестве порождающих управлений с двумя переключениями будем рассматривать четыре варианта, указанные в замечании 1, с заменой крайних значений u₁, u₂ на ${{u}_{1}}\left( {{{\alpha }_{i}}} \right)$, ${{u}_{2}}\left( {{{\alpha }_{i}}} \right)$ соответственно. При формировании подпоследовательности {z_k} считаем реализующимся (в случае двух переключений) какой-то один из этих вариантов. Тогда для предельной точки $z$ соответствующее предельное управление (если оно тоже имеет два переключения) принадлежит такому же варианту. Стало быть, для точки z в качестве возможных порождающих управлений с двумя переключениями при φ > 0 можно оставить лишь четыре варианта: ${\text{U}}{{1}^{\flat }}$, ${\text{U}}{{2}^{\flat }}$, ${\text{U}}{{3}^{\flat }}$, ${\text{U}}{{6}^{\flat }}$ (такие же, как в замечании 1).

Случай $\varphi < 0$ разбирается аналогично. Также получаем четыре варианта управлений: ${\text{U}}{{2}^{\flat }}$, ${\text{U}}{{3}^{\flat }}$, ${\text{U}}{{4}^{\flat }}$, ${\text{U}}{{5}^{\flat }}$. Замечание 2 доказано.

4. Формулы интегрирования экстремальных движений. Совокупность возможных значений φ системы (1.1) в момент ${{t}_{f}} > 0$ определяется ограничением $u \in \left[ {{{u}_{1}},{\text{\;}}{{u}_{2}}} \right]$ и представляет собой отрезок $\left[ {{{t}_{f}}{{u}_{1}},{{t}_{f}}{{u}_{2}}} \right]$. В этом и следующем разделах предполагаем, что $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right]$. Случай $\varphi \in \left[ {{{t}_{f}}{{u}_{1}},0} \right)$ будет рассмотрен в последнем разделе статьи.

В соответствии с теоремой 1 в любую точку границы $\partial G\left( {{{t}_{f}}} \right)$ трехмерного множества достижимости ведет кусочно-постоянное управление с не более чем двумя переключениями. При этом, учитывая $\varphi \geqslant 0$, в случае двух переключений можно ограничиться управлениями четырех типов: U1, U2, U3, U6 (замечание 1). То же самое справедливо и для точек, лежащих на границе φ-сечения G_φ(t_f) при $\varphi \geqslant 0$.

В разд. 4.1–4.4 будем считать, что $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$. Крайнему значению $\varphi = {{t}_{f}}{{u}_{2}}$ соответствует одноточечное множество G_φ(t_f), которое описывается в разд. 4.5.

4.1. Однопараметрические кривые четырех типов в φ-сечениях. Зафиксируем некоторое $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$. Используя моменты переключения ${{t}_{1}}$ и ${{t}_{2}}$, введем для каждого из четырех типов однопараметрическую кривую на плоскости x, y. Опираемся на то, что моменты переключения связаны между собой соотношением

где $\varphi \left( {{{t}_{0}}} \right) = 0$. Выражение (4.1) позволяет для каждого типа при помощи одного параметра описать управления, ведущие в зафиксированное φ-сечение, т.е. построить в плоскости x, y однопараметрическую кривую конечных положений с заданным φ в момент t_f.

1. Рассмотрим последовательность управлений $~{{u}_{2}},0,{{u}_{{2{\text{\;}}}}}$ с двумя моментами переключения ${{t}_{1}}$, ${{t}_{2}}$ (тип U1). При этом ${{t}_{0}} = 0 < {{t}_{1}} < {{t}_{2}} < {{t}_{f}}$.

Условие (4.1) попадания на заданное φ-сечение принимает следующий вид:

Из формулы следует, что при фиксированном φ разность ${{t}_{2}} - {{t}_{1}}$ (т.е. продолжительность среднего участка движения) является константой: ${{t}_{2}} - {{t}_{1}} = {{t}_{f}} - {{t}_{0}} - \varphi {\text{/}}{{u}_{2}}$. Учитывая ${{t}_{0}} = 0$, получаем

Взяв t₁ в качестве независимой переменной, получим при $\varphi \in \left( {0,{{t}_{f}}{{u}_{2}}} \right)$ диапазон $\left( {0,\varphi {\text{/}}{{u}_{2}}} \right)$ возможных значений t₁. Интегрируя систему (1.1) на промежутке $\left[ {0,{{t}_{f}}} \right]$ при фиксированном t₁, а затем учитывая (4.3), придем к выражению геометрического положения в момент t_f:

Формула (4.4) задает непрерывную однопараметрическую кривую (по параметру t₁) на плоскости x, y.

Возьмем новый независимый параметр ${{s}_{1}} = 2{{t}_{1}}{{u}_{2}} - \varphi $. Для него диапазон возможных значений ${{s}_{1}} \in \left( { - \varphi ,{\text{\;}}\varphi ~} \right)$ становится симметричным.

Подставляя в (4.4) выражение $\varphi \left( {{{t}_{1}}} \right) = {{t}_{1}}{{u}_{2}} = \left( {{{s}_{1}} + \varphi } \right){\text{/}}2$, получаем для $\varphi \in \left( {0,{{t}_{f}}{{u}_{2}}} \right)$ однопараметрическую кривую на плоскости x, y:

2. Действуя аналогично, устанавливаем, что движения, соответствующие типам управлений U2, U3, U6, также порождают однопараметрические кривые на плоскости x, y (при фиксированном φ). Для их описания введем обозначение

Очевидно, что при $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$ выполнено неравенство $\theta > 0$. Параметры s₂, s₃, s₆ определим через t₁ и θ:

Интегрируя систему (1.1), получаем следующие формулы:

Формулы (4.8)–(4.10) задают однопараметрические кривые на плоскости x, y, соответствующие управлениям типа U2, U3, U6 с двумя переключениями. Параметры ${{s}_{2}},{{s}_{3}},{{s}_{6}}$ изменяются в следующих диапазонах:

3. Для $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$ управления u(·) с одним переключением, удовлетворяющие ПМП, могут иметь только такую структуру: $0,{{u}_{2}}$; ${{u}_{2}},0$; ${{u}_{1}},{{u}_{2}}$; ${{u}_{2}},{{u}_{1}}$. Нетрудно убедиться, что движение, порождаемое каждым из таких вариантов, ведет в крайнюю точку хотя бы одной из кривых (4.5), (4.8)–(4.10). Управление без переключения (удовлетворяющее ПМП) является тождественно равным нулю. Соответствующее движение дает $\varphi \left( {{{t}_{f}}} \right) = 0$, $x\left( {{{t}_{f}}} \right) = {{t}_{f}}$, $y\left( {{{t}_{f}}} \right) = 0$. Это означает, что точка ${{\left( {x\left( {{{t}_{f}}} \right),y\left( {{{t}_{f}}} \right)} \right)}^{{\text{T}}}}$, отвечающая нулевому управлению, может быть в φ-сечении множества G(t_f) только при φ = 0. Получаемые значения $x\left( {{{t}_{f}}} \right)$, $y\left( {{{t}_{f}}} \right)$ совпадают со значениями, рассчитанными по формуле (4.5) для φ = 0, ${{s}_{1}} = 0$.

Таким образом, в силу теоремы 1, для $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$ при описании границы $\partial {{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ достаточно использовать кривые (4.5), (4.8)–(4.10) с замкнутыми областями определения:

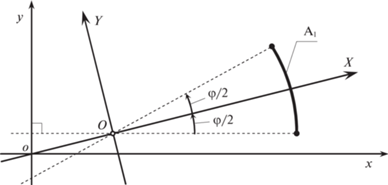
4.2. Вспомогательная система координат. Помимо исходной системы координат будем использовать вспомогательную ортогональную систему X, Y. Ось X вспомогательной системы проходит через начало отсчета исходной системы координат x, y и развернута на угол φ/2 относительно оси x (рис. 7). Начало вспомогательной системы координат расположим в точке $O = {{\left( {{\text{sin}}\varphi ,{\text{\;}}1 - {\text{cos}}\varphi } \right)}^{{\text{T}}}}$. Пересчет во вспомогательную систему X, Y из исходной системы x, y осуществляется по формуле

Вспомогательная система координат зависит только от угла φ. Формула (4.13) задает взаимно-однозначное аффинное соответствие (при фиксированном φ) между векторами ${{\left( {x,y} \right)}^{{\text{T}}}}$ и ${{\left( {X,Y} \right)}^{{\text{T}}}}$.

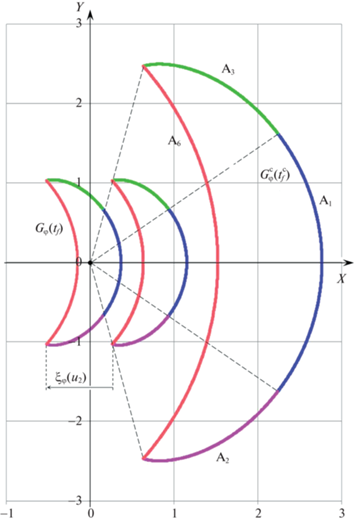
Кривые (4.5), (4.8)–(4.10), определенные для $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$ параметрами ${{s}_{1}}$, ${{s}_{2}}$, ${{s}_{3}}$, ${{s}_{6}}$ в замкнутых интервалах (4.12), пересчитаем во вспомогательную систему координат X, Y и обозначим через A₁, A₂, A₃, A₆ соответственно. Для сокращения записи положим

Имеем

Подчеркнем структурную аналогию формул (4.15)–(4.18): квадратная скобка, один и тот же коэффициент перед ней, одно и то же последнее слагаемое. Параметры ${{s}_{1}},{{s}_{2}},{{s}_{3}},{{s}_{6}},$ входящие в квадратную скобку, изменяются в диапазонах (4.12).

Кривые A₁ и A₆ представляют собой дуги окружностей. Каждая из них симметрична относительно оси X в силу симметрии относительно нуля диапазонов изменения параметров ${{s}_{1}},{{s}_{6}}$. Кривые A₂ и A₃ взаимно симметричны относительно оси X. Это следует из того, что X-компоненты точек на кривых A₂ и A₃ при ${{s}_{2}} = - {{s}_{3}}$ совпадают, а Y-компоненты отличаются только знаком.

4.3. Составная замкнутая кривая. При зафиксированном ${\text{\;}}\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right){\text{\;}}$ набор кривых A₁, A₂, A₃, A₆ содержит в себе границу множества G_φ(t_f). Рассмотрим эти кривые в последовательности A₁, A₃, A₆, A₂ с обходом их по возрастанию параметров ${{s}_{1}},{\text{\;}}{{s}_{2}},{\text{\;}}{{s}_{3}},{\text{\;}}{{s}_{6}}$. При крайних значениях (4.12) параметров имеем

В результате склейки получаем непрерывную кусочно-гладкую замкнутую кривую на плоскости X, Y. Обозначим ее символом ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ и будем называть составной. Эта кривая симметрична относительно оси X и непрерывно зависит от ${{u}_{1}}$, ${{u}_{2}}$, t_f. Структура кривой при фиксированном φ усложняется с ростом t_f. Подчеркнем, что кривая ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ составлена из кривых четырех типов и содержит в себе все точки границы множества G_φ(t_f).

На рис. 8 даны два примера кривой ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ для несимметричного случая ${{u}_{1}} = - 2$, ${{u}_{2}} = 3$ при $\varphi = 0.4\pi $. Как было отмечено выше, сохраняется симметрия кривой относительно оси X вспомогательной системы координат. Точки сочленения дуг A₁, A₃, A₆, A₂ отмечены рисками. Для значения ${{t}_{f}} = 1.3\pi $ (рис. 8, а) кривая ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ не имеет самопересечений. Для значения ${{t}_{f}} = 2.9\pi $ (рис. 8, б) на кривой ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ есть точки самопересечения.

Кривая ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ будет играть главную роль при решении основной задачи статьи, заключающейся в установлении соответствия между φ-сечениями ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ множества достижимости для канонического и несимметричного случаев.

4.4. Семейство составных кривых. Пусть $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$ и ${{f}_{1}}\left( \alpha \right)$, ${{f}_{2}}\left( \alpha \right)$ – некоторые функции, удовлетворяющие условию теоремы 2. Рассмотрим произвольную точку в множестве ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$. В силу теоремы 2 и замечания 2 найдется такое ${{\alpha }^{\flat }} \in \left( {0,1} \right]$, что в данную точку можно перейти в момент t_f  при помощи кусочно-постоянного управления с не более чем двумя переключениями и со значениями в трехэлементном множестве $\left\{ {u_{1}^{\flat },0,u_{2}^{\flat }} \right\}$, где $u_{1}^{\flat } = {{f}_{1}}({{\alpha }^{\flat }}){{u}_{1}}$, $u_{2}^{\flat } = {{f}_{2}}({{\alpha }^{\flat }}){{u}_{2}}$. При этом в случае двух переключений можно ограничиться четырьмя типами управлений: ${\text{U}}{{1}^{\flat }}$, ${\text{U}}{{2}^{\flat }}$, ${\text{U}}{{3}^{\flat }}$, ${\text{U}}{{6}^{\flat }}$.

Обозначим при помощи символа ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}}\left( \alpha \right),{{u}_{2}}\left( \alpha \right),{{t}_{f}}} \right)$ склеенную кривую, аналогичную кривой ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ и построенную с использованием формул (4.6), (4.14)–(4.18) при подстановке в них значений ${{u}_{1}}\left( \alpha \right) = {{f}_{1}}\left( \alpha \right){{u}_{1}}$, ${{u}_{2}}\left( \alpha \right) = {{f}_{2}}\left( \alpha \right){{u}_{2}}$ вместо значений ${{u}_{1}}$, ${{u}_{2}}$. Получаем, что семейство кривых ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}}\left( \alpha \right),{{u}_{2}}\left( \alpha \right),{{t}_{f}}} \right)$, где $\alpha \in \left( {0,1} \right]$, заполняет все множество ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$, т.е.

Каждая кривая ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}}\left( \alpha \right),{{u}_{2}}\left( \alpha \right),{{t}_{f}}} \right)$ (по аналогии с кривой ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$) симметрична относительно оси X вспомогательной системы координат. Поэтому в силу (4.19) получаем симметрию множества ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ относительно оси X.

4.5. Одноточечное φ-сечение в особом случае $\varphi = {{t}_{f}}{{u}_{2}}$. Крайнее значение $\varphi = {{t}_{f}}{{u}_{2}}$ реализуется на управлении $u\left( t \right) \equiv {{u}_{2}}$. Интегрируя систему (1.1), получаем точку с координатами $x\left( {{{t}_{f}}} \right) = {\text{sin}}\left( {{{t}_{f}}{{u}_{2}}} \right){\text{/}}{{u}_{2}}$, $y\left( {{{t}_{f}}} \right) = \left( {1 - {\text{cos}}\left( {{{t}_{f}}{{u}_{2}}} \right)} \right){\text{/}}{{u}_{2}}$. Пересчитаем ее во вспомогательную систему координат и обозначим символом $e\left( {{{t}_{f}}} \right)$. Имеем

Таким образом, φ-сечение ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ при $\varphi = {{t}_{f}}{{u}_{2}}$ состоит из одной точки $e\left( {{{t}_{f}}} \right)$.

5. Связь φ-сечений для несимметричного и канонического случаев. В этом разделе будет показано, что любое φ-сечение для общего несимметричного случая связано некоторым взаимно-однозначным аффинным соответствием с φ-сечением для канонического случая. Это будет означать, в частности, что φ-сечения для несимметричного случая могут быть получены на основе описания φ-сечений для канонического случая.

В рамках системы (1.1) зафиксируем некоторые значения ${{u}_{1}} < 0$, ${{u}_{2}} > 0$, ${{t}_{f}} > 0$ и $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right]$. Как и ранее, считаем ${{t}_{0}} = 0$, $z\left( {{{t}_{0}}} \right) = {{\left( {{{x}_{0}},{{y}_{0}},{{\varphi }_{0}}} \right)}^{{\text{T}}}} = {{\left( {0,0,0} \right)}^{{\text{T}}}}$.

Наряду с общим рассмотрим канонический случай, для которого положим

Отметим, что вводимый момент времени $t_{f}^{{\text{c}}}$ зависит от значений ${{u}_{1}}$, ${{u}_{2}}$, t_f и φ. Видно, что $0 \leqslant {{\varphi }^{{\text{c}}}} \leqslant t_{f}^{{\text{c}}}$. Символом $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$ обозначим φ-сечение множества достижимости в момент $t_{f}^{{\text{c}}}$ для канонического случая. По аналогии с (4.6) положим

С учетом (5.1) имеем

Прежде, чем установить формулу соответствия между φ-сечениями ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ и $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$, получим при $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$ аналогичную формулу для кривых ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ и ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\text{c}}}{\text{,}}u_{2}^{{\text{c}}},t_{f}^{{\text{c}}}} \right)$. Здесь ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\text{c}}},u_{2}^{{\text{c}}},t_{f}^{{\text{c}}}} \right)$ – замкнутая кривая в виде склейки кривых ${\text{A}}_{1}^{{\text{c}}}$, ${\text{A}}_{2}^{{\text{c}}}$, ${\text{A}}_{3}^{{\text{c}}}$, ${\text{A}}_{6}^{{\text{c}}}$, заданных формулами (4.15)–(4.18) при подстановке в них значений $u_{1}^{{\text{c}}}$, $u_{2}^{{\text{c}}}$, $t_{f}^{{\text{c}}}$ и θ^c вместо u₁, u₂, t_f, θ. А именно покажем, что кривые ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$ и ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\text{c}}},{\text{\;}}u_{2}^{{\text{c}}},{\text{\;}}t_{f}^{{\text{c}}}} \right)$, записанные во вспомогательной системе координат (она зависит только от φ), связаны соотношением

Величина ${{\xi }_{\varphi }}\left( {{{u}_{2}}} \right)$ определена формулой (4.14). Доказательство соотношения (5.3) подскажет способ рассуждений при установлении соответствия между φ-сечениями ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ и $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$.

Чтобы убедиться в справедливости соотношения (5.3), достаточно проверить его для соответствующих пар кривых: (${{{\text{A}}}_{1}}$, ${\text{A}}_{1}^{{\text{c}}}$), (${{{\text{A}}}_{2}}$, ${\text{A}}_{2}^{{\text{c}}}$), (${{{\text{A}}}_{3}}$, ${\text{A}}_{3}^{{\text{c}}}$), (${{{\text{A}}}_{6}}$, ${\text{A}}_{6}^{{\text{c}}}$). Подставляя значение $t_{f}^{{\text{c}}}$ из (5.1) в (5.2), получаем равенство θ^c = θ, где θ определяется (4.6). Поэтому, учитывая равенство φ^c = φ, делаем вывод о совпадении диапазонов (4.12) изменения параметров ${{s}_{1}}$, ${{s}_{2}}$, ${{s}_{3}}$, ${{s}_{6}}$ при задании кривых ${{{\text{A}}}_{1}}$, ${{{\text{A}}}_{2}}$, ${{{\text{A}}}_{3}}$, ${{{\text{A}}}_{6}}$ с соответствующими диапазонами для кривых ${\text{A}}_{1}^{{\text{c}}}$, ${\text{A}}_{2}^{{\text{c}}}$, ${\text{A}}_{3}^{{\text{c}}}$, ${\text{A}}_{6}^{{\text{c}}}$.

Рассмотрим кривые A₁ и ${\text{A}}_{1}^{{\text{c}}}$. Кривая A₁ задается формулой (4.15) и соответствует моменту t_f при ограничениях на управление u₁, u₂. Кривая ${\text{A}}_{1}^{{\text{c}}}$ соответствует моменту $t_{f}^{{\text{c}}}$ при ограничениях на управление $u_{1}^{{\text{c}}}$, $u_{2}^{{\text{c}}}$. С учетом того, что $u_{1}^{{\text{c}}} = - 1$, $u_{2}^{{\text{c}}} = 1$ и θ^c = θ, она имеет вид

Используя формулы (4.15), (5.4), убеждаемся в справедливости равенства

Аналогичные равенства (во вспомогательной системе координат) справедливы и для других пар кривых: (${{{\text{A}}}_{2}}$, ${\text{A}}_{2}^{{\text{c}}}$), (${{{\text{A}}}_{3}}$, ${\text{A}}_{3}^{{\text{c}}}$), (${{{\text{A}}}_{6}}$, ${\text{A}}_{6}^{{\text{c}}}$). Стало быть, выполнено соотношение (5.3).

Теорема 3. Пусть $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right]$. Сечения ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ множества достижимости исходной системы (1.1) связаны во вспомогательной системе координат с сечениями $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$ множества достижимости канонической системы (5.1) соотношением

Доказательство. Вначале будем считать, что $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$. Воспользуемся схемой, использованной при установлении равенства (5.3). Потом предположим, что $\varphi = {{t}_{f}}{{u}_{2}}$.

1. Пусть $\varphi \in \left[ {0,{{t}_{f}}{{u}_{2}}} \right)$. Для несимметричного случая рассмотрим функции

Эти функции удовлетворяют условиям, оговоренным в теореме 2.

Положим $u_{1}^{{\left( 1 \right)}}\left( \alpha \right) = f_{1}^{{\left( 1 \right)}}\left( \alpha \right){{u}_{1}}$, $u_{2}^{{\left( 1 \right)}}\left( \alpha \right) = f_{2}^{{\left( 1 \right)}}\left( \alpha \right){{u}_{2}}$. Кривые ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 1 \right)}}\left( \alpha \right),u_{2}^{{\left( 1 \right)}}\left( \alpha \right),{{t}_{f}}} \right)$ при переборе $\alpha \in \left( {0,1} \right]$ заполняют все множество ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ (разд. 4.4).

Для канонического случая, определенного в (5.1), рассмотрим функции

Положим $u_{1}^{{\left( 2 \right)}}\left( \alpha \right) = f_{1}^{{\left( 2 \right)}}\left( \alpha \right)u_{1}^{{\text{c}}}$, $u_{2}^{{\left( 2 \right)}}\left( \alpha \right) = f_{2}^{{\left( 2 \right)}}\left( \alpha \right)u_{2}^{{\text{c}}}$. Кривые ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 2 \right)}}\left( \alpha \right),u_{2}^{{\left( 2 \right)}}\left( \alpha \right),t_{f}^{{\text{c}}}} \right)$ при переборе $\alpha \in \left( {0,1} \right]$ заполняют все множество $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$.

Установим соответствие между введенными семействами кривых по формуле

Зафиксируем некоторое $\alpha \in \left( {0,1} \right]$. В силу (5.6) и (5.7) получаем

Для упрощения записи положим $u_{1}^{{\left( 1 \right)}} = u_{1}^{{\left( 1 \right)}}\left( \alpha \right)$, $u_{2}^{{\left( 1 \right)}} = u_{2}^{{\left( 1 \right)}}\left( \alpha \right)$, $u_{1}^{{\left( 2 \right)}} = u_{1}^{{\left( 2 \right)}}\left( \alpha \right)$, $u_{2}^{{\left( 2 \right)}} = u_{2}^{{\left( 2 \right)}}\left( \alpha \right)$.

Используя (5.6) и неравенство $\left( {{{u}_{2}} + {{u}_{1}}} \right) < \left( {{{u}_{2}} - {{u}_{1}}} \right)$, а также учитывая, что $\alpha \ne 0$, имеем ${{u}_{1}} \leqslant u_{1}^{{\left( 1 \right)}} < 0$, $0 < u_{2}^{{\left( 1 \right)}} \leqslant {{u}_{2}}$. Видно, что $u_{1}^{{\begin{array}{*{20}{c}} ~ \\ {\text{c}} \end{array}}} \leqslant u_{1}^{{\left( 2 \right)}} < 0$, $0 < u_{2}^{{\left( 2 \right)}} \leqslant u_{2}^{{\begin{array}{*{20}{c}} ~ \\ {\text{c}} \end{array}}}~$.

При зафиксированных значениях φ, t_f  и $t_{f}^{{\text{c}}}$ введем величины

Формулы (5.11), (5.12) аналогичны соотношениям (4.6), (5.2), в которых были задействованы управления ${{u}_{1}}$, ${{u}_{2}}$ и $u_{1}^{{\text{c}}}$, $u_{2}^{{\text{c}}}$. Используя (5.11), (5.12), вводим кривые ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 1 \right)}},u_{2}^{{\left( 1 \right)}},{{t}_{f}}} \right)$ и ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 2 \right)}},u_{2}^{{\left( 2 \right)}},t_{f}^{{\text{c}}}} \right)$. Их составные части вычисляем по формулам (4.15)–(4.18), подставляя в них вместо ${{u}_{1}}$, ${{u}_{2}}$, θ значения $u_{1}^{{\left( 1 \right)}}$, $u_{2}^{{\left( 1 \right)}}$, ${{\theta }^{{\left( 1 \right)}}}$ и $u_{1}^{{\left( 2 \right)}}$, $u_{2}^{{\left( 2 \right)}}$, θ⁽²⁾. Кривая ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 1 \right)}},u_{2}^{{\left( 1 \right)}},{{t}_{f}}} \right)$ (так же, как и кривая ${{\mathcal{A}}_{\varphi }}\left( {{{u}_{1}},{{u}_{2}},{{t}_{f}}} \right)$) лежит в множестве ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$, а кривая ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 2 \right)}},u_{2}^{{\left( 2 \right)}},t_{f}^{{\text{c}}}} \right)$ лежит в множестве $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$.

Покажем, что ${{\theta }^{{\left( 1 \right)}}} = {{\theta }^{{\left( 2 \right)}}}$. Подставляя в (5.11) выражения для $u_{1}^{{\left( 1 \right)}}$, $u_{2}^{{\left( 1 \right)}}$ из (5.9), получим

Формула (5.12) при подстановке $~t_{f}^{{{\text{c}}~}}$ из (5.1) и $u_{2}^{{\left( 2 \right)}}$ из (5, 10) принимает вид

Сравнивая (5.13) и (5.14), убеждаемся, что ${{\theta }^{{\left( 1 \right)}}} = {{\theta }^{{\left( 2 \right)}}}$.

Составляющие кривой ${{\mathcal{A}}_{\varphi }}(u_{1}^{{\left( 1 \right)}},u_{2}^{{\left( 1 \right)}},{{t}_{f}})$ обозначим через ${\text{A}}_{n}^{{\left( 1 \right)}}$, а составляющие кривой ${{\mathcal{A}}_{\varphi }}(u_{1}^{{(2)}},u_{2}^{{(2)}},t_{f}^{{\text{c}}})$ – через ${\text{A}}_{n}^{{\left( 2 \right)}}$, $n = 1,{\text{\;}}2,{\text{\;}}3,{\text{\;}}6$. Каждая составляющая ${\text{A}}_{n}^{{\left( 1 \right)}}$ кривой ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 1 \right)}},u_{2}^{{\left( 1 \right)}},{{t}_{f}}} \right)$ в соответствии с формулами (4.15)–(4.18) представима в виде

Здесь квадратная скобка ${{\left[ \begin{gathered} ... \\ ... \\ \end{gathered} \right]}_{{{\text{A}}_{n}^{{\left( 1 \right)}}}}}$ (матрица-столбец) соответствует кривой ${\text{A}}_{n}^{{\left( 1 \right)}}$ и определяется значениями φ, θ⁽¹⁾, а также параметром s_n. Для составляющих кривой ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 2 \right)}},u_{2}^{{\left( 2 \right)}},{\text{\;}}t_{f}^{{\text{c}}}} \right)$ справедлива такая же формула, только в обозначениях вместо верхнего индекса (1) нужно подставить индекс (2).

Возьмем любую кривую ${\text{A}}_{n}^{{\left( 1 \right)}}$ из четырех в составе ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 1 \right)}},u_{2}^{{\left( 1 \right)}},{{t}_{f}}} \right)$ и соответствующую ей кривую ${\text{A}}_{n}^{{\left( 2 \right)}}$ в составе ${{\mathcal{A}}_{\varphi }}\left( {u_{1}^{{\left( 2 \right)}},u_{2}^{{\left( 2 \right)}},{\text{\;}}t_{f}^{{\text{c}}}} \right)$. Запишем доказываемую формулу (5.8) для выбранных кривых:

В этой формуле квадратные скобки совпадают в силу равенства ${{\theta }^{{\left( 1 \right)}}} = {{\theta }^{{\left( 2 \right)}}}$. Используя определения величин $u_{1}^{{\left( 1 \right)}}$, $u_{2}^{{\left( 1 \right)}}$, $u_{1}^{{\left( 2 \right)}}$, $u_{2}^{{\left( 2 \right)}}$ в силу формул (5.9) и (5.10), убеждаемся, что коэффициенты

при квадратных скобках также совпадают. Чтобы установить равенство между оставшимися слагаемыми слева и справа в формуле (5.15), следует (после подстановки выражений для ${{\xi }_{\varphi }}$) проверить соотношение

Данное соотношение справедливо в силу определения величин $u_{2}^{{\left( 1 \right)}}$, $u_{2}^{{\left( 2 \right)}}$ при помощи формул (5.9), (5.10).

Таким образом, равенство (5.15) и, стало быть, равенство (5.8) доказаны. С учетом (4.19) имеем

Получаем требуемую формулу (5.5) соответствия между φ-сечениями ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ и $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$ для исходного и канонического вариантов ограничений на управление.

2. Пусть $\varphi = {{t}_{f}}{{u}_{2}}$. В этом случае множество ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ состоит из одной точки, которая во вспомогательной системе координат записывается в виде (4.20). Для канонической системы величина $t_{f}^{{\text{c}}}$ в силу (5.1) принимает значение $t_{f}^{{\text{c}}} = \varphi $. Тогда максимально возможное значение угловой координаты есть $~t_{f}^{{\text{c}}}u_{2}^{{\text{c}}} = t_{f}^{{\text{c}}} = \varphi $. Поэтому множество $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$ также состоит из одной точки, которую обозначим ${{e}^{{\text{c}}}}\left( {t_{f}^{{\text{c}}}} \right)$. Она рассчитывается по аналогии с формулой (4.20):

Подставляя $e\left( {{{t}_{f}}} \right)$ и ${{e}^{{\text{c}}}}\left( {t_{f}^{{\text{c}}}} \right)$ вместо ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ и $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$ в (5.5), получаем равенство

которое справедливо, поскольку $\varphi = {{t}_{f}}{{u}_{2}}$.

Таким образом, соотношение (5.5) выполнено и в случае, когда $\varphi = {{t}_{f}}{{u}_{2}}$. Теорема 3 доказана.

Рисунок 9 поясняет применение формулы (5.5). Исходные данные для несимметричного случая взяты в виде ${{u}_{1}} = - 2$, ${{u}_{2}} = 3$, $\varphi = 0.4\pi $, ${{t}_{f}} = 0.5\pi $. Просчитанный по этим данным момент $t_{f}^{{\text{c}}}$, который надо использовать в канонической системе, равен 1.28π. Соответствующее этому моменту множество $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$ во вспомогательной системе координат показано на рисунке справа. При умножении множества $G_{\varphi }^{{\text{c}}}\left( {t_{f}^{{\text{c}}}} \right)$ на коэффициент $\left( {1{\text{/}}{{u}_{2}} - 1{\text{/}}{{u}_{1}}} \right){\text{/}}{}_{{\text{\;}}}^{{\text{\;}}}2{\text{\;}} \approx {\text{\;}}0.417$ происходит его “сжатие” относительно нуля вспомогательной системы (изображено вторым справа). Сдвиг полученного множества вдоль оси X на величину ${{\xi }_{\varphi }}\left( {{{u}_{2}}} \right) \approx - 0.784$ дает искомое множество ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ (первое слева) для несимметричного случая.

Замечание 3. Формулу (5.5) можно переписать в исходных координатах x, y. Новая формула будет иметь тот же вид, но только в ней надо заменить сдвиг ${{\xi }_{\varphi }}\left( {{{u}_{2}}} \right)$ на

Замечание 4. В работе [20] рассмотрен случай одностороннего поворота, когда $0 = {{u}_{1}} < {{u}_{2}}$. Здесь каждое φ-сечение ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ трехмерного множества достижимости представляет собой либо сегмент круга (при $\varphi < 2\pi $), либо целый круг (при $\varphi \geqslant 2\pi $). В силу непрерывной зависимости множества достижимости от параметра ${{u}_{1}}$ (считаем, что значение u₂ закреплено) такое φ-сечение представляет собой предел в метрике Хаусдорфа φ-сечений ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ при ${{u}_{1}} \to - 0$. Подчеркнем, что при этом множества ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ для ${{u}_{1}} < 0$ не являются выпуклыми. Стало быть, формула соответствия (5.5) применима только для случая ${{u}_{1}} < 0 < {{u}_{2}}$. С ее помощью нельзя получить предельное множество для ${{u}_{1}} = 0$.

6. Случай $\varphi < 0$. Рассмотрим некоторое $\varphi \in \left[ {{{u}_{1}}{{t}_{f}},0} \right)$ при ${{t}_{f}} > 0$. Требуется получить описание множества ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$. Укажем в исходных координатах свойство симметрии, позволяющее сделать это.

Пусть u(·) – допустимое управление со значениями в промежутке $\left[ {{{u}_{1}},{{u}_{2}}} \right]$, ведущее в точку ${{\left( {x\left( {{{t}_{f}}} \right),y\left( {{{t}_{f}}} \right),\varphi \left( {{{t}_{f}}} \right)} \right)}^{{\text{T}}}} \in {{G}_{\varphi }}\left( {{{t}_{f}}} \right)$, где $\varphi \left( {{{t}_{f}}} \right) = \varphi < 0$. Наряду с исходной задачей с ограничениями u₁, u₂ рассмотрим новую задачу с ограничениями ${{\tilde {u}}_{1}} = - {{u}_{2}}$, ${{\tilde {u}}_{2}} = - {{u}_{1}}$. Получаемое в ней при том же значении t_f  трехмерное множество достижимости обозначим ${\text{\;}}\widetilde {G(}{{t}_{f}})$.

В новой задаче возьмем управление $\tilde {u}\left( t \right) = - u\left( t \right)$, $t \in \left[ {0,{{t}_{f}}} \right]$. Имеем ${{\tilde {u}}_{1}} \leqslant \tilde {u}\left( t \right) \leqslant {{\tilde {u}}_{2}}$. Специфика уравнений движения машины Дубинса проявляется в том, что получаемые в момент t текущие значения $\widetilde {{{\varphi }_{~}}}\left( t \right),{\text{\;}}\widetilde {{{x}_{{\text{\;}}}}}\left( t \right),{\text{\;}}\widetilde {{{y}_{{\text{\;}}}}}\left( t \right)$ фазовых переменных удовлетворяют соотношениям $\widetilde {{{\varphi }_{~}}}\left( t \right) = - \varphi \left( t \right)$, $\widetilde {{{x}_{{\text{\;}}}}}\left( t \right) = x\left( t \right)$, $\widetilde {{{y}_{{\text{\;}}}}}\left( t \right) = - y\left( t \right)$. При этом $\widetilde {{{\varphi }_{~}}}\left( {{{t}_{f}}} \right) > 0$.

Стало быть, чтобы найти множество ${{G}_{\varphi }}\left( {{{t}_{f}}} \right)$ при φ < 0, нужно взять множество $\widetilde {{{G}_{{\tilde {\varphi }}}}}\left( {{{t}_{f}}} \right)$ в новой задаче и отразить его относительно оси x. Таким образом, случай φ < 0 в исходной задаче сводится к случаю $\widetilde {{{\varphi }_{~}}} > 0$ в новой задаче.

Заключение. Изучается трехмерное множество достижимости для нелинейного управляемого объекта, называемого “машина Дубинса”. Предполагается, что повороты возможны как “влево”, так и “вправо”. Рассматривается случай с несимметричными, вообще говоря, возможностями (допусками) таких поворотов. Основные результаты статьи опираются на ПМП и состоят в следующем.

Известная для симметричного случая теорема о шести типах кусочно-постоянных управлений с не более чем двумя переключениями, ведущих на границу множества достижимости, распространяется на несимметричный случай. Аналогичная теорема доказана и для точек из внутренности множества достижимости (при уменьшении допусков на повороты влево и вправо).

Используемые типы управлений при фиксированном значении ${{\varphi }} \geqslant 0$ угловой координаты порождают непрерывную замкнутую кривую на плоскости геометрических координат. Совокупность таких кривых, получаемая при уменьшении допусков на повороты влево и вправо, полностью заполняет рассматриваемое φ-сечение. Это позволяет обосновать для ${{\varphi }} \geqslant 0$ формулу расчета φ-сечения множества достижимости в несимметричном случае через соответствующее сечение в каноническом симметричном случае. При этом в каноническом случае берем то же самое значение φ угловой координаты, но некоторый другой момент времени, для которого просчитывается φ-сечение. Формула имеет вид аффинного преобразования и задает взаимно-однозначное соответствие таких φ-сечений. Анализ φ-сечений при φ < 0 осуществляется на основе φ-сечений для φ > 0.

В итоге построение множества достижимости машины Дубинса в несимметричном случае сводится к каноническому случаю. В силу взаимной однозначности полученного в работе соответствия это означает, что наличие описания трехмерного множества достижимости для каких-то конкретных допусков на повороты влево и вправо позволяет получить описание множества достижимости для произвольного случая с двусторонними поворотами.

Исследование подобного вопроса в рамках случая строго одностороннего поворота [21] (поворот возможен только в одну сторону с ограничениями сверху и снизу на мгновенный радиус поворота), скорее всего, также имеет положительный ответ. Авторы попробуют обосновать это в одной из следующих работ.