Известия РАН. Теория и системы управления, 2023, № 4, стр. 50-58
К ВОПРОСУ О РЕАЛИЗАЦИИ ИНФОРМАЦИОННОЙ ТЕХНОЛОГИИ УТОЧНЕНИЯ ЭФЕМЕРИД КОСМИЧЕСКИХ АППАРАТОВ ГЛОНАСС НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ ПЕРСПЕКТИВНЫХ АППАРАТНЫХ СРЕДСТВ МЕЖСПУТНИКОВЫХ ИЗМЕРЕНИЙ
М. Н. Красильщиков a, Д. М. Кружков a, *, В. В. Пасынков a
a МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: kruzhkovd@mail.ru
Поступила в редакцию 15.03.2023
После доработки 17.03.2023
Принята к публикации 03.04.2023
- EDN: OCWQKA
- DOI: 10.31857/S0002338823040091
Аннотация
Обосновываются необходимые условия реализации информационной технологии, обеспечивающей автономность функционирования при одновременном повышении точности эфемерид и часов существующего средневысотного сегмента ГЛОНАСС. Обсуждаемая технология включает методы и алгоритмы повышения точности прогноза и уточнения эфемерид навигационных космических аппаратов в инерциальной системе координат, прогноза и уточнения эволюции параметров вращения Земли, высокоточной синхронизации бортовых часов. Уделяется внимание созданию необходимых условий реализации первой из перечисленных выше компонент предлагаемой технологии, обеспечивающей прогнозирование и уточнение эфемерид навигационных космических аппаратов в инерциальной системе координат, в том числе в автономном режиме функционирования спутниковых группировок. Компонента реализуется в форме блока специальных процедур использования аппаратуры для проведения измерений дальностей между спутниками. При этом возникает ряд технических проблем и сопутствующих ограничений, препятствующих успешному применению подобной аппаратуры в интересах решения задачи уточнения эфемерид навигационных космических аппаратов. Описаны предлагаемые авторами подходы и методы, призванные парировать часть проблем и ограничений и, в конечном итоге, повысить точность формируемых оценок эфемерид навигационных космических аппаратов на основе обработки формируемых с помощью бортовых аппаратных средств межспутниковых измерений.
Введение. Как известно в [1], улучшение потребительских характеристик современных спутниковых навигационных систем обеспечивается путем решения совокупности взаимосвязанных технических проблем, снижающих значение ключевого показателя точности навигационного поля – эквивалентной погрешности определения псевдодальности потребителя (ЭППД) навигационных сигналов [2]. Интегрально значение ЭППД определяется суммой составляющих, обусловленных следующими факторами:
погрешностями определяемых в инерциальной системе эфемерид навигационных космических аппаратов (НКА);
неопределенностью эволюционирующих значений параметров вращения Земли (смещение полюса и поправка к Всемирному времени);
уходом бортовых часов НКА относительно системной шкалы и др.
Анализ показывает [3], что одной из существенных по ее вкладу в итоговую погрешность навигационной задачи потребителя является ошибка эфемерид НКА при их прогнозировании на средних и длительных временных интервалах (от половины суток и до нескольких недель). В настоящий момент эта проблема решается на основе периодической реализации ряда процедур, приводящих в итоге к формированию в наземной инфраструктуре нового пакета точных эфемерид КА, загружаемых далее на борт. Таким образом, перманентное требование повышения точности эфемерид приводит к необходимости выполнять эти процедуры как можно чаще и более эффективно, что в результате входит в очевидное противоречие с техническими и ресурсными ограничениями, включая возможности наземной и бортовой аппаратуры. Дополнительным недостатком реализации подобных процедур является зависимость от наземной инфраструктуры и отсутствие возможности функционирования НКА ГЛОНАСС в автономном режиме. Избежать более частой загрузки данных на борт можно, например, путем реализации на борту процедур высокоточного прогнозирования движения НКА, но на текущий момент существующие и применяемые для этого инструменты неприемлемы в силу неудовлетворительной точности прогноза для средних и длительных интервалов времени. Основной проблемой, препятствующей реализации на борту высокоточного прогноза, является наличие неопределенных факторов в модели движения КА, связанных с ошибками системы ориентации КА и определением ускорения, вызываемого давлением солнечного света.
Возникающую задачу совершенствования процедур уточнения прогнозных эфемерид без участия наземной инфраструктуры предлагается решать непосредственно на борту НКА на основе обработки формируемых с использованием аппаратных средств, позволяющих проводить межспутниковые измерения (МСИ) и обмен информацией между парами НКА созвездия орбитальной группировки (ОГ) [4, 5]. Как показали результаты предварительного анализа, применения подобных средств с учетом обработки формируемых в процессе опытной эксплуатации данных в интересах решения задачи уточнения эфемерид КА, среднеквадратическое отклонение (СКО) ошибки измеренной межспутниковой дальности имеет сантиметровый порядок, что является весьма обнадеживающим. Тем не менее, трудности применения аппаратных средств для межспутниковых измерений (АС МСИ) в актуальных рабочих циклах НКА связаны, прежде всего, со следующими факторами:
наличием значительной неопределенной составляющей в ошибках измерений (не менее единиц метров);
существенным различием технических характеристик АС МСИ на разных НКА ОГ;
различными значениями задержек в антенно-фидерных системах (АФС) на разных частотах;
задержкой сигнала в плазмосфере;
релятивистскими поправками;
неопределенными погрешностями величин так называемых “выносов” фазовых центров антенн (ФЦ) НКА ГЛОНАСС относительно опорных (формулярных) значений.
С учетом сказанного задача комплексного уточнения эфемерид навигационных аппаратов всей ОГ с использованием АС МСИ требует решения отдельных частных подзадач по разработке методов и алгоритмов применения данной аппаратуры с целью устранения большей части существующих технических проблем и влияния неопределенных факторов.
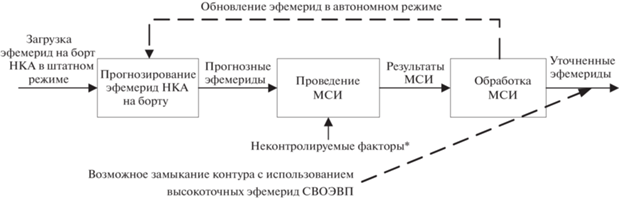
1. Техническая постановка задачи уточнения эфемерид. Как уже упоминалось, аппаратные средства для проведения МСИ являются перспективными с точки зрения возможностей реализации информационной технологии уточнения эфемерид НКА ГЛОНАСС. Наиболее вероятная функциональная схема применения подобных средств с учетом технических особенностей этой аппаратуры представлена на рис. 1.
Очевидно, что эффективному с точки зрения достижения потребной точности эфемерид использованию такой функциональной схемы препятствует наличие перечисленных выше случайных и неопределенных неконтролируемых факторов (рис. 1: неконтролируемые факторы). Необходимым условием для компенсации их влияния на процесс уточнения эфемерид является калибровка соответствующей аппаратуры НКА ГЛОНАСС. Однако в рамках функциональной схемы рис. 1 это сделать невозможно, так здесь объективно присутствуют одновременно как ошибки эфемерид, так и ошибки измерений, в результате чего фактические погрешности уточненных эфемерид не известны. Таким образом, чтобы оценить потенциальный результат использования АС МСИ для уточнения эфемерид уже на этапе разработки процедуры (рис. 1), необходимы эталонные данные, в качестве которых предлагается применять итоговые эталонные эфемериды системы высокоточного определения эфемеридно-временной информации (СВОЭВИ), поскольку такие эфемериды имеют остаточную случайную погрешность, подчиняющуюся гауссовскому распределению с известными значениями СКО и математические ожидания ошибок по бинормали, вдоль радиус-вектора и вдоль орбиты НКА [6]. Заметим, что в дальнейших экспериментах при использовании эфемерид СВОЭВП в качестве эталонных и оценке разностных измерений, содержащих уходы часов КА, необходимо также применение апостериорных частотно-временных поправок (ЧВП).
Использование эфемерид СВОЭВП в качестве эталонных позволяет “замкнуть” функциональную схему рис. 1 по невязкам эталонных и опорных эфемерид, определяемых в рамках обсуждаемой процедуры их уточнения. В результате функциональная схема процедуры уточнения эфемерид оказывается итеративной и “замкнутой” (рис. 2).
Рис. 2.
Функциональная схема использования эфемерид СВОЭВП в интересах повышения эффективности применения АС МСИ для уточнения эфемерид.
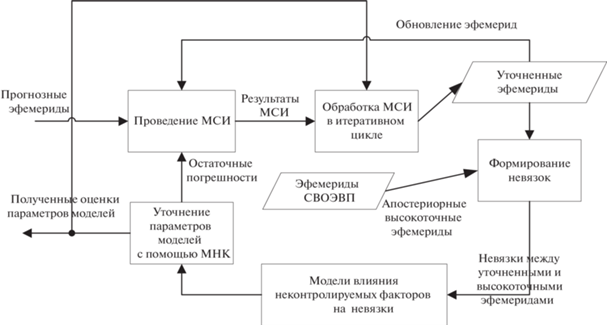
Реализация процедуры в соответствии с функциональной схемой рис. 2 требует в свою очередь формирования математической модели МСИ с учетом влияния перечисленных выше неопределенных и случайных неконтролируемых факторов. При этом предполагается, что конкретные значения параметров таких моделей должны определяться на основании проводимых экспериментов, а результаты экспериментов обрабатываться методом наименьших квадратов.
2. Математическая постановка задачи. Формализуем поставленную техническую задачу уточнения эфемерид с использованием приведенных далее математических моделей. Перспективная аппаратура проведения МСИ формирует и передает по определенной циклограмме сигнала для приема другими НКА, находящихся в зоне радиовидимости. Одновременно осуществляется прием сигнала и измерение его временного сдвига относительно шкалы бортового синхронизирующего устройства (БСУ), т.е. фактически происходит измерение беззапросной дальности. Для анализа измерений необходимо вычислить расчетные аналоги дальностей, при формировании которых будут применены высокоточные эфемериды и ЧВП (там, где необходимо) СВОЭВП. Полученные таким образом невязки будут обработаны в методе наименьших квадратов (МНК), где в число компонент оцениваемого вектора включены уточняемые параметры неконтролируемых факторов, перечисленные ранее во Введении, а в качестве частных производных МНК использованы производные от приведенных далее соотношений, описывающих различные типы расчетных аналогов измерений дальностей. Таким образом, ключевым условием успешного решения данной задачи является корректное и полное (с точки зрения возможности обработки всех накопленных измерений) математическое описание неконтролируемых факторов, поскольку, в конечном итоге, формируемые невязки расчетных и фактических измерений должны сходиться к нулю. При этом формируемые оценки должны соответствовать адекватным, предполагаемым на физическом уровне значениям. Если соответствующие модели, учитывающие влияние неконтролируемых факторов на результаты измерений, будут неполными, произойдет взаимная компенсация различных компонент вектора этих факторов, и их оценки не будут адекватными, несмотря на сходимость процедуры МНК и получение нулевых невязок.
Математическую модель измеренной межспутниковой псевдодальности (i-й НКА принимает сигнал от j-го НКА) представим в следующем виде:
(2.1)
${{S}^{{ij}}} = c{{\tau }^{{ij}}} + c(\Delta {{t}^{i}} - \Delta {{t}^{i}}^{{{\text{рел}}\left( {{\text{пм}}} \right)}}) - c(\Delta {{t}^{j}} - \Delta {{t}^{j}}^{{{\text{рел}}\left( {{\text{пд}}} \right)}}) + a_{0}^{{i{\text{пм}}}} + a_{0}^{{j{\text{пд}}}},$(2.2)
$c{{\tau }^{{ij}}} = {{\rho }^{{ij}}} + \delta {{S}_{{\text{п}}}} + \delta S_{{{\text{грав}}}}^{{ij}}~ + \,\delta S_{{{\text{пм}}}}^{i} + \delta S_{{{\text{пм}}}}^{j},$В радиотехнических трактах МСИ предполагается частотное разделение сигналов , которое (как и в случае наземных измерений) приводит к появлению так называемых литерных (систематических) задержек $a_{0}^{{i{\text{пм}}}}$ и $a_{0}^{{j{\text{пд}}}}$. Оцифровка (“привязка” измерений ко времени) осуществляется в приемной аппаратуре. “Уходы” часов приемника (i-й НКА) и передатчика (j-й НКА) имеют противоположный знак. Таким образом, при уточнении часов знак частной производной по часам для приемника и передатчика – противоположный. Релятивистская поправка, наоборот: для приемника (i-й НКА) входит в модель с отрицательным знаком, а для передатчика (j-й НКА) – с положительным.
Расчетный аналог такого измерения (так называемая “геометрическая” дальность) определяется соотношением
(2.3)
${{\rho }^{{ij}}} = D_{2}^{{ij}}({{\vec {R}}_{{{\text{пд}}}}}({{t}^{i}} - {{\rho }^{{ij}}}{\text{/}}c),{{\vec {R}}_{{{\text{пм}}}}}({{t}^{i}})),$При проведении “прямых” и “встречных” измерений (соответственно от i-го до j-го КА и наоборот) ${{S}^{{ij}}}$ и ${{S}^{{ji}}}$ на близких эпохах (в течение рабочего цикла аппаратуры АС МСИ) удается сформировать суммарно-дальномерные и разностно-дальномерные навигационные измерения. При условии необходимой синхронности по какой-то единой шкале времени формируется точечное измерение “геометрической” псевдодальности с учетом суммы и разностей калибровок (оценок задержек в аппаратуре каждого из КА) в приемо-передающих трактах НКА, участвующих во взаимных измерениях:
(2.4)
$S_{ + }^{{ij}} = ({{S}^{{ij}}} + {{S}^{{ji}}}) = c({{\tau }^{{ij}}} + {{\tau }^{{ji}}}) + a_{0}^{{i{\text{пм}}}} + a_{0}^{{j{\text{пд}}}} + a_{0}^{{j{\text{пм}}}} + a_{0}^{{i{\text{пд}}}}.$В результате появляется возможность уточнить суммарные задержки в приемо-передающих трактах каждого из КА при наличии не менее трех НКА:
(2.5)
$S_{ + }^{{ij}} = ({{S}^{{ij}}} + {{S}^{{ji}}}) = c({{\tau }^{{ij}}} + {{\tau }^{{ji}}}) + a_{0}^{{i + }} + a_{0}^{{j + }},$В (2.5) $a_{0}^{{i + }}$ и $~a_{0}^{{j + }}$ – суммарные задержки i-го и j-го НКА соответственно:
Система линейных уравнений для определения суммарных систематических задержек в приемо-передающих трактах для минимально достаточного состава из трех НКА имеет вид
где ${{\Delta }}S_{ + }^{{ij}}$ – невязка между измеренным и расчетным значением (см. рис. 2).Определитель такой системы трех уравнений с тремя неизвестными равен минус двум, и, следовательно, система имеет очевидное решение при наличии, например, высокоточных апостериорных эфемерид, что и было предложено ранее для решения данной задачи. Погрешность расчета суммарных задержек, помимо вклада случайных (шумовых) ошибок измерений, будет определяться точностью апостериорных эфемерид в проекции на межспутниковую дальность.
Уточнение суммарных задержек в приемо-передающих трактах также возможно и по совокупности прямых и встречных измерений без перехода к суммарным измерениям, но требует также знания высокоточных частотно-временных поправок. Поясним это подробнее.
В случае разностно-дальномерных измерений геометрическая задержка парируется, а модель измерения эквивалентна разности ухода часов i-го относительно j-го НКА с учетом релятивистких задержек их шкал и разностей калибровок в приемо-передающих трактах КА, участвующих во взаимных измерениях:
По аналогии с суммарными для разностных измерений можно уточнить разность задержек в приемо-передающих трактах:
С учетом (2.6) и (2.7), суммируя (2.9) с (2.6) и (2.10) с (2.7), получим
Далее, подстановкой (2.11) в (2.6) и (2.12) в (2.7), находим
Таким образом, совместная обработка суммарных и разностных измерений от не менее трех КА, реализующих прямые и встречные измерения, позволяет получить оценки задержек в приемо-передающих трактах АС МСИ. Проверка этих оценок на формулярных значениях подтверждает, что при наличии корректных оценок для суммарных (2.6), (2.7) и разностных (2.9), (2.10) значений фактические значения задержек в приемном и передающих трактах НКА разделимы, т.е. наблюдаемы, как при работе на прием и передачу на одну антенну, так и на разные.
В результате процедура уточнения влияния неконтролируемых факторов на точность эфемерид включает следующие шаги:
1. Анализ комплектации приемо-передающих трактов и антенных систем АС МСИ с точки зрения присутствия максимальных значений возможных задержек, проверка наличия априорных (формулярных или уточненных кем-либо) данных по задержкам в приемо-передающих трактах.
2. Определение невязок прямых и встречных измерений на основе апостериорной эфемеридно-временной информации (ЭВИ) и сравнение этих невязок с априорными данными (при их наличии).
3. Уточнение суммарных задержек в приемно-передающих трактах по суммарным измерениям, сравнение полученных результатов с априорными данными.
4. Уточнение разностных задержек, анализ точности средних (за сеанс) оценок, анализ технических характеристик (ТХ) БСУ по апостериорной ЭВИ, выбор НКА с лучшим и худшим БСУ в смысле стабильности и точности формируемых измерений, определение ЧВП по измерениям АС МСИ и сравнение их с апостериорными ЧВП.
5. Формирование заключения о возможности уточнения на основе предложенной процедуры и математических моделей учитываемых неконтролируемых факторов.
3. Исходные данные задачи. При подготовке материалов статьи были использованы результаты сеансов измерений, проведенных в следующих интервалах: март–апрель 2016 г. (11 НКА серии “Глонасс-М”), январь–февраль 2022 г. (4 НКА серии “Глонасс-М” и 2 НКА серии “Глонасс-К”).
Среди накопленных измерений в 2016 г. есть 12 КА, из которых по 11 КА есть встречные измерения, что позволило сформировать суммарные и разностные и провести более расширенную оценку погрешностей. Для 3 КА R05(734), R22(731), R24(735), которые присутствуют на интервале в марте–апреле 2016 г., имелись в наличии априорные исходные данные о задержках в передающем и приемном трактах, которые составили в среднем 462 и 23 нс соответственно (для каждого номера КА – свое значение). В результате выполнения специальных процедур были получены оценки погрешности вариаций задержек от среднего, которые составили не более 0.6 м для передающего тракта (734), и 0.9 м – для приемного (735). Эти отличия, безусловно, значительны, однако поскольку невязки наблюдаемых и априорных значений имеют бóльшие величины, на данном этапе анализа свойств измерений вариации менее метра можно считать незначимыми.
В начале 2022 г. проведена группа МСИ по 6 НКА с системными номерами: R09(702), R11(705) – “Глонасс-К”, R12(758), R18(754), R22(735), R24(760) – “Глонасс-М”, из которых по всем НКА есть встречные измерения, что позволило сформировать суммарные и разностные измерения и провести экспериментальную оценку с использованием новых НКА серии “Глонасс-К”.
4. Результаты. Заметим, что предварительный анализ свойств прямых измерений ${{S}^{{ij}}}$ и ${{S}^{{ji}}}$, накопленных в сеансах, показал, что некалиброванные значения задержек $a_{0}^{{i{\text{пм}}}}\, = \,{\text{с}}\Delta t{{_{{{\text{пм}}}}^{i}}^{{{{f}_{i}}}}}$, $a_{0}^{{i{\text{пд}}}}\, = \,c\Delta t{{_{{{\text{пд}}}}^{i}}^{{{{f}_{i}}}}}$, $a_{0}^{{j{\text{пд}}}}\, = \,c\Delta t{{_{{{\text{пд}}}}^{j}}^{{{{f}_{j}}}}}$, $a_{0}^{{j{\text{пм}}}} = c\Delta t{{_{{{\text{пм}}}}^{j}}^{{{{f}_{j}}}}}$, участвующих во взаимных измерениях, могут достигать десятков и иногда даже сотен метров, т.е. без калибровки такие измерения для эфемеридно-временного обеспечения (ЭВО) использоваться не могут. Иными словами, здесь необходима обработка прямых и встречных измерений, как уже указывалось, не менее, чем 3 НКА. Поэтому далее обсуждаются результаты обработки полусумм и полуразностей накопленных в проведенных сессиях измерений.
Подчеркнем еще раз, что приведенные ниже в тексте и соответствующих таблицах результаты подтверждают возможность с использованием развиваемой информационной технологией получения оценок с необходимой точностью параметров, характеризующих влияние неконтролируемых факторов на процесс уточнения эфемерид ГЛОНАСС с применением аппаратуры межспутниковых измерений. Конкретно оценивались следующие параметры: задержки в приемных и передающих трактах АС МСИ НКА $a_{0}^{{i{\text{пм}}}}$ и $a_{0}^{{i{\text{пд}}}}$, суммарные $a_{0}^{{i + }}$ и разностные $a_{0}^{{i - }}$ задержки в приемно-передающих трактах для различных пар КА ГЛОНАСС, погрешности синхронизации бортового излучателя навигационного сигнала (БИНС) и АС МСИ, входящие в состав $\Delta {{t}^{i}}$ и $\Delta {{t}^{j}}~$ как систематические ошибки, выносы ФЦ приемной и передающей антенн $\delta S_{{{\text{пм}}}}^{i}$ и $\delta S_{{{\text{пд}}}}^{j}$.
Результаты обработки полусумм измерений. Ниже в табл. 1 и 2 приведены оценки суммарной задержки, полученные в сессиях 2016 и 2022 гг. соответственно (в том числе результаты эксперимента от 2012 г., который проводился вместе с наземными станциями).
Таблица 1.
Оценки суммарной задержки по результатам сессии 2016 г.
| СТ | Номер | a+, м | sig | 2012 г. |
|---|---|---|---|---|
| R02 | 747 | 92.668 | 0.009 | |
| R03 | 744 | 91.566 | 0.010 | 91.828 |
| R04 | 742 | 89.906 | 0.009 | 90.110 |
| R05 | 734 | 78.965 | 0.009 | |
| R07 | 745 | 91.254 | 0.009 | |
| R08 | 743 | 92.579 | 0.011 | |
| R16 | 736 | 80.405 | 0.008 | |
| R17 | 751 | 90.293 | 0.008 | |
| R18 | 754 | 87.762 | 0.007 | |
| R22 | 731 | 79.666 | 0.010 | |
| R24 | 735 | 77.687 | 0.007 |
Таблица 2.
Оценки суммарной задержки в сессии 2022 г.
| СТ | Номер | a+, м | sig | 2016 г. |
|---|---|---|---|---|
| R09 | 702 | 74.717 | 0.012 | |
| R11 | 705 | 90.140 | 0.010 | |
| R22 | 735 | 77.500 | 0.013 | 77.687 |
| R18 | 754 | 87.958 | 0.012 | 87.762 |
| R12 | 758 | 88.428 | 0.013 | |
| R24 | 760 | 88.872 | 0.012 |
Таблица 3.
Задержки в трактах НКА ГЛОНАСС, рассчитанные по априорным данным
| СТ | Номер | $a_{0}^{{{\text{пм}}}}$ | $a_{0}^{{{\text{пд}}735}}$ | $a_{0}^{ + }$ (прямые) | $a_{0}^{{{\text{пм}}735}}$ | $a_{0}^{{{\text{пд}}}}$ | $a_{0}^{ - }$ (встречные) | a+/2 | a–/2 |
|---|---|---|---|---|---|---|---|---|---|
| R05-R24 | 734–735 | 8.0 | 139.9 | 147.9 | 7.2 | 135.5 | 142.6 | 145.2 | 2.6 |
| R22-R24 | 731–735 | 7.7 | 139.9 | 147.6 | 7.2 | 139.7 | 146.8 | 147.2 | 0.4 |
В табл. 1, 2 использованы следующие обозначения: спутниковая точка (СТ) – позиция НКА в орбитальной группировке, номер – системный номер, a+ – оценка суммарной задержки в метрах, sig – СКО оценки задержки.
Результаты оценки суммарных задержек показывают, что они сохраняют свои значения на длительных интервалах (до 10 лет), что говорит о приемлемости предлагаемого подхода и возможности применения данной технологии на практике. Дополнительно делалась попытка уточнения выносов антенных систем относительно центра масс НКА, что позволило снизить их СКО до 7–8 см.
Проведем также сравнение априорных значений задержек (в метрах) в приемных и передающих трактах с наблюдаемыми для 3 КА: R22(731), R24(735), R05 (734). В табл. 3 по априорным значениям упомянутых задержек проведен расчет ожидаемых задержек в прямых и встречных измерениях (без учета задержек в антенно-фидерных устройствах (АФУ), в метрах), а также ожидаемых значений полусумм и полуразностей оцениваемых задержек (в метрах).
Для указанных пар прямых и встречных измерений даже для различных литер БИНС и АС МСИ невязки задержек примерно одинаковые: прямые на 3–4 м больше априорных, а встречные – на 16 м. Таким образом, учет задержек при реализации технологии обработки МСИ должен производиться после их калибровки, а не по априорным значениям.
Измерения, соответствующие интервалу 2022 г., отражают факт появления пары НКА серии “Глонасс-К”, т.е. НКА с другой аппаратурой, что в контексте данной задачи имеет принципиальное значение. В табл. 4 приведены значения невязок прямых и встречных измерений с учетом апостериорных ЧВП для упомянутых НКА и других НКА, участвующих в сессии измерений 2022 г.
Таблица 4.
Значения невязок прямых и встречных измерений с учетом апостериорных ЧВП
| Номер | 702 | 705 | 758 | 754 | 735 | 760 | |
|---|---|---|---|---|---|---|---|
| СТ | R09 | R11 | R12 | R18 | R22 | R24 | |
| СТ | Л | –2 | 0 | –1 | –3 | –3 | 2 |
| R09 | 3 | *** | (165)/(–47.7) | (163)/(–14.2) | (152)/(–7.1) | (164)/(–11.9) | |
| R11 | 3 | (117)/(212) | *** | (179)/(+35.5) | (178)/(+31.3 | (168)/(+39.9) | (180)/(+35.8) |
| R12 | 3 | (214)/(143) | *** | (176)/(–3.9) | (167)/(+3.6) | ||
| R18 | 5 | (148)/(177) | (211)/(145) | (172)/(180) | *** | (177)/(+3.9) | |
| R22 | 6 | (145)/(160) | (206)/(130) | (170)/(163) | *** | (177)/(+3.7) | |
| R24 | 6 | (153)/(175) | (215)/(143) | (181)/(173) | (181)/(173) | *** | |
В табл. 4 дополнительно обозначены Л – номер литеры, в ячейках – значения задержек при проведении прямых и встречных измерений соответственно (в метрах). Заметен резкий рост вариаций представленных значений, который достигает 95 м (пара R09-R11). Приведем также сравнение для этих 2 КА: R11(705) и R22(735) априорных (первая строка) значений задержек (в метрах) с наблюдаемыми (вторая строка) (табл. 5).
Таблица 5.
Сравнение априорных задержек в трактах НКА с наблюдаемыми
| Номер | СТ | $a_{0}^{{{\text{пм}}}}$ | $a_{0}^{{{\text{пд}}735}}$ | $a_{0}^{ + }$ (прямые) | $a_{0}^{{{\text{пм}}735}}$ | $a_{0}^{{{\text{пд}}}}$ | $a_{0}^{ - }$ (встречные) | a+/2 | a–/2 |
|---|---|---|---|---|---|---|---|---|---|
| 705–735 | R11-R22 | 102.5 | 139.9 | 242.4 | 7.2 | 110. | 117.1 | 179.8 | 62.6 |
| 705–735 | R11-R22 | 206 | 130 | 168 | 39.9 | ||||
| Δ | –36 м | +13 м |
Заметны существенные различия между априорными и наблюдаемыми задержками, измеряемые десятками метров (третья строка Δ). Заметим, что для двух сочетаний пар “Глонасс-М” в 2016 г. было существенно лучшее согласование. Данный факт говорит о том, что априорные задержки содержат значительные неопределенности и использовать их в рабочей процедуре нецелесообразно, перейдя непосредственно к обработке измерений.
Предварительные выводы по обработке полусумм измерений. Предлагаемая процедура расчета задержек приемных и передающих трактов НКА, получаемых при обработке суммарных измерений, показывает повторяющийся результат, проверенный на 10-летнем интервале, для которого получены стабильные во времени значения суммарных задержек. Проведенная оценка выносов антенных систем показала наличие существенных отклонений от формулярных значений (примерно до 5–8 см по осям Yсв, Zсв, и до 15–25 см по Xсв, где св – связанная с НКА система координат). Реализация предлагаемых процедур может обеспечить повышение эффективности использования АС МСИ в интересах уточнения эфемерид и устранение в канале измерений систематических ошибок, вызванных неконтролируемыми факторами.
Результаты обработки полуразностей измерений. Как уже было сказано ранее, на интервале сессии 2016 г. участвовало 11 КА (R02, R03, R04, R05, R07, R08, R16, R17, R22, R24). По трем известна априорная информация о задержках МРЛ (R05, R22, R24). Расчет систематических ошибок полуразностей относительно апостериорных ЧВП приведен в табл. 6. Расчеты проведены с применением апостериорных эфемерид и ЧВП центра анализа СВОЭВИ.
Таблица 6.
Оценка разностных задержек а– (в метрах) по МСИ
| СТ | Номер | Литер | а– | sig | |
|---|---|---|---|---|---|
| БИНС | АС МСИ | ||||
| R02 | 747 | –4 | 1 | –1.447 | 0.111 |
| R03 | 744 | 5 | 1 | 6.573 | 0.113 |
| R04 | 742 | 6 | 1 | 6.016 | 0.107 |
| R05 | 734 | 1 | 2 | –1.049 | 0.107 |
| R07 | 745 | 5 | 2 | 5.301 | 0.101 |
| R08 | 743 | 6 | 2 | 6.999 | 0.132 |
| R16 | 736 | –1 | 4 | –0.342 | 0.093 |
| R17 | 751 | 4 | 5 | –0.611 | 0.097 |
| R18 | 754 | –3 | 5 | 0.045 | 0.085 |
| R22 | 731 | –3 | 6 | 6.956 | 0.122 |
| R24 | 735 | 2 | 6 | 2.040 | 0.083 |
Таким образом, были получены оценки погрешностей в разностных задержках от –1.4 до 7.0 м. Подобный разброс, предположительно, может быть обусловлен взаимной некалиброванностью трактов различных аппаратных средств НКА–БИНС и канала обмена МСИ.
5. Выводы по результатам обработки данных проведенных сессий сеансов МСИ для НКА ГЛОНАСС. Значения полусумм задержек измерений относительно стабильны во времени при определении их с использованием апостериорных эфемерид. При уточнении эфемерид можно оценивать их значения (задержек) без предварительного уточнения, например, с запросными измерениями наземного комплекса управления (НКУ). Полуразности существенно зависят от актуальных ЧВП и при текущих средствах калибровки разрешены быть не могут. Ситуацию с калибровкой, предположительно, можно будет разрешить с привлечением дополнительных средств, например, бортовых квантовых оптических систем (БКОС). Измерений БКОС должно быть достаточно для получения эталонных ЧВП, которые будут применяться в обсуждаемой процедуре как исходные данные.
Заключение. Изложены основы информационной технологии, обеспечивающей автономность функционирования при одновременном повышении точности эфемерид и часов существующего средневысотного сегмента ГЛОНАСС. Предлагаемая технология базируется на использовании бортовой аппаратуры МСИ и включает:
математические модели МСИ с учетом широкого спектра неконтролируемых факторов различной физической природы;
алгоритмы предварительного анализа характеристик результатов МСИ и их обработки с целью формирования оценок параметров, характеризующих влияние неконтролируемых факторов на процесс уточнения эфемерид ГЛОНАСС с использованием аппаратных средств проведения МСИ.
Приведены результаты экспериментальной отработки предложенной технологии, полученные на основе обработки реальных измерений на нескольких сессиях с аппаратами ГЛОНАСС. Продемонстрирована сходимость результатов оценивания систематических погрешностей МСИ, которые могли препятствовать ранее использованию подобной аппаратуры в рабочих процедурах без потери точности. Оценивались следующие параметры: задержки в приемных и передающих трактах АС МСИ КА, суммарные и разностные задержки в трактах для различных пар КА ГЛОНАСС, погрешности синхронизации БИНС и АС МСИ, выносы ФЦ антенн.
Выявлена необходимость периодического повторения экспериментальной отработки предложенной технологии, а также проведения дополнительных калибровочных процедур используемой аппаратуры. Подготовлены исходные данные для реализации технологии уточнения эфемерид НКА с помощью канала обмена информацией о МСИ.
Список литературы
Kruzhkov D.M., Pasynkov V.V. National Global Navigation Satellite System GLONASS: Features of Creation, Development and Use. M.: Moscow Aviation Institute, 2022.
[Электронный ресурс], https://glonass-iac.ru/glonass/technical, 13.03.2022.
Krasil’shchikov M.N., Kruzhkov D.M. On the Issue of Autonomous Refining of the Earth Orientation Parameters Onboard Spacecraft. Analysis of the Possibilities of Developed Information Technology // Cosmic Research. 2021. V. 59. № 5. P. 357–365.
Grechkoseev A.K. Study of Observability of Motion of an Orbital Group of Navigation Space System Using Intersatellite Range Measurements. I // Computer and Systems Sciences International. 2011. V. 50. № 2. C. 293–308.
Grechkoseev A.K. Study of Observability of Motion of an Orbital Group of Navigation Space System Using Intersatellite Range Measurements. II // Computer and Systems Sciences International. 2011. T. 50. № 3. C. 472–482.
SVOEVI, http://www.glonass-svoevp.ru, 10.12.2022.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления