Известия РАН. Теория и системы управления, 2023, № 5, стр. 43-56

Введение. Приведем систему, где материальная точка массы $m$ может скользить вдоль горизонтального жесткого невесомого стержня, вращающегося под действием внешнего момента M с заданным ограничением $\left| M \right| \leqslant {{M}_{0}}$ (рис. 1). Линейная пружина, соединяющая материальную точку с осью вращения, имеет коэффициент упругости k и длину $l$ в ненапряженном состоянии. Полагаем, что кинематические ограничения на точку не наложены (устранены конструктивно), а трение отсутствует.

Пусть $\varphi $ – угол поворота стержня, $y$ – деформация пружины, K – кинетический момент системы. Тогда ее дифференциальные уравнения движения имеют вид

Анализ поведения такой модели может на качественном уровне прояснить характерные закономерности динамики более сложных конструкций, например, в задачах ориентации космических аппаратов с нежесткими элементами, управления их прецизионными поворотными платформами и т.д. Этой тематике посвящено много работ, в том числе, в последние годы [1, 2]. Известную трудность представляет поиск управления, оптимального по быстродействию. Здесь основным подходом является применение принципа максимума Понтрягина [3], поэтому поиск управлений осуществляется в классе кусочно-постоянных функций. В системе с одной степенью свободы и в многомерной линейной системе, для которой сопряженная система имеет линейно независимые решения, особые управления (равносильные бесконечно быстрым переключениям) невозможны. В нелинейных объектах, где количество управляющих воздействий равно числу степеней свободы, особые оптимальные управления давно обнаружены [4, 5] численными экспериментами. Их можно было объяснить избыточностью ресурсов. Например, когда внешний момент вращает составной механизм, то вспомогательный момент в сочленении не обязан быть максимальным, чтобы поддерживать конфигурацию с малым суммарным моментом инерции относительно оси вращения. Напротив, для системы с двумя степенями свободы и одним управлением появление особых режимов [6] не было ожидаемым. Но их наличие прояснило, в общем случае, практическую невозможность аналитического решения задачи оптимального быстродействия, например, путем склеивания участков траекторий с постоянными значениями управлений. Применение численных методов здесь оказалось неизбежным, что вполне относится и к рассматриваемому механизму (рис. 1).

1. Свойства управляемости объекта. Вводя безразмерные переменные ${{x}_{1}} = y{\text{/}}l$, $\omega = l\sqrt {k{\text{/}}{{M}_{0}}} $, $u = M{\text{/}}{{M}_{0}}$, $p = K{\text{/}}(l\,\sqrt {m{{M}_{0}}} )$ и время $t{\kern 1pt} ' = t\sqrt {{{M}_{0}}} {\text{/}}(l\sqrt m )$, приведем уравнения движения системы (рис. 1) к нормальной форме:

Обозначим вектор состояния ${\mathbf{q}} = {{\left( {{{x}_{1}},{{x}_{2}},\varphi ,p} \right)}^{{\text{T}}}}$. Тогда в окрестности точки ${{\left( {0,0,{\text{\;}}0,0} \right)}^{{\text{T}}}}$ линеаризованная система будет неуправляемой, поскольку она распадается на две независимые подсистемы. Тем не менее, имеет место следующее свойство.

Замечание 1. Нелинейная система (1.1) является глобально управляемой, т.е. может быть переведена из любого начального состояния q₀ в любое требуемое состояние q_f  за конечное время.

Это можно показать способом, предложенным в [7], поскольку объект (рис. 1) допускает при $u \equiv 0$ стационарное вращение:

Здесь величина ${{x}_{0}} > 0$ берется произвольно, а к ней вычисляются соответствующие значения ${{p}_{0}} = \omega (1 + {{x}_{0}})\sqrt {{{x}_{0}}(1 + {{x}_{0}})} $, $\Omega = \omega \sqrt {{{x}_{0}}{\text{/}}(1 + {{x}_{0}})} $.

Введем вектор $z = {{\left( {{{z}_{1}},\,\,{{z}_{2}},{\text{\;}}{{z}_{3}}} \right)}^{{\text{T}}}}$, где ${{z}_{1}} = {{x}_{1}} - {{x}_{0}}$, ${{z}_{2}} = {{\dot {z}}_{1}}$, ${{z}_{3}} = p - {{p}_{0}}$. В линейном приближении в окрестности состояния z = 0 система примет вид

где ${{h}_{1}} = - {{\omega }^{2}} - 3p_{0}^{2}{\text{/}}{{(1 + {{x}_{0}})}^{4}}$, ${{h}_{2}} = 2{{p}_{0}}{\text{/}}{{(1 + {{x}_{0}})}^{3}} \ne 0$.

Так как $\det [{\mathbf{b}},A{\mathbf{b}}{\text{,}}{{A}^{2}}{\mathbf{b}}] = - h_{2}^{2} \ne 0$, то по критерию Калмана [8] система (1.1) локально управляема в окрестности положения относительного покоя (1.2). При этом систему (1.1) можно перевести из любого начального состояния q₀ в любую $\varepsilon $ – окрестность многообразия (1.2) за конечное время.

Действительно, используя приведенную (с учетом переносной силы инерции) потенциальную энергию

составим функцию Ляпунова

Можно показать (подробности опускаем), что функция $\left( {B({{x}_{1}}) - B({{x}_{0}})} \right)$ – положительно-определенная бесконечно большая [9]. При этом выполняется соотношение $V = E - p\Omega $, где E – полная энергия системы. Поэтому производная вдоль векторного поля системы (1.1) имеет вид

Выбирая допустимое управление из условия $signu = sign(\Omega - \dot {\varphi })$, получим $\dot {V} \leqslant 0$, причем тождество $\dot {V} \equiv 0$ возможно только в состоянии относительного покоя (1.2). Согласно утверждению из [7], этих свойств достаточно для глобальной управляемости системы (1.1), поскольку из любого начального состояния q₀ ее можно за конечное время перевести в состояние (1.2), а с учетом симметрии относительно обращения времени $t \to - t$ из состояния (1.2) можно попасть в любую точку q_f  четырехмерного фазового пространства, что и требовалось.

2. Постановка задачи и тривиальные оптимальные режимы. Далее рассмотрим задачу оптимального по быстродействию поворота системы (1.1), предварительно введя удобное начало отсчета для угла $\varphi $. Полагая, что требуемому повороту соответствует дуга $2\alpha $, назначим в середине этой дуги нулевое значение координаты $\varphi $. Аналогичную “удвоенную” запись введем и для искомого общего времени 2T движения системы, что придаст краевым условиям симметричный вид.

Задача оптимального быстродействия формулируется следующим образом: требуется определить управление u(t), $t \in \left[ {0,~\,2T} \right]$, переводящее систему (1.1) из состояния

за наименьшее время 2T (заранее неизвестное) в состояние

Используя принцип максимума Понтрягина, составим гамильтониан

Тогда оптимальное управление получит вид

где сопряженные переменные должны удовлетворять уравнениям

Ввиду однородности сопряженной системы (2.4) ее решения задаются с точностью до ненулевого сомножителя. Поэтому далее без уменьшения общности положим ${{\lambda }_{3}} \equiv 1$.

В силу замечания 1, искомое оптимальное управление существует.

Замечание 2. В задаче (1.1), (2.1)–(2.4) записанное в смещенном времени $\tilde {t} = t - T$, $\tilde {t} \in [ - T,{\kern 1pt} \;T]$, оптимальное управление $u\left( {\tilde {t}} \right)$, а также решения $\varphi \left( {\tilde {t}} \right)$, ${{x}_{2}}\left( {\tilde {t}} \right)$, ${{\lambda }_{1}}(\tilde {t})$, ${{\lambda }_{4}}(\tilde {t})$ будут нечетными функциями, а ${{x}_{1}}(\tilde {t})$, $p(\tilde {t})$, ${{\lambda }_{2}}(\tilde {t})$ – четными функциями.

Для доказательства достаточно убедиться, что в новом времени $\tilde {t}$ все соотношения (1.1), (2.1)–(2.4) инвариантны относительно замены $\tilde {t} \to - \tilde {t}$, $u \to - u$, $\varphi \to - \varphi $, ${{x}_{2}} \to - {{x}_{2}}$, ${{\lambda }_{1}} \to - {{\lambda }_{1}}$, ${{\lambda }_{4}} \to - {{\lambda }_{4}}$ при неизменных ${{x}_{1}}$, p, ${{\lambda }_{2}}.$

Из замечания 2 вытекают соотношения

характеризующие состояние системы в конце оптимальной полутраектории.

Далее поставленную задачу быстродействия будем рассматривать для взаимной вариационной задачи на максимум угла поворота $2\alpha $ при заданном времени 2T, исследуя эволюцию функций оптимального управления u(t), $t \in \left[ {0,~\,2T} \right]$ с изменением параметра Т.

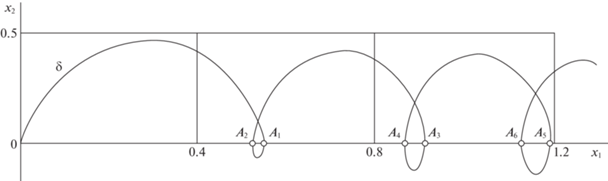
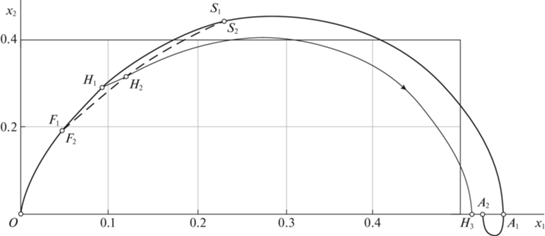
На рис. 2 для случая $\omega = 2$ в системе (1.1) на плоскости $({{x}_{1}},{{x}_{2}})$ показана фазовая кривая, выходящая из точки (0, 0) при постоянном управлении u = 1. Для краткости эту кривую будем называть линией $\delta $. Последовательные точки пересечения линии $\delta $ c осью $O{{x}_{1}}$ обозначим ${{A}_{i}}$, $i\, = \,1,2,3$, ..., где $i$ – это номер пересечения, а соответствующие им значения времени будут ${{T}_{i}}$, $i = 1,2,3,...$.

Любая из точек ${{A}_{i}}$, $i = 1,2,3,...$, может служить концом оптимальной полутраектории. Меняя в этот момент времени $t = {{T}_{i}}$ управление на $u = - 1$, получим вторую полутраекторию, симметричную первой относительно оси $O{{x}_{1}}$, согласно замечанию 2. Она завершится в точке (0, 0) в момент времени $t = 2{{T}_{i}}$. Можно показать, что такой режим из двух этапов

удовлетворяет не только краевым условиям (2.1), (2.2), но и сопряженной системе (2.4). Соответствующие решения ${{\lambda }_{j}}(t)$, $j = \overline {1,4} $, можно получить численно, интегрируя систему (1.1), (2.4) в обратном времени из состояния ${{x}_{j}}({{T}_{i}})$, $j = \overline {1,4} $, при условии ${{\lambda }_{1}}({{T}_{i}}) = {{\lambda }_{4}}({{T}_{i}}) = 0$. Параметр ${{\lambda }_{2}}({{T}_{i}})$ подбирается так, чтобы в процессе интегрирования функция ${{\lambda }_{4}}(t)$ сохраняла свой знак. Такой оптимальный режим (2.6) из двух этапов (“разгон” и “торможение”) далее назовем “тривиальным”. Его существование обусловлено лишь наличием пересечения линии $\delta $ с осью $O{{x}_{1}}$. Численный анализ показывает, что чем меньше значение $\omega $, тем больших размеров (и длительности) участок в виде арки $O{{A}_{1}}$ (рис. 2). При больших $\omega $ форма линии $\delta $ меняется: сначала в верхней полуплоскости фазовая кривая совершит несколько колебаний, прежде чем заденет ось $O{{x}_{1}}$. Чем больше $\omega $, тем больше будет таких колебаний (и тем меньше их амплитуда). При этом “среднее за период” значение величины ${{x}_{2}}(t)$ постепенно убывает, так что линия $\delta $ пересечется с осью $O{{x}_{1}}$.

На рис. 2 для случая $\omega = 2$ имеем оптимальные тривиальные полутраектории $O{{A}_{1}}$ $({{T}_{1}} \approx 2.533906)$, $O{{A}_{2}}$ $({{T}_{2}} \approx 3.040895)$, $O{{A}_{3}}$ $({{T}_{3}} \approx 4.569222)$, $O{{A}_{4}}$ $({{T}_{4}} \approx 5.184146)$ и т.д. Для остальных оптимальных режимов изображающая точка на плоскости $({{x}_{1}},{{x}_{2}})$ тоже выходит из (0, 0) по линии $\delta $, но затем в некоторый момент времени сходит с нее при переключении управления. Каждая оптимальная полутраектория, согласно условию (2.5), должна завершаться на оси $O{{x}_{1}}$.

3. Анализ движений упрощенной системы в малой окрестности начального состояния. Отдельно рассмотрим оптимальное поведение объекта при повороте на малый угол $2\alpha $. Как было отмечено выше, в малой окрестности нуля линеаризация уравнений (1.1) порождает неуправляемую систему. Поэтому вместо линейного приближения (фактически вырожденного), рассмотрим нелинейное:

полагая его качественно близким к исходной системе (1.1) при малых значениях переменных.

Для такой модели в задаче оптимального быстродействия (2.1), (2.2) вид управления (2.3) и условия (2.5) остаются прежними, но упрощается гамильтониан H = λ₁x₂ + ${{\lambda }_{2}}( - {{\omega }^{2}}{{x}_{1}} + {{p}^{2}})$ + λ₃p + + λ₄u и сопряженная система

Решения первых трех уравнений с учетом замечания 2 можно записать в виде

где T – длительность полутраектории, константа интегрирования ${{с}_{1}}$ подлежит уточнению.

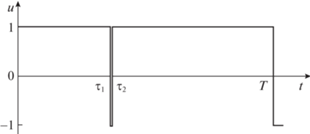
Если предположить, что функция оптимального управления (2.3) кусочно-постоянная с конечным числом моментов переключения, то четвертое уравнение (3.2) легко интегрируется на участках постоянства управления. При заданном значении T с учетом соотношений (2.5) выводится (подробности опускаем) система двух нелинейных неравенств (относительно параметров $\omega $ и ${{\tau }_{1}}$), выполнение которых гарантирует, что управление с тремя переключениями в моменты ${{\tau }_{1}}$, T, $2T - {{\tau }_{1}}$ удовлетворяет необходимым условиям оптимальности в форме (2.3), (3.2). Расчеты показывают, что для случая $\omega = 2$ эти режимы реализуются, когда ${{\tau }_{1}} > {{\tau }_{c}}$, где критическому значению ${{\tau }_{с}} \approx 1.3654$ соответствует время ${{T}_{c}} \approx 2.120637$. Для меньших параметров T оптимальное управление составится следующим образом

где ${{u}_{0}}\left( t \right)$ – особое управление, порождаемое условием ${{\lambda }_{4}}(t) \equiv 0$. Соответствующие решения системы (3.1), (3.2) (с учетом (3.3)) на каждом из трех этапов можно выписать в явной форме.

Этап 1. При $u\left( t \right) = 1$, $t \in (0,{{\tau }_{1}}]$, получим $p\left( t \right) = t$,

Этап 2. При $u\left( t \right) = - 1$, $t \in ({{\tau }_{1}},{{\tau }_{2}}]$, находим $p\left( t \right) = 2{{\tau }_{1}} - t$,

Поскольку функция (3.5) должна удовлетворить начальному ${{\lambda }_{4}}({{\tau }_{1}}) = 0$ и конечному ${{\lambda }_{4}}({{\tau }_{2}}) = 0$ условиям, то из них можно исключить константу ${{c}_{3}}$ и выразить ${{c}_{1}}$:

Этап 3. При $t \in ({{\tau }_{2}},T]$ особое управление u₀(t) определяется из условия ${{\lambda }_{4}}(t) \equiv 0$. Тождественное равенство нулю первой и второй производных функции ${{\lambda }_{4}}(t)$ по времени в силу соотношений (3.1), (3.2) даст

откуда (с учетом (3.3)) получим

Эта функция особого управления сохраняет смысл, если ее значения не нарушают ограничений $\left| u \right| \leqslant 1$. Необходимое условие оптимальности особого управления определяется неравенством Келли [10], которое в нашем случае можно представить в форме

Поскольку $\dot {p} = u$, то из (3.8) следует уравнение

которое с учетом начального условия $p({{\tau }_{2}}) = 2{{\tau }_{1}} - {{\tau }_{2}}$ имеет решение

Подставляя эту функцию во второе уравнение системы (3.1), а также используя значения ${{x}_{1}}({{\tau }_{2}})$ и ${{x}_{2}}({{\tau }_{2}})$ в конце этапа 2, можно найти в явном виде функцию

Константы интегрирования имеют вид

Из условия ${{x}_{2}}(T) = 0$ с учетом $f(T) = 0$ следует соотношение

связывающее между собой значения ${{\tau }_{1}}$, ${{\tau }_{2}}$, T. Еще одно соотношение для этих величин можно получить, подставляя выражение (3.11) в (3.9) с учетом (3.3), откуда вытекает

Приравнивая (3.6) и (3.15), получим

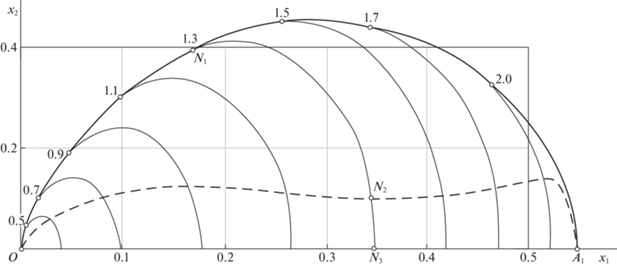
Для построения на плоскости $({{x}_{1}},{{x}_{2}})$ фазовых кривых, отвечающих трехэтапному управлению (3.4), достаточно для каждого конкретного значения ${{\tau }_{1}}$ (из диапазона $0 < {{\tau }_{1}} < {{\tau }_{c}}$) решить систему уравнений (3.13), (3.14) и (3.16), находя корни ${{\tau }_{2}}$, T, удовлетворяющие условию $T > {{\tau }_{2}} > {{\tau }_{1}}$. На рис. 3 показаны соответствующие оптимальные полутраектории системы (3.1) при $\omega = 2$. Изображающая точка движется из пункта (0, 0) при $u\left( t \right) = 1$, $t \in (0,{{\tau }_{1}}]$, по линии $\delta $ вдоль дуги $O{{J}_{1}}$ (этап 1), затем вдоль дуги ${{J}_{1}}{{J}_{2}}$ при $u\left( t \right) = - 1$, $t \in ({{\tau }_{1}},{{\tau }_{2}}]$ (этап 2), затем вдоль дуги ${{J}_{2}}{{J}_{3}}$, $t \in ({{\tau }_{2}},T]$ (этап 3), при действии особого управления (3.8). На линии $\delta $ для каждой фазовой кривой отмечены численные значения параметров ${{\tau }_{1}}$ первого переключения управления; изображенной точке ${{J}_{1}}$ соответствует ${{\tau }_{1}} = 0.9$.

Завершающие полутраектории (на рис. 3 не показаны) симметричны начальным относительно оси $O{{x}_{1}}$ и приходят в точку (0, 0), причем на каждом из трех этапов функция управления – противоположного знака. Область особых режимов на рис. 3 отделена пунктиром, а внутри этой области показаны линии с равными значениями особых управлений. В конце каждой фазовой кривой имеем значение ${{u}_{0}}(T) = 0$, что согласуется с условием ${{\lambda }_{1}}(T) = 0$ в соответствии с формулой (3.7).

Поскольку в области особых режимов неравенство (3.9) выполнено, то необходимые условия оптимальности обеспечены реализуемостью движений в силу уравнений (2.3) и (3.2). Эта реализуемость обусловлена возможностью для каждого значения ${{\tau }_{1}}$ (из диапазона $0 < {{\tau }_{1}} < {{\tau }_{c}}$) найти корни ${{\tau }_{2}}$, T системы уравнений (3.13), (3.14) и (3.16).

В использованном алгоритме с уменьшением назначаемого параметра ${{\tau }_{1}}$ убывали соответствующие величины ${{\tau }_{2}}$, T. Особый интерес (в связи с вырожденностью линеаризации для системы (3.1)) представляет предельный случай, когда ${{\tau }_{1}} \to 0$. В силу ограниченности функции p(t) в формуле (3.11) знаменатель не обращается в нуль, поэтому на этапе особого режима функция p(t) не меняет знак. Отсюда (с учетом (3.9)) следуют соотношения $2{{\tau }_{1}} - {{\tau }_{2}} > 0$ и $\omega (T - {{\tau }_{2}}) < \pi {\text{/}}2$. При достаточно малых ${{\tau }_{1}}$ и ${{\tau }_{2}}$, когда становятся приемлемыми приближения ${\text{cos}}\omega (T\, - \,{{\tau }_{2}})\, \approx \,{\text{cos}}\omega T$ + + ωτ₂sinωT  и т.п., соотношение (3.16) с сохранением компонент второго порядка малости приобретает вид

т.е. величины $\cos \omega T$ и $\cos \omega (T - {{\tau }_{2}})$ имеют разные знаки. Поскольку ${{\tau }_{2}} > {{\tau }_{1}}$, то ctgωT = = $ - \omega {{\tau }_{2}}(2 - {{\tau }_{2}}{\text{/}}{{\tau }_{1}})$ < 0, т.е. $\omega T > \pi {\text{/}}2$. Иначе говоря, при ${{\tau }_{2}} \to 0$ (и ${{\tau }_{1}} \to 0$) имеем $ctg\omega T \to 0$, что означает монотонное приближение (сверху) $T \to \pi {\text{/}}(2\omega )$. Здесь также можно показать, что в выражении для достигаемой величины угла поворота последнее (интегральное) слагаемое при ${{\tau }_{2}} \to 0$ (и ${{\tau }_{1}} \to 0$) стремится к нулю, как и первые два слагаемых. Таким образом, в пределе имеем

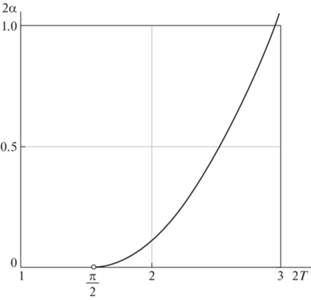
Иначе говоря, при сколь угодно малых размерах фазовых кривых, отвечающих условию ${{\tau }_{1}} \to 0$ (рис. 3), все они имеют длительность, превосходящую  $T = \pi {\text{/}}(2\omega )$. Тем самым обосновано следующее утверждение.

Замечание 3. Для системы (3.1) в задаче быстродействия (2.1), (2.2) в форме взаимной вариационной задачи (на отыскание наибольшего значения $2\alpha $ при задаваемом 2T):

1) решения не существует при $T \in \left[ {0,\;\pi {\text{/}}(2\omega )} \right]$;

2) существует критическое значение ${{T}_{c}}$, такое, что при $T \in \left( {\pi {\text{/}}(2\omega ),\;{{T}_{c}}} \right)$ оптимальное управление имеет трехэтапный вид (3.4).

На рис. 4 показана зависимость $2\alpha $ от 2T для системы (3.1) при ω = 2.

Поскольку упрощенная система (3.1) приближенно описывает поведение исходной системы (1.1) в малой окрестности нуля, то в пределе при $\alpha \to 0$ в задаче быстродействия (2.1), (2.2) тоже получим $T \to \pi {\text{/}}(2\omega )$. Говоря в терминах исходных физических переменных, при сколь угодно малом возмущении, выводящем систему (1.1) (рис. 1) из состояния покоя, понадобится времени не менее $\Delta t = \pi \sqrt {m{\text{/}}k} $ с, чтобы с помощью внешнего момента M полностью погасить колебания.

4. Численное решение задачи быстродействия (2.1), (2.2) для системы (1.1). Далее приведем результаты расчетов для системы (1.1) при конкретном значении ω = 2. Задача быстродействия (2.1), (2.2) рассматривалась в форме взаимной вариационной задачи (на отыскание наибольшего угла поворота $2\alpha $ при задаваемом времени 2T). Сценарии оптимальных движений отличались для разных диапазонов времени, которые для удобства пронумеруем римскими цифрами. Границами диапазонов оказались ранее упомянутые значения ${{T}_{i}}$, $i = 1,2,3,...$, длительностей “тривиальных” оптимальных полутраекторий $O{{A}_{i}}$, $i = 1,2,3,...$ (рис. 2).

Диапазон I: $T \in \left( {\pi {\text{/}}(2\omega ),\;{{T}_{1}}} \right)$. Как и для близкой упрощенной системы (3.1), в малой окрестности положения равновесия системы (1.1) оптимальное управление имеет вид (3.4), т.е. после участков с постоянными значениями управления $u = + 1$ и $u = - 1$ включается особое управление ${{u}_{0}}(t)$. Вид этой функции определяется тождеством ${{\lambda }_{4}}(t) \equiv 0$. Приравнивая к нулю его первую и вторую производные по времени в силу уравнений (1.1), получим

откуда выводится формула для особого управления

Эта функция сохраняет смысл, если ее значения не нарушают ограничений $\left| u \right| \leqslant 1$. Необходимое условие оптимальности особого управления определяется неравенством Келли

которое в рассматриваемой области значений ${{x}_{1}} \geqslant 0$ в силу соотношений (4.1) приобретает вид

В диапазоне I численное решение сопряженной системы осуществлялось по следующему алгоритму. Задается момент времени ${{\tau }_{1}}$ первого переключения управления, для которого ищется оптимальное продолжение траектории из точки с известными координатами ${{x}_{1}}({{\tau }_{1}})$, ${{x}_{2}}({{\tau }_{1}})$, $\varphi ({{\tau }_{1}})$, $p({{\tau }_{1}})$. Поскольку ${{\lambda }_{4}}({{\tau }_{1}}) = 0$, ${{\lambda }_{3}} \equiv 1$, то уточнению подлежат лишь значения ${{\lambda }_{1}}({{\tau }_{1}})$ и ${{\lambda }_{2}}({{\tau }_{1}})$. Они варьируются в два этапа. Сначала для каждого очередного значения ${{\lambda }_{2}}({{\tau }_{1}})$ подбирается ${{\lambda }_{1}}({{\tau }_{1}})$, чтобы при действии управления $u = - 1$ в некоторый момент времени (имеющий смысл ${{\tau }_{2}}$) выполнилось первое из равенств (4.1), т.е. система смогла войти в особый режим и далее двигаться с управлением (4.2). В момент времени (принимаемый далее за $T$), при котором верно условие ${{x}_{2}} = 0$, фиксируется значение ${{\lambda }_{1}}(T)$. Затем из множества найденных пар ${{\lambda }_{1}}({{\tau }_{1}})$, ${{\lambda }_{2}}({{\tau }_{1}})$ выбирается та, при которой обеспечивается дополнительное условие ${{\lambda }_{1}}(T) = 0$. В результате будут выполнены соотношения (2.5), свойственные оптимальным движениям. На рис. 5 на фазовой плоскости $({{x}_{1}},{{x}_{2}})$ показаны найденные оптимальные полутраектории. Типичное движение происходит сначала по дуге $O{{N}_{1}}$ при $u = + 1$, затем по дуге ${{N}_{1}}{{N}_{2}}$ при $u = - 1$. Последний участок ${{N}_{2}}{{N}_{3}}$ находится в области особых управлений, которая на рис. 5 отделена пунктирной линией.

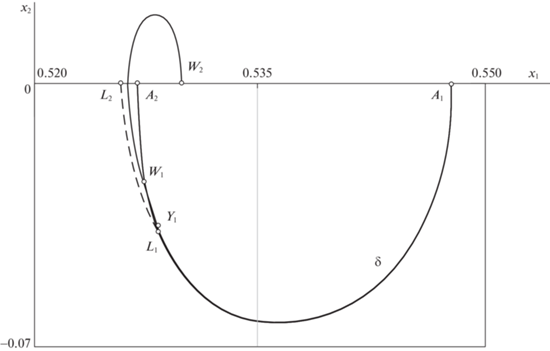
Диапазон II: $T \in \left( {{{T}_{1}},\;{{T}_{2}}} \right)$. Поскольку в конце предыдущего диапазона I точка первого переключения управления на дуге $O{{A}_{1}}$ приближалась вплотную к пункту ${{A}_{1}}$, то из соображений непрерывности можно было бы ожидать, что далее фазовые кривые будут отделяться от линии $\delta $ в точках “петлеобразной” дуги ${{A}_{1}}{{A}_{2}}$ (рис. 2). Однако анализ показывает, что ни из одной точки этой дуги не существует продолжений, которые завершались бы на оси $O{{x}_{1}}$ за время $T \in \left( {{{T}_{1}},\;{{T}_{2}}} \right)$. В конце диапазона I на графике функции u(t) оптимального управления параметры ${{\tau }_{1}}$, ${{\tau }_{2}}$, T сблизились до совпадения, дав в итоге режим с одним моментом переключения T. Далее непрерывная эволюция этой функции, как оказалось, происходит за счет “игольчатой вариации”, т.е. путем добавления двух новых сколь угодно близких моментов переключения ${{\tau }_{2}} \to {{\tau }_{1}} + 0$ (рис. 6), где ${{\tau }_{1}} \approx 0.9043$. При таком управлении на фазовой плоскости $({{x}_{1}},{{x}_{2}})$ (рис. 7) изображающая точка из положения ${{F}_{1}}$ сходит с дуги $O{{A}_{1}}$ при $u = - 1$, но после быстрого второго переключения в точке ${{F}_{2}}$ продолжает движение при $u = + 1$ до оси $O{{x}_{1}}$ сколь угодно близко к дуге $O{{A}_{1}}$. С дальнейшим увеличением длительности T на графике функции u(t) “зазор” $({{\tau }_{2}} - {{\tau }_{1}})$ растет и смещается вправо. Наибольшая разность $({{\tau }_{2}} - {{\tau }_{1}}) \approx 0.052$ достигается при ${{T}_{*}} \approx 2.773$. Это значение ${{T}_{*}}$ является пороговым в том смысле, что при $T \in \left( {{{T}_{1}},{{T}_{*}}} \right)$ оптимальные фазовые кривые попадают на ось $O{{x}_{1}}$, не заходя в нижнюю полуплоскость, а при $T \in \left( {{{T}_{*}},{{T}_{2}}} \right)$ кривые имеют завершающий “петлеобразный” фрагмент в нижней полуплоскости, т.е. дважды пересекают ось. На рис. 7 значению ${{T}_{*}}$ соответствует первое переключение при ${{\tau }_{1}} \approx 1.085$ в точке ${{H}_{1}}$, второе – в точке ${{H}_{2}}$, после чего полутраектория завершается в точке ${{H}_{3}}$. При $T \to {{T}_{2}}$ вновь $({{\tau }_{2}} - {{\tau }_{1}}) \to 0$, и при ${{\tau }_{1}} \approx 1.452$ в точке ${{S}_{1}}$ почти одновременно следует второе переключение в точке ${{S}_{2}}$, так что далее изображающая точка движется близко к дуге $O{{A}_{2}}$, заходя на ось $O{{x}_{1}}$ снизу вдоль “петли” ${{A}_{1}}{{A}_{2}}$. Эволюция графика функции $u(t)$ завершается тем, что на нем исчезает “игольчатая вставка”. На рис. 7 пунктирная дуга ${{F}_{2}}{{S}_{2}}$ является линией второго переключения управления.

В диапазоне II численное решение сопряженной системы осуществлялось путем задания моментов времени ${{\tau }_{1}}$ первого переключения управления, для каждого из которых (при известных значениях переменных ${{x}_{1}}({{\tau }_{1}})$, ${{x}_{2}}({{\tau }_{1}})$, $\varphi ({{\tau }_{1}})$, $p({{\tau }_{1}})$, ${{\lambda }_{4}}({{\tau }_{1}}) = 0$, ${{\lambda }_{3}} \equiv 1$) варьировались величины ${{\lambda }_{1}}({{\tau }_{1}})$ и ${{\lambda }_{2}}({{\tau }_{1}})$ с целью достижения условий ${{\lambda }_{1}} = 0$ и ${{\lambda }_{4}} = 0$ в момент попадания изображающей точки на ось $O{{x}_{1}}$. Этот момент времени далее принимался за $T$.

Диапазон III: $T \in \left( {{{T}_{2}},\;2{{T}_{2}} - {{T}_{1}}} \right)$. На рис. 8 в измененном масштабе показан участок ${{A}_{1}}{{A}_{2}}$ линии $\delta $ (рис. 2), лежащий ниже оси $O{{x}_{1}}$. Если переключение управления (после движения по линии $\delta $ при $u = + 1$) произойдет непосредственно перед точкой ${{A}_{2}}$, то длительность всей полутраектории слегка превысит ${{T}_{2}}$. Такое оптимальное движение (из точек дуги ${{A}_{2}}{{Y}_{1}}$ до оси $O{{x}_{1}}$) реализуется, как показывают расчеты, при действии особого управления. Крайней точке ${{Y}_{1}}$ дуги ${{A}_{2}}{{Y}_{1}}$ соответствует наименьший параметр ${{\tau }_{1}} \approx 2.9555$ и наибольшая длительность полутраектории ${{T}_{Y}} \approx 3.0828$. Поскольку особый режим наступает сразу в момент ${{\tau }_{1}}$, то для него известны не только значения ${{x}_{1}}({{\tau }_{1}})$, ${{x}_{2}}({{\tau }_{1}})$, $\varphi ({{\tau }_{1}})$, $p({{\tau }_{1}})$, ${{\lambda }_{4}}({{\tau }_{1}}) = 0$, ${{\lambda }_{3}} \equiv 1$, но и ${{\lambda }_{2}}({{\tau }_{1}})$, находимое из первого уравнения (4.1). Поэтому для численного интегрирования системы уравнений (1.1) и (2.4) достаточно подобрать величину ${{\lambda }_{1}}({{\tau }_{1}})$, варьируя ее из условия равенства нулю переменной ${{\lambda }_{1}}(t)$ в момент попадания изображающей точки на ось $O{{x}_{1}}$.

Найденные численно начальные значения особых управлений ${{u}_{0}}({{\tau }_{1}})$ (при сходе изображающих точек с дуги ${{A}_{2}}{{Y}_{1}}$ на рис. 8) уменьшаются от 0 (в точке ${{A}_{2}}$) до $ - 1$ (в точке ${{Y}_{1}}$). При дальнейшем смещении точки первого переключения по дуге ${{Y}_{1}}{{L}_{1}}$ оптимальное управление имеет структуру (3.4), т.е. этапу особого управления предшествует участок движения при $u = - 1$. Крайней точке ${{L}_{1}}$ дуги ${{Y}_{1}}{{L}_{1}}$ соответствует наименьший параметр ${{\tau }_{1}} \approx 2.9517$, наибольшая длительность полутраектории ${{T}_{L}} \approx 3.1632$ и наименьшая координата точки ${{L}_{2}}$ на оси $O{{x}_{1}}$ (рис. 8). Численный алгоритм решения сопряженной системы (2.4) здесь такой же, как и для трехэтапных управлений в диапазоне I.

Расчеты показывают, что при смещении точки первого переключения вдоль дуги ${{Y}_{1}}{{L}_{1}}$ к концу ${{L}_{1}}$ длительность $(T - {{\tau }_{2}})$ промежутка особого управления убывает вплоть до нуля, так что на рис. 8 движение по кривой ${{L}_{1}}{{L}_{2}}$ реализуется фактически при постоянном управлении $u = - 1$. Дальнейшему увеличению времени $T$ в рассматриваемом диапазоне III соответствуют функции оптимального управления с одним переключением на полутраектории. Точка переключения на дуге ${{L}_{1}}{{A}_{2}}$ смещается от ${{L}_{1}}$ к ${{A}_{2}}$ (с увеличением параметра ${{\tau }_{1}}$), причем фазовые кривые дважды пересекают ось $O{{x}_{1}}$, совершив “разворот” в верхней полуплоскости. Одна из таких кривых показана на рис. 8 в виде ${{W}_{1}}{{W}_{2}}$. Если первое переключение осуществить в точке ${{A}_{2}}$ (при ${{\tau }_{1}} = {{T}_{2}}$), то соответствующий “разворот” произойдет по линии, симметричной дуге ${{A}_{1}}{{A}_{2}}$, за такое же время (${{T}_{2}} - {{T}_{1}}$). Этот сценарий будет последним в диапазоне III.

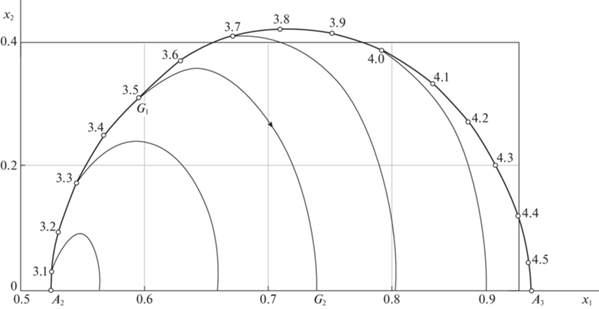
Диапазон IV: $T \in \left( {2{{T}_{2}} - {{T}_{1}},\;{{T}_{3}}} \right)$. Расчеты показывают, что каждая точка дуги ${{A}_{2}}{{A}_{3}}$ может послужить точкой единственного переключения оптимального управления, после чего фазовая кривая при $u = - 1$ достигнет оси $O{{x}_{1}}$. Численное решение сопряженной системы осуществляется путем задания параметра ${{\tau }_{1}}$ и (при известных ${{x}_{1}}({{\tau }_{1}})$, ${{x}_{2}}({{\tau }_{1}})$, $\varphi ({{\tau }_{1}})$, $p({{\tau }_{1}})$, ${{\lambda }_{4}}({{\tau }_{1}}) = 0$, ${{\lambda }_{3}} \equiv 1$) варьирования величин ${{\lambda }_{1}}({{\tau }_{1}})$ и ${{\lambda }_{2}}({{\tau }_{1}})$ с целью достижения условий ${{\lambda }_{1}} = 0$ и ${{\lambda }_{4}} = 0$ в момент времени, при котором ${{x}_{2}}(t) = 0$. На рис. 9 на фазовой плоскости $({{x}_{1}},{{x}_{2}})$ показаны завершающие участки оптимальных полутраекторий, начатых из точки (0, 0) вдоль линии $\delta $. Например, участку ${{G}_{1}}{{G}_{2}}$ соответствует первое переключение в точке ${{G}_{1}}$ в момент ${{\tau }_{1}} = 3.5$.

Рассмотренные в диапазонах II–IV сценарии далее повторяются для аналогичных по расположению участков линии $\delta $ (рис. 2). Например, диапазон V (при $T \in \left( {{{T}_{3}},\;{{T}_{4}}} \right)$) аналогичен диапазону II, т.е. эволюция функции оптимального управления претерпевает те же этапы появления “игольчатой вставки”, ее расширения и сужения вплоть до исчезновения. Диапазон VI (при $T \in \left( {{{T}_{4}},\;2{{T}_{4}} - {{T}_{3}}} \right)$) качественно повторяет диапазон III и т.д.

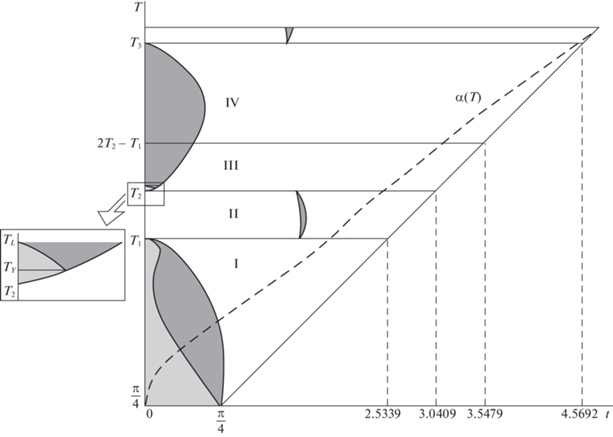
Поскольку для всех рассмотренных типов движений системы (1.1) были численно найдены решения сопряженной системы (2.4), то сами траектории удовлетворяют необходимым условиям оптимальности. Задача (2.1), (2.2) решалась в форме взаимной вариационной задачи (на отыскание наибольшего угла поворота $2\alpha $ за заданное время 2T). Множество функций оптимального управления (в зависимости от T) можно наглядно представить в виде диаграммы [11]. Ее суть в том (рис. 10), что каждое горизонтальное сечение (на высоте T) описывает одну функцию u(t), $t \in \left[ { - T,\,\,T} \right]$, где длины отрезков белого (или серого) цвета численно равны длительности участков движения при $u = - 1$ (или $u = + 1$). Участки светло-серого цвета соответствуют особым управлениям. Разделительные горизонтали (например, на высоте $T = {{T}_{1}}$, $T = {{T}_{2}}$ и т.д.) и римские номера между ними введены для указания диапазонов I–IV, рассмотренных выше. На рис. 10 показана правая (зеркальная) часть диаграммы, задающая правые части графиков u(t), $t \in \left[ {0,\,\,T} \right]$. Согласно замечанию 2, функция u(t), $t \in \left[ { - T,\,\,T} \right]$, нечетная, поэтому левая (не изображенная) часть диаграммы будет симметричной, но с заменой цветов на противоположные (как фотонегатив). Например, при $T = {{T}_{i}}$, $i = 1,2,3...$, сечения имеют вид отрезков белого цвета, т.е. $u(t) = - 1$ при $t \in \left[ {0,\,\,T} \right]$. В левой зеркальной части диаграммы соответствующие отрезки – темно-серого цвета, т.е. $u(t) = + 1$ при $t \in \left[ { - T,\,\,0} \right]$. Говоря кратко, при $T = {{T}_{i}}$, $i = 1,2,3...$, имеем режимы с одним переключением управления, названные выше “тривиальными”. В полосе с номером II располагается закрашенная область в форме чечевицы, соответствующая “вставке” в графике функции u(t) в диапазоне II. Ее самому широкому сечению (на горизонтальном уровне ${{T}_{*}}$) отвечает время движения от точки H₁ до H₂ на рис. 7. В диапазоне V, который изображен лишь частично, у аналогичной “чечевицы” максимальная ширина больше.

С диаграммой функций оптимального управления (рис. 10) совмещена пунктирная кривая, задающая график $\alpha (T)$ искомой зависимости наибольшей величины угла поворота от заданного времени движения, отложенного по вертикали.

Заключение. Рассмотрена задача оптимального по быстродействию поворота (на заданный угол) пружинного маятника (рис. 1) из одного состояния покоя в другое. Исследование осуществлено в форме взаимной вариационной задачи на максимум угла поворота при заданном времени. С учетом симметрий дифференциальных уравнений движения и сопряженной системы, связанных с симметриями краевых условий, получены численные решения, удовлетворяющие необходимым условиям оптимальности. Множество функций оптимального управления отражено на диаграмме (рис. 10).

Особенность нелинейной системы (1.1) состоит в том, что ее линеаризованная (в окрестности состояния покоя) модель не является управляемой. Поэтому для малых значений времени обратная вариационная задача не имеет решения. Для любого сколь угодно малого угла поворота требуется время, превышающее значение $\pi {\text{/}}(2\omega )$. Геометрически это означает, что множество достижимости $K(T)$ [12, с. 78] для точки $O\left( {0,0,{\text{\;}}0,0} \right)$ системы (1.1) при малых T не содержит $\varepsilon $-окрестности нуля. С увеличением значения T в диапазоне $T \in \left( {0,\;\pi {\text{/}}(2\omega )} \right)$ множество $K(T)$ расширяется по обе стороны гиперплоскости ${{x}_{2}} = 0$, имея с ней лишь одну общую точку O. Первое пересечение множества достижимости с гиперплоскостью происходит при $T = \pi {\text{/}}(2\omega )$. Для обнаружения этих свойств использовалось явное интегрирование упрощенной нелинейной системы (3.1). Это приближение в малой окрестности нуля не совпадает с “квадратичным”, однако, в отличие от него, дает решение сопряженной системы в элементарных функциях. Численные эксперименты подтвердили близость оптимальных траекторий систем (1.1) и (3.1) для малых углов поворота объекта.