Известия РАН. Теория и системы управления, 2023, № 5, стр. 16-42
БЫСТРОДЕЙСТВИЕ ГРУППЫ УПРАВЛЯЕМЫХ ОБЪЕКТОВ
a Московский авиационный институт (национальный исследовательский ун-т)
Москва, Россия
b МИСиС (национальный исследовательский технологический ун-т)
Москва, Россия
* E-mail: asbortakov@mail.ru
Поступила в редакцию 12.04.2023
После доработки 21.04.2023
Принята к публикации 05.06.2023
- EDN: OECKJA
- DOI: 10.31857/S0002338823050049
Аннотация
Рассматривается задача быстродействия группы управляемых объектов, начальное состояние каждого из которых задано, а конечное – выбирается из фиксированного набора возможных терминальных состояний (целей). Для каждого объекта требуется назначить цель и найти управление, обеспечивающее одновременное достижение группой всех выбранных целей за наименьшее время. Поскольку оптимальные по быстродействию управления отдельными объектами не решают задачу группового быстродействия, применяются так называемые минимально опаздывающие траектории. Разработана методика решения поставленной задачи, которая включает алгоритм решения минимаксной задачи назначения, процедуру использования оптимальных и минимально опаздывающих траекторий. Решена задача быстродействия группы объектов, плоское движение которых представляется траекториями Маркова–Дубинса.
Введение. Задачи группового управления имеют многочисленные приложения, в том числе при управлении подвижными объектами [1–3], в частности летательными аппаратами [4–9]. Постановки задач группового управления подвижными объектами весьма разнообразны [10]. Например, задачи сбора группы в заданной области [4], обход препятствий [2, 4, 8], перехват подвижной цели [11], управление в конфликтной среде [12]. Управляемыми динамическими системами служат математические модели роботов, летательных аппаратов, надводные и подводные корабли. Для моделирования движения беспилотных летательных аппаратов (БПЛА) [13] нередко используется модель Маркова–Дубинса [14–16] или ее обобщения [17, 18].
В статье рассматривается задача одновременного достижения точечных целей группой подвижных объектов за наименьшее время. Решение задачи проводится в несколько этапов.
На первом этапе для каждого объекта управления определяется такая цель из множества заданных, чтобы максимальное время движения всех объектов группы до целей было минимальным. Иначе говоря, находится минимальное время (рекорд) одновременного достижения всех целей. Для этого решается задача минимаксного назначения [19–21 ] или, что то же самое, линейная задача о назначениях узких мест [22, 23].
На втором этапе выясняется существование траекторий, приводящих объекты управления в назначенные цели в рекордное время. Все объекты группы делятся на “дальние” и “ближние”. “Дальние” объекты должны двигаться к своим целям оптимальным по быстродействию образом. Для них рекордное время совпадает с минимальным. Напротив, для каждого “ближнего” объекта рекордное время больше минимального. Поэтому движение “ближних” объектов не должно быть оптимальным, чтобы они не опередили “дальние”. Замедление “ближних” объектов можно выполнить разными способами. В [8] предлагается удлинять траектории, объединяя участки кратчайших путей. В [9] траектория дополняется начальным участком с неоптимальным (либо антиоптимальным, либо нейтральным) управлением. Так или иначе, получаются неопаздывающие траектории, которые приводят “ближние” объекты в конечное состояние в рекордное (но неоптимальное для них) время. Такие траектории являются субоптимальными. Как правило, они определяются либо неоднозначно, либо вообще не существуют. Если неопаздывающие траектории находятся для всех “ближних” объектов, то задача группового быстродействия решена. Если для некоторых объектов нет неопаздывающих траекторий, то повторяем двухэтапную процедуру. Снова решаем задачу минимаксного назначения (первый этап), но уже не для оптимальных, а так называемых минимально опаздывающих траекторий. Затем для нового назначения проверяем существование неопаздывающих траекторий (второй этап), но уже для нового рекорда, который хуже предыдущего. В результате итерационной процедуры либо находится решение задачи группового быстродействия, либо рекорд превысит максимально допустимое значение.
Предлагаются алгоритмы решения минимаксной задачи назначения, нахождения минимально опаздывающих траекторий, решения задачи группового быстродействия. Эффективность предлагаемых алгоритмов демонстрируется на примерах быстродействия группы объектов, плоское движение которых представляется траекториями Маркова–Дубинса.
В [8, 24, 25] рассматриваются более сложные задачи назначения для БПЛА, учитывающие препятствия, противодействие противника, периодичность попадания в цель и т.п. При этом, как правило, применяются эвристические алгоритмы или “ручная доводка” запланированных траекторий до попадающих в реальных условиях.
1. Постановки задач. Проблема оптимального по быстродействию управления группой подвижных объектов имеет комплексный характер и может быть представлена как совокупность задач оптимального управления, параметрической и дискретной оптимизации. Рассмотрим постановки соответствующих задач.
Задача минимаксного назначения (линейная задача назначения узких мест). Пусть имеется M подвижных объектов и $N$ пунктов назначения (целей), причем $N \geqslant M$. Формально для каждого объекта выбирается свой пункт назначения (без повторения номеров цели), при этом в некоторые цели подвижные объекты не будут направлены. Фактически некоторые цели могут совпадать, поэтому в них будут направлены несколько объектов. В частности, если все N целей совпадают, то получается задача сбора группы M объектов в одном месте.
Пусть известно время Tij передвижения i-го объекта в j-й пункт назначения, $i = 1,...,M$; $j = 1,...,N$. Каждому объекту ставится в соответствие свой пункт назначения: первому объекту – j1-я цель, второму – j2-я цель и т.д., последнему – jM-я цель, причем номера целей попарно не совпадают. Такое паросочетание называется назначением [26] и обозначается $({{j}_{1}},...,{{j}_{M}})$. Заметим, что назначение представляет собой размещение (без повторений) M чисел из N возможных. Качество назначения $({{j}_{1}},...,{{j}_{M}})$ характеризуется временем достижения всех целей:
Требуется найти минимальное значение T* функции (1.1) и оптимальное назначение $(j_{1}^{*},...,j_{M}^{*})$, на котором это значение достигается:
(1.2)
$T{\kern 1pt} * = \mathop {\min }\limits_{({{j}_{1}},...,{{j}_{M}})} T({{j}_{1}},...,{{j}_{M}}) = \mathop {\min }\limits_{({{j}_{1}},...,{{j}_{M}})} \mathop {\max }\limits_{i = 1,...,M} {{T}_{{i\,{{j}_{i}}}}}.$Минимизация проводится по всем размещениям $({{j}_{1}},...,{{j}_{M}})$ по M чисел из N возможных.
Отметим, что полный перебор всех размещений по M объектов из N возможных составляет $N!{\text{/}}(N - M)!$ вариантов. Наибольшее количество вариантов N! получается при M = N, когда количество подвижных объектов совпадает с количеством целей.
Для решения задачи назначения разработаны разные алгоритмы [25], в том числе пороговый алгоритм [27] и алгоритм последовательных приращений [28]. Метод ветвей и границ реализуется в предлагаемом алгоритме (см. Приложение). В нем не используются вспомогательные булевы матрицы, задающие назначение, в отличие от [21]. Для групп с небольшим количеством объектов управления алгоритм оказался вполне эффективным.
В результате решения задачи (1.2) определяются “дальние” и “ближние” подвижные объекты. Время движения “дальних” объектов до цели равно T*, а время движения “ближних” – меньше T*.
Задача группового быстродействия. Пусть на промежутке времени $[0,T]$ движение группы объектов управления описывается уравнениями
где ${{x}_{i}}(t)$ и ${{u}_{i}}(t)$ – состояние и управление i-го объекта в момент времени $t \in T$, ${{x}_{i}}(t) \in X = {{\mathbb{R}}^{{{{n}_{i}}}}}$; ${{u}_{i}}(t) \in {{U}_{i}} \subset {{\mathbb{R}}^{{{{m}_{i}}}}}$, Ui – заданное множество допустимых значений управления, $i = 1,...,M$. Функции fi непрерывны вместе с градиентами $\partial {{f}_{i}}{\text{/}}\partial {{x}_{i}}$.Начальное состояние каждого объекта группы задано:
Конечное состояние каждого объекта выбирается из множества целей $\{ {{z}_{1}},...,{{z}_{N}}\} $:
Номера целей попарно различные, т.е. ${{j}_{i}} \ne {{j}_{k}}$, если $i \ne k$. Иначе говоря, упорядоченный набор $({{j}_{1}},...,{{j}_{M}})$ представляет собой размещение (без повторений) по M чисел из N возможных, причем $M \leqslant N$. Конечные условия (1.5) определяют “точечные” цели, фиксируя тем самым правые концы траекторий подвижных объектов. Заметим, что сами цели в множестве $\{ {{z}_{1}},...,{{z}_{N}}\} $ не обязательно различные. Например, равенство ${{z}_{1}} = {{z}_{2}}$ (при M = N) означает, что в эту цель должны попасть два объекта группы. В частности, если все цели совпадают, то получаем задачу о сборе группы в одном месте в одно и то же время. Конечные условия (1.5) попадания в “точечные” цели можно заменить условиями достижения терминальных поверхностей. В этом случае правые концы траекторий становятся подвижными [29, 30].
Допустимым процессом управления $i$-м объектом считаем абсолютно непрерывную траекторию ${{x}_{i}}( \cdot )$ и ограниченное измеримое управление ${{u}_{i}}( \cdot )$, удовлетворяющие почти всюду на [0, T] дифференциальному уравнению (1.3) с терминальными условиями (1.4), (1.5). Допустимый процесс управления группой составляется из допустимых процессов управления всеми ее объектами.
Требуется определить назначение целей (1.5) и найти допустимые процессы управления объектами, при которых время T одновременного достижения всех целей будет минимальным. Иначе говоря, требуется решить задачу группового быстродействия
Как отмечалось выше, по результату $T{\kern 1pt} *$ (см. (1.2)) решения задачи назначения все объекты можно разделить на “дальние” и “ближние”. Время оптимального движения “дальних” объектов до цели равно T*, а время оптимального движения “ближних” – меньше T*. Поэтому движение “ближних” объектов необходимо замедлить. Для этого вместо оптимального управления нужно применить такое субоптимальное управление, при котором время движения цели окажется равным T*.
Задача быстродействия одного объекта. Она является частным случаем задачи группового быстродействия. Запишем кратко постановку задачи, опуская индекс $i$ – номер объекта:
Здесь x(t) и u(t) – состояние и управление в момент времени $t \in [0,T]$, $x(t) \in X = {{\mathbb{R}}^{n}}$; $u(t) \in U \subset {{\mathbb{R}}^{m}}$, $U$ – заданное множество допустимых значений управления. Постановка задачи (1.9) – классическая [31]. Возможно изменение терминальных условий. Например, вместо конечного состояния в (1.8) определить окончание процесса управления первым достижением терминальной поверхности $\Gamma $, заданной уравнением
где $\Gamma :[0, + \infty ) \times {{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{r}}$ – вектор-функция.Задача о множестве моментов достижения цели. Для управляемой системы (1.7) моментом достижения цели (заданного конечного состояния) будем называть момент времени T, для которого существует траектория системы, удовлетворяющая терминальным условиям (1.8). Иначе говоря, момент достижения – это допустимое время окончания процесса управления. Например, время T0 (решение задачи быстродействия (1.9)) является моментом достижения, причем наименьшим. В задаче о множестве моментов достижения цели требуется найти все возможные моменты достижения заданного конечного состояния, т.е. определить множество $\mathbb{T} = \mathbb{T}({{x}_{0}}\,{\text{|}}\,{{x}_{T}})$ допустимых моментов окончания процессов управления.
Заметим, что поставленная задача будет в некотором смысле двойственной к задаче нахождения множества достижимости. В самом деле, множество достижимости $\mathbb{X}(T\,{\text{|}}\,{{x}_{0}})$ образуют все возможные состояния x(T) управляемой системы в заданный момент времени T. Множество $\mathbb{T} = \mathbb{T}({{x}_{0}}\,{\text{|}}\,{{x}_{T}})$ составляют все возможные моменты достижения заданного состояния ${{x}_{T}}$. Из определений этих множеств следует равносильность включений
В постановке задачи о моментах достижения цели конечное состояние системы фиксировано. Возможны другие условия окончания, например достижение терминальной поверхности, заданной уравнением (1.10). В этом случае левый конец траектории фиксирован первым равенством в (1.8), правый – подвижный, а множество $\mathbb{T} = \mathbb{T}({{x}_{0}}\,{\text{|}}\,\Gamma )$ моментов достижения цели зависит от терминальной поверхности. Возможны и другие терминальные условия [29], например условия периодичности.
Задача минимизации опоздания. Рассмотрим задачу быстродействия (1.7)–(1.9) с дополнительным условием
где ${{T}_{*}}$ – заданное минимальное допустимое время достижения конечного состояния (цели). Не меняя решения задачи (1.7)–(1.9), функционал (1.9) можно переписать в видеВеличина $\Delta T$ равна опозданию системы при достижении ее конечного состояния по сравнению с “желаемым” временем окончания ${{T}_{*}}$. Поэтому задачу (1.12) с условием (1.11) можно назвать задачей минимизации опоздания (к назначенному сроку ${{T}_{*}}$), а искомое управление – минимально опаздывающим.
В зависимости от величины ${{T}_{*}}$ минимально опаздывающее управление имеет разный смысл. В самом деле, при ${{T}_{*}} = 0$ минимально опаздывающее управление является оптимальным по быстродействию. Такое же управление получаем при ${{T}_{*}} \leqslant {{T}_{0}}$, где T0 – решение задачи быстродействия (1.7)–(1.9). Действительно, в этом случае ограничение $T \geqslant {{T}_{*}}$ не оказывает влияния на решение задачи, так как выполняется автоматически, поскольку $T \geqslant {{T}_{0}}$.
Если ${{T}_{*}} > {{T}_{0}}$, то возможны два варианта: либо опоздание равно нулю, либо нет. В первом случае $T = {{T}_{*}}$, т.е. существует неопаздывающее управление, при котором система попадает в заданное конечное состояние в заданный момент времени ${{T}_{ * }}$. Заметим, что неопаздывающее управление обычно определяется неоднозначно. Его можно получить, если немного “ухудшить” оптимальное управление. Например, для подвижных объектов с регулируемой скоростью движения можно уменьшить величину оптимальной скорости, которая, как правило, максимально допустимая. Аналогичное уменьшение возможно для оптимальной (максимальной) тяги двигателя. Однако на практике встречаются подвижные объекты с нерегулируемой скоростью или с фиксированным ускорением. Например, это БПЛА с реактивным двигателем постоянной тяги, некоторые типы космических аппаратов и др. Для таких объектов нахождение неопаздывающего управления сложнее, чем оптимального, а иногда вообще невозможно.
Во втором случае опоздание ненулевое, т.е. $T > {{T}_{*}}$. Это означает, что неопаздывающей траектории, для которой $T = {{T}_{*}}$, не существует, а минимально опаздывающее управление является условно оптимальным, т.е. оптимальным по быстродействию с дополнительным условием (1.11).
Задача минимизации опоздания связана с задачей о времени достижения цели. Действительно, если известно множество $\mathbb{T} = \mathbb{T}({{x}_{0}}\,{\text{|}}\,{{x}_{T}})$ моментов достижения цели ${{x}_{T}}$, то минимально опаздывающему управлению для заданного значения ${{T}_{*}}$ соответствует момент
(1.13)
$T = \min \{ T \in \mathbb{T}({{x}_{0}}\,{\text{|}}\,{{x}_{T}})\,{\text{|}}\,T \geqslant {{T}_{*}}\} $Если ${{T}_{*}} \in \mathbb{T}({{x}_{0}}\,{\text{|}}\,{{x}_{T}})$, то существует субоптимальное управление, приводящее в состояние $x({{T}_{*}}) = {{x}_{T}}$. Если ${{T}_{*}}_{ * } \notin \mathbb{T}({{x}_{0}}\,{\text{|}}\,{{x}_{T}})$, то минимально опаздывающему управлению соответствует минимальное время $T \in \mathbb{T}({{x}_{0}}\,{\text{|}}\,{{x}_{T}})$, удовлетворяющее неравенству $T \geqslant {{T}_{*}}$, что и записано в (1.13).
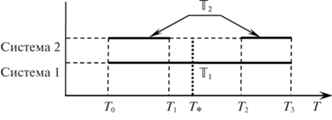
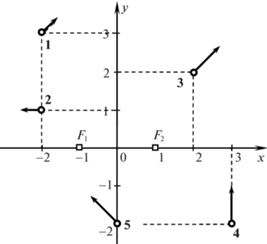
На рис. 1 полужирными линиями изображены множества ${{\mathbb{T}}_{1}} = [{{T}_{0}},{{T}_{3}}]$ и ${{\mathbb{T}}_{2}} = [{{T}_{0}},{{T}_{1}}] \cup [{{T}_{2}},{{T}_{3}}]$ моментов достижения целей для двух систем соответственно, а пунктирной линией – назначенный срок ${{T}_{*}}$. Поскольку ${{T}_{*}} \in {{\mathbb{T}}_{1}}$, первая система может попасть в конечное состояние в момент ${{T}_{*}}$. Значит, существует неопаздывающее управление, приводящее систему 1 в заданное конечное состояние в момент ${{T}_{*}}$.
Вторая система, напротив, не может достигнуть заданного конечного состояния в момент ${{T}_{*}}$, так как ${{T}_{*}} \notin {{\mathbb{T}}_{2}}$. Неопаздывающей траектории нет, но минимально опаздывающая траектория существует. Время движения до цели с минимальным опозданием равно T2.
2. Условия оптимальности для задачи быстродействия одного объекта. Задача быстродействия (1.7)–(1.9) относится к классическим задачам оптимального управления. Для ее решения применяем принцип максимума Понтрягина [31]. Составляем функцию Гамильтона–Понтрягина (ГП)
где $\psi = ({{\psi }_{1}},...,{{\psi }_{n}})$ – набор вспомогательных переменных, которые удовлетворяют сопряженной системе уравненийИз условия максимума функции ГП по управлению выражаем оптимальное управление
Составляем краевую задачу для уравнений (1.7), (2.2), дополняя дифференциальные уравнения краевыми условиями (1.8) и равенством $H(\psi (T),T,x(T),u(T)) = 0$, которое следует из условия трансверсальности.
Таким образом, задача быстродействия одного подвижного объекта сведена к двухточечной краевой задачи для системы 2n дифференциальных уравнений. Методы численного решения таких задач рассматриваются в [29, 32].
Заметим, что для получения исходных данных для задачи назначения (см. разд. 1) нужно определить минимальное время ${{T}_{{ij}}}$ достижения i-м объектом j-й цели, $i = 1,...,M$; $j = 1,...,N$. Для этого приходится решать MN задач быстродействия. Такая процедура значительно упрощается, если модель движения объекта управления простая и оптимальное управление известно.
Пример 1. Пусть на промежутке $[0,T]$ движение системы описывается уравнениями модели Маркова–Дубинса [14–16]
(2.4)
$\dot {x}(t) = V\cos \varphi (t),\quad \dot {y}(t) = V\sin \varphi (t),\quad \dot {\varphi }(t) = \omega (t),$Начальное состояние и конечное положение системы заданы
Отметим, что в конечный момент времени направление $\varphi (T)$ движения не задано, т.е. речь идет о достижении заданной точки $F({{x}_{F}},{{y}_{F}})$ на координатной плоскости.
Требуется найти наименьшее значение времени T и оптимальное управление $\omega ( \cdot )$, на котором оно достигается, т.е. решить задачу быстродействия
Можно сказать, что поставлена задача наискорейшего попадания в точечную цель.
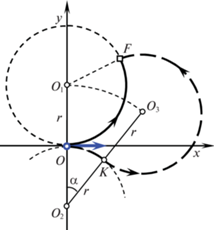
Решение этой задачи известно [14, 33]. Его можно получить, применяя принцип максимума Понтрягина [31]. Оптимальное управление оказывается кусочно-постоянным с одним переключением, причем $\omega (t) \in \{ 0,\; \pm \Omega \} $. Оптимальные траектории на плоскости $Oxy$ представляют собой гладкое соединение либо двух дуг окружностей (траектория типа CC (рис. 2)), либо дуги окружности и отрезка (траектория типа $CL$ (рис. 3, 4)). Приведем оптимальные траектории для нулевого начального состояния ${{x}_{0}} = 0$, ${{y}_{0}} = 0$, ${{\varphi }_{0}} = 0$. Без ограничения общности будем считать, что конечное положение системы – точка $F({{x}_{F}},{{y}_{F}})$ находится в верхней полуплоскости $y \geqslant 0$.
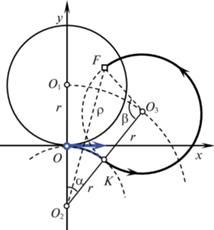
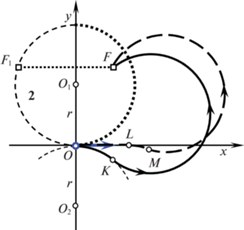
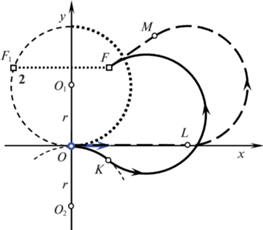
Если цель $F$ находится внутри окружности радиуса $r = V{\text{/}}\Omega $ с центром в точке ${{O}_{1}}(0,r)$, то оптимальной будет траектория типа CC. Если вне этой окружности, то оптимальной будет траектория типа $CL$. Типичные траектории CC и $CL$ представлены на рис. 2–4 соответственно. Начальное состояние и направление начальной скорости показано полужирным вектором, приложенным к началу координат, конечные положения отмечены квадратиками F, направление движения по траекториям указывается стрелками. Заметим, что $r = V{\text{/}}\Omega $ – наименьший допустимый радиус поворота.
Вычислим время ${{T}_{0}}$ движения по оптимальной траектории CC. Пусть K – точка гладкого соединения дуг окружностей с центрами ${{O}_{2}}$ и ${{O}_{3}}$. Обозначим через $\rho $ длину отрезка ${{O}_{2}}F$, а через $\alpha $ – угловую меру дуги $OK$. Тогда из треугольника ${{O}_{2}}{{O}_{3}}F$ получаем
Величина $\alpha $ равна сумме углов
(2.6)
$\alpha = \angle {{O}_{1}}{{O}_{2}}{{O}_{3}} = \angle {{O}_{1}}{{O}_{2}}F + \angle {{O}_{3}}{{O}_{2}}F = \arcsin \frac{{{{x}_{F}}}}{\rho } + \arccos \frac{{3{{r}^{2}} + {{\rho }^{2}}}}{{4r\rho }}.$Время движения находится следующим образом:
(2.7)
${{T}_{0}} = \frac{{\alpha r + (2\pi - \beta )r}}{V} = \frac{{2\pi + \alpha - \beta }}{\Omega }.$Подчеркнем, что у оптимальной траектории CC угловая величина дуги второй окружности (с центром ${{O}_{3}}$) больше $\pi $. Это обстоятельство окажется важным для построения субоптимальных траекторий.
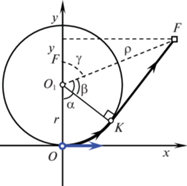
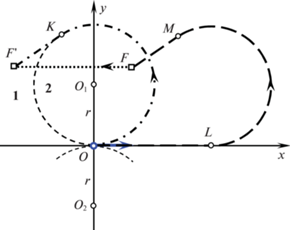
Вычислим время ${{T}_{0}}$ движения по оптимальной траектории $CL$. Пусть $K$ – точка касания прямой и окружности, $\rho $ – длина отрезка ${{O}_{1}}F$, $\alpha $ – угловая мера дуги $OK$, $\beta $ – величина угла $K{{O}_{1}}F$, а $\gamma $ – величина угла $O{{O}_{1}}F$. Предположим, что конечное положение $F({{x}_{F}},{{y}_{F}})$ принадлежит первой четверти, т.е. ${{x}_{F}} \geqslant 0$, ${{y}_{F}} \geqslant 0$ (см. рис. 3). Тогда
(2.8)
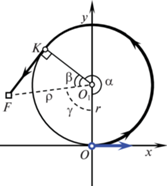
${{T}_{0}} = \frac{{\alpha r + \sqrt {{{\rho }^{2}} - {{r}^{2}}} }}{V} = \frac{\alpha }{\Omega } + \frac{{\sqrt {{{\rho }^{2}} - {{r}^{2}}} }}{V}.$Если конечное положение $F({{x}_{F}},{{y}_{F}})$ находится во второй четверти (при ${{x}_{F}} < 0$, ${{y}_{F}} \geqslant 0$ (см. рис. 4)), то приходим к той же формуле (2.8), но величина угла поворота
(2.9)
$\alpha = 2\pi - \gamma - \beta = 2\pi - \arccos \frac{{r - {{y}_{F}}}}{\rho } - \arccos \frac{r}{\rho }.$Траектории CC и CL получаются при релейном оптимальном управлении. Единственное переключение происходит в точках K (см. рис. 2–4). Момент переключения t1 определяется величиной $\alpha $ угла поворота:
Рассмотрим частные случаи. Если конечное положение F находится на окружности радиуса r с центром ${{O}_{1}}$, то оптимальная траектория – дуга этой окружности. Величина α угла поворота вычисляется по формулам
Если точка F принадлежит положительной части оси абсцисс (${{x}_{F}} > 0$, ${{y}_{F}} = 0$), то угол поворота $\alpha = 0$, а время движения
В случае ${{x}_{F}} < 0$, ${{y}_{F}} = 0$ применяются формулы (2.8), (2.9).
Если начальное состояние ненулевое, то нужно перенести начало системы координат в стартовое положение $({{x}_{0}},{{y}_{0}})$ объекта управления и повернуть ее в соответствии с направлением ${{\varphi }_{0}}$ скорости движения, при необходимости выполнить отражение в новой оси абсцисс, если ордината цели окажется отрицательной. После этого момент переключения и минимальное значение времени движения вычисляются соответственно по формулам (2.7), (2.8), (2.11), (2.12).
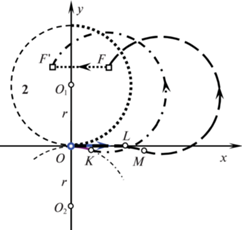
Полученные формулы (2.7), (2.8), (2.11), (2.12) показывают, что минимальное время ${{T}_{0}}$ непрерывно зависит от координат цели F на всей верхней полуплоскости, за исключением полуокружности с центром ${{O}_{1}}$ радиуса r, находящейся в первой четверти ($x \geqslant 0$, $y \geqslant 0$). При переносе точки F через эту линию изменяется тип оптимальной траектории, а время ${{T}_{0}}$ меняется скачком, так как вычисляется по разным формулам ((2.7) или (2.8)). Иначе говоря, функция цены ${{T}_{0}}(F)$ имеет конечный разрыв на этой полуокружности.
Вычислим величину скачка. Пусть точка F находится на линии разрыва (рис. 5). Дуга $OF$ (полужирная линия) является оптимальной траекторией. Минимальное время достижения цели находим по формулам (2.10), (2.11):
Кривая $OKF$ (штриховая линия) – попадающая траектория типа CC. Время движения по этой траектории вычисляется по формулам (2.5)–(2.7):
(2.14)
${{T}_{0}} = \frac{1}{\Omega }\left( {2\pi + \arcsin \frac{{{{x}_{F}}}}{\rho } + \arccos \frac{{3{{r}^{2}} + {{\rho }^{2}}}}{{4r\rho }} - \arccos \frac{{5{{r}^{2}} - {{\rho }^{2}}}}{{4{{r}^{2}}}}} \right).$Величина скачка определяется разностью величин (2.13) и (2.14):
(2.15)
$\Delta {{T}_{0}} = \frac{1}{\Omega }\left( {2\pi + \arccos \frac{{3{{r}^{2}} + {{\rho }^{2}}}}{{4r\rho }} - \arccos \frac{{5{{r}^{2}} - {{\rho }^{2}}}}{{4{{r}^{2}}}}} \right).$Следовательно, если конечное положение цели перемещается, пересекая линию разрыва в точке F в направлении к центру ${{O}_{1}}$, то минимальное время T0 увеличивается скачком на величину (2.15).
Таким образом, в классической задаче Маркова–Дубинса попадания в заданную цель функция цены всюду непрерывно зависит от позиции цели, за исключением линии разрыва, на которой она имеет скачок (2.15).
3. Методика нахождения моментов достижения цели. Известно [34], что в граничные точки множества достижимости приводят траектории, удовлетворяющие принципу максимума Понтрягина для задачи быстродействия. Следует ожидать, что граничные точки множества $\mathbb{T} = \mathbb{T}({{x}_{0}}\,{\text{|}}\,{{x}_{T}})$ также соответствуют процессам, удовлетворяющим необходимым условиям оптимальности.
Действительно, наименьший элемент T0 множества $\mathbb{T}$ является решением задачи быстродействия (1.7)–(1.9). Если множество $\mathbb{T}$ состоит, например, из двух отрезков $\mathbb{T} = [{{T}_{0}},{{T}_{1}}] \cup [{{T}_{2}},{{T}_{3}}]$, то момент T2 достижения цели – решение задачи быстродействия (1.7)–(1.9) с дополнительным условием $T \geqslant {{T}_{*}}$, где ${{T}_{*}}$ – любой момент между T1 и T2. Иначе говоря, время T2 соответствует минимально опаздывающему управлению при заданном ${{T}_{ * }}$. Таким образом, левые границы непересекающихся отрезков, входящих в множество $\mathbb{T}$, соответствуют моментам окончания процессов, удовлетворяющих принципу максимума. Для правых границ отрезков такое утверждение не доказано и, возможно, неверное.
Пример 2. Пусть на промежутке $[0,T]$ движение системы описывается уравнениями (2.4) модели Маркова–Дубинса [14–16]. Нулевое начальное состояние O и конечное положение $F({{x}_{F}},{{y}_{F}})$ определяются равенствами:
Требуется решить задачу о времени достижения цели, т.е. для каждого конечного положения F найти множество $\mathbb{T}(O\,{\text{|}}\,F)$ всех допустимых моментов T окончания процессов управления.
Решение этой задачи будем искать, предполагая, что цель $F({{x}_{F}},{{y}_{F}})$ находится в верхней полуплоскости $y \geqslant 0$. Наименьший элемент T0 множества $\mathbb{T}(O\,{\text{|}}\,F)$ является решением задачи быстродействия (см. пример 1). Поэтому для каждого момента $T > {{T}_{0}}$ нужно либо найти неопаздывающую траекторию, удовлетворяющую терминальным условиям (3.1), либо показать, что такой траектории нет.
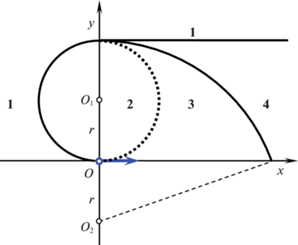
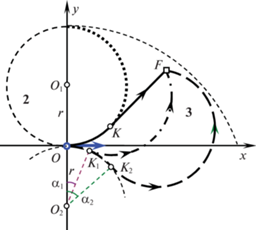
Предлагается строить неопаздывающие траектории, удлиняя оптимальные путем добавлением нового участка: либо отрезка, либо дуги окружности. В зависимости от положения цели F на координатной плоскости $Oxy$ будем строить разные неопаздывающие траектории. На рис. 6 представлены характерные области 1–4 расположения цели. Границами областей служат окружность с центром ${{O}_{1}}(0,r)$ радиуса r, дуга окружности с центром ${{O}_{2}}(0, - \,r)$ радиуса 3r, луч $y = 2r$, $x \geqslant 0$. Здесь, как и ранее, $r = V{\text{/}}\Omega $ – наименьший допустимый радиус поворота. Пунктирной полуокружностью на рис. 6 изображена линия разрыва функции цели, о которой шла речь в примере 1. Решим задачу о множестве моментов достижения цели для каждой области.
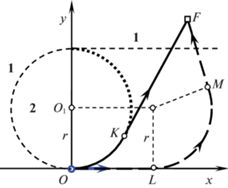
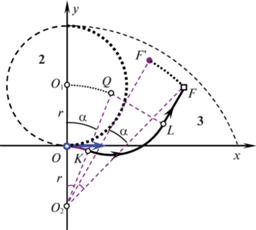
Пусть цель находится в области 1 (см. рис. 6). Оптимальная траектория $OKF$ типа CL изображена на рис. 7 полужирной линией. Минимальное время T0 достижения цели находится по формуле (2.8). Рассмотрим попадающую траекторию типа $LCL$ движения объекта управления, при котором сначала выполняется прямолинейное движение в течение времени $\tau $, потом поворот в положительном направлении и, наконец, прямолинейное движение в цель. На рис. 7 такая траектория представлена штриховой линией $OLMF$. Время T движения по этой траектории больше, чем время T0 движения по оптимальной траектории $OKF$.
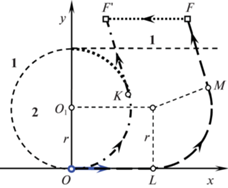
Получим зависимость времени T от продолжительности $\tau $ первого участка. Для этого вместо движения объекта управления рассмотрим перемещение цели относительно объекта управления, который будем считать неподвижным. Действительно, прямолинейному движению объекта по отрезку $OL = V\tau $ соответствует относительное перемещение цели по отрезку $FF{\kern 1pt} ' = V\tau $ (рис. 8). После этого перемещения цель окажется в точке $F{\kern 1pt} '$ области 1. Поэтому общее время движения по траектории $OLMF$ составит
где ${{T}_{0}}(F{\kern 1pt} ')$ – минимальное время движения из нулевого начального состояния в конечное состояние $F{\kern 1pt} '({{x}_{F}} - V\tau ,{{y}_{F}})$ по траектории $OKF{\kern 1pt} '$ (штрихпунктирная линия на рис. 8). Так как функция ${{T}_{0}}(F{\kern 1pt} ')$ непрерывна в области 1, а координаты точки $F{\kern 1pt} '$ непрерывно зависят от параметра $\tau $, то при любом значении $T \geqslant {{T}_{0}}$ найдется корень $\tau $ уравнения (3.2). Иначе говоря, для любого $T \geqslant {{T}_{0}}$ существует неопаздывающая попадающая траектория. Следовательно, множество моментов достижения цели в области 1 представляет собой луч $\mathbb{T}(O\,{\text{|}}\,F) = [{{T}_{0}}(F), + \infty )$.Пусть цель находится в области 2 (см. рис. 6). Оптимальная траектория $OKF$ типа CC изображена на рис. 9, 10 полужирной линией. Минимальное время T0 достижения цели находится по формуле (2.7). Рассмотрим попадающие траектории двух типов $LCC$ и $LCL$, которые представлены на рис. 9, 10 штриховыми линиями $OLMF$ соответственно. На первом участке обеих траекторий происходит прямолинейное движение объекта в течение времени $\tau $. Первый участок продолжается либо двумя поворотами (рис. 9), либо поворотом с последующим прямолинейным движением до цели (рис. 10). Первые участки попадающих траекторий отличаются длиной. У траектории LCC (на рис. 9) первый участок $OL = V\tau $ короче отрезка $F{{F}_{1}} = {{x}_{F}} - \sqrt {{{y}_{F}}(2r - {{y}_{F}})} $, а у траектории $LCL$ (на рис. 10) отрезок $OL$ больше $F{{F}_{1}}$. Время T движения по траекториям LCC или $LCL$ больше, чем время T0 движения по оптимальной траектории $OKF$.
Получим зависимость времени T от продолжительности $\tau $ первого участка. Для этого, как и ранее, вместо движения объекта управления рассмотрим перемещение цели относительно объекта управления, который будем считать неподвижным. Прямолинейному движению объекта по отрезку $OL = V\tau $ соответствует относительное перемещение цели по отрезку $FF{\kern 1pt} ' = V\tau $ (рис. 11, 12). После такого перемещения цель окажется в точке $F{\kern 1pt} '$ либо в области 2 (см. рис. 11), либо в области 1 (см. рис. 12). В обоих случаях время движения по попадающим траекториям определяется равенством (3.2), в котором, однако, минимальное время ${{T}_{0}}(F{\kern 1pt} ')$ движения из нулевого начального состояния в конечное состояние $F{\kern 1pt} '({{x}_{F}} - V\tau ,{{y}_{F}})$ по траекториям $OKF{\kern 1pt} '$ (штрихпунктирные линии на рис. 11, 12) вычисляется либо по формуле (2.7), либо по формуле (2.8) соответственно.
Функция ${{T}_{0}}(F{\kern 1pt} ')$ непрерывна в областях 1 и 2. Координаты точки $F{\kern 1pt} '$ непрерывно зависят от $\tau $. Поскольку перемещение $FF{\kern 1pt} '$ цели из области 2 в область 1 (рис. 12) не пересекает линии разрыва функции цены (пунктирной полуокружности на рис. 6). Значит, функция ${{T}_{0}}(F{\kern 1pt} ')$ непрерывно зависит от параметра $\tau $. Поэтому при любом значении $T \geqslant {{T}_{0}}$ найдется корень $\tau $ уравнения (3.2). Иначе говоря, для любого $T \geqslant {{T}_{0}}$ существует неопаздывающая попадающая траектория. Следовательно, множество моментов достижения цели в области 2 представляет собой луч $\mathbb{T}(O\,{\text{|}}\,F) = [{{T}_{0}}(F), + \infty )$.
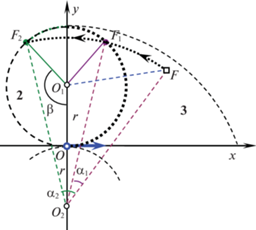
Пусть цель находится в области 3 (см. рис. 6). Оптимальная траектория типа CL достигает цель за время T0, которое находится по формуле (2.8). На рис. 13 изображены оптимальная траектория типа CL (полужирная линия), а также две траектории типа CC (штрихпунктирная и штриховая линии), попадающие в точку F. Здесь K, ${{K}_{1}}$, ${{K}_{2}}$ – точки гладкого соединения участков трех траекторий соответственно. Обозначим через ${{T}_{1}}$ и ${{T}_{2}}$ время движения по попадающим траекториям $O{{K}_{1}}F$ и $O{{K}_{2}}F$. Покажем, что множество моментов достижения цели представляет собой объединение промежутков
В самом деле, рассмотрим движение цели относительно объекта управления, который будем считать неподвижным. На рис. 14 показаны линии перемещения цели, соответствующие попадающим траекториям $O{{K}_{1}}F$ и $O{{K}_{2}}F$ движения объекта на рис. 13. Повороту $O{{K}_{1}}$ (рис. 13) соответствует перемещение $F{{F}_{1}}$ на угол ${{\alpha }_{1}} = \angle F{{O}_{2}}{{F}_{1}} = \angle O{{O}_{2}}{{K}_{1}}$, повороту $O{{K}_{2}}$ – перемещение $F{{F}_{2}}$ на угол ${{\alpha }_{2}} = \angle F{{O}_{2}}{{F}_{2}} = \angle F{{O}_{2}}{{F}_{2}}$. Вычислим время движения по траекториям $O{{K}_{1}}F$ и $O{{K}_{2}}F,$ используя перемещения цели на рис. 14. Из равных треугольников ${{O}_{1}}{{O}_{2}}{{F}_{2}}$ и ${{O}_{1}}{{O}_{2}}{{F}_{1}}$ получаем
где $\rho $ – длина отрезка ${{O}_{2}}F$. Угол ${{\alpha }_{1}}$ находим как разность углов ${{O}_{1}}{{O}_{2}}F$ и ${{O}_{1}}{{O}_{2}}{{F}_{1}}$, а угол ${{\alpha }_{2}}$ – как сумму углов ${{O}_{1}}{{O}_{2}}F$ и ${{O}_{1}}{{O}_{2}}{{F}_{1}}$:(3.4)
${{\alpha }_{1}} = \arcsin \frac{{{{x}_{F}}}}{\rho } - \arccos \frac{{3{{r}^{2}} + {{\rho }^{2}}}}{{4r\rho }},\quad {{\alpha }_{2}} = \arcsin \frac{{{{x}_{F}}}}{\rho } + \arccos \frac{{3{{r}^{2}} + {{\rho }^{2}}}}{{4r\rho }}.$Тогда время T1 и T2 движения по траекториям $O{{K}_{1}}F$ и $O{{K}_{2}}F$ вычисляется по формулам
(3.5)
${{T}_{1}} = \frac{{{{\alpha }_{1}} + \beta }}{\Omega },\quad {{T}_{2}} = \frac{{2\pi + {{\alpha }_{2}} - \beta }}{\Omega }.$Докажем теперь, что для любого момента окончания T из множества (3.3) найдется неопаздывающая траектория. Пусть ${{T}_{0}} \leqslant T \leqslant {{T}_{1}}$. Обозначим через $\tau $ время первоначального поворота $OK$ объекта управления в отрицательном направлении (рис. 15) на угол $\alpha = \Omega \,\tau $. Предполагаем, что угол $\alpha $ меньше угла ${{\alpha }_{1}}$ (рис. 14). При таком небольшом повороте относительное перемещение $FF{\kern 1pt} '$ цели будет в пределах области 3. Тогда время достижения цели будет равно
Здесь ${{T}_{0}}(F{\kern 1pt} ')$ – минимальное время движения из нулевого начального состояния в конечное положение $F{\kern 1pt} '(x{\kern 1pt} ',y{\kern 1pt} ')$, координаты которого находятся по формулам
(3.7)
$x{\kern 1pt} ' = {{x}_{F}}\cos \alpha - {{y}_{F}}\sin \alpha - r\sin \alpha ,\quad y{\kern 1pt} ' = {{x}_{F}}\sin \alpha + {{y}_{F}}\cos \alpha + r\cos \alpha - r,$Пусть теперь $T \geqslant {{T}_{2}}$. Рассмотрим траекторию типа $CLCL$ движения объекта управления (рис. 16), при котором сначала выполняется поворот в отрицательном направлении на угол ${{\alpha }_{2}}$, определяемый формулой (3.4), затем прямолинейное движение в течение времени $\tau $, потом поворот в положительном направлении и, наконец, прямолинейное движение в цель. На рис. 16 такая траектория представлена полужирной линией $O{{K}_{2}}LMF$. Время T движения по этой траектории больше, чем время T2 движения по траектории $O{{K}_{2}}F$ (штриховая линия на рис. 13). Первым двум участкам движения объекта – повороту по дуге $O{{K}_{2}}$ на угол ${{\alpha }_{2}} = \angle O{{O}_{2}}K$ и прямолинейному движению по отрезку ${{K}_{2}}L = V\tau $ соответствуют относительное перемещение цели по дуге $F{{F}_{2}}$ на угол ${{\alpha }_{2}} = \angle F{{O}_{2}}{{F}_{2}}$ и по отрезку ${{F}_{2}}F{\kern 1pt} ' = {{K}_{2}}L$. После таких перемещений цель останавливается в точке $F{\kern 1pt} '$ в области 1 относительно неподвижного объекта управления. Поэтому общее время движения по траектории типа $CLCL$ оказывается равным
где ${{T}_{0}}(F{\kern 1pt} ')$ – минимальное время движения из нулевого начального состояния в конечное положение $F{\kern 1pt} '(x{\kern 1pt} ',y{\kern 1pt} ')$, координаты которого находятся по формулам(3.9)
$x{\kern 1pt} ' = {{x}_{F}}\cos {{\alpha }_{2}} - {{y}_{F}}\sin {{\alpha }_{2}} - r\sin {{\alpha }_{2}} - V\tau ;\quad y{\kern 1pt} ' = {{x}_{F}}\sin {{\alpha }_{2}} + {{y}_{F}}\cos {{\alpha }_{2}} + r\cos {{\alpha }_{2}} - r.$Так как функция ${{T}_{0}}({{F}_{3}})$ непрерывная в области 1, а координаты (3.9) точки F3 непрерывно зависят от параметра τ, то при любом значении $T \geqslant {{T}_{2}}$ найдется корень $\tau $ уравнения (3.8). Иначе говоря, для любого $T \geqslant {{T}_{2}}$ существует неопаздывающая попадающая траектория.
Подчеркнем, что момент $T \in ({{T}_{1}},{{T}_{2}})$ не является допустимым моментом достижения цели. Первоначальному повороту объекта управления в отрицательном направлении соответствует относительное перемещение цели по дуге $F{{F}_{1}}{{F}_{2}}$ в противоположном направлении движение (рис. 14). При этом перемещении цель пересекает пунктирную полуокружность, которая, как отмечалось в примере 1, является линией разрыва функции цены. На этой дуге в точке ${{F}_{1}}$ происходит скачок (2.15) функции цены от значения T1 к значению T2. Промежуточных значений (между T1 и T2) функция цены не принимает. Поэтому не существует траекторий, достигающих цель в момент $T \in ({{T}_{1}},{{T}_{2}})$. Однако минимально опаздывающая траектория для $T\, \in \,({{T}_{1}},{{T}_{2}})$ существует. Это траектория типа CC, представленная на рис. 13 штриховой линией $O{{K}_{2}}F$. Время T2 движения по этой траектории определяется формулой (3.5).
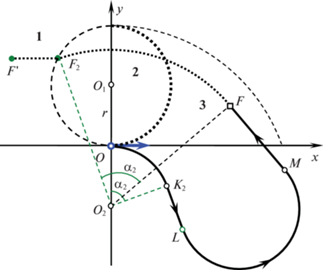
Пусть цель находится в области 4 (рис. 6). Оптимальная траектория $OKF$ типа CL изображена на рис. 17, 18 полужирной линией. Минимальное время T0 достижения цели находится по формуле (2.8). Рассмотрим попадающие траектории двух типов CCL и CLCL, которые представлены на рис. 17, 18 штриховыми линиями $O{{K}_{1}}LF$ и $O{{K}_{1}}LMF$ соответственно. На первом участке $O{{K}_{1}}$ обеих траекторий происходит поворот в отрицательном направлении на угол $\alpha $ и ${{\alpha }_{1}}$ соответственно, причем $\alpha < {{\alpha }_{1}}$. Угол $\alpha = \Omega \,\tau $, где $\tau $ – продолжительность первого участка траектории $O{{K}_{1}}LF$ (рис. 17). Угол ${{\alpha }_{1}} = \angle O{{O}_{2}}{{F}_{1}} = \arccos (3r{\text{/}}\rho )$, где ${{F}_{1}}$ – точка пересечения луча $y = 2r$, $x \geqslant 0$ окружности с центром ${{O}_{2}}$ радиуса $\rho = {{O}_{2}}F$ с границей области 4 (лучом $y = 2r$, $x \geqslant 0$). Первый участок траектории CCL продолжается поворотом в положительном направлении и прямолинейным движением в цель (см. рис. 17). За первым участком траектории CLCL следует участок прямолинейного движения продолжительности $\tau - {{\alpha }_{1}}{\text{/}}\Omega $, затем поворот в положительном направлении и, наконец, прямолинейное движение в цель. Время T движения по траекториям CCL или CLCL больше, чем время T0 движения по оптимальной траектории OKF.
Рис. 17.
Оптимальная траектория CL и перемещение цели в области 4 для неопаздывающей траектории CCL.
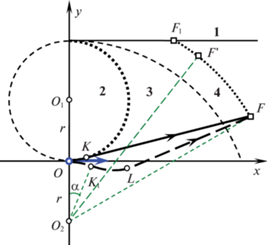
Рис. 18.
Оптимальная траектория CL и перемещение цели из области 4 для неопаздывающей траектории CLCL.
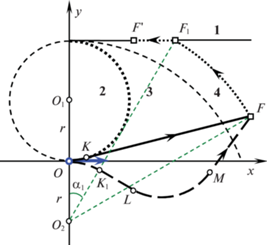
Получим зависимость времени T движения от параметра $\tau $. Рассмотрим относительное перемещение цели для обеих попадающих траекторий. Для траектории типа CCL первоначальному повороту на угол $\alpha = \angle O{{O}_{2}}{{K}_{1}}$ соответствует перемещение цели по дуге $FF{\kern 1pt} '$ той же угловой величины $\alpha = \angle F{{O}_{2}}F{\kern 1pt} '$ (рис. 17). После такого перемещения цель окажется в точке $F{\kern 1pt} '$ в области 4. Поэтому время движения по траектории $O{{K}_{1}}LF$ типа CCL вычисляется по формулам (3.6), (3.7).
Для траектории типа $CLCL$ первоначальному повороту на угол ${{\alpha }_{1}} = \angle O{{O}_{2}}{{K}_{1}}$ соответствует перемещение цели по дуге $F{{F}_{1}}$ той же угловой величины ${{\alpha }_{1}} = \angle F{{O}_{2}}F{\kern 1pt} '$ (рис. 18). После такого перемещения цель окажется в точке ${{F}_{1}}$ на границе области 1. Прямолинейному движению объекта по отрезку ${{K}_{1}}L = V(\tau - {{\alpha }_{1}}{\text{/}}\Omega )$ соответствует относительное перемещение цели по отрезку ${{F}_{1}}F{\kern 1pt} '$ той же длины (рис. 18). Конечное положение $F{\kern 1pt} '$ цели остается в области 1. Поэтому общее время движения по траектории $O{{K}_{1}}LMF$ типа CLCL вычисляется по формуле (3.6), в которой координаты конечного положения $F{\kern 1pt} '(x{\kern 1pt} ',y{\kern 1pt} ')$ цели определяются выражениями
Зависимость времени T движения от параметра $\tau $ непрерывная, поскольку при относительном перемещении $FF{\kern 1pt} '$ цели линия разрыва функции цены (пунктирная полуокружность на рис. 17, 18) не пересекается. Поэтому для любого значения $T \geqslant {{T}_{0}}$ найдется корень $\tau $ уравнения (3.6). Иначе говоря, для любого $T \geqslant {{T}_{0}}$ существует неопаздывающая попадающая траектория. Следовательно, множество моментов достижения цели в области 4 представляет собой луч $\mathbb{T}(O\,{\text{|}}\,F) = [{{T}_{0}}(F), + \infty )$.
Таким образом, в классической задаче Маркова–Дубинса множеством моментов достижения цели является либо луч $[{{T}_{0}}, + \infty )$, либо объединение двух промежутков $[{{T}_{0}},{{T}_{1}}] \cup [{{T}_{2}}, + \infty )$, где T0 – минимальное время достижения цели, а T1 и T2 – моменты, определяемые формулами (3.5). В частном случае, когда цель лежит на границе областей 2 и 3, множество моментов достижения цели будет объединением точки и луча $\{ \,{{T}_{0}}\} \cup [{{T}_{2}}, + \infty )$, поскольку в этом случае ${{T}_{1}} = {{T}_{0}}$.
4. Условия оптимальности для задачи минимизации опоздания. Задача минимизации опоздания отличается от задачи быстродействия (1.7)–(1.9) с дополнительным условием (1.11):
(4.1)
$\begin{gathered} x(0) = {{x}_{0}},\quad x(T) = {{x}_{T}}, \\ T \geqslant {{T}_{*}}, \\ \end{gathered} $Задачу (4.1) можно решать без применения метода Лагранжа. Для этого нужно модифицировать минимизируемый функционал (4.1):
Такая негладкая модификация может быть полезна при решении задачи (4.2) численными методами минимизации нулевого порядка [30] или методами недифференцируемой минимизации [36, 37].
Пример 3. Пусть на промежутке $[0,T]$ движение системы описывается уравнениями (2.4) модели Маркова–Дубинса [14–16]. Нулевое начальное состояние O и конечное положение $F({{x}_{F}},{{y}_{F}})$ определяются равенствами (3.1). Требуется решить задачу минимизации опоздания, т.е. найти минимальное время T достижения цели, которое не меньше заданной величины ${{T}_{*}}$.
Решение этой задачи фактически получено в примерах 1, 2. В самом деле, если минимально допустимое время ${{T}_{*}}$ достижения цели меньше минимального времени T0 достижения цели, то минимально опаздывающая траектория совпадает с оптимальной по быстродействию, которая найдена в примере 1. Если цель не принадлежит области 3 на рис. 6, то множество моментов достижения цели представляет собой луч $\mathbb{T}(O\,{\text{|}}\,F) = [{{T}_{0}}(F), + \infty )$, поэтому для любого назначенного срока ${{T}_{*}} \geqslant {{T}_{0}}$ существует неопаздывающая траектория (см. пример 2), которая является минимально опаздывающей. Если же цель принадлежит области 3 на рис. 6, то множество моментов достижения цели представляет собой объединение двух промежутков $\mathbb{T}(O\,{\text{|}}\,F) = [{{T}_{0}},{{T}_{1}}] \cup [{{T}_{2}}, + \infty )$, где T1 и T2 – моменты, определяемые формулами (3.5). Значит, при ${{T}_{*}} \notin ({{T}_{1}},{{T}_{2}})$ минимально опаздывающая траектория совпадает с неопаздывающей, а при ${{T}_{*}} \in ({{T}_{1}},{{T}_{2}})$ минимально опаздывающая является траекторией типа CC, представленной на рис. 13 штриховой линией $O{{K}_{2}}F$. Время T2 движения по этой траектории определяется формулой (3.5).
Таким образом, в классической задаче Маркова–Дубинса попадания в заданную цель для любого назначенного срока существует минимально опаздывающая траектория.
5. Алгоритмы решения задачи группового быстродействия. Решение задачи (1.3)–(1.6) группового быстродействия связано с нахождением оптимальных по быстродействию и минимально опаздывающих траекторий. Рассмотрим два итерационных алгоритма. В первом на каждой итерации используются множества моментов достижения целей, а минимально опаздывающие траектории строятся один раз после нахождения оптимального назначения. Во втором алгоритме на каждой итерации находятся минимально опаздывающие траектории, а множества моментов достижения целей не применяются. Выбор алгоритма зависит от трудоемкости решения вспомогательных задач. Процедура построения множеств моментов достижения для каждого объекта управления и каждой цели требует, как правило, больших вычислительных ресурсов. Однако эта процедура, используемая в первом алгоритме, выполняется один раз. Во втором алгоритме на каждой итерации нужно для каждого объекта управления и каждой цели найти минимально опаздывающие траектории. Нахождение каждой такой траектории по вычислительным затратам обычно сравнимо с поиском оптимальной траектории. Количество итераций конечное, но заранее неизвестное. Если для решения достаточно малого числа итераций, то выгоднее использовать второй алгоритм, если итераций много, то лучше применять первый алгоритм.
Поскольку численная реализация каждого алгоритма весьма сложная, она связана с многократным решением задач оптимального управления, желательно использовать аналитические методы, упрощающие решение. Например, вместо оптимального управления применять рациональное управление, если оно находится сравнительно просто, а по качеству близко к оптимальному. Либо упростить модель движения объектов управления так, чтобы оптимальные траектории можно было получить аналитически. Решить задачу группового быстродействия с простыми моделями движения, а полученное управление проверить на прикладных моделях, описывающих реальное движение.
Алгоритм I решения задачи группового быстродействия с известными множествами моментов достижения цели. Пусть в задаче (1.3)–(1.6) группового быстродействия для каждого объекта управления и каждой цели известны множества ${{\mathbb{T}}_{{ij}}} = \mathbb{T}({{x}_{{i0}}}\,{\text{|}}\,{{z}_{j}})$ моментов достижения цели, $i = 1,...,M$; $j = 1,...,N$. Минимальный момент T* одновременного достижения цели определяется равенством
(5.1)
$T{\kern 1pt} * = \mathop {\min }\limits_{({{j}_{1}},...,{{j}_{M}})} \min \bigcap\limits_{i = 1,...,M}^{} {{{\mathbb{T}}_{{i{{j}_{i}}}}}} .$Здесь первая операция минимизация проводится по всем размещениям $({{j}_{1}},...,{{j}_{M}})$ по M чисел из N возможных. Каждое размещение определяет назначение (паросочетание): первому подвижному объекту назначается j1-я цель, второму – j2-я цель и т.д. Второй минимум в формуле (5.1) обозначает выбор минимального элемента пересечения числовых множеств. Для решения вспомогательных задач назначения, возникающих на каждой итерации, применяется алгоритм, приведенный в Приложении. Алгоритм решения задачи группового быстродействия следующий.
Шаг 0. Назначаем нулевой не опережаемый срок ${{T}_{*}} = 0$ достижения целей и переходим к шагу 1.
Шаг 1. Составляем матрицу минимальных допустимых моментов достижений целей с элементами ${{T}_{{ij}}} = \min \{ t \in {{\mathbb{T}}_{{ij}}}\,{\text{|}}\,t \geqslant {{T}_{*}}\} $.
Шаг 2. Решаем задачу минимаксного назначения с матрицей $({{T}_{{ij}}})$. Получаем оптимальное назначение $(j_{1}^{*},...,j_{M}^{*})$ и рекорд
(5.2)
$T{\kern 1pt} * = T(j_{1}^{*},...,j_{M}^{*}) = \mathop {\min }\limits_{({{j}_{1}},...,{{j}_{M}})} \mathop {\max }\limits_{i = 1,...,M} {{T}_{{i{{j}_{i}}}}}$.Шаг 3. Проверяем реализуемость рекорда T*. Если $T{\kern 1pt} * \in {{\mathbb{T}}_{{i{{j}_{i}}}}}$ для всех $i = 1,...,M$, то переходим к шагу 4, поскольку минимальный момент T* одновременного достижения целей найден. В противном случае увеличиваем не опережаемый срок, полагая ${{T}_{*}} = T{\kern 1pt} *$, и переходим к шагу 1.
Шаг 4. Находим неопаздывающие траектории для момента T* одновременного достижения целей. Решение задачи закончено.
Поясним работу алгоритма. На первой итерации, поскольку не опережаемый срок – нулевой, матрица (Tij) заполняется оптимальными по быстродействию моментами достижения целей. Решая минимаксную задачу назначения, получаем первый рекорд T*. Заметим, что $T{\kern 1pt} * > {{T}_{*}}$, так как все элементы матрицы (Tij) не меньше ${{T}_{*}}$. В шаге 3 алгоритма выясняется, могут ли все подвижные объекты попасть в назначенные цели в рекордное время T*. Если могут, то задача решена, осталось только построить неопаздывающие траектории (см. шаг 4). Если нет, то после увеличения минимального срока ${{T}_{*}} = T{\kern 1pt} *$ достижения целей возвращаемся к шагу 1. На второй и последующих итерациях (в шаге 1) матрица (Tij) заполняется моментами окончания минимально опаздывающих к назначенному сроку ${{T}_{*}}$ траекторий. Заметим, что число итераций конечное, поскольку количество возможных размещений равно $N!/(N - M)!$.
Алгоритм II решения задачи группового быстродействия при помощи минимально опаздывающих траекторий.
Шаг 0. Назначаем нулевой не опережаемый срок ${{T}_{*}} = 0$ достижения целей и переходим к шагу 1.
Шаг 1. Составляем матрицу (Tij) моментов достижения целей минимально опаздывающими к сроку ${{T}_{*}}$ траекториями. Элемент Tij является решением задачи минимизации опоздания i-го объекта при достижении j-й цели:
(5.3)
$\begin{gathered} {{x}_{i}}(0) = {{x}_{{i\,0}}},\quad {{x}_{i}}(T) = {{z}_{j}}, \\ T \geqslant {{T}_{*}}, \\ \end{gathered} $Шаг 2. Решаем задачу минимаксного назначения с матрицей $({{T}_{{ij}}})$. Получаем оптимальное назначение $(j_{1}^{*},...,j_{M}^{*})$ и рекорд (5.2).
Шаг 3. Проверяем реализуемость рекорда T*. Полагаем ${{T}_{*}} = T{\kern 1pt} *$ и решаем задачу (5.3) минимизации опоздания i-го объекта при достижении $j_{i}^{*}$-й цели, $i = 1,...,M$. Получаем моменты ${{T}_{{ij_{i}^{ * }}}}$ достижения целей минимально опаздывающими к сроку T* траекториями. Если ${{T}_{{ij_{i}^{ * }}}} = {{T}_{*}}$ для всех $i = 1,...,M$, то все траектории неопаздывающие и решение задачи закончено. Если равенство ${{T}_{{ij_{i}^{ * }}}} = {{T}_{*}}$ нарушается ходя бы для одного объекта, то имеются опаздывающие траектории. Поэтому переходим к шагу 1. (Элементы ${{T}_{{ij_{i}^{ * }}}}$, $i = 1,...,M$, матрицы (Tij) в шаге 1 повторно искать не надо.)
Оба алгоритма за конечное число шагов приводят к одному и тому же результату – минимальному времени одновременного достижения цели. Однако неопаздывающее управление объектами, а также решение задачи назначения находятся неоднозначно. Поэтому процессы управления, соответствующие оптимальному результату, могут отличаться.
Пример 4. Пусть на промежутке времени $[0,T]$ движение группы M подвижных объектов управления описывается уравнениями (2.4) модели Маркова–Дубинса [14–16]:
(5.4)
${{\dot {x}}_{i}}(t) = {{V}_{i}}\cos {{\varphi }_{i}}(t),\quad {{\dot {y}}_{i}}(t) = {{V}_{i}}\sin {{\varphi }_{i}}(t),\quad {{\dot {\varphi }}_{i}}(t) = {{\omega }_{i}}(t),\quad i = 1,...,M,$Начальное состояние каждого объекта группы задано равенствами
(5.5)
${{x}_{i}}(0) = {{x}_{{i\,0}}},\quad y(0) = {{y}_{{i\,0}}},\quad \varphi (0) = {{\varphi }_{{i\,0}}},\quad i = 1,...,M.$Конечное положение выбирается из множества целей $\{ {{F}_{1}}({{x}_{{{{F}_{1}}}}},{{y}_{{{{F}_{1}}}}}),...,{{F}_{N}}({{x}_{{{{F}_{N}}}}},{{y}_{{{{F}_{N}}}}})\} $:
(5.6)
${{x}_{i}}(T) = {{x}_{{{{F}_{{{{j}_{i}}}}}}}},\quad {{y}_{i}}(T) = {{y}_{{{{F}_{{{{j}_{i}}}}}}}},\quad i = 1,...,M.$Номера целей в (5.6) попарно различные, т.е. ${{j}_{i}} \ne {{j}_{k}}$, если $i \ne k$. Иначе говоря, упорядоченный набор $({{j}_{1}},...,{{j}_{M}})$ представляет собой размещение (без повторений) по M чисел из N возможных, причем $M \leqslant N$. Конечные условия (5.6) определяют “точечные” цели на координатной плоскости $Oxy$. Заметим, что цели в множестве $\{ {{F}_{1}},...,{{F}_{N}}\} $ не обязательно различные. Например, равенство ${{F}_{1}} = {{F}_{2}}$ (при M = N) означает, что в эту цель должны попасть два объекта группы. В частности, если все цели совпадают, то получаем задачу о сборе группы в одном месте в одно и то же время.
Требуется определить назначение целей и найти допустимые процессы управления объектами, при которых время T одновременного достижения всех целей будем минимальным. Иначе говоря, требуется решить задачу группового быстродействия
В задаче (5.4)–(5.7) столкновения подвижных объектов исключаются. Можно считать, что речь идет о движении группы БПЛА, которые летят на разных высотах. Кроме того, нет фазовых ограничений, запрещенных для движения областей, конфликтных ситуаций, связанных с действиями противника [8, 25].
Рассмотрим академический пример быстродействия группы из пяти подвижных объектов, которые направляются в две точечные цели, причем в одну цель должны попасть два объекта, а в другую – три. Значения параметров моделей движения, начальные состояния и положения целей следующие:
(5.8)
$\begin{gathered} {{x}_{{10}}} = - 2,\quad {{y}_{{1\,0}}} = 3,\quad {{\varphi }_{{10}}} = \pi {\text{/}}4;\quad {{x}_{{20}}} = - 2,\quad {{y}_{{20}}} = 1,\quad {{\varphi }_{{20}}} = \pi ;\quad {{x}_{{30}}} = 2,\quad {{y}_{{30}}} = 2, \\ {{\varphi }_{{30}}} = \pi {\text{/}}4;\quad {{x}_{{40}}} = 3,\quad {{y}_{{40}}} = - 2,\quad {{\varphi }_{{40}}} = \pi {\text{/}}2;\quad {{x}_{{50}}} = 0,\quad {{y}_{{50}}} = - 2,\quad {{\varphi }_{{50}}} = 3\pi {\text{/}}4; \\ \end{gathered} $Для задачи назначения цели F1 и F2 “клонируются”. В равенствах (5.8) одна цель указывается дважды, а другая – трижды. На рис. 19 начальные состояния подвижных объектов изображены окружностями с приложенными к ним векторами скорости, цели F1 и F2 – квадратиками. Объекты перенумерованы полужирными цифрами.
Решение поставленной задачи будем искать, применяя описанные выше алгоритмы. Чтобы использовать первый алгоритм, нужно для каждого объекта найти множество моментов достижения каждой цели. Учитывая решение примера 2, получаем
Здесь ${{\mathbb{T}}_{{ij}}}$ – множество моментов достижения i-м объектом j-й цели с учетом “клонирования” (5.8). Изолированная точка в множестве ${{\mathbb{T}}_{{42}}}$ соответствует частному положению цели ${{F}_{2}}$ на границе областей 2 и 3 для 4-го объекта управления.
На шаге 0 алгоритма I полагаем ${{T}_{*}} = 0$ и переходим к шагу 1.
Шаг 1 (первая итерация). Составляем матрицу минимальных допустимых моментов достижений целей с элементами ${{T}_{{ij}}} = \min \{ t \in {{\mathbb{T}}_{{ij}}}\,{\text{|}}\,t \geqslant {{T}_{*}}\} $. Так как ${{T}_{*}} = 0$, то выбираем минимальные элементы множеств ${{\mathbb{T}}_{{ij}}}$:
(5.9)
$({{T}_{{ij}}}) = \left( {\begin{array}{*{20}{c}} {{\text{4}}{\text{.7606}}}&{4.9689}&{{\text{4}}{\text{.7606}}}&{{\text{4}}{\text{.9689}}}&{{\text{4}}{\text{.9689}}} \\ {4.7124}&{{\text{6}}{\text{.3099}}}&{{\text{4}}{\text{.7124}}}&{{\text{6}}{\text{.3099}}}&{{\text{6}}{\text{.3099}}} \\ {{\text{5}}{\text{.6469}}}&{{\text{5}}{\text{.3616}}}&{{\text{5}}{\text{.6469}}}&{5.3616}&{{\text{5}}{\text{.3616}}} \\ {{\text{2}}{\text{.5708}}}&{{\text{1}}{\text{.5708}}}&{{\text{2}}{\text{.5708}}}&{{\text{1}}{\text{.5708}}}&{1.5708} \\ {{\text{1}}{\text{.1252}}}&{{\text{5}}{\text{.5321}}}&{1.1252}&{{\text{5}}{\text{.5321}}}&{{\text{5}}{\text{.5321}}} \end{array}} \right).$В матрице (5.9) третий столбец совпадает с первым, а четвертый и пятый – со вторым, что соответствует “клонированию” целей (5.8).
Шаг 2 (первая итерация). Решаем задачу минимаксного назначения при помощи алгоритма, приведенного в Приложении. Для матрицы (5.9) получаем назначение (2, 1, 4, 5, 3) с рекордом $T{\text{*}} = {\text{5}}{\text{.3616}}$. В матрице (5.9) элементы найденного назначения выделены полужирным курсивом. Время достижения целей при этом назначении записаны в табл. 1. Как видим, для третьего объекта назначенная цель “дальняя”, а для остальных объектов все цели “ближние”.
Таблица 1.
Первое минимаксное назначение
| Объект | Цель | Время достижения |
|---|---|---|
| 1 | F2 | 4.9689 |
| 2 | F1 | 4.7124 |
| 3 | F4 = F2 | 5.3616 |
| 4 | F5 = F2 | 1.5708 |
| 5 | F3 = F1 | 1.1252 |
Шаг 3 (первая итерация). Проверяем реализуемость рекорда $T{\kern 1pt} * = {\text{5}}{\text{.3616}}$. Так как $T{\kern 1pt} * \notin {{\mathbb{T}}_{{45}}}$ и $T{\kern 1pt} * \notin {{\mathbb{T}}_{{53}}}$, то полученное назначение нельзя реализовать. За время $T{\kern 1pt} *$ четвертый объект не может попасть во вторую цель, а пятый – в первую. Поэтому увеличиваем не опережаемый срок, полагая ${{T}_{*}} = 5.3616$, и переходим к шагу 1.
Шаг 1 (вторая итерация). Составляем матрицу минимальных допустимых моментов достижений целей с элементами ${{T}_{{ij}}} = \min \{ t \in {{\mathbb{T}}_{{ij}}}\,{\text{|}}\,t \geqslant {{T}_{*}}\} $. Так как ${{T}_{*}} = 5.3616$, то выбираем элементы множеств ${{\mathbb{T}}_{{ij}}}$, соответствующие минимально опаздывающим траекториям:
(5.10)
$({{T}_{{ij}}}) = \left( {\begin{array}{*{20}{c}} {{\text{5}}{\text{.3616}}}&{5.3616}&{{\text{5}}{\text{.3616}}}&{{\text{5}}{\text{.3616}}}&{{\text{5}}{\text{.3616}}} \\ {5.3616}&{{\text{6}}{\text{.3099}}}&{{\text{5}}{\text{.3616}}}&{{\text{6}}{\text{.3099}}}&{{\text{6}}{\text{.3099}}} \\ {{\text{5}}{\text{.6469}}}&{{\text{5}}{\text{.3616}}}&{{\text{5}}{\text{.6469}}}&{5.3616}&{{\text{5}}{\text{.3616}}} \\ {{\text{5}}{\text{.3616}}}&{{\text{5}}{\text{.6397}}}&{5.3616}&{{\text{5}}{\text{.6397}}}&{{\text{5}}{\text{.6397}}} \\ {{\text{6}}{\text{.4366}}}&{{\text{5}}{\text{.5321}}}&{{\text{6}}{\text{.4366}}}&{{\text{5}}{\text{.5321}}}&{5.5321} \end{array}} \right).$Шаг 2 (вторая итерация). Решаем задачу минимаксного назначения с матрицей (5.10), получаем назначение (2, 1, 4, 5, 3) с рекордом $T{\kern 1pt} * = {\text{5}}{\text{.5321}}$. В матрице (5.10) элементы найденного назначения выделены полужирным курсивом. Время достижения целей при этом назначении записаны в табл. 2. Как видим, для пятого объекта назначенная цель “дальняя”, а для остальных объектов все цели “ближние”.
Таблица 2.
Второе минимаксное назначение
| Объект | Цель | Время достижения цели |
|---|---|---|
| 1 | F2 | 5.3616 |
| 2 | F1 | 5.3616 |
| 3 | F4 = F2 | 5.3616 |
| 4 | F3 = F1 | 5.3616 |
| 5 | F5 = F2 | 5.5321 |
Шаг 3 (вторая итерация). Проверяем реализуемость рекорда $T{\kern 1pt} * = {\text{5}}{\text{.5321}}$. Так как величина T* принадлежит множествам ${{\mathbb{T}}_{{12}}}$, ${{\mathbb{T}}_{{21}}}$, ${{\mathbb{T}}_{{34}}}$, ${{\mathbb{T}}_{{43}}}$, ${{\mathbb{T}}_{{55}}}$, то полученное назначение (2, 1, 4, 5, 3) реализовать можно. Наименьший момент $T{\kern 1pt} * = {\text{5}}{\text{.5321}}$ одновременного достижения целей найден. Переходим к шагу 4.
Шаг 4. Находим неопаздывающие траектории для момента $T{\kern 1pt} * = {\text{5}}{\text{.5321}}$ одновременного достижения целей. В примере 3 поиск неопаздывающей траекторий каждого типа сведен к решению нелинейного уравнения с одним неизвестным $\tau $ – продолжительностью движения по дополнительному участку. В табл. 3 приведены параметры полученных траекторий.
Таблица 3.
Неопаздывающие траектории
| Объект | Цель | Тип траектории | Моменты переключения управления |
|---|---|---|---|
| 1 | F2 | LCL | 0.413 2.0084 3.1121 |
| 2 | F1 | LCL | 0.53 3.8539 1.158 |
| 3 | F4 = F2 | LCL | 0.15 4.4484 0.94 |
| 4 | F3 = F1 | LCL | 1.7 3.1416 0.7 |
| 5 | F5 = F2 | CC | 0.6619 4.8702 |
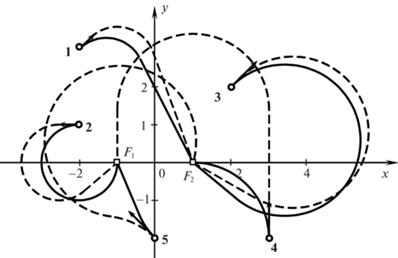
На рис. 20 полужирными линиями изображены оптимальные траектории при первом назначении, а штриховыми – неопаздывающие траектории для второго назначения. Заметим, что на второй итерации четвертому и пятому объектам были назначены другие цели, чем при первой.
Рис. 20.
Оптимальные траектории при первом назначении (полужирные линии), неопаздывающие траектории для второго назначения (штриховые линии).
Используем для решения алгоритм II.
Шаг 0. Назначаем нулевой не опережаемый срок ${{T}_{*}} = 0$ достижения целей и переходим к шагу 1.
Шаг 1 (первая итерация). Составляем матрицу (Tij) моментов достижения целей минимально опаздывающими к сроку ${{T}_{*}} = 0$ траекториями. Элемент ${{T}_{{ij}}}$ является решением задачи быстродействия (см. пример 1). Получаем матрицу (5.9).
Шаг 2 (первая итерация). Решаем задачу минимаксного назначения при помощи алгоритма, приведенного в Приложении. Для матрицы (5.9) получаем назначение (2, 1, 4, 5, 3) с рекордом $T{\kern 1pt} * = {\text{5}}{\text{.3616}}$. В матрице (5.9) элементы найденного назначения выделены полужирным курсивом. Время достижения целей при этом назначении записаны в табл. 1. Как видим, для третьего объекта назначенная цель “дальняя”, а для остальных объектов все цели “ближние”.
Шаг 3 (первая итерация). Проверяем реализуемость рекорда $T{\kern 1pt} * = {\text{5}}{\text{.3616}}$. Полагаем ${{T}_{*}} = T{\kern 1pt} *$ = = 5.3616 и решаем задачу минимизации опоздания для найденного назначения (см. пример 3). Получаем
Поскольку ${{T}_{{45}}} \ne {{T}_{*}}$ (и ${{T}_{{52}}} \ne {{T}_{*}}$), значит, имеются опаздывающие траектории. Поэтому назначение не реализуемо, переходим к шагу 1.
Шаг 1 (вторая итерация). Составляем матрицу (Tij) моментов достижения целей минимально опаздывающими к сроку ${{T}_{*}} = {\text{5}}{\text{.3616}}$ траекториями. Получаем матрицу (5.10).
Шаг 2 (вторая итерация). Решаем задачу минимаксного назначения для матрицы (5.10). Получаем назначение (2, 1, 4, 5, 3) с рекордом $T{\kern 1pt} * = {\text{5}}{\text{.5321}}$. В матрице (5.10) элементы найденного назначения выделены полужирным курсивом.
Шаг 3 (вторая итерация). Проверяем реализуемость рекорда $T{\kern 1pt} * = {\text{5}}{\text{.5321}}$. Полагаем ${{T}_{*}} = T{\kern 1pt} *$ = = 5.5321 и решаем задачу минимизации опоздания для найденного назначения (см. пример 3). Получаем ${{T}_{{12}}} = {{T}_{{21}}} = {{{\text{T}}}_{{{\text{34}}}}} = {{{\text{T}}}_{{{\text{43}}}}} = {{{\text{T}}}_{{{\text{55}}}}} = {\text{5}}{\text{.3616}}$. Так как все траектории назначения неопаздывающие, значит, это назначение реализуемо. Решение задачи закончено, параметры неопаздывающих траекторий группы представлены в табл. 3.
Оба алгоритма привели к одному и тому же решению. Это совпадение обусловлено тем, что решение задачи назначения и построение минимально опаздывающих траекторий выполнялось в обоих алгоритмах одними и теми же методами. Если применять другие методы, то получим разные неопаздывающие траектории и, возможно, разные назначения. При этом, конечно, минимальное время одновременного достижения целей находится однозначно любым точным алгоритмом.
Заключение. Поставлена задача минимизации опоздания динамической системы, которая является модификацией задачи быстродействия, а также задача поиска множества моментов достижения терминального состояния. Обе задачи тесно связаны с задачей группового быстродействия. Предложены два алгоритма решения задачи быстродействия группы подвижных объектов, а именно минимизации времени одновременного достижения всех целей. Эффективность этих алгоритмов в общем случае зависит от динамики управляемых систем. В статье приведена конкретная реализация обоих алгоритмов для модели Маркова–Дубинса, т.е. задача группового быстродействия машин Маркова–Дубинса полностью решена. Это решение можно использовать при планировании траекторий летательных аппаратов в многочисленных приложениях. Дальнейшие исследования в этом направлении связаны с известными обобщениями задач группового управления: учетом взаимодействий между объектами группы, противодействием противника, наличием запрещенных для движения областей и т.п.
Список литературы
Каляев И.А., Гайдук А.Р., Капустян С.Г. Модели и алгоритмы коллективного управления в группах роботов. М.: Физматлит, 2009.
Куржанский А.Б. Задача управления групповым движением. Общие соотношения // Докл. РАН. 2009. Т. 426. № 1. С. 20–25.
Габасов Р., Дмитрук Н.М., Кириллова Ф.М. Оптимальное децентрализованное управление группой динамических объектов // ЖВМ и МФ. 2008. Т. 48. № 4. С. 593–600.
Евдокименков В.Н., Красильщиков М.Н., Оркин С.Д. Управление смешанными группами пилотируемых и беспилотных летательных аппаратов в условиях единого информационно-управляющего поля. М.: Изд-во МАИ, 2015.
Гончаренко В.И., Желтов С.Ю., Князь В.А., Лебедевa Г.Н., Михайлинa Д.А., Царева О.Ю. Интеллектуальная система планирования групповых действий беспилотных летательных аппаратов при наблюдении наземных мобильных объектов на заданной территории // Изв. РАН. ТиСУ. 2021. № 3. С. 39–56.
Tsourdos A., White B., Shanmugavel M. Cooperative Path Planning of Unmanned Aerial Vehicles. N. Y.: Wiley&Sons, 2011.
Jia Zeng, Xiaoke Yang, Lingyu Yang, Gongzhang Shen. Modeling for UAV Resource Scheduling Under Mission Synchronization // J. Systems Engineering and Electronics. 2010. V. 21. № 5. P. 821–826.
Babel L. Coordinated Target Assignment and UAV Path Planning with Timing Constraints // J. Intelligent & Robotic Systems. 2019. V. 94 (3–4). P. 857–869.
Бортаковский А.С., Щелчков К.А. Задачи группового быстродействия летательных аппаратов // Тр. МАИ. 2018. № 99. http://mai.ru//upload/iblock/33c/Bortakovskiy_ SHCHelchkov_rus.pdf.
Poudel S., Moh S. Task Assignment Algorithms for Unmanned Aerial Vehicle Networks: A Comprehensive Survey // Vehicular Communications. 2022. V. 35. P. 100469.
Бузиков М.Э., Галяев А.А. Перехват подвижной цели машиной Дубинса за кратчайшее время // АиТ. 2021. № 5. С. 3–19.
Галяев А.А., Рубинович Е.Я. Планирование движения подвижных объектов в конфликтной среде // Аналитическая механика, устойчивость и управление: Тр. XI Междунар. Четаевской конф. (пленарные доклады). Казань: Изд-во КНИТУ-КАИ, 2017. С. 71–90.
Mohsan S.A.H., Othman N.Q.H., Li Y. et al. Unmanned Aerial Vehicles (UAVs): Practical Aspects, Fpplications, Open Challenges, Security Issues, and Future Trends. Intel Serv Robotics. 2023. V. 16. P. 109–137.
Марков А.А. Несколько примеров решения особого рода задач о наибольших и наименьших величинах // Сообщения Харьк. мат. общества. Сер. 2. Т. I. 1889. С. 250–276.
Dubins L.E. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents // American. Mathematics. 1957. V. 79. № 3. P. 497–516.
Isaacs R. Games of Pursuit // Scientific Report of the RAND Corporation. Santa Monica, 1951.
Бортаковский А.С. Оптимальные по быстродействию траектории плоского движения с неограниченной кривизной // Изв. РАН. ТиСУ. 2022. № 4. С. 38–48.
Пацко В.С., Федотов А.А. Трехмерное множество достижимости для машины Дубинса: сведение общего случая ограничений на повороты к каноническому // Изв. РАН. ТиСУ. 2023. № 4. С. 25–49.
Диниц Е.А. О решении двух задач о назначении // Исследования по дискретной оптимизации. М.: Наука, 1976. С. 333–348.
Глебов Н.И. Об одном обобщении минимаксной задачи о назначениях // Дискретн. анализ и исслед. операций. 2004. Т. 11. Вып. 4. С. 36–43.
Серая О.В. Минимаксная задача назначения // Восточно-Европейский журнал передовых технологий. 2009. Т. 3. № 3(39). С. 8–11.
Fulkerson D.R., Glicksberg I., Gross O. A Production Line Assignment Problem. Tech. Rep. RM-1102, The Rand Corporation. Santa Monica. CA, 1953.
Burkard R., Dell’Amico M., Martello S. Assignment Problems: Revised Reprint. Siam, 2012. T. 125.
Gottlieb Y.; Shima T. UAVs Task and Motion Planning in the Presence of Obstacles and Prioritized Targets // Sensors. 2015. V. 15. P. 29734–29764. https://doi.org/10.3390/s151129734
Zhu X., Peng R. Optimal Routing, Aborting and Hitting Strategies of UAVs Executing Hitting the Targets Considering the Defense Range of Targets // Reliability Engineering and System Safety. 2021. V. 215. P. 107811.
Кофман А., Анри-Лабордер А. Методы и модели исследования оптимизации. Целочисленное программирование. М.: Мир, 1976.
Garfinkel R. An Improved Algorithm for the Bottleneck Assignment Problem // Oper. Res. 1971. V. 19. P. 1747–1751.
Derigs U., Zimmermann U. An Augmenting Path Method for Solving Linear Bottleneck Assignment Problems // Computing. 1978. V. 19. P. 285–295.
Федоренко Р.П. Приближенное решение задач оптимального управления. М.: Наука, 1978.
Васильев Ф.П. Методы оптимизации. М.: Факториал Пресс, 2002.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Физматгиз, 1961.
Грачев Н.И., Евтушенко Ю.Г. Библиотека программ для решения задач оптимального управления // ЖВМ и МФ. 1979. Т.10. № 2. С. 367−387.
Cockayne E.J., Hall G.W.C. Plane Motion of a Particle Subject to Curvature Constraints // SIAM J. Control and Optimization. 1975. V. 13. № 1. P. 197−220.
Ли Э.Б., Маркус Л. Основы теории оптимального управления. М.: Наука, 1972.
Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука, 1974.
Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983.
Кларк Ф. Оптимизация и негладкий анализ. М.: Наука, 1988.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления