Известия РАН. Теория и системы управления, 2023, № 6, стр. 67-80

ОПТИМАЛЬНОЕ ПОДАВЛЕНИЕ КОЛЕБАНИЙ В ЗАДАЧЕ РАСКРУЧИВАНИЯ ДВУХМАССОВОЙ СИСТЕМЫ

С. А. Васенин^a, *, С. А. Решмин^a

^a ИПМех РАН
Москва, Россия

Поступила в редакцию 10.05.2023
После доработки 17.06.2023
Принята к публикации 31.07.2023

EDN: FNEJMB
DOI: 10.31857/S0002338823060112

Аннотация

Рассматривается управляемая механическая система многих тел, состоящая из несущего диска, который вращается вокруг своей оси, закрепленной в пространстве, и несомого диска, присоединенного к нему при помощи невесомых упругих элементов. Представленные тела находятся в одной плоскости. Исследуется задача о минимизации амплитуды радиальных колебаний. Для решения данной задачи на достаточно большом интервале используются два численных метода: метод последовательных приближений в пространстве управлений и метод Ньютона. Изучены свойства фазовых траекторий системы в зависимости от начальных состояний дисков. Обнаружены различные режимы раскрутки дисков. С помощью процедуры сглаживания для оптимального управления построено непрерывное управление, уменьшающее амплитуду радиальных колебаний.

Введение. Процессы раскрутки механических систем присутствуют во многих технических устройствах. Важность исследования данного явления обусловлена большим количеством механических объектов, процессы которых напрямую или косвенно связаны с разными модификациями процессов раскрутки и вращения. В работе рассматривается модель колеса, представляющая собой систему двух взаимосвязанных дисков, соединенных между собой невесомыми упругими пружинами. Для данной системы ставится задача о раскручивании с одновременным подавлением радиальных упругих колебаний (имеется в виду изменение расстояния между осями вращения дисков). Принимается во внимание нелинейность в модели упругого взаимодействия, обусловленная тем, что упругие элементы ориентированы по-разному, что позволяет влиять на амплитуду радиальных колебаний, применяя только управляющий крутящий момент. Для построения управления на большом интервале времени предлагается использовать метод последовательных приближений [1] и метод Ньютона, часто применяющийся для решения соответствующей краевой задачи принципа максимума Л.С. Понтрягина [2]. В предыдущей работе [3] была продемонстрирована эвристическая методика применения простейшего варианта метода последовательных приближений. Для построения управления на большом интервале времени предлагалось разбивать его на последовательность коротких интервалов и использовать на них метод последовательных приближений. В результате было получено субоптимальное управление на большом интервале времени, успешно минимизирующее амплитуду радиальных колебаний. Данный подход возник из-за отсутствия сходимости простейшего варианта метода последовательных приближений на длительном интервале времени.

Хочется также отметить, что управления, найденные разными способами применения метода последовательных приближений, имеют отличия. В работе было получено управление при помощи метода последовательных приближений с улучшенной сходимостью, которое быстрее минимизирует амплитуду радиальных колебаний механической системы.

Предполагается, что возможности прикладываемого к одному из дисков моментов велики, так что в процессе управления угол крутильной деформации, т.е. разность углов вращения дисков, может изменяться сколь угодно быстро в заданных пределах. Указанный угол кручения выбирается в качестве нового управления, которое гасит амплитуду радиальных колебаний. Выбором допустимого диапазона изменения управления (угла кручения) можно обеспечить дополнительно и требуемую раскрутку системы в целом.

Отметим, что существуют работы, например [4], численные методы расчета оптимального программного управления которых используют эволюционные алгоритмы, не основанные на решении краевой задачи принципа максимума. Ограничения на величину управляющего воздействия часто учитываются в задачах управления техническими системами. Поиск и оценка числа переключений релейного оптимального управления проводились в публикациях [5–8]. В [9] получено аналитическое оптимальное по энергии управление гармоническим осциллятором, причем задача рассматривалась на конечном интервале времени. Сложные задачи с ограничениями на управление были исследованы в [10, 11]. Отметим, что в работах [12, 13] рассматривались похожие по структуре механические системы, для которых присутствовала возможность влияния на центробежную силу инерции за счет вращения. В данной статье такая возможность отсутствовала. Оптимальное изменение ориентации двухмассовой системы проводилось в [14–17]. В [18] исследовалась динамика механического изотропного стержневого упругого подвеса. Многомерные осцилляторы с нелинейным затуханием рассматривались в [19, 20]. Задача построения общего ограниченного управления, приводящего системы из произвольного числа осцилляторов в заданное состояние, была представлена в [21, 22]. В [23] предлагается алгоритм стабилизации движения тросовой системы с квадратичным критерием оптимальности, как в данной работе, в окрестности местной вертикали, основанный на принципе динамического программирования Беллмана [24].

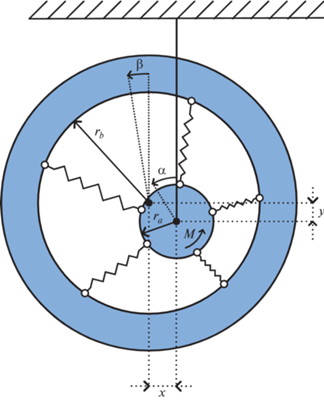
1. Постановка задачи управления двухмассовой системой. Рассматривается задача оптимального управления для механической системы, состоящей из двух дисков, расположенных в одной плоскости и соединенных между собой при помощи невесомых предварительно растянутых пружин, концы которых не защемлены шарнирно-неподвижными опорами (рис. 1). Радиус первого диска равен r_a. Радиус внутренней полости второго диска равен ${{r}_{b}}$. Углы поворотов дисков обозначены через $\alpha $ и $\beta $ и отсчитываются от вертикали. Оси вращения параллельны, причем ось вращения первого диска жестко закреплена снизу кронштейном к неподвижному основанию, которое обозначено штриховкой. Положение центра масс второго характеризуется относительными координатами $x,\;y$ в прямоугольной системе координат в плоскости, которая перпендикулярна осям вращения. Таким образом, при $x = 0$ и $y = 0$ оси вращения совпадают. Влияние силы тяжести на систему не учитывается.

Рис. 1.

Двухмассовая система

Предполагается, что при малых $x,\;y,\;\alpha - \beta $ потенциальная энергия Π взаимодействия разложима в двумерный ряд Тейлора по переменным ${{r}^{2}}$ и ${{\varphi }^{2}}$, где ${{r}^{2}} = {{x}^{2}} + {{y}^{2}}$, ${{\varphi }^{2}} = {{\left( {\alpha - \beta } \right)}^{2}}$, и приближенно задается следующим выражением: Π = $\frac{1}{2}[k_{r}^{0}({{x}^{2}}\, + \,{{y}^{2}})\, + \,k_{\varphi }^{0}{{(\alpha \, - \,\beta )}^{2}}]$ + $\frac{1}{4}[k_{r}^{r}{{({{x}^{2}}\, + \,{{y}^{2}})}^{2}}\, + \,2k_{r}^{\varphi }({{x}^{2}}\, + \,{{y}^{2}}){{(\alpha \, - \,\beta )}^{2}}\, + \,k_{\varphi }^{\varphi }$(α – – β)⁴] + ..., где $k_{r}^{0}$, $k_{\varphi }^{0}$, $k_{r}^{r}$, $k_{r}^{\varphi }$, $k_{\varphi }^{\varphi }$ – заданные постоянные коэффициенты.

Определим коэффициенты $k_{r}^{0}$, $k_{\varphi }^{0}$, $k_{r}^{r}$, $k_{r}^{\varphi }$, $k_{\varphi }^{\varphi }$ в случае, когда в качестве упругих элементов выступают линейные пружины, у которых график “нагрузка–деформация” представляет собой прямую линию. Рассмотрим систему из $N$ пружин жесткости $k$, причем длина в свободном состоянии каждой из них равна $l < {{r}_{b}} - {{r}_{a}}$. Для расчета коэффициентов упругой модели будем использовать следующие соотношения, полученные в [25] для $N \geqslant 5$:

$k_{r}^{0} = kN\left( {1 - \frac{l}{{2\left( {{{r}_{b}} - {{r}_{a}}} \right)}}} \right),\quad k_{\varphi }^{0} = kN\left( {1 - \frac{l}{{{{r}_{b}} - {{r}_{a}}}}} \right){{r}_{b}}{{r}_{a}},\quad k_{r}^{\varphi } = \frac{{kNl{{r}_{a}}{{r}_{b}}}}{{4{{{\left( {{{r}_{b}} - {{r}_{a}}} \right)}}^{3}}}},$

$k_{r}^{r} = - \frac{{kNl}}{{16{{{\left( {{{r}_{b}} - {{r}_{a}}} \right)}}^{3}}}},\quad k_{\varphi }^{\varphi } = - \frac{{kN}}{6}\left( {1 - \frac{{l\left( {{{r}_{a}}^{2} + {{r}_{a}}{{r}_{b}} + {{r}_{b}}^{2}} \right)}}{{{{{\left( {{{r}_{b}} - {{r}_{a}}} \right)}}^{3}}}}} \right){{r}_{a}}{{r}_{b}}.$

Введем обозначения радиальной и крутильной жесткости:

(1.1)

${{k}_{r}} = k_{r}^{0} + k_{r}^{r}({{x}^{2}} + {{y}^{2}}) + k_{r}^{\varphi }{{(\alpha - \beta )}^{2}},\quad {{k}_{\varphi }} = k_{\varphi }^{0} + k_{r}^{\varphi }({{x}^{2}} + {{y}^{2}}) + k_{\varphi }^{\varphi }{{(\alpha - \beta )}^{2}}.$

Отметим, что значение $k_{r}^{\varphi }$ всегда принимает положительное значение и $k_{r}^{\varphi }$ является единственным коэффициентом, присутствующим как в выражении для радиальной жесткости, так и в выражении для крутильной жесткости. Опишем влияние, оказываемое данным коэффициентом на коэффициенты ${{k}_{r}}$ и ${{k}_{\varphi }}$, с позиции физических соображений. При увеличении значений $\left| x \right|,\;\left| y \right|$ слагаемое в крутильной жесткости с коэффициентом $k_{r}^{\varphi }$ вызывает рост значения ${{k}_{\varphi }}$, а при увеличении значения $\left| {\alpha - \beta } \right|$ слагаемое в радиальной жесткости с коэффициентом $k_{r}^{\varphi }$ вызывает рост значения ${{k}_{r}}$. Фактически это означает, что из-за нарастания отклонений по одной из степеней свободы будет нарастать возвращающая сила, препятствующая нарастанию отклонений по иным степеням свободы.

Учитывая выражение для кинетической энергии

${\rm K} = \frac{1}{2}[{{I}_{a}}{{\dot {\alpha }}^{2}} + {{I}_{b}}{{\dot {\beta }}^{2}} + {{m}_{b}}({{\dot {x}}^{2}} + {{\dot {y}}^{2}})],$

составим уравнения Лагранжа второго рода:

${{I}_{a}}\ddot {\alpha } + {{k}_{\varphi }}(\alpha - \beta ) = M,\quad {{I}_{b}}\ddot {\beta } - {{k}_{\varphi }}(\alpha - \beta ) = 0,\quad {{m}_{b}}\ddot {x} + {{k}_{r}}x = 0,\quad {{m}_{b}}\ddot {y} + {{k}_{r}}y = 0.$

Для данной системы ставится следующая задача: за счет выбора момента $M(t)$ требуется раскрутить систему, уменьшая, насколько это возможно, радиальные колебания в процессе управления.

Для определения крутящего момента $M(t)$, уменьшающего радиальные колебания системы, в данной работе предлагается ввести вспомогательную ограниченную управляющую функцию, представляющую собой разность углов поворотов:

$u(t) = \alpha (t) - \beta (t),\quad 0 \leqslant u(t) \leqslant {{u}_{0}},$

где ${{u}_{0}}$ – заданная постоянная, которая должна быть достаточно мала, чтобы выполнялось сделанное ранее предположение о разложимости в многомерный ряд Тейлора потенциальной энергии $\Pi $.

Если допустить, что угол кручения $u(t)$, его вторая производная $\ddot {u}(t)$, а также координаты $x(t)$, $y(t)$ центра масс второго диска известны, то искомый момент может быть представлен в виде

(1.2)

$M(t) = M(u(t),\ddot {u}(t),x(t),y(t)).$

Подробная запись этой зависимости будет дана в разд. 6. Исходная система уравнений движения трансформируется в соотношения

(1.3)

$\alpha (t) = \beta (t) + u(t),\quad {{I}_{b}}\ddot {\beta } = {{k}_{\varphi }}(u,x,y)u,$

(1.4)

${{m}_{b}}\ddot {x} + {{k}_{r}}(u,x,y)x = 0,\quad {{m}_{b}}\ddot {y} + {{k}_{r}}(u,x,y)y = 0,$

где в соответствии с (1.1) использованы следующие выражения для радиальной и крутильной жесткости:

(1.5)

${{k}_{r}}(u,x,y) = k_{r}^{0} + k_{r}^{r}({{x}^{2}} + {{y}^{2}}) + k_{r}^{\varphi }{{u}^{2}},\quad {{k}_{\varphi }}(u,x,y) = k_{\varphi }^{0} + k_{r}^{\varphi }({{x}^{2}} + {{y}^{2}}) + k_{\varphi }^{\varphi }{{u}^{2}}.$

Видно, что уравнения (1.4) не зависят явно от углов $\alpha $ и $\beta $. Поэтому задачу подавления колебаний системы (1.4) можно решать отдельно с использованием методов теории оптимального управления, выбрав подходящий терминальный функционал. Функция $u(t)$ предполагается кусочно-непрерывной. При этом неотрицательность вспомогательной управляющей функции, а следовательно, правой части второго уравнения (1.3) обеспечивает постепенное раскручивание системы. Задача управления рассматривается на конечном заданном интервале времени $t \in \left[ {0,\;T} \right].$

В результате для решения поставленной задачи оптимального управления будет построена вспомогательная управляющая функция, оптимально уменьшающая радиальные колебания системы. Однако при кусочно-непрерывном законе управления $u(t)$ выражение (1.2) не имеет смысла, так как вторая производная $\ddot {u}(t)$ не существует в точках разрыва. Применяя для $u(t)$ процедуру сглаживания (см. разд. 6) и используя выражение (6.2) для нахождения крутящего момента как функции от сглаженной вспомогательной управляющей функции $u(t)$, получим искомый крутящий момент $M(t)$.

Так как в данной задаче крутящий момент $M(t)$ будет найден через вспомогательную функцию $u(t)$, можно предполагать, что разность углов поворотов дисков является новым управлением для рассматриваемой системы. Из данного заключения следует, что на начальном этапе первые два уравнения (см. (1.3)) можно не рассматривать, а рассматривать только оставшиеся два (см. (1.4)).

Введем новые переменные: ${{{v}}_{x}}$ – скорость изменения координаты x, ${{{v}}_{y}}$ – скорость изменения координаты $y$. Перейдем к системе четырех уравнений первого порядка, описывающих двумерный осциллятор:

(1.6)

$\dot {x} = {{{v}}_{x}},\quad {{{\dot {v}}}_{x}} = \frac{{ - x{{k}_{r}}}}{{{{m}_{b}}}},\quad \dot {y} = {{{v}}_{y}},\quad {{{\dot {v}}}_{y}} = \frac{{ - y{{k}_{r}}}}{{{{m}_{b}}}}.$

Коэффициенты k_r и ${{k}_{\varphi }}$ заданы с помощью (1.5). Системе отвечают начальные условия:

$x(0) = {{x}_{0}},\quad {{{v}}_{x}}(0) = {{{v}}_{{x0}}},\quad y(0) = {{y}_{0}},\quad {{{v}}_{y}}(0) = {{{v}}_{{y0}}}.$

2. Методика применения метода последовательных приближений. В данном разделе описана методика применения метода последовательных приближений: простейшего варианта метода и метода с улучшенной сходимостью.

Пусть рассматривается задача оптимального управления механической системой на фиксированном интервале со свободным правым концом траектории. При постановке задачи необходимо, прежде всего, выписать дифференциальные уравнения движения, например уравнения Лагранжа второго рода. Далее для построения оптимального управления или экстремалей нужно, во-первых, составить соотношения принципа максимума, во-вторых, численно решить их с использованием метода последовательных приближений [1].

Для решения первой подзадачи (составления краевой задачи) следует ввести сопряженные переменные, составить гамильтониан, выписать сопряженную систему, найти общий вид управления, максимизирующего гамильтониан в каждый момент времени, добавить начальные условия для основных переменных и граничные условия для сопряженных переменных на правом конце траектории (условия трансверсальности).

Для решения второй подзадачи (численного решения краевой задачи) следует выбрать и использовать подходящую модификацию численного метода последовательных приближений в пространстве управлений для задачи оптимального управления со свободным правым концом [1]. Сначала изложим простейший вариант этого метода.

Управляемая система описывается уравнениями с начальными условиями и ограничениями:

(2.1)

$\frac{{dx}}{{dt}} = f(t,x,u),\quad x({{t}_{0}}) = {{x}_{0}},\quad u(t) \in U,\quad t \geqslant {{t}_{0}}.$

Здесь $x = ({{x}_{1}}, \ldots ,{{x}_{n}})$ – $n$-мерный вектор фазовых координат, $u = ({{u}_{1}}, \ldots ,{{u}_{m}})$ – $m$-мерный вектор управляющих функций, t – время, $f = ({{f}_{1}}, \ldots ,{{f}_{n}})$ – заданная вектор-функция, ${{x}_{0}}$ – постоянный вектор, ${{t}_{0}}$ – начальный момент времени, $U$ – замкнутое множество $m$-мерного пространства. Допустимыми управлениями будем называть кусочно-непрерывные функции $u(t)$, удовлетворяющие ограничению (2.1).

Поставим задачу об определении допустимого управления $u(t)$, минимизирующего линейный терминальный функционал:

(2.2)

$J = (c,x(T)),\quad T > {{t}_{0}}.$

Здесь $T$ – заданный момент времени, $с = ({{с}_{1}}, \ldots ,{{c}_{n}})$ – ненулевой постоянный вектор, скобками обозначено скалярное произведение векторов. Предположим, что поставленная задача имеет решение в классе допустимых управлений $u(t)$, это решение будем называть оптимальным управлением. К виду (2.2) приводится после введения дополнительных фазовых координат широкий класс интегральных функционалов [26].

Согласно принципу максимума Л.С. Понтрягина [2, 26], введем $n$-мерный вектор p = = $({{p}_{1}}, \ldots ,{{p}_{n}})$ сопряженных переменных, функцию Гамильтона $H$ и запишем сопряженную систему и условия трансверсальности:

(2.3)

$H(t,x,p,u) = (p,f(t,x,u)),$

(2.4)

$\frac{{d{{p}_{i}}}}{{dt}} = - \frac{{\partial H}}{{\partial {{x}_{i}}}} = - \sum\limits_{j = 1}^n {{{p}_{j}}} \frac{{\partial {{f}_{j}}(t,x,u)}}{{\partial {{x}_{i}}}},\quad p(T) = - c.$

Согласно принципу максимума, искомое оптимальное управление доставляет функции $H$ из (2.3) максимум по $u \in U$ при любом $t \in [{{t}_{0}},T],$ если $x$ и $p$ удовлетворяют уравнениям и граничным условиям (2.1) и (2.4).

В качестве начального приближения ${{u}^{1}}(t)$ зададим некоторое допустимое управление. Метод состоит из последовательных итераций; $k$-я итерация заключается в следующем $(k = 1,2, \ldots ){\text{:}}$

1) решая задачу Коши (2.1) с управлением $u = {{u}^{k}}(t),$ определяем траекторию $x = {{x}^{k}}(t)$ на интервале $[{{t}_{0}},T];$

2) решая задачу Коши (2.4) “справа налево” от момента $t = T$ до $t = {{t}_{0}}$ при $u = {{u}^{k}}(t)$, $x = {{x}^{k}}(t),$ находим сопряженные переменные ${{p}^{k}}(t)$ на интервале $[{{t}_{0}},T];$

3) определяем управление ${{u}^{{k + 1}}}(t)$ на интервале $[{{t}_{0}},T]$ из условия

(2.5)

$H(t,{{x}^{k}}(t),{{p}^{k}}(t),{{u}^{{k + 1}}}(t)) = \mathop {\max }\limits_{u \in U} H(t,{{x}^{k}}(t),{{p}^{k}}(t),u)$

и после этого переходим к следующей итерации.

Если процесс последовательных приближений сходится, то продолжаем его до тех пор, пока последующие приближения не будут отличаться друг от друга в пределах заданной точности. Полученное решение будет удовлетворять принципу максимума.

Описанный простейший вариант итерационного процесса не всегда сходится и в случае нашей системы такое произошло. Рассмотрим прием, позволяющий добиться сходимости итераций [1]. Обозначим через $Ф$ оператор, который каждому допустимому управлению ${{u}^{k}}(t)$ ставит в соответствие новое приближение по схеме, приведенной выше (см. (2.5)):

${{u}^{{k + 1}}}(t) = Ф({{u}^{k}}(t)),\quad k = 1,2, \ldots $

Тогда новое приближение модифицированного метода определяется по следующей схеме:

${{u}^{{k + 1}}}(t) = \left\{ \begin{gathered} {{u}^{k}}(t),\quad t \notin [t{\kern 1pt} ',t_{{}}^{{''}}] \subset [{{t}_{0}},T], \hfill \\ Ф({{u}^{k}}(t)),\quad t \in [t{\kern 1pt} ',t_{{}}^{{''}}]. \hfill \\ \end{gathered} \right.$

Здесь интервал $[t{\kern 1pt} ',t_{{}}^{{''}}]$, входящий в интервал $[{{t}_{0}},T]$, выбирается так, чтобы обеспечить условие

${{J}^{{k + 1}}} < {{J}^{k}},$

где ${{J}^{k}}$, ${{J}^{{k + 1}}}$ – значения функционала, отвечающие управлениям u^k, ${{u}^{{k + 1}}}.$

Подбор чисел $t{\kern 1pt} '$, $t_{{}}^{{''}}$ на каждой итерации происходит следующим образом:

$\begin{gathered} t{\kern 1pt} ' = t{\kern 1pt} * - \frac{h}{2},\quad t_{{}}^{{''}} = t{\kern 1pt} * + \frac{h}{2}, \\ t{\kern 1pt} * = \arg \;\mathop {\max }\limits_{t \in [{{t}_{0}},T]} [H({{p}^{k}}(t),{{x}^{k}}(t),{{u}^{{k + 1}}}(t),t) - H({{p}^{k}}(t),{{x}^{k}}(t),{{u}^{k}}(t),t)], \\ \end{gathered} $

где h – параметр, выбираемый произвольно. Процесс итераций заканчивается, когда для управления будет выполнен принцип максимума.

3. Методика применения метода Ньютона. Для построения оптимального управления или экстремалей нужно, во-первых, составить соотношения принципа максимума, во-вторых, численно решить их с использованием метода Ньютона.

Для решения первой подзадачи (составления краевой задачи) следует выполнить набор последовательных стандартных действий, а именно ввести сопряженные переменные, составить гамильтониан, выписать сопряженную систему, найти общий вид управления, максимизирующего гамильтониан в каждый момент времени, добавить начальные условия для основных переменных и граничные условия для сопряженных переменных на правом конце траектории (условия трансверсальности).

Для решения второй подзадачи (численного решения краевой задачи) следует использовать численный метод типа “пристрелки”. Начальные значения сопряженных переменных считаются варьируемыми параметрами. Исходная система интегрируется совместно с сопряженной системой в прямом времени при управлении, максимизирующем гамильтониан в каждый момент времени. Цель – обеспечить выполнение условий трансверсальности на правом конце траектории. Задача рассматривается формально как задача решения системы нескольких уравнений, заданных неявно. Число уравнений равно числу варьируемых параметров. Для выбора варьируемых параметров на следующей итерации и обеспечения сходимости к искомому решению используется метод Ньютона:

$\begin{gathered} z = ({{p}_{1}}(0), \ldots ,{{p}_{n}}(0)),\quad F(z) = 0,\quad F = ({{F}_{1}}, \ldots ,{{F}_{n}}), \\ {{z}^{{k + 1}}} = {{z}^{k}} - {{W}^{{ - 1}}}F,\quad W = \frac{{\partial {{F}_{i}}}}{{\partial {{z}_{j}}}},\quad i,j = 1, \ldots ,n, \\ \end{gathered} $

где z – вектор начальных значений сопряженных переменных, $F(z)$ – вектор из условий трансверсальности на правом конце, W – матрица Якоби. Так как условия трансверсальности на правом конце явно не зависят от начальных значений сопряженных переменных, то для определения матрицы Якоби применим выражение

$\frac{{\partial {{F}_{i}}}}{{\partial {{z}_{j}}}} \approx \frac{{{{F}_{i}}({{z}_{1}},{{z}_{2}}, \ldots ,{{z}_{j}} + {{\delta }_{j}}, \ldots ,{{z}_{n}}) - {{F}_{i}}({{z}_{1}},{{z}_{2}}, \ldots ,{{z}_{j}}, \ldots ,{{z}_{n}})}}{{{{\delta }_{j}}}}.$

Процесс итераций заканчивается, когда будут выполнены условия трансверсальности на правом конце.

4. Краевая задача принципа максимума. Введем вспомогательную переменную ${{x}_{0}}$ и выберем функционал типа Майера, соответствующий минимизации амплитуды радиальных колебаний системы в течение всего процесса:

$J = {{x}_{0}}(T),\quad {{\dot {x}}_{0}} = {{f}_{0}} = \frac{1}{2}k_{r}^{0}({{x}^{2}} + {{y}^{2}}),\quad {{x}_{0}}(0) = 0.$

Данный функционал имеет вид (2.2), где $c = \left( {1,0,0,0,0} \right)$.

Для решения задачи с таким функционалом используем принцип максимума. Введем соответствующие сопряженные переменные:

${{p}_{0}}(t),\quad {{p}_{1}}(t),\quad {{p}_{2}}(t),\quad {{p}_{3}}(t),\quad {{p}_{4}}(t),$

причем ${{p}_{0}}(t) = $ const $ = - 1.$ Запишем гамильтониан:

$\begin{gathered} H = \left( {p,f} \right) = - \frac{1}{2}k_{r}^{0}({{x}^{2}} + {{y}^{2}}) + {{p}_{1}}{{{v}}_{x}} - \frac{{{{p}_{2}}x[k_{r}^{0} + k_{r}^{r}({{x}^{2}} + {{y}^{2}}) + k_{r}^{\varphi }{{u}^{2}}]}}{{{{m}_{b}}}} + \\ \, + {{p}_{3}}{{{v}}_{y}} - \frac{{{{p}_{4}}y[k_{r}^{0} + k_{r}^{r}({{x}^{2}} + {{y}^{2}}) + k_{r}^{\varphi }{{u}^{2}}]}}{{{{m}_{b}}}}. \\ \end{gathered} $

Здесь в скалярном произведении p – вектор сопряженных переменных, f – вектор-функция, у которой компоненты с ненулевым индексом задают правую часть системы. Сопряженная система имеет вид

$\begin{gathered} {{{\dot {p}}}_{1}} = - \frac{{\partial H}}{{\partial x}} = k_{r}^{0}x + \frac{{{{p}_{2}}[k_{r}^{\varphi }{{u}^{2}} + k_{r}^{0} + k_{r}^{r}({{x}^{2}} + {{y}^{2}})]}}{{{{m}_{b}}}} + \frac{{2k_{r}^{r}{{p}_{2}}{{x}^{2}}}}{{{{m}_{b}}}} + \frac{{2k_{r}^{r}{{p}_{4}}xy}}{{{{m}_{b}}}},\quad {{{\dot {p}}}_{2}} = - \frac{{\partial H}}{{\partial {{{v}}_{x}}}} = - {{p}_{1}}, \\ {{{\dot {p}}}_{3}} = - \frac{{\partial H}}{{\partial y}} = k_{r}^{0}y + \frac{{{{p}_{4}}[k_{r}^{\varphi }{{u}^{2}} + k_{r}^{0} + k_{r}^{r}({{x}^{2}} + {{y}^{2}})]}}{{{{m}_{b}}}} + \frac{{2k_{r}^{r}{{p}_{4}}{{y}^{2}}}}{{{{m}_{b}}}} + \frac{{2k_{r}^{r}{{p}_{2}}xy}}{{{{m}_{b}}}},\quad {{{\dot {p}}}_{4}} = - \frac{{\partial H}}{{\partial {{{v}}_{y}}}} = - {{p}_{3}}. \\ \end{gathered} $

Граничные условия (условия трансверсальности) для полученной системы заданы на правом конце траектории:

${{p}_{1}}(T) = 0,\quad {{p}_{2}}(T) = 0,\quad {{p}_{3}}(T) = 0,\quad {{p}_{4}}(T) = 0.$

Оптимальное управление должно максимизировать гамильтониан, поэтому полагаем

$u(t) = \left\{ {\begin{array}{*{20}{c}} {0,\quad {{p}_{2}}x + {{p}_{4}}y > 0,} \\ {{{u}_{0}},\quad {{p}_{2}}x + {{p}_{4}}y \leqslant 0.} \end{array}} \right.$

5. Численное построение экстремалей при оптимальном управлении. При расчете были использованы следующие параметры системы с ненулевой начальной скоростью и ненулевым начальным отклонением центра масс второго диска (его начальный угол и начальная угловая скорость равны нулю):

${{m}_{a}} = 1\,\,{\text{кг}},\quad {{m}_{b}} = 1~\,\,{\text{кг}},\quad {{r}_{a}} = 0.621\,\,{\text{м}},\quad {{r}_{b}} = 0.644\,\,{\text{м,}}\quad {{I}_{a}} = 0.193\,\,{\text{кг}}\,\,{{{\text{м}}}^{2}},\quad {{I}_{b}} = 0.208\,\,{\text{кг}}\,\,{{{\text{м}}}^{{\text{2}}}}{\text{,}}$

$k = 10\,\,{\text{Н/м,}}\quad l = 0.012\,\,{\text{м,}}\quad N = 10,\quad T = 80\,\,{\text{с,}}\quad {{u}_{0}} = 0.01\,\,{\text{рад,}}$

$x(0) = 0.02{\text{\;м,}}\quad {{{v}}_{x}}(0) = - 0.01\,\,{\text{м/с}},\quad y(0) = 0.02\,\,{\text{м}},\quad {{{v}}_{y}}(0) = 0.01\,\,{\text{м/с}}{\text{.}}$

Получены следующие коэффициенты упругой модели:

$k_{r}^{0} = 75\,\,{\text{Н/м}},\quad k_{\varphi }^{0} = 20{\text{\;Н}}\,\,{\text{м,}}\quad k_{r}^{\varphi } = 9375\,\,{\text{Н/м,}}\quad k_{r}^{r} = - 5857\,\,{\text{Н/}}{{{\text{м}}}^{{\text{3}}}}{\text{,}}\quad k_{\varphi }^{\varphi } = 7500\,\,{\text{Н}}\,\,{\text{м}}{\text{.}}$

Отметим, что параметры системы подбирались так, чтобы слагаемые большего порядка малости в разложении потенциальной энергии были малы по сравнению со слагаемыми меньшего порядка малости. Преобразуя потенциальную энергию следующим образом:

$\Pi = \frac{1}{4}({{x}^{2}} + {{y}^{2}})[2k_{r}^{0} + k_{r}^{r}({{x}^{2}} + {{y}^{2}}) + k_{r}^{\varphi }{{\left( {\alpha - \beta } \right)}^{2}}] + \frac{1}{4}{{\left( {\alpha - \beta } \right)}^{2}}[2k_{\varphi }^{0} + k_{r}^{\varphi }({{x}^{2}} + {{y}^{2}}) + k_{\varphi }^{\varphi }{{\left( {\alpha - \beta } \right)}^{2}}],$

можно заметить, что если коэффициенты при квадратичных слагаемых рядах Тейлора будут в несколько раз больше, чем слагаемые в квадратных скобках преобразованной потенциальной энергии с коэффициентами $k_{r}^{r}$, $k_{r}^{\varphi }$, $k_{\varphi }^{\varphi }$, то будет обеспечено выполнение нужного нам условия. Варьируемыми параметрами для определения коэффициентов $k_{r}^{0}$, $k_{\varphi }^{0}$, $k_{r}^{r}$, $k_{r}^{\varphi }$, $k_{\varphi }^{\varphi }$ будут ${{r}_{a}},\;{{r}_{b}},\;l$. Поэтому потребуется составить систему из трех уравнений, где также будет учтено соотношение $l < {{r}_{b}} - {{r}_{a}}$. Для нахождения данных параметров системы были составлены следующие соотношения:

$\left\{ \begin{gathered} k_{r}^{0} = 80u_{0}^{2}, \hfill \\ k_{r}^{0} = k_{\varphi }^{\varphi }{{u}_{0}}, \hfill \\ l = 0.5\left( {{{r}_{b}} - {{r}_{a}}} \right). \hfill \\ \end{gathered} \right.$

Покажем, что при данных параметрах системы слагаемые четвертого порядка принимают меньшие значения, чем слагаемые второго порядка:

$\begin{gathered} {{\Pi }_{{\max }}} = \frac{1}{2}[k_{r}^{0}(x_{{\max }}^{2} + y_{{\max }}^{2}) + k_{\varphi }^{0}u_{{\max }}^{2}] + \frac{1}{4}[k_{r}^{r}{{(x_{{\max }}^{2} + y_{{\max }}^{2})}^{2}} + 2k_{r}^{\varphi }(x_{{\max }}^{2} + y_{{\max }}^{2})u_{{\max }}^{2} + k_{\varphi }^{\varphi }u_{{\max }}^{4}], \\ {{\Pi }_{{\max }}} = 0.031 + 0.0013,\quad \left| {{{x}_{{\max }}}} \right| = \left| {{{y}_{{\max }}}} \right| = 0.02,\quad \left| {{{u}_{{\max }}}} \right| = 0.01. \\ \end{gathered} $

Из закона сохранения кинетического момента и радиальности упругой силы следует, что фазовая траектория центра масс диска $b$ будет стремиться к окружности, радиус которой может быть получен приближенно из следующих равенств:

${{m}_{b}}{{\vec {r}}_{0}} \times {{{\vec {v}}}_{0}} = {{m}_{b}}\vec {r} \times {\vec {v}},\quad {\vec {v}} = \vec {\omega } \times \vec {r},\quad \left| {\vec {\omega }} \right| = \sqrt {\frac{{k_{r}^{0}}}{{{{m}_{b}}}}} .$

При вышеуказанных параметрах радиус окружности принял значение $\left| {\vec {r}} \right| = 0.0068$ м. Численным методом последовательных приближений и методом Ньютона было получено оптимальное управление, успешно минимизирующее амплитуду радиальных колебаний механической системы.

Для более быстрой сходимости численного метода последовательных приближений в качестве начального приближения было взято управление в виде обратной связи, имеющее следующий вид:

${{u}_{{{\text{init}}}}}(t) = \left\{ {\begin{array}{*{20}{c}} {{{u}_{0}},\quad (x\dot {x} > 0) \cap (y\dot {y} > 0),} \\ {0,\quad (x\dot {x} \leqslant 0) \cup (y\dot {y} \leqslant 0).} \end{array}} \right.$

Данное управление было выбрано из следующих физических соображений. Допустим, что начальные условия для $x,\;{{{v}}_{x}}$ и $y,{{{v}}_{y}}$ совпадают. Тогда из уравнений (1.6) следует, что $x$ будет изменяться так же, как и y. Получается, что уравнение ${{m}_{b}}\ddot {x} + (k_{r}^{0} + 2k_{r}^{r}{{x}^{2}} + k_{r}^{\varphi }{{u}^{2}})x = 0$ совпадает с уравнением одномерного осциллятора с нелинейной пружиной и дополнительной управляющей силой. В работе данная дополнительная сила должна обеспечивать уменьшение энергии на участках, где произведение $x\dot {x}$ положительно, и не влиять на систему в ином случае. Обобщением на двумерный случай служит выражение ${{u}_{{{\text{init}}}}}(t)$, имеющее тенденцию к подавлению колебаний.

Для нахождения начального приближения метода Ньютона для решения краевой задачи принципа максимума использовалась следующая методика. Первоначально были найдены начальные значения сопряженных переменных для построения оптимального управления, как описано выше, на интервале времени длительностью $\Delta T$. В качестве начального приближения для этого интервала были взяты нулевые начальные условия для сопряженных переменных. Далее происходил последовательный процесс увеличения длительности данного интервала времени с шагом по времени $\Delta T$, где последующие начальные значения сопряженных переменных брались из предыдущего по длительности интервала времени. В таблице 1 представлены начальные приближения метода Ньютона для последовательности интервалов времени.

Таблица 1.

Начальные приближения в методе Ньютона

Интервал времени	${{p}_{1}}(0)$	${{p}_{2}}(0)$	${{p}_{3}}(0)$	${{p}_{4}}(0)$
[0, 10]	0	0	0	0
[0, 20]	–6.2476149729	0.0558616915	–6.2514938495	–0.0636194428
[0, 30]	–10.7938393835	0.1378480362	–10.8035365526	–0.1572423726
[0, 40]	–13.7405216169	0.2605788340	–13.7492193386	–0.2779742774
[0, 50]	–15.8863496236	0.4296283883	–15.8951768600	–0.4472828611
[0, 60]	–17.4251969814	0.6755285405	–17.4349274146	–0.6949894072
[0, 70]	–18.4961040840	1.0140680430	–18.5058913761	–1.0336426276
[0, 80]	–19.2388848848	1.5026903304	–19.2486687961	–1.5222581530

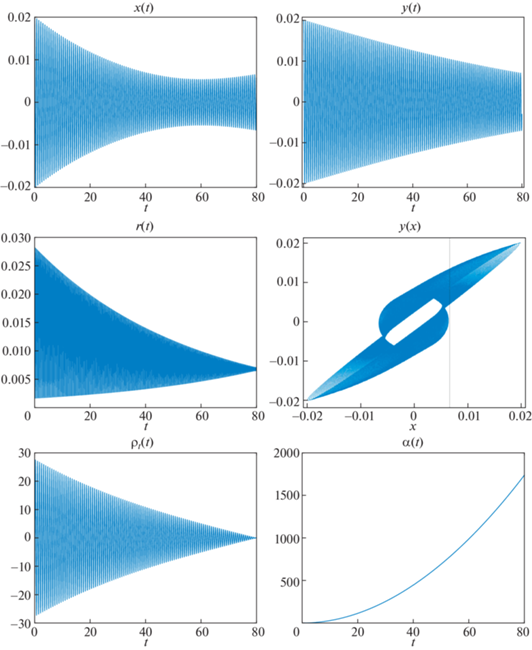
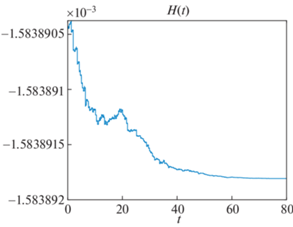
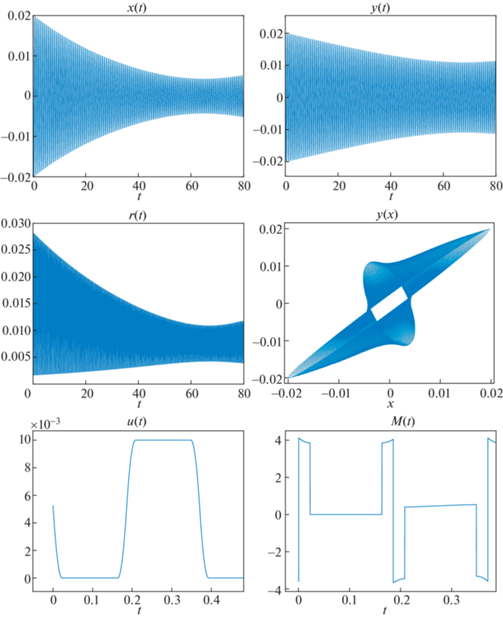
На рис. 2 представлены результаты численного моделирования. Сопряженная переменная ${{p}_{1}}$ сначала колеблется с убывающей амплитудой, а потом, когда колебания полностью пропадают, принимает нулевое терминальное значение. Поведение сопряженных переменных ${{p}_{2}}$, ${{p}_{3}}$, ${{p}_{4}}$ аналогично, поэтому графики для них не приводятся. Функционал $J$ имеет в конце процесса раскрутки примерно следующее значение: 0.4239601. Для контроля точности представлен график для Гамильтониана (рис. 3) в течение процесса раскрутки. Из данного графика видно, что Гамильтониан является приблизительно постоянным, что свидетельствует о правильности и точности проделанных вычислений.

Рис. 2.

Результаты численного моделирования при оптимальном управлении

Рис. 3.

Контроль точности полученных результатов

Заметим из графиков, что частота колебаний $r(t)$ выше по сравнению с частотой колебаний $x(t)$ и $y(t)$. На рис. 4 демонстрируются графики для $x(t)$ (штриховая линия), $y(t)$ (штрих-пунктирная линия), $r(t)$ (сплошная линия). Частота колебаний у $r(t)$ больше примерно в 2 раза из-за того, что в момент максимума амплитуды $x(t)$ амплитуда $y(t)$ примерно равна 0. Верно данное утверждение и в обратном порядке.

Рис. 4.

Сравнение частот колебаний $x(t)$, $y(t)$, $r(t)$

Для оценивания эффективности построенного управления сравним его с другим управлением, определяемым по схеме:

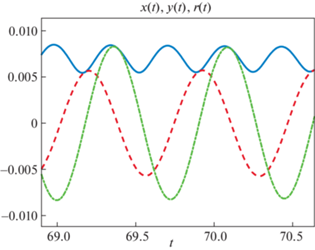
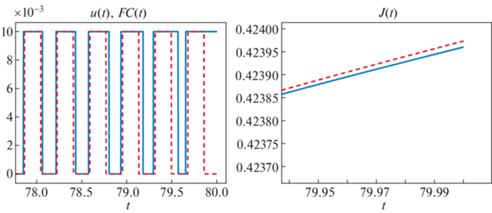
$FC(t) = \left\{ {\begin{array}{*{20}{c}} {{{u}_{0}},\quad x\dot {x} + y\dot {y} > 0,} \\ {0,\quad x\dot {x} + y\dot {y} \leqslant 0.} \end{array}} \right.$

Данное управление относится к классу управлений с обратной связью и отличается от управления ${{u}_{{{\text{init}}}}}(t)$, однако из-за примерно похожего принципа действия успешно минимизирует радиальные колебания. Для сравнения построим $u(t)$, $FC(t)$ на одном графике (см. рис. 5, где показан процесс в течение временного подынтервала, присутствуют отличия управлений). Аналогично поступим и с функцией $J(t)$, используя данные, полученные при интегрировании системы при двух управлениях $u(t)$, $FC(t)$. Сплошная линия на графиках соответствует управлению $u(t)$, штриховая – управлению $FC(t)$.

Рис. 5.

Сравнение управлений

Было обнаружено, что управления $u(t)$, $FC(t)$ имеют относительно похожий характер переключения, но также существуют и отличия, присутствующие в конце рассматриваемого интервала времени (рис. 5). На графике $J(t)$ показано, что при оптимальном управлении $u(t)$ функционал $J$ принимает меньшее значение, чем при управлении $FC(t)$. Однако значение, принимаемое функционалом $J$ при управлении в виде обратной связи, не сильно больше и имеет примерно следующее значение: ${\text{0}}{\text{.4239731}}{\text{.}}$ Поэтому можно утверждать, что данное управление является квазиоптимальным управлением.

6. Процедура сглаживания оптимального управления. Функция оптимального управления представляет собой кусочно-постоянную функцию с некоторым приблизительно постоянным периодом переключения. Процедура сглаживания протекала следующим образом.

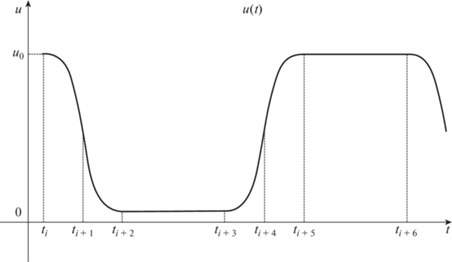
Для каждой точки, в которой происходит переключение управления, необходимо построить отрезок времени, в котором осуществляется устранение разрыва управления. Центром данных отрезков будут точки переключения, а концы отрезка находятся в точках, где управление принимает значения ${{u}_{0}}$ или 0. Отметим, что данный отрезок времени должен быть во много раз меньше периода переключения управления.

Далее из концов отрезка необходимо провести имеющие одинаковый по модулю, но разный по знаку главный коэффициент $q$ ветви двух парабол следующего общего вида:

$u = \pm q{{(t - {{t}_{i}})}^{2}} + b,\quad {\text{где}}\quad b = \left[ \begin{gathered} 0, \hfill \\ {{u}_{0}}, \hfill \\ \end{gathered} \right.\quad q > 0.$

Нулевое значение коэффициента $b$ соответствует положительному знаку перед коэффициентом $q$, а значение ${{u}_{0}}$ коэффициента $b$ – отрицательному знаку перед коэффициентом $q$. Точкой соединения двух парабол выступают точки переключения оптимального управления (середины отрезков), в которых управление принимает значение ${{u}_{0}}{\text{/}}2$. Предлагается следующая итерационная схема определения управления на интервалах времени (рис. 6):

$u = \left\{ \begin{gathered} - q{{(t - {{t}_{i}})}^{2}} + {{u}_{0}},\quad t \in [{{t}_{i}},{{t}_{{i + 1}}}], \hfill \\ q{{(t - {{t}_{{i + 2}}})}^{2}},\quad t \in [{{t}_{{i + 1}}},{{t}_{{i + 2}}}], \hfill \\ 0,\quad t \in [{{t}_{{i + 2}}},{{t}_{{i + 3}}}], \hfill \\ q{{(t - {{t}_{{i + 3}}})}^{2}},\quad t \in [{{t}_{{i + 3}}},{{t}_{{i + 4}}}], \hfill \\ - q{{(t - {{t}_{{i + 5}}})}^{2}} + {{u}_{0}},\quad t \in [{{t}_{{i + 4}}},{{t}_{{i + 5}}}], \hfill \\ {{u}_{0}},\quad t \in [{{t}_{{i + 5}}},{{t}_{{i + 6}}}]. \hfill \\ \end{gathered} \right.$

Здесь ${{t}_{{i + 1}}}$, ${{t}_{{i + 4}}}$ – моменты, когда оптимальное управление должно менять свое значение, ${{t}_{i}}$, ${{t}_{{i + 2}}}$, ${{t}_{{i + 3}}}$, ${{t}_{{i + 5}}}$ – вершины парабол. Получим выражение для определения крутящего момента на данных интервалах времени. Для этого рассмотрим следующие уравнения Лагранжа:

${{I}_{a}}\ddot {\alpha } + {{k}_{\varphi }}(\alpha - \beta ) = M,\quad {{I}_{b}}\ddot {\beta } - {{k}_{\varphi }}(\alpha - \beta ) = 0.$

Вычитанием из первого уравнения второго уравнения, домноженного на коэффициент ${{I}_{a}}{\text{/}}{{I}_{b}}$, можно получить следующее выражение для определения крутящего момента:

(6.1)

$M = {{I}_{a}}\left( {\ddot {\alpha } - \ddot {\beta }} \right) + {{k}_{\varphi }}\left( {1 + \frac{{{{I}_{a}}}}{{{{I}_{b}}}}} \right)\left( {\alpha - \beta } \right).$

Заметим, что выражение для определения крутящего момента может быть переписано следующим образом:

(6.2)

$M = {{I}_{a}}\ddot {u} + \tilde {M}(u,x,y),\quad {\text{где}}\quad \tilde {M}(u,x,y) = [k_{\varphi }^{0} + k_{r}^{\varphi }({{x}^{2}} + {{y}^{2}}) + k_{\varphi }^{\varphi }{{u}^{2}}]\left( {1 + \frac{{{{I}_{a}}}}{{{{I}_{b}}}}} \right)u.$

Тогда итерационная схема определения крутящего момента на интервалах времени (рис. 6) примет следующий вид:

$M = \left\{ \begin{gathered} - 2{{I}_{a}}q + \tilde {M}(u,x,y),\quad t \in [{{t}_{i}},{{t}_{{i + 1}}}], \hfill \\ 2{{I}_{a}}q + \tilde {M}(u,x,y),\quad t \in [{{t}_{{i + 1}}},{{t}_{{i + 2}}}], \hfill \\ 0,\quad t \in [{{t}_{{i + 2}}},{{t}_{{i + 3}}}], \hfill \\ 2{{I}_{a}}q + \tilde {M}(u,x,y),\quad t \in [{{t}_{{i + 3}}},{{t}_{{i + 4}}}], \hfill \\ - 2{{I}_{a}}q + \tilde {M}(u,x,y),\quad t \in [{{t}_{{i + 4}}},{{t}_{{i + 5}}}], \hfill \\ \tilde {M}(u,x,y),\quad t \in [{{t}_{{i + 5}}},{{t}_{{i + 6}}}]. \hfill \\ \end{gathered} \right.$

Рис. 6.

Схема для процедуры сглаживания оптимального управления

7. Численное моделирование при непрерывном управлении. При расчете были использованы следующие параметры системы с ненулевой начальной скоростью и ненулевым начальным отклонением центра масс второго диска (его начальный угол и начальная угловая скорость равны нулю):

${{m}_{a}} = 1\,\,{\text{кг,}}\quad {{m}_{b}} = 1\,\,{\text{кг,}}\quad {{r}_{a}} = 0.621\,\,{\text{м,}}\quad {{r}_{b}} = 0.644\,\,{\text{м,}}\quad {{I}_{a}} = 0.193\,\,{\text{кг}}\,\,{{{\text{м}}}^{{\text{2}}}}{\text{,}}\quad {{I}_{b}} = 0.208~\,\,{\text{кг}}\,\,{{{\text{м}}}^{2}},$

$k = 10\,\,{\text{Н/м,}}\quad l = 0.012\,\,{\text{м,}}\quad N = 10,\quad T = 80~\,\,{\text{с}},\quad {{u}_{0}} = 0.01~\,\,{\text{рад,}}\quad q = 10\,\,{\text{рад/}}{{{\text{с}}}^{{\text{2}}}}{\text{,}}$

$x(0) = 0.02\,\,{\text{м,}}\quad {{{v}}_{x}}(0) = - 0.01\,\,{\text{м/с,}}\quad y(0) = 0.02\,\,{\text{м,}}\quad {{{v}}_{y}}(0) = 0.01\,\,{\text{м/с}}{\text{.}}$

Получены следующие коэффициенты упругой модели:

$k_{r}^{0} = 75\,\,{\text{Н/м}},\quad k_{\varphi }^{0} = 20\,\,{\text{Н}}\,\,{\text{м}},\quad k_{r}^{\varphi } = 9375\,\,{\text{Н/м,}}\quad k_{r}^{r} = - 5857\,\,{\text{Н/}}{{{\text{м}}}^{{\text{3}}}}{\text{,}}\quad k_{\varphi }^{\varphi } = 7500\,\,{\text{Н}}\,\,{\text{м,}}$

а также следующие результаты (рис. 7). Функционал в конце процесса раскрутки принял примерное значение 0.4463841. Отметим, что при увеличении значения коэффициента q фазовая траектория центра масс диска $b$ будет иметь вид окружности к концу процесса раскрутки.

Рис. 7.

Результаты моделирования при применении процедуры сглаживания

Заключение. Описана постановка задачи оптимального подавления упругих колебаний, возникающих при раскрутке двухмассовой механической системы. Развит и проиллюстрирован алгоритм применения метода последовательных приближений с улучшенной сходимостью и метода Ньютона. Обнаружено квазиоптимальное управление в виде обратной связи, успешно минимизирующее амплитуду радиальных колебаний механической системы. Данный подход может быть использован в технических устройствах, минимизирующих амплитуду упругих колебаний раскручиваемых систем. Эффективность данного подхода заключается в том, что применение данного управления в технических системах не требует затрат на численный расчет управления. С помощью процедуры сглаживания для оптимального управления построено непрерывное управление, уменьшающее амплитуду радиальных колебаний.

Список литературы

Крылов И.А., Черноусько Ф.Л. О методе последовательных приближений для решения задач оптимального управления // ЖВМиМФ. 1962. Т. 2. № 6. С. 1132–1139.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1983.
Решмин С.А., Васенин С.А. Применение метода последовательных приближений при решении краевых задач принципа максимума на примере задачи управления раскручиванием двухмассовой системы // Modern European Researches. 2022. № 3 (Т. 1). С. 186–196.
Дивеев А.И., Константинов С.В. Исследование практической сходимости эволюционных алгоритмов оптимального программного управления колесным роботом // Изв. РАН. ТиСУ. 2018. № 4. С. 80–106.
Garcia Almuzara J.L., Flügge-Lotz I. Minimum Time Control of a Nonlinear System // J. Differen. Equations. 1968. V. 4. № 1. P. 12–39.
Ovseevich A.I. Complexity of the Minimum-Time Damping of a Physical Pendulum // SIAM J. on Control and Optimization. 2014. V. 52. № 1. P. 82–96.
Решмин С.А. Бифуркация в задаче быстродействия для нелинейной системы второго порядка // ПММ. 2009. Т. 73. Вып. 4. С. 562–572.
Решмин С.А. Пороговая абсолютная величина релейного управления при наискорейшем приведении спутника в желаемое угловое положение // Изв. РАН. ТиСУ. 2018. № 5. С. 30–41.
Галяев А.А., Лысенко П.В. Оптимальное по энергии управление гармоническим осциллятором // АиТ. 2019. № 1. С. 21–37.
Лавровский Э.К. О быстродействии в задаче управления вертикальным положением маятника с помощью перемещения его основания // Изв. РАН. ТиСУ. 2021. № 1. С. 42–51.
Каюмов О.Р. Оптимальное по быстродействию перемещение тележки с маятником // Изв. РАН. ТиСУ. 2021. № 1. С. 30–41.
Решмин С.А. Применение метода Ньютона при решении краевых задач принципа максимума на примере задачи об оптимальном раскручивании двухмассовой системы // Modern European Researches. 2021. № 2 (Т. 1). С. 114–122.
Каюмов О.Р. Оптимальный по быстродействию поворот пружинного маятника // Изв. РАН. ТиСУ. 2023. № 5. C. 43–56.
Розенблат Г.М. Об оптимальном повороте твердого тела при помощи внутренних сил // Доклады Российской академии наук. Математика, информатика, процессы управления. 2022. Т. 505. № 1. С. 92–99.
Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы // ДАН. 2018. Т. 480. № 5. С. 528–532.
Черноусько Ф.Л., Шматков А.М. Оптимальное управление поворотом твердого тела при помощи внутренней массы // Изв. РАН. ТиСУ. 2019. № 3. С. 10–23.
Наумов Н.Ю., Черноусько Ф.Л. Переориентация твердого тела, управляемого посредством подвижной внутренней массы // Изв. РАН. ТиСУ. 2019. № 2. С. 98–105.
Привалов Е.А., Жбанов Ю.К. Стержневая конструкция упругого подвеса инертной массы // Изв. РАН. МТТ. 2018. № 5. С. 19–28.
Журавлев В.Ф. Двумерный осциллятор Ван дер Поля с внешним управлением // Нелинейная динамика. 2016. Т. 12. № 2. С. 211–222.
Журавлев В.Ф. Пространственный осциллятор Ван-дер-Поля. Технические приложения // Изв. РАН. МТТ. 2020. № 1. С. 158–164.
Овсеевич А.И., Федоров А.К. Управление в форме синтеза для успокоения системы осцилляторов // АиТ. 2015. № 11. С. 3–17.
Ананьевский И.М., Овсеевич А.И. Управляемое перемещение линейной цепочки осцилляторов // Изв. РАН. ТиСУ. 2021. Т. 5. № 5. С. 18–26.
Воеводин П.С., Заболотнов Ю.М. О стабилизации движения электродинамической тросовой системы на околоземной орбите // Изв. РАН. МТТ. 2019. № 4. С. 48–62.
Беллман Р. Динамическое программирование. М.: Изд-во иностр. лит., 1960.
Решмин С.А. Качественный анализ силы тяги при вращении ведущего колеса с невесомой шиной // Тр. Математического ин-та им. В.А. Стеклова. 2021. Т. 315. С. 211–221.
Розоноэр Л.И. Принцип максимума Л.С. Понтрягина в теории оптимальных систем. I // АиТ. 1959. Т. 20. Вып. 10. С. 1320–1334.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал