Известия РАН. Теория и системы управления, 2023, № 6, стр. 60-66
НАВЕДЕНИЕ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА С ТЕПЛОВИЗИОННЫМ КОРРЕЛЯЦИОННО-КОНТРАСТНЫМ АЛГОРИТМОМ АВТОСОПРОВОЖДЕНИЯ В УСЛОВИЯХ ИНФОРМАЦИОННОГО ПРОТИВОДЕЙСТВИЯ
В. А. Болдинов a, *, В. А. Бухалёв b, А. А. Скрынников a, c, Б. Л. Шапиро b
a Московский авиационный ин-т (национальный исследовательский ун-т)
Москва, Россия
b Московский научно-исследовательский телевизионный ин-т
Москва, Россия
c Государственный научно-исследовательский ин-т авиационных систем
Москва, Россия
* E-mail: viktorboldinov@mail.ru
Поступила в редакцию 11.05.2023
После доработки 30.06.2023
Принята к публикации 31.07.2023
- EDN: GPTPAT
- DOI: 10.31857/S0002338823060045
Аннотация
Рассматривается задача построения алгоритма автосопровождения наземного объекта для системы наведения беспилотного летательного аппарата. В состав системы наведения входят следящий тепловизионный координатор цели с комбинированным корреляционно-контрастным алгоритмом пеленгации и бесплатформенная инерциальная навигационная система. Наведение происходит в условиях информационного противодействия, вызывающего случайные перерывы информации и случайные изменения мощности помех, которые фиксируются соответствующими индикаторами. Получен комбинированный помехоустойчивый алгоритм автосопровождения, использующий показания индикаторов перерывов информации и мощности помех и измерения углов пеленга и основанный на теории систем со случайной скачкообразной структурой. Приведен пример, иллюстрирующий работу алгоритма и демонстрирующий удовлетворительную точность автосопровождения.
Введение. Алгоритмы автосопровождения в тепловизионных и телевизионных системах наведения (СН) беспилотных летательных аппаратов (БПЛА) на наземные объекты можно разделить на два класса: контрастные и корреляционные.
В контрастных алгоритмах происходит выделение некоторых элементов изображения по контрасту с окружающим фоном, формирование из них объектов, которые могут рассматриваться в качестве гипотетических целей, выбор одного из них как цели наведения, формирование угла рассогласования между направлениями на цель и продольной оси следящего координатора для выполнения автосопровождения и наведения БПЛА [1].
В корреляционных алгоритмах угол рассогласования определяется по критерию максимального совпадения наблюдаемого изображения с эталоном, первоначально записанным в памяти компьютера и периодически обновляемым в процессе наведения. При этом совпадение текущего наблюдаемого изображения и эталона формируется на основе определения их взаимной корреляционной функции [2].
В состав СН входит бесплатформенная инерциальная навигационная система (БИНС), которая работает либо автономно, либо корректируется с командного пункта или системой спутниковой навигации. Информационное противодействие наведению БПЛА приводит к увеличению мощности помех в измерительных каналах вплоть до полного прекращения поступления информации об угловых координатах цели [2–4].
В статье рассматривается задача построения комбинированного корреляционно-контрастного алгоритма автосопровождения при наведении БПЛА на наземный объект по заданной траектории в условиях информационного противодействия.
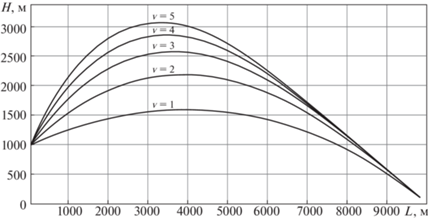
1. Постановка задачи. Математическая формулировка задачи имеет следующий вид. Требуемая траектория БПЛА в вертикальной плоскости описывается формулами [4]
(1.1)
$\bar {\varepsilon }(t) = ({{\bar {\varepsilon }}_{0}} - {{\bar {\varepsilon }}_{n}}){{\left( {\frac{\tau }{{{{t}_{n}}}}} \right)}^{\nu }} + {{\bar {\varepsilon }}_{n}},\quad \bar {\omega }(t) = \frac{\nu }{{{{t}_{n}}}}({{\bar {\varepsilon }}_{0}} - {{\bar {\varepsilon }}_{n}}){{\left( {\frac{\tau }{{{{t}_{n}}}}} \right)}^{{\nu - 1}}}$Формулы (1.1) эквивалентны системе уравнений [4]:
(1.2)
$\dot {\bar {\varepsilon }}(t) = \bar {\omega }{\kern 1pt} (t),\quad \dot {\bar {\omega }}{\kern 1pt} (t) = {{\tau }^{{ - 1}}}(t)(1 - \nu ){\kern 1pt} \bar {\omega }{\kern 1pt} (t),$(1.3)
$\bar {\varepsilon }(0) = {{\bar {\varepsilon }}_{0}},\quad \bar {\varepsilon }({{t}_{n}}) = {{\bar {\varepsilon }}_{n}},\quad \bar {\omega }{\kern 1pt} (0) = t_{n}^{{ - 1}}\nu {\kern 1pt} ({{\bar {\varepsilon }}_{n}} - {{\bar {\varepsilon }}_{0}}),\quad \bar {\omega }{\kern 1pt} ({{t}_{n}}) = 0.$Реальная траектория отличается от требуемой и описывается уравнениями [4]
(1.4)
$\dot {\varepsilon }(t) = \omega (t),\quad \dot {\omega }(t) = {{\tau }^{{ - 1}}}(t)\left[ {2\omega \left( t \right) + u\left( t \right) + \xi \left( t \right)} \right],$(1.5)
$u\left( t \right) = - \left[ {{{\tau }^{{ - 1}}}\left( t \right){{c}_{\varepsilon }}{{{\hat {\varepsilon }}}^{{\text{о}}}}\left( t \right) + {{c}_{\omega }}{{{\hat {\omega }}}^{{\text{о}}}}\left( t \right) + \left( {\nu + 1} \right)\bar {\omega }\left( t \right)} \right].$В законе управления (1.5) ${{c}_{\varepsilon }}$ и ${{c}_{\omega }}$ – параметрически оптимизированные постоянные коэффициенты, а ${{\hat {\varepsilon }}^{{\text{o}}}}\left( t \right)$ и ${{\hat {\omega }}^{o}}\left( t \right)$ – оценки переменных ${{\varepsilon }^{{\text{о}}}}\left( t \right) \triangleq \varepsilon \left( t \right) - \bar {\varepsilon }\left( t \right)$ и ${{\omega }^{{\text{о}}}}\left( t \right) \triangleq \omega \left( t \right) - \bar {\omega }\left( t \right)$.
В угломерных каналах следящего координатора цели измеряются сигналы ${{z}^{i}}\left( t \right)$, $i = 1,2$:
(1.6)
$\begin{gathered} {{z}^{1}}\left( t \right) = \delta ({{s}^{{\left( 1 \right)}}}\left( t \right),2)\left[ {\varepsilon \left( t \right) - \hat {\varepsilon }\left( t \right)} \right] + \sqrt {{{Q}^{{\left( 1 \right)}}}({{\sigma }^{{\left( 1 \right)}}}\left( t \right))} {{\zeta }^{{\left( 1 \right)}}}\left( t \right), \\ {{z}^{2}}\left( t \right) = \delta ({{s}^{{\left( 2 \right)}}}\left( t \right),2)\left[ {\varepsilon \left( t \right) - \hat {\varepsilon }\left( t \right)} \right] + {{\tau }^{{ - 1}}}\sqrt {{{Q}^{{\left( 2 \right)}}}({{\sigma }^{{\left( 2 \right)}}}\left( t \right))} {{\zeta }^{{\left( 2 \right)}}}\left( t \right), \\ \end{gathered} $(1.7)
$\varphi _{k}^{{\left( i \right)}}(\sigma _{{k + 1}}^{{\left( i \right)}} = j\left| {\sigma _{k}^{{\left( i \right)}} = j} \right.) = 1 - \sum\limits_{\nu = 1,\nu \ne j}^{{{N}^{{\left( i \right)}}}} {\varphi _{k}^{{\left( i \right)}}\left( {\nu \left| j \right.} \right)} .$Структура ${{s}^{{\left( i \right)}}}\left( t \right)$ наблюдается с помощью индикатора, выходной сигнал которого ${{r}^{{\left( i \right)}}}\left( t \right)$ (или в дискретной форме $r_{k}^{{\left( i \right)}} = {{r}^{{\left( i \right)}}}\left( {{{t}_{k}}} \right)$) – условная марковская цепь, заданная условными вероятностями переходов при фиксированном $s_{k}^{{\left( i \right)}}$: $\pi _{{k + 1}}^{{\left( i \right)}}\left( {r_{{k + 1}}^{{\left( i \right)}}\left| {r_{k}^{{\left( i \right)}},s_{{k + 1}}^{{\left( i \right)}}} \right.} \right)$.
Разница в формулах для ${{z}^{{\left( 1 \right)}}}\left( t \right)$ и ${{z}^{{\left( 2 \right)}}}\left( t \right)$ в (1.6) объясняется различным характером ошибок измерения в контрастных и корреляционных пеленгаторах: в первых отношение “сигнал–шум” по мере приближения к цели увеличивается приблизительно прямо пропорционально квадрату дальности до цели, а в корреляционных пеленгаторах, наоборот, уменьшается обратно пропорционально квадрату дальности вследствие роста дисперсии ошибки измерения угла рассогласования $\varepsilon \left( t \right) - \hat {\varepsilon }\left( t \right)$, вызванной периодической перезаписью эталона изображения.
Структура ${{\sigma }^{{\left( i \right)}}}\left( t \right)$ наблюдается с помощью индикатора ${{\rho }^{{\left( i \right)}}}\left( t \right)$ (или в дискретной форме $\rho _{k}^{{\left( i \right)}} = {{\rho }^{{\left( i \right)}}}\left( {{{t}_{k}}} \right)$) – условная марковская цепь с ${{N}^{{\left( i \right)}}}$ состояниями: $\rho _{k}^{{\left( i \right)}} = \overline {1,{{N}^{{\left( i \right)}}}} $, заданная условными вероятностями переходов $\psi _{{k + 1}}^{{\left( i \right)}}\left( {\rho _{{k + 1}}^{{\left( i \right)}}\left| {\rho _{k}^{{\left( i \right)}},\sigma _{{k + 1}}^{{\left( i \right)}}} \right.} \right)$.
Вероятности переходов индикаторов перерыва информации и индикаторов мощности помех описываются формулами (верхний индекс $i$ опущен для простоты записи):
(1.8)
${{\pi }_{{k + 1}}}\left( {{{r}_{{k + 1}}}\left| {{{r}_{k}},{{s}_{{k + 1}}}} \right.} \right) = \left\{ \begin{gathered} 1 - \pi _{{k + 1}}^{r},\quad {{r}_{{k + 1}}} \ne {{r}_{k}}, \hfill \\ \pi _{{k + 1}}^{r},\quad {{r}_{{k + 1}}} = {{r}_{k}}, \hfill \\ \end{gathered} \right.$(1.9)
${{\psi }_{{k + 1}}}\left( {{{\rho }_{{k + 1}}}\left| {{{\rho }_{k}},{{\sigma }_{{k + 1}}}} \right.} \right) = \left\{ \begin{gathered} 1 - \pi _{{k + 1}}^{\rho },\quad {{\rho }_{{k + 1}}} \ne {{\rho }_{k}}, \hfill \\ \pi _{{k + 1}}^{\rho },\quad \quad \,{{\rho }_{{k + 1}}} = {{\rho }_{k}}, \hfill \\ \end{gathered} \right.$Требуется построить алгоритм автосопровождения цели, основанный на измерениях угловых координат ${{z}^{{\left( i \right)}}}\left( t \right)$ и показаниях индикаторов перерывов информации ${{r}^{{\left( i \right)}}}\left( t \right)$ и индикаторов мощности помех ${{\rho }^{{\left( i \right)}}}\left( t \right)$ в контрастном (i = 1) и корреляционном (i = 2) пеленгаторах, а также на показаниях БИНС.
2. Алгортм автосопровождения. Приближенно-оптимальный алгоритм, базирующийся на теории систем со случайной скачкообразной структурой (ССС) [4, 5] состоит из следующих блоков: 1) классификаторы перерывов информации, вычисляющие вероятности перерывов $\hat {p}_{k}^{{\left( i \right)}}(s_{k}^{{\left( i \right)}})$; 2) идентификаторы перерывов информации, определяющие оценки ${{\hat {s}}^{{\left( i \right)}}}\left( t \right)$ состояний ${{s}^{{\left( i \right)}}}\left( t \right)$; 3) классификаторы и идентификаторы мощности помех, расчитывающие оценки ${{\hat {Q}}^{{\left( i \right)}}}\left( t \right)$, $i = 1,2$; 4) фильтр, вычисляющий оценку $\hat {\varepsilon }\left( t \right)$ угла визирования цели $\varepsilon \left( t \right)$.
Алгоритм описывается следующими уравнениями.
1. Кассификатор перерывов информации:
(2.1)
$\begin{gathered} \hat {p}_{{k + 1}}^{{\left( i \right)}}\left( 1 \right) = {{\left[ {1 + \frac{{\tilde {p}_{{\left( {k + 1} \right)}}^{{\left( i \right)}}\left( 2 \right)\pi _{{k + 1}}^{{\left( i \right)}}\left( {r_{{k + 1}}^{{\left( i \right)}}\left| {r_{k}^{{\left( i \right)}},2} \right.} \right)}}{{\tilde {p}_{{\left( {k + 1} \right)}}^{{\left( i \right)}}\left( 1 \right)\pi _{{k + 1}}^{{\left( i \right)}}\left( {r_{{k + 1}}^{{\left( i \right)}}\left| {r_{k}^{{\left( i \right)}},1} \right.} \right)}}} \right]}^{{ - 1}}},\quad \hat {p}_{{k + 1}}^{{\left( i \right)}}\left( 2 \right) = 1 - \hat {p}_{{k + 1}}^{{\left( i \right)}}\left( 1 \right), \\ \tilde {p}_{{k + 1}}^{{\left( i \right)}}\left( 1 \right) = q_{k}^{{\left( i \right)}}\left( {1\left| 1 \right.} \right)\hat {p}_{k}^{{\left( i \right)}}\left( 1 \right) + q_{k}^{{\left( i \right)}}\left( {1\left| 2 \right.} \right)\hat {p}_{k}^{{\left( i \right)}}\left( 2 \right),\quad \tilde {p}_{{k + 1}}^{{\left( i \right)}}\left( 2 \right) = 1 - \tilde {p}_{{k + 1}}^{{\left( i \right)}}\left( 1 \right). \\ \end{gathered} $2. Идентификатор перерывов информации:
(2.2)
$\begin{gathered} {{s}^{{\left( i \right)}}}\left( t \right) = \left\{ \begin{gathered} 1\quad {\text{при}}\quad {{{\hat {p}}}^{{\left( i \right)}}}\left( 1 \right) \geqslant p_{{{\text{пор}}}}^{{\left( i \right)}}, \hfill \\ 2\quad {\text{при}}\quad {{{\hat {p}}}^{{\left( i \right)}}}\left( 1 \right) < p_{{{\text{пор}}}}^{{\left( i \right)}}, \hfill \\ \end{gathered} \right. \\ {{{\hat {p}}}^{{\left( i \right)}}}\left( 1 \right) = \hat {p}_{{k + 1}}^{{\left( i \right)}}\left( 1 \right) + \frac{{\hat {p}_{k}^{{\left( i \right)}}\left( 1 \right)}}{2},\quad i = 1,2, \\ \end{gathered} $3. Классификатор мощности помех:
(2.3)
$\begin{gathered} \hat {P}_{{k + 1}}^{{\left( i \right)}}(\sigma _{{k + 1}}^{{\left( i \right)}}) = \frac{{\tilde {P}_{{k + 1}}^{{\left( i \right)}}(\sigma _{{k + 1}}^{{\left( i \right)}})\psi _{{k + 1}}^{{\left( i \right)}}(\rho _{{k + 1}}^{{\left( i \right)}}\left| {\rho _{k}^{{\left( i \right)}},\sigma _{{k + 1}}^{{\left( i \right)}}} \right.)}}{{\sum\limits_{\sigma _{{k + 1}}^{{\left( i \right)}}} {\tilde {P}_{{k + 1}}^{{\left( i \right)}}(\sigma _{{k + 1}}^{{\left( i \right)}})\psi _{{k + 1}}^{{\left( i \right)}}(\rho _{{k + 1}}^{{\left( i \right)}}\left| {\rho _{k}^{{\left( i \right)}},\sigma _{{k + 1}}^{{\left( i \right)}}} \right.)} }}, \\ \tilde {P}_{{k + 1}}^{{\left( i \right)}}(\sigma _{{k + 1}}^{{\left( i \right)}}) = \sum\limits_{\sigma _{k}^{{\left( i \right)}}} {\varphi _{{k + 1}}^{{\left( i \right)}}(\sigma _{{k + 1}}^{{\left( i \right)}}\left| {\sigma _{k}^{{\left( i \right)}}} \right.)} \hat {P}_{k}^{{\left( i \right)}}(\sigma _{k}^{{\left( i \right)}}),\quad \sigma _{k}^{{\left( i \right)}} = \overline {1,N} . \\ \end{gathered} $4. Идентификатор мощности помех:
(2.4)
$\begin{gathered} \hat {Q}_{k}^{{\left( i \right)}} = \sum\limits_{\sigma _{k}^{{\left( i \right)}}} {\hat {P}_{k}^{{\left( i \right)}}(\sigma _{k}^{{\left( i \right)}})} Q_{k}^{{\left( i \right)}}(\sigma _{k}^{{\left( i \right)}}),\quad \sigma _{k}^{{\left( i \right)}} = \overline {1,N} , \\ {{{\hat {Q}}}^{{\left( i \right)}}}\left( t \right) = \hat {Q}_{{k + 1}}^{{\left( i \right)}} + \frac{{\hat {Q}_{k}^{{\left( i \right)}}}}{2}. \\ \end{gathered} $5. Фильтр:
(2.5)
$\hat {\varepsilon }\left( t \right) = \hat {\omega }\left( t \right) + \delta ({{\hat {s}}^{{\left( 1 \right)}}}\left( t \right),2)k_{\varepsilon }^{{\left( 1 \right)}}\left( t \right){{\tau }^{{ - 1}}}{{z}^{{\left( 1 \right)}}}\left( t \right) + \delta ({{\hat {s}}^{2}}\left( t \right),2)k_{\varepsilon }^{{\left( 2 \right)}}\left( t \right){{z}^{{\left( 2 \right)}}}\left( t \right),$3. Пример. Рассмотрим пример представленной задачи при следующих исходных данных: $\Delta f = 0.1$ Гц, $\Delta t = 0.1$ с, $s_{k}^{{\left( i \right)}} = 1,\;2$, $\sigma _{k}^{{\left( i \right)}} = 1,\;2$, $Q_{k}^{{\left( i \right)}} = [Q_{{\min }}^{{\left( i \right)}},Q_{{\max }}^{{\left( i \right)}}]$.
Результаты имитационного математического моделирования представлены на рис. 2–5.
Рис. 2.
Структура перерывов информации и их распознавание в контрастном и корреляционном пеленгаторах
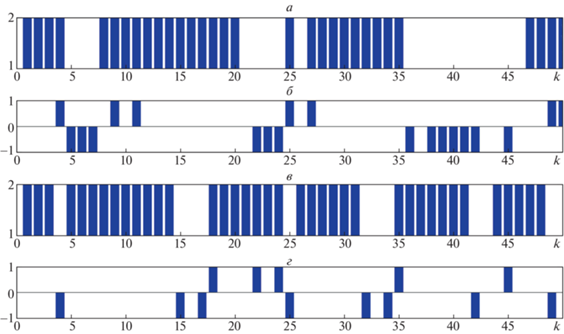
Рис. 3.
Структура изменения мощности помех и распознавание изменения мощности помех в контрастном и корреляционном пеленгаторах
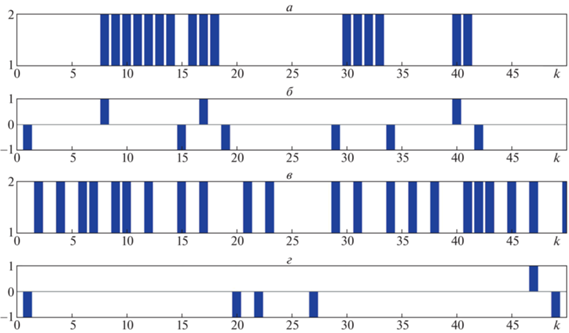
На графиках рис. 2 изображено: а – перерывы информации в контрастном пеленгаторе, где $s_{k}^{{\left( 1 \right)}} = 1$ – “есть перерыв”, а $s_{k}^{{\left( 1 \right)}} = 2$ – “нет перерыва”; б – распознавание перерывов информации $\Delta s_{k}^{{\left( 1 \right)}} = s_{k}^{{\left( 1 \right)}} - \hat {s}_{k}^{{\left( 1 \right)}}$, где $\Delta s_{k}^{{\left( 1 \right)}} = 0$ – “правильные решения”, $\Delta s_{k}^{{\left( 1 \right)}} = 1$ – “пропуск сигнала”, а $\Delta s_{k}^{{\left( 1 \right)}} = - 1$ – “ложная тревога”; в, г – результаты, аналогичные а и б, только для второго (корреляционного) пеленгатора.
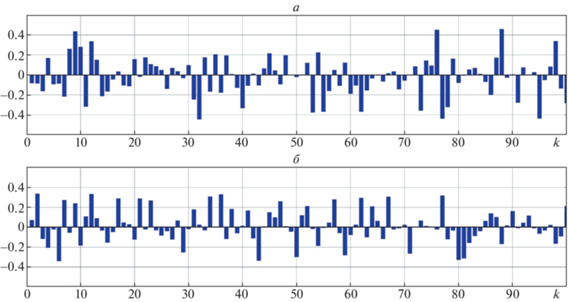
На графиках рис. 3 отображено: а – структура изменения мощности помех в контрастном пеленгаторе, где $\sigma _{k}^{{\left( 1 \right)}} = 1$ – “минимальная мощность помех $Q_{{\min }}^{{(1)}}$”, а $\sigma _{k}^{{\left( 1 \right)}} = 2$ – “максимальная мощность помех $Q_{{\max }}^{{(1)}}$”; б – распознавание мощности помех в контрастном пеленгаторе $\Delta \sigma _{k}^{{\left( 1 \right)}} = \sigma _{k}^{{\left( 1 \right)}} - \hat {Q}_{k}^{{\left( 1 \right)}}$, где $\Delta \sigma _{k}^{{\left( 1 \right)}} = 0$ – “правильные решения”, а $\Delta \sigma _{k}^{{\left( 1 \right)}} = 1$ – “ошибочные решения”; в, г – результаты, аналогичные а и б, только для корреляционного пеленгатора.
На графиках рис. 4 рассмотрены помехи (ошибок измерений) в контрастном ($\zeta _{k}^{{\left( 1 \right)}}$) и корреляционном ($\zeta _{k}^{{\left( 2 \right)}}$) пеленгаторах, представляющие собой центрированные гауссовские белые шумы с мощностью $Q_{k}^{{\left( 1 \right)}}$ и $Q_{k}^{{\left( 2 \right)}}$ соответственно.
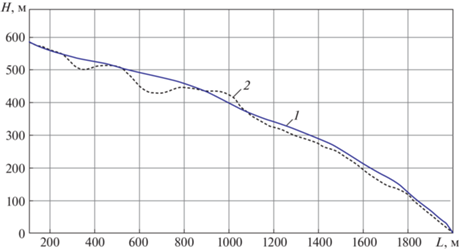
На рис. 5 приведены траектории полета БПЛА в вертикальной плоскости с углом пеленга цели ${{\varepsilon }_{k}}$ (траектория 1) и его оценкой ${{\hat {\varepsilon }}_{k}}$ (траектория 2), полученной разработанным корреляционно-контрастным алгоритмом автосопровождения цели тепловизионной СН БПЛА.
Заключение. Предложен метод построения приближенно-оптимального алгоритма автосопровождения неподвижного наземного объекта комбинированной СН БПЛА. СН включает в себя контрастный и корреляционный тепловизионные пеленгаторы и БИНС, которые могут работать как вместе, так и по отдельности в зависимости от условий применения и характеристик информационного противодействия.
Противодействие приводит к значительному и неточно определяемому изменению отношения “сигнал–шум” вплоть до перерывов в поступлении информации о координатах объекта. Алгоритм автосопровождения, построенный на основе теории систем ССС, обладает свойством сходимости оценок угловых координат объекта в указанных условиях.
Список литературы
Ллойд Дж. Системы тепловидения. М.: Мир, 1978.
Бухалëв В.А., Болдинов В.А., Сухачев А.Б., Шапиро Б.Л. Управление беспилотным летательным аппаратом с тепловизионным корреляционным координатором в условиях низкочастотных помех // Информационно-измерительные и управляющие системы. 2019. № 7. Т. 17. С. 13–20.
Баханов Л.Е., Давыдов А.Н., Корниенко В.Н. и др. Системы управления вооружением истребителей. Основы интеллекта многофункционального самолета. Под ред. Федосова Е.А. М.: Машиностроение, 2005. 400 с.
Бухалёв В.А., Скрынников А.А., Болдинов В.А. Алгоритмическая помехозащита беспилотных летательных аппаратов. М.: ФИЗМАТЛИТ, 2018. 192 с.
Бухалёв В.А. Распознавание, оценивание и управление в системах со случайной скачкообразной структурой. М.: Наука. ФИЗМАТЛИТ, 1996. 287 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления