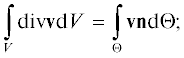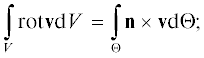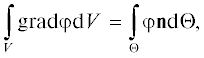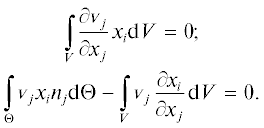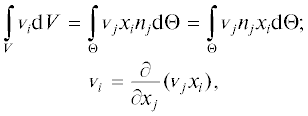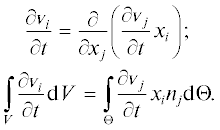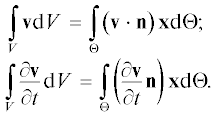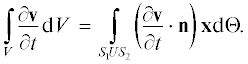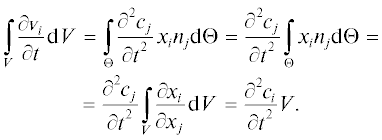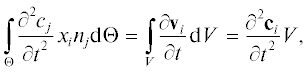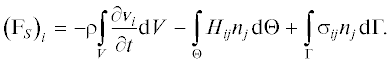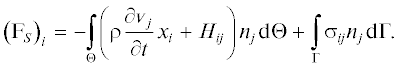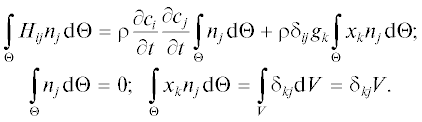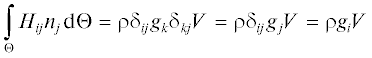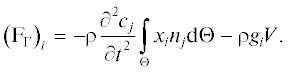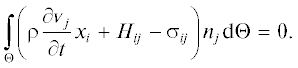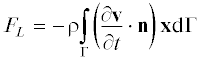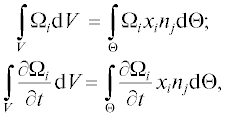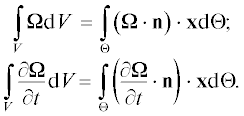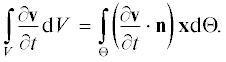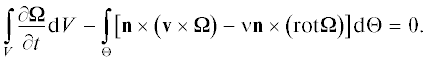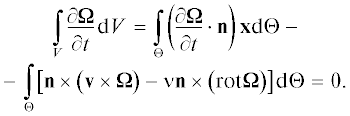Теплоэнергетика, 2021, № 12, стр. 33-44

Методы упрощения математической модели расчета течений в проточной части гидравлических турбин

S. Fialová^a, *, F. Pochylý^a, А. В. Волков^b, А. В. Рыженков^b, А. А. Дружинин^b, **

^a Brno University of Technology (Технический университет г. Брно), Victor Kaplan Department of Fluids Engineering (кафедра механики жидкостей им. В. Каплана)
61669 Brno, Technická 2896/2, Czech Republic

^b Национальный исследовательский университет “Московский энергетический институт”
111250 Москва, Красноказарменная ул., д. 14, Россия

^* E-mail: Fialova@fme.vutbr.cz
^** E-mail: Alexey2959@mail.ru

Поступила в редакцию 30.04.2021
После доработки 25.05.2021
Принята к публикации 26.05.2021

DOI: 10.1134/S0040363621120031

Полный текст (PDF)

Аннотация

В представленной работе внимание уделено фундаментальным исследованиям одной из серьезных проблем, возникающих при эксплуатации гидравлических турбин, – образованию вихревого жгута за рабочим колесом. Отмечается, что в настоящее время рабочий диапазон этих машин требует расширения из-за динамично меняющейся нагрузки энергетических сетей в суточном и сезонном циклах, что приводит к увеличению времени работы гидравлических турбин в нерасчетных или нежелательных зонах эксплуатации, в том числе и характеризующихся риском образования вихревого жгута разной степени интенсивности. Для описания этого сложного движения жидкости была разработана математическая модель, описывающая движение вихревого жгута за рабочим колесом гидравлических турбин. В данной статье рассматриваются главным образом фундаментальные вопросы создания математической модели. Показаны методы упрощения математической записи уравнений структуры вихревого жгута, образующегося в проточной части. Используемые в данном случае уравнения математической физики, содержащие зависимую переменную, и их прикладное применение к жидкостям, где они принимают форму уравнений Навье – Стокса, описывают изменения во времени выбранных величин в контролируемом объеме, создаваемом потоком, проходящим через границу объема. Показано, что граничные условия имеют большое влияние на нестационарные вихревые структуры. Сформулирован частный случай для потенциального силового поля с использованием тензора напряжений, которому подчиняются уравнения равновесия. Это дает возможность описать сложное движение в жидкостях, не прибегая к применению громоздкой формы записи уравнений Навье – Стокса для вихревых структур.

Ключевые слова: нестационарное течение, вихревые структуры, несжимаемая жидкость, уравнения Навье–Стокса, нестационарный член, теорема о дивергенции, метод конечных объемов

Исследование течения нестационарных вихревых структур жидкости в сложных каналах по-прежнему представляет собой важную проблему механики жидкости. Теоретический анализ такого течения основан на уравнениях Навье – Стокса [1–3] и во многих случаях чрезвычайно сложен даже для класса так называемых ньютоновских жидкостей [4]. Доказательство существования единственности и гладкости математического решения системы уравнений Навье – Стокса было объявлено Математическим институтом Клэя одной из семи проблем тысячелетия. Отсутствие же такого доказательства существенно ограничивает понимание течения нестационарных вихревых структур жидкости. Глобально определенные гладкие решения существуют только для двухмерных течений, для трехмерных течений были найдены только слабые решения, удовлетворяющие уравнениям в среднем, а не поточечно. Такие трудности получения аналитических решений делают приближенные численные решения уравнений Навье – Стокса чрезвычайно важными. В настоящее время среди численных методов, используемых для решения многих задач, преобладает метод конечных (контрольных) объемов [3, 5].

Образование вихревых структур зависит от граничных условий и вязкости жидкости [6]. Это приводит к тому, что частные решения уравнений Навье – Стокса становятся очень сложными, если граница области жидкости сложная и нерегулярная, изменяется во времени, т.е. если поток нестационарен и/или окружающее тело не является абсолютно твердым [7]. Эта ситуация является характерной при анализе взаимодействия жидкость – конструкция. В последние десятилетия необходимость проведения такого анализа постоянно возрастала [8–10]. Кроме того, неньютоновские жидкости, например такая, как бингамовская жидкость [11, 12], делают решение этого уравнения еще более сложным.

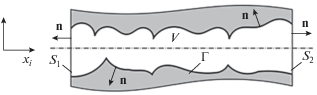
Исследование влияния граничных условий на образование вихревых структур в области жидкости V может быть упрощено благодаря использованию операторов rot (вращения), div (дивергенции) и grad (градиента), в результате чего уравнение Навье – Стокса становится менее громоздким. Еще одно упрощение достигается при использовании теоремы о дивергенции Гаусса – Остроградского [4, 13, 14], что позволяет вместо поиска поля переменной v ограничиться интегрированием потоков, нормальных к границе области (рис. 1):

(1)

(2)

(3)

где ${\mathbf{v}}$ – скорость жидкости; n – единичный вектор, связанный с границей области жидкости; Θ – полная граница области жидкости; $\varphi $ – скалярное поле области жидкости.

Рис. 1.

Взаимодействие тела V_т с областью жидкости объемом V с полной границей непрерывной области жидкости ${{\Theta }} = {{\Gamma }} \cup S,$ ${{\Gamma }} = {{{{\Gamma }}}_{1}} \cup {{{{\Gamma }}}_{2}} \cup {{{{\Gamma }}}_{3}}.$ ${{{{\Gamma }}}_{1}},{{{{\Gamma }}}_{2}},{{{{\Gamma }}}_{3}}$ – “кусочные” границы непрерывной области V; S – поверхность тела V_т

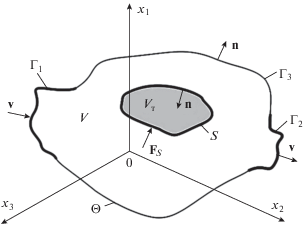
Очевидно, что изменение зависимой переменной ${\mathbf{v}}$ внутри области V зависит от значений ${\mathbf{v}}$ на ее границе Θ. Задавая компоненту вектора ${\mathbf{v}}$ нормальную к Θ, можно повлиять на формирование вихревых структур внутри области V. Более сложная ситуация возникает, когда переменная ${\mathbf{v}}$ зависит от времени t. В общем случае это можно записать в виде

(4)

${\mathbf{v}} = {\mathbf{v}}\left( {{\mathbf{x}},t} \right),$

где x – декартова система координат.

НОВАЯ ФОРМА УРАВНЕНИЙ НАВЬЕ – СТОКСА ДЛЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ИНЕРЦИАЛЬНОМ ПРОСТРАНСТВЕ

Несжимаемая жидкость характеризуется постоянной плотностью ρ = const, для которой уравнение неразрывности имеет вид

(5)

${\text{div}}{\mathbf{v}} = \frac{{\partial {{{v}}_{i}}}}{{\partial {{x}_{i}}}} = 0,$

где ${{{v}}_{i}}$ – i-я компонента скорости v; ${{x}_{i}}$ – i-я координата вектора x.

Для несжимаемой жидкости уравнения Навье – Стокса могут быть преобразованы либо в операторную, либо в тензорную форму с использованием нотационной конвенции Эйнштейна о суммировании [1, 2, 7, 15, 16].

В операторной форме уравнения выглядят так:

(6)

$\rho \frac{{\partial {\mathbf{v}}}}{{\partial t}} + \rho \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{v}} + \nabla p + \eta \nabla \times {\mathbf{\Omega }} = \rho {\mathbf{g}},$

где $\nabla $ – оператор Лапласа; $p$ – давление; $\eta $ – динамический коэффициент вязкости жидкости; ${\mathbf{g}}$ – ускорение свободного падения, а завихренность потока ${\mathbf{\Omega }}$ рассчитывается следующим образом:

(7)

${\mathbf{\Omega }} = \nabla \times {\mathbf{v}}.$

В тензорной форме эти же уравнения можно записать в виде

(8)

$\rho \frac{{\partial {{{v}}_{i}}}}{{\partial t}} + \rho \frac{\partial }{{\partial {{x}_{j}}}}\left( {{{{v}}_{i}}{{{v}}_{j}}} \right) + \frac{{\partial p}}{{\partial {{x}_{i}}}} + \eta {{\varepsilon }_{{ijk}}}\frac{{\partial {{\Omega }_{k}}}}{{\partial {{x}_{j}}}} = \rho {{g}_{i}};$

(9)

${{\Omega }_{k}} = {{\varepsilon }_{{k1m}}}\frac{{\partial {{{v}}_{m}}}}{{\partial {{x}_{l}}}},$

где x_i и ${{x}_{j}}$ – i-я и j-я компоненты вектора x; v_i, ${{{v}}_{j}}$ и ${{v}_{m}}$ – i-я, j-я и m-я компоненты вектора v; ${{\varepsilon }_{{ijk}}},$ ε_k1m – тензоры Леви–Чивиты; ${{g}_{i}}$ – i-я компонента вектора g.

Если применить теорему Гаусса – Остроградского (о дивергенции) к уравнению (8) [13, 14], то это позволит исследовать силы, действующие на жидкость, и понять влияние граничных условий на образование вихревых структур. С этой целью множители ${{g}_{i}}$ и $\frac{{\partial {{{v}}_{i}}}}{{\partial t}}$ в (8) необходимо изменить в соответствии с [17]. Ускорение свободного падения обычно выражается как потенциал некоторой скалярной функции [16]

(10)

${{g}_{i}} = \frac{\partial }{{\partial {{x}_{i}}}}\left( {{{g}_{j}}{{x}_{j}}} \right)\,\,\,\,{\text{или}}\,\,\,\,g = \nabla \left( {{\mathbf{g}} \cdot {\mathbf{x}}} \right).$

Доказать справедливость этой формулы можно следующим образом:

(11)

$\frac{\partial }{{\partial {{x}_{i}}}}\left( {{{g}_{j}}{{x}_{j}}} \right) = {{g}_{j}}\frac{{\partial {{x}_{j}}}}{{\partial {{x}_{i}}}} = {{g}_{j}}{{\delta }_{{ij}}} = {{g}_{i}},$

где ${{\delta }_{{ij}}}$ – дельта-функция Кронекера.

Из уравнения неразрывности (5) следует, что

(12)

$\frac{{\partial {{{v}}_{j}}}}{{\partial {{x}_{j}}}}{{x}_{i}} = 0.$

Интегрирование уравнения (12) по всей области V (см. рис. 1) приводит его к виду

Поскольку справедливо равенство $\frac{{\partial {{x}_{i}}}}{{\partial {{x}_{j}}}} = {{\delta }_{{ij}}},$ то после применения теоремы Гаусса – Остроградского можно записать

(13)

где ${{n}_{j}}$ – j-я компонента вектора n.

Действительно, дифференцируя правую часть (13) с учетом уравнения неразрывности, можно получить

(14)

${{{v}}_{i}} = \frac{{\partial {{{v}}_{j}}}}{{\partial {{x}_{j}}}}{{x}_{i}} + {{{v}}_{j}}\frac{{\partial {{x}_{i}}}}{{\partial {{x}_{j}}}} = {{{v}}_{j}}{{\delta }_{{ij}}} = {{{v}}_{i}}.$

Уравнение (14) позволяет провести новый качественный, а также количественный анализ уравнений Навье – Стокса.

Дифференцирование уравнения неразрывности (5) по времени дает

$\frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{{\partial {{{v}}_{j}}}}{{\partial t}}} \right) = 0.$

После использования процедуры, аналогичной примененной для (12)–(14), можно получить

(15)

Интегральные уравнения (13) и (14) можно записать также в векторной форме

(16)

Физический смысл уравнений (16) может быть очень полезен для описания нестационарных вихревых структур внутри области V [18–21]. Очевидно, что локальное ускорение внутри объема V зависит только от граничных условий. Уравнение (16) позволяет сделать очень важный вывод: локальные ускорения в области V проявляются на границе Θ только через свои компоненты в направлении, нормальном к границе.

Примеры предпочтительного применения уравнений Навье – Стокса в новой форме

Далее для иллюстрации представлены три простых примера.

Пример 1. “Твердая трубка”. Предполагается, что граница Γ (рис. 2) неподвижна и на ней выполняется гипотеза прилипания жидкости, т.е. ${\mathbf{v}} = 0$ на Γ и ${\mathbf{v}} = {{{\mathbf{v}}}_{{1~}}}$ на границе тела ${{S}_{1}}$ и ${\mathbf{v}} = {{{\mathbf{v}}}_{{2~}}}$ на границе тела ${{S}_{2}}.$ Таким образом, ${{\Theta }} = {{S}_{1}} \cup {{S}_{2}}$ и уравнение (8) принимает следующий вид:

(17)

Рис. 2.

Непрерывная область V с 2D-границей ${{\Theta }} = \Gamma \cup {{S}_{1}} \cup {{S}_{2}}$

Очевидно, что ускорением жидкости внутри области V можно управлять с помощью подходящего выбора граничных условий на границе ${{S}_{1}} \cup {{S}_{2}}.$

Пример 2. Рассматривается непрерывная область V с границей Θ (см. рис. 1). Предполагается, что граница Θ колеблется со скоростью поступательного движения $\frac{{\partial {\mathbf{c}}}}{{\partial t}}$ (${\mathbf{c}}$ – перемещение). Следовательно, на Θ граничным выступает условие ${\mathbf{v}} = \frac{{\partial {\mathbf{c}}}}{{\partial t}}.$ В этом случае (15) приводится к следующему виду:

Тогда

(18)

где ${{c}_{i}}$ и ${{c}_{j}}$ – компоненты перемещения c.

Несомненным достоинством уравнения (18) является тот факт, что оно получено с использованием (15) без необходимости знать распределение скорости жидкости в области V.

Пример 3. Предполагается, что граница Γ неподвижна во времени, т.е. ${\mathbf{v}} = 0.$ Тело, занимающее область ${{V}_{{\text{т}}}}$ (см. рис. 1), совершает небольшие колебания вокруг оси x₁ с угловой скоростью ${{{{\omega }}}_{1}} = {{\omega }}\left( t \right).$ Тогда

$\begin{gathered} {\mathbf{\omega }} = \left( {{{\omega }_{1}} = \omega \,;0;0} \right);\,\,{\mathbf{u}} = {\mathbf{\omega }} \times {\mathbf{x}}; \\ {{u}_{j}} = {{\varepsilon }_{{j1k}}}{{\omega }_{l}}{{x}_{k}} = {{\varepsilon }_{{j1k}}}\omega {{x}_{k}}. \\ \end{gathered} $

Уравнение (15) можно преобразовать и получить его в форме

(19)

$\int\limits_V {\frac{{\partial {{{v}}_{i}}}}{{\partial t}}{\text{d}}V} = \int\limits_S {\frac{{{{\partial }^{2}}{{u}_{j}}}}{{\partial {{t}^{2}}}}{{x}_{i}}{{n}_{j}}{\text{d}}S} = {{\varepsilon }_{{j1k}}}\frac{{{{\partial }^{2}}\omega }}{{\partial {{t}^{2}}}}\int\limits_S {{{x}_{k}}{{x}_{i}}{{n}_{j}}{\text{d}}S} ,$

где S – граница области ${{V}_{{\text{т}}}}.$

Так как ${{x}_{k}} = \frac{1}{2}\frac{\partial }{{\partial {{x}_{k}}}}\left( {{{x}_{j}}{{x}_{j}}} \right),$ то после подстановки этого соотношения в (19) и использования теоремы о дивергенции можно получить

$\int\limits_V {\frac{{\partial {{{v}}_{i}}}}{{\partial t}}{\text{d}}V} = - {{\varepsilon }_{{i1k}}}\frac{1}{2}\frac{{{{\partial }^{2}}\omega }}{{\partial {{t}^{2}}}}\int\limits_S {{{{\left| {\mathbf{x}} \right|}}^{2}}{{n}_{k}}{\text{d}}S} .$

Уравнение (19) было получено без необходимости определения поля скоростей внутри тела ${{V}_{{\text{т}}}}.$

Эти три примера, очевидно, только простые случаи прикладного применения уравнения (15). Далее это уравнение используется для расчета сил, действующих на тело, и анализируется влияние граничных условий на нестационарные вихревые структуры. Подставляя (11) и (15) в уравнения Навье – Стокса (8), можно получить

(20)

$\begin{gathered} \frac{\partial }{{\partial {{x}_{j}}}}\left\{ {\left[ {\rho \frac{{\partial {{{v}}_{j}}}}{{\partial t}}{{x}_{i}} + \rho \left( {{{{v}}_{i}}{{{v}}_{j}}} \right) - \rho {{\delta }_{{ij}}}{{g}_{k}}{{x}_{k}}} \right] + } \right. \\ \left. { + \,\,\left[ {{{\delta }_{{ij}}}p + \eta {{\varepsilon }_{{ijk}}}{{\Omega }_{k}}} \right]} \right\} = 0. \\ \end{gathered} $

Уравнение (20) представляет собой новую форму уравнений Навье – Стокса для несжимаемой жидкости. Для дальнейшего анализа (20) вводится новый тензор

(21)

${{H}_{{ij}}} = \rho {{{v}}_{i}}{{{v}}_{j}} - \rho {{g}_{k}}{{x}_{k}}{{\delta }_{{ij}}}.$

Если ввести систему координат, удовлетворяющую условиям

(22)

$~{\mathbf{x}} = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}} = H} \right);\,\,\,\,{\mathbf{g}} = \left( {0,0, - g} \right),$

то можно записать

(23)

${\mathbf{g}} \cdot {\mathbf{x}} = {{g}_{k}}{{x}_{k}} = - gH$

и, следовательно,

(24)

${{H}_{{ij}}} = \rho {{{v}}_{i}}{{{v}}_{j}} + \rho gH{{\delta }_{{ij}}}.$

Полученный тензор является одной из составляющих тензора плотности потока импульса.

Тензор напряжений имеет вид

(25)

${{\sigma }_{{ij}}} = {{\pi }_{{ij}}} + {{\tau }_{{ij}}},$

где ${{\pi }_{{ij}}}$ и ${{\tau }_{{ij}}}$ представляют собой нормальные и касательные напряжения.

В случае ньютоновской жидкости это приводит к следующему выражению:

(26)

$\begin{gathered} {{\sigma }_{{ij}}} = - p~{{\delta }_{{ij}}} + \eta ~{{{v}}_{{ij}}};~\,\,\,\, \\ {{{v}}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{{v}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{v}}_{j}}}}{{\partial {{x}_{i}}}}} \right). \\ \end{gathered} $

Используя уравнения (20) и (26), можно записать уравнения Навье – Стокса в новой форме следующим образом:

(27)

$\frac{\partial }{{\partial {{x}_{j}}}}\left( {\rho \frac{{\partial {{{v}}_{j}}}}{{\partial t}}{{x}_{i}} + {{H}_{{ij}}} - {{\sigma }_{{ij}}}} \right) = 0.$

Уравнения Навье – Стокса в стандартной форме выглядят так:

(28)

$\rho \frac{{\partial {{{v}}_{i}}}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{j}}}}\left( {{{H}_{{ij}}} - {{\sigma }_{{ij}}}} \right) = 0.$

Уравнение (27) более удобно по сравнению с (28) для численного решения нестационарных задач с использованием метода конечных объемов.

РАСЧЕТ НАГРУЗОК, ДЕЙСТВУЮЩИХ НА ГРАНИЦУ ЖИДКОСТЬ – ТВЕРДОЕ ТЕЛО

Анализ нестационарных сил, действующих между жидкостью и твердым (жестким или упругим) телом, является важной частью современных исследований. Такие силы особенно часто возникают в гидравлических турбинах [8–10].

Гидравлические турбины и лопастные насосы обычно имеют неподвижные лопасти и проектируются для определенных рабочих условий, а затем функционируют в небольшом диапазоне режимов, близких к оптимальному. В настоящее время требуется расширение рабочего диапазона этих машин из-за очень изменчивой динамики энергосетей. Расширение же рабочего диапазона сопровождается образованием нестационарных вихревых структур и, как следствие, усилением нагрузки на отдельные элементы гидромашины.

Для компьютерного 3D-моделирования необходимо очень большое машинное время, поэтому нужно заранее провести всесторонний качественный анализ задачи, особенно анализ влияния граничных условий на процесс вычислений. И именно для этой цели могут быть успешно применены уравнения Навье – Стокса в новой форме (27).

На рис. 1 показана сила ${{{\mathbf{F}}}_{S}},$ описывающая воздействие жидкости на поверхность тела S; i-я компонента этой силы может быть выражена следующим образом [2, 15]:

(29)

${{\left( {{{{\text{F}}}_{S}}} \right)}_{i}} = - \int\limits_S {{{\sigma }_{{ij}}}{{n}_{j}}{\text{d}}S} .$

Чтобы рассчитать эту силу, необходимо знать распределение давления по поверхности S и компоненты тензора скоростей деформации ${{{v}}_{{ij}}}$ [см. (26)]. Хотя распределение давления можно измерить достаточно точно, градиенты составляющих скорости на сложной движущейся поверхности определить экспериментально практически невозможно. Более того, во многих случаях нельзя использовать ни один из методов измерений, поскольку поверхность S может располагаться внутри лопасти. Поэтому часто для определения силы ${{{\mathbf{F}}}_{S}}$ применяется другая формула, полученная из уравнений Навье –Стокса после их интегрирования по области V. После интегрирования уравнений Навье – Стокса стандартного вида получается следующее соотношение для расчета i-й компоненты силы ${{{\mathbf{F}}}_{S}}{\text{:}}$

(30)

Следует отметить, что недостатком этого уравнения является необходимость оценки составляющих скорости по всему объему. Оно не позволяет также выявить влияние изменения граничных условий на значение интеграла $\int_V {\frac{{\partial {{{v}}_{i}}}}{{\partial t}}~{\text{d}}V} .$ Поэтому предложенная новая форма уравнений Навье –Стокса (27) обеспечивает гораздо более многообещающие возможности, поскольку после их интегрирования по области V формула для расчета i-й компоненты силы ${{F}_{S}}$ имеет следующий вид:

(31)

Очевидно, что граничные условия оказывают определяющее влияние на локальное ускорение $\frac{{\partial {{{v}}_{i}}}}{{\partial t}},$ а также позволяют оптимизировать и контролировать компоненты силы ${{{\mathbf{F}}}_{S}}.$ Во многих случаях решения прикладных задач наблюдается противоположная ситуация: кинематика движения тела известна, а силу ${{{\mathbf{F}}}_{\Gamma }},$ действующую на границу Γ, необходимо оценить. В этом случае (см. рис. 1) для i-й компоненты этой силы выполняется следующее соотношение:

(32)

$\begin{gathered} {{\left( {{{{\text{F}}}_{\Gamma }}} \right)}_{i}} = - \int\limits_\Gamma {{{\sigma }_{{ij}}}{{n}_{j}}~{\text{d}}\Gamma } = \\ = \,\, - \int\limits_\Theta {\left( {\rho \frac{{\partial {{{v}}_{j}}}}{{\partial t}}{{x}_{i}} + {{H}_{{ij}}}} \right)} \,{{n}_{j}}~{\text{d}}\Theta - {{\left( {{{{\text{F}}}_{S}}} \right)}_{i}}. \\ \end{gathered} $

Использование новой формы уравнений Навье – Стокса, например, для описания поступательного движения судна является, казалось бы, простым прикладным вариантом (см. пример 2 и рис. 2). После подстановки в (32) соотношения (24) в виде

$\int\limits_\Theta {{{H}_{{ij}}}{{n}_{j}}} {\text{d}}\Gamma = \int\limits_\Theta {(\rho {{v}_{i}}{{v}_{j}} + {{\delta }_{{ij}}}\rho {{g}_{k}}{{x}_{k}}){{n}_{j}}} {\text{d}}\Theta $

с учетом ${{{v}}_{i}} = \frac{{\partial {{c}_{i}}}}{{\partial t}}$ на S и ${{{v}}_{i}} = 0$ на Γ можно записать

Следовательно,

Это уравнение с использованием (18) можно переписать в виде

(33)

${{\left( {{{{\text{F}}}_{\Gamma }}} \right)}_{i}} = - \,\rho V\left( {{{g}_{i}} + \frac{{{{\partial }^{2}}{{c}_{i}}}}{{\partial {{t}^{2}}}}} \right).$

Из этого уравнения видно, что сила ${{{\mathbf{F}}}_{\Gamma }}$ может быть рассчитана без знания полей давления и скорости [20, 21]. Поэтому уравнение (27) полезно не только для оценки действующих сил, оно также необходимо для анализа граничных условий, поскольку вместо интегрирования по всему объему сложной непрерывной области V можно интегрировать только вдоль границы любой непрерывной области и тем самым сократить время вычислений. Таким образом, можно записать следующее уравнение:

(34)

Уравнения (27) и (34) позволяют оценить влияние граничных условий на значение результирующей силы. Более того, уравнение (34) может быть использовано для проведения численных расчетов методом конечных объемов [3, 21].

Для несложной непрерывной замкнутой области ΔV, описанной границей ΔΓ, можно получить следующий вид уравнения (34):

(35)

$\int\limits_{{{\Delta \Gamma }}} {\left( {\rho \frac{{\partial {{{v}}_{j}}}}{{\partial t}}{{x}_{i}} + {{H}_{{ij}}} - {{\sigma }_{{ij}}}} \right)} \,{{n}_{j}}~{\text{d}}\Delta \Gamma = 0$

или

(36)

$\rho \int\limits_{{{\Delta }}V} {\frac{{\partial {{{v}}_{i}}}}{{\partial t}}{\text{d}}\Delta V} + \int\limits_{{{\Delta \Gamma }}} {\left( {{{H}_{{ij}}} - {{\sigma }_{{ij}}}} \right){{n}_{j}}~{\text{d}}\Delta \Gamma } = 0.$

В уравнении (36) нестационарный член может быть выражен через средние значения

(37)

$\int\limits_{{{\Delta }}V} {\frac{{\partial {{{v}}_{i}}}}{{\partial t}}{\text{d}}\Delta V} = \frac{{\partial {{{{\hat {v}}}}_{i}}}}{{\partial t}}\Delta V.$

Уравнение (37) предусматривает при исследовании нестационарного потока использование относительно малых конечных объемов. В противном случае следует применять уравнение (35).

ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ АНАЛИТИЧЕСКОГО ПОДХОДА

Образование вихревого жгута в проточной части гидротурбин за рабочим колесом является одной из серьезных проблем при их эксплуатации. Поскольку рассмотренные ранее три примера были только демонстрационными, далее представлен важный пример с применением аналитического подхода к определению нестационарных сил в гидравлических турбинах, вызванных местным ускорением.

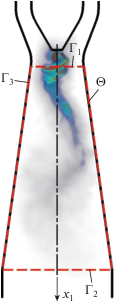
На рис. 3 изображен диффузор, в котором движется нестационарный поток. Течение внутри диффузора создается вихревым генератором (рабочим колесом гидравлической турбины), расположенным перед границей ${{\Gamma }_{1}}.$ На этом рисунке тонированием показано нестационарное поле давления. Оно вызвано неустойчивостью, описываемой конвективными (нелинейными) членами в уравнениях Навье – Стокса.

Рис. 3.

Генератор вихрей и границы (моделирование течения жидкости в отсасывающей трубе гидравлической турбины)

Сила, действующая на поверхность тела, определяется следующим соотношением:

(38)

${{F}_{L}} = - \,\rho \int\limits_V {\frac{{\partial {v}}}{{\partial t}}{\text{d}}V} .$

Эта сила, вызванная нестационарным полем скорости внутри области V, приложена к стенкам диффузора ${{\Gamma }_{3}}.$ Однако уравнение (38) неудобно для анализа, поскольку силу ${{F}_{L}}$ в этом случае можно определить только численными методами. Если же выразить эту силу с помощью поверхностного интеграла

(39)

и учесть условие прилипания жидкости на границе ${{\Gamma }_{3}}$

(40)

${{F}_{L}} = - \rho \int\limits_{{{{{\Gamma }}}_{1}} \cup {{{{\Gamma }}}_{2}}} {\left( {\frac{{\partial {v}}}{{\partial t}} \cdot {\mathbf{n}}} \right){\mathbf{x}}{\text{d}}{{{{\Gamma }}}_{L}}~} ;\,\,\,\,{{{{\Gamma }}}_{L}} = {{{{\Gamma }}}_{1}} \cup {{{{\Gamma }}}_{2}},$

то в результирующем уравнении (40) сила определяется только граничными условиями на границе $\Gamma $.

Если выбрать подходящую систему координат, то, анализируя формулу (40), можно сделать много полезных выводов. Например, на границе ${{\Gamma }_{1}}$ поле скорости является стационарным, т.е. ${v} = {v}\left( x \right).$ Кроме того, глядя на выражение (40), легко прийти к выводу, что силовое воздействие жидкости на боковую стенку диффузора (на границе Г₃) равно нулю (${{F}_{{L3}}} = 0$), причем без проведения численных расчетов.

Результирующее силовое воздействие жидкости на границе ${{\Gamma }_{3}},$ определенное численно, показано на рис. 4, где изображены колебания проекций результирующей силы на соответствующие оси во времени при следующих граничных условиях:

(41)

${{{{\Gamma }}}_{1}}{\text{:}}\,\,{v} = {v}\left( x \right);\,\,\,\,{{{{\Gamma }}}_{3}}{\text{:}}\,\,{v} = 0;\,\,\,\,{{{{\Gamma }}}_{2}}{\text{:}}\,\,p = 0.$

Рис. 4.

Пульсации составляющих членов результирующей силы в декартовой системе координат, отражающих влияние местного ускорения на изменение результирующей силы жидкости во времени; по оси абсцисс отложено время расчетно-численного моделирования рассматриваемого процесса. x₁, x₂, x₃ – оси декартовой системы координат; пульсации проекций результирующей силы на соответствующие оси декартовой системы координат: 1 – ${{F}_{{{{x}_{1}}}}};$ 2 – ${{F}_{{{{x}_{2}}}}};$ 3 – ${{F}_{{{{x}_{3}}}}}$

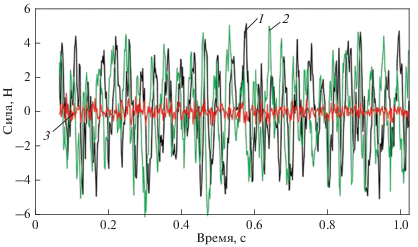
Расчет был выполнен авторами настоящей статьи с использованием метода конечных объемов и модели турбулентности, изложенной в [22].

ВЫВОД УРАВНЕНИЙ НАВЬЕ – СТОКСА В НОВОЙ ФОРМЕ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ

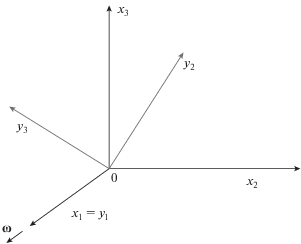
В этом разделе рассматриваются декартова система координат x_i и другая система ${{y}_{i}},$ которая вращается с постоянной угловой скоростью ${\mathbf{\omega }}$ вокруг оси ${{x}_{1}}$ (рис. 5). Далее будет анализироваться влияние на течение жидкости только гравитационных сил, и уравнения Навье – Стокса запишутся в виде [23]

(42)

$\begin{gathered} \rho \frac{{\partial {{w}_{i}}}}{{\partial t}} + \rho \frac{\partial }{{\partial {{y}_{j}}}} \times \\ \times \,\,\left( {{{w}_{i}}{{w}_{j}} - \frac{1}{2}{{{\left| {\mathbf{u}} \right|}}^{2}}{{{{\delta }}}_{{ij}}} + 2{{u}_{i}}{{w}_{j}} - {{{\hat {\sigma }}}_{{ij}}}} \right) = 0, \\ \end{gathered} $

где w_i, w_j – i-я и j-я компоненты вектора относительной скорости w; ${\mathbf{u}}$ – окружная скорость; ${{y}_{j}}$ – j-я комонента радиус-вектора y.

Рис. 5.

Декартовы системы координат ${\mathbf{x}}$ и y; ${\mathbf{x}}$ – фиксированная, а ${\mathbf{y}}$вращается вокруг оси x₁ с постоянной угловой скоростью ${\mathbf{\omega }} = {{{{\omega }}}_{1}}$

Тензор напряжений ${{\hat {\sigma }}_{{ij}}}$ определяется следующим образом:

(43)

${{\hat {\sigma }}_{{ij}}} = - p{{{{\delta }}}_{{ij}}} + 2{{\eta }}{{w}_{{ij}}} = - p{{{{\delta }}}_{{ij}}} + {{\eta }}\left( {\frac{{\partial {{w}_{i}}}}{{\partial {{y}_{j}}}} + \frac{{\partial {{w}_{j}}}}{{\partial {{y}_{i}}}}} \right),$

где ${{y}_{i}}$ – i-я комонента радиус-вектора y.

Для несжимаемой жидкости уравнение неразрывности можно записать в виде

(44)

${\text{div}}{\mathbf{w}} = \frac{{\partial {{w}_{i}}}}{{\partial {{y}_{i}}}} = 0.$

Далее применяется тот же подход, что ранее был применен для инерциальной системы. Исходная форма уравнений Навье – Стокса может быть переписана следующим образом:

(45)

${{w}_{i}} = \frac{\partial }{{\partial {{y}_{j}}}}\left( {{{w}_{j}}{{y}_{i}}} \right);\,\,\,\,~\frac{{\partial {{w}_{i}}}}{{\partial t}} = \frac{\partial }{{\partial {{y}_{j}}}}\left( {\frac{{\partial {{w}_{j}}}}{{\partial t}}{{y}_{i}}} \right);$

(46)

$\begin{gathered} \int\limits_{\hat {V}} {{{w}_{i}}{\text{d}}\hat {V}} = \int\limits_{\hat {\Theta }} {{{w}_{j}}{{y}_{i}}{{{\hat {n}}}_{j}}{\text{d}}\hat {\Theta }} ; \\ \int\limits_{\hat {V}} {\frac{{\partial {{w}_{i}}}}{{\partial t}}{\text{d}}\hat {V}} ~ = \int\limits_{\hat {\Theta }} {\frac{{\partial {{w}_{j}}}}{{\partial t}}{{y}_{i}}{{{\hat {n}}}_{j}}{\text{d}}\hat {\Theta }} , \\ \end{gathered} $

или в векторной форме

(47)

$\begin{gathered} \int\limits_{\hat {V}} {{\mathbf{w}}{\text{d}}\hat {V}} = \int\limits_{\hat {\Theta }} {\left( {{\mathbf{w}} \cdot {\mathbf{\hat {n}}}} \right) \cdot {\mathbf{y}}{\text{d}}\hat {\Theta }} ; \\ \int\limits_{\hat {V}} {\frac{{\partial {\mathbf{w}}}}{{\partial t}}{\text{d}}\hat {V}} ~ = \int\limits_{\hat {\Theta }} {\left( {\frac{{\partial {\mathbf{w}}}}{{\partial t}} \cdot {\mathbf{\hat {n}}}} \right)} \cdot {\mathbf{y}}{\text{d}}\hat {\Theta }. \\ \end{gathered} $

В уравнениях (46) и (47) $\hat {V}$ – сложная непрерывная область; $\hat {\Theta }$ – граница области жидкости в неинерциальной системе координат; ${\mathbf{\hat {n}}}$ – единичный вектор, относящйся к жидкости.

Из приведенных уравнений вытекает еще одно важное следствие. Вектор локального ускорения в области V трансформируется в свою нормальную составляющую вдоль границы области. Если граница (стенка) непроницаема, то $\frac{{\partial {\mathbf{w}}}}{{\partial t}} \cdot {\mathbf{\hat {n}}} = 0.$ Для упрощения формы и прояснения физического смысла отдельных членов в уравнение (42) вводится по аналогии с инерциальной системой новый тензор ${\mathbf{\hat {H}}}$. Для его ij-й компоненты можно записать формулу

(48)

${{\hat {H}}_{{ij}}} = \rho \left( {{{w}_{i}}{{w}_{j}} - \frac{1}{2}{{{\left| {\mathbf{u}} \right|}}^{2}}{{\delta }_{{ij}}} + 2{{u}_{i}}{{w}_{j}}} \right).$

Первый член в формуле (48) описывает конвективный перенос импульса, второй и третий выражают влияние тангенциальной скорости и кориолисова ускорения. После подстановки (48) в (42) можно получить

(49)

$\rho \frac{{\partial {{w}_{i}}}}{{\partial t}} + \frac{\partial }{{\partial {{y}_{j}}}}\left( {{{{\hat {H}}}_{{ij}}} - {{{\hat {\sigma }}}_{{ij}}}} \right) = 0.$

Уравнения Навье – Стокса в новой форме в неинерциальной (вращающейся) системе могут быть получены с использованием уравнения (35)

(50)

$\frac{\partial }{{\partial {{y}_{j}}}}\left( {\rho \frac{{\partial {{w}_{j}}}}{{\partial t}}{{x}_{i}} + {{{\hat {H}}}_{{ij}}} - {{{\hat {\sigma }}}_{{ij}}}} \right) = 0.$

Что касается формальной аналогии между уравнениями (50) и (27), все результаты, полученные ранее, могут быть последовательно применены и здесь.

Силовое воздействие жидкости на тело с поверхностью $\hat {S}$ можно выразить следующим образом:

(51)

${{\left( {{{{\hat {F}}}_{{\widehat S}}}} \right)}_{i}} = - \int\limits_{\hat {S}} {{{\sigma }_{{ij}}}{{{\hat {n}}}_{j}}{\text{d}}\hat {S}} .$

Рассмотрение влияния граничных условий может быть также основано на интегральной форме уравнения (50). Путем его интегрирования по всей области $\hat {V}$ и применения теоремы Гаусса – Остроградского (о дивергенции) получается следующее уравнение:

(52)

$\int\limits_{\hat {\Theta }} {\left( {\rho \frac{{\partial {{w}_{j}}}}{{\partial t}}{{x}_{i}} + {{{\hat {H}}}_{{ij}}} - {{{\hat {\sigma }}}_{{ij}}}} \right)} {{\hat {n}}_{j}}{\text{d}}\hat {\Theta } = 0.$

Уравнение (52) можно также использовать для новой формулировки метода конечных объемов в неинерциальном пространстве.

РАСЧЕТ ЗАВИХРЕННОСТИ ПОТОКА ЖИДКОСТИ В ИНЕРЦИАЛЬНОМ ПРОСТРАНСТВЕ

Исследование нестационарных вихревых структур можно проводить на основе уравнений, описывающих завихренность Ω [1, 2, 15]: ${\mathbf{\Omega }} = \nabla \times {\mathbf{v}} = {\text{rot}}{\mathbf{v}}.$ Если конвективные члены в уравнениях Навье –Стокса выражаются формулой

(53)

$\left( {{\mathbf{v}} \cdot {{\Delta }}} \right){\mathbf{v}} = \frac{1}{2}\nabla \left( {{{{\left| {\mathbf{v}} \right|}}^{2}}} \right) - {\mathbf{v}} \times {\mathbf{\Omega }},$

а удельная механическая энергия ${{Y}_{L}}$ определяется по следующей формуле:

(54)

${{Y}_{L}} = \frac{{{{{\left| {\mathbf{v}} \right|}}^{2}}}}{2} + \frac{p}{\rho } + \left( {{\mathbf{g}} \cdot {\mathbf{x}}} \right),$

то уравнения Навье – Стокса (6) можно записать в следующем виде:

(55)

$\frac{{\partial {\mathbf{v}}}}{{\partial t}} + \nabla \left( {{{Y}_{L}}} \right) - \left( {{\mathbf{v}} \times {\mathbf{\Omega }}} \right) + \nu \nabla \times {\mathbf{\Omega }} = 0,$

где $\nu $ – кинематический коэффициент вязкости.

В результате применения оператора rot к уравнению (55) получается уравнение для завихренности Ω:

(56)

$\frac{{\partial {\mathbf{\Omega }}}}{{\partial t}} - \nabla \times \left( {{\mathbf{v}} \times {\mathbf{\Omega }}} \right) + \nu \nabla \times \left( {\nabla \times {\mathbf{\Omega }}} \right) = 0.$

С учетом определения завихренности (7) можно переписать уравнение неразрывности в следующем виде:

(57)

${\text{div}}{\mathbf{\Omega }} = \frac{{\partial {{\Omega }_{i}}}}{{\partial {{x}_{i}}}} = 0.$

Если преобразовать (57), применяя процедуру, аналогичную описанной ранее, можно получить следующие уравнения:

(58)

${{{{\Omega }}}_{i}} = \frac{\partial }{{\partial {{x}_{j}}}}\left( {{{{{\Omega }}}_{j}}{{x}_{i}}} \right);\,\,\,\,\frac{{\partial {{{{\Omega }}}_{i}}}}{{\partial t}} = \frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{{\partial {{{{\Omega }}}_{j}}}}{{\partial t}}{{x}_{i}}} \right);$

(59)

или их формулировку в векторном виде

(60)

Из анализа уравнения (60) можно сделать следующий важный вывод: если внутри области V возникает нестационарное вихревое поле, то существует и нестационарная завихренность на границе, и наоборот. При этом вектор завихренности коллинеарен вектору нормали к границе. Эти вихревые поля очень опасны, потому что они сопровождаются пульсациями как скорости, так и давления. Доказательство этого факта следует из уравнения

(61)

Для оценки влияния граничных условий на трудоемкость расчетов важно интегрировать (56) по всей области V

С учетом уравнения (60) можно получить

(62)

Это уравнение показывает, что нестационарная завихренность зависит от граничных условий и формы границы Θ исследуемой области.

РАСЧЕТ ЗАВИХРЕННОСТИ ПОТОКА ЖИДКОСТИ В НЕИНЕРЦИАЛЬНОМ ПРОСТРАНСТВЕ

Для вывода уравнения завихренности в неинерциальном пространстве $\widehat {\mathbf{\omega }}$ используется уравнение (42), записанное в векторной форме, и его конвективный член согласно [23] выражается следующим образом:

(63)

$\left( {{\mathbf{w}} \cdot \nabla } \right) \cdot {\mathbf{w}} = \nabla \frac{1}{2}{{\left| {\mathbf{w}} \right|}^{2}} - {\mathbf{w}} \times {\mathbf{\hat {\omega }}};$

(64)

${\mathbf{\hat {\omega }}} = \nabla \times {\mathbf{w}}.$

Затем вводится удельная механическая энергия ${{Y}_{{\mathbf{w}}}},$ выраженная через относительную скорость w:

(65)

${{Y}_{{\mathbf{w}}}} = \frac{1}{2}{{\left| {\mathbf{w}} \right|}^{2}} + \frac{p}{\rho }.$

Далее к уравнению (42) применяется оператор rot, в результате получается следующее уравнение для расчета завихренности в неинерциальном пространстве:

(66)

$\frac{{\partial {\mathbf{\hat {\omega }}}}}{{\partial t}} - \nabla \times \left( {{\mathbf{w}} \times {\mathbf{\hat {\omega }}}} \right) + \nu \nabla \times \left( {\nabla \times {\mathbf{\hat {\omega }}}} \right) = 0.$

С учетом определения завихренности (64) уравнение неразрывности для завихренности можно записать следующим образом:

(67)

${\text{div}}{\mathbf{\hat {\omega }}} = \frac{{\partial {{{\hat {\omega }}}_{i}}}}{{\partial {{y}_{i}}}} = 0.$

С использованием процедур, изложенных ранее, можно вывести следующие уравнения для завихренности в неинерциальном пространстве:

(68)

$\begin{gathered} {{{\hat {\omega }}}_{i}} = \frac{\partial }{{\partial {{y}_{j}}}}\left( {{{{\hat {\omega }}}_{j}}{{y}_{i}}} \right); \\ \frac{{\partial {{{\hat {\omega }}}_{i}}}}{{\partial t}} = \frac{\partial }{{\partial {{y}_{j}}}}\left( {\frac{{\partial {{{\hat {\omega }}}_{j}}}}{{\partial t}}{{y}_{i}}} \right); \\ \end{gathered} $

(69)

$\begin{gathered} \int\limits_{\hat {V}} {{{{\hat {\omega }}}_{i}}{\text{d}}\hat {V}} = \int\limits_{\hat {\Theta }} {{{{\hat {\omega }}}_{j}}{{y}_{i}}{{{\hat {n}}}_{j}}{\text{d}}\hat {\Theta }} ; \\ \int\limits_{\hat {V}} {\frac{{\partial {{{\hat {\omega }}}_{i}}}}{{\partial t}}{\text{d}}\hat {V}} ~ = \int\limits_{\hat {\Theta }} {\frac{{\partial {{{\hat {\omega }}}_{j}}}}{{\partial t}}{{y}_{i}}{{{\hat {n}}}_{j}}{\text{d}}\hat {\Theta }} , \\ \end{gathered} $

или в векторной форме

(70)

$\begin{gathered} \int\limits_{\hat {V}} {{\mathbf{\hat {\omega }}}{\text{d}}\hat {V}} = \int\limits_{\hat {\Theta }} {\left( {{\mathbf{\hat {\omega }}} \cdot {\mathbf{\hat {n}}}} \right) \cdot {\mathbf{y}}{\text{d}}\hat {\Theta }} ; \\ \int\limits_{\hat {V}} {\frac{{\partial {\mathbf{\hat {\omega }}}}}{{\partial t}}{\text{d}}\hat {V}} ~ = \int\limits_{\hat {\Theta }} {\left( {\frac{{\partial {\mathbf{\hat {\omega }}}}}{{\partial t}} \cdot {\mathbf{\hat {n}}}} \right) \cdot {\mathbf{y}}{\text{d}}\hat {\Theta }} . \\ \end{gathered} $

Здесь

(71)

${\mathbf{v}} = {\mathbf{u}} + {\mathbf{w}};\,\,\,\,~{\mathbf{\Omega }} = {\text{rot}}{\mathbf{v}} = 2\omega {\mathbf{k}} + {\mathbf{\hat {\omega }}},$

где ${\mathbf{k}}$ – единичный вектор.

Из уравнения (70) следует важный вывод. Результирующее изменение завихренности ${\mathbf{\omega }}$ во времени порождает нормальную составляющую завихренности на границе $\hat {\Theta }$ [24]. Если подставить уравнение (70) в (66), то получим новую форму уравнения для завихренности в неинерциальной (вращающейся) системе координат y_i. Уравнение (66) можно переписать в следующем виде:

$\frac{{\partial {{{\hat {\omega }}}_{i}}}}{{\partial t}} - {{{{\varepsilon }}}_{{ijk}}}\frac{\partial }{{\partial {{y}_{j}}}}{{\left( {{\mathbf{w}} \times {\mathbf{\hat {\omega }}}} \right)}_{k}} + \nu {{{{\varepsilon }}}_{{ijk}}}\frac{\partial }{{\partial {{y}_{j}}}}{{\left( {{\text{rot}}{\mathbf{\hat {\omega }}}} \right)}_{k}} = 0,$

или

(72)

$\frac{\partial }{{\partial {{y}_{j}}}}\left[ {\left( {\frac{{\partial {{{\hat {\omega }}}_{j}}}}{{\partial t}}{{y}_{i}}} \right) - {{{{\varepsilon }}}_{{ijk}}}{\kern 1pt} {{{\left( {{\mathbf{w}} \times {\mathbf{\hat {\omega }}}} \right)}}_{k}} + \nu {{{{\varepsilon }}}_{{ijk}}}{\kern 1pt} {{{\left( {{\text{rot}}{\mathbf{\hat {\omega }}}} \right)}}_{k}}} \right] = 0.$

Уравнение (72) представляет собой новую форму уравнения для завихренности во вращающейся системе координат ${{y}_{i}}$. Его интегральный вариант можно записать следующим образом:

(73)

$\int\limits_{\hat {\Theta }} {\left[ {\left( {\frac{{\partial {{{\hat {\omega }}}_{j}}}}{{\partial t}}{{y}_{i}}} \right) - {{{{\varepsilon }}}_{{ijk}}}{\kern 1pt} {{{\left( {{\mathbf{w}} \times {\mathbf{\hat {\omega }}}} \right)}}_{k}}{\kern 1pt} + \nu {{{{\varepsilon }}}_{{ijk}}}{\kern 1pt} {{{\left( {{\text{rot}}{\mathbf{\hat {\omega }}}} \right)}}_{k}}} \right]} \,{{n}_{j}}{\text{d}}\hat {\Theta } = 0,$

или в векторной форме

(74)

$\begin{gathered} \int\limits_{\hat {V}} {\frac{{\partial {\mathbf{\hat {\omega }}}}}{{\partial t}}{\text{d}}\hat {V}} ~ = \int\limits_{\hat {\Theta }} {\left( {\frac{{\partial {\mathbf{\hat {\omega }}}}}{{\partial t}} \cdot {\mathbf{\hat {n}}}} \right) \cdot {\mathbf{y}}{\text{d}}\hat {\Theta }} - \\ - \,\,\int\limits_{\hat {\Theta }} {\left[ {{\mathbf{\hat {n}}} \times \left( {{\mathbf{w}} \times {\mathbf{\hat {\omega }}}} \right) - \nu {\mathbf{\hat {n}}} \times \left( {{\text{rot}}{\mathbf{\hat {\omega }}}} \right)} \right]{\text{d}}\hat {\Theta }} = 0. \\ \end{gathered} $

ОБОБЩЕНИЕ ПРИМЕНЯЕМОГО ПОДХОДА

Формы уравнения, подобные уравнению (5), используются также при решении других задач математической физики, например уравнений Максвелла [25]. Таким образом, полученные в данной работе результаты могут быть обобщены и для других типов векторных полей. Если предположить, что в декартовой системе координат существует векторное поле ${\mathbf{a}} = {\mathbf{a}}\left( {{\mathbf{x}},t} \right)$ и ${\text{div}}{\mathbf{a}} = 0,$ то для вектора ${\mathbf{a}}$ может быть определена следующая процедура:

(75)

${{a}_{i}} = \frac{\partial }{{\partial {{x}_{j}}}}\left( {{{a}_{j}}{{x}_{i}}} \right);\,\,\,\,~\frac{{\partial {{a}_{i}}}}{{\partial t}} = \frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{{\partial {{a}_{j}}}}{{\partial t}}{{x}_{i}}} \right);$

(76)

$\int\limits_V {{\mathbf{a}}{\text{d}}V} = \int\limits_\Theta {\left( {{\mathbf{a}} \cdot {\mathbf{n}}} \right){\mathbf{x}}~{\text{d}}\Theta } ;$

(77)

$\int\limits_V {\frac{{\partial {\mathbf{a}}}}{{\partial t}}{\text{d}}V} = \int\limits_\Theta {\left( {\frac{{\partial {\mathbf{a}}}}{{\partial t}} \cdot {\mathbf{n}}} \right){\mathbf{x}}~d\Theta } .$

В математической физике вектор ${\mathbf{a}}$ может иметь различный физический смысл, например, это может быть вектор скорости, вектор вихря или вектор магнитной индукции. Из приведенных выражений видно, что объемные интегралы от ${\mathbf{a}}$ и $\frac{{\partial {\mathbf{a}}}}{{\partial t}}$ преобразуются в поверхностные. Поэтому для понимания физики процессов, описываемых уравнениями Навье – Стокса, очень важно получить математическое описание явлений, обусловленных векторным полем ${\mathbf{a}}$ и происходящих в пределах области V. Предложенный в настоящей работе подход может быть применен при решении уравнений Максвелла.

ВЫВОДЫ

1. Новые формы уравнений Навье – Стокса для несжимаемой жидкости позволяют преобразовать объемный интеграл от завихренности потока жидкости в поверхностный интеграл от ее составляющей в нормальном направлении к границе области.

2. Предложеннный в настоящей работе подход может быть успешно применен для расчета взаимодействия упругого или движущегося тела с жидкостью как в инерциальном, так и в неинерциальном пространстве.

3. Предложенные процедуры позволяют получать новые формы уравнения неразрывности и уравнения для расчета завихренности потока жидкости.

4. На основе выведенных интегральных выражений можно оценить влияние граничных условий, а также силовые эффекты, возникающие при взаимодействии жидкости с телом. Применение теоремы Гаусса – Остроградского к уравнениям Навье – Стокса позволяет ограничиться интегрированием только вдоль границы, т.е. отпадает необходимость знать поле скорости во всем исследуемом объеме. Таким образом, все расчеты вихревых структур можно значительно упростить.

5. Представленный подход не ограничивается ньютоновскими жидкостями, которые представляют собой обычную основу для теоретического анализа потока с использованием уравнений Навье – Стокса. Новизна предлагаемого подхода состоит в простом преобразовании интеграла по объему от нестационарного члена в поверхностный интеграл.

6. Преобразованные уравнения (в их общих формах или непосредственно в некоторых из представленных конкретных форм) могут быть полезны при разработке численных методов (например, метода конечных элементов) и особенно при оптимизации нестационарного векторного поля (скорости) по всей площади. В большинстве случаев значения соответствующих величин (например, скорости) представляют большой интерес только на входных и выходных поверхностях исследуемого объема.

7. Полученные уравнения могут применяться при решении преобразованных уравнений Максвелла.

Список литературы

Katz J. Introductory fluid mechanics. Cambridge University Press, 2010.
Morrison F.A. An introduction to fluid mechanics. Cambridge University Press, 2013.
Arfken G.B., Weber H.J., Harris F.E. Mathematical methods for physicists: A comprehensive guide. 6th ed. Academic Press, 2005.
Smirnov V.I. A course of higher mathematics. V. 2. Elsevier, 1964.
Eymard R., Gallouët T., Herbin R. Handbook of numerical analysis. Elsevier, 2000.
Pochylý F., Stejskal J. Rotational flow in centrifugal pump meridian using curvilinear coordinates // J. Fluids Eng. 2016. V. 138. № 8. P. 081101 (6 pages). https://doi.org/10.1115/1.4032756
Ladyzhenskaya O.A. The mathematical theory of viscous incompressible flows. Mathematics and its applications. V. 2 / Translated from the Russian by R.A. Silverman and J. Chu. 2nd ed. New York:London:Paris: Gordon and Breach Science Publishers, 1969.
Pochylý F., Malenovský E., Pohanka L. New approach for solving the fluid–structure interaction eigenvalue problem by modal analysis and the calculation of steady-state or unsteady responses // J. Fluids Struct. 2013. V. 37. P. 171–184. https://doi.org/10.1016/j.jfluidstructs.2012.09.001
Paidoussis M.P. Fluid-structure interactions. V. 1, 2. Elsevier Academic Press, 1998.
Axisa F., Antunes J. Modeling of mechanical systems: Fluid-structure interaction. Elsevier, 2007.
Ferrofluids. Magnetically controllable fluids and their applications / Ed. by S. Odenbach. Springer, 2002.
Modelling of hydrophobic surfaces by the Stokes problem with the stick-slip boundary conditions / R. Kučera, V. Šátek, J. Haslinger, S. Fialová, F. Pochylý // J. Fluids Eng. 2017. V. 139. Is. 1. P. 011202 (9 pages).https://doi.org/10.1115/1.4034199
Pfeffer W.F. The divergence theorem and sets of finite perimeter. N.Y.: Chapman and Hall/CRC, 2012. https://doi.org/10.1201/b11919
Ženíšek A. Surface integral and Gauss–Ostrogradskij theorem from the view point of aplications // Appl. Math. 1999. V. 44. Is. 3. P. 169–241.
Landau L.D., Lifschitz E.M. The classical theory of fields. 4th revised ed. Butteworth–Heinemann, 1987.
De Grott S.R., Mazur P. Non-equlibrium thermodynamics. North-Holland, Amsterdam, Dover Publications Inc.; N.Y.: Wiley, 1962.
Pochylý F., Fialová S., Krutil J. New mathematical model of certain class of continuum mechanics problems // Eng. Mech. 2014. V. 21. № 1. P. 61–66.
Pasche S., Avellan F., Gallaire F. Part load vortex rope as a global unstable mode // J. Fluids Eng. 2017. V. 139. Is. 5. P. 051102 (11 pages). https://doi.org/10.1115/1.4035640
Proper orthogonal decomposition of self-induced instabilities in decelerated swirling flows and their mitigation through axial water injection / D. Štefan, P. Rudolf, S. Muntean, R. Susan-Resiga // J. Fluids Eng. 2017. V. 139. Is. 8. P. 081101 (25 pages). https://doi.org/10.1115/1.4036244
Klas R., Fialová S. Pulse flow of liquid in flexible tube. EFM Praha, 2018.
Pochylý F., Klas R., Fialová S. Application of modified Navier–Stokes equations to determine the unsteady force effects of a heterogeneous liquid. EFM Praha, 2018.
Menter F. Stress-blended eddy simulation (SBES) – a new paradigm in hybrid RANS-LES modeling // Progress in Hybrid RANS-LES Modelling. Springer, 2018. P. 27–37. https://doi.org/10.1007/978-3-319-70031-1_3.
Pochylý F., Fialová S., Krausová H. Variants of Navier–Stokes equations // Engineering Mechanics 2012: Book of extended abstracts. Svratka, CZ: Association for Engineering Mechanics, 2012. P. 1011–1016.
Richter T. Fluid-structure interactions. Springer International Publishing, 2017.
Jiles D. Introduction to magnetism and magnetic materials. CRC Press, 2016.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплоэнергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал