Теплоэнергетика, 2021, № 2, стр. 79-85

Модель выхода продуктов деления из бассейна расплава во время тяжелой аварии в реакторе с жидкометаллическим охлаждением

Э. В. Усов^a, *, В. И. Чухно^a, И. А. Климонов^a, В. Д. Озрин^a, Н. А. Мосунова^a, В. Ф. Стрижов^a

^a Институт проблем безопасного развития атомной энергетики РАН
115191 Москва, Большая Тульская ул., д. 52, Россия

Поступила в редакцию 17.01.2020
После доработки 22.05.2020
Принята к публикации 24.06.2020

DOI: 10.1134/S0040363621020065

Аннотация

Сценарии аварий, подразумевающие несрабатывание системы активных и пассивных защит реактора, являются наиболее тяжелыми по своим последствиям, поскольку сопровождаются плавлением твэлов, тепловыделяющих сборок и всей активной зоны и, как следствие, выходом продуктов деления (ПД) из расплава топлива и конструкционных материалов. Расположение реакторных установок вблизи населенных пунктов требует понимания того, к каким последствиям приведут гипотетические аварии с разрушением активной зоны. Наиболее важной является информация о количестве вышедших в окружающую среду ПД. Для оценки возможной дозовой нагрузки на персонал и окружающую среду при гипотетической аварии необходимы данные по выходу радиоактивных нуклидов из поврежденной, в том числе расплавленной, активной зоны. В настоящей работе представлены подходы, которые могут быть использованы для расчета количества вышедших продуктов деления из расплава топлива. В основе предложенных подходов – общие закономерности поведения и выхода примесей из жидких растворов. Для моделирования этого процесса решается система дифференциальных уравнений. Предложенные подходы были реализованы в виде программного модуля для расчета выхода ПД из расплава. С использованием разработанного модуля была решена тестовая задача по выходу ПД из расплава оксидного топлива, а также выполнен анализ результатов реальных экспериментов, проведенных в Национальной лаборатории в Ок-Ридже. Показана удовлетворительная сходимость расчетных данных по выходу из расплава как нелетучих (Ce, Sr), так и летучих (Xe, Kr) продуктов деления.

Ключевые слова: реактор на быстрых нейтронах, тяжелая авария, летучие и нелетучие продукты деления, расплав, ЕВКЛИД/V2, SAFR/V1

Для анализа тяжелых аварий в реакторных установках на быстрых нейтронах (быстрых реакторах) в ИБРАЭ РАН разрабатывается вторая версия интегрального кода ЕВКЛИД [1, 2]. В состав этого кода входят следующие модули: теплогидравлический, твэльный, нейтронно-физический, расчета переноса продуктов деления в теплоносителе и помещениях АЭС, тяжелоаварийный [3, 4]. Последний из перечисленных модулей позволяет рассчитывать процессы плавления твэла, перемещения расплава по твэлу, выброса расплава в теплоноситель, диссоциации нитридного топлива, выхода ПД из расплава.

Во время тяжелой аварии в реакторной установке, когда материал активной зоны реактора плавится и перемещается, в нижней части реактора может образовываться бассейн расплава, который нагревается остаточным теплом, выделяющимся в результате радиоактивного распада продуктов деления, содержащихся в расплаве. Повышение температуры в бассейне активирует выход газообразных продуктов деления из бассейна. Бόльшая часть летучих продуктов деления (Xe, Kr, Cs, I) выходят из расплавленного топлива уже при формировании бассейна расплава, в то время как менее летучие продукты могут оставаться в конденсированном состоянии в расплаве из-за низкого давления насыщенных паров. Выход оставшихся в расплаве благородных газов и летучих/слаболетучих продуктов деления в большей степени определяется движением газонаполненных пузырей в расплаве. Выход нелетучих ПД зависит от конвективно-диффузионного переноса ПД в расплаве и их испарения с открытой поверхности расплава. К летучим ПД относятся следующие элементы: Cs, Cr, Mn, Kr, Te, Xe; к слаболетучим и нелетучим – Am, Ba, Ce, Cm, Co, Fe, Mn, Mo, Np, Nd, Ni, Sr, La, Pu, Ru, U, Zr.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЫХОДА ПД С ЗЕРКАЛА РАСПЛАВА

В этом разделе детально рассматривается процесс выноса веществ с зеркала расплава во время испарения ПД. Расплав топлива с ПД может быть представлен как идеальный раствор. В этом случае в соответствии с законом Рауля давление пара вещества над раствором (в модели идеального раствора) можно рассчитать по формуле

(1)

$p = {{x}_{s}}{{p}_{s}}\left( T \right),$

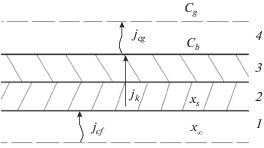
где ${{x}_{s}}$ – мольная доля ПД в приповерхностном слое раствора (расплава); ${{p}_{s}}$ – давление насыщенных паров над чистым веществом, индекс “$s$” относится к веществу в насыщенном состоянии; $T$ – температура расплава.

Выход ПД из расплава может быть разделен на три этапа (рис. 1). На первом этапе происходит конвективно-диффузионный перенос ПД из объема расплава к его поверхности, затем в результате испарения ПД переходят в приповерхностный слой газа (второй этап) и далее из приповерхностного слоя переносятся в газовый объем (третий этап).

Рис. 1.

Схема выхода ПД с зеркала расплава. 1 – внутренний объем расплава; 2 – приповерхностный слой расплава; 3 – приповерхностный слой газа; 4 – газовый объем

Поток массы из объема расплава в приповерхностный слой (см. рис. 1) можно определить по выражению

(2)

${{j}_{{cf}}} = {{\alpha }_{{cf}}}\left( {{{C}_{\infty }} - {{C}_{s}}} \right),$

где ${{\alpha }_{{cf}}}$ – коэффициент массопереноса к поверхности расплава для заданного продукта деления; ${{C}_{\infty }}$ – массовая концентрация ПД в объеме расплава; ${{C}_{s}}$ – массовая концентрация ПД на поверхности расплава. Индекс “$cf$” относится к конвективному переносу в жидком расплаве, а индекс $\infty $ – к объему расплава на большом удалении от поверхности.

Поток массы (2) можно выразить через мольные доли продуктов деления в растворе ${{x}_{\infty }},$ ${{x}_{s}}$ следующим образом:

(3)

${{j}_{{cf}}} = {{\alpha }_{{cf}}}\left( {{{x}_{\infty }} - {{x}_{s}}} \right){{{{N}_{{tot}}}M} \mathord{\left/ {\vphantom {{{{N}_{{tot}}}M} V}} \right. \kern-0em} V}.$

Здесь ${{N}_{{tot}}}$ – полное количество молей вещества в расплаве; $M$ – молярная масса ПД; $V$ – объем расплава.

Если предположить, что ПД составляют малую долю расплава топлива, то

${{N}_{{tot}}} = {{{{m}_{m}}} \mathord{\left/ {\vphantom {{{{m}_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}},$

где ${{M}_{m}}$ и ${{m}_{m}}$ – масса и молярная масса расплава; индекс “$m$” означает расплав.

Молекулярный перенос с приповерхностного слоя расплава в приповерхностный слой газа (см. рис. 1) описывается следующим выражением:

(4)

${{j}_{k}} = 2\sqrt {{M \mathord{\left/ {\vphantom {M {\left( {2{\pi }RT} \right)}}} \right. \kern-0em} {\left( {2{\pi }RT} \right)}}} \left[ {{{x}_{s}}{{p}_{s}}\left( T \right) - {{p}_{{b\infty }}}} \right].$

Здесь $R$ – универсальная газовая постоянная; ${{p}_{{b\infty }}}$ – парциальное давление пара вещества на некотором удалении от поверхности (расстояние порядка длины свободного пробега), индекс “$b\infty $” относится к слою газа на удалении от поверхности на расстоянии порядка длины свободного пробега молекулы.

При использовании массовой концентрации молекул, кг/м³, формула (4) примет вид

${{j}_{k}} = 2\sqrt {{{RT} \mathord{\left/ {\vphantom {{RT} {\left( {2\pi M} \right)}}} \right. \kern-0em} {\left( {2\pi M} \right)}}} \left[ {{{x}_{s}}{{C}_{s}}\left( T \right) - {{C}_{{b\infty }}}} \right],$

а в мольных долях

${{j}_{k}} = 2\sqrt {{{RT} \mathord{\left/ {\vphantom {{RT} {\left( {2\pi M} \right)}}} \right. \kern-0em} {\left( {2\pi M} \right)}}} \,{{C}_{s}}\left( T \right)\left[ {{{x}_{s}} - {{{{C}_{{b\infty }}}} \mathord{\left/ {\vphantom {{{{C}_{{b\infty }}}} {{{C}_{s}}\left( T \right)}}} \right. \kern-0em} {{{C}_{s}}\left( T \right)}}} \right].$

На третьем этапе происходит конвективно-диффузионный перенос ПД из приповерхностного слоя газа в газовый объем (см. рис. 1)

(5)

${{j}_{{cg}}} = {{\alpha }_{{cg}}}\left( {{{C}_{{b\infty }}} - {{C}_{g}}} \right),$

где ${{C}_{g}}$ – концентрация молекул в буферном слое газа, индекс “$cg$” означает конвективный перенос в газе.

В долях давления насыщения формула (5) примет вид

${{j}_{{cg}}} = {{\alpha }_{{cg}}}{{C}_{s}}\left( T \right)\left[ {{{{{C}_{{b\infty }}}} \mathord{\left/ {\vphantom {{{{C}_{{b\infty }}}} {{{C}_{s}}\left( T \right)}}} \right. \kern-0em} {{{C}_{s}}\left( T \right)}} - {{{{C}_{g}}} \mathord{\left/ {\vphantom {{{{C}_{g}}} {{{C}_{s}}\left( T \right)}}} \right. \kern-0em} {{{C}_{s}}\left( T \right)}}} \right].$

С использованием приведенных формул, а также условия баланса массы можно записать

${{j}_{{cf}}} = {{j}_{k}} = {{j}_{{cg}}}.$

Потоки, выраженные через массовые доли, имеют вид

$\begin{gathered} {{{\text{d}}m} \mathord{\left/ {\vphantom {{{\text{d}}m} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = S\left\{ {{{{\left( {{{\alpha }_{{cf}}}{{{{N}_{{tot}}}M} \mathord{\left/ {\vphantom {{{{N}_{{tot}}}M} V}} \right. \kern-0em} V}} \right)}}^{{ - 1}}} + {{{\left[ {2\sqrt {{{RT} \mathord{\left/ {\vphantom {{RT} {\left( {2\pi M} \right)}}} \right. \kern-0em} {\left( {2\pi M} \right)}}} \,{{C}_{s}}} \right]}}^{{ - 1}}} + } \right. \\ {{\left. { + \,\,{{{\left( {{{\alpha }_{{cg}}}{{C}_{s}}} \right)}}^{{ - 1}}}} \right\}}^{{ - 1}}}\left( {{{x}_{\infty }} - {{{{C}_{g}}} \mathord{\left/ {\vphantom {{{{C}_{g}}} {{{C}_{s}}}}} \right. \kern-0em} {{{C}_{s}}}}} \right), \\ \end{gathered} $

где $S$ – площадь поверхности расплава; x_∞ = = ${{\left( {{{{{C}_{\infty }}} \mathord{\left/ {\vphantom {{{{C}_{\infty }}} M}} \right. \kern-0em} M}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{{C}_{\infty }}} \mathord{\left/ {\vphantom {{{{C}_{\infty }}} M}} \right. \kern-0em} M}} \right)} {\left( {{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}} \right)}}} \right. \kern-0em} {\left( {{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}} \right)}}$ – мольная доля; ${{\rho }_{m}}$ – плотность расплава.

Концентрация насыщения может быть найдена по формуле для определения давления насыщения:

${{C}_{s}}\left( T \right) = {{{{p}_{s}}\left( T \right)M} \mathord{\left/ {\vphantom {{{{p}_{s}}\left( T \right)M} {\left( {RT} \right)}}} \right. \kern-0em} {\left( {RT} \right)}}.$

РАСЧЕТ КОЭФФИЦИЕНТОВ МАССООТДАЧИ

Коэффициент массоотдачи ПД в жидкости может быть рассчитан с учетом аналогии между массо- и теплоотдачей с использованием безразмерного коэффициента массоотдачи – числа Шервуда ${\text{Sh}}$ – от плоской горизонтальной поверхности

${{\alpha }_{{cf}}} = {\text{Sh}}{D \mathord{\left/ {\vphantom {D L}} \right. \kern-0em} L},$

где $D$ – коэффициент диффузии молекул i-го вещества в расплаве; $L$ – линейный размер поверхности расплава, который может быть оценен по соотношению $L = \sqrt {{{4S} \mathord{\left/ {\vphantom {{4S} \pi }} \right. \kern-0em} \pi }} .$

Число Шервуда для естественной конвекции определяется по формуле [5]

${\text{Sh}} = 0.27{{\left( {{\text{GrSc}}} \right)}^{{0.25}}}.$

Здесь ${\text{Gr}} = \frac{{g{{L}^{3}}}}{{{\nu }_{m}^{2}}}\frac{{\left| {{{C}_{\infty }} - {{C}_{s}}} \right|}}{{{{C}_{\infty }}}}$ – число Грасгофа; Sc = = ν_m/D – число Шмидта; ${{{\nu }}_{m}}$ – кинематический коэффициент вязкости расплава; $g$ – ускорение свободного падения.

Коэффициент диффузии молекул в жидкости может быть рассчитан с использованием соотношения Стокса–Эйнштейна:

$D = {{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} {\left( {3\pi {{\mu }_{m}}d} \right)}}} \right. \kern-0em} {\left( {3\pi {{\mu }_{m}}d} \right)}},$

где ${{k}_{{\text{B}}}}$ – постоянная Больцмана; ${{\mu }_{m}}$ – динамический коэффициент вязкости расплава; $d$ – размер молекулы ПД.

Коэффициент массоотдачи в газовой фазе также определяется с помощью вышеприведенных соотношений. Для расчета коэффициента диффузии молекул ПД в газе была использована формула из [6] в несколько модифицированном виде:

$\begin{gathered} D = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}\sqrt {{{k_{{\text{B}}}^{{\text{3}}}} \mathord{\left/ {\vphantom {{k_{{\text{B}}}^{{\text{3}}}} {{{\pi }^{3}}}}} \right. \kern-0em} {{{\pi }^{3}}}}} \sqrt {\left[ {{{{{N}_{{\text{A}}}}} \mathord{\left/ {\vphantom {{{{N}_{{\text{A}}}}} {\left( {2{{M}_{g}}} \right)}}} \right. \kern-0em} {\left( {2{{M}_{g}}} \right)}}} \right] + \left[ {{{{{N}_{{\text{A}}}}} \mathord{\left/ {\vphantom {{{{N}_{{\text{A}}}}} {(2M)}}} \right. \kern-0em} {(2M)}}} \right]} \times \\ \times \,\,{{4{{p}^{{ - 1}}}{{T}^{{3/2}}}} \mathord{\left/ {\vphantom {{4{{p}^{{ - 1}}}{{T}^{{3/2}}}} {{{{\left( {d + {{d}_{a}}} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {d + {{d}_{a}}} \right)}}^{2}}}}, \\ \end{gathered} $

где ${{d}_{a}}$ – эффективный диаметр молекулы буферного слоя газа над атмосферой (аргон или пары натрия); ${{N}_{{\text{A}}}}$ – число Авогадро; ${{M}_{g}}$ – молекулярная масса буферного газа.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЫХОДА ЛЕТУЧИХ ПД В ВИДЕ ПУЗЫРЕЙ

Летучие ПД могут выходить не только с зеркала расплава, но и из бассейна в виде формирующихся и всплывающих пузырей, в которых испаряются ПД. Рост пузыря определяется скоростью диффузии ПД в пузырь из окружающей жидкости. В работе [7] на основе данных Скривена [8] было получено следующее выражение для оценки скорости роста пузыря:

(6)

$\begin{gathered} {{{{C}_{m}}} \mathord{\left/ {\vphantom {{{{C}_{m}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}} = 2{{\beta }^{3}}{\text{exp}}\left( {3{{\beta }^{2}}} \right) \times \\ \times \,\,\int\limits_\beta ^\infty {{{\xi }^{{ - 2}}}{\text{exp}}\left( { - {\kern 1pt} {{\xi }^{2}} - 2{{\beta }^{3}}{{\xi }^{{ - 1}}}} \right){\text{d}}\xi {\kern 1pt} } . \\ \end{gathered} $

Здесь ${{C}_{m}}$ – массовая концентрация ПД в расплаве, определяемая как сумма массовых концентраций всех летучих ПД: ${{C}_{m}} = \sum\nolimits_i {{{C}_{{i\infty }}}} $ (${{C}_{{i\infty }}} = {{{{m}_{{i{\text{ПД}}}}}} \mathord{\left/ {\vphantom {{{{m}_{{i{\text{ПД}}}}}} V}} \right. \kern-0em} V},$ ${{m}_{{i{\text{ПД}}}}}$ – масса i-го компонента ПД); ${{\rho }_{g}}$ – плотность смеси ПД в газовом пузыре; $\beta = {{{{D}_{b}}} \mathord{\left/ {\vphantom {{{{D}_{b}}} {\left( {4\sqrt {{{D}_{i}}t} } \right)}}} \right. \kern-0em} {\left( {4\sqrt {{{D}_{i}}t} } \right)}}$ – безразмерный параметр роста, который определяет скорость роста пузыря в зависимости от разности концентраций в объеме раствора и концентрации насыщения; ${{D}_{b}}$ – диаметр пузыря; ${{D}_{i}}$ – коэффициент диффузии i-го ПД; $t$ – время; $\xi = {r \mathord{\left/ {\vphantom {r {{{R}_{{{\text{max}}}}}}}} \right. \kern-0em} {{{R}_{{{\text{max}}}}}}}$ – автомодельная переменная [8] ($r$ – радиус пузыря в момент времени t; ${{R}_{{{\text{max}}}}} = {{{{D}_{b}}} \mathord{\left/ {\vphantom {{{{D}_{b}}} 2}} \right. \kern-0em} 2}$ – максимальный радиус пузыря).

Плотность смеси ПД в газовом пузыре вычисляется по формуле

${{\rho }_{g}} = \sum\limits_i {{{x}_{{i\infty }}}} {{{{p}_{{si}}}\left( T \right){{M}_{i}}} \mathord{\left/ {\vphantom {{{{p}_{{si}}}\left( T \right){{M}_{i}}} {\left( {RT} \right)}}} \right. \kern-0em} {\left( {RT} \right)}},$

где индекс “i” соответствует i-му компоненту летучих ПД.

В полученном выражении (6) предполагается, что летучие ПД подчиняются уравнению состояния идеального газа. В приведенных выражениях учтено, что полная концентрация ПД в расплаве и в газовой фазе складывается из концентраций отдельных ПД.

При $\beta \geqslant 5.0$ используется асимптотическое приближение [8]

$\begin{gathered} \varphi \left( \beta \right) = 2{{\beta }^{3}}{\text{exp}}\left( {3{{\beta }^{2}}} \right)\int\limits_\beta ^\infty {{{\xi }^{{ - 2}}}{\text{exp}}\left( { - {\kern 1pt} {{\xi }^{2}} - 2{{\beta }^{3}}{{\xi }^{{ - 1}}}} \right){\text{d}}\xi } \approx \\ \approx \sqrt {{\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}} \left( {\beta - {4 \mathord{\left/ {\vphantom {4 9}} \right. \kern-0em} 9}} \right), \\ \end{gathered} $

а при $\beta \leqslant 0.5$ [8]

$\varphi \left( \beta \right) \approx 2{{\beta }^{2}}.$

Для промежуточных значений $0.5 < \beta < 5.0$ используется линейная интерполяция.

Если известно значение $\beta ,$ то можно найти частоту образования пузырей минимального диаметра [8] $f$ как обратную величину времени роста до этого диаметра:

(7)

$f = {{t}^{{ - 1}}} = {{16{\kern 1pt} {\kern 1pt} {{\beta }^{2}}{{D}_{i}}} \mathord{\left/ {\vphantom {{16{\kern 1pt} {\kern 1pt} {{\beta }^{2}}{{D}_{i}}} {{{d}_{b}}^{2}}}} \right. \kern-0em} {{{d}_{b}}^{2}}};\,\,\,\,{{D}_{b}}\left( t \right) = {{d}_{b}} = 4\beta \sqrt {{{D}_{i}}t} ,$

где_{${{D}_{i}}$ – коэффициент диффузии; ${{d}_{b}} = \sqrt {{\sigma \mathord{\left/ {\vphantom {\sigma {\left( {{{\rho }_{m}}g} \right)}}} \right. \kern-0em} {\left( {{{\rho }_{m}}g} \right)}}} $ – минимальный диаметр пузыря, значение которого принято равным капиллярной постоянной;
${\sigma }$ – коэффициент поверхностного натяжения.

Скорость образования пузырей минимального диаметра рассчитывается по формуле

${{{\text{d}}{{n}_{1}}} \mathord{\left/ {\vphantom {{{\text{d}}{{n}_{1}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {{f{{s}_{n}}} \mathord{\left/ {\vphantom {{f{{s}_{n}}} V}} \right. \kern-0em} V},$
где ${{n}_{1}}$ – число пузырей минимального диаметра (индекс “1”); ${{s}_{n}}$ – число центров, участвующих в образовании пузырей.

Образовавшиеся пузыри начинают всплывать. В процессе всплытия размер пузырей увеличивается
как из-за продолжения их роста, так и вследствие коагуляции. Стоит отметить, что закон
роста всплывающего пузыря отличается от закона Скривена, принятого в настоящей работе
для оценки скорости роста пузыря. Доработка подходов к учету различных эффектов –
задача будущих исследований.

Диапазон размеров пузырей разбивается на конечное число фракций: k = 1, …, N. Первая фракция соответствует пузырям, имеющим диаметр, равный минимальному:

${{D}_{{b1}}} = {{d}_{b}}.$
Изменение числа пузырей k-го размера из-за их слияния имеет следующий вид [9]:

${{{\text{d}}{{n}_{k}}} \mathord{\left/ {\vphantom {{{\text{d}}{{n}_{k}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = 0.5\sum\limits_{i + j = k} {{{B}_{{ij}}}{{n}_{i}}{\kern 1pt} {\kern 1pt} {{n}_{j}}} - \sum\limits_{i = 1}^N {{{B}_{{ik}}}{{n}_{i}}{\kern 1pt} {\kern 1pt} {{n}_{k}}} .$
Первая сумма этого выражения отвечает за образование пузырей k-го размера из пузырей меньшего размера, а вторая – за их исчезновение вследствие
слияния с другими пузырями. Далее предполагается, что основной механизм слияния пузырей
– их столкновение. Тогда скорость коагуляции

${{B}_{{ij}}} = 0.25\pi {{\left( {{{D}_{{bi}}} + {{D}_{{bj}}}} \right)}^{2}}\left| {{{U}_{i}} - {{U}_{j}}} \right|,$
где ${{U}_{i}}$ – скорость i-го пузыря; ${{U}_{j}}$ – скорость j‑го пузыря.

Изменение числа пузырей из-за их роста можно определить по выражению

${{{\text{d}}{{n}_{k}}} \mathord{\left/ {\vphantom {{{\text{d}}{{n}_{k}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {{{{n}_{{k - 1}}}} \mathord{\left/ {\vphantom {{{{n}_{{k - 1}}}} {{{\tau }_{{kk - 1}}}}}} \right. \kern-0em} {{{\tau }_{{kk - 1}}}}} - {{{{n}_{k}}} \mathord{\left/ {\vphantom {{{{n}_{k}}} {{{\tau }_{{k + 1k}}}}}} \right. \kern-0em} {{{\tau }_{{k + 1k}}}}},$
где ${{\tau }_{{kk - 1}}}$ – время роста пузыря размером ${{D}_{{bk - 1}}}$ до пузыря размером ${{D}_{k}}.$ Значение этого времени можно получить из (7):

${{\tau }_{{kk - 1}}} = {{\left( {D_{{bk}}^{2} - D_{{bk - 1}}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {D_{{bk}}^{2} - D_{{bk - 1}}^{2}} \right)} {\left( {16D{{\beta }^{2}}} \right)}}} \right. \kern-0em} {\left( {16D{{\beta }^{2}}} \right)}}.$
Уменьшение числа пузырей из-за их всплытия на поверхность равно отношению концентрации
пузырей ко времени их всплытия, определяемого отношением глубины бассейна $H$ к скорости движения пузырей ${{U}_{k}}{\text{:}}$

${{{\text{d}}{{n}_{k}}} \mathord{\left/ {\vphantom {{{\text{d}}{{n}_{k}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = - {{{{U}_{k}}{{n}_{k}}} \mathord{\left/ {\vphantom {{{{U}_{k}}{{n}_{k}}} H}} \right. \kern-0em} H}.$
Скорость движения пузыря вычисляется по выражению

${{U}_{k}} = {{\left( {{{4g{{D}_{{bk}}}{{\zeta }_{{bk}}}} \mathord{\left/ {\vphantom {{4g{{D}_{{bk}}}{{\zeta }_{{bk}}}} 3}} \right. \kern-0em} 3}} \right)}^{{0.5}}},$
где ${{\zeta }_{{bk}}}$ – коэффициент трения пузыря о жидкость.

Для расчета коэффициента трения пузыря используется формула из работы [9], которая, по утверждениям самих авторов, автоматически учитывает изменение коэффициента
трения газового пузыря при изменении его формы. Необходимо отметить, что для поиска
скорости движения пузыря решается нелинейное уравнение с использованием метода Ньютона.

Итоговое изменение числа пузырей k-го размера может быть представлено следующим образом [10]

$\left. \begin{gathered} {{{\text{d}}{{n}_{1}}} \mathord{\left/ {\vphantom {{{\text{d}}{{n}_{1}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {{f{{s}_{n}}} \mathord{\left/ {\vphantom {{f{{s}_{n}}} V}} \right. \kern-0em} V} - {{{{n}_{1}}} \mathord{\left/ {\vphantom {{{{n}_{1}}} {{{{\tau }}_{{21}}}}}} \right. \kern-0em} {{{{\tau }}_{{21}}}}} - \sum\limits_{i = 1}^N {{{B}_{{i1}}}{{n}_{i}}{\kern 1pt} {{n}_{1}}} - {{{{U}_{1}}{{n}_{1}}} \mathord{\left/ {\vphantom {{{{U}_{1}}{{n}_{1}}} {H;}}} \right. \kern-0em} {H;}} \hfill \\ ... \hfill \\ {{{\text{d}}{{n}_{k}}} \mathord{\left/ {\vphantom {{{\text{d}}{{n}_{k}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {{{{n}_{{k - 1}}}} \mathord{\left/ {\vphantom {{{{n}_{{k - 1}}}} {{{{\tau }}_{{kk - 1}}}}}} \right. \kern-0em} {{{{\tau }}_{{kk - 1}}}}} - {{{{n}_{k}}} \mathord{\left/ {\vphantom {{{{n}_{k}}} {{{{\tau }}_{{k + 1k}}}}}} \right. \kern-0em} {{{{\tau }}_{{k + 1k}}}}} + \hfill \\ + \,\,0.5\sum\limits_{i + j = k} {{{B}_{{ij}}}{{n}_{i}}{\kern 1pt} {{n}_{j}}} - \sum\limits_{i = 1}^N {{{B}_{{ik}}}{{n}_{i}}{\kern 1pt} {{n}_{k}}} - {{{{U}_{k}}{{n}_{k}}} \mathord{\left/ {\vphantom {{{{U}_{k}}{{n}_{k}}} {H.}}} \right. \kern-0em} {H.}} \hfill \\ \end{gathered} \right\}$
При решении этой системы могут быть получены значения ${{n}_{k}}$ в любой момент времени. В свою очередь, зная ${{n}_{k}},$ можно вычислить число пузырей заданного размера ${{N}_{k}},$ покидающих бассейн расплава в единицу времени:

$\frac{{{\text{d}}{{N}_{k}}}}{{{\text{d}}t}} = {{n}_{k}}{{U}_{k}}S.$
Отсюда полный объем газов ${{V}_{g}},$ выходящих с поверхности расплава в единицу времени,

$\frac{{{\text{d}}{{V}_{g}}}}{{{\text{d}}t}} = \sum\limits_{k = 1}^N {\frac{1}{6}\pi D_{{bk}}^{3}{{n}_{k}}{{U}_{k}}S} $
и, соответственно, масса i-го летучего продукта деления, выходящего в единицу времени,

$\frac{{{\text{d}}{{m}_{i}}}}{{{\text{d}}t}} = {{\rho }_{i}}\left( T \right)\sum\limits_{k = 1}^N {\frac{1}{6}\pi D_{{bk}}^{3}{{n}_{k}}{{U}_{k}}S} .$
Здесь ${{\rho }_{i}}\left( T \right)$ – плотность (массовая концентрация) ПД в пузыре при температуре $T,$ которая рассчитывается по уравнению состояния идеального газа с учетом закона Рауля

${{\rho }_{i}} = \frac{{{{{{C}_{{i\infty }}}} \mathord{\left/ {\vphantom {{{{C}_{{i\infty }}}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}}}{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}\frac{{{{p}_{{si}}}\left( T \right){{M}_{i}}}}{{RT}}.$
В итоге уравнение для расчета изменения концентрации ПД в газовой фазе над расплавом
выглядит следующим образом:

$\begin{gathered} {{V}_{g}}{{{\text{d}}{{C}_{g}}} \mathord{\left/ {\vphantom {{{\text{d}}{{C}_{g}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = S\left\{ {\frac{1}{{{{\alpha }_{{cf}}}}} + {{{\left[ {2\sqrt {{{RT} \mathord{\left/ {\vphantom {{RT} {\left( {2\pi M} \right)}}} \right. \kern-0em} {\left( {2\pi M} \right)}}} \,{{C}_{s}}} \right]}}^{{ - 1}}} \times } \right. \\ {{\left. { \times \,\,\frac{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{{{C}_{s}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{s}}\left( T \right)} M}} \right. \kern-0em} M}}} + \frac{1}{{{{\alpha }_{{cg}}}}}\frac{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{{{C}_{s}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{s}}\left( T \right)} M}} \right. \kern-0em} M}}}} \right\}}^{{ - 1}}} \times \\ \times \,\,\left[ {{{C}_{\infty }} - {{C}_{g}}\frac{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{{{C}_{s}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{s}}\left( T \right)} M}} \right. \kern-0em} M}}}} \right] + \frac{{{{{{C}_{\infty }}} \mathord{\left/ {\vphantom {{{{C}_{\infty }}} M}} \right. \kern-0em} M}}}{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{C}_{s}}\left( T \right) \times \\ \times \,\,\sum\limits_{k = 1}^N {\frac{1}{6}\pi D_{{bk}}^{3}{{n}_{k}}{{U}_{k}}S} . \\ \end{gathered} $
Последний член этого уравнения описывает выход ПД в составе пузырей.
Уравнение для определения изменения концентрации ПД в расплаве

$V{{{\text{d}}{{C}_{\infty }}} \mathord{\left/ {\vphantom {{{\text{d}}{{C}_{\infty }}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = - {{V}_{g}}{{{\text{d}}{{C}_{g}}} \mathord{\left/ {\vphantom {{{\text{d}}{{C}_{g}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}.$
Полная масса ПД в атмосфере над расплавом составляет

$m\left( t \right) = \sum\limits_i {V{{C}_{{ig}}}\left( t \right)} ,$
где ${{C}_{{ig}}}\left( t \right)$ – концентрация i-го ПД в атмосфере над расплавом.}

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Разработанная модель была реализована в составе тяжелоаварийного модуля SAFR/V1 [3, 4] интегрального кода ЕВКЛИД/V2 [1, 2]. Для демонстрации правильности программной реализации заложенных моделей были проведены расчеты задач с известным аналитическим решением, а для оценки погрешности расчетов выполнено моделирование экспериментов по выходу ПД из расплава топлива.

Далее приводится вывод аналитического решения. Изменение массы нелетучего ПД в атмосфере над расплавом находится путем решения следующего уравнения:

(8)

$\begin{gathered} \frac{{{\text{d}}{{m}_{g}}}}{{{\text{d}}t}} = S{{\left[ {\frac{1}{{{{\alpha }_{{cf}}}}} + \frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{2\sqrt {\frac{{RT}}{{2\pi M}}} {{C}_{s}}\left( T \right)}} + \frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{\alpha }_{{cg}}}{{C}_{s}}\left( T \right)}}} \right]}^{{ - 1}}} \times \\ \times \,\,\left( {{{C}_{\infty }} - {{C}_{g}}\frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{C}_{s}}\left( T \right)}}} \right). \\ \end{gathered} $

Масса продуктов деления, оставшихся в расплаве, равна

(9)

$\frac{{{\text{d}}{{m}_{m}}}}{{{\text{d}}t}} = - \frac{{{\text{d}}{{m}_{g}}}}{{{\text{d}}t}},$

что отражает закон сохранения массы.

Выражение для массы продуктов деления можно переписать так:

(10)

${{m}_{m}} = V{{C}_{\infty }}{\text{,}}\,\,\,\,{{m}_{g}} = {{V}_{g}}{{C}_{g}}.$

В этом случае система уравнений (8)–(10) преобразуется к виду

(11)

$\left. \begin{gathered} {{V}_{g}}\frac{{{\text{d}}{{C}_{g}}}}{{{\text{d}}t}} = S{{\left[ {\frac{1}{{{{\alpha }_{{cf}}}}} + \frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{2\sqrt {\frac{{RT}}{{2\pi M}}} \,{{C}_{s}}\left( T \right)}} + \frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{\alpha }_{{cg}}}{{C}_{s}}\left( T \right)}}} \right]}^{{ - 1}}}{\kern 1pt} \times \\ \times \,\,\left[ {{{C}_{\infty }} - {{C}_{g}}\frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{C}_{s}}\left( T \right)}}} \right]; \\ V\frac{{{\text{d}}{{C}_{\infty }}}}{{{\text{d}}t}} = - S{{\left[ {\frac{1}{{{{\alpha }_{{cf}}}}} + \frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{2\sqrt {\frac{{RT}}{{2\pi M}}} \,{{C}_{s}}\left( T \right)}} + \frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{\alpha }_{{cg}}}{{C}_{s}}\left( T \right)}}} \right]}^{{ - 1}}}{\kern 1pt} \times \\ \times \,\,\left[ {{{C}_{\infty }} - {{C}_{g}}\frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{C}_{s}}\left( T \right)}}} \right]. \\ \end{gathered} \right\}$

Систему уравнений (11) можно записать следующим образом:

$\left. \begin{gathered} \frac{{{\text{d}}{{C}_{g}}}}{{{\text{d}}t}} = \frac{S}{{{{V}_{g}}}}{{{\alpha }}_{{eff}}}\left( {{{C}_{\infty }} - {{C}_{g}}\frac{{{{{{{\rho }}_{m}}M} \mathord{\left/ {\vphantom {{{{{\rho }}_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{C}_{s}}\left( T \right)}}} \right); \hfill \\ \frac{{{\text{d}}{{C}_{\infty }}}}{{{\text{d}}t}} = - \frac{S}{V}{{{\alpha }}_{{eff}}}\left( {{{C}_{\infty }} - {{C}_{g}}\frac{{{{{{{\rho }}_{m}}M} \mathord{\left/ {\vphantom {{{{{\rho }}_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{C}_{s}}\left( T \right)}}} \right). \hfill \\ \end{gathered} \right\}$

Здесь

${{\alpha }_{{eff}}} = {{\left( {\frac{1}{{{{\alpha }_{{cf}}}}} + \frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{2\sqrt {\frac{{RT}}{{2\pi M}}\,} {{C}_{s}}\left( T \right)}} + \frac{{{{{{\rho }_{m}}M} \mathord{\left/ {\vphantom {{{{\rho }_{m}}M} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{\alpha }_{{cg}}}{{C}_{s}}\left( T \right)}}} \right)}^{{ - 1}}}.$

Система (11) представляет собой линейную систему дифференциальных уравнений, решение которой ищется в виде

${{C}_{g}} = {{C}_{1}}{{{\text{e}}}^{{{\lambda }t}}},\,\,\,\,{{C}_{\infty }} = {{C}_{2}}{{{\text{e}}}^{{{\lambda }t}}}.$

В результате подстановки этих выражений в (11) получаем

$\left. \begin{gathered} \left[ {{\lambda } + \frac{S}{{{{V}_{g}}}}{{\alpha }_{{eff}}}\frac{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{{{C}_{s}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{s}}\left( T \right)} M}} \right. \kern-0em} M}}}} \right]{{C}_{1}} - \frac{S}{{{{V}_{g}}}}{{\alpha }_{{eff}}}{{C}_{2}} = 0; \hfill \\ - \frac{S}{V}{{\alpha }_{{eff}}}\frac{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{{{C}_{s}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{s}}\left( T \right)} M}} \right. \kern-0em} M}}}{{C}_{1}} + \left( {{\lambda } + \frac{S}{V}{{\alpha }_{{eff}}}} \right){{C}_{2}} = 0. \hfill \\ \end{gathered} \right\}$

Нетривиальные решения могут быть только в том случае, если определитель системы равен 0, поэтому значения $\lambda $ могут быть найдены при решении характеристического уравнения.

Общее решение имеет вид

(12)

${{C}_{{ig}}} = - \frac{V}{{{{V}_{g}}}}A{{{\text{e}}}^{{{\lambda }t}}} + \frac{{{{{{C}_{{si}}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{{si}}}\left( T \right)} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}}}{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}B,\,\,\,\,{{C}_{{i\infty }}} = A{{{\text{e}}}^{{{\lambda }t}}} + B.$

При t = 0 (начальное условие): ${{C}_{{ig}}} = 0$ и ${{C}_{{i\infty }}} = {{C}_{0}},$ тогда

(13)

$\begin{gathered} {{C}_{g}} = \left\{ {1 - {\text{exp}}\left[ { - S{{\alpha }_{{eff}}}\left( {\frac{1}{V} + \frac{1}{{{{V}_{g}}}}\frac{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{{{{{C}_{s}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{s}}\left( T \right)} M}} \right. \kern-0em} M}}}} \right)t} \right]} \right\} \times \\ \times \,\,\frac{{\frac{{{{{{C}_{s}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{s}}\left( T \right)} M}} \right. \kern-0em} M}}}{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}V}}{{\frac{{{{{{C}_{s}}\left( T \right)} \mathord{\left/ {\vphantom {{{{C}_{s}}\left( T \right)} M}} \right. \kern-0em} M}}}{{{{{{\rho }_{m}}} \mathord{\left/ {\vphantom {{{{\rho }_{m}}} {{{M}_{m}}}}} \right. \kern-0em} {{{M}_{m}}}}}}{{V}_{g}} + V}}{{C}_{0}}. \\ \end{gathered} $

Активность A рассчитывается по формуле

$A = {{\lambda }_{d}}{{C}_{g}},$

где ${{\lambda }_{d}}$ – постоянная распада для данного изотопа.

На рис. 2 представлены результаты расчета и аналитического решения для выхода нелетучих ПД с зеркала расплава в виде зависимости активности (числа частиц, умноженных на постоянную распада) от времени. Как можно видеть из рисунка, результаты аналитического решения хорошо согласуются с расчетными данными.

Рис. 2.

Зависимость активности А продуктов деления от времени (выход нелетучих ПД из расплава). 1 – расчет по ЕВКЛИД/V2; 2 – аналитическое решение

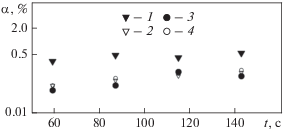
Рисунок 3 иллюстрирует зависимость от времени доли выхода летучих ПД (ксенона и криптона) из расплава диоксида урана, а рис. 4 – нелетучих ПД (стронция и церия). В экспериментах, проведенных в Национальной лаборатории в Ок-Ридже [11], топливо удерживалось в расплавленном состоянии в течение определенного промежутка времени, в котором происходил выход ПД. Плавление таблеток общей массой 29 г осуществлялось путем пропускания электрического тока через вольфрамовый стержень, который был вставлен в отверстие таблеток. Таблетки топлива обдувались гелием, который уносил вышедшие из печи ПД. Эти рисунки показывают удовлетворительное согласие расчетных и экспериментальных данных для выхода как нелетучих, так и летучих продуктов деления.

Рис. 3.

Доля выхода из расплава топлива летучих ПД: ксенона (1, 2) и криптона (3, 4) – в зависимости от времени. 1, 4 – эксперимент [11]; 2, 3 – расчет авторов

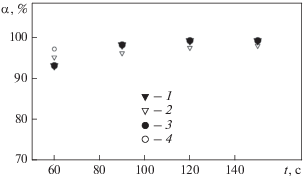
Рис. 4.

Доля выхода из расплава топлива нелетучих ПД: стронция (1, 2) и церия (3, 4) – в зависимости от времени. Обозначения см. рис. 3

ВЫВОДЫ

1. Механизмы выхода летучих и нелетучих продуктов деления из расплава различны и описываются разными дифференциальными уравнениями.

2. Предложенные механизмы выхода продуктов деления позволяют с хорошей точностью моделировать выход ПД в реальных экспериментах.

Список литературы

Верификация кода ЕВКЛИД/V2 на основе экспериментов с разрушением элементов активной зоны реактора с жидкометаллическим теплоносителем / А.А. Бутов, В.С. Жданов, И.А. Климонов, И.Г. Кудашов, А.Э. Кутлиметов, П.Д. Лобанов, Н.А. Мосунова, А.А. Сорокин, В.Ф. Стрижов, Э.В. Усов, В.И. Чухно // Теплоэнергетика. 2019. № 5. С. 16–24. https://doi.org/10.1134/S0040363619050035
Физические модели для расчета разрушений твэла и активной зоны реактора с жидкометаллическим теплоносителем, реализованные в коде ЕВКЛИД/V2 / А.А. Бутов, В.С. Жданов, И.А. Климонов, И.Г. Кудашов, А.Э. Кутлиметов, Н.А. Мосунова, В.Ф. Стрижов, А.А. Сорокин, С.А. Фролов, Э.В. Усов, В.И. Чухно // Теплоэнергетика. 2019. № 5. С. 5–15. https://doi.org/10.1134/S0040363619050023
Моделирование процессов плавления твэла и затвердевания расплава, образующегося при термическом разрушении твэла быстрого реактора, с помощью модуля SAFR/V1 интегрального кода ЕВКЛИД/V2 / Э.В. Усов, А.А. Бутов, В.И. Чухно, И.А. Климонов, И.Г. Кудашов, В.С. Жданов, Н.А. Прибатурин, Н.А. Мосунова, В.Ф. Стрижов // Атомная энергия. 2018. Т. 124. Вып. 3. С. 123–126.
Моделирование перемещения расплава по поверхности твэла быстрого реактора при тяжелой аварии с помощью модуля SAFR/V1 интегрального кода ЕВКЛИД/V2 / Э.В. Усов, А.Л. Бутов, В.И. Чухно, И.А. Климонов, И.Г. Кудашов, В.С. Жданов, Н.А. Прибатурин, Н.А. Мосунова, В.Ф. Стрижов // Атомная энергия. 2018. Т. 124. Вып. 4. С. 197–200.
Дрейцер Г.А. Теплообмен при свободной конвекции. М.: МАИ, 2002.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Физическая кинетика. Т. 10. М.: Физматлит, 2002.
McClure P.R., Leonard M.T., Razani A. A model for fission product release from liquid metal pool: Development and sensitivity investigation // Nucl. Sci. Eng. 1993. V. 114. Is. 2. P. 102–111. https://doi.org/10.13182/NSE93-A24021
Scriven L.E. On the dynamic of phase growth // Chem. Eng. Sci. 1959. V. 10. Is. 1–2. pp. 1–13. https://doi.org/10.1016/0009-2509(59)80019-1
Friedlander S. Smoke, dust, and haze. Fundamentals of aerosol dynamics. N.Y.: Oxford University Press, 2000.
Loth E. Quasi-steady shape and drag of deformable bubbles and drops // Int. J. Multiphase Flow. 2008. V. 34. Is. 6. P. 523–546. https://doi.org/10.1016/j.ijmultiphaseflow.2007.08.010
Release of fission products during in-pile melting of UO₂ / W.E. Browning, C.E. Miller, R.P. Shields, B.F. Roberts // Nucl. Sci. Eng. 1964. V. 18. P. 151–162. https://doi.org/10.13182/NSE64-1

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплоэнергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал