Теплоэнергетика, 2023, № 2, стр. 71-77
Разработка методики построения суррогатных моделей оборудования на примере модели гидравлики устройства газоудаления
И. А. Коновалов a, А. Н. Соколов a, А. А. Баринов a, Т. К. Зырянова b, *
a АО “Опытное конструкторское бюро машиностроения им. И.И. Африкантова”
603074 г. Нижний Новгород, Бурнаковский проезд, д. 15, Россия
b Нижегородский государственный технический университет им. Р.Е. Алексеева
603950 г. Нижний Новгород, ул. Минина, д. 24, Россия
* E-mail: ats@nntu.ru
Поступила в редакцию 08.07.2022
После доработки 23.08.2022
Принята к публикации 30.08.2022
Аннотация
В настоящее время перед энергетическим машиностроением стоит актуальная задача повышения эффективности и безопасности проектируемого оборудования. Из-за роста сложности разрабатываемых агрегатов требуется все более детальный анализ теплогидравлических процессов (в том числе с применением трехмерных кодов вычислительной гидродинамики), что приводит к увеличению затрат времени на проведение моделирования. В то же время повышение эффективности сложных теплогидравлических систем со множеством варьируемых технических параметров, влияющих на работоспособность системы, может быть обосновано с помощью математических алгоритмов многокритериальной оптимизации, требующих проведения большого количества вариантных расчетов (или экспериментов) рассматриваемой системы. В этом случае применение кодов вычислительной гидродинамики для моделирования отдельных геометрически сложных элементов в оптимизационном цикле становится затруднительным, поскольку приводит к неприемлемым временным затратам. Данная проблема может быть решена с использованием аппроксимационной зависимости (суррогатной модели) входных и выходных параметров, построенной на базе некоторой обучающей выборки, полученной в ходе расчета или эксперимента, вместо исходной сложной вычислительной математической модели. Однако в этом случае с повышением размерности задачи требуется увеличение обучающей выборки. В рамках данной работы предлагается способ представления суррогатной модели большой размерности в виде совокупности аппроксимационных зависимостей с меньшим числом размерностей, что позволяет обучать более точные модели на меньших выборках. Рассмотрена методика генерации обучающих выборок, а также представлена методология построения гидравлических суррогатных моделей энергетического оборудования на примере устройства газоудаления для атомной электростанции малой мощности. Получено хорошее соответствие построенной суррогатной модели с результатами численного моделирования.
В настоящее время в атомном машиностроении все большее распространение получает концепция цифровых двойников как отдельных единиц проектируемого оборудования, так и атомных электростанций в целом [1]. Понятие цифрового двойника, пройдя путь от “тренажера” до инструмента проектирования, подразумевает все более детальное моделирование теплогидравлических процессов, происходящих в контурах ядерных энергетических установок. Современные цифровые модели, в том числе виртуальной АЭС, базируются на использовании множества физических моделей, предназначенных для описания различных физических и химических процессов контурной теплогидравлики и различающихся по уровню сложности применяемых математических моделей [2 ] . При этом физико-химические явления, возникающие в отдельных геометрически сложных элементах оборудования реакторных установок, на сегодняшний день могут быть реалистично смоделированы только с использованием трехмерных кодов вычислительной гидродинамики.
Несмотря на впечатляющие успехи в развитии как информационных технологий, так и их аппаратной базы, полноценное применение CFD-кодов для инженерных расчетов и в составе цифровых двойников оборудования остается весьма ограниченным ввиду необходимости задействовать огромные вычислительные мощности для проведения трехмерного моделирования теплогидравлических процессов в приемлемые сроки. В дополнение к этому, в случае применения алгоритмов многопараметрической оптимизации к моделируемому оборудованию временные затраты многократно возрастают.
Обозначенная проблема может быть решена посредством использования суррогатной модели рассматриваемого оборудования, которая подразумевает многомерную аппроксимацию входных и выходных параметров. Установление аппроксимационной зависимости с приемлемой точностью напрямую с использованием одного метода возможно далеко не во всех случаях, в связи с чем актуальной задачей является разработка методики построения подобных суррогатных моделей для реального оборудования.
СУРРОГАТНАЯ МОДЕЛЬ
Основная идея суррогатного моделирования заключается в замене математической модели многомерной аппроксимацией входных и выходных параметров на основе статистических зависимостей.
Для данной задачи можно ввести следующие специфические терминологию и обозначения:
${\mathbf{D}}$ – K-мерное непрерывное пространство поиска;
${\mathbf{x}}$ – набор (вектор) размерности K варьируемых параметров ${\mathbf{x}} \in {\mathbf{D}} \subset {{\Re }^{K}}.$ Как правило, каждый варьируемый параметр набора имеет свой физически обусловленный диапазон значений ${{{\text{x}}}_{i}} \in \left[ {x_{i}^{0},x_{i}^{1}} \right]$ (здесь $x_{i}^{0}$ соответствует нижней границе диапазона i-го параметра, $x_{i}^{1}$ – верхней границе);
${\mathbf{f}}\left( {\mathbf{x}} \right)$ – целевая функция, некоторая величина, отвечающая конкретному набору (вектору) варьируемых параметров (например, коэффициент гидравлического сопротивления дроссельного устройства в зависимости от его геометрических характеристик, параметров среды и т.д.);
бюджет расчетов N – максимальное число вариантных расчетов, доступное для проведения расчетного анализа, обусловленное различными факторами, главные из которых – доступное процессорное время и средняя вычислительная сложность одного расчета;
${\mathbf{X}}\left( {1:N} \right)$ – дискретное подмножество ${\mathbf{D}},$ план вариации, представляющий собой некоторую совокупность векторов ${\mathbf{x}}$ в количестве N, сгенерированных для проведения вариантных расчетов.
Таким образом, решение задачи построения суррогатной модели сводится к нахождению совокупности аппроксимирующих функций ${\mathbf{\bar {f}}}\left( {\mathbf{x}} \right),$ удовлетворяющей условию ${\mathbf{\bar {f}}}\left( {\mathbf{x}} \right) = {\mathbf{f}}\left( {\mathbf{x}} \right) + \Delta {\mathbf{f}}\left( {\mathbf{x}} \right),$ где $\Delta {\mathbf{f}}\left( {\mathbf{x}} \right)$ – погрешность аппроксимации.
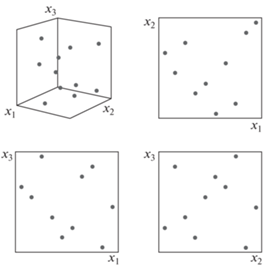
Генерация плана вариации ${\mathbf{X}}$ может выполняться с использованием различных подходов, однако для решения рассматриваемой задачи был выбран метод латинского гиперкуба (Latin Hypercube Sampling), при котором доступный бюджет из N расчетов распределяют по пространству поиска таким образом, чтобы получались однозначные и регулярные проекции из N точек на каждую его размерность (рис. 1).
Рис. 1.
Пространство поиска для K = 3 параметров в подходе латинского гиперкуба (бюджет из N = 10 вариантных расчетов, показан один из возможных вариантов)
Значения целевой функции ${\mathbf{f}}\left( {\mathbf{x}} \right),$ рассчитанные для ${\mathbf{X}},$ можно обозначить как ${\mathbf{Y}}.$ Тогда совокупность значений $\left\{ {{\mathbf{X}},{\mathbf{Y}}} \right\}$ есть обучающая выборка для модели ${\mathbf{\bar {f}}}\left( {\mathbf{x}} \right).$
Предлагаемая методика построения суррогатной модели заключается в определении таких совокупностей $\left\{ {{\mathbf{X}}{\kern 1pt} ',{\mathbf{Y}}{\kern 1pt} '} \right\},$ ${\mathbf{X}}{\kern 1pt} ' \in {\mathbf{X}},{\text{ }}{\mathbf{Y}}{\kern 1pt} ' \in {\mathbf{Y}},$ для которых коэффициенты взаимной корреляции $\left| {{\mathbf{R}}\left( {\widehat {{\mathbf{X}}{\kern 1pt} ',{\mathbf{Y}}{\kern 1pt} '}} \right)} \right| \geqslant 0.2$ [3]. При этом, если вектор входных параметров ${{{\mathbf{x}}}_{i}},$ ${{{\mathbf{x}}}_{i}} \in {\mathbf{X}}$ не коррелирует ни с одним из векторов выходных параметров ${\mathbf{y}},$ ${\mathbf{y}} \in {\mathbf{Y}},$ но известна физическая природа процесса, целесообразно введение вектора промежуточных параметров ${\mathbf{\tilde {y}}}$ такого, что $\left| {{\mathbf{R}}\left( {\widehat {{{{\mathbf{x}}}_{i}},{\mathbf{\tilde {y}}}}} \right)} \right| \geqslant 0.2 \wedge \left| {{\mathbf{R}}\left( {\widehat {{\mathbf{\tilde {y}}},{{{\mathbf{y}}}_{j}}}} \right)} \right| \geqslant 0.2.$ Например, если для коэффициента гидравлического сопротивления (КГС) $\xi $ и расхода потока $Q$ коэффициент корреляции $\left| {R\left( {\widehat {\xi ,Q}} \right)} \right| < 0.2$ и при этом $\xi $ аналитически связан со скоростью потока $u,$ которая, в свою очередь, зависит от расхода потока $Q$ (т.е. со статистической точки зрения $\left| {R\left( {\widehat {\xi ,u}} \right)} \right| \geqslant 0.2 \wedge \left| {R\left( {\widehat {u,Q}} \right)} \right| \geqslant 0.2$), можно установить аппроксимационную зависимость $\xi = f\left[ {u = f\left( Q \right)} \right].$
Определенная таким образом совокупность аппроксимационных зависимостей и составляет суррогатную модель
(1)
${\mathbf{y}} = {\mathbf{\bar {f}}}\left( {\mathbf{x}} \right) = \left\{ \begin{gathered} {{y}_{0}} = {{f}_{0}}\left( {{\mathbf{x}}_{0}^{'}} \right); \hfill \\ ... \hfill \\ {{y}_{n}} = {{f}_{n}}\left( {{\mathbf{x}}_{m}^{'}} \right). \hfill \\ \end{gathered} \right.,\,\,\,\,{{{\mathbf{x}}}_{{0:m}}} \in {\mathbf{x}};$ПОСТАНОВКА ЗАДАЧИ
В инженерной практике устройства газоудаления рассматриваются в составе сложных теплогидравлических систем, динамический (или итерационный) расчет которых не позволяет применять CFD-коды для моделирования отдельных элементов системы ввиду значительных затрат времени. В рамках данной работы был предложен альтернативный подход – многомерная аппроксимация КГС сопла на основе анализа статистических зависимостей входных и выходных параметров. Далее рассматривается методология построения суррогатной модели на примере модели устройства газоудаления, представляющего собой эжектор с подключением трех сдувок – трубопроводов газоудаления, подключенных к горловине основного канала при угле между соседними сдувками 120°. Проточная часть устройства газоудаления показана на рис. 2.
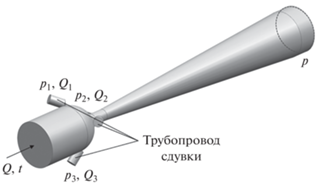
Рис. 2.
Проточная часть устройства газоудаления. Q – расход основного потока, м3/с; Q1–Q3 – расход среды по сдувкам, м3/с; t – температура среды, °C; р – статическое давление в системе, Па; р1–р3 – статическое давление на входе в сдувки, Па
Принцип работы устройства заключается в эжектировании потоков из сдувок вследствие падения статического давления в горловине канала, обусловленного повышением скорости основного потока. При этом расчет КГС сдувок и сопла, характеризующего перепад давления между входным и выходным сечениями сопла, является сложной задачей, не поддающейся расчету по справочным зависимостям ввиду сильной несимметричности потока в горловине сопла из-за различных давлений на входах в сдувки и возникающей вследствие этого асимметрии потока. В описанном случае задача построения суррогатной модели устройства газоудаления заключается в определении зависимости коэффициентов гидравлических сопротивлений и давления в горловине $\left\{ {\xi ,\,\,{{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}},{{р}_{{{\text{гор}}}}}} \right\}$ от входных параметров $\left\{ {Q,t,р,{{р}_{1}},{{р}_{2}},{{р}_{3}}} \right\}$ (здесь $\xi $ – КГС, характеризующий перепад давления между входным и выходным сечениями сопла; ${{\xi }_{1}} - {{\xi }_{3}}$ – КГС, характеризующие перепады давления между входом в сдувки и горловиной канала; ргор – статическое давление в горловине устройства, Па).
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Начальным этапом при построении суррогатной модели является генерация обучающей выборки, включающая в себя определение значений целевой функции ${\mathbf{f}}\left( {\mathbf{x}} \right) = \left\{ {\xi ,\,\,{{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}},{{р}_{{{\text{гор}}}}}} \right\}.$ Решение этой задачи возможно с использованием CFD-моделирования. В данной работе расчеты выполнялись в трехмерной стационарной постановке задачи с помощью численного решения системы уравнений Навье – Стокса в программном комплексе STAR-CCM+. Для численного интегрирования использовали метод контрольного объема, построенного на основе полиэдральной конечно-элементной сетки (рис. 3) с характерными размерами ячеек расчетной сетки 1.5 мм (0.075 мм для сдувок). Профиль скорости вблизи стенки определяли с использованием логарифмической пристеночной функции (высокий ${{y}^{ + }}$). Для повышения точности численного решения вблизи стенки были сгенерированы два призматических слоя расчетной сетки. Общая толщина пристенного призматического слоя составляла 0.5 мм (0.075 мм для сдувок).
Скалярные метрики точности моделей pSeven
| Зависимость | R2 | RMS | Q95 |
|---|---|---|---|
| ${{u}_{1}} = f\left( {р,{{р}_{1}},{{р}_{2}}} \right)$ | 0.994 | 0.077 | 0.179 |
| ${{\xi }_{1}} = f\left( {{{u}_{1}}} \right)$ | 0.998 | 0.041 | 0.089 |
| $\Delta р = f\left( {{{р}_{1}},{{р}_{2}},{{р}_{3}},Q} \right)$ | 0.986 | 0.120 | 0.079 |
| ${{\xi }_{2}} = f\left( {{{р}_{2}},\Delta р} \right)$ | 0.985 | 0.122 | 0.244 |
| ${{u}_{3}} = f\left( {р,{{р}_{2}},{{р}_{3}},{{u}_{1}}} \right)$ | 0.998 | 0.041 | 0.086 |
| ${{\xi }_{3}} = f\left( {{{u}_{3}}} \right)$ | 0.999 | 0.019 | 0.040 |
| ${{р}_{{{\text{гор}}}}} = f\left( Q \right)$ | 0.987 | 0.092 | 0.044 |
Поскольку устройство газоудаления работает в области очень малых газосодержаний, для упрощения расчетов в данной статье рассматривается течение однофазной несжимаемой жидкости. Для моделирования турбулентного потока в каналах устройства газоудаления использована стандартная k–ε-модель. В качестве граничных условий при расчете заданы скорость основного потока на входе, давление на выходе, а также давления на входе в сдувки.
На входе в сопло и выходе из него моделировали успокоительные участки длиной 5 калибров, предназначенные на входе для формирования реалистичного входного профиля скорости, на выходе – для уменьшения влияния граничного условия “давление на выходе” на явления, протекающие непосредственно в канале.
МЕТОДИКА ОБРАБОТКИ ДАННЫХ
Начальный этап построения суррогатной модели заключается в генерации K-мерной (в рассматриваемом случае 12-мерной, включая дополнительные параметры) обучающей выборки метода латинского гиперкуба. С помощью результатов статистической обработки данных обучающей выборки делаются выводы об уровнях взаимной корреляции тех или иных пар параметров. С учетом анализа полученных таким образом коэффициентов взаимной корреляции при построении суррогатной модели устройства газоудаления систему (1) можно представить в виде
(2)
$\begin{gathered} \left\{ {\xi ,{{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}},{{р}_{{{\text{гор}}}}}} \right\} = {\mathbf{\bar {f}}}\left( {Q,t,р,{{р}_{1}},{{р}_{2}},{{р}_{3}}} \right) = \\ = \left\{ \begin{gathered} \Delta р = f\left( {{{р}_{1}},{{р}_{2}},{{р}_{3}},Q} \right); \hfill \\ \xi = f\left( {\Delta р} \right); \hfill \\ {{\xi }_{2}} = f\left( {{{р}_{2}},\Delta р} \right); \hfill \\ {{u}_{1}} = f\left( {р,{{р}_{1}},{{р}_{2}}} \right); \hfill \\ {{\xi }_{1}} = f\left( {{{u}_{1}}} \right); \hfill \\ {{u}_{3}} = f\left( {р,{{р}_{2}},{{р}_{3}},{{u}_{1}}} \right); \hfill \\ {{\xi }_{3}} = f\left( {{{u}_{3}}} \right); \hfill \\ {{р}_{{{\text{гор}}}}} = f\left( Q \right), \hfill \\ \end{gathered} \right. \\ \end{gathered} $Коэффициент гидравлического сопротивления сопла Вентури $\xi $ вычисляется по формуле
(3)
$\xi = \frac{{2\Delta р}}{{\rho {{u}^{2}}}} = \frac{{2\Delta р}}{{\rho {{{\left[ {Q{{{\left( {0.25\pi {{d}^{2}}} \right)}}^{{ - 1}}}} \right]}}^{2}}}},$Для установления аппроксимационных зависимостей (2) использовали различные методы: для $\Delta р$ и ${{\xi }_{2}}$ – метод поверхности отклика (Response Surface Model) [4]; для ${{u}_{1}}$ – регрессию гауссовского процесса (Gaussian Process) [5]; для ${{\xi }_{1}},$ ${{u}_{3}},$ ${{\xi }_{3}}$ – метод многомерной регрессии гауссовского процесса (High-Dimensional Approximation Gaussian Process) [6]. Аппроксимацию производили с помощью программного обеспечения для многокритериальной оптимизации “pSeven” [7]. Блок-схема суррогатной модели, составленная таким образом в pSeven, представлена на рис. 4.
АНАЛИЗ РЕЗУЛЬТАТОВ
На рис. 5 приведены результаты расчета общего КГС сопла по выражениям (2), (3) в сравнении со значениями обучающей выборки, полученными в ходе CFD-моделирования.
Рис. 5.
Зависимость общего коэффициента гидравлического сопротивления от расхода основного потока. 1 – обучающая выборка; 2 – верификационная выборка
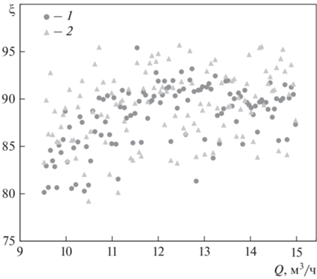
Результаты расчета значений параметров, определенные по аппроксимационным зависимостям (2) с помощью программы pSeven с использованием различных методов, в сравнении с результатами CFD-моделирования (обучающая выборка) представлены на рис. 6, 7. Поскольку при обучении модели существует вероятность ее переобучения (когда она точно предсказывает значения зависимых переменных в точках обучающей выборки, но при этом сильно ошибается в промежуточных точках, отличных от обучающей выборки), для проверки корректности обучения аппроксимационных моделей была сгенерирована верификационная выборка – новый план вариации независимых переменных, отличный от плана вариации обучающей выборки, для которого рассчитаны модельные значения зависимых переменных, но сгенерированный в тех же диапазонах варьирования. В этом случае о корректности модели можно судить по совпадению общего характера (тренда) значений обучающей и верификационной выборок. Значения аппроксимационной модели (2), рассчитанные для верификационной выборки, также приведены на рис. 6, 7.
Рис. 6.
Зависимость общего перепада давления на сопле от расхода основного потока. 1, 2 – см. рис. 5; 3 – модельные значения
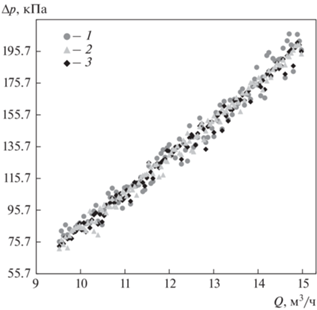
Рис. 7.
Зависимость коэффициента гидравлического сопротивления сдувки 1 (а), сдувки 2 (б) и сдувки 3 (в) от расхода основного потока. Обозначения см. рис. 6
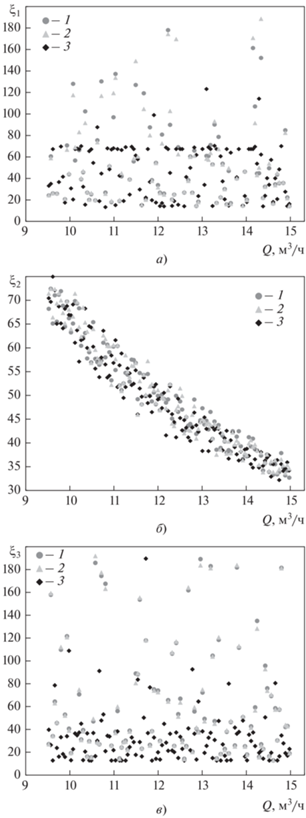
Как можно заметить, тренды изменения искомых КГС для верификационной выборки на представленных рисунках совпадают с трендами обучающей выборки, что свидетельствует о корректности построенных аппроксимационных моделей. Качественно разные характеры зависимости КГС от расхода основного потока на рис. 7 могут быть объяснены конструктивными особенностями системы, в которой функционирует рассматриваемый эжектор: давление на входе в сдувку 2, а следовательно, и ее КГС напрямую зависят от расхода основного потока, поскольку она подключена к автономному контуру насоса, обеспечивающего циркуляцию основного потока через горловину эжектора. Сдувки 1 и 3 подключены к другим агрегатам системы, поэтому их КГС практически не зависит от расхода основного потока.
Для оценки точности моделей, сгенерированных встроенными средствами pSeven (зависимости, представленные на рис. 4), использовались значения коэффициентов детерминации R2, среднеквадратического отклонения RMS (root mean square) и 95-го перцентиля Q95 (95-й перцентиль показывает, что для 95% точек верификационной выборки абсолютная ошибка меньше указанного значения).
Выражение для коэффициента детерминации модели, характеризующего долю дисперсии зависимой переменной, вызванной самой аппроксимационной моделью, выглядит следующим образом:
(4)
${{R}^{2}} = 1 - \frac{{\sum\limits_{i = 1}^n {{{{\left( {{{u}_{i}} - {{{\tilde {u}}}_{i}}} \right)}}^{2}}} }}{{\sum\limits_{i = 1}^n {{{{\left( {{{u}_{i}} - {{{\bar {u}}}_{i}}} \right)}}^{2}}} }},$Чем ближе значение R2 к 1, тем качественнее построена аппроксимационная зависимость.
Среднеквадратическое отклонение модельных значений от верификационной выборки вычисляют по формуле
(5)
${\text{RMS}} = \sqrt {\frac{1}{{n\left( {n - 1} \right)}}\sum\limits_{i = 1}^n {{{{\left( {{{{\tilde {u}}}_{i}} - {{u}_{i}}} \right)}}^{2}}} .} $Чем меньше RMS, тем меньше отклонение предсказанных моделью значений от значений верификационной выборки.
Значения скалярных метрик точности моделей приведены в таблице.
ВЫВОДЫ
1. Результаты применения построенной в работе суррогатной модели сложного гидравлического устройства для расчета значения коэффициента гидравлического сопротивления по обучающей и тестовой выборкам входных данных позволяют судить о корректности представленной методики ввиду совпадения трендов выходных данных.
2. Суррогатная модель дает возможность значительно сократить время, затрачиваемое на расчет гидравлических характеристик рассматриваемого устройства.
3. Суррогатные модели могут быть использованы в том числе на этапе планирования экспериментальных исследований, поскольку позволяют определить объем и направленность экспериментов.
Список литературы
Виртуально-цифровая АЭС – современный инструмент поддержки жизненного цикла атомных энергоблоков с ВВЭР / Г.В. Аркадов, А.П. Жукавин, А.Е. Крошилин, И.А. Паршиков, С.Л. Соловьев, А.В. Шишов // Теплоэнергетика. 2014. № 10. С. 3–11. https://doi.org/10.1134/S0040363614100014
Возможности по применению программно-технического комплекса “Виртуально-цифровая АЭС с ВВЭР” для обеспечения безопасности эксплуатации АЭС / С.М. Гололобов, А.А. Дружаев, А.А. Семенов, В.А. Чернаков // Сб. тезисов докл. 13-й Междунар. науч.-практ. конф. по атомной энергетике “Безопасность, эффективность, ресурс”. Севастополь, 3–6 октября 2017 г. С. 19–20.
Бендат Д., Пирсол А. Прикладной анализ случайных данных: пер. с англ. М.: Мир, 1989.
Стемпицкий В.Р. Метод поверхности откликов в статическом проектировании технологии ИМС // Сб. материалов Междунар. науч.-техн. семинара “Современные проблемы проектирования и производства радиоэлектронных средств”. НовоПолоцк, 29–31 мая 2000 г. С. 99–102.
Беляев М., Бурнаев Е., Капушев Е. Вычислительно-эффективный алгоритм построения регрессии на основе гауссовских процессов в случае структурированных выборок // Журн. вычислит. математики и математ. физики. 2016. Т. 56. № 4. С. 507–522.
Бурнаев Е.В., Ерофеев П.Д., Приходько П.В. Выделение главных направлений в задаче аппроксимации на основе гауссовских процессов // Труды МФТИ. Информатика, математическое моделирование, экономика. 2013. Т. 5. № 3. С. 24–35.
Свидельство о государственной регистрации программы для ЭВМ 2019612369, Feb. 19, 2019. Программа для автоматизации инженерных расчетов, интеллектуального анализа данных и оптимизации pSeven 6.14. ООО “ДАТАДВАНС”.
Дополнительные материалы отсутствуют.
Инструменты
Теплоэнергетика