Теплоэнергетика, 2023, № 3, стр. 20-39

Моделирование методом VOF процессов конденсации неподвижного и движущегося насыщенного пара на поверхности горизонтальной трубы

К. Б. Минко^a, *, В. И. Артемов^a, А. А. Клементьев^a

^a Национальный исследовательский университет “Московский энергетический институт”
111250 Москва, Красноказарменная ул., д. 14, Россия

^* E-mail: minkokb@gmail.com

Поступила в редакцию 19.09.2022
После доработки 10.10.2022
Принята к публикации 26.10.2022

DOI: 10.56304/S0040363623030050

Полный текст (PDF)

Аннотация

Исследованиям процессов пленочной конденсации неподвижного и движущегося пара на внешней поверхности одиночной трубы и разнообразных трубных пучков посвящено большое количество работ. Несмотря на это, локальные характеристики теплоотдачи и детали взаимодействия стекающего конденсата с движущимся потоком пара, которые могут оказывать существенное влияние на характеристики процесса конденсации в трубных пучках, недостаточно изучены. В статье представлены результаты моделирования конденсации практически неподвижного, а также движущегося насыщенного пара на поверхности горизонтального цилиндра. В качестве основы математической модели двухфазного потока использован метод VOF (Volume of Fluid), который реализован в открытом исследовательском коде ANES. Главное преимущество предлагаемого метода моделирования заключается в возможности явно определять поверхность раздела фаз без каких-либо допущений. Для моделирования межфазного массообмена использовалась модифицированная модель Lee. Предложен алгоритм автоматического подбора константы в данной модели исходя из заданных свойств теплоносителя и параметров расчетной сетки. Выполнена валидация модели с использованием классических решений Нуссельта для вертикальной пластины и горизонтального цилиндра, известных расчетных корреляций и результатов расчета с помощью упрощенной модели конденсации, предложенной в предыдущих работах авторов настоящей статьи. Представлена информация об отрывных диаметрах капель, динамике нагрева капель переохлажденного конденсата после их срыва с поверхности трубы и влиянии внешнего орошения трубы на интенсивность конденсации. Полученные данные сравниваются с имеющимися экспериментальными результатами.

Ключевые слова: конденсация, массообмен, горизонтальная труба, межфазная поверхность, численное моделирование, метод VOF, модифицированная модель Lee, нисходящее движение пара, орошение конденсатом

Исследованиям процессов пленочной конденсации неподвижного и движущегося чистого пара на внешней поверхности одиночной трубы и трубных пучков посвящено большое число работ [1, 2]. Тем не менее многие практически важные процессы, определяющие интенсивность конденсации в трубных пучках, остаются по-прежнему почти не изученными. К их числу относятся взаимодействие стекающего конденсата с движущимся потоком пара, а также орошение трубы конденсатом, образовавшимся на других трубах пучка. Авторы обзорной статьи [3] отмечают противоречивость имеющихся рекомендаций по учету влияния этих эффектов на процесс конденсации. Известно, что наличие конденсата в межтрубном пространстве оказывает существенное воздействие на перепад давления в трубном пучке, который может значительно возрастать [4]. При общем низком давлении в системе увеличение перепада давления в конденсаторе является негативным эффектом, в том числе и по причине существенного падения температуры насыщения по ходу движения пара. Из-за сложности экспериментального исследования совокупно протекающих процессов при конденсации на трубных пучках в значительной степени затруднены разработка более совершенных методик расчета и проектирование эффективных конденсаторов с опорой только на опытные данные и традиционные модели для описания пленки конденсата. Поэтому актуальность использования новых методов анализа упомянутых выше процессов не вызывает сомнений.

Цель настоящей работы – моделирование процессов конденсации практически неподвижного и движущегося пара на поверхности горизонтальной охлаждаемой трубы методом VOF. Очевидное преимущество этого метода заключается в возможности явно определять поверхность раздела фаз без каких-либо допущений. Основная проблема при использовании метода VOF при моделировании процесса конденсации – создание эффективных алгоритмов расчета источников массы жидкой фазы (или источников энергии) вследствие фазового перехода и перемещения межфазной поверхности. Следует отметить, что некоторые алгоритмы, например CISIT [5], хорошо зарекомендовавшие себя при моделировании процессов в отсутствие фазовых переходов (традиционный VOF) или процессов кипения, оказываются неэффективными для моделирования процессов конденсации. Причины возникновения этой особенности будут рассмотрены при обсуждении алгоритма VOF, использованного в настоящей работе.

Различные подходы к моделированию массообмена методом VOF систематизированы в недавно вышедшей обзорной работе [6]. Существующие модели для упомянутых ранее источников можно условно разделить на два класса: модели “поверхностных” и “сглаженных” источников. В первом случае источники локализованы только в одной “двухфазной” расчетной ячейке по “толщине” межфазной поверхности, содержащей фронт фазового перехода. В [6] этот класс моделей подразделяется на две группы, различающиеся методами расчета источников/стоков массы: модели, основанные на уравнении Герца – Кнудсена для плотности массового потока на межфазной поверхности [7], и модели, использующие универсальные условия совместности на поверхности раздела фаз при фазовых переходах умеренной интенсивности (“energy jump condition”) [8]. В моделях второго класса предполагается, что фронт фазового перехода имеет некоторую конечную “толщину” и распространяется на несколько расчетных ячеек, содержащих обе фазы. Тем самым источники/стоки массы и энергии в результате фазового перехода “размазываются” на две-три расчетные ячейки. Вероятно, для моделирования процессов конденсации наиболее удачной моделью этого класса оказалась модель W.H. Lee [9]. Ее физическая интерпретация чрезвычайно проста: источник энергии за счет фазового перехода (конденсации) пропорционален разности температуры насыщения и температуры двухфазной смеси в ячейке. Основной недостаток этой модели заключается в произвольности выбора некоторой константы $С{\kern 1pt} ',$ которую Lee назвал “time relaxation parameter” [9] (в [9] эта константа обозначена символом λ_d).

Несмотря на то что в [6] практически для всех упомянутых моделей и алгоритмов расчета массообмена методом VOF предполагается возможность использовать их и для моделирования конденсации, количество работ, в которых исследуется данный процесс, весьма ограничено. Примечательно, что из 250 работ, включенных в библиографические ссылки [6], нет ни одной публикации, которая была бы посвящена расчету процессов конденсации на поверхности горизонтальных труб.

Авторы настоящей статьи ограничатся кратким обзором работ, в которых используется метод VOF для моделирования пленочной конденсации на поверхности горизонтальных труб. Для более детального рассмотрения применения метода VOF для моделирования различных режимов конденсации внутри охлаждаемых труб следует обратиться к упомянутой ранее обзорной публикации [6].

В работе 2006 г. [10] предпринята, по-видимому, одна из первых попыток моделирования методом VOF конденсации на поверхности горизонтальной трубы нисходящего потока насыщенного водяного пара при давлении 0.1 МПа и скорости 10 м/с (труба имела эллиптическое сечение). Авторы [10] указывают на использование стационарной версии метода VOF. Описанные в статье результаты не дают ответа на многие вопросы, связанные с деталями постановки задачи и способом получения стационарного решения, численной реализацией алгоритмов и используемым кодом. Особенности моделирования процесса стекания образовавшегося конденсата также не обсуждаются. Очевидно, что срыв конденсата в виде капель не может быть смоделирован в стационарной постановке.

В работах [11, 12] авторы представили результаты численного исследования процессов конденсации практически неподвижного пара пентана на гладких и оребренных трубах методом VOF, в том числе в трехмерной постановке. Авторы предложили оригинальный подход к моделированию массообмена, в котором источник в уравнении энергии для фиксации температуры насыщения в контрольном объеме, содержащем межфазную поверхность, на каждом шаге по времени постепенно возрастает в процессе “внутренних” итераций и, в отличие от модели Lee [9], не требует подбора эмпирического параметра релаксации $С{\kern 1pt} '.$ Расчеты выполнялись с использованием кода OpenFOAM. Предварительно модель валидировалась на одномерной задаче Стефана (конденсация воды и пентана). Расчет конденсации пентана на горизонтальной трубе дал примерно на 10% более низкие результаты, чем решение Нуссельта. В [11, 12] предполагалась симметрия относительно вертикальной плоскости, содержащей ось трубы, которая ограничивала расчетную область. Интересно отметить, что задание различных граничных условий на фрагменте этой плоскости (в двумерной постановке – на фрагменте вертикальной линии) ниже поверхности трубы приводило к различным режимам стекания конденсата (капельному, ручейковому). При образовании капель значения средних коэффициентов теплоотдачи оказывались примерно на 5% ниже аналогичных значений для ручейкового режима.

В работе [13] с использованием модели VOF в сочетании с моделью Lee выполнено моделирование конденсации практически неподвижного насыщенного пара различных хладагентов. Хотя авторы привели выражения для константы $С{\kern 1pt} '$ в модели Lee из документации кода ANSYS Fluent (ANSYS Fluent Theory Guide) [14], подбор константы был проведен в результате серии тестовых расчетов. Важно, что для всех рассчитанных режимов конденсации в [13] применялось одно значение $С{\kern 1pt} '$ = 5 × 10⁶ с^–1. Результаты моделирования конденсации пропана (температура насыщения ${{T}_{{sat}}}$ = 308.15 К, отношение плотностей жидкой и паровой фаз равно 17.4) и хладагента R1234ze(E) (${{T}_{{sat}}}$ = 313.15 К, отношение плотностей – 15.5) находятся в хорошем соответствии с экспериментальными данными [15] и теорией Нуссельта. Авторы [13] проанализировали влияние поверхностного натяжения на поведение жидкой пленки конденсата вблизи точки его срыва с поверхности трубы. Из-за недостаточного размера расчетной области ниже поверхности трубы им не удалось смоделировать динамику срыва капель конденсата при высоких тепловых нагрузках ($\Delta T = {{T}_{{sat}}} - {{T}_{w}} = 100\,\,{\text{К,}}$ где ${{T}_{w}}$ – температура стенки), так как предотрывной размер вытянутой капли конденсата выходил за пределы расчетной области. В этом режиме наблюдалась несимметричная относительно вертикальной оси трубы динамика образования капли конденсата на нижней половине трубы. Данный эффект, разумеется, невозможно воспроизвести в симметричной постановке, используемой в работах [11, 12].

Несколько неожиданными представляются результаты [13], обработанные в виде среднего коэффициента теплоотдачи $\left\langle \alpha \right\rangle $ в зависимости от ${{T}_{{sat}}}$ при фиксированном перепаде температуры $\Delta T$ для различных хладагентов. Для пропана кривые $\left\langle \alpha \right\rangle = f({{T}_{{sat}}})$ при разных $\Delta T$ имеют локальный максимум в окрестности ${{T}_{{sat}}} \approx 268\,\,{\text{К,}}$ и с уменьшением ${{T}_{{sat}}}$ коэффициент теплоотдачи уменьшается на 10–15%. Такое поведение $\left\langle \alpha \right\rangle $ противоречит теории Нуссельта, в соответствии с которой $\left\langle \alpha \right\rangle = f({{T}_{{sat}}})$ монотонно возрастает с уменьшением ${{T}_{{sat}}}$ в результате изменения теплофизических свойств среды. Следует отметить, что при снижении ${{T}_{{sat}}}$ до 233.15 К отношение плотностей для пропана достигает 220, что выше на порядок отношения плотностей в режимах, которые использовались для верификации. Попытки авторов [13] объяснить полученные результаты, ссылаясь на уравнение Герца – Кнудсена, вряд ли уместны, так как используемые в модели уравнения исключительно феноменологические, а константа $С{\kern 1pt} '$ в модели Lee, хотя и имеет отдаленное отношение к уравнению Герца – Кнудсена, была выбрана, как упоминалось ранее, постоянной для всех хладагентов и режимов конденсации. Далее авторы статьи еще обратятся к этим данным [13] при обсуждении результатов настоящей работы.

За исключением [10], исследования, в которых методом VOF моделировался бы процесс конденсации на горизонтальном цилиндре водяного пара, авторам настоящей статьи не известны. Возможно, это объясняется в несколько раз большим значением отношения плотностей жидкой и паровой фаз воды по сравнению с хладонами и огромной теплотой фазового перехода. Известно, что эти обстоятельства осложняют устойчивость некоторых алгоритмов, положительно зарекомендовавших себя применительно к конденсации хладонов. Из-за существенно большего значения отношения плотностей фаз для воды (1600 для 100 кПа и 28 000 для 5 кПа) временной шаг расчета катастрофически снижается (на порядок и более) и усиливается чувствительность расчетных схем к выбранному способу аппроксимации потоков на гранях контрольного объема. Указанные обстоятельства с учетом относительно низкой эффективности распараллеливания расчетов (их запуска на нескольких процессорах) для двумерных задач, содержащих относительно небольшое число контрольных объемов, приводят к тому, что некоторые двумерные расчеты для воды по необходимым временным ресурсам сопоставимы с трехмерными расчетами для хладонов.

В настоящей работе предложен и реализован в исследовательском коде ANES алгоритм автоматического подбора константы модели Lee [9] исходя из заданных свойств теплоносителя и параметров расчетной сетки и проведено моделирование процессов конденсации на горизонтальной трубе движущегося потока пара, в том числе и водяного. Валидация модели выполнена с привлечением известного решения Нуссельта для случая неподвижного пара и имеющихся данных для пара, движущегося с умеренными скоростями. Представлены анализ динамики срыва капель конденсата и данные о влиянии на теплоотдачу орошения трубы сверху заданным расходом конденсата.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ VOF

В модели VOF двухфазная среда описывается односкоростной и однотемпературной гомогенной моделью, истинные свойства фаз которой считаются постоянными. Модель включает в себя следующую систему уравнений:

(1)

$\frac{{\partial \varphi }}{{\partial \tau }} + {\text{div}}\left( {U\varphi } \right) = \frac{{{{M}_{{gl}}}}}{{{{\rho }_{l}}}};$

(2)

${\text{div}}\left( U \right) = {{M}_{{gl}}}\left( {\frac{1}{{{{\rho }_{l}}}} - \frac{1}{{{{\rho }_{g}}}}} \right);$

(3)

$\frac{{\partial \left( {\rho {{U}_{k}}} \right)}}{{\partial \tau }} + {\text{div}}\left( {\rho U{{U}_{k}} - \mu \nabla {{U}_{k}}} \right) = - \frac{{\partial {{p}_{{rgh}}}}}{{\partial {{x}_{k}}}} + {{F}_{{b,k}}};$

(4)

$\frac{{\partial \left( {\rho {{c}_{p}}T} \right)}}{{\partial \tau }} + {\text{div}}\left( {\rho {{c}_{p}}UT - \lambda \nabla T} \right) = {{Q}_{{gl}}}.$

Система уравнений модели состоит из уравнения баланса объемной доли жидкой фазы φ (1), уравнения неразрывности (2), записанного через плотность объемного потока среды, т.е. скорость, уравнений движения (3) и энергии (4) [16]. В ней приняты следующие обозначения: $\tau $ – время c; $U$ – вектор скорости, м/с; ${{M}_{{gl}}}$ – межфазная объемная плотность потока массы, направленная из газовой фазы в жидкую фазу, кг/(м³ · c); ${{\rho }_{l}}$ и ${{\rho }_{g}}$ – истинные плотности жидкой и газовой фаз, кг/м³; ${{U}_{k}}$ – k-я проекция скорости, м/с; $\mu $ – динамический коэффициент вязкости среды, Па ⋅ с; F_b,k – проекция вектора ${{F}_{b}} = \left[ { - \left( {{{\rho }_{l}} - {{\rho }_{g}}} \right)\left( {g \cdot x} \right) + \sigma K} \right]\nabla \varphi $ на ось k; $g$ – вектор ускорения свободного падения, м/с²; $x$ – радиус-вектор точки расчетной области, м; $K$ – кривизна межфазной поверхности, м^–1; σ – поверхностное натяжение, Н/м; ${{p}_{{rgh}}} = p - \rho \left( {g \cdot x} \right)$ – статическое давление за вычетом локального гидростатического столба, Па; p – давление, Па; $\rho ,$ ${{c}_{p}},$ $T,$ $\lambda $ – плотность, кг/м³, теплоемкость, Дж/(кг ⋅ К), температура, К, и коэффициент теплопроводности, Вт/(м ⋅ К), среды соответственно; ${{Q}_{{gl}}} = \,\,\,{{M}_{{gl}}}{{h}_{{lg}}}$ – источник энергии, Вт/м³; ${{h}_{{lg}}}$ – теплота фазового перехода, Дж/кг.

Плотность $\rho ,$ динамический коэффициент вязкости $\mu ,$ объемная теплоемкость $\rho {{c}_{p}}$ и коэффициент теплопроводности $\lambda $ среды в каждой расчетной ячейке определяются как среднеобъемные величины по формуле

$f = \varphi {{f}_{l}} + (1 - \varphi ){{f}_{g}},\,\,\,\,f \in (\rho ,\mu ,\rho {{c}_{p}},\lambda ).$

Здесь и далее подстрочный индекс l обозначает параметры жидкой фазы, а g – параметры газовой фазы.

МОДЕЛИРОВАНИЕ МЕЖФАЗНОГО МАССООБМЕНА

Главное отличие модели VOF от обычной гомогенной модели двухфазного потока – использование уравнения (1) для явного определения положения межфазной поверхности путем “сжатия” области с $0 < \varphi < 1$ до слоя из одной – трех ячеек расчетной сетки. Для этого в различных традиционных версиях VOF без массообмена применяются специальные численные схемы высокого порядка точности, модель “донор–акцептор”, предложенная в работе [16], и очевидное предположение, что межфазная поверхность перемещается вместе с двухфазной смесью. Типичным примером такой схемы является схема CICSAM [17], используемая в данной работе. Межфазная поверхность рассматривается как поверхность постоянного уровня $\varphi $ = 0.5, что позволяет определить ее форму и площадь в ячейке. Для большинства схем характерен двухшаговый алгоритм предиктор – корректор. На предиктор-шаге решаются дискретные аналоги уравнения (1), на корректор-шаге производится коррекция $\varphi $ в ячейках расчетной области с нефизическими значениями φ ($\varphi < 0$ или $\varphi > 1$). Чаще всего используется “перелив” жидкости (при $\varphi > 1$) в соседние ячейки через грани ячейки с вытекающими потоками или “долив” жидкости (при $\varphi < 0$) из соседних ячеек (см., например, [5, 17]).

При наличии массообмена на фазовой границе (${{M}_{{gl}}} \ne 0$) ситуация существенным образом меняется. В этом случае вектор скорости движения межфазной поверхности не совпадает с вектором скорости смеси. Это приводит к принципиальному различию моделирования кипения (${{M}_{{gl}}} < 0$) и конденсации $\left( {{{M}_{{gl}}} > 0} \right)$), так как источниковые члены в уравнениях (1) и (2) меняют знак на противоположный. На дискретном уровне уравнение неразрывности (2) для ячейки с узловой точкой Р при ${{\rho }_{g}} < < {{\rho }_{l}}$ можно записать в виде

(5)

$\sum\limits_k {{{V}_{k}}} \approx - {{\left( {\frac{{{{M}_{{gl}}}}}{{{{\rho }_{g}}}}} \right)}_{P}}\Delta {{V}_{P}},\,\,\,\,{{V}_{k}} = \left( {{{U}_{k}}{{n}_{k}}} \right)\Delta {{A}_{k}},$

где ${{V}_{k}}$ – объемный поток, вытекающий через k‑ю грань ячейки P, м³/с; ${{n}_{k}}$ – внешняя нормаль к грани; $\Delta {{V}_{P}}$ – объем ячейки P, м³; $\Delta {{A}_{k}}$ – площадь k-й грани, м².

При использовании “поверхностного” источника в случае кипения $\left( {{{M}_{{gl}}} < 0} \right)$ для ячейки, с-одержащей межфазную поверхность, левая часть (5) положительна, что гарантирует наличие вытекающих потоков и возможность “переноса” межфазной поверхности в другие ячейки, ранее содержавшие только жидкость, на корректор-шаге. При моделировании конденсации $\left( {{{M}_{{gl}}} > 0} \right)$ левая часть (5) отрицательна, что может приводить к отсутствию вытекающих потоков даже в многомерной постановке. Такая ситуация возникает, в частности, при моделировании одномерной пленочной конденсации (задача Стефана). В этом случае на корректор-шаге невозможно скомпенсировать рост объемной доли жидкости в ячейке с $\varphi > 1$ и “переместить” фронт конденсации в соседнюю ячейку. Авторам настоящей статьи известны две работы [10, 18], в которых “поверхностная” модель используется для моделирования конденсации, однако особенности схем и алгоритмов применяемого метода VOF в них не обсуждаются.

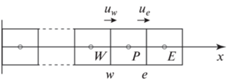
Для сглаженной модели массообмена процесс конденсации протекает не в одной ячейке, а в слое из двух-трех ячеек. Стоит рассмотреть особенности процессов на примере одномерной конденсации пентана при $p$ = 10⁵ Па, $\Delta T$ = 20 К (задача Стефана). Результаты, которые будут обсуждаться далее, получены авторами статьи при использовании модифицированной модели Lee. На рис. 1 изображены три контрольных объема расчетной области, обозначенные индексами W, P и E.

Рис. 1.

Фрагмент сетки ячеек для одномерной задачи Стефана. u_w, u_e – скорости на гранях w и e контрольного объема

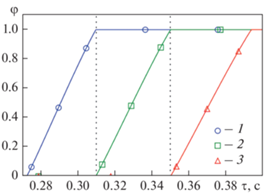
На рис. 2 приведены зависимости объемной доли конденсата в выбранных ячейках от времени. На первый взгляд, на этом рисунке представлена очевидная динамика последовательного и практически линейного по времени наполнения ячеек конденсатом. После наполнения конденсатом ячейки W фронт фазового перехода перемещается в ячейку Р. Далее картина наполнения ячеек конденсатом тиражируется. Однако на самом деле моделируемые процессы протекают несколько иначе. На рис. 3 представлены статьи баланса дискретного по пространству уравнения (1) для ячейки Р :

${{\left( {\frac{{\partial \varphi }}{{\partial \tau }}} \right)}_{P}} = {{\tilde {F}}_{{w,in}}} + {{\tilde {F}}_{{e,in}}} + {{S}_{\varphi }},$

где ${{\tilde {F}}_{{w,in}}} = {{u}_{w}}{{\varphi }_{w}}{{\Delta {{A}_{w}}} \mathord{\left/ {\vphantom {{\Delta {{A}_{w}}} {\Delta {{V}_{P}}}}} \right. \kern-0em} {\Delta {{V}_{P}}}},$ ${{\tilde {F}}_{{e,in}}} = - {{u}_{e}}{{\varphi }_{e}}{{\Delta {{A}_{e}}} \mathord{\left/ {\vphantom {{\Delta {{A}_{e}}} {\Delta {{V}_{P}}}}} \right. \kern-0em} {\Delta {{V}_{P}}}}$ – объемные втекающие в ячейку Р потоки жидкой фазы $\varphi ,$ отнесенные к объему ячейки, с^–1; ${{S}_{\varphi }} = {{\left( {{{{{M}_{{gl}}}} \mathord{\left/ {\vphantom {{{{M}_{{gl}}}} {{{\rho }_{l}}}}} \right. \kern-0em} {{{\rho }_{l}}}}} \right)}_{p}}$ – источниковый член в уравнении (1) для ячейки Р, с^–1.

Рис. 2.

Временные зависимости объемной доли жидкой фазы φ в трех ячейках: 1 – W; 2 – P; 3 – E

Рис. 3.

Зависимости составляющих баланса уравнения для $\varphi $ $\gamma \in \left( {{{{\tilde {F}}}_{{e,in}}};{{{\tilde {F}}}_{{w,in}}};{{S}_{\varphi }};{{{\left( {{{\partial \varphi } \mathord{\left/ {\vphantom {{\partial \varphi } {\partial \tau }}} \right. \kern-0em} {\partial \tau }}} \right)}}_{P}}} \right)$ от времени для ячейки P: $\gamma {\kern 1pt} {\text{:}}$ 1 – ${{\tilde {F}}_{{e,in}}};$ 2 – ${{\tilde {F}}_{{w,in}}};$ 3 – ${{S}_{\varphi }};$ 4 – ${{\left( {{{\partial \varphi } \mathord{\left/ {\vphantom {{\partial \varphi } {\partial \tau }}} \right. \kern-0em} {\partial \tau }}} \right)}_{P}}$

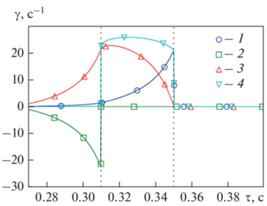
В момент времени, например $\tau $ = 0.28 с, объемная доля жидкой фазы в ячейке W не превосходит $\varphi $ = 0.2, в ячейке Р она практически равна нулю (см. рис. 2). Тем не менее, в ячейке Р уже “работают” источники тепла и массы за счет сглаженной модели фазового перехода (температура в ячейке Р оказывается ниже, чем ${{T}_{{sat}}}$) и тем самым генерируется жидкая фаза. Практически вся образовавшаяся в ячейке Р жидкая фаза перетекает в виде двухфазной смеси (так как на грани w реализуется условие $0 < {{\varphi }_{w}} < 1$) в ячейку W, наполняя ее (совместно с источником жидкой фазы ${{M}_{{gl}}} > 0$ в ячейке W) конденсатом. На рис. 3 хорошо видно, что на всем протяжении заполнения ячейки W конденсатом поток $\varphi $ на грани w ячейки Р – вытекающий, так как ${{\tilde {F}}_{{w,in}}} < 0.$ В это же время ячейка Р снабжается паром, поступающим из ячейки Е (см. рис. 3). В момент достижения ${{\varphi }_{w}} = 1$ ($\tau = 0.31\;{\text{с}}$) поток φ, вытекающий из ячейки Р через грань w, становится равным нулю в силу уравнения (2) и принудительного зануления источника в ячейке W при ${{\varphi }_{W}} = 1,$ при этом ${{\varphi }_{P}} \approx {{10}^{{ - 2}}},$ т.е. ячейка Р является двухфазной. Далее подобная картина повторяется, но с ячейками Р и Е. Таким образом, размазывание фронта фазового перехода на несколько ячеек позволяет избежать проблем, характерных для моделей со строго локализованным фронтом, определяемым из условия $\varphi $ = 0.5.

В работах [19, 20] предложен оригинальный алгоритм создания сглаженного источника массы на основе поверхностного источника. Смысл алгоритма заключается в удалении источника из ячейки с межфазной поверхностью и задании в прилежащих ячейках двух источников с разными знаками: в случае кипения – отрицательного источника массы в жидкости и положительного в паре. Этот алгоритм был успешно реализован в [20] для описания процесса пузырькового кипения. Применялся ли он для моделирования процессов конденсации, авторам настоящей статьи неизвестно.

Ранее отмечалось, что в большинстве работ по пленочной конденсации используется модель Lee [9], в рамках которой источник в уравнении энергии (4) для ячеек с $0 < \varphi < 1$ можно записать в следующем упрощенном линеаризованном относительно температуры виде:

(6)

${{Q}_{{gl}}} = \tilde {С}({{T}_{{sat}}} - T),$

где $\tilde {С}$ – величина, имеющая достаточно большое значение, Вт/(м³ ⋅ К).

В этом случае температура в ячейке будет близка к ${{T}_{{sat}}}$ (но не равна ей), а левая часть уравнения энергии будет описывать приток (при конденсации) или отток (при кипении) тепла в ячейках с идущим процессом массообмена. В [9] объемный источник тепла при конденсации задается в виде

(7)

$\begin{gathered} {{Q}_{{gi}}} = {{M}_{{gl}}}{{h}_{{lg}}} = \\ = {{С{\kern 1pt} '{{h}_{{lg}}}{{\rho }_{g}}\left( {1 - \varphi } \right)\Delta {{T}_{{gl}}}} \mathord{\left/ {\vphantom {{С{\kern 1pt} '{{h}_{{lg}}}{{\rho }_{g}}\left( {1 - \varphi } \right)\Delta {{T}_{{gl}}}} {{{T}_{{sat}}}}}} \right. \kern-0em} {{{T}_{{sat}}}}},\,\,\,\,\Delta {{T}_{{gl}}} > 0, \\ \end{gathered} $

где $\Delta {{T}_{{gl}}} = {{T}_{{sat}}} - T$ – перепад температуры в ячейке, в которой происходит фазовый переход, К.

Появление множителя (1 – φ) в выражении (7) объясняется использованием в модели приведенной плотности газовой фазы ${{\rho }_{g}}(1 - \varphi ).$ Применение этого множителя полезно тем, что источник зануляется в ячейках с $\varphi $ = 1. Зануление источника в паровой фазе ($\varphi = 0$) определяется нарушением условия $\Delta {{T}_{{gl}}} > 0.$

Основной недостаток оригинальной модели Lee (7) – неопределенность параметра $С{\kern 1pt} ',$ значение которого подбирается для конкретной задачи экспериментальным путем. Значения этого параметра, принятые в различных работах, изменяются в очень широких пределах – от значения 0.2, использованного Lee, до значения 5 × 10⁶ в работе [13].

В [21] авторы предложили модификацию модели Lee, в которой постоянная модели $С{\kern 1pt} '$ определяется шагом интегрирования по времени. Минусом модели оказалось условие использования слишком малого шага по времени. В упомянутых выше работах [11, 12] реализована итерационная процедура, позволяющая, по словам авторов, снять излишне жесткое ограничение на шаг по времени.

Для определения источника в настоящей работе модель Lee была модифицирована исходя из следующих соображений. Поверхностная плотность теплового потока ${{q}_{w}}$ при конденсации определяется как

${{q}_{w}} = {{\lambda }_{l}}\frac{{\Delta T}}{l},$

где $l$ – характерный линейный масштаб (например, толщина жидкой пленки), м; $\Delta T$ – характерный перепад температуры по условиям задачи, К.

С учетом (6) баланс тепла для контрольного объема можно записать в виде

${{\lambda }_{l}}\frac{{\Delta T}}{l} = \frac{{{{Q}_{{gl}}}\Delta {{V}_{P}}}}{{\Delta A}} = \frac{{\tilde {C}\Delta {{T}_{{gl}}}\Delta {{V}_{{CV}}}}}{{\Delta A}}$

или

$\tilde {C} = \frac{{\Delta T}}{{\Delta {{T}_{{gl}}}}}\frac{{\Delta {{x}_{{CV}}}}}{l}\frac{{{{\lambda }_{l}}}}{{{{{\left( {\Delta {{x}_{{CV}}}} \right)}}^{2}}}},$

где $\Delta {{x}_{{CV}}} = \left( {{{\Delta {{V}_{{CV}}}} \mathord{\left/ {\vphantom {{\Delta {{V}_{{CV}}}} {\Delta A}}} \right. \kern-0em} {\Delta A}}} \right)$ – характерный размер контрольного объема, м.

Очевидно, что для сжатия “толщины” фронта фазового перехода необходимо выполнение следующих неравенств: ${{\Delta T} \mathord{\left/ {\vphantom {{\Delta T} {\Delta {{T}_{{gl}}}}}} \right. \kern-0em} {\Delta {{T}_{{gl}}}}} > > 1$ и ${{\Delta {{x}_{{CV}}}} \mathord{\left/ {\vphantom {{\Delta {{x}_{{CV}}}} l}} \right. \kern-0em} l} < < 1.$ Второе условие обеспечивается правильным подбором расчетной сетки. Для линейного профиля температур внутри жидкой пленки, характерного для задач конденсации, можно считать, что ${{\Delta T} \mathord{\left/ {\vphantom {{\Delta T} {\Delta {{T}_{{gl}}}}}} \right. \kern-0em} {\Delta {{T}_{{gl}}}}} = {l \mathord{\left/ {\vphantom {l {\Delta {{x}_{{CV}}}}}} \right. \kern-0em} {\Delta {{x}_{{CV}}}}}.$ В этом случае для $\tilde {С}$ справедливо следующее соотношение:

$\tilde {C} = \frac{{{{\lambda }_{l}}}}{{{{{\left( {\Delta {{x}_{{CV}}}} \right)}}^{2}}}}.$

После добавления в выражение для объемного теплового потока (6) ограничителя $2\left( {1 - \varphi } \right),$ позволяющего занулить ${{Q}_{{gl}}}$ при $\varphi = 1$ и вырождающегося в 1 в ячейке с фронтом $(\varphi = 0.5),$ получается итоговое соотношение

(8)

${{Q}_{{gl}}} = 2\left( {1 - \varphi } \right)\frac{{{{\lambda }_{l}}}}{{{{{\left( {\Delta {{x}_{{CV}}}} \right)}}^{2}}}}\Delta {{T}_{{gl}}}.$

Сравнивая соотношение (8) с выражением (7), можно вывести следующее соотношение для упомянутой выше константы Lee:

(9)

$C{\kern 1pt} ' = \frac{{2{{\lambda }_{l}}{{T}_{{sat}}}}}{{{{\rho }_{g}}{{h}_{{lg}}}{{{\left( {\Delta {{x}_{{CV}}}} \right)}}^{2}}}}.$

Расчет константы при моделировании конденсации выполнялся автоматически на основе представленного соотношения (9). В качестве характерного размера контрольного объема был выбран его минимальный размер.

ОСОБЕННОСТИ ЧИСЛЕННОГО АЛГОРИТМА

Система основных уравнений сохранения (1)–(4) дискретизировалась на структурных сетках в полярной системе координат методом контрольного объема. Для решения уравнения (1) применялся алгоритм CICSAM [17]. Гидродинамические уравнения решались с использованием алгоритма PIMPLE [22], являющегося комбинацией алгоритмов SIMPLE [23] и PISO [24]. В отличие от алгоритма PISO, в алгоритме PIMPLE проводятся итерации на шаге по времени, однако их число существенно меньше, чем в SIMPLE, ввиду возможности отказа от использования нижней релаксации.

Источник тепла вследствие фазового перехода в дискретных аналогах уравнения энергии определялся по модели Lee с константой $С{\kern 1pt} ',$ рассчитанной по соотношению (9).

Кривизна межфазной поверхности K вычислялась по формуле

$K = - div({{n}_{{int}}}),\,\,\,\,{{n}_{{int}}} = \frac{{\nabla \bar {\varphi }}}{{\left| {\nabla \bar {\varphi }} \right|}},$

где ${{n}_{{int}}}$ – нормаль к межфазной границе.

Дискретный аналог этой формулы был получен интегрированием по контрольному объему. Для определения сглаженного поля объемной доли жидкости $\bar {\varphi }$ применялся итерационный алгоритм “значение в центре ячейки – значения в вершинах ячейки” согласно рекомендациям работы [5].

Алгоритм PIMPLE в процессе итерационного решения приводит к удовлетворению уравнения неразрывности, записанного относительно объемных потоков (2); уравнения движения (3) и энергии (4) записаны относительно массовых конвективных потоков. Как показали численные эксперименты, для удовлетворения уравнения неразрывности, записанного относительно массовых потоков, необходимо для расчета плотности на гранях ячейки использовать значения $\varphi $ на гранях, полученные при решении уравнения (1) методом CICSAM. Общепринятое вычисление значения $\varphi $ на грани на основе линейной интерполяции значений в ее ячейках-соседях дает заметные ошибки в задачах с массообменом на фазовой границе.

Для тестирования численных алгоритмов, реализованных в CFD-коде ANES [22], были решены две задачи: одномерная плоская пленочная конденсация (задача Стефана) и конденсация на вертикальной пластине, для которых имеются аналитические решения. Описание результатов представлено в дополнительных материалах к настоящей статье.

ФИЗИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

В работе рассматривается конденсация пентана и воды при атмосферном давлении на поверхности гладкого горизонтального цилиндра. Свойства теплоносителей считаются постоянными и представлены в табл. 1 [25].

Таблица 1.

Свойства теплоносителей пентана и воды при атмосферном давлении

Свойство	Теплоноситель
Свойство	пентан	вода
Плотность, кг/м³:
жидкости ${{\rho }_{l}}$	610.10	958.370
газа ${{\rho }_{g}}$	2.93890	0.59766
Теплоемкость, Дж/(кг · К):
жидкости ${{с}_{{p,l}}}$	2365.7	4215.6
газа ${{c}_{{p,g}}}$	1762.2	2079.9
Коэффициент теплопроводности, Вт/(м · К):
жидкости ${{\lambda }_{l}}$	107.41 × 10^–3	679.08 × 10^–3
газа ${{\lambda }_{g}}$	15.254 × 10^–3	25.093 × 10^–3
Динамический коэффициент вязкости, Па · с:
жидкости ${{\mu }_{l}}$	199.24 × 10^–6	281.66 × 10^–6
газа ${{\mu }_{g}}$	7.194 × 10^–6	12.231 × 10^–6
Поверхностное натяжение $\sigma $, Н/м	14.304 × 10^{– 3}	58.917 × 10^–3
Теплота фазового перехода ${{h}_{{lg}}}$, Дж/кг	357.89 × 10³	2256.50 × 10³
Температура насыщения ${{T}_{{sat}}}$, К	308.828 (35.678°C)	373.150 (100.000°C)

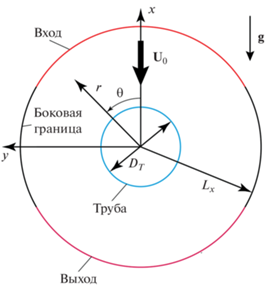
Расчетная область показана на рис. 4. Диаметр цилиндра принят равным ${{D}_{T}}$ = 25.4 мм, диаметр расчетной области ${{L}_{x}} = 3{{D}_{T}}.$ Входная $( - 60 \leqslant \theta \leqslant 60^\circ ),$ где θ – угол, и выходная $(120 \leqslant \theta \leqslant 240^\circ )$ границы проницаемы для жидкости, остальные границы расчетной области непроницаемые. На входной границе задавался постоянный вектор скорости ${{U}_{0}},$ направленный вдоль вектора ускорения свободного падения $g{\text{,}}$ на боковых границах – условия равенства нулю касательных напряжений. На выходе фиксировалось распределение давления ${{p}_{{rgh}}} = \left( {{{\rho }_{g}} - \rho } \right)\left( {g \cdot x} \right)$ исходя из известного распределения статического давления в паре. Для остальных переменных использовались стандартные выходные граничные условия. Если граница становилась входной, то считалось, что в расчетную область поступает насыщенный пар при температуре ${{T}_{{sat}}}.$ На стенке фиксировалась постоянная температура ${{T}_{w}},$ соответствующая заданному перепаду температур $\Delta T = {{T}_{{sat}}} - {{T}_{w}}.$

Рис. 4.

Постановка задачи

В начальный момент времени задавалась толщина пленки, полученная из решения Нуссельта:

(10)

$\frac{{\delta \left( \theta \right)}}{{{{\delta }_{0}}}} = {{\left[ {\frac{4}{{3{{{\left( {\sin \theta } \right)}}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}}}\int\limits_0^\theta {{{{\left( {\sin \theta {\kern 1pt} '} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}d\theta {\kern 1pt} '} } \right]}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}};$

(11)

${{\delta }_{0}} = {{\left( {\frac{{3{{\lambda }_{l}}\Delta T{{\nu }_{l}}{{D}_{T}}}}{{2g\Delta \rho {{h}_{{lg}}}}}} \right)}^{{0.25}}},$

где ${{\nu }_{l}}$ – кинематический коэффициент вязкости, м²/с.

Данное распределение использовалось до углов ±160°, при которых толщина пленки фиксировалась и далее оставалась постоянной. Начальное значение температуры принималось равным ${{T}_{{sat}}},$ скорости пара и жидкости полагались равными нулю.

ВЫБОР РАСЧЕТНОЙ СЕТКИ И ТЕСТИРОВАНИЕ СЕТОЧНОЙ НЕЗАВИСИМОСТИ

Пример использованной сетки представлен на рис. 5. Параметры сетки по радиусу определялись автоматически на основе базового размера – толщины пленки из решения Нуссельта ${{\delta }_{0}}$ [уравнение (11)]. Первая подобласть представляет собой кольцевой слой толщиной ${{\delta }_{0}}$ у поверхности трубы с равномерной сеткой и количеством контрольных объемов по радиусу ${{N}_{{r,1}}}.$ Вторая подобласть – переходный слой до расстояния $5{{\delta }_{0}}$ от поверхности трубы, в котором сетка равномерно увеличивается от размера контрольного объема на границе первой подобласти с логарифмичностью 1.02 (размер контрольного объема изменялся в геометрической прогрессии с коэффициентом прогрессии 1.02). Третья подобласть – слой толщиной ${{{{D}_{T}}} \mathord{\left/ {\vphantom {{{{D}_{T}}} 4}} \right. \kern-0em} 4},$ в котором сетка равномерно увеличивается от размера последнего контрольного объема во второй подобласти с логарифмичностью ${{\gamma }_{{r,3}}}.$ Наконец, четвертая подобласть – кольцевой слой от границы третьей подобласти до границы расчетной области с постоянными размерами контрольного объема, равными размеру последнего контрольного объема в третьей подобласти.

Рис. 5.

Пример используемой сетки

Сетка по углу θ была либо равномерная, либо с логарифмическим сгущением к точке отрыва конденсата. Коэффициент логарифмичности – ${{\gamma }_{\varphi }}$ (применялся для каждой половины расчетной области).

Для определения зависимости решения от сетки было выполнено моделирование конденсации пентана для ${{U}_{0}}$ = 0.1 м/с и $\Delta T$ = 20 К. Параметры сеток представлены в табл. 2.

Таблица 2.

Параметры используемых сеток

Номер сетки	${{N}_{{r,1}}}$	${{\gamma }_{{r,3}}}$	${{N}_{\varphi }}$	${{\gamma }_{\varphi }}$	Общее число контрольных объемов	Количество временны́х шагов для расчета 3.0 с, тыс.
1	10	1.2	256	1.00	31 232	110
2	10	1.2	256	1.02	31 232	129
3	10	1.1	512	1.01	93 184	130
4	15	1.1	512	1.01	102 912	201
5 (базовая)	20	1.1	512	1.01	111 104	260
6	30	1.1	512	1.01	121 856	348

На рис. 6 показано изменение коэффициента теплоотдачи и площади (задача двумерная), занятой жидкой фазой, во времени при расчетах на разных сетках. Значения коэффициента теплоотдачи определялись как $\alpha = {{{{q}_{{w,ave}}}} \mathord{\left/ {\vphantom {{{{q}_{{w,ave}}}} {\Delta T}}} \right. \kern-0em} {\Delta T}},$ где ${{q}_{{w,ave}}}$ – средняя по поверхности цилиндра плотность теплового потока в текущий момент времени, Вт/м². Для сравнения все значения нормируются на значения, определенные по соотношению Нуссельта для горизонтального цилиндра при тех же граничных условиях, что и в настоящей постановке:

(12)

${{\alpha }_{{Nu,T}}} = 0.728{{\left( {\frac{{\lambda _{l}^{3}g\Delta \rho {{h}_{{lg}}}}}{{{{\nu }_{l}}\Delta T{{D}_{T}}}}} \right)}^{{0.25}}}.$

Рис. 6.

Временные зависимости относительных коэффициента теплоотдачи (а) и площади жидкой фазы (б) (конденсация пентана при ${{U}_{0}}$= 0.1 м/с, $\Delta T$ = = 20 К, р = 0.1 МПа). Номер линии соответствует номеру сетки в табл. 2

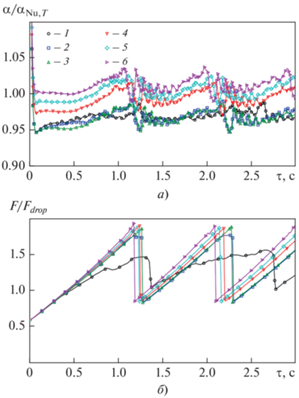
В качестве масштаба для площади применялось значение, соответствующее характерному размеру отрывающейся капли (см. раздел далее).

Видно, что для сеток № 2–6 (см. табл. 2) все локальные характеристики незначительно различаются, при этом для сеток № 4–6 разница в значениях отношения ${\alpha \mathord{\left/ {\vphantom {\alpha {{{\alpha }_{{Nu,T}}}}}} \right. \kern-0em} {{{\alpha }_{{Nu,T}}}}}$ составляет 1–2%. В результате осреднения значений ${\alpha \mathord{\left/ {\vphantom {\alpha {{{\alpha }_{{Nu,T}}}}}} \right. \kern-0em} {{{\alpha }_{{Nu,T}}}}}$ в интервале времени между первым и вторым отрывами капли были получены следующие значения для сетки с номером:

1…………………………………………...……………..0.970

2…………………………………...……………………..0.968

3…………………………………………………………..0.968

4…………………………………………………………..0.960

5………...………………………………………………..1.000

6…………………………………………………………..1.000

При использовании сетки № 1 отрыв капли не происходил, верхняя часть сформировавшейся капли размазывалась и уносилась в виде отдельных “капель” размером в несколько контрольных объемов. При этом средний коэффициент теплоотдачи хорошо согласуется с решением Нуссельта, так как во многом определяется толщиной пленки с наветренной стороны трубы. Возможно, именно этим и объясняются достаточно правдоподобные результаты работы [10], полученные с помощью стационарной версии модели VOF и относительно грубой расчетной сетки.

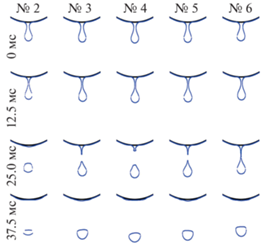
Сетка № 2 обеспечивает минимальное разрешение срывающейся капли. Начиная с сетки № 3 дальнейшее улучшение сетки слабо сказывается на динамике срыва капли. На рис. 7 представлена динамика срыва капель для сеток № 2–6. Время на рисунке указано относительно времени формирования крупной вытянутой капли. Небольшое различие результатов связано с тем, что шаг их записи составлял 0.0125 с, что вместе с незначительной разницей в коэффициентах теплоотдачи (см. рис. 6) приводило к некоторому смещению зафиксированных моментов срыва капель, полученных на разных сетках.

Рис. 7.

Динамика отрыва капель конденсата, полученная при использовании сеток № 2–6 (конденсация пентана при ${{U}_{0}}$= 0.1 м/с, $\Delta T$ = 20 К, р = 0.1 МПа)

РЕЗУЛЬТАТЫ РАСЧЕТА

Далее будут обсуждаться результаты моделирования процессов конденсации для пентана $({{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}} = 207.6)$ и воды $({{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}} = 1603)$ при атмосферном давлении. Устойчивость численных алгоритмов при решении уравнений (1)–(4) может быть обеспечена только при условии Co < 1, где $Co = \frac{{\Delta \tau {{u}_{{\max }}}}}{{\Delta {{x}_{{CV}}}}}$ – число Куранта, ${{u}_{{\max }}}$ – модуль максимальной скорости в ячейке с фазовой границей, м/с, $\Delta {{x}_{{CV}}}$ – характерный размер ячейки, м. Воспользовавшись аналитическим решением одномерной задачи Стефана для конденсации, можно показать, что максимальная скорость характерна для подтекающего к межфазной поверхности пара ${{u}_{g}} \approx - {{u}_{i}}\left( {{{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}}} \right),$ где ${{u}_{i}} = {{ - {{m}_{s}}\sqrt {{{a}_{l}}} } \mathord{\left/ {\vphantom {{ - {{m}_{s}}\sqrt {{{a}_{l}}} } {\sqrt \tau }}} \right. \kern-0em} {\sqrt \tau }}$ – скорость движения межфазной поверхности, м/с; ${{a}_{l}}$ – температуропроводность, м²/с; ${{m}_{s}} = {{\left( {1 + \frac{2}{{Ja{\text{*}}}}} \right)}^{{ - \frac{1}{2}}}},$ $Ja* = {{{{c}_{{pl}}}({{T}_{{sat}}} - {{T}_{w}})} \mathord{\left/ {\vphantom {{{{c}_{{pl}}}({{T}_{{sat}}} - {{T}_{w}})} {\Delta {{h}_{{lg}}}}}} \right. \kern-0em} {\Delta {{h}_{{lg}}}}}$ – число Якоба. Значения ${{m}_{s}}\sqrt {{{a}_{l}}} $ при ΔT = 20 К для пентана (7.3 × 10^–5 м ⋅ с^–1/2) и воды (5.7 × 10^–5 м ⋅ с^–1/2) различаются примерно на 30%, поэтому основное влияние на скорость подтекающего газа оказывает отношение плотностей фаз. Окончательное выражение для шага по времени может быть представлено в виде

$\Delta \tau = Co\frac{{\Delta {{x}_{{CV}}}}}{{{{u}_{g}}}} = Co\frac{{\sqrt \tau \Delta {{x}_{{CV}}}}}{{{{m}_{s}}\sqrt {{{a}_{l}}} }}\frac{{{{\rho }_{l}}}}{{{{\rho }_{g}}}}.$

Радикальные различия значений ${{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}}$ для пентана и воды привели к тому, что при заданном перепаде температур $\Delta T$ = 20 К и скорости пара ${{U}_{0}}$ = 0.1 м/с максимальные шаги по времени на выбранных сетках не превышали 1.2 × 10^–5 с для пентана и 3 × 10^–6 с для воды. При этом характерное время между отрывами капель отличалось почти в 2.5 раза (оно составляло приблизительно 1 с для пентана и около 2.5 с для воды). Тем самым временные ресурсы компьютера, необходимые для расчета одного периода между отрывами капель, различались практически на порядок.

На рис. 8 представлено распределение толщины жидкой пленки пентана по периметру трубы. Ее значение нормировано на значение ${{\delta }_{0}},$ определенное по формуле (11). Для сравнения показано также распределение, следующее из решения Нуссельта (10).

Рис. 8.

Распределение толщины пленки по периметру трубы (относительный масштаб толщины пленки и диаметра трубы искажены для наглядности) при конденсации пентана при ${{U}_{0}}$ = 0.1 м/с, $\Delta T$ = 20 К). 1 – результаты расчета; 2 – решение Нуссельта

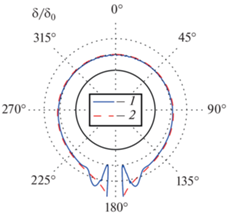
Распределение скорости в жидкой пленке конденсата при $\theta $ = 90° приведено на рис. 9. Результаты сравниваются с кривыми, рассчитанными по формулам

(13)

$u = \frac{g}{{{{\nu }_{l}}}}\left( {\delta y - \frac{1}{2}{{y}^{2}}} \right);$

(14)

$u = \frac{g}{{{{\nu }_{l}}}}\left( {\delta y - \frac{1}{2}{{y}^{2}}} \right) + \frac{{{{\tau }_{g}}}}{{{{\mu }_{l}}}}y.$

Рис. 9.

Распределение относительной скорости в пленке при $\theta $ = 90° (конденсация пентана при $\Delta T$ = = 20 К, ${{U}_{0}}$ = 0.1 м/с). 1 – результаты моделирования (закрашенная область показывает среднеквадратическое отклонение от среднего значения); 2 – уравнение (13); 3 – уравнение (14); 4 – распределение жидкой фазы в пленке

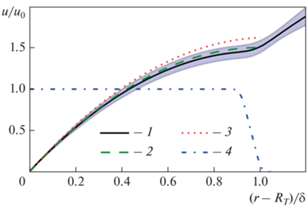
В качестве масштаба скорости выбрана величина

${{u}_{0}} = \frac{1}{3}\frac{{g{{\delta }^{2}}}}{{{{\nu }_{l}}}},$

где $\delta $ – толщина пленки, м.

При оценке касательного напряжения на стенке использовалось следующее приближенное соотношение [1]:

${{\tau }_{g}} = \frac{{2{{U}_{0}}\left\langle \alpha \right\rangle \Delta T}}{{{{h}_{{lg}}}}}.$

Видно, что толщина пленки претерпевает незначительные пульсации, при этом распределение скорости хорошо согласуется с теоретическими зависимостями. Характерная зависимость коэффициента теплоотдачи от времени представлена на рис. 10. Значение коэффициента нормировано на значение, полученное по соотношению (12). Вертикальные линии на рисунке соответствуют времени отрыва капель конденсата, за которое принималось среднее время между двумя соседними временами вывода результатов ($\Delta \tau $ = 0.0125 с), в течение которого исчезал тонкий перешеек между пленкой и каплей (см. рис. 7).

Рис. 10.

Зависимость относительного коэффициента теплоотдачи от времени при конденсации пентана при $\Delta T$= 20 К и ${{U}_{0}}$ = 0.1 м/с. Интервалы между отрывами капель, с: 1 – 0.92; 2 – 0.95; 3 – 0.94; 4 – 0.92

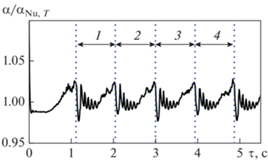
Пульсации значений коэффициента теплоотдачи связаны с колебаниями толщины пленки конденсата из-за возвратного движения пленки сразу после срыва капли. Эквивалентный диаметр срывающихся с поверхности пленки капель составлял 3.4–3.6 мм для пентана и 5.5 мм для воды, что соответствует зависимости ${{d}_{{drop}}} = Ab,$ где $b = \sqrt {{\sigma \mathord{\left/ {\vphantom {\sigma {\left( {\Delta \rho g} \right)}}} \right. \kern-0em} {\left( {\Delta \rho g} \right)}}} $ – капиллярная постоянная, а значение коэффициента $A$ = 2.2–2.4. Полученные данные о размерах капель несколько отличаются от рекомендованных в работе [26] (А = 3). Как будет показано далее, это отличие связано с разной кривизной поверхностей плоской и трехмерной капель.

Зависимости средних коэффициентов теплоотдачи от $\Delta T$ для пентана и воды при низкой скорости паров 0.1 м/с представлены на рис. 11. Отклонение рассчитанных значений коэффициента теплоотдачи от значений, предсказанных теорией Нуссельта (12), не превышает 5%.

Рис. 11.

Зависимости среднего коэффициента теплоотдачи от $\Delta T$ для пентана (а) и воды (б) при ${{U}_{0}}$ = = 0.1 м/с. Точки – результаты моделирования; сплошная линия – зависимость Нуссельта (±5%); штриховая – отклонение ±5%

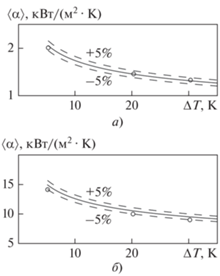
С увеличением переохлаждения стенки частота срыва капель увеличивается из-за роста плотности теплового потока и интенсивности массообмена, при этом их характерный размер не изменяется.

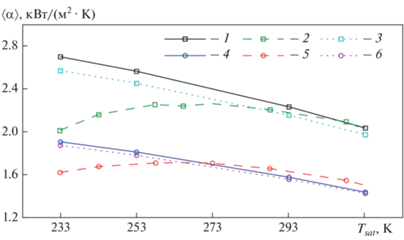
Для сравнения с расчетными данными [13], упомянутыми выше, были выполнены расчеты для пропана при температуре ${{T}_{{sat}}},$ изменяющейся от 233.15 до 313.15 К, и двух значений $\Delta T$: 5 и 20 К. Полученные результаты (рис. 12) хорошо согласуются с решением Нуссельта (12) и не подтверждают установленного в [13] снижения числа Нуссельта при ${{T}_{{sat}}}$ < 263.15 K. Эквивалентный диаметр отрывающихся капель в этих режимах хорошо согласуется с ранее описанными результатами для пентана и воды.

Рис. 12.

Зависимости среднего коэффициента теплоотдачи от ${{T}_{{sat}}}$ для пропана при $\Delta T$ = 5 К (1, 2, 3) и $\Delta T$ = 20 К (4, 5, 6). 1, 4 – решение Нуссельта; 2, 5 – результаты работы [13]; 3, 6 – результаты настоящей работы

На рис. 13 для сравнения представлены результаты расчетов и экспериментов [27] по нагреву падающих капель конденсата. Для нахождения условной температуры капли на некоторых расстояниях от нижней образующей трубы вдоль вертикальной оси в расчетах определялась минимальная по времени среднеобъемная температура ${{T}_{{ave}}},$ зафиксированная в круглой области диаметром 1.6 мм. Размер области осреднения 1.6 мм выбран исходя из информации о размерах датчика температуры в работе [27]. Число Рейнольдса пленки вычислялось по формуле

$\operatorname{Re} = \frac{{4\left\langle \alpha \right\rangle \Delta T\frac{{\pi {{D}_{T}}}}{2}}}{{{{h}_{{lg}}}{{\mu }_{l}}}}.$

Рис. 13.

Зависимость переохлаждения “капель” конденсата пентана от расстояния до нижней образующей трубы (положение координатных осей соответствует [27]). Результаты моделирования: 1 – $\operatorname{Re} $ = 65, $\Delta T$ = 20 К; 2 – $\operatorname{Re} $ = 88, $\Delta T$ = 30 К; 3 – экспериментальные данные [27], $\operatorname{Re} $ = 140, $\Delta T$ = 35 К

Неопределенность некоторых режимных параметров (диаметр трубы, марка хладона) в [27] дает основание утверждать, что результаты расчетов соответствуют данным экспериментов на качественном уровне. На расстоянии 10 мм от трубы переохлаждение падающих капель уменьшается в 2 раза вследствие конденсации пара на поверхности капель.

Для оценки влияния скорости пара на процесс конденсации пентана и воды выполнены расчеты при $\Delta T$ = 20 К и ${{U}_{0}}$ = 0.1–3.0 м/с. Указанные скорости соответствуют числам Рейнольдса ${{\operatorname{Re} }_{g}} = {{\rho }_{g}}{{{{U}_{0}}{{D}_{T}}} \mathord{\left/ {\vphantom {{{{U}_{0}}{{D}_{T}}} {{{\mu }_{g}}}}} \right. \kern-0em} {{{\mu }_{g}}}}$ от 10³ до 3 × 10⁴ для пентана и от 120 до 3700 для воды. При этом значения динамического напора $\Pi = {{{{\rho }_{g}}U_{0}^{2}} \mathord{\left/ {\vphantom {{{{\rho }_{g}}U_{0}^{2}} 2}} \right. \kern-0em} 2}$ изменялись от 0.37 до 13.20 Па для пентана и от 0.003 до 2.700 Па для воды. На рис. 14 представлены полученные в настоящей работе зависимости степени интенсификации теплоотдачи при конденсации ${{\left\langle \alpha \right\rangle } \mathord{\left/ {\vphantom {{\left\langle \alpha \right\rangle } {{{\alpha }_{{Nu,T}}}}}} \right. \kern-0em} {{{\alpha }_{{Nu,T}}}}}$ от скорости движения пара. Для сравнения на рис. 14 приводятся также данные, рассчитанные по формулам Fujii [28]

(15)

$\begin{gathered} \left\langle \alpha \right\rangle = \frac{{{{\lambda }_{l}}}}{{{{D}_{T}}}}\left[ {0.656{{{\left( {\frac{{{{\rho }_{l}}{{U}_{0}}{{D}_{T}}}}{{{{\mu }_{l}}}}} \right)}}^{2}} \times } \right. \\ \times \,\,{{\left. {{{{\left( {1 + \sqrt {\frac{{{{\rho }_{g}}{{\mu }_{g}}}}{{{{\rho }_{l}}{{\mu }_{l}}}}} \frac{{{{\mu }_{l}}{{h}_{{lg}}}}}{{{{\lambda }_{l}}\Delta T}}} \right)}}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + \frac{{0.276\rho _{l}^{2}D_{T}^{3}{{h}_{{lg}}}g}}{{{{\mu }_{l}}{{\lambda }_{l}}\Delta T}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}} \\ \end{gathered} $

и Rose [29]

(16)

$\begin{gathered} \left\langle \alpha \right\rangle = \frac{{{{\lambda }_{l}}}}{{{{D}_{T}}}}{{\operatorname{Re} }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{0.9 + 0.728{{F}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{{\left( {1 + 3.44{{F}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + F} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}, \\ F = \frac{{{{\mu }_{l}}{{h}_{{lg}}}g{{D}_{T}}}}{{{{\lambda }_{l}}\Delta TU_{0}^{2}}}. \\ \end{gathered} $

Рис. 14.

Зависимости относительного коэффициента теплоотдачи от скорости набегающего потока при $\Delta T$ = 20 К для пентана (а) и воды (б). Расчет: 1 – по формуле (15); 2 – по формуле (16); результаты: 3 – расчета по упрощенной модели [30]; 4 – настоящей работы с интервалом отклонения ±10%

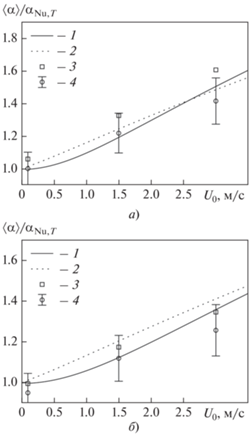
На этом же рисунке показаны зависимости, полученные с использованием упрощенной модели [30].

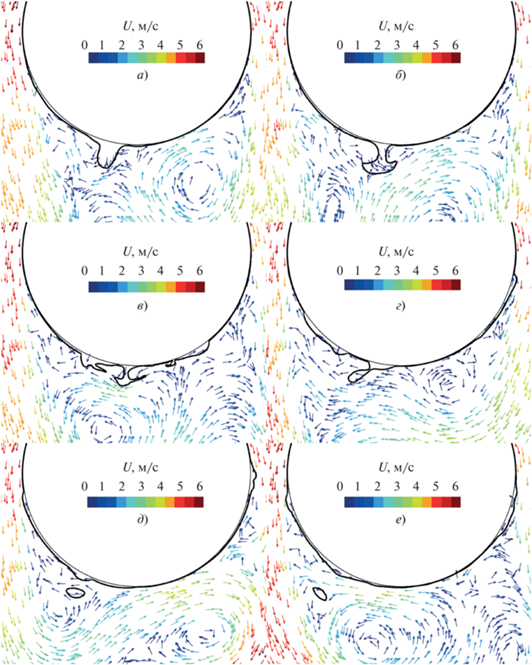
С ростом скорости взаимодействие потока пара с пленкой конденсата на нижней части трубы усложняется. Происходит периодический несимметричный срыв капель конденсата из-за наличия группы вихрей в ближнем следе за цилиндром. При этом в процессе отрыва капель иногда формируются вторичные капли конденсата и наблюдается периодический “заброс” пленки конденсата в область $\theta < 180^\circ .$ Для примера на рис. 15 приведена динамика срыва капли пентана при ${{U}_{0}} = 3\,\,{\text{м/с,}}$ период между кадрами на рисунке составляет 0.0125 с.

Рис. 15.

Поле скорости и динамика формирования срывающихся капель конденсата пентана при $\Delta T$ = 20 К, ${{U}_{0}}$ = 3.0 м/с. а–е – кадры, сделанные с интервалом 0.0125 с

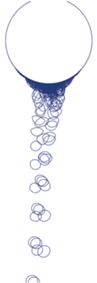
Для режима конденсации пентана при скорости пара, равной 1.5 м/с, на рис. 16 представлены изолинии $\varphi = 0.5$ для всех шагов записи результатов ($\Delta \tau $ = 12.5 мс) на протяжении 3.5 с. На рисунке хорошо видна траектория всех капель, которые образовались и сорвались с поверхности цилиндра. Отсутствие симметрии относительно вертикальной оси в последовательном срыве капель связано, вероятно, с несимметричным ростом и срывом первой капли под действием несимметричных вихревых структур в паре и влиянием сложившейся картины на последующую динамику образования капель.

Рис. 16.

Изолинии $\varphi $ = 0.5, построенные для всех шагов записи результатов ($\Delta \tau $ = 12.5 мс) на протяжении 3.5 с (конденсация пентана при скорости ${{U}_{0}}$ = 1.5 м/с и $\Delta T$ = 20 К)

На рис. 17 для сравнения представлены распределения толщины пленки по периметру цилиндра для скорости 1.5 м/c, полученные в настоящей работе и с использованием упрощенной модели [30]. Данные для модели VOF обрабатывались следующим образом: сначала на каждом шаге выдачи результатов рассчитывалось распределение толщины пленки, которая определялась как сумма радиальных размеров контрольного объема, умноженных на долю жидкости в них, при фиксированном угле θ, затем значения осреднялись по времени.

Рис. 17.

Распределение толщины пленки по периметру при конденсации пентана (а) и воды (б) при скорости ${{U}_{0}}$ = 1.5 м/с и $\Delta T$ = 20 К. Результаты расчета с использованием метода VOF (1) и упрощенной модели [30] (2)

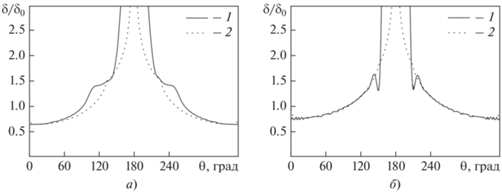
Наблюдается хорошее согласие распределений, полученных методом VOF и по разработанной ранее упрощенной модели, что вполне закономерно, так как скорость пара невелика. Анализ результатов показал, что наибольшее рассогласование отмечается в области формирования капли и в определении положения точки отрыва пограничного слоя от поверхности пленки, после которого толщина жидкой пленки резко увеличивается.

Дополнительно рассмотрена постановка задачи, в которой на оси симметрии над трубой был расположен капилляр, через который подавалась жидкая фаза пентана с фиксированным расходом. Периодически срывавшиеся с капилляра капли попадали на поверхность трубы, и тем самым моделировалось ее орошение. Расстояние между срезом капилляра и поверхностью трубы равнялось $7b$ = 10.7 мм. Расход определялся по соотношению

${{G}_{l}} = k\frac{{{{\alpha }_{{{\text{Nu}},T}}}\Delta T\pi {{D}_{T}}}}{{{{h}_{{lg}}}}},$

где коэффициент $k$ задавался в качестве входного параметра.

Моделирование было выполнено для четырех значений коэффициента $k$ = 1, 2, 3, 5, что примерно соответствовало второй, третьей, четвертой и шестой трубам в вертикальном ряду трубного пучка. Динамика срыва и падения капель при $k = 1$ представлена на рис. 18.

Рис. 18.

Конденсация пентана при наличии орошения при $k$ = 1, ${{U}_{0}}$ = 0.1 м/с, $\Delta T$ = 20 К

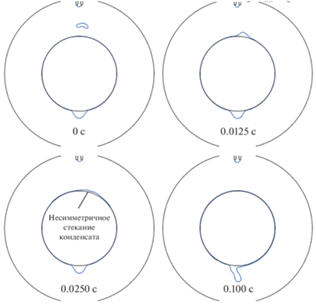
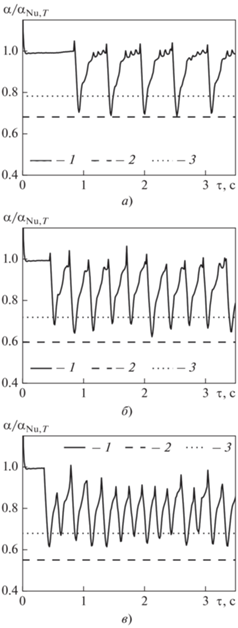
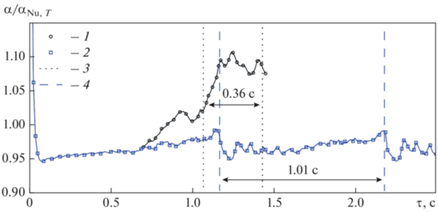
Изменение коэффициента теплоотдачи во времени показано на рис. 19. Видно, что при попадании конденсата на трубу коэффициент теплоотдачи резко снижается, а затем постепенно восстанавливается практически до исходного значения.

Рис. 19.

Зависимости относительного коэффициента теплоотдачи от времени при $\Delta T$ = 20 К и различных значениях $k{\text{:}}$ а – 1; б – 2; в – 3. 1 – результаты настоящей работы; 2, 3 – значения для N-й трубки, рассчитанные по формулам из [31] и [32] соответственно

Для сравнения на рис. 19 приведены также значения коэффициентов теплоотдачи по модели Jakob [31]:

$\frac{{\left\langle {{{\alpha }_{{i = N}}}} \right\rangle }}{{{{\alpha }_{{{\text{Nu}},T}}}}} = {{N}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}} - {{\left( {N - 1} \right)}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}$

и модели Kern [32]:

$\frac{{\left\langle {{{\alpha }_{{i = N}}}} \right\rangle }}{{{{\alpha }_{{{\text{Nu}},T}}}}} = {{N}^{{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}}}} - {{\left( {N - 1} \right)}^{{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}}}},$

где $N = k + 1.$

Зависимости на рис. 19 были осреднены начиная с момента удара второй капли и до момента последнего удара капли на рассчитанном интервале времени.

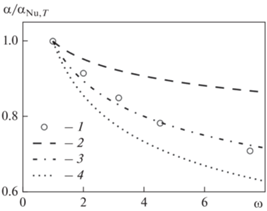
Зависимости относительного среднего коэффициента теплоотдачи от значения $\omega $ представлены на рис. 20. Параметр $\omega $ определялся по формуле

$\omega = \frac{{{{G}_{\sum }}}}{{{{G}_{{l,cond}}}}} = \frac{{{{G}_{l}} + {{G}_{{l,cond}}}}}{{{{G}_{{l,cond}}}}},$

где ${{G}_{l}}$ – удельный расход, орошающий трубку, кг/(м · с), ${{G}_{{l,cond}}}$ – удельный расход конденсата, образовавшегося на трубке, кг/(м · с).

Рис. 20.

Зависимости относительного коэффициента теплоотдачи от параметра $\omega $. 1 – результаты настоящей работы; 2 – $s = 0.07$ [33]; 3 – $s = 0.16$ [34]; 4 – $s = 0.223$ [35]

Сравнение результатов расчета выполнено с зависимостями вида

$\frac{{\left\langle {{{\alpha }_{{i = N}}}} \right\rangle }}{{{{\alpha }_{{Nu,T}}}}} = {{\omega }^{{ - s}}},$

где параметру s придавали значения согласно рекомендациям разных авторов:$s = 0.07$ [33], $s = 0.16$ [34], $s = 0.223$ [35].

Видно, что полученные результаты хорошо согласуются с зависимостью, предложенной в [34].

МОДЕЛИРОВАНИЕ КОНДЕНСАЦИИ НЕПОДВИЖНОГО ПАРА В ТРЕХМЕРНОЙ ПОСТАНОВКЕ

Для проверки работоспособности используемых моделей и алгоритмов массообмена и выяснения степени влияния размерности задачи на полученные результаты было выполнено моделирование конденсации в трехмерной постановке (3D). Рассматривалась конденсация неподвижного пара пентана на поверхности горизонтальной трубы при $\Delta T$ = 20 К и атмосферном давлении. Ширина расчетной области вдоль оси трубы ${{L}_{z}}$ была принята равной $2\pi \sqrt 2 b$ в соответствии с рекомендациями [11, 26]. Двумерная сетка № 2 использовалась в качестве базовой в радиальном и угловом направлениях, по координате z вдоль оси трубы область была разбита на 64 контрольных объема одинакового размера. При z = 0 и z = L_z ставились периодические граничные условия. Выбор сетки № 2 обусловлен исключительно экономией вычислительных ресурсов и вполне удовлетворительными результатами по отрыву капель, полученными в двумерной постановке (2D).

Трехмерная задача инициализировалась с использованием двумерных полей в момент времени 0.7 с. На рис. 21 для сравнения представлены коэффициенты теплоотдачи для 3D- и 2D-постановок. Средние значения ${{\left\langle \alpha \right\rangle } \mathord{\left/ {\vphantom {{\left\langle \alpha \right\rangle } {{{\alpha }_{{Nu,T}}}}}} \right. \kern-0em} {{{\alpha }_{{Nu,T}}}}}$ между моментами отрыва первой и второй капель для 2D- и 3D-постановок составили 0.97 и 1.08 соответственно. Важно отметить, что время между срывами капель в 3D-постановке практически в 3 раза меньше по сравнению со временем в 2D-постановке. Данное различие легко объясняется разными объемами капель, отрывающихся с 1 м погонной длины трубы:

$\begin{gathered} \frac{{\Delta {{\tau }_{{3D}}}}}{{\Delta {{\tau }_{{2D}}}}} \approx \frac{1}{{{{L}_{z}}}}\frac{{\pi d_{{drop}}^{3}}}{6}\frac{4}{{\pi d_{{drop}}^{2}}} = \frac{2}{3}\left( {\frac{{A_{{3D}}^{3}}}{{A_{{2D}}^{2}}}} \right)\frac{b}{{2\pi \sqrt 2 b}} = \\ = 0.05\left( {\frac{{A_{{3D}}^{3}}}{{A_{{2D}}^{2}}}} \right) \approx 0.23 - 0.36, \\ \end{gathered} $

где ${{A}_{{{\text{2D}}}}},$ ${{A}_{{{\text{3D}}}}}$ – константы в соотношении ${{d}_{{drop}}} = Ab$ для 2D- и 3D-постановок.

Рис. 21.

Зависимости относительного коэффициента теплоотдачи от времени для 3D- и 2D-постановок. 1, 3 ‒ 3D; 2, 4 ‒ 2D; вертикальные линии – момент времени отрыва капель

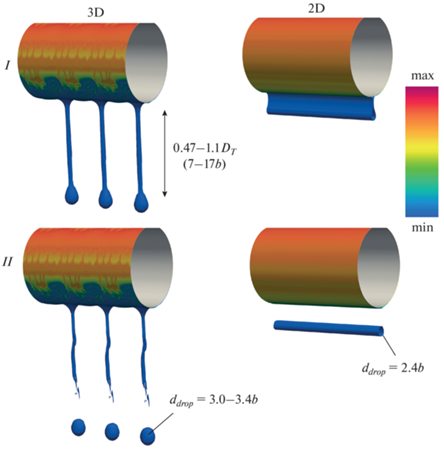
На рис. 22 показан вид капли сразу после отрыва от пленки для 3D- и 2D-вариантов. Для наглядности результатов моделирования изображение слева на рисунке построено путем трехкратного повторения вдоль оси z картины, полученной на выбранной длине трубы L_z (в действительности на длине L_z отрывалась одна капля), а для 2D (справа на рисунке) – простым растяжением вдоль z плоской картины. Для 3D-варианта такое представление результатов соответствует постановке задачи, так как по оси z используются периодические граничные условия и возможно масштабирование результатов расчета на трубу любой протяженности, если длина последней кратна длине расчетной области. Отрыв капли в расчетной области происходит несимметрично, ближе к ее правой границе. Эквивалентные диаметры капель после отрыва в трехмерном варианте оказались равными ${{d}_{{drop}}} = 3.4b$ для первой капли и ${{d}_{{drop}}} = 3.0b$ для второй, что примерно в $\sqrt 2 $ раза превышает диаметр двумерной капли (диаметр цилиндрической капли). Данное отличие, как указывалось ранее, вероятно, связано с двукратным различием кривизны поверхностей сферы и цилиндра. Тон поверхности и шкала на рис. 22 соответствуют интенсивности конденсации. Для 3D-варианта видно возникновение трехмерных структур на нижней половине поверхности цилиндра.

Рис. 22.

Вид первой капли сразу после отрыва с пленки для 3D- и 2D-постановок. I, II – кадры, сделанные с периодом 12.5 мс

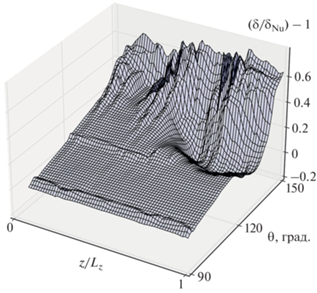
На рис. 23 представлено распределение толщины пленки в виде $\left[ {\left( {{\delta \mathord{\left/ {\vphantom {\delta {{{\delta }_{{{\text{Nu}}}}}}}} \right. \kern-0em} {{{\delta }_{{{\text{Nu}}}}}}}} \right) - 1} \right]$ по длине трубы для углов $\theta $ от 0 до 150° в момент времени перед отрывом капли. Видно существенное локальное уменьшение толщины пленки $\left[ {\left( {{\delta \mathord{\left/ {\vphantom {\delta {{{\delta }_{{Nu}}}}}} \right. \kern-0em} {{{\delta }_{{Nu}}}}}} \right) - 1 \approx - 0.2} \right]$ при приближении к нижней образующей трубы.

Рис. 23.

Распределение толщины пленки по длине трубы в момент времени перед отрывом капли для угла θ от 90 до 150°

ВЫВОДЫ

1. Выполненная валидация реализованной в исследовательском коде ANES модифицированной модели массообмена Lee для расчета методом VOF процессов конденсации пара на поверхности горизонтальной трубы показала, что полученные в двумерной постановке данные по теплоотдаче при конденсации практически неподвижных паров пентана и воды хорошо согласуются с теорией Нуссельта.

2. Для умеренных скоростей движения паров пентана и воды (U₀$ \leqslant $ 3.0 м/с) результаты по средней теплоотдаче с погрешностью, не превышающей $ \pm 10\% ,$ согласуются с зависимостями, предложенными в [28, 29], а также с результатами расчетов по упрощенной модели авторов [30].

3. Результаты расчетов диаметров отрывающихся капель при конденсации пентана в двумерной (с учетом различия радиусов кривизны объемной и плоской капель) и трехмерной постановках неплохо согласуются с имеющимися экспериментальными данными. Полученные данные о прогреве падающей капли за счет конденсации пара на ее поверхности качественно воспроизводят результаты работы [27].

4. Вследствие существования вихревых структур в движущемся паре картина формирования и отрыва капель оказывается несимметричной относительно плоскости, содержащей вертикальный диаметр трубы.

5. Результаты расчетов теплоотдачи с учетом орошения трубы конденсатом наилучшим образом соответствуют зависимости Wilson [34]. При этом пульсации коэффициента теплоотдачи достигают 20–30%, а поведение жидкой пленки во многом отличается от монотонной зависимости, следующей из решения Нуссельта.

6. Зафиксировано наличие заметной неоднородности интенсивности массообмена на поверхности трубы при моделировании в 3D-постановке. Срыв конденсата в 3D-постановке существенно отличается от такового в 2D-постановке.

7. Использованная в работе модифицированная модель Lee может быть рекомендована для расчетов методом VOF процессов конденсации движущегося пара.

В дальнейшем авторы планируют проведение систематических расчетов для 3D-постановки.

Список литературы

Гогонин И.И. Исследование теплообмена при пленочной конденсации пара. Новосибирск: Изд-во СО РАН, 2015.
Федоров В.А., Мильман О.О. Конденсаторы п-аротурбинных установок. М.: Изд-во МГТУ им. Н.Э. Баумана, 2013.
Comprehensive review of pure vapour condensation outside of horizontal smooth tubes / C. Bonneau, C. Josset, V. Melot, B. Auvity // Nucl. Eng. Des. 2019. V. 349. P. 92–108. https://doi.org/10.1016/j.nucengdes.2019.04.005
Grant C. An experimental investigation of drop wise and film wise condensation of low pressure steam in tube banks: PhD thesis. Edinburgh: Heriot-Watt University, 1999.
Tsui Y.Y., Lin S.W. A VOF-based conservative interpolation scheme for interface tracking (CISIT) of two-fluid flows // Numer. Heat Transfer. Part B: Fundamentals. 2013. V. 63. Is. 4. P. 263–283. https://doi.org/10.1080/10407790.2013.756251
Kharangate C.R., Mudawar I. Review of computational studies on boiling and condensation // Int. J. Heat Mass Transfer. 2017. V. 108. Part A. P. 1164–1196. https://doi.org/10.1016/j.ijheatmasstransfer.2016.12.065
Knudsen M. The kinetic theory of gases: some modern aspects (Methuen’s monographs physical subjects). L.: Methuen and Co. 1934.
Ягов В.В. Теплообмен в однофазных средах и при фазовых превращениях. М.: Издательский дом МЭИ, 2014.
Lee W.H. A pressure iteration scheme for two-phase flow modeling // Multiphase transport: fundamentals, reactor safety, applications / Ed. by T.N. Veziroglu. Washington, DC: Hemisphere Publishing, 1980. P. 407–432.
Aghanajafi C., Hesampour K. Heat transfer analysis of a condensate flow by VOF method // J. Fusion Energy. 2006. V. 25. Is. 3. P. 219–223. https://doi.org/10.1007/s10894-006-9025-6
Kleiner T., Rehfeldt S., Klein H. CFD model and simulation of pure substance condensation on horizontal tubes using the volume of fluid method // Int. J. Heat Mass Transfer. 2019. V. 138. P. 420–431. https://doi.org/10.1016/j.ijheatmasstransfer.2019.04.054
Detailed CFD simulations of pure substance condensation on horizontal annular low finned tubes including a parameter study of the fin slope / T. Kleiner, A. Eder, S. Rehfeldt, H. Klein // Int. J. Heat Mass Transfer. 2020. V. 163. P. 120363. https://doi.org/10.1016/j.ijheatmasstransfer.2020.120363
Li S., Ju Y. Numerical study on the condensation characteristics of various refrigerants outside a horizontal plain tube at low temperatures // Int. J. Therm. Sci. 2022. V. 176. P. 107508. https://doi.org/10.1016/j.ijthermalsci.2022.107508
ANSYS Fluent Theory Guide. Canonsburg: ANSYS Inc., 2018.
Condensation heat transfer of R134a, R1234ze(E) and R290 on horizontal plain and enhanced titanium tubes / W.-T. Ji, G.-H. Chong, C.-Y. Zhao, H. Zhang, W.-Q. Tao // Int. J. Refrig. 2018. V. 93. P. 259–268. https://doi.org/10.1016/j.ijrefrig.2018.06.013
Hirt C.W., Nichols B. Volume of fluid (VOF) method for dynamics of free boundaries // J. Comput. Phys. 1981. V. 39. Is. 1. P. 201–225. https://doi.org/10.1016/0021-9991(81)90145-5
Ubbink O., Issa R.I. A method for capturing sharp fluid interfaces on arbitrary meshes // J. Comput. Phys. 1999. V. 153. Is. 1. P. 26–50. https://doi.org/10.1006/jcph.1999.6276
Zhang Y., Faghri A., Shafii M.B. Capillary blocking in forced convective condensation in horizontal miniature channels // J. Heat Transfer. 2001. V. 123. Is. 3. P. 501–511. https://doi.org/10.1115/1.1351808
Hardt S., Wondra F. Evaporation model for interfacial flows based on a continuum-field representation of the source terms // J. Comput. Phys. 2008. V. 227. Is. 11. P. 5871–5895. https://doi.org/10.1016/j.jcp.2008.02.020
Kunkelmann C. Numerical modeling and investigation of boiling phenomena: PhD thesis. Darmstadt, Germany: Technische Universität Darmstadt, 2011.
Rattner A.S., Garimella S. Simple mechanistically consistent formulation for volume-of-fluid based computations of condensing flows // J. Heat Transfer. 2014. V. 136. Is. 7. P.071501. https://doi.org/10.1115/1.4026808
Код ANES. [Электрон. ресурс.] http://anes.ch12655. tmweb.ru/
Патанкар С. Численные методы решения задач тепломассообмена и динамики жидкости / пер. с англ. М.: Энергоатомиздат, 1984.
Issa R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting // J. Comput. Phys. 1986. V. 62. Is. 1. P. 40–65. https://doi.org/10.1016/0021-9991(86)90099-9
Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library CoolProp / I.H. Bell, J. Wronski, S. Quoilin, V. Lemort // Ind. Eng. Chem. Res. 2014. V. 53. Is. 6. P. 2498–2508. https://doi.org/10.1021/ie4033999
Yung D., Lorenz J.J., Ganic E.N. Vapor/liquid interaction and entrainment in falling film evaporators // J. Heat Transfer. 1980. V. 102. Is. 1. P. 20–25. https://doi.org/10.1115/1.3244242
Kutateladze S.S., Gogonin I.I., Sosunov V.I. The influence of condensate flow rate on heat transfer in film condensation of stationary vapour on horizontal tube banks // Int. J. Heat Mass Transfer. 1985. V. 28. Is. 5. P. 1011–1018. https://doi.org/10.1016/0017-9310(85)90283-2
Fujii T., Uehara H., Kurato C. Laminar filmwise condensation of flowing vapour on a horizontal cylinder // Int. J. Heat Mass Transfer. 1972. V. 15. Is. 2. P. 235–246. https://doi.org/10.1016/0017-9310(72)90071-3
Rose J.W. Effect of pressure gradient in forced convection film condensation on a horizontal tube // Int. J. Heat Mass Transfer. 1984. V. 27. Is. 1. P. 39–47. https://doi.org/10.1016/0017-9310(84)90235-7
Минко К.Б., Артемов В.И., Клементьев А.А. Валидация модели жидкой пленки конденсата на поверхности гладкого горизонтального цилиндра при различных направлениях движения пара // Теплоэнергетика. 2022. № 12. С. 40–53. https://doi.org/10.56304/S0040363622120062
Jakob M. Heat transfer. N.Y.: John Wiley & Sons, 1949.
Kern D.Q. Process heat transfer. N.Y.: McGraw Hill, 1950.
Фукс С.Н. Теплоотдача при конденсации движущегося пара в горизонтальном трубном пучке // Теплоэнергетика. 1957. № 1. С. 35‒38.
Wilson J.L. The design of condensers by digital computers // Chem. Eng. Symp. Ser. 1972. V. 35. P. 21–27.
Grant I.D.R., Osment B.D.J. The effect of condensate drainage on condenser performance: Techn. Rep. 350. East Kilbride, Glasgow: National Engineering Laboratory, 1968.

Дополнительные материалы

скачать ESM.docx

Приложение 1.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплоэнергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал