Теплофизика высоких температур, 2019, T. 57, № 1, стр. 83-93
Численный анализ характеристик теплообмена при радиационно-конвективном нагреве конуса, затупленного по сфере
К. Н. Ефимов 1, В. А. Овчинников 1, А. С. Якимов 1, *, С. А. Гаар 1
1 Национальный исследовательский Томский государственный университет,
Томск,, Россия
* E-mail: yakimovas@mail.ru
Поступила в редакцию 11.05.2017
После доработки 10.10.2017
Принята к публикации 14.07.2017
Аннотация
Проведен численный анализ процесса нестационарного теплообмена в композиционном материале при действии лазерного излучения умеренной интенсивности на основе тепловой модели разрушения теплозащитного покрытия конической части тела. При многократном импульсном воздействии получены различные режимы термохимического разрушения покрытия из углепластика и графита В-1 конической части тела. Найдено, что в экранировке лазерного излучения продуктами разрушения тела определяющую роль играют газообразные продукты пиролиза, частицы конденсированной фазы и пары углеродного материала.
ВВЕДЕНИЕ
В конце прошлого века и в начале нового столетия в исследованиях по импульсному воздействию высококонцентрированного потока энергии уделялось большое внимание вопросам взаимодействия лазерного излучения с образующимися продуктами разрушения [1–10]. В работах [1–5, 7, 9, 10] показано, что воздействие импульсного излучения на композиционные материалы сопровождается как испарением, так и выбросом фрагментов вещества в твердой фазе (диспергированием материала). В [1] указано, что пренебрежение взаимодействием продуктов выброса с потоком энергии может привести к ошибкам в определении параметров разрушения вещества, поскольку экранировка способна существенно изменять пространственно-временные характеристики потока. При воздействии импульса излучения умеренной интенсивности (${{10}^{8}}$−${{10}^{{10}}}$ Вт/м2) на мишенях из эбонита или графита [4, 5] обнаружена существенная степень экранирующего действия лазерного эрозионного плазменного факела. Показано, что в экранирующем действии лазерного эрозионного плазменного факела, заключающемся в поглощении и рассеянии лазерного излучения, определяющую роль играют частицы конденсированной фазы. В [4] установлено, что потери на отражение и рассеяние лазерного эрозионного плазменного факела достигают максимального значения при плотностях потока ~${{10}^{{10}}}$ Вт/м2 и в случае эбонита составляют 50%.
Математическое моделирование процесса тепломассообмена и горения композиционных материалов в высокоэнтальпийных потоках обсуждается в [11–14]. В данной статье дается численный анализ процесса термохимического разрушения углепластика при воздействии лазерного излучения умеренной интенсивности $q{\text{*}}$ ≈ ${{10}^{9}}$ Вт/м2 с учетом конвективного нагрева композиционного материала. При этом для простоты анализа спектральный состав излучения не учитывается.
ПОСТАНОВКА ЗАДАЧИ
Предполагается, что в пограничном слое имеются пять компонентов: $O,{{O}_{2}},N,$ ${{N}_{2}},NO,$ которые участвуют в трех равновесных химических реакциях: ${{O}_{2}} \leftrightarrow 2O,$ ${{N}_{2}} \leftrightarrow 2N,$ $NO \leftrightarrow N\, + O.$ Распределение концентраций компонент на внешней границе пограничного слоя находилось по методике [15]. Температура ${{T}_{e}} = {{T}_{{e0}}}{{\bar {p}}^{\Phi }},$ Φ = = ${{({{\gamma }_{{{\text{ef}}}}} - 1)} \mathord{\left/ {\vphantom {{({{\gamma }_{{{\text{ef}}}}} - 1)} {{{\gamma }_{{{\text{ef}}}}}}}} \right. \kern-0em} {{{\gamma }_{{{\text{ef}}}}}}},$ безразмерное давление $\bar {p} = {{{{P}_{e}}} \mathord{\left/ {\vphantom {{{{P}_{e}}} {{{P}_{{e0}}}}}} \right. \kern-0em} {{{P}_{{e0}}}}}$ и эффективный показатель адиабаты ${{\gamma }_{{{\text{ef}}}}}$ определялись согласно [16].
Для описания термохимического разрушения углепластика используются уравнения, предложенные в [11], а граничные условия, учитывающие “механический” унос материала, взяты из [12]. Кроме того, учитывается сопряженная постановка задачи прогрева составного тела (см. рис. 1) внутри конденсированной фазы и пиролиз композиционного материала конической части оболочки.
Рис. 1.
Схема обтекания тела: 1 − пористое сферическое затупление; 2, 3 − коническая часть тела из композиционного материала.

При относительно небольших значениях плотности потока энергии лазерного излучения, когда внутреннюю задачу можно анализировать в достаточной мере независимо от внешней, для описания кинетики поверхностного испарения используется так называемая тепловая модель [2], основанная на решении уравнения теплопроводности для области с движущейся границей раздела фаз с соответствующими краевыми условиями.
На конической части тела рассматривается девятикомпонентная модель, где под преобладающими компонентами понимаются все компоненты, вклад от которых в полную энтальпию газа ${{h}_{w}} = \sum\nolimits_{i = 1}^9 {{{h}_{i}}{{c}_{{iw}}}} $ (где ${{c}_{{iw}}}$ − массовая концентрация i-го компонента, i = 1, 2, …, 9, h − энтальпия) хотя бы в отдельных точках потока составляет 5% и больше. Поэтому, в отличие от [13, 14], в гетерогенных химических реакциях ниже добавлена дополнительно реакция образования циана [8, 17].
Как и в [6], при интерполяции параметров ослабления излучения продуктами горения считается, что его оптическая толщина пропорциональна расходу продуктов термохимического разрушения теплозащитного материала. В первом приближении такой процесс по аналогии с законом Бугера–Ламберта [18] представим в виде
где ${{(\rho v)}_{\Sigma }}$ − суммарный массовый унос с поверхности углепластика, ${{q}_{*}}$ − плотность потока энергии лазерного излучения в отсутствие вдува, ξ − эмпирический коэффициент (размерностью ${{{\text{м }}}^{{\text{2}}}}$ с/кг), который зависит от типа материала, оптических свойств частиц дисперсной фазы и состава газообразных продуктов термохимического разрушения композиционного материала. Индексы “звездочка” и Σ приписываются характерной и суммарной величине, r – радиационному потоку тепла, w – параметрам внешней границе тела.Физический смысл (1) очевиден: чем больше суммарная массовая скорость вдува продуктов термохимического разрушения в пограничный слой, тем выше концентрация конденсированных частиц и многоатомных газообразных продуктов разрушения вблизи поверхности твердого тела и тем сильнее происходит ослабление падающего лучистого потока.
Кроме того, для расчета процесса нагрева надо знать также временную структуру импульса излучения. В первом приближении режим излучения может быть описан ступенчатой функцией времени [18]:
(2)
$\left\{ \begin{gathered} W(t) = 0,\,\,\,\,\,t < {{t}_{{2i - 1}}}, \hfill \\ W(t) = 1,\,\,\,\,{{t}_{{2i - 1}}} \leqslant t \leqslant {{t}_{{2i}}},\,\,\,\,i = 1,2, \ldots ,N, \hfill \\ W(t) = 0,\,\,\,\,t > {{t}_{{2i}}}, \hfill \\ \end{gathered} \right.$Здесь и ниже t − текущее время; s, η − составляющие естественной системы координат; ${{t}_{i}}$ − фиксированный момент времени; ${{R}_{N}}$ − радиус сферического затупления; ${{\bar {s}}_{1}}$ = 3, ${{\bar {s}}_{2}}$ = 4.771, ${{\eta }_{1}}$ = = 180°, ${{\eta }_{2}}$ = 205°. В дальнейшем при численных расчетах были выбраны три пика лазерного излучения i = 1–3 в (2) и ${{t}_{1}}$ = 10.001, ${{t}_{2}}$ = 10.002, ${{t}_{3}}$ = = 10.005, ${{t}_{4}}$ = 10.006, ${{t}_{5}}$ = 10.009, ${{t}_{6}}$ = 10.01 с.
Физика процесса в конденсированной фазе на конической части тела такова [11–14]: под воздействием высокотемпературного потока температура ${{T}_{2}}$ увеличивается до температуры разложения смолы, затем начинается пиролиз с образованием углеродистого остатка (кокса), который удерживается внутри матрицы армирующих волокон. При ${{T}_{{2w}}}$ > 1000 К углеродистая поверхность разрушается в результате взаимодействия с компонентами диссоциированного воздуха. Газы пиролиза могут фильтроваться к границе раздела сред $n$ = 0, вдуваться в пограничный слой и вместе с продуктами окисления, горения, сублимации углепластика и частицами твердой фазы снижать поступающий к телу радиационно-конвективный поток тепла.
При постановке задачи примем следующие допущения:
1) число Рейнольдса в набегающем гиперзвуковом потоке воздуха достаточно велико (${{\operatorname{Re} }_{\infty }} \gg 1$) и в окрестности поверхности тела сформировался пограничный слой;
2) воздух на внешней границе пограничного слоя находится в состоянии термохимического равновесия и представляет собой пятикомпонентную смесь $O,{{O}_{2}},N,{{N}_{2}},NO;$
3) явления переноса в пограничном слое рассматриваются при упрощающих предположениях о равенстве коэффициентов диффузии; число Льюиса Le = 1;
4) для расчета состава на границе раздела газообразной и к-фаз используем аналогию процесса тепло- и массообмена [11];
5) тепловое состояние полусферической оболочки в области 1 (рис. 1) определяется из решения нестационарного уравнения сохранения энергии для пористого сферического затупления в рамках однотемпературной модели и квазистационарного уравнения для скорости фильтрации охлаждающего газа в порах;
6) фильтрующийся газ в области 1 считается однородным, его молекулярная масса равна молекулярной массе воздуха, а плотность газовой фазы находится из уравнения состояния идеального газа;
7) величина потока массы по нормали n к обтекаемой поверхности значительно больше, чем по касательным к ней;
8) на внешней поверхности конической части тела при $s \geqslant {{s}_{A}}$ протекают следующие гетерогенные процессы [8, 12, 13, 17, 19]:
(3)
$\begin{gathered} 1)\,\,C\, + {{O}_{2}} \to C{{O}_{2}},\,\,\,\,2)\,\,2C\, + {{O}_{2}} \to 2CO, \\ {\text{3)}}\,\,{\text{C}} + {\text{O}} \to {\text{CO,}}\,\,\,\,\,4)\,\,C\, + {\text{C}}{{O}_{2}} \to 2CO, \\ {\text{5)}}\,\,{\text{C}} + {\text{N}} \to {\text{CN,}}\,\,\,\,6)\,\,{\text{O}} + {\text{O}} + {\text{C}} \to {{{\text{O}}}_{{\text{2}}}} + {\text{C,}} \\ {\text{7)}}\,\,{\text{N}} + {\text{N}} + {\text{C}} \to {{{\text{N}}}_{{\text{2}}}} + {\text{C,}}\,\,{\text{8)}}\,\,{\text{C}} \Leftrightarrow {{{\text{C}}}_{1}},\,\,9)\,\,{\text{C}} \Leftrightarrow {{{\text{C}}}_{3}}; \\ \end{gathered} $9) армирующие нити композиционного материала (волокна углерода) не плавятся;
10) энергия лазерного излучения поглощается на поверхности, т.е. пробег излучения в твердом теле мал по сравнению с глубиной прогрева в течении представляющего интерес периода времени;
11) условием диспергирования частиц наполнителя (углерода) считаем достижение предельной плотности армирующего волокна: ${{\rho }_{c}}[x(t),t] = {{\rho }_{{c*}}};$
12) механизм диспергирования связан с “выстреливанием” частиц, и скорость этих частиц может превышать скорость фильтрации [12]:
Используя (4), найдем массовые скорости образования (исчезновения) компонентов в результате гетерогенных реакций:
Выражения для массовых скоростей уноса имеют вид [13]
(5)
$\begin{gathered} {{(\rho v)}_{{2w}}} = {{\varphi }_{2}}\rho _{w}^{{(2)}}\left[ {\left( {\frac{{{{m}_{6}}}}{{{{m}_{2}}}} - 1} \right){{c}_{{2w}}}{{B}_{1}} + \left( {2\frac{{{{m}_{5}}}}{{{{m}_{2}}}} - 1} \right){{c}_{{2w}}}{{B}_{2}}} \right. + \\ \left. { + \,\,\left( {\frac{{{{m}_{5}}}}{{{{m}_{1}}}} - 1} \right){{c}_{{1w}}}{{B}_{3}} + \left( {2\frac{{{{m}_{5}}}}{{{{m}_{6}}}} - 1} \right){{c}_{{6w}}}{{B}_{4}} + \left( {\frac{{{{m}_{7}}}}{{{{m}_{3}}}} - 1} \right){{k}_{5}}{{c}_{{3w}}}} \right], \\ {{(\rho v)}_{{3w}}} = {{\varphi }_{2}}\sum\limits_{i = 8}^9 {\frac{{{{m}_{i}}{{A}_{{ci}}}(P_{{ci}}^{*} - {{P}_{{ci}}})}}{{{{{(2\pi R{{T}_{{2w}}}{{m}_{i}})}}^{{0.5}}}}}} , \\ {{B}_{i}} = {{k}_{i}}\exp \left( {{{ - {{E}_{i}}} \mathord{\left/ {\vphantom {{ - {{E}_{i}}} {R{{T}_{{2w}}}}}} \right. \kern-0em} {R{{T}_{{2w}}}}}} \right),\,\,\,\,i = \overline {1,4} , \\ (\rho v)_{w}^{{(2)}} = \sum\limits_{i = 1}^3 {{{{(\rho v)}}_{{iw}}}} ,\,\,\,\,{{(\rho v)}_{\Sigma }} = (\rho v)_{w}^{{(2)}} + {{z}_{1}}{{(\rho v)}_{{1w}}}. \\ \end{gathered} $Обоснование седьмого допущения дано в [14], а девятого в [17]. C − обозначение твердофазного углерода, входящего в состав теплозащитного покрытия. На границе конденсированной и газовой фаз присутствуют пять компонентов: $CO,C{{O}_{2}},CN,{{C}_{1}},{{C}_{3}},$ которые возникают в семи гетерогенных реакциях горения и сублимации из (3). Там же учитываются две реакции каталитической рекомбинации компонентов ${{O}_{2}},{{N}_{2}}$ [19]. В пограничном слое отсутствует аргон, а на поверхности конуса – сублимирующая компонента ${{C}_{2}}$, так как по данным [8, 17] их величины в рассмотренном диапазоне температур меньше 1 и 5% соответственно.
На основании допущений 5–7, для пористой сферической оболочки $0 < s < {{s}_{A}}$ при одномерном процессе фильтрации вдуваемого газа в направлении нормали к поверхности в рассматриваемой системе координат, связанной с осью симметрии тела, имеем [12–14]
(6)
$\frac{{\partial [{{{(\rho v)}}^{{(1)}}}{{\varphi }_{1}}{{r}_{1}}{{F}_{1}}]}}{{\partial n}} = 0,$(7)
$\begin{gathered} {{(\rho {{c}_{p}})}_{1}}(1 - {{\varphi }_{1}})\frac{{\partial {{T}_{1}}}}{{\partial t}} = \frac{1}{{{{r}_{1}}{{F}_{1}}}}\left\{ {\frac{\partial }{{\partial n}}\left[ {{{r}_{1}}{{F}_{1}}{{\lambda }_{1}}(1 - {{\varphi }_{1}})\frac{{\partial {{T}_{1}}}}{{\partial n}}} \right]} \right. + \\ + \,\,\frac{\partial }{{\partial s}}\left[ {\frac{{{{r}_{1}}{{\lambda }_{1}}}}{{{{F}_{1}}}}(1 - {{\varphi }_{1}})\frac{{\partial {{T}_{1}}}}{{\partial s}}} \right] + \left. {\frac{\partial }{{\partial \eta }}\left[ {\frac{{{{F}_{1}}{{\lambda }_{1}}}}{{{{r}_{1}}}}\left( {1 - {{\varphi }_{1}}} \right)\frac{{\partial {{T}_{1}}}}{{\partial \eta }}} \right]} \right\} + \\ + \,\,c_{{pg}}^{{(1)}}\left( {\rho v} \right)_{w}^{{(1)}}\frac{{{{r}_{{1w}}}}}{{{{r}_{1}}{{F}_{1}}}}\frac{{\partial {{T}_{1}}}}{{\partial n}}, \\ \end{gathered} $(8)
$A{{\mu }_{1}}{{v}^{{(1)}}} + B{{\varphi }_{1}}{{\rho }^{{(1)}}}{{v}^{{(1)}}}\left| {{{v}^{{(1)}}}} \right| = - \frac{{\partial P}}{{\partial n}},$(9)
$\begin{gathered} P = \frac{{{{\rho }^{{(1)}}}R{{T}_{1}}}}{M},\,\,\,\,{{F}_{1}} = \frac{{{{R}_{N}} - n}}{{{{R}_{N}}}},\,\,\,\,{{r}_{1}} = ({{R}_{N}} - n)\sin (\bar {s}), \\ {{\mu }_{1}}\sim \sqrt {{{T}_{1}}} ,\,\,\,\,{{\lambda }_{1}}\sim \sqrt {{{T}_{1}}} ,\,\,\,\,{{\varphi }_{1}} = {\text{const}}{\text{.}} \\ \end{gathered} $Для конической части тела (${{s}_{A}} < s < {{s}_{k}}$) уравнения сохранения энергии и массы в подвижной системе координат для углепластика в области 2 и 3 на рис. 1 записываются в виде [11, 12]
(10)
$\begin{gathered} {{\rho }_{c}}{{c}_{{p2}}}\left( {\frac{{\partial {{T}_{2}}}}{{\partial t}} - \psi \frac{{\partial {{T}_{2}}}}{{\partial n}}} \right) + c_{{pg}}^{{(2)}}G\frac{{\partial {{T}_{2}}}}{{\partial n}} = \frac{\partial }{{\partial n}}\left( {{{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial n}}} \right) + \\ + \,\,\frac{\partial }{{\partial s}}\left( {{{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial s}}} \right) + \frac{1}{{r_{2}^{2}}}\frac{\partial }{{\partial \eta }}\left( {{{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial \eta }}} \right) - {{Q}_{c}}\frac{{d{{\rho }_{c}}}}{{dt}}, \\ \end{gathered} $(11)
$\begin{gathered} \frac{{d{{\rho }_{c}}}}{{dt}} = \left( {\frac{{\partial {{\rho }_{c}}}}{{\partial t}} - \psi \frac{{\partial {{\rho }_{c}}}}{{\partial n}}} \right) = \\ = \left\{ \begin{gathered} - {{k}_{c}}{{\rho }_{{c0}}}\left( {\frac{{{{\rho }_{c}} - {{\rho }_{{c*}}}}}{{{{\rho }_{{c0}}}}}} \right)\exp \left( { - \frac{{{{E}_{c}}}}{{R{{T}_{2}}}}} \right),\,\,\,\,\,\,\,\,{{\rho }_{c}} > {{\rho }_{{c*}}}, \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{\rho }_{c}} \leqslant {{\rho }_{{c*}}}, \\ \end{gathered} \right. \\ c_{{pg}}^{{(i)}} = {{b}_{1}} + {{b}_{2}}{{T}_{i}},\,\,\,\,i = 1,2, \\ {{r}_{2}} = \left( {{{R}_{N}} - n} \right)\cos \theta + \left( {s - {{s}_{A}}} \right)\sin \theta ,\,\,\,\,G = \int\limits_0^l {\frac{{d{{\rho }_{c}}}}{{dt}}dn,} \\ \psi = {{\left[ {\sum\limits_{i = 2}^3 {{{{(\rho v)}}_{{iw}}} + {{z}_{1}}{{{(\rho v)}}_{{1w}}}} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{i = 2}^3 {{{{(\rho v)}}_{{iw}}} + {{z}_{1}}{{{(\rho v)}}_{{1w}}}} } \right]} {{{\rho }_{{cw}}}}}} \right. \kern-0em} {{{\rho }_{{cw}}}}},\,\,\,\,{{(\rho v)}_{{1w}}} = {{G}_{w}}. \\ \end{gathered} $Для графита В-1 при i = 2 в области 2 и подложки из асбестоцемента в области 3 получим
(12)
$\begin{gathered} {{\rho }_{i}}{{c}_{{pi}}}\left( {\frac{{\partial {{T}_{i}}}}{{\partial t}} - \psi \frac{{\partial {{T}_{i}}}}{{\partial n}}} \right) = \frac{\partial }{{\partial n}}\left( {{{\lambda }_{i}}\frac{{\partial {{T}_{i}}}}{{\partial n}}} \right) + \\ + \,\,\frac{\partial }{{\partial s}}\left( {{{\lambda }_{i}}\frac{{\partial {{T}_{i}}}}{{\partial s}}} \right) + \frac{1}{{r_{2}^{2}}}\frac{\partial }{{\partial \eta }}\left( {{{\lambda }_{i}}\frac{{\partial {{T}_{i}}}}{{\partial \eta }}} \right),\,\,\,\,i = 2,3. \\ \end{gathered} $Для определения температуры частиц дисперсной среды из [12] имеем $T_{{2w}}^{s} = {{T}_{2}}(t - t*),$ где ${{t}_{*}}$ − время достижения предельной плотности ${{\rho }_{{c*}}}.$ Эта формула соответствует случаю, когда за время отрыва ${{t}_{*}}$ частица не успела обменяться энергией с окружающей газовой средой и сохранила ту температуру, которая была на момент начала отрыва.
Систему уравнений (6)–(8), (10)–(12) необходимо решать с учетом начальных
(13)
${{\left. {{{T}_{i}}} \right|}_{{t = 0}}} = {{T}_{0}},\,\,\,\,i = 1,2,3,\,\,\,\,{{\left. {{{\rho }_{c}}} \right|}_{{t = 0}}} = {{\rho }_{{c0}}}.$На обтекаемой внешней поверхности оболочки ($n = 0$) имеют место условия [13, 14] при $0 \leqslant \eta < 2\pi \,:$
(14)
${{q}_{{1w}}} - (1 - {{\varphi }_{1}}){{\varepsilon }_{1}}\sigma T_{{1w}}^{4} = {{\left. { - {{\lambda }_{1}}\left( {1 - {{\varphi }_{1}}} \right)\left( {\frac{{\partial {{T}_{1}}}}{{\partial n}}} \right)} \right|}_{w}},$(15)
$\begin{gathered} {{Q}_{\Sigma }} = {{\left. { - {{\lambda }_{2}}\left( {\frac{{\partial {{T}_{2}}}}{{\partial n}}} \right)} \right|}_{w}},\,\,\,\,{{Q}_{\Sigma }} = {{Q}_{w}},\,\,\,\,t < {{t}_{{2i - 1}}}, \\ t > {{t}_{{2i}}},\,\,\,\,i = 1{\kern 1pt} --{\kern 1pt} 3,\,\,\,\,{{Q}_{\Sigma }} = {{Q}_{w}} + W{{q}_{r}},\,\,\,\,{{t}_{{2i - 1}}} \leqslant t \leqslant {{t}_{{2i}}}, \\ \end{gathered} $(16)
$\begin{gathered} {{Q}_{w}} = {{q}_{{2w}}} - \left( {{{h}_{w}} - {{h}_{c}}} \right)\sum\limits_{i = 2}^3 {{{{\left( {\rho v} \right)}}_{{iw}}} - {{z}_{1}}{{{\left( {\rho v} \right)}}_{{1w}}}\left( {h_{w}^{s} - {{h}_{c}}} \right) - } \\ - \,\,{{\left( {\rho v} \right)}_{{1w}}}\left( {{{h}_{w}} - {{h}_{g}}} \right) - {{\varphi }_{2}}{{\varepsilon }_{2}}\sigma T_{{2w}}^{4}, \\ \end{gathered} $(17)
$\begin{gathered} {{q}_{{1w}}} = {{\alpha }_{1}}({{h}_{{e0}}} - {{H}_{w}}),\,\,\,\,{{q}_{{2w}}} = {{\alpha }_{2}}({{h}_{{e0}}} - {{h}_{w}}), \\ h_{w}^{s} = {{c}_{{p2}}}T_{{2w}}^{s},\,\,\,\,{{h}_{g}} = \int\limits_0^{{{T}_{2}}} {c_{{pg}}^{{(2)}}d{{T}_{2}}} ,\,\,\,\,{{H}_{w}} = {{T}_{{1w}}}{{b}_{1}} + {{{{b}_{2}}T_{{1w}}^{2}} \mathord{\left/ {\vphantom {{{{b}_{2}}T_{{1w}}^{2}} 2}} \right. \kern-0em} 2}. \\ \end{gathered} $На внутренней поверхности полусферы DE и конической части тела DC выполняются соотношения [14]
(18)
${{\left. {{{\lambda }_{1}}\left( {1 - {{\varphi }_{1}}} \right)\frac{{\partial {{T}_{1}}}}{{\partial n}}} \right|}_{{n = {{L}_{0}}}}} = \delta \left( {{{T}_{{1,{{L}_{0}}}}} - {{T}_{0}}} \right),\,\,\,\,0 \leqslant s < {{s}_{A}},$(19)
${{\left. {{{\rho }_{c}}} \right|}_{{n = l}}} = {{\rho }_{{c0}}},\,\,\,\,{{\left. {{{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial n}}} \right|}_{{n = l}}} = 0,\,\,\,\,{{s}_{A}} \leqslant s \leqslant {{s}_{k}}.$На кольце сопряжения сфера–конус AD при $s = {{s}_{A}}$ и на линии EF при $n = {{n}_{*}}$ используются условия идеального контакта
(20)
$\begin{gathered} {{\left. {\frac{{{{\lambda }_{1}}\left( {1 - {{\varphi }_{1}}} \right)}}{{{{F}_{1}}}}\frac{{\partial {{T}_{1}}}}{{\partial s}}} \right|}_{{s = {{s}_{A}} - 0}}} = {{\left. {{{\lambda }_{i}}\frac{{\partial {{T}_{i}}}}{{\partial s}}} \right|}_{{s = {{s}_{A}} + 0}}}, \\ {{\left. {{{T}_{1}}} \right|}_{{s = {{s}_{A}} - 0}}} = {{\left. {{{T}_{i}}} \right|}_{{s = {{s}_{A}} + 0}}},\,\,\,\,i = 2,3, \\ \end{gathered} $(21)
${{\left. {{{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial n}}} \right|}_{{n = n* - 0}}} = {{\left. {{{\lambda }_{3}}\frac{{\partial {{T}_{3}}}}{{\partial n}}} \right|}_{{n = n* + 0}}},\,\,\,\,{{\left. {{{T}_{2}}} \right|}_{{n = n* - 0}}} = {{\left. {{{T}_{3}}} \right|}_{{n = n* + 0}}},$(22)
${{\left. {\frac{{\partial {{T}_{i}}}}{{\partial s}}} \right|}_{{s = {{s}_{k}}}}} = 0,\,\,\,\,i = 2,3.$На внешней и внутренней поверхностях области сферического затупления имеет место равенство давлений в порах и во внешней среде
(23)
${{\left. {{{P}_{w}}} \right|}_{{n = 0}}} = {{P}_{e}}(s,\eta ),\,\,\,{{\left. P \right|}_{{n = {{L}_{0}}}}} = {{P}_{{{{L}_{0}}}}}.$При отсутствии плоскости симметрии течения имеют место условия периодичности
(24)
${{T}_{i}}(t,n,s,\eta ) = {{T}_{i}}(t,n,s,\eta + 2\pi ),\,\,\,\,i = 1{\kern 1pt} --{\kern 1pt} 3,$Здесь и ниже A и B − вязкостный и инерционный коэффициенты в нелинейном законе Дарси (8); ${{r}_{{1w}}},{{r}_{i}},i = 1,2,{{F}_{1}}$ − коэффициенты Ламе; $\left( {\rho v} \right)_{w}^{{(1)}}$ − расход газа-охладителя с поверхности сферического затупления; G − массовый расход газообразных продуктов разложения углепластика; $\left( {\rho v} \right)_{w}^{{(2)}}$ − массовый унос с углеродной поверхности конической части тела без учета диспергирования; ρ − плотность; ${{\rho }_{c}}\psi $ − массовая скорость перемещения поверхности разрушения; ${{{{Q}_{c}}d{{\rho }_{c}}} \mathord{\left/ {\vphantom {{{{Q}_{c}}d{{\rho }_{c}}} {dt}}} \right. \kern-0em} {dt}}$ − тепло, поглощенное в результате реакции пиролиза углепластика; ${{\varphi }_{1}}$ − пористость сферического затупления; M − молекулярная масса; V − скорость; ${{\varphi }_{2}}$ − доля каркаса конической части тела; ${{M}_{\infty }}$ − число Маха; ${{H}_{\infty }}$ − высота полета тела; ${{L}_{0}}$ − начальная толщина оболочки; θ − угол конусности; β − угол атаки; $n$ − нормаль к поверхности направлена вглубь оболочки; ψ − линейная скорость перемещения поверхности разрушения; $x(t)$ − граница раздела газообразной и конденсированной фазы (глубина выгорания); ${{E}_{i}},{{k}_{i}},$ i =1–4 − энергия активации и предэкспонент i‑й гетерогенной реакции оболочки конической части тела; ${{k}_{c}},$ ${{E}_{c}}$ и ${{Q}_{c}}$ − предэкспонент, энергия активации и тепловой эффект реакции пиролиза.
Индексы e и e0 соответствуют величинам на внешней границе пограничного слоя и на внешней границе в точке торможения; нижний индекс 1 − характеристикам сферы; 2 − конусу из углепластика или графита В-1 без подложки; 2, 3 − величинам в области 2, 3 (графиту и асбестоцементу), g − газовой фазе на сферической и конической части тела, ∞ − величинам невозмущенного газового потока; lam, tur, 0 − характеристикам ламинарного, турбулентного переноса и начальным условиям; L − внутренней оболочке сферической части тела; $k$ − периферийному участку оболочки; верхние индексы 1, 2 − характеристикам газовой фазы на сфере и конусе в теле, черта сверху − безразмерный параметр, z − время окончания теплового воздействия, ef − эффективной величине, с − углепластик, “звездочка” − характерная величина, m − максимальная величина.
Балансовые соотношения для массовых концентраций компонент (${{c}_{{iw}}}$) запишем, используя закон Фика для диффузионных потоков и аналогию процессов тепло- и массообмена [11, 12]:
При задании теплового потока из газовой фазы ${{q}_{w}}$ воспользуемся формулами работы [20] для пространственного случая при ламинарном и турбулентном режимах течения в пограничном слое. Для ослабления теплового потока при вдуве газа-охладителя, совпадающего по составу с набегающим воздушным потоком, будем использовать формулы из [11]. При этом на пористой сферической части в системе координат, связанной с точкой торможения, имеем для ламинарного режима течения в пограничном слое [11, 14, 20]
(25)
$\begin{gathered} {{q}_{{1w}}} = {{\alpha }_{1}}({{h}_{{e0}}} - {{H}_{w}}),\,\,\,\,{{\alpha }_{{lam}}} = 1.05V_{\infty }^{{1.08}}{{({{{{\rho }_{\infty }}} \mathord{\left/ {\vphantom {{{{\rho }_{\infty }}} {{{R}_{N}}}}} \right. \kern-0em} {{{R}_{N}}}})}^{{0.5}}} \times \\ \times \,\,[0.55 + 0.45{\text{cos}}(2\tilde {s})], \\ {{\alpha }_{1}} = {{\alpha }_{{lam}}}\exp [ - 0.6{{(\rho v)_{w}^{{(1)}}} \mathord{\left/ {\vphantom {{(\rho v)_{w}^{{(1)}}} {{{\alpha }_{{lam}}}}}} \right. \kern-0em} {{{\alpha }_{{lam}}}}}], \\ \tilde {s} = \arccos (\cos \bar {s}\cos \beta + \sin \bar {s}\sin \beta \cos \eta ), \\ {{h}_{{e0}}} = {{V_{\infty }^{2}} \mathord{\left/ {\vphantom {{V_{\infty }^{2}} 2}} \right. \kern-0em} 2} + {{h}_{\infty }},\,\,\,\,{{0}_{1}} \leqslant \tilde {s} \leqslant \tilde {s}{\text{*}}{\text{.}} \\ \end{gathered} $Для турбулентного режима течения в пограничном слое [14, 20] следует
(26)
$\begin{gathered} {{q}_{{1w}}} = {{\alpha }_{1}}({{h}_{{e0}}} - {{H}_{w}}),\,\,\,\,{{\alpha }_{{{\text{tur}}}}} = \frac{{16.4V_{\infty }^{{1.25}}\rho _{\infty }^{{0.8}}}}{{R_{N}^{{0.2}}{{{(1 + {{{{H}_{w}}} \mathord{\left/ {\vphantom {{{{H}_{w}}} {{{h}_{{e0}}}}}} \right. \kern-0em} {{{h}_{{e0}}}}})}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}} \times \\ \times \,\,(3.75{\text{sin}}\tilde {s} - 3.5{{\sin }^{2}}\tilde {s}), \\ {{\alpha }_{1}} = {{\alpha }_{{tur}}}\exp [ - 0.37{{(\rho v)_{w}^{{(1)}}} \mathord{\left/ {\vphantom {{(\rho v)_{w}^{{(1)}}} {{{\alpha }_{{tur}}}}}} \right. \kern-0em} {{{\alpha }_{{tur}}}}}],\,\,\,\,\tilde {s}* < \tilde {s} < {{{\tilde {s}}}_{A}}, \\ \end{gathered} $Чтобы оценить влияние вдува на тепловой поток в завесной зоне, воспользуемся результатами [21] и формулами, приведенными в [22], полученными на основе обработки результатов точных численных расчетов пространственного турбулентного пограничного слоя и вязкого ударного слоя
(27)
$\begin{gathered} {{q}_{{2w}}} = {{\alpha }_{2}}(1 - {{k}_{1}}{{b}^{{{{k}_{2}}}}})({{h}_{{e0}}} - {{h}_{w}}), \\ {{\alpha }_{2}} = {{\alpha }_{w}}\exp [ - 0.37{{(\rho v)_{w}^{{(2)}}} \mathord{\left/ {\vphantom {{(\rho v)_{w}^{{(2)}}} {{{\alpha }_{w}}}}} \right. \kern-0em} {{{\alpha }_{w}}}}], \\ {{\alpha }_{w}} = \frac{{16.4V_{\infty }^{{1.25}}\rho _{\infty }^{{0.8}}}}{{R_{N}^{{0.2}}{{{(1 + {{{{h}_{w}}} \mathord{\left/ {\vphantom {{{{h}_{w}}} {{{h}_{{e0}}}}}} \right. \kern-0em} {{{h}_{{e0}}}}})}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}\frac{{2.2\bar {p}({{{{u}_{e}}} \mathord{\left/ {\vphantom {{{{u}_{e}}} {{{v}_{m}}}}} \right. \kern-0em} {{{v}_{m}}}})}}{{{{\varsigma }^{{0.4}}}\bar {r}_{2}^{{0.2}}}}, \\ {{{\bar {r}}}_{2}} = \cos \theta + (\bar {s} - {{{\bar {s}}}_{A}})\sin \theta ,\,\,\,\,\bar {p} = {{{{P}_{e}}} \mathord{\left/ {\vphantom {{{{P}_{e}}} {{{P}_{{e0}}}}}} \right. \kern-0em} {{{P}_{{e0}}}}}, \\ {{{{u}_{e}}} \mathord{\left/ {\vphantom {{{{u}_{e}}} {{{v}_{m}}}}} \right. \kern-0em} {{{v}_{m}}}} = {{(1 - {{{\bar {p}}}^{\chi }})}^{{0.5}}},\,\,\,\,\varsigma = ({{\gamma }_{{{\text{ef}}}}} - 1 + {{{2 \mathord{\left/ {\vphantom {2 {M_{\infty }^{2}}}} \right. \kern-0em} {M_{\infty }^{2}}})} \mathord{\left/ {\vphantom {{{2 \mathord{\left/ {\vphantom {2 {M_{\infty }^{2}}}} \right. \kern-0em} {M_{\infty }^{2}}})} {({{\gamma }_{{{\text{ef}}}}}}}} \right. \kern-0em} {({{\gamma }_{{{\text{ef}}}}}}} + 1), \\ {{{\tilde {s}}}_{A}} \leqslant \tilde {s} \leqslant {{{\tilde {s}}}_{B}},\,\,\,\,\chi = {{({{\gamma }_{{{\text{ef}}}}} - 1)} \mathord{\left/ {\vphantom {{({{\gamma }_{{{\text{ef}}}}} - 1)} {{{\gamma }_{{{\text{ef}}}}}}}} \right. \kern-0em} {{{\gamma }_{{{\text{ef}}}}}}}. \\ \end{gathered} $При законе расхода газа-охладителя
имеем(28)
$\begin{gathered} b = \frac{{2{{{(\rho v)}}_{w}}({{0}_{1}})\{ 1 - \cos {{{\tilde {s}}}_{A}} + a[{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3} - \cos {{{\tilde {s}}}_{A}} + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}{{{\cos }}^{3}}{{{\tilde {s}}}_{A}}]\} }}{{{{\alpha }_{w}}(\bar {s} - {{{\bar {s}}}_{A}})[2\cos \theta + (\bar {s} - {{{\bar {s}}}_{A}})\sin \theta ]}}, \\ \cos {{{\tilde {s}}}_{A}} = \cos {{{\bar {s}}}_{A}}\cos \beta + \sin {{{\bar {s}}}_{A}}\sin \beta \cos \eta , \\ {{{\bar {s}}}_{A}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \theta . \\ \end{gathered} $МЕТОДИКА РАСЧЕТА, ТЕСТОВЫЕ ПРОВЕРКИ И ИСХОДНЫЕ ДАННЫЕ
Краевая задача (6)–(8), (10)–(15), (18)–(24) решена численно локально-одномерным методом расщепления [23]. Использована неявная, абсолютно устойчивая, монотонная разностная схема с суммарной погрешностью аппроксимации О(τ + $H_{n}^{2} + H_{s}^{2}$ + $H_{\eta }^{2}$), где ${{H}_{n}},$ ${{H}_{s}},$ ${{H}_{\eta }}$ − шаги по пространству вдоль координат n, s, $\eta $ соответственно; τ − шаг по времени. Для проверки программы численного расчета в пористом теле использовалась последовательность сгущающихся сеток по пространству ${{h}_{1}}$ = ${{h}_{n}}$ = 5 × 10–4 м, ${{h}_{2}} = {{h}_{{s1}}}$ = = 8.75 × 10–2 (на сфере), ${{h}_{3}} = {{h}_{{s2}}}$ = 8.55 × 10–2 (на конусе), ${{h}_{4}} = {{h}_{\eta }}$ = 0.087 и брались ${{H}_{{1,i}}} = 2 \times {{h}_{i}},$ ${{H}_{{2,i}}} = {{h}_{i}},$ ${{H}_{{3,i}}} = {{{{h}_{i}}} \mathord{\left/ {\vphantom {{{{h}_{i}}} 2}} \right. \kern-0em} 2},$ ${{H}_{{4,i}}} = {{{{h}_{i}}} \mathord{\left/ {\vphantom {{{{h}_{i}}} 4}} \right. \kern-0em} 4},$ i = 1–4. Температура каркаса фиксировалась по глубине тела в различные моменты времени. Во всех вариантах задача решалась с переменным шагом по времени, который выбирался из условия заданной точности, одинаковой для всех шагов по пространству. Различие относительной погрешности по температуре падало и к моменту времени t = ${{t}_{z}}$ составляло ${{\Delta }_{1}}$ = 9.3%, ${{\Delta }_{2}}$ = 5.2%, ${{\Delta }_{3}}$ = 2.4%. Приведенные ниже результаты расчета получены для шагов по пространству ${{H}_{{3,i}}} = {{{{h}_{i}}} \mathord{\left/ {\vphantom {{{{h}_{i}}} 2}} \right. \kern-0em} 2},$ i = 1–4.
Квазистационарное уравнение неразрывности (6) ${{(\rho v)_{w}^{{(1)}}{{r}_{{1w}}}} \mathord{\left/ {\vphantom {{(\rho v)_{w}^{{(1)}}{{r}_{{1w}}}} {({{F}_{1}}{{r}_{1}})}}} \right. \kern-0em} {({{F}_{1}}{{r}_{1}})}}$ = $ - {{\rho }^{{(1)}}}{{\varphi }_{1}}{{v}^{{(1)}}}$ (знак минус обусловлен тем, что нормальная координата n направлена вглубь тела (см. рис. 1), а охладитель течет в противоположном направлении) совместно с первым выражением (9), нелинейным законом Дарси (8) и граничными условиями (23) можно проинтегрировать и найти расход газа в области 1 [14]:
(29)
$\begin{gathered} (\rho v)_{w}^{{(1)}}(s,\eta ,t) = \\ = \frac{{{{{\left[ {2B(P_{{{{L}_{0}}}}^{2} - P_{w}^{2}){{{{\varphi }_{1}}M{{D}_{{{{L}_{0}}}}}} \mathord{\left/ {\vphantom {{{{\varphi }_{1}}M{{D}_{{{{L}_{0}}}}}} R}} \right. \kern-0em} R} + E_{{{{L}_{0}}}}^{2}} \right]}}^{{0.5}}} - {{E}_{{{{L}_{0}}}}}}}{{2B{{D}_{{{{L}_{0}}}}}}}, \\ \end{gathered} $Давление на внутренней “холодной” поверхности сферической оболочки ($n = {{L}_{0}}$) задано в виде
где k − некоторая постоянная. Это обеспечивало необходимый расход охладителя (в частности, не была достигнута температура плавления каркаса из пористого металла [11]) на участке теплового воздействия от t = 0 до t = ${{t}_{z}}$ (${{t}_{z}}$ = 12 с отвечает времени окончания теплового воздействия).Рассматривается вариант транспирационного охлаждения носовой части, обеспечивающий высокую интенсивность вдува, при которой тепловой поток в ламинарной области становится пренебрежимо малым (уменьшается почти на три порядка).
Расчеты обтекания конуса, затупленного по сфере, с углом полураствора $\theta = {{10}^{^\circ }}$ потоком химически равновесного воздуха под углом атаки $\beta = {{5}^{^\circ }}$ проводились для следующих условий, которые соответствуют параметрам: ${{V}_{\infty }} = 5.5$ км/с, ${{H}_{\infty }}$ = 2.4 × 104 м, ${{T}_{{e0}}}$ = 6739 К, ${{P}_{{e0}}}$ = 13.59 × 105 H/м2, ${{h}_{{e0}}}$ = 1.5418 × 107 Дж/кг, ${{R}_{N}}$ = 0.2 м, ${{L}_{0}}$ = 0.01 м. Кинетические константы (4) реакций (3) брались из [12, 24], энтальпия графита ${{h}_{c}}$ рассчитывалась по формуле [25], а энтальпии ${{h}_{i}},\,\,i = \overline {1,9} $ и теплоемкости компонент химических реакций – из [26].
Теплофизические характеристики пористого затупления соответствовали пористой стали: ${{\varepsilon }_{1}} = 0.8,$ ${{\lambda }_{1}}$ = 2.92 + 4.5 × 10–3${{T}_{1}}$ Вт/(м К), ${{\rho }_{1}}{{c}_{{p1}}}$ = = (1252 + $0.544{{T}_{1}}$) × 103 Дж/(K м3), A = 2.3 × 1011 1/м2, B = 5.7 × 105 1/м [27]. Теплофизические характеристики конической части тела отвечают углепластику [14] или графиту В-1 [28] и асбестоцементу [29]:
Приводимые ниже результаты получены при ${{T}_{0}}$ = 293 К, ${{\rho }_{\infty }} = 4.75 \times {{10}^{{ - 3}}}$ (с2 кгс)/м4, δ = = 100 Вт/(м2 K), ${{q}_{*}}$ = ${{10}^{9}}$ Вт/м2, ${{\rho }_{3}} = \,\,1800$ кг/м3, ${{с }_{{p3}}} = \,\,837$ Дж/(кг К), ${{\lambda }_{3}} = \,\,0.349$ Вт/(м К), М = = 29 кг/кмоль, ${{\varepsilon }_{2}} = 0.9,$ ξ = 1 (м2 с)/кг. В табл. 1 приведены безразмерные параметры, используемые для решения краевой задачи, а в табл. 2 плотность углепластика и термокинетические постоянные реакции пиролиза.
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РЕШЕНИЯ
На рис. 2а показаны зависимости от времени конвективного теплового потока ${{q}_{{2w}}}$ из газовой фазы (1) и энтальпии поверхности ${{h}_{w}}$ (2), а на рис. 2б – профили температуры поверхности (1) и суммарного теплового потока ${{Q}_{\Sigma }}$ (2) в конденсированную фазу в фиксированном сечении (${{\bar {s}}_{1}} = 3,\,\,{{\eta }_{1}} = 180^\circ $) затупленного конуса в завесной зоне. Сплошные кривые соответствуют характеристикам углепластика, штриховые – параметрам графита В-1 без подложки. Зависимости для массовой концентрации компонентов (сплошные кривые) и массового уноса ${{(\rho v)}_{\Sigma }}$ (штриховые кривые) с поверхности углепластика приведены на рис. 3а. Аналогичные зависимости для концентраций компонентов и массового уноса с поверхности графита даны на рис. 3б. Видно, что при воздействии высокоэнтальпийного потока увеличивается температура поверхности ${{T}_{{2w}}},$ появляется окись углерода ${{c}_{{5w}}}$ [13] и массовый унос ${{(\rho v)}_{\Sigma }}.$ После включения первого импульса излучения при $t > {{t}_{1}}$ температура поверхности возрастает (рис. 2б), начинает увеличиваться концентрация циана ${{c}_{{7w}}}$ (см. рис. 3) и появляется сублимационная составляющая ${{c}_{{7w}}}$ (см. рис. 3). В то же время величина конвективного потока ${{q}_{{2w}}}$ уменьшается (см. кривую 1 на рис. 2а) в силу возрастания температуры (сплошная кривая на рис. 2б) и увеличения энтальпии ${{h}_{w}}$ (кривая 2 на рис. 2а) из-за роста компонента ${{c}_{{9w}}}$ (см. рис. 3а).
Рис. 2.
Зависимость конвективного теплового потока из газовой фазы (1) и энтальпии поверхности (2) в фиксированном сечении конической части тела от времени (а) и зависимость температуры поверхности (1) и суммарного теплового потока в конденсированную фазу (2) в фиксированном сечении от времени (б).
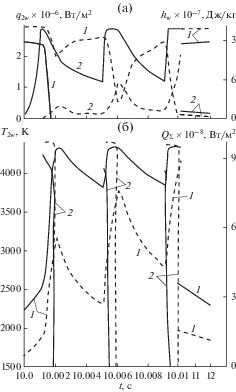
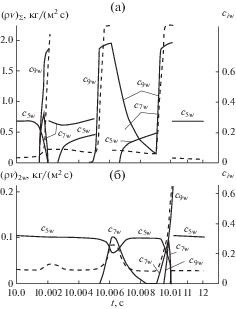
Рис. 3.
Зависимость массовой концентрации компонентов (сплошные кривые) и суммарного массового уноса (штриховая) в фиксированном сечении от времени: (а) – характеристики углепластика, (б) – параметры графита В-1 без подложки.
Кроме того, здесь имеет место ослабление ${{q}_{{2w}}},$ согласно (27), в результате вдува в пограничный слой продуктов термохимического разрушения композиционного материала конической части тела.
Отметим, что лучистый поток ${{q}_{r}}$ (1) и суммарный тепловой поток ${{Q}_{\Sigma }}$ (15) в конденсированную фазу (рис. 2б) также уменьшаются. Затем со временем величина ${{(\rho \text{v})}_{\Sigma }}$ стабилизируется для углепластика из-за экранирующего влияния прококсованного слоя [13, 14], толщина которого по мере прогрева углепластика увеличивается [13]. В дальнейшем после прекращения лучистого нагрева ($t > {{t}_{2}}$) величина ${{T}_{{2w}}}$ уменьшается в результате обтекания тела относительно холодным (по сравнению с температурой поверхности) конвективным потоком газовой фазы (рис. 2а).
После включения следующих пиков лазера ${{t}_{i}},\,\,i = 2,\,3$ картина в распределении профилей указанных характеристик теплообмена повторяется. Однако уже в предварительно прогретом теле температура поверхности на участке действия второго импульса лазерного излучения может быть выше, чем в первом пике. Поэтому величина ${{(\rho v)}_{\Sigma }}$ при втором и третьем импульсном нагружении на участке лучистого прогрева определяется составляющей уноса за счет сублимации углеродной поверхности тела (см. сплошные кривые ${{c}_{{9w}}}$ на рис. 3а и 3б при ${{t}_{3}} \leqslant t \leqslant {{t}_{6}}$). Последнее приводит к ослаблению импульса излучения, что связано с экранировкой лучистой составляющей как продуктами гетерогенных химических реакций, так и частицами дисперсной фазы. В результате ${{Q}_{\Sigma }}$ уменьшается из-за отбора тепла при переизлучении и сублимации поверхности углепластика.
При отсутствии радиационного нагрева ($t > {{t}_{6}}$) прогрев материала на конической части ${{\Delta }_{*}}$ = = $({{\bar {s}}_{1}} \leqslant \bar {s} \leqslant {{\bar {s}}_{2}},{{\eta }_{1}} \leqslant \eta \leqslant {{\eta }_{2}})$ тела осуществляется суммарным тепловым потоком ${{Q}_{w}}$ из (16), величина которого на два порядка меньше ${{Q}_{\Sigma }}$ для $t \leqslant {{t}_{6}}$ и поэтому не приведена на рис. 2б при $t > {{t}_{6}}.$ В результате падения ${{Q}_{w}}$ прогрев углепластика замедляется, а температура поверхности уменьшается до момента окончания теплового воздействия. Как и следовало ожидать, величина ${{(\rho v)}_{\Sigma }}$ в этот период определяется преимущественно составляющими ${{(\rho v)}_{{1w}}},$ ${{(\rho v)}_{{2w}}}$ из (5), а суммарный тепловой поток ${{Q}_{w}}$ − составляющей за счет диспергирования и пиролиза композиционного материала.
На рис. 4–6 приведены зависимости от продольной координаты $\bar {s}$ температуры поверхности ${{T}_{{1w}}},{{T}_{{2w}}},$ массового уноса ${{(\rho v)}_{\Sigma }}$ с конической части тела из углепластика (сплошные кривые), графита В-1 (штриховые кривые), расхода со сферического затупления $(\rho v)_{w}^{{(1)}}$ (29) (кривая 5) и конвективного теплового потока ${{q}_{{1w}}},\,{{q}_{{2w}}}$ (26)–(28) в плоскости симметрии течения (η = 0°–180°) на наветренной и подветренной сторонах. Кривые 1−4 на рис. 4–8 отвечают моментам времени t: 1 – 5, 2 – 10.002, 3 – 10.01, 4 – 12 с. На рис. 7, 8 даны распределения по окружной координате η для ${{\bar {s}}_{1}}$ = 3 температуры поверхности ${{T}_{{2w}}}$ и суммарного массового уноса ${{(\rho v)}_{\Sigma }}$ с конической части тела из углепластика (сплошные кривые) и графита (штриховые кривые). Из рис. 4 и 7 видно, что наибольшая температура поверхности тела реализуется на подветренной стороне конуса ${{\Delta }_{*}}$ в области пятна попадания лазерного излучения. В этой же области ${{\Delta }_{*}}$ на подветренной стороне конуса формируется наибольший массовый унос с поверхности (см. рис. 5 и 8), который может экранировать (ослаблять) лучистый поток тепла согласно формуле (1).
Рис. 4.
Распределение температуры поверхности в плоскости симметрии течения (η = 0°–108°) на наветренной и подветренной сторонах тела от продольной координаты.
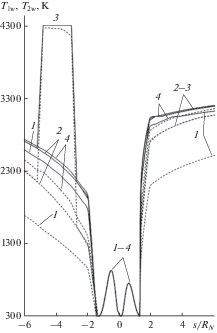
Рис. 5.
Распределение массового уноса на поверхности сферически затупленного конуса в плоскости симметрии течения (η = 0°–180°) на наветренной и подветренной сторонах тела от продольной координаты.

Рис. 6.
Распределение конвективного теплового потока в плоскости η = 0°–180° от продольной координаты.

Рис. 7.
Зависимость температуры поверхности в сечении ${{\bar {s}}_{1}}$ = 3 на конусе от окружной координаты.

Рис. 8.
Зависимость суммарного массового уноса с поверхности тела для ${{\bar {s}}_{1}}$ = 3 от окружной координаты.

Анализ характеристик тепло- и массообмена пористой сферической оболочки из стали, приведенных на рис. 4–6, показывает, что заданный вдув газа-охладителя (см. на рис. 5 кривую 5) не дает превышения критической температуры затупления ${{T}_{*}}$ = 1600 К [11] до $t = {{t}_{z}}$ за счет ослабления теплового потока согласно (25), (26). К тому же здесь имеет место поглощение тепла при фильтрации газа в порах проницаемого сферического затупления. При этом максимальная температура поверхности на пористой сфере отвечает максимальному тепловому потоку из газовой фазы.
Для практики представляет интерес величина температуры внутренней стенки сферического затупления, которая для проницаемой стали составила ${{T}_{{1{{L}_{0}}}}}$ = 293 К при ${{L}_{0}}$ = 0.01 м в момент $t = {{t}_{z}}$. На конической части тела в сечении ${{\bar {s}}_{1}} = 3,\eta = 180^\circ $ величина температуры внутренней стенки для углепластика не превысила ${{T}_{{2l}}}$ = 293 К, а для графита без подложки при ${{L}_{0}}$ = 0.01 м составила ${{T}_{{2l}}}$ = = 1730 К в момент $t = {{t}_{z}}$. Для графита с подложкой из асбестоцемента (толщиной 0.0025 м) при ${{L}_{0}}$ = = 0.01 м получаем ${{T}_{{2l}}}$ = 896 К, а при толщине подложки 0.005 м − ${{T}_{{2l}}}$ = 352 К.
Последний результат по графиту В-1 (в рассмотренном температурном диапазоне теплопроводность графита В-1 в 25–30 раз превышает теплопроводность углепластика, удельные теплоемкости у них различаются в полтора раза [14, 28]) показывает, что для снижения внутренней температуры стенки необходимо использовать на конической части тела составной композиционный материал.
Уменьшение или увеличение параметра ξ в два раза в формуле для ослабления лучистой составляющей (1) при ${{z}_{1}} = 1,$ а также увеличение в два раза ${{z}_{1}}$ в последней формуле равенств (5) при ξ = 1 не приводит к существенному замедлению процесса прогрева углепластика или графита В-1 и к качественному изменению результатов решения задачи. В то же время при ${{q}_{r}} = q{\text{*}}$ (ξ = 0, ${{z}_{1}} = 1$) температура поверхности углепластика во втором ($t \geqslant {{t}_{4}}$) и третьем пике лазера достигает максимальной температуры ${{T}_{{2w}}}$ = 4697−4703 К. Это приводит к более интенсивному прогреву композиционного материала и значительному массовому уносу материала с поверхности углепластика (более чем в 22 раза). Очевидно, что столь высокое значение характеристик тепломассообмена не будет реализовано на практике из-за механического уноса углепластика и ослабления падающего лучистого потока продуктами термохимического разрушения.
Отсутствие тепла за счет конвективного нагрева в суммарном тепловом потоке на участке действия второго и третьего пика лазера (${{t}_{3}} \leqslant t \leqslant {{t}_{6}}$) не приводит к изменению характеристик тепломассообмена, приведенных на рис. 2−8. Дело в том, что в период пиков излучения (W = 1) ${{q}_{r}}$ более чем на порядок превосходит ${{q}_{{2w}}},$ а при W = 0 величина ${{Q}_{\Sigma }}$ из выражений (16) определяется в основном уносом энергии за счет термохимического разрушения углепластика.
Следует отметить, что формулы для плотностей конвективного теплового и диффузионного потоков ${{q}_{{2w}}}$ и ${{J}_{{iw}}}$ теряют физический смысл в период сильного термохимического разрушения материала, так как они получены с использованием понятий и методов теории пограничного слоя, который при интенсивном вдуве продуктов разрушения оттесняется. Однако ограниченность формулы для ${{q}_{{2w}}}$ практически не отражается на численных результатах, поскольку величина суммарного теплового потока ${{Q}_{\Sigma }}$ в период действия излучения в основном определяется лучистой составляющей. Этот вывод согласуется с данными математического эксперимента при ${{q}_{{2w}}}$ = 0, приведенного выше.
ЗАКЛЮЧЕНИЕ
Разработана математическая модель термохимического разрушения затупленного по сфере конуса при действии лазерного излучения умеренной интенсивности на углеграфитовые теплозащитные материалы. Получено, что в экранировке лазерного излучения продуктами термохимического разрушения углепластика определяющую роль на начальном этапе взаимодействия излучения с телом играют газообразные продукты пиролиза и частицы конденсированной фазы. При повторном импульсном нагружении экранировка для ${{T}_{{2w}}}$ > 3800 К может осуществляться преимущественно парами углеродного материала и частицами твердой фазы.
Список литературы
Виленская Г.Г., Немчинов И.В. Явление вспышки поглощения излучения ОКГ и связанные с ним газодинамические эффекты // Докл. АН СССР. 1969. Т. 186. № 5. С. 1048.
Анисимов С.И., Имас Я.А., Романов Г.C., Ходыко Ю.В. Действие излучения большой мощности на металлы. М.: Наука, 1970. 212 с.
Бункин Ф.В., Кириченко Н.А., Лукьянчук Б.С. Термохимическое действие лазерного излучения // УФН. 1982. Т. 138. № 9. С. 43.
Минько Л.Я., Гончаров В.К., Лопарев А.Н. Исследование отражения лазерного излучения при его разрушающем действии на непрозрачные диэлектрики // ФХОМ. 1979. № 1. С. 31.
Лопарев А.Н., Минько Л.Я. Роль частиц в экранирующем действии собственных лазерных эрозионных плазменных факелов // ФХОМ. 1985. № 2. С. 26.
Домбровский Л.А., Юкина Э.П., Колпаков А.В., Иванов В.А. Методика расчета теплового разрушения углепластика под действием интенсивного инфракрасного излучения // ТВТ. 1993. Т. 31. № 4. С. 619.
Климков Ю.М., Майоров В.С., Хорошев М.В. Взаимодействие лазерного излучения с веществом. Учеб. пособ. M.: МИИГАиК, 2014. 108 с.
Горский В.В. Теоретические основы расчета абляционной тепловой защиты. М.: Научный мир, 2015. 688 с.
Горский В.В., Евдокимов И.М., Запривода А.В., Реш В.Г. Ослабление радиационного теплового потока парами материала при лазерной резке стеклопластика // ТВТ. 2014. Т. 52. № 1. С. 126.
Цветков В.Б., Царькова О.Г., Гарнов С.В. и др. Моделирование температурных полей в плоских мишенях при воздействии интенсивного лазерного излучения // Тр. Ин-та общ. физики РАН им. А.М. Прохорова. 2014. Т. 70. С. 83.
Полежаев Ю.В., Юревич Ф.Б. Тепловая защита. М.: Энергия, 1976. 392 с.
Гришин А.М., Фомин В.М. Сопряженные и нестационарные задачи механики реагирующих сред. Новосибирск: Наука, 1984. 318 с.
Зинченко В.И., Якимов А.С. Режимы термохимического разрушения углефенольного композиционного материала под действием теплового потока // ФГВ. 1988. Т. 24. № 2. С. 141.
Гришин А.М., Голованов А.Н., Зинченко В.И., Ефимов Е.К., Якимов А.С. Математическое и физическое моделирование тепловой защиты. Томск: Изд-во Томск. ун-та, 2011. 358 с.
Лапин Ю.В. Турбулентный пограничный слой в сверхзвуковых потоках газа. М.: Наука, 1982. 372 с.
Лунёв В.В., Магомедов К.М., Павлов В.Г. Гиперзвуковое обтекание притупленных конусов с учетом равновесных физико-химических превращений. М.: Изд.-во ВЦ АН СССР, 1968. 203 с.
Скала Дж. Сублимация графита при гиперзвуковых скоростях // РТК. 1965. Т. 3. № 9. С. 87.
Рыкалин Н.Н., Углов А.А., Зуев И.В., Кокора А.Н. Лазерная и электронно-лучевая обработка материалов. Спр. М.: Машиностроение, 1985. 496 с.
Никитин П.В., Овсянников В.М., Холодков Н.В. Разрушение композиционного материала на органической основе в высокотемпературном потоке газа // ИФЖ. 1986. Т. 50. № 3. С. 363.
Землянский Б.А., Степанов Г.И. О расчете теплообмена при пространственном обтекании тонких затупленных конусов гиперзвуковым потоком воздуха // Изв. АН СССР. МЖГ. 1981. № 5. С. 173.
Харченко В.Н. Теплообмен в гиперзвуковом турбулентном пограничном слое при вдуве охлаждающего газа через щель // ТВТ. 1972. Т. 10. № 1. С. 101.
Буреев А.В., Зинченко В.И. Расчет обтекания сферически затупленного конуса при различных режимах течения в ударном слое и вдуве газа с поверхности // ПМТФ. 1991. № 2. С. 72.
Самарский А.А. Введение в теорию разностных схем. М.: Наука, 1971. 552 с.
Toshiyuki S., Kazuhisa F., Keisuke A., Takeharu S. Experimental Study of Graphite Ablation in Nitrogen Flow // J. Thermophys. Heat Transfer. 2008. V. 22. № 3. P. 382.
Бучнев Л.М., Смыслов А.И., Дмитриев И.А. и др. Экспериментальное исследование энтальпии квазимонокристалла графита и стеклоуглерода в интервале температур 300–3800 К // ТВТ. 1987. Т. 25. № 6. С. 1120.
Гурвич Л.В., Хачкурузова Г.А., Вейц И.В., Медведева В.А. Термодинамические свойства индивидуальных веществ / Под ред. Глушко В.П. М.: Изд-во АН СССР, 1962. Т. 2. 916 с.
Алифанов О.М., Трянин А.П., Ложкин А.Л. Экспериментальное исследование метода определения коэффициента внутреннего теплообмена из решения обратной задачи // ИФЖ. 1987. Т. 52. № 3. С. 460.
Соседов В.П. Свойства конструкционных материалов на основе углерода. Спр. М.: Металлургия, 1975. 335 с.
Соколов П.Н. Технология производства асбестоцементных изделий. М.: Промстройиздат, 1951. 352 с.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур



