1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 57, № 1, 2019

Теплофизика высоких температур, 2019, T. 57, № 1, стр. 121-126

Развитие простой модели следа от пары цилиндров: двухчастотная мода течения

Г. В. Гембаржевский 1, *, А. К. Леднев 1, К. Ю. Осипенко 1

1 Институт проблем механики им. А.Ю. Ишлинского РАН,
Москва, Россия

* E-mail: gvgemb@ipmnet.ru

Поступила в редакцию 11.09.2017
После доработки 05.06.2018
Принята к публикации 11.09.2017

Полный текст (PDF)

Аннотация

Для интерпретации обнаруженного ранее эффекта перестройки гидродинамического режима ближнего следа от двух цилиндров под действием тлеющего разряда развивается простая одномерная модель такого перемежающегося течения. При не слишком близком расположении цилиндров след предполагается сформированным из двух дорожек Кармана. Модель отличается учетом нелинейного взаимодействия дорожек Кармана в области их формирования в окрестности цилиндров; при этом допущение о слабости взаимодействия не используется. Обнаружено, что в рамках модели, помимо одночастотных глобальных мод, в некоторой области параметров модели существует двухчастотная асимметричная мода следа. В турбулентном следе она реализуется в режиме перемежаемости с симметричной модой.

ВВЕДЕНИЕ

Ближний след за плохообтекаемыми телами с его выраженной крупномасштабной когерентной вихревой структурой представляет теоретический интерес как классический пример развивающегося турбулентного течения. В то же время течения подобного типа широко распространены в различных технических устройствах, где требуется интенсификация процессов переноса, например в быстропроточных лазерах, в камерах сгорания. В ходе технического прогресса внимание исследователей смещается от аэродинамики нейтральных газов в сторону изучения плазменных течений [1]. Ввиду присущей динамике плазмы неустойчивости такая эволюция сопровождается существенным усложнением решаемых принципиальных и прикладных задач. С другой стороны, одновременно появляются дополнительные возможности по целенаправленной перестройке режимов течения под действием прилагаемых электрических и магнитных полей. В частности, широко исследуется возможность перестройки различного рода нейтральных газовых течений с помощью актюаторов на коронном, диэлектрическом барьерном, дуговом разрядах (например, [2–4]). В таком контексте естественной выглядит задача модификации плазменного течения с помощью разрядного актюатора того или иного типа. Течение низкотемпературной неравновесной плазмы характерно для мощных быстропроточных электроразрядных лазеров. Определяющие характеристики – предельная мощность и качество излучения таких лазеров – существенно зависят от гидродинамических характеристик потока рабочей среды в резонаторной камере (она же – разрядная камера лазера). Соответственно, требуется оптимизация структуры неравновесного турбулентного потока плазмы в условиях тлеющего разряда в разрядной камере [5, 6], т.е. в ближнем следе соответствующего (механического) турбулизатора потока, расположенного на входе в камеру, посредством подбора его характеристик. Дальнейшую настройку – оптимизацию поля турбулентных характеристик течения – удобно проводить с помощью разрядных актюаторов.

ОСНОВНЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

Вероятно, наиболее простое средство турбулизации потока в большом объеме – это установка цилиндра или ряда параллельных цилиндров, расположенных в плоскости, перпендикулярной невозмущенному потоку. Для подобного течения с помощью специально разработанного датчика скорости плазмы тлеющего разряда и газа [7] обнаружено, что под действием разряда происходит перестройка гидродинамического режима ближнего следа от пары близко расположенных параллельных цилиндров. В эксперименте [8] диэлектрические цилиндры были установлены на входе в разрядную камеру быстропроточного СО2-лазера, вплотную за водоохлаждаемым катодом, на относительном расстоянии между осями цилиндров ${T \mathord{\left/ {\vphantom {T D}} \right. \kern-0em} D} \approx 2.2.$ Число Рейнольдса, рассчитанное по диаметру цилиндров и невозмущенной скорости втекающего газа, составило $\operatorname{Re} \sim 1000.$ Соответствующая фотография разрядной камеры установки Лантан-2, представляющая собой вид через боковое смотровое окно под 45° к направлению втекающего газа, приведена на рис. 1. В этой конфигурации было обнаружено, что в режиме несамостоятельного тлеющего разряда, с увеличением погонной плотности тока на катоде в области значений ∼1 А/м спектр пульсаций скорости азотной плазмы плавно перестраивается от распределения с единственным сравнительно узким пиком спектральной мощности к распределению с двумя пиками [8]. При этом новый пик появляется на сравнительно низкой частоте (НЧ) ~0.80 кГц, а высокочастотный (ВЧ) пик остается расположенным на прежней частоте (~1.12 кГц) нейтрально-газового течения. Более того, при плотностях тока $j \geqslant 1.5\,\,{{\text{A}} \mathord{\left/ {\vphantom {{\text{A}} {\text{м }}}} \right. \kern-0em} {\text{м }}}$ большая часть мощности квазикогерентных пульсаций скорости плазмы перераспределяется из ВЧ- в НЧ-пик.

Рис. 1.

Пара цилиндров-турбулизаторов на входе потока в разрядную камеру.

Для анализа происходящей перестройки течения весьма желательна визуализация течения. Однако в условиях установки Лантан-2 визуализация течения за вертикально расположенными цилиндрами существенно затруднена непрозрачностью верхней и нижней стенок разрядной камеры, смотровые окна есть только в боковых стенках (рис. 1). В сложившихся условиях единственный выход – это максимально использовать развернутую модель течения, по возможности простую, в анализе экспериментальных данных по осцилляциям скорости.

МАЛОМЕРНОЕ МОДЕЛИРОВАНИЕ СЛЕДА

В настоящее время развитые вихревые течения, в том числе течения при учете различных осложняющих обстоятельств (например, фазовых переходов), удается моделировать с различной степенью детализации (см. [9]). Что касается следовых течений от цилиндров, то уже достаточно давно их моделирование принято проводить не только в рамках уравнений Навье–Стокса или их обобщений, но и строить маломерные аналитические модели. Для следа уединенного цилиндра это может быть модель двумерного течения в форме классической дорожки Кармана “точечных вихрей” в идеальной жидкости. Также широко используются одномерные динамические модели дорожки, это так называемые модель типа Ландау–Стюарта (ЛС) и модель дорожки-осциллятора Ван дер Поля (ВдП). Здесь уместно отметить, что простые маломерные модели обладают рядом достоинств. С одной стороны, их использование позволяет пролить свет на физику исследуемых (зачастую достаточно сложных) явлений. С другой стороны, подобные модели могут быть весьма полезны в практических приложениях, например в вопросах многопараметрической оптимизации изделий, при построении перспективных систем автоматического регулирования течения в реальном масштабе времени.

Модель ЛС (“бифуркации Ландау–Хопфа” в терминах теории динамических систем) была сформулирована и обоснована на “физическом” уровне строгости применительно к задаче ламинарно-турбулентного перехода во внутренних гидродинамических течениях Л.Д. Ландау в 1944 г. [10]. Уравнение ЛС – это эволюционное уравнение и формулируется относительно комплексной медленно изменяющейся амплитуды ${{A}_{{(t)}}}$ осцилляций при установившемся их пространственном распределении (в данном случае применения уравнения ЛС к осцилляциям скорости в следе за цилиндром типа дорожки Кармана). Уравнение ЛС принято записывать в форме

(1)
$\frac{{\partial A}}{{\partial t}} = {{\varepsilon }_{{{\text{LS}}}}}\left[ {{{\lambda }_{{{\text{LS}}}}} - {{\mu }_{{{\text{LS}}}}}{{{\left| A \right|}}^{2}}} \right]A.$
Здесь εLS – малый действительный положительный параметр, а ${{\lambda }_{{{\text{LS}}}}}$ и ${{\mu }_{{{\text{LS}}}}}$ – комплексные параметры модели. К настоящему времени применение уравнения ЛС для моделирования ламинарного режима течения ближнего следа за цилиндром в форме классической дорожки Кармана (для чисел Рейнольдса течения в интервале 47 $ < \operatorname{Re} < 180$) получило “строгое” обоснование. Это обоснование базируется на успешности асимптотического разложения решения соответствующей граничной задачи для двумерных уравнений Навье–Стокса по малому параметру надкритичности ${{\varepsilon }_{{{\text{LS}}}}} = {{\left( {{{{\operatorname{Re} }}_{{{\text{cr}}}}}} \right)}^{{ - 1}}} - {{\left( {\operatorname{Re} } \right)}^{{ - 1}}} \ll 1,$ ${{\operatorname{Re} }_{{{\text{cr}}}}} \approx 47$ (см., например, [11]). Так, рассчитанные численно параметры модели ЛС хорошо согласуются с соответствующими экспериментально измеренными значениями.

Для маломерного моделирования ближнего следа цилиндра в форме дорожки Кармана, наряду с моделью ЛС, используется также модель осциллятора ВдП [12, 13], являющаяся простейшей, но общей моделью автогенератора произвольной природы, с “мягким” возбуждением вблизи порога генерации. В гидродинамике эту модель принято использовать при исследовании задач “аэроупругого резонанса” (vortex induced vibrations), не говоря уже о ее широком применении в других областях естествознания [14]. Модельное уравнение ВдП может быть записано в безразмерном виде

(2)
$\frac{{{{\partial }^{2}}X}}{{\partial {{t}^{2}}}} + X = \varepsilon \left[ {1 - {{X}^{2}}} \right]\frac{{\partial X}}{{\partial t}}.$

Оно сформулировано относительно действительной величины X, пропорциональной поперечной составляющей скорости течения в любой характерной точке следа – дорожки Кармана. Как и в модели ЛС, осцилляции скорости в различных точках сформировавшейся дорожки Кармана предполагаются жестко синхронизованными, причем различие в их фазе определяется только скоростью сноса дорожки как целого (аналогично модели Кармана). При этом пространственное распределение относительных амплитуд осцилляций в различных точках считается фиксированным (как и в модели ЛС). Действительный положительный параметр ε модели ВдП, вообще говоря, не обязательно мал, но мал в случае моделирования дорожек Кармана (в согласии с тем, что отмечалось для соответствующего параметра ${{\varepsilon }_{{{\text{LS}}}}}$ модели ЛС). Фигурирующее в уравнении (2) время обезразмерено на период установившихся осцилляций в дорожке Кармана $t = {{\omega }_{0}}{{t}_{{{\text{phys}}}}}.$

Решение уравнения ВдП (2) в случае малых $\varepsilon $ следует искать в форме осцилляций с медленно меняющейся амплитудой и фазой. На этом пути обнаруживается, что соответствующие укороченные (усредненные) уравнения для амплитуды и фазы осцилляций в модели ВдП эквивалентны уравнениям для действительной и мнимой частей уравнения (1) модели ЛС, но только при дополнительном условии $\operatorname{Im} {{\mu }_{{{\text{LS}}}}} = 0.$ Последнее ограничение обусловлено тем, что в стандартной модели ВдП не учитывается дополнительный (квадратичный по амплитуде осцилляций) набег фазы колебаний в процессе релаксации, имеющий место в модели ЛС. Явление “срывного флаттера” упруго закрепленного цилиндра при его обтекании потоком газа подробно рассматривается в [12] в рамках модели типа ВдП.

В практических приложениях часто представляют интерес следовые течения значительных поперечных размеров, соответственно порождаемые группой параллельных цилиндров. В связи с этим следующим необходимым шагом является обобщение моделей следовых течений на учет взаимодействия дорожек Кармана от соседних цилиндров. Как правило, в рамках одномерного моделирования такое взаимодействие учитывается в простейшей форме посредством дополнительных линейных по зависимым переменным членов, включаемых в уравнения ЛС [15] или ВдП [13], описывающие след уединенного цилиндра. Такой подход подкрепляется аргументом слабости взаимодействия дорожек Кармана в случае не слишком близкого расположения порождающих след цилиндров.

Развиваемая модель турбулентного следа пары цилиндров, предложенная в рамках работ по гранту РФФИ № 13-01-00742-а [16], также основывается на уравнениях типа ВдП для управляющих параметров двух дорожек Кармана ${{X}_{i}},$ представляющих относительную амплитуду осцилляций поперечной составляющей скорости течения в соответствующей дорожке Кармана. В несколько модифицированном виде (с учетом малости параметра $\left| \Delta \right| \ll 1$) уравнения модели [17, 18] следующие:

(3)
$\begin{gathered} \frac{{{{d}^{2}}{{X}_{1}}}}{{d{{t}^{2}}}} + {{X}_{1}}\left[ {1 - \Delta ({{\rho }^{2}} - 4)} \right] - \\ - \,\,\varepsilon \left[ {1 - X_{1}^{2} - \lambda X_{2}^{2} - l{{X}_{1}}{{X}_{2}}} \right]\frac{{d{{X}_{1}}}}{{dt}} = {{h}_{1}}, \\ \end{gathered} $
(4)
$\begin{gathered} \frac{{{{d}^{2}}{{X}_{2}}}}{{d{{t}^{2}}}} + {{X}_{2}}\left[ {1 - \Delta ({{r}^{2}} - 4)} \right] - \\ - \,\,\varepsilon \left[ {1 - X_{2}^{2} - \lambda X_{1}^{2} - l{{X}_{1}}{{X}_{2}}} \right]\frac{{d{{X}_{2}}}}{{dt}} = {{h}_{2}}. \\ \end{gathered} $

Отметим, что модельные уравнения (3), (4) турбулентного следа неоднородные; их правые части ${{h}_{{\,i}}}$ представляют собой случайные процессы – источник стохастизации турбулентного следа (некоторый аналог сил Ланжевена). Других принципиальных отличий модели по сравнению со случаем ламинарного следа (${{h}_{i}} = 0$) не предполагается. Иными словами, в сформировавшемся турбулентном следе ($\operatorname{Re} \sim 1000$) от цилиндров достаточно малого аспектного отношения (в опытах [8] ${H \mathord{\left/ {\vphantom {H D}} \right. \kern-0em} D} \approx 3.5$) доминирует крупномасштабная двумерная структура квазикармановских дорожек. Соответственно, для турбулентного режима следа можно в первом приближении использовать такую же модель ламинарного следа, но обобщенную на учет источника стохастизации ${{h}_{i}} \ne 0.$

Прочие отличительные особенности модели следующие. Первое с целью охватить максимальную область применимости модели следа взаимодействие дорожек учтено с помощью нелинейного члена уравнений, а именно посредством квадратичной формы общего вида с коэффициентами $\lambda ,l$ при скорости изменения управляющего параметра. При этом на интенсивность взаимодействия формирующихся дорожек Кармана – осцилляторов ВдП (локализованного в окрестности порождающих след цилиндров) не накладывается ограничений, т.е. значения параметров модели $\lambda ,l$ a priori произвольные. Как было обнаружено [16], такая модель (для случая $\Delta = 0$) дает достаточно богатый набор одночастотных квазиламинарных мод следа, но спектр их собственных частот, к сожалению, остался полностью вырожденным. Для устранения отмеченного недостатка, была явно учтена зависимость частоты осцилляций от их амплитуды, ожидаемая из общих соображений и имеющаяся в модели ЛС следа. Эта зависимость была учтена в модели посредством введения параметра Δ [17], что составляет вторую особенность нашей модели как модели типа ВдП. Тогда оказывается, что с учетом малости параметра Δ, для случая следа уединенного цилиндра укороченные уравнения представленной модели становятся полностью эквивалентными соответствующим уравнениям модели ЛС. Более того, из требования эквивалентности двух моделей следа вытекает условие отрицательности соответствующего параметра модели ВдП $\Delta < 0.$ Здесь еще раз подчеркнем, что модель ЛС для ламинарного следа от уединенного цилиндра обоснована как экспериментально, так и теоретически.

Аналитическое исследование несколько более сложной, чем (3), (4), модели на поиск одночастотных глобальных мод ламинарного следа показало наличие пяти таких устойчивых мод, при этом вырождение мод по частоте осцилляций оказалось полностью снятым для случая $\Delta \ne 0$ [17]. В принципе, этот набор одночастотных мод позволяет объяснить основные черты наблюдаемого спектра пульсаций скорости [8], причем не единственным образом [17, 18]. В рамках модели плазменное течение при повышенных плотностях тока можно интерпретировать как перемежающееся течение при конкуренции между модой синфазной синхронизации одинаковых дорожек за цилиндрами и асимметричной одночастотной модой с частично подавленной дорожкой за одним из цилиндров при развитой дорожке за вторым. Наряду с этой интерпретацией возможна и другая: в плазменном течении наблюдалась перемежаемость между модами синфазной и противофазной синхронизации одинаковых дорожек Кармана за цилиндрами [18]. Здесь необходимо отметить, что у обоих рассмотренных вариантов интерпретации экспериментальных данных в рамках развиваемой модели оставался принципиальный недостаток. Это – несогласованность с имеющимися публикациями по следам цилиндров. Согласно различным работам по визуализации следов двух цилиндров при достаточном их сближении ${T \mathord{\left/ {\vphantom {T D}} \right. \kern-0em} D} \leqslant 2,$ устойчиво наблюдается след с развитой дорожкой Кармана за одним из цилиндров и частично подавленной дорожкой за вторым цилиндром: асимметричный отклоненный след “biased wake” [19–21]. При этом частоты срыва вихрей в двух дорожках различаются [21–24]. Это – двухчастотный режим следа пары цилиндров. Соответственно, был проведен поиск такого двухчастотного режима в рамках развиваемой модели: системы тех же уравнений (3), (4).

ДВУХЧАСТОТНАЯ ГЛОБАЛЬНАЯ МОДА СЛЕДА В РАМКАХ ЧЕТЫРЕХПАРАМЕТРИЧЕСКОЙ МОДЕЛИ

Модель ближнего следа от двух цилиндров представляет собой систему двух уравнений (3), (4). Она содержит четыре действительных параметра $0 < \varepsilon ,\Delta ,\lambda ,l,$ из которых только два последних отвечают за нелинейное взаимодействие дорожек. На основании малости параметра $\varepsilon < 1,$ что обосновано экспериментально [25], для решения системы (3), (4) следует воспользоваться методом Крылова–Боголюбова. Тогда осредненные (“укороченные”) уравнения для медленных амплитуд $\rho ,\,r$ и фаз колебаний $\theta ,\,\Psi $

(5)
$\begin{gathered} {{X}_{1}} = \rho \cos \left( {\int\limits_0^t {\left[ {1 - 0.5\Delta ({{\rho }^{2}} - 4)} \right]{\kern 1pt} d\tau + \theta } } \right), \\ {{X}_{2}} = r\cos \left( {\int\limits_0^t {\left[ {1 - 0.5\Delta ({{r}^{2}} - 4)} \right]{\kern 1pt} d\tau + \psi } } \right) \\ \end{gathered} $
принимают вид

(6)
$\begin{gathered} \frac{{d{{\rho }^{2}}}}{{dt}} = \\ = \varepsilon {{\rho }^{2}}\left[ {1 - \frac{{{{\rho }^{2}} + \lambda {{r}^{2}}\left( {2 - \cos (2P)} \right) + l\rho r\cos (P)}}{4}} \right] + {{h}_{\rho }}, \\ \end{gathered} $
(7)
$\begin{gathered} \frac{{d{{r}^{2}}}}{{dt}} = \\ = \varepsilon {{r}^{2}}\left[ {1 - \frac{{{{r}^{2}} + \lambda {{\rho }^{2}}\left( {2 - \cos (2P)} \right) + l\rho r\cos (P)}}{4}} \right] + {{h}_{r}}, \\ \end{gathered} $
(8)
$\begin{gathered} \frac{{dP}}{{dt}} = \frac{\Delta }{2}({{r}^{2}} - {{\rho }^{2}}) - \\ - \,\,\frac{\varepsilon }{8}\left[ {\lambda ({{\rho }^{2}} + {{r}^{2}})\sin 2P + 2l\rho r\sin P} \right] + {{h}_{P}}. \\ \end{gathered} $

Здесь в уравнениях модели (6)–(8) учтена малость параметра $\left| \Delta \right| \ll 1$ и введено обозначение для полной относительной фазы осцилляций в двух дорожках Кармана

(9)
$P = \int\limits_0^t {\left[ {\frac{\Delta }{2}\left( {{{r}^{2}} - {{\rho }^{2}}} \right)} \right]} {\kern 1pt} d\tau + \theta - \psi .$

Пять точек покоя системы уравнений (6)–(8) при нулевых стохастизирующих членах ${{h}_{i}} = 0$ представляют одночастотные глобальные моды ламинарного следа [17]. Четыре из них оказались устойчивыми относительно бесконечно малых возмущений, а пятая асимметричная $A{{S}_{{\rho {\kern 1pt} r}}}$ [17] оказалась неустойчивой в рамках модели (6)–(8) всюду в области своего формального существования.

Конфигурацию асимметричной двухчастотной моды будем искать как квазистационарное решение системы уравнений (6)–(8) модели в отсутствие стохастизации ${{h}_{i}} = 0.$ При этом в отличие от одночастотных мод, полная относительная фаза осцилляций в двух дорожках Кармана (9) предполагается линейной функцией времени плюс малые осциллирующие добавки:

(10)
${{\rho }^{2}},{{r}^{2}} \approx {\text{const,}}$
(11)
$P \approx {\text{const}} + \Omega t.$

Для первого грубого приближения полностью пренебрегаем осциллирующими слагаемыми в правых частях уравнений (6)–(8). В результате получаем, что однопараметрическое семейство решений вида (10), (11) реализуется вдоль прямой $\lambda = 0.5.$ Для этого семейства квадраты амплитуд осцилляций в двух дорожках Кармана связаны соотношением

(12)
${{\rho }^{2}} + {{r}^{2}} = 4$
при произвольном в остальном соотношении между амплитудами. Все решения семейства оказываются нейтрально устойчивыми (относительно бесконечно малых возмущений) вдоль направления (12) и устойчивыми в ортогональном направлении.

Соответствующее прямое численное исследование системы (6)–(8) показывает, что двухчастотная асимметричная мода существует и устойчива относительно малых возмущений в области $0 < 0.5 - \lambda \ll 1$ для умеренно больших значений параметра $\left| l \right|.$ Существенное расщепление частот осцилляций в двух дорожках Кармана наблюдается вблизи граничного значения параметра модели $\lambda \approx 0.5,$ причем расщепление тем больше, чем ближе к граничному значению 0.5. Пример установившейся динамики следа в форме двух дорожек Кармана приведен на рис. 2 для случая $\varepsilon = 0.30,$ $\Delta = - 0.16,$ $\lambda = 0.49,$ $l = 4.0.$

Рис. 2.

Временнáя развертка осцилляций скорости в двух дорожках Кармана от пары цилиндров в квазиламинарном установившемся режиме, ${{X}_{1}}(t)$ и ${{X}_{2}}(t)$ (со сдвигом на три единицы): двухчастотная асимметричная (а) и одночастотная симметричная (б) моды следа.

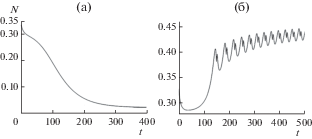
В турбулентном следе (${{h}_{i}} \ne 0$ в (3)–(8)) эти две моды должны формировать перемежающееся течение. Следует отметить, что форма осцилляций скорости по установившейся асимметричной моде заметно отличается от гармонической, не так как в случае конкурирующей симметричной моды синфазных дорожек. Некоторое представление о процессе релаксации следа в определенную квазиламинарную глобальную моду дает рис. 3. На рисунке проиллюстрирована зависимость от времени коллективной переменной – асимметрии следа $N = \frac{{{{\rho }^{2}} - {{r}^{2}}}}{{2({{\rho }^{2}} + {{r}^{2}})}}$ в случае $\varepsilon = 0.16,$ $\Delta = - 0.16,$ $\lambda = 0.49,\,\,l = 3.0.$ Начальные данные ${{N}_{{(0)}}}$ для расчета эволюции взяты вблизи границы между областями притяжения симметричной синфазной моды и асимметричной двухчастотной моды следа, при этом по разные стороны от этой границы для вариантов 3a и 3б соответственно. По полученному результату можно отметить, что для начальных условий, близких к границе между областями притяжения различных глобальных мод, процесс релаксации следа в установившееся состояние занимает значительное время (в масштабах ε–1).

Рис. 3.

Динамика коллективной переменной следа – асимметрии N: (a) – релаксация на симметричную моду синфазных дорожек для ${{N}_{{(0)}}} = 0.32,$ (б) – релаксация на асимметричную двухчастотную моду для ${{N}_{{(0)}}} = 0.33.$

ЗАКЛЮЧЕНИЕ

1. Развита модель турбулентного перемежающегося следа от пары цилиндров, причем учтен нелинейный характер взаимодействия квазикармановских вихревых дорожек в области их формирования ${x \mathord{\left/ {\vphantom {x D}} \right. \kern-0em} D} \leqslant 3{\kern 1pt} - {\kern 1pt} 5.$

2. В модели в явном виде учтена зависимость частоты осцилляций скорости в дорожках Кармана от амплитуды осцилляций. Учет проведен в такой форме, чтобы для уединенного цилиндра модель становилась полностью эквивалентной модели Ландау–Стюарта этого течения, которую считаем обоснованной экспериментально и теоретически для ламинарного режима течения.

3. В рамках модели продемонстрировано существование двухчастотной глобальной квазиламинарной моды следа, перемежающейся с одночастотными модами.

4. Отмечается высокая вероятность проявления этой двухчастотной моды в экспериментах с переключаемым плазменным следом [8, 18]. Однако для однозначной интерпретации таких экспериментальных данных требуется дополнительная экспериментальная информация по относительной фазе осцилляций в двух дорожках Кармана, составляющих след.

Разрабатываемая модель следа является обобщением модели, предложенной в рамках исследований поддержанных грантом РФФИ № 13-01-00742, и может служить в качестве обоснования к заявке № 19-01-00105 на конкурс “А” РФФИ.Авторы признательны Э.В. Теодоровичу за полезную дискуссию.

Список литературы

  1. Суржиков С.Т. Физическая механика газовых разрядов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006.

  2. Sosa R., Artana G., Benard N., Moreau E. Mean Lift Generation on Cylinders Induced with Plasma Actuators // Exp. Fluids. 2011. V. 51. P. 853.

  3. Казанский П.Н., Климов А.И., Моралев И.А. Управление воздушным потоком вблизи кругового цилиндра с помощью ВЧ-актюатора. Влияние параметров разряда на аэродинамическое сопротивление цилиндра // ТВТ. 2012. Т. 50. Вып. 3. С. 346.

  4. Битюрин В.А., Завершинский И.П., Климов А.И., Молевич Н.Е., Моралев И.А., Мунхоз Д., Поляков Л.Б., Сугак С.С. Обтекание цилиндра с электрической дугой, вращающейся в магнитном поле // ТВТ. 2016. Т. 54. № 4. С. 632.

  5. Panchenko V.Ya., Zavalov Yu.N., Galushkin M.G., Grishaev R.V., Golubev V.S., Dubrov V.D. The Development of Turbulence in the Active Medium of a Fast-flow Gas-discharge Laser // Laser Phys. 2006. V. 16. Is. 1. P. 40.

  6. Huang H., Wang Y. Kinetic Modeling and Optimum Design of the Discharge Tube for the CO2 Laser with Computational Fluid Dynamics Method // Opt. Eng. 2010. V. 49. № 11. P. 114201.

  7. Гембаржевский Г.В., Генералов Н.А., Косынкин В.Д. Датчик пульсаций скорости турбулентного газового потока в условиях тлеющего разряда // ПТЭ. 1993. № 3. С. 149.

  8. Гембаржевский Г.В. Электроразрядный эффект в плазменном течении следа: перераспределение энергии пульсаций в область низких частот // Письма в ЖТФ. 2009. Т. 35. Вып. 5. С. 95.

  9. Вараксин А.Ю. Воздушные торнадоподобные вихри: математическое моделирование // ТВТ. 2017. Т. 55. № 2. С. 291.

  10. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 6. Гидродинамика. М.: Наука, 1986. С. 137.

  11. Sipp D., Lebedev A. Global Stability of Base and Mean Flows: a General Approach and its Application to Cylinder and Open Cavity Flows // J. Fluid Mech. 2007. V. 593. P. 333.

  12. Ланда П.С. Срывной флаттер как один из механизмов возбуждения автоколебаний линий электропередачи // Изв. вузов. Прикладная нелинейная динамика. 2009. Т. 17. № 2. С. 3.

  13. Simiu E., Scanlan R.H. Wind Effects on Structures: An Introduction to Wind Engineering N.Y.–Chichester–Brisbane–Toronto: John Willey & Sons, 1978.

  14. Кузнецов А.П., Селиверстова Е.С., Трубецков Д.И., Тюрюкина Л.В. Феномен уравнения Ван дер Поля // Изв. вузов. Прикладная нелинейная динамика. 2014. Т. 22. № 4. С. 3.

  15. Peschard I., Le Gal P. Coupled Wakes of Cylinders // Phys. Rev. Lett. 1996. V. 77. № 15. P. 3122.

  16. Gembarzhevskii G.V., Lednev A.K. Reduced Order Model for Effect of Pulsation Energy Redistribution in Cylinders Wake Induced by Glow Discharge // Proc. 12th Workshop on Magneto-Plasma Aerodynamics / Ed. Bityurin V.A. M.: JIHT RAS, 2013. P. 67.

  17. Гембаржевский Г.В., Леднев А.К., Осипенко К.Ю. Моделирование эволюции плазменного следа пары цилиндров под действием электрического разряда // Письма в ЖТФ. 2015. Т. 41. Вып. 23. С. 40.

  18. Gembarzhevskii G.V., Lednev A.K., Osipenko K.Yu. Mode Intermittence in a Wake from Two Cylinders // J. Physics: Conf. Series. 2017. V. 815. P. 012020.

  19. Bearman P.W., Wadcock A.J. The Interaction between a Pair of Circular Cylinders Normal to a Streem // J. Fluid Mech. 1973. V. 61. Part 3. P. 499.

  20. Ishigai S., Nishikawa E., Nishimura K., Cho K. Experimental Study on Structure of Gas Flow in Tube Banks with Tube Axes Normal to Flow. Part 1. Karman Vortex Flow Around two Tubes at Various Spacing // Bull. Jap. Soc. Mech. Eng. 1972. V. 15. № 86. P. 949.

  21. Spivak H.M. Vortex Frequency and Flow Pattern in the Wake of Two Parallel Cylinders at Varied Spacing Normal to an Air Stream // J. Aeronaut. Sci. 1946. V. 13. P. 289.

  22. Kiya M., Arie M., Tamura H., Mori H. Vortex Shedding from Two Circular Cylinders in Staggered Arrangement // J. Fluids Eng. 1980. V. 102. № 2. P. 166.

  23. Sumner D. Two Circular Cylinders in Cross-flow: A Review // J. Fluids Structures. 2010. V. 26. P. 849.

  24. Alam Md.M., Zhou Y., Wang X.W. The Wake of Two Side-by-side Square Cylinders // J. Fluid Mech. 2011. V. 669. P. 432.

  25. Gembarzhevskii G.V. The Effect of Flow Structure Transformation Induced by Electric Discharge and its Simple Model // VI Int. Conf. on Plasma Physics and Plasma Technology. Minsk, Belarus: Institute of Physics NAS, 2009. V. 1. P. 27.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал