Теплофизика высоких температур, 2019, T. 57, № 1, стр. 20-25

ВВЕДЕНИЕ

Нанофокусировка световой энергии на вершине металлического микроострия − важнейшее явление, лежащее в основе перспективных нанотехнологических приложений. Нанофокусировка проявляется в необычайно резком возрастании интенсивности поверхностной плазмонно-поляритонной волны при симметричном ее схождении к нановершине острия [1–3] и формировании наноразмерной области концентрации световой энергии. Это явление объясняется тем, что на геометрически идеальном металлическом острие возможно существование осесимметричной электромагнитной стоячей волны с сингулярностью электрического поля на вершине [4]. Как показывают эксперименты [5, 6], эта волна может эффективно возбуждаться сходящейся к вершине поверхностной плазмонно-поляритонной TM (transverse magnetic) волной с той же осевой симметрией поля. Наличие сингулярности электрического поля хорошо объясняется в квазистатическом приближении, которое выполняется в окрестности нановершины металлического микроострия.

Реальная вершина микроострия не идеальна и имеет закругление на вершине. В [7, 8] для нахождения распределения электрического поля на закругленной вершине одиночного микроострия поверхность вершины аппроксимировалась параболоидом вращения. Задача решена в параболоидальной системе координат в квазистационарном приближении численным методом разложения решения по гармоникам уравнения Лапласа с последующим удовлетворением граничным условиям. Доказано, что размер фокального распределения (в окрестности максимума распределения энергии поля на вершине) убывает пропорционально радиусу закругления вершины, что принципиально объясняет нанофокусировку (при уменьшении радиуса вершины острия до нанометровых размеров размер фокальной области уменьшается в той же пропорции). В [9] показано, что размер фокального распределения существенно не меняется, когда рассматриваемое металлическое острие расположено у плоской границы раздела полупространства, заполненного диэлектриком или металлом. Задача решалась тем же численным методом, а полупространство учитывалось методом зеркальных отражений.

В настоящей работе обсуждается фокальное распределение поля при нахождении вершины острия вблизи плоской границы многослойного материала. Для учета влияния на фокальное распределение поля многопленочной структуры используется оригинальный обобщенный метод зеркальных отражений [10]. Важность проблемы нахождения фокального распределения поля определяется тем, что оно, например, позволяет оценить размеры области полимеризации в поверхностной пленке мономера на поверхности многопленочной структуры у вершины острия при сканировании им поверхности.

МЕТОД РЕШЕНИЯ ЗАДАЧИ

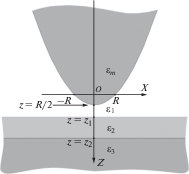
Рассмотрим металлическое острие с наноразмерным радиусом закругления вершины R. Пусть поверхность острия вблизи вершины представляется (осесимметричной относительно оси Z) параболоидом вращения $z = {R \mathord{\left/ {\vphantom {R 2}} \right. \kern-0em} 2} - {{({{x}^{2}} + {{y}^{2}})} \mathord{\left/ {\vphantom {{({{x}^{2}} + {{y}^{2}})} {2R}}} \right. \kern-0em} {2R}}$ (рис. 1). Предположим, что вблизи острия находится первая плоская граница пленки $z = {{z}_{1}}$, где ${{z}_{1}} \geqslant {R \mathord{\left/ {\vphantom {R 2}} \right. \kern-0em} 2},$ а вторая граница рассматриваемой пленки толщиной h будет $z = {{z}_{2}},$ где ${{z}_{2}} = {{z}_{1}} + h.$ Комплексные диэлектрические проницаемости металла острия, внешней однородной среды, пленки и полубесконечной среды при $z \geqslant {{z}_{2}}$ обозначим ${{\varepsilon }_{m}},$ ${{\varepsilon }_{1}},$ ${{\varepsilon }_{2}}$ и ${{\varepsilon }_{3}}$ соответственно (рис. 1).

При решении задачи используем комплексное представление гармонических полей с временной зависимостью $\exp \left( { - i\omega t} \right),$ где $\omega $ − циклическая частота. Задачу вблизи вершины можно решать в квазистатической формулировке [8], при которой потенциал электрического поля Φ удовлетворяет уравнению Лапласа $\Delta \Phi = 0,$ а нормальные и тангенциальные составляющие электрического поля на поверхности острия и двух плоских границах пленки должны соответствовать известным граничным условиям:

на поверхности острия

на первой границе пленки

на второй границе пленки

Будем искать осесимметричное решение уравнения Лапласа, имеющее максимум поля на вершине острия и соответствующее фокусировке на нем симметричной поверхностной плазмонной TM-волны. Кроме того, для автоматического удовлетворения граничных условий на плоских поверхностях пленки (2) и (3) воспользуемся обобщенным методом зеркальных отражений, который будет изложен ниже. Пусть потенциал зарядов, находящихся на параболоидальном металлическом острие, в пространстве с проницаемостью ${{\varepsilon }_{1}}$ описывается функцией ${{\Phi }_{{{\text{tip}}}}}\left( {\mathbf{r}} \right)$ = $ = {{\Phi }_{{{\text{tip}}}}}\left( {x,y,z} \right),$ где радиус-вектор ${\mathbf{r}} = \left( {x,y,z} \right)$ проведен из начала координат в точку нахождения потенциала. Пусть потенциал индуцированных зарядов на границах пленки (из уравнений Максвелла следует, что внутри однородного диэлектрика нет поляризационных зарядов, они могут быть только на границе) в пространстве с проницаемостью ${{\varepsilon }_{1}}$ равен ${{\Phi }_{{{\text{ind}}}}}\left( {\mathbf{r}} \right) = {{\Phi }_{{{\text{ind}}}}}\left( {x,y,z} \right).$ Тогда, полный потенциал в области, заполненной диэлектриком с проницаемостью ${{\varepsilon }_{1}}$, составляет

Пусть потенциалы электрического поля, возбуждаемого зарядами острия в областях с ${{\varepsilon }_{2}}$ и ${{\varepsilon }_{3}},$ т.е. в пленке и в полупространстве за пленкой, равны ${{\Phi }_{2}}\left( {\mathbf{r}} \right) = {{\Phi }_{2}}\left( {x,y,z} \right)$ и ${{\Phi }_{3}}\left( {\mathbf{r}} \right) = {{\Phi }_{3}}\left( {x,y,z} \right).$

Найдем теперь общий вид потенциала острия ${{\Phi }_{{{\text{tip}}}}}\left( {\mathbf{r}} \right),$ удовлетворяющий уравнению Лапласа в однородном диэлектрическом пространстве (без слоистой структуры) снаружи и внутри острия, причем на границе острия должны удовлетворяться граничные условия (1). Введем параболоидальные координаты [11] (систему параболических координат вращения) $\left( {\alpha ,\beta ,\psi } \right),$ которые связаны с прямоугольными декартовыми координатами $\left( {x,\,y,\,z} \right)$ формулами

где c – масштабный постоянный множитель. В рассматриваемой системе координат с началом в точке O и осью Z (см. рис. 1) уравнение Лапласа для электрического потенциала $\Phi $ внутри и снаружи острия при аксиальной симметрии (Φ не зависит от $\psi $) можно записать следующим образом [11]:

Общее решение (6) известно [11] и определяется выражением

где p, ${{B}_{1}},$ ${{B}_{2}},$ ${{C}_{1}},$ ${{C}_{2}}$ – константы; ${{J}_{0}},$ ${{Y}_{0}}$ – функции Бесселя первого и второго рода нулевого порядка; ${{I}_{0}},$ ${{K}_{0}}$ – модифицированные функции Бесселя первого и второго рода нулевого порядка. Суммирование производится по решениям с различными значениями констант.

Пусть граница параболоидального острия определяется уравнением $\beta = {{\beta }_{0}}.$ Из (5) следует, что граница острия $\beta = {{\beta }_{0}}$ в декартовых координатах $\left( {x,\,y,\,z} \right)$ определяется уравнением $z = {{c\beta _{0}^{2}} \mathord{\left/ {\vphantom {{c\beta _{0}^{2}} 2}} \right. \kern-0em} 2} - {{({{x}^{2}} + {{y}^{2}})} \mathord{\left/ {\vphantom {{({{x}^{2}} + {{y}^{2}})} {2c\beta _{0}^{2}}}} \right. \kern-0em} {2c\beta _{0}^{2}}}.$ Несложно показать, что радиус кривизны вершины острия равен $R = c\beta _{0}^{2}.$

В дальнейшем рассмотрении будем использовать осесимметричные решения уравнения Лапласа. Поэтому для выполнения граничных условий на всей поверхности вращения острия достаточно удовлетворить их на линии пересечения граничной поверхности острия с любой плоскостью симметрии, проходящей через ось Z. В качестве такой плоскости выберем плоскость (x, z). Легко доказать, что в данном симметричном случае достаточно рассмотреть выполнение граничных условий только на границе пересечения полуплоскости $y = 0$ при $x \geqslant 0$ и поверхности параболоидального острия.

Имея в виду общность дальнейшего изложения, перейдем на плоскости $\left( {x,z} \right)$ к безразмерным координатам: $\tilde {x} = {x \mathord{\left/ {\vphantom {x R}} \right. \kern-0em} R},$ $\tilde {z} = {z \mathord{\left/ {\vphantom {z R}} \right. \kern-0em} R}$ и $\tilde {\alpha } = {\alpha \mathord{\left/ {\vphantom {\alpha {{{\beta }_{0}}}}} \right. \kern-0em} {{{\beta }_{0}}}},$ $\tilde {\beta } = {\beta \mathord{\left/ {\vphantom {\beta {{{\beta }_{0}}}}} \right. \kern-0em} {{{\beta }_{0}}}}.$ Безразмерные параболоидальные $\left( {\tilde {\alpha },\tilde {\beta }} \right)$ и декартовы координаты на плоскости $\left( {\tilde {x},\tilde {z}} \right)$ связаны между собой формулами $\tilde {\alpha } = \sqrt {\sqrt {{{{\tilde {x}}}^{2}} + {{{\tilde {z}}}^{2}}} - \tilde {z}} $ и $\tilde {\beta } = {{\tilde {x}} \mathord{\left/ {\vphantom {{\tilde {x}} {\sqrt {\sqrt {{{{\tilde {x}}}^{2}} + {{{\tilde {z}}}^{2}}} - \tilde {z}} }}} \right. \kern-0em} {\sqrt {\sqrt {{{{\tilde {x}}}^{2}} + {{{\tilde {z}}}^{2}}} - \tilde {z}} }}$ при положительных $\tilde {x}$ [8]. В этих координатах граница острия будет определяться функцией $\tilde {z} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} - {{{{{\tilde {x}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\tilde {x}}}^{2}}} 2}} \right. \kern-0em} 2},$ а уравнение Лапласа (6) в безразмерных координатах имеет вид

Если из решения уравнения Лапласа найти осесимметричный потенциал, являющийся функцией только $\tilde {\alpha }$ и $\tilde {\beta },$ то нормальные и тангенциальные размерные компоненты поля с двух сторон границы диэлектрика (среды с ${{\varepsilon }_{1}}$) и металла можно записать в виде

Нормируем потенциал на его значение U в максимуме поля на вершине острия, тогда можно перейти от размерного к безразмерному потенциалу $\tilde {\Phi } = {\Phi \mathord{\left/ {\vphantom {\Phi U}} \right. \kern-0em} U}$ и от размерных составляющих полей к их безразмерным величинам:

В нормированных декартовых координатах в плоскости $\left( {\tilde {x},\,\,\tilde {z}} \right)$ компоненты нормированного электрического поля будут иметь вид ${{\tilde {E}}_{{\tilde {x}}}} = - {{\partial{ \tilde {\Phi }}} \mathord{\left/ {\vphantom {{\partial{ \tilde {\Phi }}} {\partial{ \tilde {x}}}}} \right. \kern-0em} {\partial{ \tilde {x}}}},$ ${{\tilde {E}}_{{\tilde {z}}}} = - {{\partial{ \tilde {\Phi }}} \mathord{\left/ {\vphantom {{\partial{ \tilde {\Phi }}} {\partial{ \tilde {z}}}}} \right. \kern-0em} {\partial{ \tilde {z}}}}.$

Итак, исходя из общего решения (7), будем искать решение граничной задачи для электрического поля в окрестности острия, предполагая, что потенциалы ${{\tilde {\Phi }}_{{{\text{tip}}}}}$ снаружи ($\beta \geqslant {{\beta }_{0}}$) и внутри ($\beta \leqslant {{\beta }_{0}}$) границы металлического острия имеют вид соответственно

где ${{A}_{j}},$ ${{B}_{j}}$ и ${{\lambda }_{j}}$ – константы. Значения ${{\lambda }_{j}}$ можно выбрать в виде ${{\lambda }_{j}} = {{{{\mu }_{j}}} \mathord{\left/ {\vphantom {{{{\mu }_{j}}} L}} \right. \kern-0em} L},$ где ${{\mu }_{j}},$ $j = 1,\,2,\,...\,,\,N$ − первые N корней уравнения Бесселя ${{J}_{0}}\left( {{{\mu }_{j}}} \right) = 0,$ а L – некоторое безразмерное расстояние от вершины, удовлетворяющее граничным условиям на поверхности острия. В пределе $N \to \infty $ система функций ${{J}_{0}}\left( {{{\lambda }_{j}}\tilde {\alpha }} \right)$ и вышеуказанный выбор ${{\lambda }_{j}}$ на отрезке $0 \leqslant \tilde {\alpha } \leqslant L$ образуют полную систему функций [12].

Отметим, что выбор функциональных зависимостей (8) из общего решения (7) обусловлен естественными требованиями к сконцентрированному у вершины полю (которые и выделяют указанные зависимости однозначным образом): а) снаружи острия потенциал поля должен уменьшаться при удалении от его поверхности, быть конечным и максимальным на вершине острия; б) внутри металла острия потенциал должен быть конечным в начале координат. Кроме того, электрический потенциал должен быть непрерывен при переходе через границу.

Учтем теперь индуцированные заряды, возникающие в многослойной пленке. Как показано в [12], функцию ${{\tilde {\Phi }}_{{{\text{ind}}}}}\left( {\tilde {x},\tilde {z}} \right),$ соответствующую ${{\tilde {\Phi }}_{{{\text{tip,1}}}}}\left( {\tilde {x},\tilde {z}} \right)$ из (8), можно представить в виде

где ${{H}_{j}}\left( {\tilde {x},\tilde {z}} \right)$ зависят от ${{\lambda }_{j}}.$ В данной работе не приводится громоздкий вывод выражения для ${{H}_{j}}\left( {\tilde {x},\tilde {z}} \right),$ который подробно изложен в [10]. Приведем лишь результат: где

Идея вывода выражения для ${{\tilde {\Phi }}_{{{\text{ind}}}}}$ проста. Потенциал ${{\tilde {\Phi }}_{{{\text{tip,1}}}}}$ можно в принципе разложить на потенциалы точечных зарядов. Для каждого точечного заряда можно найти потенциал индуцированного поля как в области между острием и первой пленкой, так и между пленок. Просуммировав потенциалы по всем зарядам, получим выражение для ${{\tilde {\Phi }}_{{{\text{ind}}}}},$ ${{\tilde {\Phi }}_{2}}$ и ${{\tilde {\Phi }}_{3}}$ из ${{\tilde {\Phi }}_{{{\text{tip,1}}}}}$ (см. [10]).

Таким образом, если подставить (8) и (9) в (1), используя (4), получим систему линейных уравнений относительно ${{A}_{j}}$ и ${{B}_{j}}$ вида

Здесь не выписаны функции ${{a}_{j}}\left( {{{\lambda }_{j}},\tilde {x}} \right),$ ${{b}_{j}}\left( {{{\lambda }_{j}},\tilde {x}} \right),$ ${{c}_{j}}\left( {{{\lambda }_{j}},\tilde {x}} \right)$ и ${{d}_{j}}\left( {{{\lambda }_{j}},\tilde {x}} \right)$ в явном виде, так как их легко получить при указанной тривиальной, но громоздкой подстановке.

РЕЗУЛЬТЫ РАСЧЕТОВ И ОБСУЖДЕНИЕ

Уравнения (10), (11) решались методом коллокаций [13]. Указанные уравнения записывались в $\left( {N - 1} \right)$ регулярно расположенных точках на поверхности острия. В результате получены $\left( {2N - 2} \right)$ линейных алгебраических уравнений с $2N$ неизвестными коэффициентами ${{A}_{j}}$ и ${{B}_{j}}.$ Для получения однозначного решения добавлены еще два уравнения приравниванием потенциалов на вершине острия (снаружи и внутри острия) к единице. В результате решения полученной системы из $2N$ уравнений найдены ${{A}_{j}}$ и ${{B}_{j}}$ и по ним распределения потенциала и электрического поля во всем пространстве. При этом полученное распределение потенциала автоматически нормировалось на единицу на вершине острия.

Диэлектрическая проницаемость металла острия приближенно описывалась формулой Друдэ ${{\varepsilon }_{m}} = 1 - {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {\left( {{{\omega }^{2}} + i\omega \Gamma } \right)}}} \right. \kern-0em} {\left( {{{\omega }^{2}} + i\omega \Gamma } \right)}},$ где ${{\omega }_{p}}$ – плазменная частота металла, Γ – коэффициент, учитывающий потери. Для серебра принимались следующие параметры: ${{\omega }_{p}} \approx 1.36 \times {{10}^{{16}}}$ с^–1, $\Gamma \approx 2 \times {{10}^{{14}}}$ с^–1 [14]. Удобно выражать ${{\varepsilon }_{m}}$ через нормированную частоту $\varpi = {\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{p}}}}} \right. \kern-0em} {{{\omega }_{p}}}}$ и нормированный коэффициент поглощения $\gamma = {\Gamma \mathord{\left/ {\vphantom {\Gamma {{{\omega }_{p}}}}} \right. \kern-0em} {{{\omega }_{p}}}}$ по формуле ε_m = = $1 - {1 \mathord{\left/ {\vphantom {1 {\left( {{{\varpi }^{2}} + i\varpi \gamma } \right)}}} \right. \kern-0em} {\left( {{{\varpi }^{2}} + i\varpi \gamma } \right)}}.$ Для серебра $\gamma = {\text{0}}{\text{.01471}}{\text{.}}$

Рассмотрены два примера применения описанной теории.

Пример № 1. Рассмотрено распределение максимального значения электрического поля в окрестности серебряного острия (${{\varepsilon }_{m}} = {{\varepsilon }_{{{\text{Ag}}}}}$), расположенного около тонкой диэлектрической пленки с ${{\varepsilon }_{2}} = 4.$ Пленка располагалась на границе диэлектрического полупространства с ${{\varepsilon }_{3}} = 2.$ Диэлектрическая проницаемость области между острием и верхней поверхностью пленки полагалась равной единице (${{\varepsilon }_{1}} = 1$). В безразмерных (нормированных на радиус кривизны вершины) единицах длины толщина пленки принималась равной $\tilde {h} = 1,$ а координаты верхней и нижней границ пленки – ${{\tilde {z}}_{1}} = 1$ и ${{\tilde {z}}_{2}} = 2.$ Нормированная циклическая частота излучения составляла $\tilde {\omega } = 0.62252.$

Результаты вычисления пространственного распределения (линии уровня) модуля электрического поля показаны на рис. 2а. На рис. 2б приведены зависимости распределения поля рис. 2а вдоль прямых линий, параллельных оси острия, на которых хорошо видны скачки электрического поля на границе диэлектриков, соответствующие изменению диэлектрических постоянных. На рис. 2б хорошо видны границы острия и пленок.

Из рис. 2 следует важный физический результат данных исследований: электрическое поле сконцентрировано (сфокусировано) в ближайшей окрестности вершины микроострия, включая малую область внутри ближайшей диэлектрической пленки. Кроме того, видно, что электрическое поле проникает под пленку, в полупространство под ней, хотя и с существенным ослаблением. Знание этого ослабления может быть полезно в технических приложениях, в которых необходимо осуществить воздействие через пленку.

Пример № 2. Рассмотрена предыдущая задача, но диэлектрическая пленка (${{\varepsilon }_{2}} = 4$) заменена на серебряную (${{\varepsilon }_{2}} = {{\varepsilon }_{{{\text{Ag}}}}}$) той же толщины. Результаты вычисления пространственного распределения (линии уровня) модуля электрического поля показаны на рис. 3а. На рис. 3б приведены зависимости распределения поля рис. 3а вдоль тех же прямых линий, что и в примере № 1, параллельных оси острия, на которых, в частности, продемонстрированы скачки электрического поля на границе сред.

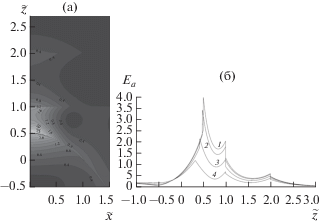
По сравнению с предыдущей задачей в случае серебряной пленки распределение поля более остро локализовано в окрестности фокуса, поле от острия проникает заметно глубже в полупространство с ${{\varepsilon }_{3}} = 2$ за пленкой. Кроме того, поле в фокальном пятне на поверхности серебряной пленки ближе по величине к полю на вершине острия по сравнению с предыдущим случаем (рис. 2).

Особо отметим, что полученные распределения поля приведены в нормированных (на радиус кривизны вершины R) координатах. Это означает, что при фокусировке на нановершине микроострия (R в нанометровом диапазоне) будет получаться фокальное пятно нанометровых размеров.

Из рассмотренных примеров следует, что с помощью металлического острия, на вершину которого сфокусирована поверхностная плазмонная волна, можно засвечивать тонкую пленку мономера фоторезиста и, сканируя острием вдоль ее поверхности, создавать поверхностные полимерные структуры, которые могут быть использованы в стандартных технологических приложениях, например, таких как создание шаблонов для копирования микросхем известными методами нанолитографии [15, 16]. Подобное устройство может применяться для изучения поверхностного распределения рамановского (комбинационного) излучения от молекул на границе поверхностной металлической или диэлектрической пленки при ее сканировании возбужденным наноострием. Более того, второй рассмотренный в работе пример показывает, что обсуждаемым устройством можно засвечивать фоторезист и под тонкой пленкой металла, что дает дополнительные технологические возможности. Наконец, результаты настоящей работы могут быть применены для создания наноградиентных тонкопленочных структур [17–19] или рассмотрения явлений электронной эмиссии из металлических острий [20].

ЗАКЛЮЧЕНИЕ

Разработан метод нахождения фокального распределения электрического поля в окрестности нановершины металлического микроострия, расположенного вблизи слоистой пленочной структуры, при возбуждении вершины сходящейся по поверхности острия к вершине поверхностной плазмонной TM-волной. В качестве примера такой пленочной структуры рассмотрена одна пленка материала, расположенная на плоской границе полупространства. Предложенный метод может быть обобщен на случай многопленочной структуры. Показано, что присутствие диэлектрической или металлической пленки вблизи острия не разрушает фокусирующих свойств наноострия.