Теплофизика высоких температур, 2019, T. 57, № 1, стр. 150-153

Акустические волны в вязкоупругих пузырьковых средах

Д. А. Губайдуллин¹, А. А. Никифоров^1, *

¹ Институт механики и машиностроения ФИЦ Казанский научный центр РАН
Татарстан, Казань, Россия

Поступила в редакцию 19.11.2017
После доработки 05.06.2018
Принята к публикации 13.03.2018

DOI: 10.1134/S0040364419010290

Аннотация

Теоретически исследовано распространение акустических волн в вязкоупругой пузырьковой среде. Приведена линеаризованная система дифференциальных уравнений возмущенного движения такой среды, выведено дисперсионное соотношение. На примере вязкоупругой пузырьковой среды, представляющей собой полидиметилсилоксан с внедренными полидисперсными воздушными пузырьками, рассчитаны зависимости фазовой скорости и коэффициента затухания от частоты колебаний, дано сравнение с известными экспериментальными данными.

ВВЕДЕНИЕ

Распространение акустических волн в пузырьковых средах продолжает оставаться предметом активных исследований. При моделировании динамики пузырьковых систем часто используется континуальный подход, когда двухфазная среда моделируется совокупностью взаимодействующих и взаимопроникающих континуумов [1]. Этот и другие подходы моделирования, а также фундаментальные проблемы физики пузырьковых систем на основе общих принципов описания двухфазных сред изложены в [2]. Основные методы построения уравнений движения двухфазной среды и анализ особенностей континуального подхода приведены в [3]. Поведение пузырьковой среды описывается осредненными уравнениями механики сплошной среды в эйлеровых переменных и дополняется уравнением Рэлея–Плессета для одиночного пузырька. В большинстве моделей, реализуемых в рамках континуального подхода, несущая среда рассматривается как идеальная, а вязкость учитывается лишь в процессах взаимодействия между несущей средой (жидкостью) и несомыми включениями (газовыми пузырями). В [4] в рамках континуального подхода [1] приведены условия, при которых проявляется сжимаемость несущей среды для задач акустики пузырьковых жидкостей, и предложено развитие модели пузырьковых жидкостей с учетом акустической разгрузки пузырьков. Полученные решения сопоставлены с экспериментальными результатами. Некоторые уточнения результатов этой работы приведены в [5]. Аналитическое решение задачи о пульсациях газового пузырька под действием внешних колебаний давления получено в [6], подробно описаны границы применимости допущения о гомобаричности давления внутри пузырька. Несущая фаза пузырьковой среды может обладать и вязкоупругими свойствами, это необходимо учитывать, например, в биомедицинской акустике [7] и при получении метаматериалов с особыми акустическими свойствами [8]. В [7] изучается механика одиночного пузырька в биологических вязкоупругих тканях. В [8] исследуется искусственная вязкоупругая среда, обладающая высокой дисперсией, демонстрирующая пики в затухании и фазовую скорость как функции частоты, которые не могут быть точно описаны без учета упругости несущей фазы.

В настоящей работе дано развитие теоретической модели в рамках континуального подхода [1], описывающей динамику акустических волн в полидисперсной вязкоупругой пузырьковой среде с учетом межфазного теплообмена.

ДИСПЕРСИОННОЕ СООТНОШЕНИЕ

Для анализа волновых процессов в пузырьковой жидкости часто используется односкоростная схема, учитывающая основную особенность такой среды – радиальную инерцию и вязкость жидкости [1]. В рамках допущений континуального подхода [1] в системе координат, связанной с невозмущенной средой, записываются линеаризованные уравнения сохранения масс, числа пузырьков, импульса и уравнение неразрывности в пузырьках:

(1)

$\frac{{\partial \rho _{j}^{'}}}{{\partial t}} + {{\rho }_{{j0}}}\frac{{\partial \text{v}{\text{'}}}}{{\partial x}} = 0,\,\,\,\,j = l,g,$

(2)

$\frac{{\partial n{\text{'}}}}{{\partial t}} + {{n}_{0}}\frac{{\partial \text{v}{\text{'}}}}{{\partial x}} = 0,\,\,\,\,n = \int\limits_{{{a}_{{\min }}}}^{{{a}_{{\max }}}} {N(a)da} ,$

(3)

$\left( {{{\rho }_{{l0}}} + {{\rho }_{{g0}}}} \right)\frac{{\partial \text{v}{\text{'}}}}{{\partial t}} + \frac{{\partial p_{l}^{'}}}{{\partial x}} = 0,$

(4)

$\begin{gathered} \frac{{\partial p_{g}^{'}}}{{\partial t}} = - 3{{\gamma }_{g}}{{p}_{0}}\frac{{w{\text{'}}}}{a} - 3\left( {{{\gamma }_{g}} - 1} \right)\frac{q}{a},\,\,\,\,w{\text{'}} = \frac{{\partial a{\text{'}}}}{{\partial t}}, \\ \rho {\kern 1pt} {}_{j}\, = \rho _{j}^{^\circ }{{\alpha }_{j}},\,\,\,\,{{\alpha }_{l}} + {{\alpha }_{g}} = 1,\,\,\,\,{{\alpha }_{g}} = \frac{4}{3}\pi \int\limits_{{{a}_{{\min }}}}^{{{a}_{{\max }}}} {N(a){{a}^{3}}da} . \\ \end{gathered} $

Здесь и далее $\rho ^\circ ,$ $\rho $ – истинная и средняя плотности; $\text{v}$ – скорость; $p$ – давление; $n$ – число пузырьков в единице объема смеси; ${{\gamma }_{g}}$ – показатель адиабаты газа; $w$ – скорость радиального движения пузырьков; $\alpha $ – объемное содержание; $N(a)$ – функция распределения пузырьков газа по размерам; a – радиус пузырька; $x$ – координата; $t$ – время. Нижние индексы $l$ и $g$ относятся к параметрам жидкой и газовой фаз соответственно, индексом 0 обозначено первоначально невозмущенное состояние. Штрихи обозначают возмущения параметров.

Для несущей среды используется линеаризованное уравнение состояния акустически сжимаемой жидкости

(5)

$p_{l}^{'}\, = C_{l}^{2}\rho _{l}^{{'^\circ }},$

где ${{C}_{l}}$ – скорость звука в жидкости, для дисперсной фазы – уравнение состояния совершенного газа

(6)

${{p}_{g}} = \rho _{g}^{^\circ }{{R}_{g}}{{T}_{g}},$

где ${{R}_{g}}$ – газовая постоянная.

Согласно [4], для определения интенсивности межфазного теплообмена $q$ принимается следующее соотношение:

(7)

$\begin{gathered} q = (i\omega )ap_{g}^{'}{{[y\operatorname{cth} (y) - 1]} \mathord{\left/ {\vphantom {{[y\operatorname{cth} (y) - 1]} {{{y}^{2}}}}} \right. \kern-0em} {{{y}^{2}}}}, \\ y = \sqrt {{{ - i\omega {{a}^{2}}} \mathord{\left/ {\vphantom {{ - i\omega {{a}^{2}}} {{{\kappa }_{g}}}}} \right. \kern-0em} {{{\kappa }_{g}}}}} ,\,\,\,\,{{\kappa }_{g}} = \frac{{{{\lambda }_{g}}}}{{{{c}_{g}}\rho _{{g0}}^{^\circ }}}. \\ \end{gathered} $

Здесь $\omega $ – частота возмущений; ${{\kappa }_{g}},$ ${{\lambda }_{g}}$ – коэффициенты температуропроводности и теплопроводности газа; ${{c}_{g}}$ – теплоемкость газовой фазы при постоянном давлении. Соотношение (7) получается из решения уравнения теплопроводности для газового пузырька с соответствующими граничными условиями. Следует отметить, что решения задачи о теплоотдаче на поверхности пульсирующего пузырька типа (7) получены на основе допущения об однородности распределения давления по объему пузырька. Это допущение выполняется, если радиальная скорость стенок пузырька много меньше скорости звука в газе. Согласно оценке, приведенной в [6], если время ${{t}_{1}} = {{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {{{C}_{g}}}}} \right. \kern-0em} {{{C}_{g}}}}$ (${{C}_{g}}$ – скорость звука в газовой фазе), за которое звуковая волна проходит расстояние порядка радиуса пузырька ${{a}_{0}},$ много меньше времени периода пульсаций внешнего давления ${{t}_{2}} = {1 \mathord{\left/ {\vphantom {1 \omega }} \right. \kern-0em} \omega },$ то распределение давления внутри пузырька будет практически однородным. Таким образом, должно выполняться условие [6]

$\frac{{{{t}_{1}}}}{{{{t}_{2}}}} = \frac{{{{a}_{0}}\omega }}{{{{C}_{g}}}} \ll 1.$

При значениях параметров ${{a}_{0}} \sim {{10}^{{ - 4}}},$ $\omega \sim {{10}^{5}},$ ${{C}_{g}} \sim 300$ условие гомобаричности выполняется.

При описании радиального движения, согласно уточнению, приведенному в [4], полагается, что возмущение массовой радиальной скорости жидкости на поверхности раздела фаз $w{\text{'}}$ состоит из двух слагаемых: $w{\text{'}} = w_{R}^{'} + w_{A}^{'}.$ Слагаемое $w_{A}^{'},$ учитывающее сжимаемость несущей фазы, определяется из решения задачи о разгрузке сферического пузырька в жидкости в акустическом приближении [4]:

(8)

$w_{A}^{'} = \frac{{p_{g}^{'} - p_{l}^{'}}}{{\rho _{{l0}}^{ \circ }{{C}_{l}}\alpha _{{g0}}^{\beta }}},\,\,\,\,\beta = \frac{1}{6}.$

Аналогично [5], используется уточнение формулы (8) для акустических поправок из [4], для чего $\beta $ полагается равной 1/6 вместо 1/3. Слагаемое $w_{R}^{'},$ описывающее динамику вязкоупругой жидкости вокруг пузырька, определяется уравнением Рэлея–Плессета:

$a\frac{{{{d}^{2}}a}}{{d{{t}^{2}}}} + \frac{3}{2}{{\left( {\frac{{da}}{{dt}}} \right)}^{2}} = \frac{{p(a) - p(\infty )}}{{\rho _{l}^{ \circ }}}.$

Для расчета давления на границе пузырька радиусом a в несжимаемой вязкоупругой жидкости используется [7]

$p(a) = {{p}_{1}} - \frac{{2\sigma }}{a} - \int\limits_a^\infty {\frac{{{{\tau }_{{rr}}}}}{r}dr} ,$

где $\sigma $ – коэффициент поверхностного натяжения, ${{\tau }_{{rr}}}$ – радиальная (нормальная) компонента тензора напряжений на поверхности пузырька, r – радиальная координата. Интеграл от ${{\tau }_{{rr}}}$ определяет вклад вязкоупругости несущей фазы в колебания пузырька и, согласно [7], определяется выражением

$3\int\limits_a^\infty {\frac{{{{\tau }_{{rr}}}}}{r}dr} = - \left[ {\frac{{4G}}{{3{{a}^{3}}}}\left( {{{a}^{3}} - a_{0}^{3}} \right) + \frac{{4\mu }}{a}\frac{{da}}{{dt}}} \right].$

Здесь $G$ – модуль сдвига, $\mu $ – динамическая вязкость.

Если радиус пузырька изменяется по гармоническому закону $a(t)\sim {{a}_{0}}\exp ( - i\omega t),$ с учетом линеаризации уравнение Рэлея–Плессета имеет вид

(9)

${{a}_{0}}\frac{{\partial w_{R}^{'}}}{{\partial t}} = \frac{{p_{g}^{'} - p_{l}^{'}}}{{\rho _{{l0}}^{ \circ }}} - \frac{{4\mu _{l}^{*}}}{{{{a}_{0}}\rho _{{l0}}^{ \circ }}}a{\text{'}},$

где $\mu _{l}^{*} = {{G}_{l}} - i\omega {{\mu }_{l}}$ – комплексный модуль сдвига, ${{G}_{l}}$ определяет его упругую часть, $\omega {{\mu }_{l}}$ – вязкую часть.

Таким образом, получается замкнутая система уравнений (1)–(9), решение которой ищется в виде плоских прогрессивных волн для возмущений параметров пузырьковой жидкости $\psi {\text{'}}$ ($\psi = p,\,\rho ,\,\text{v},...$):

(10)

$\psi {\text{'}} = {{A}_{\psi }}\exp [i(K{\text{*}}x - \omega t)].$

Здесь ${{A}_{\psi }}$ – амплитуда возмущения параметра $\psi ,$ ${{K}_{*}} = K + i{{K}_{{{\text{**}}}}}$ – комплексное волновое число, ${{K}_{{{\text{**}}}}}$ – линейный коэффициент затухания, фазовая скорость определяется как ${{C}_{p}} = {\omega \mathord{\left/ {\vphantom {\omega K}} \right. \kern-0em} K}$. Из условия существования нетривиального решения (10) системы (1)–(9) получается следующая зависимость комплексного волнового числа ${{K}_{*}}$ от частоты возмущений $\omega {\kern 1pt} {\text{:}}$

(11)

$\begin{gathered} {{\left( {\frac{{{{K}_{*}}}}{\omega }} \right)}^{2}} = \frac{1}{{C_{f}^{2}}} + \\ + \,\,\int\limits_{{{a}_{{\min }}}}^{{{a}_{{\max }}}} {\frac{{4\pi aN(a){{\alpha }_{{l0}}}{{\rho }_{{l0}}}Q}}{{3{{\gamma }_{g}}{{p}_{0}} + \left( {4{{G}_{l}} - {{\omega }^{2}}\rho _{{l0}}^{ \circ }{{a}^{2}} - i4{{\mu }_{l}}} \right)S}}} da, \\ \end{gathered} $

$\begin{gathered} {{C}_{f}} = {{{{C}_{l}}} \mathord{\left/ {\vphantom {{{{C}_{l}}} {{{\alpha }_{{l0}}}}}} \right. \kern-0em} {{{\alpha }_{{l0}}}}},\,\,\,\,S = \frac{Q}{{1 - i\omega {{t}_{A}}}}, \\ Q = 1 + 3({{\gamma }_{g}} - 1){{(y{\text{cth(}}y{\text{)}} - 1)} \mathord{\left/ {\vphantom {{(y{\text{cth(}}y{\text{)}} - 1)} {{{y}^{2}}}}} \right. \kern-0em} {{{y}^{2}}}}, \\ {{t}_{a}} = {a \mathord{\left/ {\vphantom {a {\left( {{{C}_{l}}{{{{\text{(}}{{\alpha }_{{g0}}}{\text{)}}}}^{\beta }}} \right)}}} \right. \kern-0em} {\left( {{{C}_{l}}{{{{\text{(}}{{\alpha }_{{g0}}}{\text{)}}}}^{\beta }}} \right)}}{\text{,}}\,\,\,\,\beta = \frac{1}{6}. \\ \end{gathered} $

РЕЗУЛЬТАТЫ РАСЧЕТОВ

В работе [8] представлены результаты измерений зависимостей фазовой скорости и коэффициента затухания акустических волн в образце с полидисперсными воздушными пузырьками, внедренными в упругую несущую среду. В качестве несущей среды использовался полидиметилсилоксан (PDMS RTV-615) – материал из силиконового каучука с добавлением отвердителей. Для функции распределения пузырьков по размерам принималось соотношение [8]

(12)

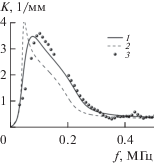
$\begin{gathered} N{\text{(}}a{\text{)}} = \frac{{{{N}_{0}}}}{{\sqrt {2\pi } \varepsilon a}}{\text{exp}}\left( { - \frac{{{{{\left( {{\text{ln}}\left( {{a \mathord{\left/ {\vphantom {a {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}} \right)} \right)}}^{2}}}}{{2{{\varepsilon }^{2}}}}} \right), \\ {{N}_{0}} = \frac{{3{{\alpha }_{{g0}}}}}{{4\pi a_{0}^{3}{\text{exp}}\left( {{{9{{\varepsilon }^{2}}} \mathord{\left/ {\vphantom {{9{{\varepsilon }^{2}}} 2}} \right. \kern-0em} 2}} \right)}} \\ \end{gathered} $

с параметрами ${{a}_{0}} = 0.15$ мм, $\varepsilon = 0.25$ в диапазоне от ${{a}_{{\min }}} = 0.05$ мм до ${{a}_{{\max }}} = 0.35$ мм. Объемное содержание пузырьков ${{\alpha }_{{g0}}} = 0.02.$ В численных расчетах использовались следующие значения теплофизических параметров при ${{p}_{0}} = 0.1\,\,{\text{М П а ,}}$ ${{T}_{0}} = 300\,\,{\text{K:}}$ для воздуха $\rho _{{g0}}^{ \circ } = 1.3\,\,{\text{к г /}}{{{\text{м }}}^{{\text{3}}}},$ ${{\gamma }_{g}} = 1.4,$ ${{\lambda }_{g}} = 0.0026\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\left( {{\text{м }}\,{{\rm K}}} \right)}}} \right. \kern-0em} {\left( {{\text{м }}\,{{\rm K}}} \right)}},$ c_g = $1006\,\,{{{\text{Д ж }}} \mathord{\left/ {\vphantom {{{\text{Д ж }}} {{\text{(к г }}\,{{\rm K});}}}} \right. \kern-0em} {{\text{(к г }}\,{{\rm K});}}}$ для полидиметилсилоксана ${{C}_{l}} = 1020\,\,{\text{м /с ,}}$ $\rho _{{l0}}^{ \circ }$ = = 965 кг/м³. Для определения действительной и мнимой частей модуля сдвига, согласно [8], применялись следующие выражения: G_l = = $(0.6 + 0.7f)\,\,{\text{М П а ,}}$ ${{\mu }_{l}} = (0.2 + 1.8f)\,\,{\text{М П а ,}}$ где $f$ – частота возмущений (МГц).

На рис. 1 и 2 сравниваются результаты расчетов по предложенной модели при использовании дисперсионного соотношения (11) с данными эксперимента [8]. Также приводятся результаты расчета с теми же параметрами смеси, но по модели, изложенной в [9] без учета упругости несущей фазы. В последнем случае коэффициент затухания и фазовая скорость определяются неправильно, частоты максимальных значений и амплитуды меньше экспериментальных данных. Эти результаты свидетельствуют о том, что модель, в которой упругость несущей фазы не учитывается, для описания динамики акустических волн в полидиметилсилоксане с пузырьками воздуха не годится. Предложенная модель вязкоупругой пузырьковой среды существенно лучше описывает эксперимент. Хотя в расчетах по обеим моделям наблюдается характерный для пузырьковых сред вид кривых фазовой скорости и коэффициента затухания [1], при учете упругости несущей фазы заметен сдвиг пиковых значений кривых в сторону более высоких частот. Для модели [9] пик затухания акустических волн приходится на частоту, соответствующую резонансной частоте Миннаэрта:

${{f}_{{\text{M}}}} = \frac{1}{{2\pi {{a}_{0}}}}\sqrt {\frac{{3{{\gamma }_{g}}{{p}_{0}}}}{{\rho _{{l0}}^{ \circ }}}} .$

Рис. 1.

Зависимость фазовой скорости от частоты возмущений для полидисперсной смеси геля с воздушными пузырьками: 1 – расчет по (11), 2 – расчет по [9], 3 – эксперимент [8].

Рис. 2.

Зависимость коэффициента затухания от частоты возмущений для полидисперсной смеси геля с воздушными пузырьками: 1 – расчет по (11), 2 – расчет по [9], 3 – эксперимент [8].

Радиус ${{a}_{0}}$ – параметр используемой функции распределения (12). В случае учета упругости, максимальное значение смещается и соответствует резонансной частоте

${{f}_{{\text{M}}}} = \frac{1}{{2\pi {{a}_{0}}}}\sqrt {\frac{{3{{\gamma }_{g}}{{p}_{0}} + 4{{G}_{l}}}}{{\rho _{{l0}}^{ \circ }}}} ,$

которая превышает резонансную частоту Миннаэрта, что и наблюдается в эксперименте [8].

ЗАКЛЮЧЕНИЕ

Сопоставление с экспериментальными результатами показало применимость представленной теоретической модели для описания динамики акустических волн в вязкоупругих пузырьковых средах.

Список литературы

Нигматулин Р.И. Динамика многофазных сред. Ч. 1, 2. М.: Наука, 1987.
Avdeev A.A. Bubble Systems. Switzerland: Springer Int. Publ., 2016.
Вараксин А.Ю. Гидрогазодинамика и теплофизика двухфазных потоков: проблемы и достижения // ТВТ. 2013. Т. 51. № 3. С. 421.
Нигматулин Р.И., Шагапов В.Ш., Вахитова Н.К. Проявление сжимаемости несущей жидкости при распространении волн в пузырьковой среде // ДАН СССР. 1989. Т. 304. № 5. С. 1077.
Нигматулин Р.И., Губайдуллин Д.А., Федоров Ю.В. Звуковые волны в двухфракционных полидисперсных пузырьковых жидкостях // ДАН. 2012. Т. 447. № 3. С. 284.
Авдеев А.А. Пульсации газового пузыря в акустическом поле (резонанс и границы политропического приближения) // ТВТ. 2014. Т. 52. № 6. С. 875.
Yang X., Church C.C. A Model for the Dynamics of Gas Bubbles in Soft Tissue // J. Acoust. Soc. Am. 2005. V. 118. № 6. P. 3595.
Leroy V., Strybulevych A.L., Page J.H., Scanlon M.G. Influence of Positional Correlations on the Propagation of Waves in a Complex Medium with Polydisperse Resonant Scatterers // Phys. Rev. E. 2011. V. 83. № 4. 046605.
Губайдуллин Д.А., Никифоров А.А. Взаимодействие акустического сигнала с неподвижной дискретно-слоистой средой, содержащей слой пузырьковой жидкости // ТВТ. 2017. Т. 55. № 1. С. 102.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал