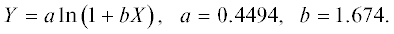Теплофизика высоких температур, 2019, T. 57, № 1, стр. 4-10
Особенности учета атом-атомного и ион-атомного взаимодействия в газах при наличии процессов диссоциации
А. Л. Хомкин 1, *, А. С. Шумихин 1, **
1 Объединенный институт высоких температур РАН,
Москва, Россия
* E-mail: alhomkin@mail.ru
** E-mail: shum_ac@mail.ru
Поступила в редакцию 03.03.2018
После доработки 05.06.2018
Принята к публикации 15.05.2018
Аннотация
Рассмотрена проблема выбора потенциала взаимодействия “свободных” частиц и расчета вириальных поправок на межатомное и ион-атомное взаимодействие в химических моделях с реакциями диссоциации. Проведен критический анализ используемых в литературе потенциалов. Предложены простые формулы для расчета вириальных поправок с учетом ограничений фазового пространства двух частиц. Даны некоторые рекомендации по их использованию.
ВВЕДЕНИЕ
К настоящему времени достигнут большой прогресс в статистической теории неидеальных (плотных) газов и плазмы [1, 2]. Одним из распространенных методов расчета уравнения состояния, равновесного состава и на их основе кинетических коэффициентов стал метод смеси и построенные на его основе химические, многокомпонентные газоплазменные модели. Возникает вопрос, почему такое разнообразие химических моделей [3], например, для водорода, инертных газов и паров металлов [4–10], если все они строятся на достаточно строгих и общих теоретических результатах. Большинство различий между моделями обусловлено выбором межчастичных потенциалов и способом расчета поправок на взаимодействие “свободных” частиц как нейтральных, так и заряженных. И следует признать, что единое мнение в этом вопросе до настоящего времени отсутствует.
Происхождение этой проблемы давно установлено и связано с переходом от физической к химической модели (модели смеси) [11]. Действительно, в физической модели рассмотрение начинается с ансамбля “исходных” частиц, например электронов и ядер для плазмы. Потенциал взаимодействия между ними известен – это кулоновский потенциал. Атомы возникают как результат взаимодействия электронов и ядер. А как будут взаимодействовать электроны и ядра в модели смеси, будучи продуктами ионизации атомов? Аналогичный вопрос возникает, конечно, и при рассмотрении атомарно-молекулярной смеси. Потенциал взаимодействия двух атомов водорода хорошо известен, он рассчитывается квантово-механически [1]. Но в многочисленных реализациях модели смеси для газоплазменных состояний потенциал взаимодействия диссоциированных или ионизованных частиц (иногда называются “свободными”) атомов, электронов и ионов, как правило, отличается от потенциала взаимодействия исходных частиц [3–10]. Если в атомарно-молекулярной смеси решить уравнения диссоциативного равновесия для “свободных” атомов, взаимодействующих с исходным потенциалом, вновь получим существенное количество молекул.
Последовательный расчет термодинамических функций атомарной плазмы в рамках метода исходных частиц выполнен в пионерской работе Веденова и Ларкина [12], а для частично диссоциированных молекулярных газов в работе Семенова [13]. Однако использование полученных результатов в расчетах при переходе к высоким плотностям и к большому числу компонент оказалось затруднительным. Дело в том, что численные методы и весьма популярная жидкостная теория возмущений применительно к атомарно-молекулярным и газоплазменным смесям требует для своей реализации аналитические потенциалы взаимодействия продуктов ионизации и диссоциации. Основы последовательной теории, формально приводящей к такому потенциалу, заложены в работах [14, 15], но конкретные аналитические соотношения до сих пор не получены в связи со сложностью потенциала и его зависимостью от импульса относительного движения частиц.
Проблема существует уже в простейшем варианте модели смеси – в идеальном приближении, когда взаимодействие между частицами смеси отсутствует. Рассмотрим идеальную атомарную плазму, состоящую из электронов, ионов и атомов. Это неплохое приближение для экспресс-расчетов, но в нем содержится парадокс: атомы существуют в результате кулоновского взаимодействия электронов и ядер, но оно отсутствует между свободными ионами и электронами. Аналогичный парадокс характерен и для частично диссоциированного молекулярного водорода, да и для других молекулярных газов.
Речь в данной ситуации может идти лишь о псевдопотенциале, и таковой был предложен Хиллом в [16] для описания взаимодействия “свободных” атомов в атомарно-молекулярной смеси. Зависимость псевдопотенциала “по Хиллу” от температуры ограничила область его применения. При переходе к большим плотностям, возникающим при сжатии частично диссоциированных молекулярных газов, весьма популярным стал потенциал “экспонента-6”, предложенный еще в [17]. Он "получен” как сумма синглетного и триплетного термов межатомного потенциала при усреднении по суммарному спину. Этот потенциал, хотя и не имеет строгого теоретического обоснования, получил довольно широкое распространение [4, 5, 18, 19]. В некоторых работах для учета ион-атомного взаимодействия вириальные поправки рассчитываются с использованием классического вириального коэффициента для поляризационного потенциала, обрезанного на “размере” атома, несмотря на наличие в смеси связанных ион-атомных частиц (молекулярных ионов водорода, например) [20]. Как возможный выбор псевдопотенциалов в [7] предложен оригинальный феноменологический способ расчета поправки на взаимодействие тяжелых частиц в виде степенной функции объема, зависящей от нескольких параметров. Этот способ требует “настройки” – подборки параметров для каждой рассматриваемой газоплазменной смеси. К псевдопотенциальной группе можно отнести и известный потенциал “с полочкой” (см. [2]) для описания взаимодействия “свободных” электронов и ионов в частично ионизованной плазме. В серии работ [21, 22] для водорода предложено учитывать межатомное взаимодействие как коллективное, когезионное, не зависящее от температуры и зависящее только от плотности.
В настоящей работе выполнен сравнительный анализ вышеупомянутых подходов для учета межатомного и ион-атомного взаимодействий на примере частично диссоциированного и ионизованного водорода. Предложены простые расчетные формулы для вириальных поправок “по Хиллу”. На основе анализа поправок в достаточно широком диапазоне реальных плотностей и температур сформулированы конкретные рекомендации для их использования в химических моделях. Проблема электрон-ионного псевдопотенциала рассмотрена в [23].
ОСНОВНЫЕ СООТНОШЕНИЯ
Ограничим рассмотрение атом-атомным и ион-атомным взаимодействиями. В принципе соответствующие потенциалы взаимодействия или их компоненты (например, дальнодействующие ветви) можно вычислить аналитически, но чаще используются феноменологические потенциалы, среди которых наиболее популярны потенциалы Леннарда-Джонса
(1)
${{V}_{{n,m}}}\left( {\Delta E,\sigma ,r} \right) = \frac{{\Delta E\quad{{{\left( {{n \mathord{\left/ {\vphantom {n m}} \right. \kern-0em} m}} \right)}}^{{{n \mathord{\left/ {\vphantom {n {\left( {n - m} \right)}}} \right. \kern-0em} {\left( {n - m} \right)}}}}}}}{{1 - \left( {{m \mathord{\left/ {\vphantom {m n}} \right. \kern-0em} n}} \right)}}\left[ {{{{\left( {\frac{\sigma }{r}} \right)}}^{n}} - {{{\left( {\frac{\sigma }{r}} \right)}}^{m}}} \right],$Введем межатомный ${{V}_{{aa}}}\left( r \right) = {{V}_{{12,6}}}\left( {\Delta {{E}_{{aa}}},{{\sigma }_{{aa}}},r} \right)$ и ион-атомный ${{V}_{{ia}}}\left( r \right) = {{V}_{{12,4}}}\left( {\Delta {{E}_{{ia}}},{{\sigma }_{{ia}}},r} \right)$ потенциалы взаимодействия. Первая поправка на взаимодействие частиц определяется вторым вириальным коэффициентом. Вводя безразмерные переменные ${{{\varepsilon }}_{{aa}}} = {\beta }\Delta {{E}_{{aa}}},$ $x = {r \mathord{\left/ {\vphantom {r {{{\sigma }_{{aa}}}}}} \right. \kern-0em} {{{\sigma }_{{aa}}}}}\quad$ (${\beta } = {1 \mathord{\left/ {\vphantom {1 {kT}}} \right. \kern-0em} {kT}}$ – обратная температура), для межатомного взаимодействия, например, имеем
(2)
${{B}_{{aa}}}\left( {{{\sigma }_{{aa}}},{{{\varepsilon }}_{{aa}}}} \right) = \frac{{4\pi \sigma _{{aa}}^{3}}}{3}\quad{{F}_{{aa}}}\left( {{{{\varepsilon }}_{{aa}}}} \right),$(3)
${{F}_{{aa}}}\left( {{{{\varepsilon }}_{{aa}}}} \right) = 3\mathop \smallint \limits_0^\infty {{x}^{2}}\left[ {\exp \left( { - 4{{{\varepsilon }}_{{aa}}}\left( {\frac{1}{{{{x}^{{12}}}}} - \frac{1}{{{{x}^{6}}}}} \right)} \right) - 1} \right]dx.$Аналогично можно факторизовать вириальный коэффициент и для ион-атомного взаимодействия.
В работах Хилла показано, что в газах, в которых возможны химические реакции, вместо (2), (3) необходимо использовать модифицированный второй вириальный коэффициент:
(4)
$B_{{aa}}^{H}\left( {{{\sigma }_{{aa}}},{{{\varepsilon }}_{{aa}}}} \right) = \frac{{4\pi \sigma _{{aa}}^{3}}}{3}F_{{aa}}^{H}\left( {{{{\varepsilon }}_{{aa}}}} \right),$(5)
$\begin{gathered} F_{{aa}}^{H}\left( {{{{\varepsilon }}_{{aa}}}} \right) = 3\mathop \smallint \limits_0^1 {{x}^{2}}dx\left[ {{\text{exp}}\left( { - {\beta }{{V}_{{aa}}}\left( x \right)} \right) - 1} \right] + \\ + \,\,3\mathop \smallint \limits_1^\infty {{x}^{2}}dx\left[ {\exp \left( { - {\beta }{{V}_{{aa}}}\left( x \right)} \right)\frac{{{\Gamma }\left( {\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right) - {\beta }{{V}_{{aa}}}\left( x \right)} \right)}}{{{\Gamma }\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}} - 1} \right]. \\ \end{gathered} $Первое слагаемое в (5) описывает вклад отталкивательной ветви потенциала, а второе – вклад его притягивательной ветви. Отличие (5) от (3) состоит в том, что для области, где потенциал ${{V}_{{aa}}}\left( r \right)$ отрицательный, интегрирование во втором слагаемом проводится по ограниченному фазовому пространству, соответствующему положительным энергиям относительного движения атомов, т.е. состояниям непрерывного спектра движения двух тел. Вклады отталкивательных ветвей (3), (5) не меняются.
В [24] на основе формулы (5) рассмотрен псевдопотенциал “по Хиллу”. Его отталкивательная ветвь $({{V}_{{aa}}}\left( r \right) > 0)$ не меняется и совпадает с исходной, а притягивательная ветвь вводится с помощью соотношений:
(8)
$Y = X - {\text{ln}}\left[ {1 - \frac{2}{{\sqrt \pi }}\mathop \smallint \limits_0^X {{{\text{e}}}^{{ - t}}}\sqrt t dt} \right].$В (6)–(8) $X$ – исходный безразмерный потенциал с обратным знаком, а $Y$ – соответствующий псевдопотенциал “по Хиллу”.
В [24] предложена приближенная, но весьма точная формула, которую будем называть формулой Муленко. Для притягивательной ветви потенциала она имеет вид
На рис. 1 сравниваются расчеты по (7) и соответствующему приближенному выражению
(9)
$R\left( X \right) = {{{\text{e}}}^{Y}} = {\text{exp}}\left( X \right){{{\Gamma }\left( {\frac{3}{2},X} \right)} \mathord{\left/ {\vphantom {{{\Gamma }\left( {\frac{3}{2},X} \right)} {{\Gamma }\left( {\frac{3}{2}} \right)}}} \right. \kern-0em} {{\Gamma }\left( {\frac{3}{2}} \right)}},$Рис. 1.
Зависимость притягивательной ветви псевдопотенциала от исходного потенциала X: 1 – расчет по точной формуле (9), 2 – по формуле Муленко (10).

Для температурного множителя вириального коэффициента “по Хиллу” (5) можно предложить простую аналитическую формулу. Переходя к безразмерным переменным в (5), получим для межатомного потенциала (1) при n = 12, m = 6
(11)
$FM_{{aa}}^{H}\left( {\varepsilon } \right) = 1.2{\varepsilon }\left( {1 - 0.01{\varepsilon }} \right)$(12)
$FM_{{ia}}^{H}\left( {\varepsilon } \right) = 4.29{\varepsilon }\left( {1 - 0.0063{\varepsilon }} \right).$Графики функций ${{F}_{{aa}}}\left( {\varepsilon } \right),$ $F_{{aa}}^{H}\left( {\varepsilon } \right),$ $FM_{{aa}}^{H}\left( {\varepsilon } \right),$ представленные на рис. 2, демонстрируют отличие вириального коэффициента “по Хиллу” от вириального коэффициента (2), (3), а также его близость к расчету по приближенной формуле (11). Аналогично выглядят зависимости и для ион-атомного взаимодействия.
Рис. 2.
Температурный множитель второго вириального коэффициента: 1 – ${{F}_{{aa}}}\left( {\varepsilon } \right)$ по (3), 2 – $F_{{aa}}^{H}\left( {\varepsilon } \right)$ “по Хиллу” (5), 3 – $FM_{{aa}}^{H}\left( {\varepsilon } \right),$ приближенная формула (11).

РАСЧЕТНЫЕ ФОРМУЛЫ
Для использования формул (4), (5) в расчетах необходимо выбрать константы ${\varepsilon }$ и $\sigma {\text{.}}$ Константа ${\varepsilon }$ связана с энергией диссоциации молекулы водорода в расчетах $B_{{aa}}^{H}\left( {{{\sigma }_{{aa}}},{\varepsilon }} \right)$ или молекулярного иона в расчетах $B_{{ia}}^{H}\left( {{{\sigma }_{{ia}}},{\varepsilon }} \right).$ Для выбора константы $\sigma $ есть два варианта. В [24] предложено определить ее через равновесное расстояние атомов в молекуле или молекулярном ионе ${{r}_{{{\text{min}}}}}.$ Однако возможен и другой вариант, предложенный Ликальтером в [25]. Им для описания ион-атомного вириального коэффициента “по Хиллу” использован поляризационный потенциал притяжения без отталкивания
Для такого потенциала интеграл в (6) сходится, и приходим к формуле Ликальтера для ион-атомного вириального коэффициента “по Хиллу”
Ликальтером получено ${{C}_{1}} = 1.61,$ авторами в [10] рекомендовано ${{C}_{1}} = 1.2$ для приближенного учета отталкивания. Представляется, что для учета взаимодействия частиц в непрерывном спектре разумно связать параметр $\sigma $ с притягивательной веткой потенциала, тем более что она может быть рассчитана теоретически. Для ион-атомного потенциала она определяется формулой (13), а для межатомного можно воспользоваться соотношением
Таблица.
Два варианта выбора параметров потенциала взаимодействия
| Атом–атом | |
|---|---|
| ${\varepsilon } = {\beta }{{D}_{{aa}}}$ | |
| $\sigma = {{{{r}_{{{\text{min}}}}}} \mathord{\left/ {\vphantom {{{{r}_{{{\text{min}}}}}} {{{2}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}}}} \right. \kern-0em} {{{2}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}}}$ | $\sigma = {{a}_{0}}{{\left( {\frac{{{{C}_{{VdW}}}Ry}}{{2{{D}_{{aa}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}$ |
| Ион–атом | |
| ${\varepsilon } = {\beta }{{D}_{{ia}}}$ | |
| $\sigma = {{{{r}_{{{\text{min}}}}}} \mathord{\left/ {\vphantom {{{{r}_{{{\text{min}}}}}} {{{3}^{{{1 \mathord{\left/ {\vphantom {1 8}} \right. \kern-0em} 8}}}}}}} \right. \kern-0em} {{{3}^{{{1 \mathord{\left/ {\vphantom {1 8}} \right. \kern-0em} 8}}}}}}$ | $\sigma = {{a}_{0}}\left( {\frac{{2{{\alpha }_{D}}Ry}}{{3\sqrt 3 {{D}_{{ia}}}}}} \right)$ |
Использование приближенных формул (11), (12) сводит расчет вириальных поправок “по Хиллу” к алгебраическим вычислениям, хотя в исходном виде они содержали двойное интегрирование.
Для описания взаимодействия “свободных” частиц химически реагирующей смеси часто используется потенциал
(14)
${\Phi }\left( {\Delta E,\sigma ,r} \right) = \frac{{\Delta E}}{{\alpha - 6}}\left\{ {6{\kern 1pt} {\text{exp}}\left[ {\alpha \left( {1 - \frac{r}{\sigma }} \right)} \right] - \alpha {{{\left( {\frac{\sigma }{r}} \right)}}^{6}}} \right\}.$В (14) отталкивательный член описывается экспоненциальной функцией, а притягивательный – степенной аналогично (1). Для краткости такой потенциал называется “экспонента-6”. Для межатомных, атом-молекулярных и межмолекулярных взаимодействий в частично диссоциированным водороде [4, 5] $\alpha = 13{\kern 1pt} --{\kern 1pt} 11,\quad$ $\Delta E = \left( {20{\kern 1pt} --{\kern 1pt} 36} \right) \times {{10}^{{ - 4}}}$ эВ. Для азота [18] и кислорода [19] константы α близки к водородным, а ΔE намного выше, $\Delta E = \left( {600{\kern 1pt} --{\kern 1pt} 700} \right) \times {{10}^{{ - 4}}}$ эВ, но все равно на порядки величины меньше реальной энергии диссоциации молекул, составляющих от нескольких эВ для водорода до десятка эВ для азота. Поправки на взаимодействие рассчитываются с использованием классического вириального коэффициента (2), (3). Весьма популярны они и в жидкостной теории возмущений при интегрировании с корреляционными функциями базовой системы твердых шаров [4, 5]. По мнению авторов, такая популярность этих потенциалов неоправданна, так как теоретическое обоснование у них слабое. Сумма триплетной и синглетной ветвей потенциала в реальных условиях не реализуется. Складываются соответствующие вириальные коэффициенты, тогда притягивательный терм “по Больцману” всегда дает больший вклад. Формально, можно говорить о сложении термов лишь в пределе высоких температур, где поправки малы. Главная особенность и достоинство потенциала “экспонента-6”, на взгляд авторов, – преимущественно отталкивательный характер взаимодействия “свободных” частиц при практически полном отсутствии притяжения в диапазоне существования частичной диссоциации. Это – область температур порядка 1 эВ.
Возможен еще один способ учета межатомного взаимодействия – когезионные силы сцепления, характерные для жидких щелочных металлов. В [26] на основе теории Бардина в решеточном приближении рассчитана когезия атомарного водорода ${{E}_{{{\text{coh}}}}}{\kern 1pt} \left( y \right),$ где $y = {{{{{\left( {\left( {{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}} \right)\pi {{n}_{a}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \mathord{\left/ {\vphantom {{{{{\left( {\left( {{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}} \right)\pi {{n}_{a}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}$ – радиус атомарной ячейки Вигнера–Зейтца в боровских радиусах, ${{n}_{a}}$ – концентрация атомов. Для атомарного водорода она может быть аппроксимирована универсальной функцией UBER [27] (в эВ):
(15)
${{E}_{{{\text{coh}}}}}\left( y \right) = - 2.5\left( {1 + \frac{{y - 1.55}}{{0.42}}} \right){\text{exp}}\left( { - \frac{{y - 1.55}}{{0.42}}} \right).$С использованием (15) в [26] предсказан фазовый переход пар–жидкость в гипотетическом водороде – атомарном без молекул. Воспользуемся этой величиной для предельных оценок роли межатомного взаимодействия при переходе к высоким плотностям.
Проведем классификацию подходов, используемых для учета эффектов неидеальности. Рассмотрим использование метода исходных частиц (МИЧ) и метод смеси (МС) в каноническом (КА) и большом каноническом (БКА) ансамблях.
МИЧ в КА. Нет проблем в теории молекулярных и инертных газов без химических реакций. Потенциалы взаимодействия достаточно хорошо известны. Возможно теоретическое рассмотрение флюидных, жидкостных и твердотельных состояний с использованием жидкостной теории возмущений и численных методов. Последовательный учет образования связанных состояний практически невозможен. Сюда можно отнести теорию электролитов Дебая–Хюккеля с кулоновским потенциалом взаимодействия между зарядами [2], но без учета бьерумовских пар (в плазме атомов). По мнению авторов, именно это обстоятельство создает известные проблемы при переходе к большим плотностям.
МИЧ в БКА. С использованием потенциала взаимодействия между “исходными” частицами получены первые члены разложения большого термодинамического потенциала по степеням активности, которое описывает образование связанных состояний и взаимодействие частиц в непрерывном спектре. Получены фундаментальные результаты для атомарной плазмы [12] и диссоциированных молекулярных газов [13]. Использование результатов в многокомпонентных моделях смеси практически невозможно. Аналитически выйти за рамки полученных соотношений трудно. Часть квантового вириального коэффициента, связанная с взаимодействием частиц в непрерывном спектре, рассмотрена Хиллом [16] и может быть использована в моделях смеси в качестве первой поправки на взаимодействие “свободных” частиц [9].
МС в КА. Теоретический метод расчета термодинамических функций, состава, а на их основе электрофизических и оптических характеристик газоплазменных систем в широком диапазоне параметров [3] считается в настоящее время наиболее распространенным. Последовательный вывод модели смеси фактически отсутствует. Имеются нерешенные до настоящего времени вопросы, и среди них главный – выбор потенциалов и учет взаимодействия “свободных” частиц. Учету взаимодействия “свободных” заряженных частиц посвящены сотни статей, но эта тема не закрыта до сих пор и исследования продолжаются [2]. Особенно остро встает вопрос об учете кулоновского взаимодействия при переходе в область ионизованного флюида [28]. Нет единого мнения и при расчете поправок на межатомное и ион-атомное взаимодействия.
РАСЧЕТЫ ВИРИАЛЬНЫХ КОЭФФИЦИЕНТОВ И АНАЛИЗ РЕЗУЛЬТАТОВ
Вириальные коэффициенты имеют размерность объема, а безразмерные поправки к свободной энергии и другим термодинамическим функциям описываются соотношениями вида ${{n}_{a}}{{B}_{{aa}}}$ или ${{n}_{a}}{{B}_{{ia}}}.$ Для когезионной поправки имеем ${{n}_{a}}\beta {{E}_{{{\text{coh}}}}}\left( y \right).$
На рис. 3 нанесены вириальные поправки “по Хиллу” для двух вариантов их расчета (см. таблицу) в зависимости от $y.$ Они отрицательны, что отвечает притяжению “свободных” частиц. Температура равна 0.45
эВ, $\varepsilon = $ 10. Интервал значений $y = 25{\kern 1pt} --{\kern 1pt} 2.5$ соответствует диапазону плотности атомов ${{10}^{{20}}}{\kern 1pt} --{\kern 1pt} {{10}^{{23}}}$ см–3,  – твердотельным концентрациям. Можно сделать вывод, что в газовой и даже в области
флюида межатомные поправки, рассчитанные “по Хиллу”, невелики. Значительно меньше
поправка, вычисленная с потенциалом “экспонента-6” (14) (на рис. 3 не показана). Обращает на себя внимание близость поправок “по Хиллу” между собой
и с когезионной. Видно большое отличие от классической (2), (3). Весьма важно подчеркнуть
плавный переход поправок “по Хиллу” в когезионную, что может служить определенным
обоснованием ее использования в предложенной ранее модели “3+” [28].
– твердотельным концентрациям. Можно сделать вывод, что в газовой и даже в области
флюида межатомные поправки, рассчитанные “по Хиллу”, невелики. Значительно меньше
поправка, вычисленная с потенциалом “экспонента-6” (14) (на рис. 3 не показана). Обращает на себя внимание близость поправок “по Хиллу” между собой
и с когезионной. Видно большое отличие от классической (2), (3). Весьма важно подчеркнуть
плавный переход поправок “по Хиллу” в когезионную, что может служить определенным
обоснованием ее использования в предложенной ранее модели “3+” [28].
Рис. 3.
Вириальные поправки ${{n}_{a}}{{B}_{{aa}}}\quad$для межатомного взаимодействия при ${\varepsilon } = 10$: 1 – расчет “по Хиллу”, первый вариант; 2 – то же по второму варианту; 3 – прямой классический вариант; 4 – когезионная поправка.

На рис. 4 ${\varepsilon } = 0.1,$ что соответствует высокой температуре ∼45 эВ. При высоких температурах вириальные поправки, рассчитанные “по Хиллу” (первый вариант), и прямые совпадают, что обусловлено определяющим влиянием отталкивания. Некоторое отклонение расчета по второму варианту понятно. Точно описывая дальнодействующую часть потенциала, он вносит погрешность в отталкивательную ветвь, главную при высоких температурах. Все поправки невелики и связаны с межатомным отталкиванием. Когезионная энергия этот эффект не описывает. Заметим, что при таких температурах вопрос о межатомных поправках вообще не очень актуален. В смеси практически нет молекул, да и атомов тоже.
Рис. 4.
Вириальные поправки ${{n}_{a}}{{B}_{{aa}}}$ для межатомного взаимодействия при ${\varepsilon } = 0.1$: обозначения те же, что и на рис. 3.

Общая картина для ион-атомных поправок схожая. Выпишем аналитические формулы для атом-атомной ${{n}_{a}}B_{{aa}}^{H}$ и ион-атомной ${{n}_{a}}B_{{ia}}^{H}$ поправок, рассчитанных по второму варианту:
(16)
$\begin{gathered} {{n}_{a}}B_{{aa}}^{H}\left( {{\varepsilon },y} \right) = \frac{1}{{{{y}^{3}}}}{{\left[ {\frac{{{{C}_{{VdW}}}Ry}}{{2{{D}_{{aa}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}1.213{\varepsilon }\left( {1 - 0.01{\varepsilon }} \right), \\ {\varepsilon } = {\beta }{{D}_{{aa}}}; \\ {{n}_{a}}B_{{ia}}^{H}\left( {{\varepsilon },y} \right) = \frac{1}{{{{y}^{3}}}}{{\left[ {\frac{{2{{\alpha }_{D}}Ry}}{{3\sqrt 3 {{D}_{{ia}}}}}} \right]}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}4.29{\varepsilon }\left( {1 - 0.0063{\varepsilon }} \right), \\ {\varepsilon } = {\beta }{{D}_{{ia}}}. \\ \end{gathered} $Удивительно, что расчетные формулы для вириальных коэффициентов “по Хиллу” заметно проще классических вириальных (2), (3). Расчетная формула Ликальтера для ${{n}_{a}}B_{{ia}}^{H}$ имеет следующий вид:
(17)
${{n}_{a}}B_{{ia}}^{H} = \frac{{3.6}}{{{{y}^{3}}}}{{\left( {{{\alpha }_{D}}\quad{\beta }Ry} \right)}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}.$На рис. 5 представлены зависимости от плотности ион-атомных вириальных поправок “по Хиллу” (5) с использованием приближенной формулы Муленко (16), а также по формуле Ликальтера (17). Для расчета параметров ${\varepsilon },\sigma $ выбран второй вариант. Расчеты близки. Некоторое отличие расчета по формуле Ликальтера связано с влиянием отталкивания при высоких температурах. С уменьшением температуры результаты расчетов сближаются (рис. 6). Важно подчеркнуть, что ион-атомные поправки “по Хиллу” в газовой области ($y > 5$) невелики и для экспресс-расчетов их вполне можно определять по приближенной формуле (16).
Рис. 5.
Вириальные поправки на ион-атомное взаимодействие для водорода (второй вариант) при ${\beta }{{D}_{{ia}}} = 1$: 1 – расчет “по Хиллу” (5), 2 – по формуле Муленко (16), 3 – по (17).

Рис. 6.
Вириальные поправки на ион-атомное взаимодействие для водорода при ${\beta }{{D}_{{ia}}} = 5{\text{:}}$ обозначения те же, что и на рис. 5.

На рис. 7 представлены ион-атомные поправки для различных температур в зависимости от плотности. При низких температурах они значительны, но надо иметь в виду, что в термодинамические функции атомарной компоненты эти поправки входят с множителем ${{n}_{i}}$ (концентрации ионов). Это существенно уменьшает их вклад в связи с исчезновением ионов при уменьшении температуры.
НЕКОТОРЫЕ ВЫВОДЫ И РЕКОМЕНДАЦИИ
Выполненные в настоящей работе расчеты межатомных и ион-атомных вириальных поправок “по Хиллу” показывают, что их можно использовать в достаточно широкой области состояний, не прибегая к малообоснованным псевдопотенциалам [5]. Для продвижения в область больших плотностей следует учитывать когезионные силы сцепления. К сожалению, когезионная энергия не рассчитана впрямую для атомарных газов, образующих устойчивые молекулярные состояния. К таковым относятся кислород, азот и т.д. Расчет когезионной энергии для них весьма важен для интерпретации экспериментов по ударному сжатию. В водороде и дейтерии когезионная связь между “свободными” атомами приводит к диссоциативному фазовому переходу [21, 22] из молекулярного газа в атомарную жидкость.
ЗАКЛЮЧЕНИЕ
Рассмотрены вириальные поправки на межатомное и ион-атомное взаимодействия “по Хиллу”, т.е. рассчитанные в фазовом пространстве состояний непрерывного спектра двух частиц. Представлены простые, но достаточно точные формулы для расчета этих поправок. Обсуждаются различные подходы, используемые в литературе для расчета этих поправок. Даны практические рекомендации для учета атом-атомных и ион-атомных эффектов неидеальности в плотных газоплазменных состояниях.
Список литературы
Hirschfelder J.O., Curtiss C.F., Byron B.R. Molecular Theory of Gases and Liquids. N.Y.: Wiley, 1954.
Фортов В.Е., Храпак А.Г., Якубов И.Т. Физика неидеальной плазмы. М.: Физматлит, 2010.
Иосилевский И.Л. Общая характеристика термодинамического описания низкотемпературной плазмы (НТП) // Энциклопедия низкотемпературной плазмы. Вводн. т. I. М.: Наука, 2000. С. 275.
Saumon D., Chabrier G. Fluid Hydrogen at High Density: Pressure Ionization // Phys. Rev. A. 1992. V. 46. P. 2084.
Juranek H., Redmer R. Self-consistent Fluid Variational Theory for Presuure Dissociation in Dense Hydrogen // J. Chem. Phys. 2000. V. 112. №. 8. P. 3780.
Potekhin A.Y. Ionization Equilibrium of Hot Hydrogen Plasma // Phys. Plasmas. 1996. V. 3. P. 4156.
Грязнов В.К. Термодинамика низкотемпературной плазмы в квазихимическом представлении // Энциклопедия низкотемпературной плазмы. Вводн. т. I. М.: Наука, 2000. С. 299.
Апфельбаум Е.М. Расчет теплофизических свойств плазмы титана и цинка // ТВТ. 2017. Т. 55. № 1. С. 3.
Муленко И.А., Олейникова Е.Н., Хомкин А.Л. Широкодиапазонная модель неидеальной плазмы сложного состава // Энциклопедия низкотемпературной плазмы. Т. III-1. М.: Наука, 2000. С. 277.
Хомкин А.Л., Шумихин А.С. Уравнение состояния, состав и проводимость плазмы паров металлов // ТВТ. 2014. Т. 52. № 3. С. 335.
Гефтер В.М., Мика В.И., Семенов А.М. Расчет состава и термодинамических свойств неидеальных химически реагирующих газов // Обзоры по теплофизическим свойствам веществ. № 3. М.: ИВТАН, 1976.
Веденов А.А., Ларкин А.И. Уравнение состояния плазмы // ЖЭТФ. 1959. Т. 36. С. 1139.
Семенов А.М. Расчет термодинамических свойств пара натрия из первых принципов // ДАН СССР. 1984. Т. 278. № 4. С. 866.
Воробьев В.С., Хомкин А.Л. Метод канонического преобразования в термодинамике частично ионизованной плазмы // Теор. и матем. физика. 1971. Т. 8. С. 109.
Girardeau M.D. Second-Quantization Representation for Systems of Atoms, Nuclei, and Electrons // Phys. Rev. Lett. 1971. V. 27. P. 1416.
Хилл Т. Статистическая механика. М.: Изд-во иностр. лит., 1960.
Ross M., Ree F.H. Repulsive Forces of Simple Molecules and Mixtures at High Density and Temperature // J. Chem. Phys. 1980. V. 73. P. 6146.
Chen Q.F., Cai L.C., Zhang Y., Gu Y.J., Jing F.Q. Self-consistent Fluid Variational Theory for the Dissociation of Dense Nitrogen // J. Chem. Phys. 2006. V. 124. P. 074510.
Chen Q.F., Cai L.C., Zhang Y., Gu Y.J. The Dissociation and Equation of State of Dense Fluid Oxygen at High Pressures and High Temperatures // J. Chem. Phys. 2008. V. 128. P. 104512.
Redmer R., Ropke G., Beule D., Ebeling W. Electrical Conductivity in Dense Hydrogen Fluid and Metal Plasmas // Contrib. Plasma Phys. 1999. V. 39. P. 25.
Хомкин А.Л., Шумихин А.С. Диссоциация и диссоциативный фазовый переход в плотном водороде // ЖЭТФ. 2012. Т. 141. С. 101.
Хомкин А.Л., Шумихин А.С. Аномальная сжимаемость и металлизация дейтерия и водорода при высоких давлениях // ЖЭТФ. 2014. Т. 146. С. 518.
Хомкин А.Л., Шумихин А.С. Степень ионизации в окрестности критических точек классических кулоновских систем // ТВТ. 2015. Т. 53. № 5. С. 645.
Муленко И.А., Соловей В.Б., Хомкин А.Л., Цуркин В.Н. О температурной зависимости вириальных коэффициентов в химически реагирующих системах // ТВТ. 1999. Т. 37. № 3. С. 518.
Ликальтер А.А. Взаимодействие атомов с электронами и ионами в плазме // ЖЭТФ. 1969. Т. 56. С. 240.
Хомкин А.Л., Шумихин А.С. Фазовый переход в металлическое состояние в плотном атомарном водороде (гипотетическом, без молекул) // Физика плазмы. 2013. Т. 39. С. 958.
Banerjia A., Smith J.R. Origins of the Universal Binding-Energy Relation // Phys. Rev. B. 1988. V. 37. P. 6632.
Хомкин А.Л., Шумихин А.С. Особенности расчета уравнения состояния, состава и проводимости плотных, закритических паров металлов – плазменного флюида // ЖЭТФ. 2017. Т. 152. С. 1393.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур