Теплофизика высоких температур, 2019, T. 57, № 3, стр. 464-468

ВВЕДЕНИЕ

Данная работа является продолжением исследований, представленных в [1]. В статье анализируется влияние равновесной температуры и степени диспергированности объемного содержания пузырьковой фазы на динамику отражения и прохождения акустической волны при “косом” падении на границу раздела пузырьковой и “чистой” жидкостей. Здесь используется терминология и обозначения, принятые в [1].

Случай “косого” падения акустического сигнала на границу раздела между парогазокапельной средой и воздухом рассмотрен в [2]. На основе расчетов, проведенных авторами, показано, что в случае падения волны на границу раздела со стороны парогазокапельной смеси существует критический угол падения, при котором волна полностью отражается. Также этими же авторами рассмотрен случай распространения звука в тумане [3]. Для “холодной” жидкости, когда в пузырьках присутствует только газ, задача об отражении и прохождении волн на границе пузырьковой и “чистой” жидкостей изучена в [4]. Исследования позволили определить значения критических углов падения, при которых также возможно полное отражение волны от границы раздела.

В работах [5, 6] были рассмотрены случаи распространения начального локализованного по поперечной координате волнового импульса в однородной пузырьковой смеси и кусочно-неоднородной по объемному содержанию пузырьков области, находящейся между двумя плоскопараллельными стенками. В случае смеси с неоднородным распределением объемного содержания газа распространение импульсного сигнала в кусочно-неоднородной по объемному содержанию пузырьков области сопровождается образованием в поперечном направлении профилей давления с пиками вблизи границ между слоями, что обусловлено различием скорости волны в слоях с отличающимися объемными содержаниями газа [5]. При исследовании воздействия на пузырьковую жидкость плоским ударником с параболическим профилем по поперечной координате установлено, что за счет двумерных эффектов происходит фокусировка волны вдоль линии симметрии [6].

Особенности ударного и изоэнтропического воздействия на газожидкостные среды исследованы в работе [7]. На основе численных расчетов получены параметры падающих и отраженных ударных волн в газожидкостной среде для случаев изотермического, адиабатического и ударного сжатий газовой компоненты. Проведено сравнение расчетов с экспериментальными данными по распространению и отражению от преграды акустических и ударных волн в парогазожидкостных смесях.

В работе [8] на основе двумерной модели газожидкостной среды с цилиндрической симметрией численно исследован процесс формирования и распространения ударной волны в воде при наличии в ней пенного слоя. Получены оценки эффективности пространственного взаимодействия волнового импульса с пенной преградой в условиях, приближенных к реальным задачам защиты промышленных объектов от технологических взрывов.

ОСНОВНЫЕ УРАВНЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

Рассмотрим двумерные акустические волны. Вертикальную ось $0x$ направим перпендикулярно к плоскости раздела между однофазной и двухфазной средами в сторону “чистой” жидкости, а начало координат ($x = 0$) положим на границе раздела. Горизонтальная ось $0y$ направлена вдоль границы раздела (рис. 1).

Рис. 1.

Схематическое изображение расчетной области.

Пусть жидкость в зоне $x > 0$ находится при температуре ${{T}_{0}}$ и давлении ${{p}_{0}},$ а в жидкости в зоне $x < 0,$ находящейся при той же температуре и давлении, имеются сферические пузырьки радиусом ${{a}_{0}}$, которые содержат пар и нерастворимый в жидкой фазе газ. Данная система описывается уравнениями (1)–(12) из [1]. Стоит отметить, что если состояние жидкости достаточно далеко от критического, то выполняются условия ${{p}_{{\upsilon 0}}} = {{p}_{s}}({{T}_{0}})$ согласно [9].

Пусть на плоскую границу раздела между жидкостью и газонасыщенной жидкостью под некоторым углом падает плоская гармоническая волна (рис. 1). Будем полагать, что, как и в случае обычных однофазных сред, отраженная от границы и преломленная волны представляют плоские гармонические волны [10]. Тогда в зоне воды малые возмущения составляют сумму из двух гармонических волн, а в зоне пузырьковой жидкости – одну гармоническую волну. Возмущения, соответствующие падающей, отраженной и преломленной волнам, отметим верхними значками (0), (r) и (s). В рамках принятой модели пузырьковой жидкости вязкостные и теплообменные процессы учитываются лишь при межфазных взаимодействиях, смесь односкоростная, тензор напряжений шаровой, жидкость изотермическая. Следовательно, на границе $x = 0,$ как и в случае однофазных сред, можно ограничиться лишь двумя граничными условиями ‒ непрерывности давления и нормальной компоненты скорости:

В (1) ${{\theta }^{{(0)}}},$ ${{\theta }^{{(r)}}}$ и ${{\theta }^{{(s)}}}$ – углы падения; ${{\upsilon }^{{(0)}}},$ ${{\upsilon }^{{(r)}}}$ и ${{\upsilon }^{{(s)}}}$ – возмущения скорости, соответствующие плоским падающим, отраженным и преломленным волнам.

Основная методика расчета была приведена в [1]. Напомним лишь ее ключевые моменты.

Для волновых чисел K⁽⁰⁾ и K^(r) (из [1]) имеет место ${{K}^{{(0)}}} = {{K}^{{(r)}}} = {\omega \mathord{\left/ {\vphantom {\omega {{{C}_{\ell }}}}} \right. \kern-0em} {{{C}_{\ell }}}}.$

Волновое число K^(s) определяется из дисперсионного уравнения

Вывод дисперсионного уравнения (2) подробно описан в [1].

Для коэффициентов отражения и преломления получим [1]

Волновое число ${{K}^{{(0)}}}$ определяется из дисперсионного уравнения (2). Для коэффициентов преломления и отражения в этом случае будем иметь

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Как отмечалось в [1], проведение экспериментальных работ по рассматриваемой тематике представляется весьма сложным. Поэтому для апробации полученных результатов было проведено сравнение с [4]. На рис. 2–4 представлено сравнение результатов, полученных в настоящей работе с использованием начальных данных из [4]. Начальный радиус пузырьков в расчетах брался равным ${{a}_{0}} = {{10}^{{ - 3}}}$ м. Штриховые линии на перечисленных рисунках соответствуют данным [4], а сплошные – это результаты, полученные авторами по описанной выше модели.

Рис. 2.

Дисперсионные кривые при различных значениях начального объемного содержания пузырьков.

Рис. 3.

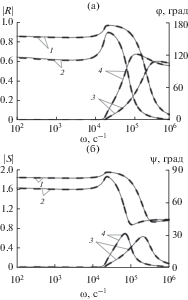
Влияние начального объемного содержания пузырьков ${{\alpha }_{0}}$ на модули (1, 2) и аргументы (3, 4) $\varphi $ и $\psi $ коэффициентов отражения и преломления при “косом” падении волны со стороны “чистой” жидкости на границу раздела: 1, 3 ‒ ${{\alpha }_{0}} = {{10}^{{ - 2}}};$ 2, 4 – ${{\alpha }_{0}} = {{10}^{{ - 3}}}.$

Рис. 4.

Влияние начального объемного содержания пузырьков ${{\alpha }_{0}}$ на модули (1, 2) и аргументы (3, 4) $\varphi $ и $\psi $ коэффициентов отражения и преломления при “косом” падении волны со стороны пузырьковой жидкости на границу раздела: 1, 3 ‒ ${{\alpha }_{0}} = {{10}^{{ - 2}}};$ 2, 4 – ${{\alpha }_{0}} = {{10}^{{ - 3}}}.$

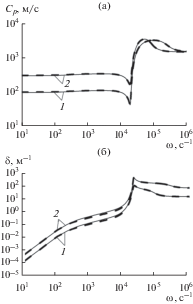
На рис. 2 линия 1 соответствует начальному объемному содержанию пузырьков ${{\alpha }_{0}} = {{10}^{{ - 2}}},$ а линия 2 – ${{\alpha }_{0}} = {{10}^{{ - 3}}}.$ На рис. 2б заметно некоторое отличие в результатах, что связано с отсутствием в пузырьках паровой компоненты [4]. Стоит отметить, что такое различие наблюдается для низкочастотного диапазона ($\omega \leqslant {{\omega }_{R}},$ ${{\omega }_{R}} = a_{0}^{{ - 1}}\sqrt {{{3\gamma {{p}_{0}}} \mathord{\left/ {\vphantom {{3\gamma {{p}_{0}}} {\rho _{{\ell 0}}^{0}}}} \right. \kern-0em} {\rho _{{\ell 0}}^{0}}}} $ – миннаэртовская частота собственных колебаний пузырьков). Это связано с тем, что при низких частотах повышается роль фазовых переходов и за счет них парогазовые пузырьки с небольшим массовым содержанием инертного газа становятся менее упругими.

На рис. 3, 4 представлено сравнение зависимостей модулей (линии 1 и 2) и аргументов (линии 3 и 4) $\varphi $ и $\psi $ коэффициентов отражения и преломления от круговой частоты гармонических волн, падающих со стороны “чистой” жидкости на пузырьковую смесь (рис. 3) и со стороны пузырьковой жидкости в “чистую” жидкость (рис. 4). Видно удовлетворительное совпадение с результатами, полученными ранее. Это дает возможность считать, что использование фундаментальных законов механики и хорошее совпадение с данными предыдущих работ позволяет говорить о достоверности результатов, изложенных в настоящей статье.

На рис. 5 (${{a}_{0}} = {{10}^{{ - 3}}}$ м) и 6 (${{a}_{0}} = {{10}^{{ - 6}}}$ м) приведены зависимости угла преломления от угла падения при трех значениях температуры среды: ${{T}_{0}} = 300$ (штриховая линия), $353$ (пунктирная линия) и 373 К (сплошная линия). Следует отметить, что, согласно формуле (19) из [1], угол преломления ${{\theta }^{{(s)}}}$ является комплексным числом, поскольку волновое число ${{K}^{{(s)}}}$ для пузырьковой системы комплексное. Чтобы формально избавиться от комплексности ${{\theta }^{{(s)}}},$ в формуле (19) из [1] вместо ${{K}^{{(s)}}}$ достаточно использовать действительную часть волнового числа, т.е. $\operatorname{Re} ({{K}^{{(s)}}}).$ Такое допущение означает пренебрежение диссипативными процессами в плане определения акустической жесткости среды. Как показывают расчеты [11], действительная часть комплексной величины, определенной из формулы (19) в [1], практически идентична значению, когда за волновое число принимается только его действительная часть. Поэтому в дальнейшем под углом преломления будем понимать действительную часть ${{\theta }^{{(s)}}}.$ Здесь надо отметить, что для ${{T}_{0}} = 373$ К диссипация за счет фазовых переходов сильно влияет на значение угла преломления.

Рис. 5.

Зависимость угла преломления от угла падения со стороны “чистой” жидкости (а) и со стороны пузырьковой жидкости (б) при ${{\alpha }_{0}} = {{10}^{{ - 2}}}$ и ${{a}_{0}} = {{10}^{{ - 3}}}$ м: 1 – $\omega = {{10}^{2}}\,\,{{{\text{c}}}^{{ - 1}}},$ 2 – 10³, 3 – 10⁴.

Для случая падения волны из “чистой” жидкости в зону пузырьковой жидкости угол преломления для всех случаев не превышает 5° (рис. 5а и 6а). Это связано с низким значением фазовой скорости, особенно при ${{T}_{0}} = 373$ К. Здесь угол преломления не превышает 3°. Волна в “чистой” жидкости для всех углов падения ${{\theta }^{{(0)}}}$ в пузырьковую жидкость проникает практически перпендикулярно к поверхности раздела. Из рис. 5а и 6а также видно, что во всем диапазоне изменения угла падения ($0 \leqslant {{\theta }^{{(0)}}} \leqslant 90^\circ $) для рассматриваемых частот угол преломления меньше прямого угла (${{\theta }^{{(s)}}} < 90^\circ $). Следовательно, при любом угле падения акустическая волна всегда проникает из “чистой” жидкости в зону пузырьковой жидкости.

Для случая, когда волна падает со стороны пузырьковой жидкости на границу раздела (рис. 5б), линии, соответствующие начальной температуре среды ${{T}_{0}} = 300$ и $353$ К, уже на малых углах падения (${{\theta }^{{(0)}}} \leqslant 5^\circ $) достигают значения ${{\theta }^{{(s)}}} \sim 90^\circ .$ Следовательно, и в данном случае акустическая волна не проникнет через границу раздела, поэтому пузырьковый слой в “чистой” жидкости обладает свойствами звукового канала. Наряду с этим для начальной температуры среды ${{T}_{0}} = 373$ К видим немного иную картину. Угол отражения в максимальном своем значении достигает величины ${{\theta }^{{(s)}}} \approx 70^\circ .$ Таким образом, для системы, находящейся при температуре 373 К, формально не происходит полного внутреннего отражения. Однако в этом случае из-за большого коэффициента затухания и малой фазовой скорости (что отражается в значении мнимой части $n_{y}^{{(s)}}$ или $\cos {{\theta }^{{(s)}}}$) проникающая в “чистую” жидкость волна полностью затухает вблизи границы раздела сред. Следовательно, и в этом случае фактически реализуется полное внутреннее отражение.

В пузырьковой жидкости с начальным размером пузырьков ${{a}_{0}} = {{10}^{{ - 6}}}$ м (рис. 6б) наряду с начальной температурой важное влияние на значение угла преломления оказывает и частота возмущений. При температуре 373 К для частот, близких к частоте собственных колебаний пузырьков, угол отражения в максимальном своем значении достигает величины ${{\theta }^{{(s)}}} \approx 70^\circ .$ Аналогично случаю ${{a}_{0}} = {{10}^{{ - 3}}}$ м, для системы, находящейся при температуре 373 К, формально не происходит полного внутреннего отражения. Однако в этом случае из-за большого коэффициента затухания и малой фазовой скорости (что отражается в значении мнимой части $n_{y}^{{(s)}}$ или $\cos {{\theta }^{{(s)}}}$) проникающая в “чистую” жидкость волна полностью затухает вблизи границы раздела сред. Следовательно, и в этом случае реализуется полное внутреннее отражение.

Рис. 6.

Зависимость угла преломления от угла падения со стороны “чистой” жидкости (а) и со стороны пузырьковой жидкости (б) при ${{\alpha }_{0}} = {{10}^{{ - 2}}}$ и ${{a}_{0}} = {{10}^{{ - 6}}}$ м: 1 – $\omega = {{10}^{5}}\,\,{{{\text{c}}}^{{ - 1}}},$ 2 – 10⁶, 3 – 10⁷.

ЗАКЛЮЧЕНИЕ

Для рассмотренных начальных температур ${{T}_{0}} = 300$ и $353$ К показано, что при падении акустической волны со стороны пузырьковой жидкости на границу раздела для низкочастотных волн ($\omega < {{\omega }_{R}}$) при углах, больших критического угла падения, она полностью отражается от границы раздела. Например, при углах падения, превышающих значение ${{\theta }^{{(0)}}} = 10^\circ ,$ угол преломления асимптотически приближается к значению ${{\theta }^{{(s)}}} = 90^\circ .$ Установлено, что в данном случае пузырьковый слой в “чистой” жидкости обладает свойствами звукового канала. Наряду с этим для начальной температуры среды ${{T}_{0}} = 373$ К наблюдается иная картина. Угол отражения в максимальном своем значении достигает величины ${{\theta }^{{(s)}}} \approx 70^\circ .$ Следовательно, для системы, находящейся при температуре 373 К, формально не происходит полного внутреннего отражения. Однако в этом случае из-за большого значения величины коэффициента затухания и малого значения фазовой скорости (что отражается в значении мнимой части $n_{y}^{{(s)}}$ (или $\cos {{\theta }^{{(s)}}}$)) проникающая в “чистую” жидкость волна полностью затухает вблизи границы раздела сред. Таким образом, фактически реализуется полное внутреннее отражение.

Показано, что при падении волны со стороны “чистой” жидкости на границу раздела, она при любом угле падения проходит в пузырьковую жидкость (см. также [1]).

Данная работа расширяет результаты, которые были получены ранее в [12].

Работа В.Ш. Шагапова и М.Н. Галимзянова поддержана средствами государственного бюджета по госзаданию на 2017‒2019 годы (№ 0246-2019-0052). Работа И.И. Вдовенко частично поддержана грантом РФФИ (№ 17-41-020582-р_а).