Теплофизика высоких температур, 2019, T. 57, № 3, стр. 408-415

ВВЕДЕНИЕ

Почти столетие назад, в первой половине прошлого века стало понятным, что на процессы теплообмена, протекающие во многих технических устройствах, может оказывать влияние сила тяжести. Одними из первых приближенно оценили это влияние применительно к течению и теплообмену в вертикальной трубе с постоянной температурой стенки авторы работы [1], опубликованной в 1942 году. В начале 50-х годов прошлого века в трудах выдающегося советского ученого Г.А. Остроумова обращается внимание на существующую “неясность научных представлений о конвективных процессах в поле силы тяжести” [2, 3] и в значительной степени восполнен этот пробел. В частности, впервые решена задача о ламинарной смешанной конвекции при установившемся подъемном и опускном течениях в круглой трубе с граничными условиями второго рода. Примечательно, что ни в одной из публикаций зарубежных авторов по данной тематике работы Г.А. Остроумова не упоминаются – они либо им неизвестны, либо замалчиваются.

К настоящему времени появилось достаточно много исследований в рассматриваемом направлении для круглой трубы при граничных условиях первого и второго рода, причем как для развитого течения и теплообмена, так и на начальном участке. Результаты некоторых из этих исследований приведены в монографиях [4, 5]. Отметим наиболее значимые из имеющихся работ. В [6] аналитическое решение задачи об установившейся ламинарной смешанной конвекции в вертикальной круглой трубе с постоянной плотностью теплового потока на стенке распространено на случай наличия в потоке жидкости внутренних источников тепла. Автором [7] предложен другой метод решения указанной задачи, однако он применим лишь при совпадении направлений вынужденной и свободной конвекции (т.е. при подъемном течении и нагревании или при опускном течении и охлаждении). В работе [8] найдены границы и характер влияния термогравитации на течение и теплообмен в наклонных, в частности вертикальных, круглых трубах на начальном участке при граничном условии второго рода. Проведено аналитическое решение системы уравнений конвективного теплообмена для малых отклонений температуры и составляющих вектора скорости от их известных значений при вынужденной конвекции.

В отличие от течения в круглой трубе, течение в плоском канале с граничными условиями второго рода рассмотрено лишь в нескольких работах. Наиболее содержательное исследование установившейся смешанной конвекции, включающее формулы для профилей скорости, температуры и числа Нуссельта, провел автор [9]. Однако аналитический метод, использованный в [9], как и в [7] для течения в круглой трубе, применим лишь при совпадении направлений вынужденной и свободной конвекции. Для такого же случая в [10] построено приближенное аналитическое решение указанной задачи на начальном участке для двух граничных условий – первого и второго рода. В [11] аналитическим методом рассмотрено влияние термогравитации и переменной вязкости капельной жидкости на профили скорости, коэффициенты сопротивления трения, числа Нуссельта при линейном распределении температуры между поверхностями вертикального плоского канала. В [12] получено аналитическое решение задачи о смешанной конвекции при подъемном течении в плоском вертикальном канале для случая, когда плотности теплового потока на горячей q_h и холодной q_c стенках различны: q_c = kq_h, $ - 1 \leqslant k \leqslant 1.$ Метод решения, предложенный в этой работе, аналогичен примененному в [9] и может использоваться только для неотрицательного изменения по длине канала средней массовой температуры жидкости. Получено, что, когда холодная стенка является адиабатической (k = 0) или охлаждается с той же плотностью теплового потока, с которой нагревается горячая стенка (k = –1), при достаточно сильном влиянии свободной конвекции у холодной стенки появляются возвратные течения. Такое же явление, как будет показано ниже, наблюдается и при симметричном охлаждении. Число Нуссельта на горячей стенке ниже, чем при симметричном обогреве, но превышает число Нуссельта на холодной стенке. При определенном значении параметра k имеется разрыв числа Нуссельта на холодной стенке, связанный с близкими значениями температуры холодной стенки и средней массовой температуры жидкости.

Так как отсутствуют сведения о тепловых и гидродинамических величинах в противоположном направлении вынужденной и свободной конвекции при течении в плоском канале, решение указанной задачи интересно с точки зрения развития теории конвективного теплообмена. Очевидно, что качественно зависимости для тепловых и гидродинамических величин будут подобны известным зависимостям при течении в круглой трубе, но количественно они могут существенно различаться, что подтверждают результаты представленной работы. Отметим, что ранее не было изучено влияние силы плавучести на коэффициент сопротивления трения и на другие составляющие коэффициента гидравлического сопротивления. Это относится как к течению в плоском канале, так и к течению в круглой трубе.

Исследования в данном направлении имеют не только теоретическое, но и практическое значение. Плоский канал является предельным случаем прямоугольного щелевого канала с малым отношением длин его сторон. Такие каналы широко применяются в различных теплообменных устройствах. Как правило, течение в элементах этих теплообменных аппаратов является турбулентным, тем более что влияние силы плавучести способствует переходу от ламинарного режима к турбулентному. Об этом свидетельствуют имеющиеся экспериментальные данные, приведенные, например, в [4, 13], и теоретические работы [10, 14]. Однако в определенных условиях может происходить ламинаризация потока, в частности в результате действия термического ускорения, что показано в ставшей классической работе [15]. Турбулентность подавляется, и критическое число Рейнольдса возрастает при течении электропроводной жидкости в продольном магнитном поле [16]. Заметим, что жидкие металлы являются перспективными теплоносителями для ядерных энергетических установок нового поколения, а также термоядерных реакторов, в бланкетах которых могут использоваться прямоугольные каналы [17].

ПОСТАНОВКА ЗАДАЧИ

Решалась система уравнений движения и энергии для стабилизированного ламинарного течения жидкости с постоянными свойствами в плоском вертикальном канале. В уравнении движения учитывалась сила плавучести, в уравнении энергии пренебрегалось аксиальной теплопроводностью, сжимаемостью и диссипацией.

Здесь u – продольная составляющая скорости; t – температура; p – давление; х и у – продольная и поперечная координаты; $\rho ,\mu ,\lambda ,$ c_p – плотность, динамический коэффициент вязкости, теплопроводность, изобарная теплоемкость; g – ускорение силы тяжести.

Уравнения (1), (2) решаются со следующими граничными условиями. На стенке канала при y = h/2 (h – ширина канала) u = 0, $ - {{\lambda dt} \mathord{\left/ {\vphantom {{\lambda dt} {dy}}} \right. \kern-0em} {dy}} = {{q}_{{\text{c}}}}$ (q_c – плотность теплового потока на стенке); на оси при y = 0 ${{du} \mathord{\left/ {\vphantom {{du} {dy}}} \right. \kern-0em} {dy}} = {{dt} \mathord{\left/ {\vphantom {{dt} {dy}}} \right. \kern-0em} {dy}} = 0.$

Изменение плотности в поле силы тяжести в данной постановке задачи обычно учитывается только в первом члене уравнения движения (1). Верхний знак этого члена здесь и далее соответствует одинаковому направлению вектора скорости и ускорения силы тяжести, т.е. опускному течению, нижний знак – подъемному течению.

Полагая величину ρβ постоянной ($\beta = - \frac{1}{\rho }{{\left( {\frac{{\partial \rho }}{{\partial t}}} \right)}_{p}}$ – коэффициент термического расширения), этот член представим в виде $g{{\rho }_{0}}[{{{{\rho }_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{\text{c}}}}} {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}} + \beta ({{t}_{{\text{c}}}} - t)],$ где ${{\rho }_{{\text{c}}}}$ и ${{\rho }_{0}}$ – плотности при температуре стенки t_c и некоторой определяющей температуре, при которой берутся значения всех физических свойств жидкости, считающихся постоянными.

Для стабилизированного теплообмена при постоянной плотности теплового потока на стенке, проинтегрировав уравнение энергии (2) по сечению канала, получим

где ${{t}_{{\text{ж }}}} = \frac{2}{{h{{u}_{0}}}}\int_0^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} {tudy} $ – средняя массовая температура жидкости, ${{u}_{0}} = \frac{2}{h}\int_0^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} {udy} $ – средняя по сечению скорость.

Приведем уравнения (1), (2) к безразмерному виду, используя указанное выше выражение:

Здесь $U = {u \mathord{\left/ {\vphantom {u {{{u}_{0}}}}} \right. \kern-0em} {{{u}_{0}}}},$ $\vartheta = 2{\lambda }({{t}_{{\text{c}}}} - {{t)} \mathord{\left/ {\vphantom {{t)} {({{q}_{{\text{c}}}}h)}}} \right. \kern-0em} {({{q}_{{\text{c}}}}h)}},$ $Y = {{2y} \mathord{\left/ {\vphantom {{2y} h}} \right. \kern-0em} h}$ – безразмерные продольная скорость, температура, расстояние от оси трубы; $P = \frac{{{{h}^{2}}}}{{4\mu {{u}_{0}}}}$$\left( { - \frac{{dp}}{{dx}} \pm g{{\rho }_{{\text{c}}}}} \right)$ – безразмерный параметр, включающий, как будет показано ниже, гидравлическое и гидростатическое сопротивление.

Уравнения (3), (4) решаются со следующими граничными условиями. На стенке канала при Y = 1 $U = \vartheta = 0;$ на оси при Y = 0 ${{dU} \mathord{\left/ {\vphantom {{dU} {dY}}} \right. \kern-0em} {dY}}$ = $ = {{d\vartheta } \mathord{\left/ {\vphantom {{d\vartheta } {dY}}} \right. \kern-0em} {dY}} = 0.$

Решение задачи зависит от единственного режимного параметра $G = {{{\text{G}}{{{\text{r}}}_{q}}} \mathord{\left/ {\vphantom {{{\text{G}}{{{\text{r}}}_{q}}} {(8\operatorname{Re} )}}} \right. \kern-0em} {(8\operatorname{Re} )}},$ где Gr_q = = ${{g\beta {{q}_{{\text{c}}}}{{h}^{4}}} \mathord{\left/ {\vphantom {{g\beta {{q}_{{\text{c}}}}{{h}^{4}}} {(\lambda {{\nu }^{2}})}}} \right. \kern-0em} {(\lambda {{\nu }^{2}})}}$ – число Грасгофа, базирующееся на плотности теплового потока на стенке, $\operatorname{Re} = {{{{u}_{0}}h} \mathord{\left/ {\vphantom {{{{u}_{0}}h} \nu }} \right. \kern-0em} \nu }$ – число Рейнольдса.

Заметим, что параметр ${{{\text{G}}{{{\text{r}}}_{q}}} \mathord{\left/ {\vphantom {{{\text{G}}{{{\text{r}}}_{q}}} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}$ указан автором [8, 12] как определяющий при течении в вертикальных трубах и присутствует в других работах, например в [10]. Однако в ряде работ, например в [3, 6, 7, 9], параметр, от которого зависит решение задачи, называется числом Рэлея, что является некорректным с физической точки зрения. Число Рэлея – это произведение числа Грасгофа ${\text{Gr}} = {{g\beta \Delta {\text{t}}{{{\text{h}}}^{3}}} \mathord{\left/ {\vphantom {{g\beta \Delta {\text{t}}{{{\text{h}}}^{3}}} {{{\nu }^{2}}}}} \right. \kern-0em} {{{\nu }^{2}}}},$ базирующегося на разности температур Δt, и числа Прандтля Pr = μc_p/λ: Ra = GrPr. Число Рэлея, как правило, используется при исследовании свободной, а не смешанной конвекции, когда имеются вторичные течения. Конечно, можно искусственно, как это сделано в упомянутых выше работах, в определение числа Грасгофа, базирующегося на разности температур, вместо Δt/h подставить величину $А = \frac{{d{{t}_{{\text{ж }}}}}}{{dx}} = \frac{{2{{q}_{{\text{c}}}}}}{{\rho {{c}_{p}}{{u}_{0}}h}}.$ В результате действительно получим ${{{\text{G}}{{{\text{r}}}_{q}}} \mathord{\left/ {\vphantom {{{\text{G}}{{{\text{r}}}_{q}}} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }} = {\text{Gr}}\Pr .$ Тем самым создается ложное представление о том, что на решение рассматриваемой задачи влияет число Прандтля.

ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ

Продифференцировав (3) два раза и используя (4), получим для U дифференциальное уравнение четвертого порядка

и четыре граничных условия для него: при Y = 0 ${{dU} \mathord{\left/ {\vphantom {{dU} {dY}}} \right. \kern-0em} {dY}}$ = ${{{{d}^{3}}U} \mathord{\left/ {\vphantom {{{{d}^{3}}U} {d{{Y}^{3}}}}} \right. \kern-0em} {d{{Y}^{3}}}} = 0;$ при Y = 1 $U = 0,$ ${{{{d}^{2}}U} \mathord{\left/ {\vphantom {{{{d}^{2}}U} {d{{Y}^{2}}}}} \right. \kern-0em} {d{{Y}^{2}}}} = - P.$ Функция Р находится из интегрального уравнения неразрывности $\int_0^1 {UdY} = 1.$

Имея решение уравнения (5), можно с помощью (4) вычислить профиль температуры $\vartheta (Y) = \int_Y^1 {\left( {\int_0^Y {UdY} } \right)dY} ,$ безразмерный температурный напор $\Delta \vartheta = {{\vartheta }_{{\text{ж }}}} = \int_0^1 {\vartheta UdY} $ и число Нуссельта ${\text{Nu}} = {{{{q}_{{\text{c}}}}h} \mathord{\left/ {\vphantom {{{{q}_{{\text{c}}}}h} {[({{t}_{{\text{c}}}}}}} \right. \kern-0em} {[({{t}_{{\text{c}}}}}} - {{t}_{{\text{ж }}}})\lambda ] = {2 \mathord{\left/ {\vphantom {2 {\Delta \vartheta }}} \right. \kern-0em} {\Delta \vartheta }}.$

Проинтегрировав по сечению канала уравнение движения, получим соотношение для коэффициента гидравлического сопротивления ξ^p = = ${{ - ({{dp} \mathord{\left/ {\vphantom {{dp} {dx}}} \right. \kern-0em} {dx}})2h} \mathord{\left/ {\vphantom {{ - ({{dp} \mathord{\left/ {\vphantom {{dp} {dx}}} \right. \kern-0em} {dx}})2h} {{{\rho }_{0}}u_{0}^{2}}}} \right. \kern-0em} {{{\rho }_{0}}u_{0}^{2}}}$

где ${{\xi }^{\tau }} = - \frac{8}{{\operatorname{Re} }}{{\left( {\frac{{dU}}{{dY}}} \right)}_{{Y = 1}}}$ – коэффициент сопротивления трения. Остальные члены в правой части этого соотношения являются коэффициентами гидростатического сопротивления, вызванного силой плавучести. Коэффициент $\xi _{0}^{g} = \mp {{2gh} \mathord{\left/ {\vphantom {{2gh} {u_{0}^{2}}}} \right. \kern-0em} {u_{0}^{2}}}$ обусловлен вкладом веса столба жидкости в перепад давления, необходимый для прокачки; $\xi _{x}^{g} = {{ \pm 32Gx} \mathord{\left/ {\vphantom {{ \pm 32Gx} {(h{\text{Pe}}\operatorname{Re} )}}} \right. \kern-0em} {(h{\text{Pe}}\operatorname{Re} )}}$ – линейным изменением средней массовой температуры жидкости вдоль трубы; $\xi _{1}^{g} = \mp \frac{{8G}}{{\operatorname{Re} }}\int_0^1 {\vartheta dY} $ = $ \mp \frac{{8G}}{{\operatorname{Re} }}\bar {\vartheta }$ – разницей между температурой стенки и средней по сечению температурой; $\xi _{2}^{g} = \pm 8G{{\Delta \vartheta } \mathord{\left/ {\vphantom {{\Delta \vartheta } {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}$ – температурным напором (разницей между температурой стенки и средней массовой температурой жидкости). Заметим, что для функции Р справедливо выражение

РЕШЕНИЕ ДЛЯ ПОДЪЕМНОГО ТЕЧЕНИЯ

В случае нагревания и подъемного течения (что равносильно охлаждению и опускному течению) второй член уравнения (5) имеет положительный знак. Общее решение этого уравнения примет вид

Значения четырех констант С находятся из граничных условий. В частности, С₁ = С₂, С₃ = –С₄. Для функции Р, используя условие постоянства средней по сечению скорости, получим следующую зависимость:

Распределение скорости по сечению трубы определяется выражением

Результаты расчета показаны на рис. 1. При отсутствии влияния силы плавучести (G = 0), т.е. в чисто вынужденном течении, профиль скорости представляет собой параболу U = 1.5(1 – Y  ²). В случае большого влияния силы плавучести вблизи стенки на профиле скорости появляется максимум, а в центре канала наблюдается возвратное течение.

Для безразмерной температуры получим

Профиль температуры представлен на рис. 2. При больших значениях параметра G уменьшается разница между температурой стенки и температурой в потоке жидкости, а распределение температуры в большей части сечения канала становится равномерным.

Безразмерный температурный напор найдем, используя выражения (6), (7):

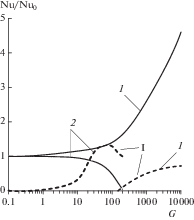
Зависимость числа Нуссельта, отнесенного к его значениям при отсутствии влияния силы плавучести Nu₀ = 4.12, от режимного параметра G показана на рис. 3. Видно, что число Нуссельта при подъемном течении и нагревании может увеличиться в несколько раз благодаря возрастанию градиента скорости вблизи стенки. Расчеты показали, что при течении в плоском канале наблюдается более существенное влияние силы плавучести на теплоотдачу, чем при течении в круглой трубе [4].

Осредняя безразмерную температуру (7) по сечению канала, получим

Эта величина входит в коэффициент гидростатического сопротивления $\xi _{1}^{g}$. Коэффициент сопротивления трения ${{\xi }^{\tau }}$ пропорционален величине ${{\left( {\frac{{dU}}{{dY}}} \right)}_{{Y = 1}}},$ которая вычисляется из (6):

На рис. 4 приведены все составляющие коэффициента гидравлического сопротивления (кроме $\xi _{0}^{g},$ который зависит от ширины канала h и средней по сечению скорости u₀), отнесенные к его значению при вынужденной конвекции ${{\xi }_{0}} = {{\xi }^{р }} = {{\xi }^{\tau }} = {{24} \mathord{\left/ {\vphantom {{24} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}.$ Коэффициент сопротивления $\xi _{x}^{g}$ построен для значения приведенной длины $Х = {x \mathord{\left/ {\vphantom {x {(h{\text{Pe}})}}} \right. \kern-0em} {(h{\text{Pe}})}},$ равной трем длинам начального термического участка при вынужденной конвекции Х = 0.06. Вклад этого коэффициента в гидравлическое сопротивление, так же как и коэффициента $\xi _{1}^{g},$ обусловленного температурным напором, способствует уменьшению перепада давления. Напротив, сопротивление трения, которое заметно возрастает благодаря увеличению градиента скорости на стенке, и сопротивление $\xi _{1}^{g},$ вызванное разностью температуры стенки и средней по сечению температуры, приводит к увеличению гидравлического сопротивления. Однако при больших Х и G становится определяющим вклад $\xi _{x}^{g}$ и коэффициент гидравлического сопротивления может достигнуть отрицательных значений, возникнет так называемая самотяга.

Представляет интерес влияние силы плавучести на гидравлическое сопротивление при умеренных значениях параметра G. Для стабилизированного теплообмена при ламинарном течении жидкости в плоском канале средняя по сечению температура превышает среднюю массовую температуру жидкости, а разность безразмерных температур $\Delta \vartheta - \bar {\vartheta } = 0.0858$ [4]. Таким образом, с учетом того, что при малых значениях параметра G → 0 ${{\xi }^{р }} - \xi _{0}^{g} - \xi _{x}^{g} = {{\xi }_{0}} = {{24} \mathord{\left/ {\vphantom {{24} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }},$ $\delta \xi = (\xi _{1}^{g} + {{\xi _{2}^{g})} \mathord{\left/ {\vphantom {{\xi _{2}^{g})} {({{\xi }^{р }} - \xi _{0}^{g}}}} \right. \kern-0em} {({{\xi }^{р }} - \xi _{0}^{g}}}$ – ‒ $\xi _{x}^{g}) = - 0.0286G.$ При G ≈ 10 величина $\left| {\delta \xi } \right|$ проходит через максимальное значение $\left| {\delta \xi } \right|$ ≈ 0.25, а затем меняет знак, т.е. средняя массовая температура жидкости становится выше средней по сечению температуры (рис. 3). Этот эффект обусловлен особенностями профилей скорости и температуры, показанных на рис. 1, 2. Отличие средней по сечению температуры от средней массовой температуры жидкости при сильном влиянии силы плавучести возрастает с увеличением G. Если принять, что эти температуры равны, т.е. $\xi _{1}^{g}$ = $ - \xi _{2}^{g},$ то расчет коэффициента гидравлического сопротивления приведет к заметной ошибке, которая показана на рис. 3. Отсюда следует вывод, что для точного расчета гидравлического сопротивления при существенном влиянии силы плавучести необходимо иметь данные о коэффициенте сопротивления трения, числе Нуссельта (т.е. температурном напоре $\Delta \vartheta $) и средней по сечению температуре $\bar {\vartheta }.$

РЕШЕНИЕ ДЛЯ ОПУСКНОГО ТЕЧЕНИЯ

В случае нагревания и опускного течения (что равносильно охлаждению и подъемному течению) второй член уравнения (5) имеет отрицательный знак. Общее решение этого уравнения принимает вид

Значения четырех констант С находятся из граничных условий. В частности, С₁ = С₂, С₄ = 0. Для функции Р получим следующую зависимость:

Распределение скорости по сечению трубы определяется выражением

Результаты расчета представлены на рис. 5. В отличие от подъемного течения, сила плавучести приводит к существенному уменьшению скорости вблизи стенки; в этой области при больших значениях параметра G наблюдаются мощные возвратные течения. Примечательно, что особенность решения системы уравнений движения и энергии такова, что при Y = 0.58 значения скорости для всех параметров G одинаковы – все кривые на рис. 4 пересекаются в одной точке. Аналогичной особенностью обладает решение для круглой трубы, приведенное в [4].

Для безразмерной температуры получим

Рассчитанные профили температуры показаны на рис. 6. В отличие от подъемного течения, влияние силы плавучести приводит к росту разности температур стенки и в потоке жидкости, а также к более неравномерному распределению температуры по сечению канала.

Для безразмерного температурного напора, определяющего число Нуссельта и коэффициент сопротивления $\xi _{2}^{g},$ получено следующее выражение:

Зависимость отношения Nu/Nu₀ от режимного параметра G показана на рис. 3.

Анализ задачи показал, что при опускном течении решение возможно провести для существенно меньших значений параметра G, чем при подъемном течении. При G > 200 температурный напор становится настолько большим, что число Нуссельта стремится к нулю, что видно на рис. 3. Дальнейшее увеличение значения G приводит к физически необоснованным результатам. Сопоставление результатов расчета с данными для круглой трубы, приведенными в [4], показало, что при течении в плоском канале наблюдается более существенное влияние силы плавучести на теплоотдачу.

Для средней по сечению температуры, определяющей коэффициент сопротивления $\xi _{1}^{g},$ и градиента скорости на стенке, определяющего коэффициент сопротивления трения, получены следующие выражения:

Зависимость коэффициентов сопротивления от параметра G показана на рис. 7. Коэффициент сопротивления трения значительно ниже своего значения при вынужденной конвекции ξ₀ и с ростом G становится отрицательным, так как у стенки появляются возвратные течения (см. рис. 4). Сопоставим значения ${{{{\xi }^{\tau }}} \mathord{\left/ {\vphantom {{{{\xi }^{\tau }}} {{{\xi }_{0}}}}} \right. \kern-0em} {{{\xi }_{0}}}}$ для одинаковых G при подъемном и опускном течениях. В последнем случае сила плавучести влияет на коэффициент сопротивления трения, как и на число Нуссельта, в гораздо большей степени.

Коэффициенты $\xi _{1}^{g}$ и $\xi _{2}^{g}$ имеют знаки, противоположные их знакам при подъемном течении; $\xi _{1}^{g}$ способствует уменьшению коэффициента гидравлического сопротивления, а $\xi _{2}^{g}$ вносит положительный вклад в ${{\xi }^{р }}.$ Сумма этих коэффициентов по отношению к коэффициенту гидравлического сопротивления $\delta \xi $ показана на рис. 3. В отличие от подъемного течения она всегда положительна, т.е. средняя по сечению температура, как и при вынужденной конвекции, превышает среднюю массовую температуру жидкости. Разница этих температур заметно выше, чем при подъемном течении. Сравнивая на рис. 4 и 7 коэффициент гидравлического сопротивления (без учета $\xi _{x}^{g}$) при подъемном и опускном течениях, можно сделать вывод, что в последнем случае влияние силы плавучести существенно выше и направлено на увеличение ${{\xi }^{р }}.$ Способствует росту гидравлического сопротивления и вклад в него коэффициента $\xi _{x}^{g}.$

ЗАКЛЮЧЕНИЕ

Математическое описание задачи о ламинарной установившейся смешанной конвекции в плоском вертикальном канале сведено к обыкновенному дифференциальному уравнению четвертого порядка. Решением этого уравнения является комбинация экспоненциальных и тригонометрических функций. Решение зависит от режимного параметра, пропорционального числу Грасгофа ${\text{G}}{{{\text{r}}}_{q}} = {{g\beta {{q}_{{\text{c}}}}{{h}^{4}}} \mathord{\left/ {\vphantom {{g\beta {{q}_{{\text{c}}}}{{h}^{4}}} {(\lambda {{\nu }^{2}})}}} \right. \kern-0em} {(\lambda {{\nu }^{2}})}},$ базирующемуся на заданной плотности теплового потока на стенке, и обратно пропорционального числу Рейнольдса.

Получены аналитические выражения для профилей скорости, температуры, чисел Нуссельта и коэффициентов сопротивления при подъемном и опускном течениях и нагревании (соответственно при опускном и подъемном течениях и охлаждении).

Показано, что для нагревания и опускного течения физически обосновано решение лишь при ограниченном значении режимного параметра.

Для подъемного и опускного течения при небольшом значении параметра Gr_q/Re теплоотдача и сопротивление трения зависят от него в одинаковой степени, хотя влияние силы плавучести для этих случаев имеет противоположный характер. С возрастанием значения режимного параметра наблюдается более существенное влияние силы плавучести на число Нуссельта и коэффициент сопротивления трения при опускном течении по сравнению с подъемным течением.

Результаты расчета свидетельствуют о том, что влияние силы плавучести на теплоотдачу при течении в плоском канале более значительно, чем при течении в круглой трубе, особенно для нагревания и опускного течения. Если при подъемном течении число Нуссельта для круглой трубы приблизительно на 15% ниже, чем для плоского канала, то при опускном течении это различие достигает сотен процентов.