Теплофизика высоких температур, 2019, T. 57, № 4, стр. 543-547

О тепловых солитонах при волновом теплопереносе в ограниченных областях

В. Ф. Формалев^1, *, С. А. Колесник^1, **

¹ Московский авиационный институт (национальный исследовательский университет)
125993 Москва, Россия

^* E-mail: formalev38@yandex.ru
^** E-mail: sergey@oviont.com

Поступила в редакцию 24.11.2018
После доработки 25.12.2018
Принята к публикации 25.12.2018

DOI: 10.1134/S0040364419040045

Аннотация

В работе моделируется волновой теплоперенос на основе анализа динамики изолированной тепловой волны (теплового солитона). Изолированная тепловая волна возникает под действием теплового импульса, действующего в течение короткого времени, и продвигается по холодной области. В отличие от непрерывного теплового процесса в неравновесном состоянии, когда возникает подвижной фронт бегущей тепловой волны в полубесконечном теле, тепловой солитон имеет два фронта: передний и задний, между которыми отмечено распределение температур по пространственной переменной. На этих фронтах наблюдаются разрывы первого рода температурного распределения с уменьшающейся амплитудой за счет диссипации тепловой энергии. Достигнув противоположной границы, солитон отражается не так, как механическая волна. Сначала окрестность противоположной границы нагревается до определенного уровня, а затем солитон движется по холодному пространству в противоположную сторону с уменьшающейся амплитудой. Приводятся результаты аналитического решения задачи волнового теплопереноса на основе уравнения теплопроводности гиперболического типа с учетом релаксационных явлений.

ВВЕДЕНИЕ

Теплоперенос в условиях локального неравновесия между градиентами температур и тепловыми потоками связан с дискретным состоянием среды, поскольку время столкновения между частицами, называемое временем релаксации, как раз и есть упомянутое в [1] время. Закон теплопроводности при волновом теплопереносе отличается от классического градиентного закона Фурье слагаемым, равным произведению времени релаксации на скорость изменения теплового потока. Поскольку время релаксации – малая величина (~10^–12–10^–14 c), то, для того чтобы это слагаемое имело заметное значение, необходимы очень высокие скорости нагрева. Этот закон теплопроводности называют законом Вернотта–Каттанео–Лыкова (ВКЛ). Уравнение теплопроводности на основе данного закона является волновым уравнением теплопроводности, имеющим гиперболический тип в отличие от уравнения параболического типа на основе закона Фурье [2].

Сложность решения задач теплопереноса на основе волнового уравнения теплопроводности гиперболического типа заключается в возникновении подвижных по пространству и времени фронтов, на которых наблюдаются разрывы температурных профилей и тепловых потоков, причем амплитуды этих разрывов уменьшаются со временем за счет диссипации энергии.

Если тело полубесконечное, то в нем возникают бегущие тепловые волны с уменьшающимися амплитудами разрывов. Такие явления рассматривались в работах Карташова Э.М. [3], Формалева В.Ф., Колесника С.А., Кузнецовой Е.Л. [4–9], Кудинова В.А., Кудинова И.В. и др. [10].

В приведенных работах описано математическое моделирование бегущих тепловых волн в полубесконечных средах. Однако волновой теплоперенос в ограниченных средах не рассматривался, поскольку отражение тепловых волн от противоположной границы существенно отличается от отражения механических волн. Тепловая волна, достигнув противоположной теплоизолированной границы, полностью поглощается ею с повышением температуры, а затем от противоположной границы идет обратная тепловая волна, которая складывается с другой тепловой волной, идущей от левой границы к правой.

Целью данной работы является изучение на основе математического моделирования динамики движения по пространству и времени изолированной тепловой волны в ограниченном стержне в прямом и обратном направлениях с диссипацией тепловой энергии.

ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ

Ставится задача об исследовании динамики движения и отражения изолированной тепловой волны (солитона) в конечном стержне под действием мгновенного теплового импульса величиной ${{T}_{0}},$ действующего на левой границе стержня в течение времени ${{t}_{1}}$ (такое время называют носителем импульса). Поскольку тепловой импульс имеет П-образную форму с разрывами первого рода на переднем по времени и заднем фронтах, то следует ожидать, что теплоперенос вдоль пространственной переменной (вдоль стержня), определяемый на основе решения начально-краевой задачи для волнового уравнения гиперболического типа, будет представлять собой подвижный солитон вдоль пространственной переменной с двумя фронтами температурного профиля (передним и задним), на которых формируются разрывы первого рода. Такие задачи теплопереноса возникают в квантовой механике при облучении тел мощными импульсами тепловой энергии различной природы.

Математическая формулировка проблемы для распределения температур $T\left( {x,t} \right)$ имеет следующий вид:

(1)

${{\tau }_{p}}\frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}} + \frac{{\partial T}}{{\partial t}} = a\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}},\,\,\,\,0 < x < l,\,\,\,\,t > 0,$

(2)

$T\left( {x,0} \right) = 0,\,\,\,\,0 \leqslant x \leqslant l,$

(3)

$\frac{{\partial T\left( {x,0} \right)}}{{\partial t}} = 0,\,\,\,\,0 \leqslant x \leqslant l,$

(4)

$T\left( {0,t} \right) = {{T}_{0}}\left[ {\eta \left( t \right) - \eta \left( {t - {{t}_{1}}} \right)} \right] = \varphi \left( t \right),\,\,\,\,t > 0,$

(5)

$\frac{{\partial T\left( {l,t} \right)}}{{\partial x}} = 0,\,\,\,\,t > 0.$

Здесь ${{\tau }_{p}}$ – время релаксации, т.е. время отставания плотности теплового потока $q\left( {x,t} \right)$ от градиента температур в соответствии с законом ВКЛ

(6)

$q\left( {x,t} \right) = - \lambda \frac{{\partial T\left( {x,t} \right)}}{{\partial x}} - {{\tau }_{p}}\frac{{\partial q\left( {x,t} \right)}}{{\partial t}},$

на основе которого выведено уравнение волнового теплопереноса (1) [2]; $\eta \left( z \right)$ – функция Хевисайда ($\eta \left( z \right) = 1$ при $z > 0,$ $\eta \left( z \right) = 0$ при $z < 0$); $x,t$ – пространственная переменная и время; $a$ – температуропроводность в м²/с.

Поскольку время релаксации ${{\tau }_{p}}$ в твердых телах имеет порядок 10^–12–10^–14 с, то в задаче (1)–(5) целесообразно перейти к безразмерным переменным, для чего уравнение (1) умножим на ${{\tau }_{p}}$ и разделим на $\tau _{p}^{2}.$ После этого введем следующие безразмерные величины:

(7)

$\begin{gathered} \bar {T}\left( {x,t} \right) = {{T\left( {x,t} \right)} \mathord{\left/ {\vphantom {{T\left( {x,t} \right)} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}},\,\,\,\,\bar {t} = {t \mathord{\left/ {\vphantom {t {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}},\,\,\,\,\bar {x} = \frac{x}{{\sqrt {a{{\tau }_{p}}} }}, \\ \bar {l} = {l \mathord{\left/ {\vphantom {l {\sqrt {a{{\tau }_{p}}} }}} \right. \kern-0em} {\sqrt {a{{\tau }_{p}}} }},\,\,\,\,{{{\bar {t}}}_{1}} = {{{{t}_{1}}} \mathord{\left/ {\vphantom {{{{t}_{1}}} {{{\tau }_{p}}.}}} \right. \kern-0em} {{{\tau }_{p}}.}} \\ \end{gathered} $

Вводя безразмерные переменные (7) в соотношения (1)–(5), получим задачу о волновом теплопереносе в безразмерном виде:

(8)

$\frac{{{{\partial }^{2}}\bar {T}}}{{\partial {{{\bar {t}}}^{2}}}} + \frac{{\partial{ \bar {T}}}}{{\partial{ \bar {t}}}} = \frac{{{{\partial }^{2}}\bar {T}}}{{\partial {{{\bar {x}}}^{2}}}},\,\,\,\,0 < \bar {x} < \bar {l},\,\,\,\,\bar {t} > 0,$

(9)

$\bar {T}\left( {\bar {x},0} \right) = 0,\,\,\,\,0 \leqslant \bar {x} \leqslant \bar {l},$

(10)

$\frac{{\partial{ \bar {T}}\left( {\bar {x},0} \right)}}{{\partial{ \bar {t}}}} = 0,\,\,\,\,0 \leqslant \bar {x} \leqslant \bar {l},$

(11)

$\bar {T}\left( {0,\bar {t}} \right) = 1\left[ {\eta \left( {\bar {t}} \right) - \eta \left( {\bar {t} - {{{\bar {t}}}_{1}}} \right)} \right],\,\,\,\,\bar {t} > 0,$

(12)

$\frac{{\partial{ \bar {T}}\left( {\bar {l},\bar {t}} \right)}}{{\partial{ \bar {x}}}} = 0,\,\,\,\,\bar {t} > 0.$

Поскольку скорость $V$ тепловой волны определяется выражением $V = \sqrt {{a \mathord{\left/ {\vphantom {a {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}}} $ [11], то из выражения $V = {x \mathord{\left/ {\vphantom {x t}} \right. \kern-0em} t}$ имеем $V = \sqrt {a{{\tau }_{p}}} {{\bar {x}} \mathord{\left/ {\vphantom {{\bar {x}} {{{\tau }_{p}}\bar {t}}}} \right. \kern-0em} {{{\tau }_{p}}\bar {t}}} = \sqrt {{a \mathord{\left/ {\vphantom {a {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}}} {{\bar {x}} \mathord{\left/ {\vphantom {{\bar {x}} {\bar {t}}}} \right. \kern-0em} {\bar {t}}},$ т.е. из $\sqrt {{a \mathord{\left/ {\vphantom {a {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}}} = \sqrt {{a \mathord{\left/ {\vphantom {a {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}}} {{\bar {x}} \mathord{\left/ {\vphantom {{\bar {x}} {\bar {t}}}} \right. \kern-0em} {\bar {t}}}$ следует, что $\bar {t} = \bar {x}.$

Для решения задачи (8)–(12) применим метод функции источника (Грина). Для получения функции Грина $G\left( {x,\xi ,t} \right)$ поместим источник единичной мощности в точке $x = \xi $ и в соответствии с общей теорией, используя нулевые условия этой функции на пространственно-временнóй границе, приходим к вспомогательной задаче для функции $G\left( {x,\xi ,t} \right)$

(13)

$\frac{{{{\partial }^{2}}G}}{{\partial {{t}^{2}}}} + \frac{{\partial G}}{{\partial t}} = \frac{{{{\partial }^{2}}G}}{{\partial {{x}^{2}}}},\,\,\,\,0 < x < l,\,\,\,\,\,t > 0,$

(14)

$G\left( {x,\xi ,0} \right) = 0,\,\,\,\,0 \leqslant x \leqslant l,\,\,\,\,\xi \in \left( {0,l} \right),$

(15)

$\frac{{\partial G\left( {x,\xi ,0} \right)}}{{\partial t}} = 1\delta \left( {x - \xi } \right),\,\,\,\,0 \leqslant x \leqslant l,\,\,\,\,\xi \in \left( {0,l} \right),$

(16)

$G\left( {0,\xi ,t} \right) = 0,\,\,\,\,t > 0,\,\,\,\,\xi \in \left( {0,l} \right),$

(17)

$\frac{{\partial G\left( {l,\xi ,t} \right)}}{{\partial x}} = 0,\,\,\,\,t > 0,\,\,\,\,\xi \in \left( {0,l} \right).$

Если решение задачи (13)–(17) для функции $G\left( {x,\xi ,t} \right)$ получено, то решение задачи (8)–(12) находится в форме интеграла по времени $\tau < t$ [12]

(18)

$\bar {T}\left( {\bar {x},\bar {t}} \right) = \int\limits_0^{\bar {t}} {\varphi \left( \tau \right){{{\left[ {\frac{\partial }{{\partial \xi }}G\left( {\bar {x},\xi ,\bar {t} - \tau } \right)} \right]}}_{{\xi = 0}}}d\tau .} $

C помощью подстановки

(19)

$G\left( {x,\xi ,t} \right) = V\left( {x,\xi ,t} \right)\exp \left( {\mu t} \right)$

приведем уравнение (13) к классическому уравнению гиперболического типа. Подставляя (19) в (13) и приравнивая к нулю коэффициент при ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial t}}} \right. \kern-0em} {\partial t}},$ получим $\mu = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$ Тогда задача (13)–(17) трансформируется в задачу

(20)

$\frac{{{{\partial }^{2}}V}}{{\partial {{t}^{2}}}} - \frac{1}{4}V = \frac{{{{\partial }^{2}}V}}{{\partial {{x}^{2}}}},\,\,\,\,0 < x < l,\,\,\,\,t > 0,\,\,\,\,\xi \in \left( {0,l} \right),$

(21)

$V\left( {x,\xi ,0} \right) = 0,\,\,\,\,0 \leqslant x \leqslant l,\,\,\,\,\xi \in \left( {0,l} \right),$

(22)

$\frac{{\partial V\left( {x,\xi ,0} \right)}}{{\partial t}} = 1\delta \left( {x - \xi } \right),\,\,\,\,0 \leqslant x \leqslant l,\,\,\,\,\xi \in \left( {0,l} \right),$

(23)

$V\left( {0,\xi ,t} \right) = 0,\,\,\,\,t > 0,\,\,\,\,\xi \in \left( {0,l} \right),$

(24)

$\frac{{\partial V\left( {l,\xi ,t} \right)}}{{\partial x}} = 0,\,\,\,\,t > 0,\,\,\,\,\,\xi \in \left( {0,l} \right).$

Задачу (20)–(24) можно решить методом разделения переменных, представив $V = X\left( x \right)\theta \left( t \right).$ Собственные значения ${{\lambda }_{n}}$ и соответствующие им собственные функции ${{X}_{n}}\left( x \right)$ соответствующей задачи Штурма–Лиувилля имеют вид

(25)

${{\lambda }_{n}} = \frac{{\pi \left( {1 + 2n} \right)}}{{2l}}{\kern 1pt} ,\,\,\,\,{{X}_{n}}\left( x \right) = \sin {\kern 1pt} \left( {{{\lambda }_{n}}x} \right){\kern 1pt} ,\,\,\,\,n = 0,1,2,...,$

а функция ${{\theta }_{n}}\left( t \right){\text{:}}$

(26)

${{\theta }_{n}}\left( t \right) = {{A}_{n}}\sin \left( {t\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} } \right) + {{B}_{n}}\cos \left( {t\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} } \right),$

(27)

$\begin{gathered} V\left( {x,t} \right) = \sum\limits_{n = 1}^\infty {{{\theta }_{n}}\left( t \right){{X}_{n}}\left( x \right)} = \\ = \sum\limits_{n = 1}^\infty {\left[ {{{A}_{n}}\sin \left( {t\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} } \right)} \right.} + \\ + \,\,\left. {{{B}_{n}}\cos \left( {t\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} } \right)} \right]\sin \left( {{{\lambda }_{n}}x} \right). \\ \end{gathered} $

Удовлетворяя (27) начальным условиям (21) и (22), получим коэффициенты ${{A}_{n}},$ ${{B}_{n}}$

${{A}_{n}}\left( \xi \right) = \frac{2}{l}\frac{{\sin \left( {{{\lambda }_{n}}\xi } \right)}}{{\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} }},\,\,\,\,{{B}_{n}} = 0.$

Таким образом, функция (27) имеет вид

(28)

$\begin{gathered} V\left( {x,\xi ,t} \right) = \sum\limits_{n = 0}^\infty {\frac{2}{l}\frac{{\sin \left( {{{\lambda }_{n}}\xi } \right)}}{{\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} }}} \times \\ \times \,\,\sin \left( {t\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} } \right)\sin \left( {{{\lambda }_{n}}x} \right). \\ \end{gathered} $

Здесь $\lambda _{n}^{2} \geqslant {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}.$ Если $\lambda _{n}^{2} < {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$ $\left( {n < \frac{l}{{2\pi }} - \frac{1}{2}} \right),$ то решением задачи (20)–(24) будет функция

$\begin{gathered} V\left( {x,\xi ,t} \right) = \sum\limits_{n = 0}^N {\frac{2}{l}\frac{{\sin \left( {{{\lambda }_{n}}\xi } \right)}}{{\sqrt {\left| {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right|} }}{\text{sh}}\left( {t\sqrt {\left| {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right|} } \right)} \times \\ \times \,\,\sin \left( {{{\lambda }_{n}}x} \right) + \sum\limits_{n = N + 1}^\infty {\frac{2}{l}\frac{{\sin \left( {{{\lambda }_{n}}\xi } \right)}}{{\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} }}} \times \\ \times \,\,\sin \left( {t\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} } \right)\sin \left( {{{\lambda }_{n}}x} \right), \\ \end{gathered} $

где $N < \frac{l}{{2\pi }} - \frac{1}{2},$ т.е. $N$ равно нижнему целому числа $\frac{l}{{2\pi }} - \frac{1}{2}.$

С учетом (19) и (29) решением задачи (13)–(17) для функции источника $G\left( {x,\xi ,t} \right)$ будет функция

(30)

$\begin{gathered} G\left( {x,\xi ,t} \right) = \sum\limits_{n = 1}^N {\left( {\frac{2}{l}\frac{{{{e}^{{{{ - t} \mathord{\left/ {\vphantom {{ - t} 2}} \right. \kern-0em} 2}}}}}}{{\sqrt {\left| {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right|} }}{\text{sh}}\left( {t\sqrt {\left| {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right|} } \right)} \right)} \times \\ \times \,\,\sin \left( {{{\lambda }_{n}}x} \right)\sin \left( {{{\lambda }_{n}}\xi } \right) + \,\, \\ + \,\,\sum\limits_{N + 1}^\infty {\left( {\frac{2}{l}\frac{{{{e}^{{{{ - t} \mathord{\left/ {\vphantom {{ - t} 2}} \right. \kern-0em} 2}}}}}}{{\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} }}\sin \left( {t\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} } \right)} \right)} \times \\ \times \,\,\sin \left( {{{\lambda }_{n}}x} \right)\sin \left( {{{\lambda }_{n}}\xi } \right). \\ \end{gathered} $

Подставляя (30) в (18), получим решение задачи (13)–(17) для функции $\bar {T}\left( {\bar {x},\bar {t}} \right)$ в следующем виде:

(31)

$\begin{gathered} \bar {T}\left( {\bar {x},\bar {t}} \right) = \int\limits_0^{\bar {t}} {\varphi \left( \tau \right){{{\left( {\frac{\partial }{{\partial \xi }}G\left( {\bar {x},\xi ,\bar {t} - \tau } \right)} \right)}}_{{\xi = 0}}}} d\tau = \\ = \int\limits_0^{\bar {t}} {\left[ {\eta \left( \tau \right) - \eta \left( {\tau - {{{\bar {t}}}_{1}}} \right)} \right]} \times \\ \times \,\,\sum\limits_{n = 0}^N {\left[ {\frac{2}{{\bar {l}}}\frac{{{{e}^{{{{ - \left( {\bar {t} - \tau } \right)} \mathord{\left/ {\vphantom {{ - \left( {\bar {t} - \tau } \right)} 2}} \right. \kern-0em} 2}}}}}}{{\sqrt {\left| {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right|} }}{\text{sh}}\left( {\left( {\bar {t} - \tau } \right)\sqrt {\left| {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right|} } \right)} \right] \times } \\ \times \,\,{{\lambda }_{n}}\sin \left( {{{\lambda }_{n}}\bar {x}} \right)d\tau + \int\limits_0^t {\left[ {\eta \left( \tau \right) - \eta \left( {\tau - {{{\bar {t}}}_{1}}} \right)} \right]} \times \\ \times \,\,\sum\limits_{n = N + 1}^\infty {\left[ {\frac{2}{{\bar {l}}}\frac{{{{e}^{{{{ - \left( {\bar {t} - \tau } \right)} \mathord{\left/ {\vphantom {{ - \left( {\bar {t} - \tau } \right)} 2}} \right. \kern-0em} 2}}}}}}{{\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} }}\sin \left( {\left( {\bar {t} - \tau } \right)\sqrt {\lambda _{n}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} } \right)} \right]} \times \\ \times \,\,{{\lambda }_{n}}\sin \left( {{{\lambda }_{n}}\bar {x}} \right)d\tau , \\ \end{gathered} $

где

${{\lambda }_{n}} = \frac{{\pi \left( {1 + 2n} \right)}}{{2\bar {l}}},\,\,\,\,n = 0,1,2,...\,\,.$

Функция (31) – решение исходной задачи (8)–(12) волнового теплопереноса изолированной тепловой волны (солитона).

АНАЛИЗ РЕЗУЛЬТАТОВ

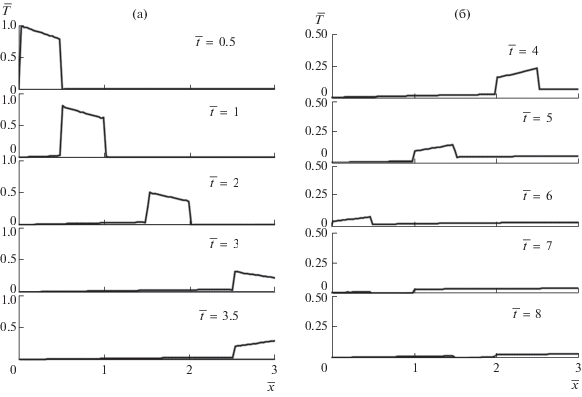
По формуле (31) выполнены расчеты волнового теплопереноса в ограниченных телах для отдельного теплового солитона. Результаты приведены на рисунке. Показана динамика движения изолированной тепловой волны в ограниченном стержне в условиях, когда правая граница теплоизолирована $\left( {\frac{{\partial T\left( {l,t} \right)}}{{\partial x}} = 0} \right).$ Для каждого из десяти моментов времени приведены амплитуды изолированной тепловой волны, координаты по $x$ и скорости ее движения. При этом, поскольку $\bar {t}$ = $\bar {x},$ носитель по времени тепловой волны (временнóй промежуток, на котором амплитуды волны больше нуля, а вне этого промежутки равны нулю) равен носителям по пространственной переменной. В рассматриваемом примере носитель по времени ${{\bar {t}}_{1}}$ принимался равным 0.5, а безразмерная длина стержня $\bar {l}$ – равной 3. Так что динамика движения тепловой волны по пространственной переменной показана на шести отрезках. Амплитуда исходной тепловой волны, входящей в тело на левой границе, равна единице, т.е. максимальная относительная температура $\bar {T} = {T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$ = 1, а абсолютная температура ${{T}_{0}}$ может быть произвольной.

Рис. 1.

Динамика движения тепловой изолированной волны в ограниченном пространстве.

В каждый момент времени на каждом пространственном носителе тепловая волна при движении от левой границы к правой имеет два фронта: передний и задний. Изолированная волна на указанных фронтах имеет разрывы температуры первого рода, причем передние фронты имеют меньшие уровни температур по сравнению с задними фронтами, а между ними распределение температур соответствует формуле (31). При этом перед передним фронтом температура равна начальному условию (в данном случае нулю), а за левым фронтом температурный профиль отличается от начального на незначительную величину.

Достигнув правого конца, энергия тепловой волны полностью уходит на повышение температуры правой границы (рис. а, для $\bar {t}$ = 3.5). Поскольку слева от правой границы температура приближенно равна начальной, то формируется подвижная изолированная тепловая волна в противоположном направлении (обратная волна) (рис. б). В обратной волне фронты меняются местами: задний фронт становится передним, а передний – задним. Теперь на переднем фронте температура ниже, чем на заднем, а между ними распределение температур определяется в соответствии с формулой (31).

Достигнув левого конца, тепловой солитон отражается (тепловым образом), вследствие чего возникает волна в прямом направлении с постепенно уменьшаемой амплитудой.

Таким образом, при многократном отражении от границ ограниченного тела тепловая волна затухает, поглощая всю энергию солитона и образуя температурное поле, слабо отличное от начального распределения.

Следует ожидать, что при наличии серии солитонов, входящих с левой границы тела, отраженные от правой границы волны складываются или поглощаются прямой волной.

В силу малых величин времени релаксации ${{\tau }_{p}}\sim {{10}^{{ - 12}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 14}}}$ с физическая длина $l$ имеет величину нескольких длин свободного пробега, а время – нескольких наносекунд. Таким образом, рассматриваемая проблема имеет место при исследовании теплопереноса в релятивистской механике.

ЗАКЛЮЧЕНИЕ

На основе нового аналитического решения задачи о волновом теплопереносе изолированной тепловой волны (солитона) в ограниченных телах исследована динамика движения ее в пространственно-временнóй области, установлен механизм отражения тепловой волны от границ тела, получены вторичные волны при отражении от правой границы, а затем вторичной волны от левой границы к правой и т.д. При этом носители изолированных тепловых волн по пространственной переменной не изменяются, а амплитуды температур передних и задних фронтов изолированных волн подвержены разрывам первого рода.

Работа выполнена при поддержке Российского научного фонда (проект № 16-19-10 340).

Список литературы

Соболев С.Л. Процессы переноса и бегущие волны в условиях локально-неравновесных систем // УФН. 1991. Т. 161. № 3. С. 5.
Шашков А.Г., Бубнов А.В., Яновский С.Ю. Волновые явления теплопроводности. М.: УРСС, 2004. 248 с.
Карташов Э.М. Математическое моделирование теплопроводности с двухфазным запаздыванием // ИФЖ. 2015. Т. 89. № 2. С. 338.
Формалев В.Ф. О тепловых ударных волнах в нелинейных твердых средах // ТВТ. 2012. Т. 50. № 6. С. 799.
Формалев В.Ф., Колесник С.А., Кузнецова Е.Л. О волновом теплопереносе на временах, сравнимых с временем релаксации при интенсивном конвективно-кондуктивном теплообмене // ТВТ. 2018. Т. 56. № 3. С. 412.
Formalev V.F., Kolesnik S.A. Temperature-dependent Anisotropic Bodies Thermal Conductivity Tensor Components Identification Method // Int. J. Heat Mass Transfer. 2018. V. 123. P. 994.
Формалев В.Ф., Колесник С.А., Кузнецова Е.Л. О волновом теплопереносе в окрестности начального момента времени при интенсивном конвективно-кондуктивном нагреве // ТВТ. 2018. Т. 56. № 3. С. 412.
Формалев В.Ф., Колесник С.А. Аналитическое исследование теплопереноса в анизотропной полосе при задании тепловых потоков на границах // ИФЖ. 2016. Т. 89. № 4. С. 973.
Формалев В.Ф., Колесник С.А., Кузнецова Е.Л. Нестационарный теплоперенос в анизотропном полупространстве в условиях теплообмена с окружающей средой, имеющей заданную температуру // ТВТ. 2016. Т. 54. № 6. С. 876.
Кудинов И.В., Кудинов В.А., Котова Е.В. Дополнительные граничные условия в нестационарных задачах теплопроводности // ТВТ. 2017. Т. 55. № 4. С. 556.
Лыков А.В. Тепломассообмен. Справочник. М.: Энергия, 1978. 480 с.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1972. 736 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал