Теплофизика высоких температур, 2019, T. 57, № 4, стр. 548-559

ВВЕДЕНИЕ

Механизмы, приводящие к генерации вихрей различного типа, представляют большой интерес для метеорологии и служб, обеспечивающих защиту населения от природных катастроф [1–7]. В настоящее время ежегодно в США и во многих других странах наблюдается большое количество торнадо. Например, в 1925 г. на территорию США обрушился один из самых смертоносных смерчей в истории – торнадо Трех Штатов (категория F5); за 3.5 часа оно пронеслось по нескольким штатам со скоростью 100 км/ч. В результате погибли 695 человек, более 2000 получили ранения, 50 000 человек остались без домов¹¹. Из малого вихря, образующегося в атмосфере над океаном, может образоваться циклон (антициклон), представляющий собой гигантский атмосферный вихрь с пониженным (повышенным) давлением в центре и наличием градиентов температуры и давления. Известно, что развитие циклона (антициклона) составляет три стадии: начальная, стадия наибольшего развития и распад. Для начальной стадии, когда вихрь может еще разрушиться и не образовать то или иное атмосферное явление, характерны невысокие перепады давления и высокий градиент температуры, скорости ветра во фронтальной зоне превышают 20 м/с на высоте 5 км [1–4]. Именно на начальной стадии образования вихря могут быть эффективны различные способы внешнего воздействия.

В связи с плохой предсказуемостью места, времени и силы таких атмосферных явлений, исследования условий зарождения вихрей в атмосфере и, особенно, способов воздействия на них могут поспособствовать более точному временнóму и пространственному прогнозированию этих явлений и использованию эффективных способов разрушения смерчей. Для решения названных проблем важно выделить факторы, вызывающие неустойчивости в атмосфере и порождающие природные явления с необычайной разрушительной мощью, такие как ураганы и торнадо.

Целью данной работы является изучение свойств отдельных сосредоточенных вихрей, системы таких вихрей и возможностей их использования для создания на пути торнадо препятствий, проходя через которые, оно ослабевает и распадается на серию вихрей малой интенсивности. Эти малые вихри затухают за счет сил вязкости воздуха и силы трения о поверхность. Поскольку место и время зарождения торнадо плохо прогнозируются и часто находятся далеко от необходимых источников энергии, представляет большой интерес способ быстрой организации системы препятствий именно в нужном месте и в нужное время.

Частные случаи вихревых течений, в которых направления векторов завихренности и скорости коллинеарны, относятся к классу течений Громеки–Бельтрами [8–11] и Н.Е. Жуковского [12]. В работе [8] показана возможность нахождения поля скоростей в сосредоточенном вихре, когда выполняется условие

Здесь ${\mathbf{u}}$ – скорость среды, k – неизвестный параметр, который находится в процессе решения задачи.

Для более детального анализа распределения скоростей, давлений и температуры в сосредоточенном вихре специального типа для невязкой среды с учетом силы Кориолиса необходимо найти полное решение системы уравнений неразрывности и движения с учетом условия (1):

Под сосредоточенным вихрем будем понимать течение, сосредоточенное внутри цилиндра заданного радиуса. Вихри такого типа представляют отдельный случай. Возможность их реализации и использования в природе требует специального анализа.

1. СТАЦИОНАРНЫЙ СОСРЕДОТОЧЕННЫЙ ВИХРЬ С ДВУМЯ КОМПОНЕНТАМИ СКОРОСТИ В ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ

С учетом (1) уравнение сохранения импульса Эйлера для среды [13] распадается на систему линейных уравнений для скорости (1) и на неоднородное уравнение для нахождения распределения давления:

В случае, когда две компоненты вектора скорости ${\mathbf{u}} = \left( {0,{{u}_{\varphi }}\left( r \right),{{u}_{z}}\left( r \right)} \right)$ зависят только от радиуса, решение данной задачи для сосредоточенного вихря радиуса $R$ получено в [8]. Воспроизведем его здесь в удобной форме и найдем распределение давления в вихре с учетом силы Кориолиса. Система уравнений $\left[ {\nabla \times {\mathbf{u}}} \right] \equiv {\mathbf{\Omega }} = k{\mathbf{u}}$ в цилиндрической системе координат и в проекциях на оси ${{{\mathbf{e}}}_{r}},{{{\mathbf{e}}}_{z}}$ сводятся к двум уравнениям:

Из системы (4) получаем уравнение Бесселя для функции ${{u}_{z}}\left( r \right)$

При граничных условиях на отрезке $\left[ {0,R} \right]$

Из первого уравнения системы (4) находим распределение угловой скорости внутри сосредоточенного вихря

Константы ${{C}_{j}}$ остаются неопределенными. Далее остановимся на монотонном распределении скорости ${{u}_{z}}\left( {\tilde {r}} \right)$ по радиусу, считая, что известен расход воздуха в вихре $G.$ В этом частном случае ограничимся лишь первым членом в приведенных выше решениях. Тогда, используя выражение для расхода

Таким образом, при заданном расходе распределение скоростей и завихренности в сосредоточенном вихре радиуса $R$ имеет вид

Зависимость давления от радиуса

Для нахождения распределения давления в вихре воспользуемся уравнением (4) и рассмотрим два отдельных случая.

Случай a. Сила Кориолиса отсутствует. В данном примере ограничиваемся малыми числами Маха, поэтому можно считать $\rho = {\text{const}}{\text{.}}$ В этом случае из уравнения (2) при ${{\Omega }_{k}} = 0$ получаем

(10)

$\frac{p}{\rho } + \frac{{{{{\mathbf{u}}}^{2}}}}{2} = \Pi .$

Здесь $\Pi $ – произвольная константа.

Зная зависимость квадрата модуля скорости от радиуса

$\begin{gathered} {{{\mathbf{u}}}^{2}}\left( r \right) = u_{z}^{2}\left( r \right) + u_{\varphi }^{2}\left( r \right) = {{\left[ {\frac{G}{\rho }\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2\pi {{R}^{2}}}}\frac{1}{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}}} \right]}^{2}} \times \\ \times \,\,\left[ {J_{0}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\frac{r}{R}} \right) + J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\frac{r}{R}} \right)} \right] \\ \end{gathered} $

и полагая, что давление равно атмосферному $p = {{p}_{0}}{\text{ п р и }}\,\,r = R,$ можно найти константу $\Pi ,$ входящую в уравнение (10). При этом условии имеем

(11)

$p\left( \xi \right) = \left\{ \begin{gathered} {{p}_{0}} - \frac{1}{{2\rho }}{{\left( {\frac{G}{{\pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{2}} \right)}^{2}}\left[ {\frac{{J_{0}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right) + J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right)}}{{J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}} - 1} \right],\,\,\,\,\,0 \leqslant \xi \leqslant 1; \hfill \\ {{p}_{0}} = {\text{const}},\,\,\,\,\xi > 1, \hfill \\ \end{gathered} \right.\,\,\,\,\,\,\xi = \frac{r}{R}.$

Для построения графиков удобно пользоваться безразмерными параметрами:

$\xi = \frac{r}{R},\,\,\,\,\tilde {u} = \frac{{u\rho {{R}^{2}}}}{G},\,\,\,\,\tilde {\Omega } = \frac{{\Omega \rho {{R}^{3}}}}{G},\,\,\,\,\tilde {p} = \frac{p}{{{{p}_{0}}}}.$

На рис. 1–3 показаны распределения безразмерных скоростей, завихренностей и давления в пределах вихря. Анализируя изменение давления, можно видеть, что данный вихрь всегда является циклоном. Относительное изменение давления в циклоне ${{p\left( 0 \right)} \mathord{\left/ {\vphantom {{p\left( 0 \right)} {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}$ зависит от параметра $a = {G \mathord{\left/ {\vphantom {G {\pi {{R}^{2}}}}} \right. \kern-0em} {\pi {{R}^{2}}}}{\kern 1pt} {\text{:}}$

$\frac{{p\left( 0 \right)}}{{{{p}_{0}}}} = 1 - \frac{1}{{2\rho {{p}_{0}}}}{{\left( {\frac{{a\mu _{1}^{{\left( 0 \right)}}}}{2}} \right)}^{2}}\left[ {\frac{1}{{J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}} - 1} \right].$

Рис. 1.

Распределение безразмерных вертикальной (1) и угловой (2) компонент скорости по безразмерному радиусу.

Рис. 2.

Распределение безразмерных вертикальной (1) и угловой (2) компонент вектора завихренности по радиусу.

Рис. 3.

Распределение безразмерного давления $\tilde {p} = {p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}$ в пределах вихря.

Для достижения давления 700 мм рт. ст. на оси вихря данный параметр должен быть порядка $ \sim {\kern 1pt} 70$ (кг/м³)/(м/с). При расходе $10$ кг/с вихрь будет очень малого радиуса: $R = 0.21{\text{ м }}{\text{.}}$

Выше рассмотрен случай, когда расход направлен вдоль оси z. Если изменить направление движения среды, то каждая компонента скорости изменит свой знак на противоположный. При этом, естественно, распределение давления по-прежнему описывается уравнением (11).

Случай b. Влияние силы Кориолиса при постоянной плотности. Снова воспользуемся уравнением (2), когда ${{\Omega }_{k}} \ne 0.$ Проводя в уравнении (2) интегрирование, имеем

$\frac{p}{\rho } + \frac{{{{{\mathbf{u}}}^{2}}}}{2} + 2\int {[{{{\mathbf{\Omega }}}_{k}} \times {\mathbf{u}}]dr} = \Pi .$

Используя условие на границе вихря $p = {{p}_{0}}\;{\text{п р и }}\;r = R,$ находим распределение давления в вихре с учетом силы Кориолиса, также представляя его в безразмерном виде $\left( {\tilde {p} = {p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}} \right){\kern 1pt} {\text{:}}$

(12)

$\tilde {p}\left( \xi \right) = \left\{ \begin{gathered} 1 - \frac{1}{{2\rho {{p}_{0}}}}{{\left( {\frac{{G\mu _{1}^{{\left( 0 \right)}}}}{{2\pi {{R}^{2}}}}} \right)}^{2}}\left[ {\frac{{J_{0}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right) + J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right)}}{{J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}} - 1} \right] - \frac{{G{{\Omega }_{k}}}}{{\pi R}}\frac{{{{J}_{0}}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right)}}{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}},\,\,\,\,0 \leqslant \xi \leqslant 1; \hfill \\ 1,\,\,\,\,\xi > 1. \hfill \\ \end{gathered} \right.$

С учетом силы Кориолиса сосредоточенный вихрь при движении воздуха вверх является всегда циклоном. Однако, когда воздух в вихре направлен вниз, при определенных размерах вихря он может быть антициклоном (рис. 4).

Рис. 4.

Распределение давления по радиусу при наличии и отсутствии силы Кориолиса.

Как видно из рис. 4, при параметрах вихря ${{R}_{{\min }}} \approx 37{\text{ м }},$ G = 10 кг/c в центре будет повышенное давление, однако перепады давления очень малы. Поэтому можно считать такой вихрь изобарическим.

Случай c. Специальный. $2[{{{\mathbf{\Omega }}}_{k}} \times {\mathbf{u}}] - \left[ {{\mathbf{u}} \times {\mathbf{\Omega }}} \right] = 0,$ $\nabla \cdot {\mathbf{u}} = 0.$

Если выполняется условие

(13)

$\left[ {{\mathbf{\Omega }} \times {\mathbf{u}}} \right] + 2[{{{\mathbf{\Omega }}}_{k}} \times {\mathbf{u}}] = \left[ {\left( {{\mathbf{\Omega }} + 2{{{\mathbf{\Omega }}}_{k}}} \right) \times {\mathbf{u}}} \right] = 0,$

то в (1) соотношение ${\mathbf{\Omega }} = k{\mathbf{u}}$ можно заменить на

(14)

$(\Omega + 2{{\Omega }_{k}}) = k{\mathbf{u}}{\kern 1pt} .$

В этом случае система уравнений, позволяющая найти поле скоростей, сводится к следующей:

(15)

$\left\{ \begin{gathered} - \frac{{d{{u}_{z}}}}{{dr}} = k{{u}_{\varphi }}, \hfill \\ \frac{1}{r}\frac{{d\left( {r{{u}_{\varphi }}} \right)}}{{dr}} = k{{u}_{z}} + 2{{\Omega }_{k}}. \hfill \\ \end{gathered} \right.$

Теперь вместо уравнения (5) для функции ${{u}_{z}}\left( r \right)$ приходим к уравнению

(16)

$\frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{d{{u}_{z}}}}{{dr}}} \right) + k\left( {k{{u}_{z}} + 2{{\Omega }_{k}}} \right) = 0.$

Его решение имеет вид

${{u}_{z}}\left( r \right) = \sum\limits_{j = 1}^\infty {\left[ {{{C}_{j}}{{J}_{0}}\left( {\mu _{j}^{{\left( 0 \right)}}\frac{r}{R}} \right) - 2{{\Omega }_{k}}\frac{R}{{\mu _{j}^{{\left( 0 \right)}}}}} \right]} {\kern 1pt} .$

Соответственно, для угловой скорости и компонент завихренности получаем

${{u}_{\varphi }} = \sum\limits_{j = 1}^\infty {{{C}_{j}}{{J}_{1}}\left( {\mu _{j}^{{\left( 0 \right)}}\frac{r}{R}} \right)} ,$

$\begin{gathered} {{\Omega }_{z}}\left( r \right) = \sum\limits_{j = 1}^\infty {\left[ {{{C}_{j}}\frac{{\mu _{j}^{{\left( 0 \right)}}}}{R}{{J}_{0}}\left( {\mu _{j}^{{\left( 0 \right)}}\frac{r}{R}} \right) - 2{{\Omega }_{k}}} \right]} , \\ {{\Omega }_{\varphi }}\left( r \right) = \sum\limits_{j = 1}^\infty {\left[ {{{C}_{j}}\frac{{\mu _{j}^{{\left( 0 \right)}}}}{R}{{J}_{1}}\left( {\mu _{j}^{{\left( 0 \right)}}\frac{r}{R}} \right)} \right]} {\kern 1pt} . \\ \end{gathered} $

Видно, что угловая скорость не изменилась по сравнению с предыдущим случаем. Считая, как и выше, что известен расход воздуха в вихре (7), находим константу

${{C}_{1}} = \frac{{{{\Omega }_{k}}R}}{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}}\left( {\frac{G}{{\rho \pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2{{\Omega }_{k}}R}} + 1} \right).$

В результате получаем следующие зависимости скоростей и компонент вектора завихренности от радиуса:

(17)

$\begin{gathered} {{u}_{z}}\left( r \right) = {{\Omega }_{k}}R\left[ {\left( {\frac{G}{{\rho \pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2{{\Omega }_{k}}R}} + 1} \right)\frac{{{{J}_{0}}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right)}}{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}} - \frac{2}{{\mu _{1}^{{\left( 0 \right)}}}}} \right], \\ {{u}_{\varphi }} = {{\Omega }_{k}}R\left( {\frac{G}{{\rho \pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2{{\Omega }_{k}}R}} + 1} \right)\frac{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right)}}{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}}, \\ {{\Omega }_{z}}\left( r \right) = {{\Omega }_{k}}\left[ {\left( {\frac{G}{{\rho \pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2{{\Omega }_{k}}R}} + 1} \right)\frac{{{{J}_{0}}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right)}}{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}}\mu _{1}^{{\left( 0 \right)}} - 2} \right], \\ {{\Omega }_{\varphi }}\left( r \right) = {{\Omega }_{k}}\left( {\frac{G}{{\rho \pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2{{\Omega }_{k}}R}} + 1} \right)\frac{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right)}}{{{{J}_{1}}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}}\mu _{1}^{{\left( 0 \right)}}. \\ \end{gathered} $

Сила Кориолиса, как видно из (17), оказывает сильное воздействие на скорость только на больших расстояниях от центра вихря, и первое слагаемое в этих формулах при $r \to R$ много больше второго. Поэтому в вихрях такого типа решение при $r \to R$ соответствует рис. 1, 2. Используя формулы (17), найдем квадрат скорости, который понадобится для определения распределения давления:

$\begin{gathered} {{u}^{2}}\left( r \right) = \Omega _{k}^{2}{{R}^{2}}{{\left( {\frac{G}{{\rho \pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2{{\Omega }_{k}}R}} + 1} \right)}^{2}} \times \\ \times \,\,\frac{1}{{J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}}\left[ {J_{0}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\frac{r}{R}} \right) + J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\frac{r}{R}} \right)} \right] \\ \end{gathered} $

и с учетом условия $p = {{p}_{0}},$ $r = R$ находим константу П, входящую в уравнение (10):

$\Pi = {{p}_{0}} + \frac{{\rho \Omega _{k}^{2}{{R}^{2}}}}{2}{{\left( {\frac{G}{{\rho \pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2{{\Omega }_{k}}R}} + 1} \right)}^{2}}.$

Теперь распределение давления в вихре определяется формулой

(18)

$\tilde {p}\left( \xi \right) = \left\{ \begin{gathered} 1 - \frac{{\rho \Omega _{k}^{2}{{R}^{2}}}}{{2{{p}_{0}}}}{{\left( {\frac{G}{{\rho \pi {{R}^{2}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{2{{\Omega }_{k}}R}} + 1} \right)}^{2}} \times \hfill \\ \times \,\,\left[ {\frac{{J_{0}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right) + J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}\xi } \right)}}{{J_{1}^{2}\left( {\mu _{1}^{{\left( 0 \right)}}} \right)}} - 1} \right],\,\,\,\,\xi \leqslant 1; \hfill \\ 1,\,\,\,\,\xi > 1. \hfill \\ \end{gathered} \right.$

В этом случае учитывалась сила Кориолиса, однако направление расхода уже не может сильно повлиять на распределение давления. Также перепад давления при данном решении является максимальным (рис. 5).

Рис. 5.

Распределение давления: пунктир – случай a, штрихпунктир – b, сплошная – специальный случай c.

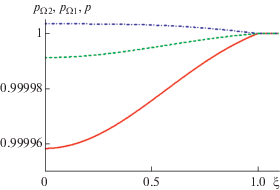
При тех же параметрах вихря, что и в случае b $\left( {R \approx 37{\text{ м }},G = 10{\text{ }}{{{\text{к г }}} \mathord{\left/ {\vphantom {{{\text{к г }}} {\text{с }}}} \right. \kern-0em} {\text{с }}}} \right)$, давление будет сильнее меняться, однако его перепады все равно очень малы, поэтому данный вихрь также можно считать изобарическим.

Исследуем зависимость среднего значения завихренности в пределах вихря

(19)

$\left\langle \Omega \right\rangle = \frac{1}{{\pi {{R}^{2}}}}\int\limits_0^R {{{\Omega }_{z}}\left( r \right)2\pi rdr} = \frac{2}{{{{R}^{2}}}}\int\limits_0^R {{{\Omega }_{z}}\left( r \right)rdr} $

от расхода и радиуса области, занятой вихрем. Используя уравнения (17), (19) и проводя интегрирование, имеем

(20)

$f\left( {G,R} \right) = \frac{{\left\langle \Omega \right\rangle }}{{{{\Omega }_{k}}}} = \frac{G}{{{{R}^{3}}}}\frac{{\mu _{1}^{{\left( 0 \right)}}}}{{\rho \pi {{\Omega }_{k}}}}.$

Сравним зависимость (20) от радиуса при трех расходах $G = 1,\,\,10,\,\,100{\text{ }}{{{\text{к г }}} \mathord{\left/ {\vphantom {{{\text{к г }}} {\text{с }}}} \right. \kern-0em} {\text{с }}}{\text{.}}$ Радиус вихря, при котором средняя завихренность сравняется с интенсивностью Кориолиса, $R = 20.5,\;44,\;95{\text{ м }}$ соответственно. Для любого расхода чем меньше радиус вихря, тем быстрее растет средняя завихренность с увеличением расхода.

Зная распределение скоростей и давлений в сосредоточенном вихре, можно найти двумерное распределение температуры из уравнения энергии

$\frac{{\partial T}}{{\partial t}} + {{u}_{r}}\frac{{\partial T}}{{\partial r}} + {{u}_{z}}\frac{{\partial T}}{{\partial z}} = \chi \left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial T}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}}} \right] + \frac{{q(r,z)}}{{\rho {{c}_{\text{v}}}}}.$

Здесь $q$ – источник внешнего тепловыделения; $\chi = {\lambda \mathord{\left/ {\vphantom {\lambda {\rho {{c}_{\text{v}}}}}} \right. \kern-0em} {\rho {{c}_{\text{v}}}}}$ – коэффициент температуропроводности; $\lambda ,\rho ,{{c}_{\text{v}}}$ – теплопроводность, плотность воздуха и удельная теплоемкость соответственно. Как будет показано далее, это уравнение может быть использовано для создания сосредоточенного вихря посредством внешнего воздействия $q(r,z).$

2. СТАЦИОНАРНЫЙ СОСРЕДОТОЧЕННЫЙ ВИХРЬ С ТРЕМЯ КОМПОНЕНТАМИ СКОРОСТИ, ЗАВИСЯЩИМИ ОТ ВЕРТИКАЛЬНОЙ И РАДИАЛЬНОЙ КООРДИНАТЫ

Сосредоточенный вихрь ${\mathbf{\Omega }}\left( {r,z} \right) = \nabla \times {\mathbf{u}}\left( {r,z} \right)$ = $ = k \cdot {\mathbf{u}}\left( {r,z} \right),$ полученный в работе [8] и детально рассмотренный в предыдущем параграфе, содержал две компоненты скорости, зависящие только от радиуса. Не меньший интерес представляют сосредоточенные вихри с тремя компонентами скорости, зависящими не только от радиуса, но и от вертикальной координаты:

С учетом силы Кориолиса система уравнений движения распадается на уравнение

Кроме данной системы уравнений, вектор скорости должен удовлетворять уравнению неразрывности, записанному в цилиндрической системе координат:

Решение системы (22) необходимо искать с учетом выполнения (23). Подход к решению этой системы с учетом (23) состоит в том, что уравнение неразрывности выполняется тождественно, если искать решение в виде

(26)

Дальнейшее решение задачи, позволяющее найти распределения скоростей по радиусу вихря и по высоте, зависит от выбора конкретных граничных условий.

Вихрь радиуса $R$ с потоком, втекающим в слой толщиной $H$

Общее решение второго уравнения (26) имеет вид

(27)

$Z(z) = {{C}_{1}}\exp ( - i\lambda z) + {{C}_{2}}\exp (i\lambda z).$

Константа $\lambda $ находится из граничных условий, полагающих, что скорость втекающего потока на высоте $H$ равна нулю:

(28)

$Z(z = 0) \ne 0,$

(29)

$Z(z = H) = 0.$

С учетом первого граничного условия (28) решение для функции Z(z) имеет вид

(30)

$Z(z) = C\cos (\lambda z).$

Используя второе граничное условие (29), находим

(31)

${{\lambda }_{n}} = \frac{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + \pi n}}{H},\,\,\,\,n = 0,1,\,...,\infty .$

Первое уравнение из (26) является дифференциальным уравнением Бесселя первого порядка, и, заменяя ${{k}^{2}} - {{\lambda }^{2}} = {{K}^{2}},$ перепишем его в виде

(32)

$\frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r\frac{{\partial S}}{{\partial r}}} \right] + S\left( {{{K}^{2}} - \frac{1}{{{{r}^{2}}}}} \right) = 0.$

Для решения (32) используем граничные условия для функции S(r), аналогичные (6):

(33)

$S({{r}_{0}}) = 0,\,\,\,\,{{\left. {\frac{d}{{dr}}S} \right|}_{{r = 0}}} = 0.$

С учетом (33) решение (32) может быть записано в виде бесконечной суммы функций Бесселя первого порядка

(34)

$S(r) = \sum\limits_{j = 1}^\infty {{{C}_{j}}{{J}_{1}}\left( {\mu _{j}^{{(1)}}\frac{r}{{{{r}_{0}}}}} \right).} $

где $\mu _{j}^{{\left( 1 \right)}}$ – нули функции Бесселя первого порядка ${{J}_{1}}(K{{r}_{0}}) = {{J}_{1}}(\mu _{j}^{{(1)}}) = 0.$

Подставляя найденные решения (30), (34) в (25), для азимутальной составляющей скорости получаем

(35)

${{u}_{\varphi }}(r,z) = \sum\limits_{n = 0}^\infty {\sum\limits_{j = 1}^\infty {{{C}_{{jn}}}{{J}_{1}}} \left( {\mu _{j}^{{(1)}}\frac{r}{R}} \right)\cos ({{\lambda }_{n}}z).} $

Зная значения $\mu _{j}^{{\left( 1 \right)}}$ и ${{\lambda }_{n}}$, находим k_jn

$\begin{gathered} {{k}_{{jn}}} = \sqrt {{{{\left( {\frac{{\mu _{j}^{{(1)}}}}{R}} \right)}}^{2}} + {{{\left( {\frac{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + \pi n}}{H}} \right)}}^{2}}} , \\ j = 1,\,\,2,\,\, \ldots ,\,\,\infty ,\,\,\,\,n = 0,\,\,1,\,\, \ldots ,\,\,\infty . \\ \end{gathered} $

Радиальную скорость получим из первого уравнения системы (22):

(36)

${{u}_{r}}(r,z) = \sum\limits_{n = 0}^\infty {\sum\limits_{j = 1}^\infty {{{C}_{{jn}}}} \frac{{{{\lambda }_{n}}}}{{{{k}_{{jn}}}}}{{J}_{1}}\left( {\mu _{j}^{{(1)}}\frac{r}{R}} \right)\sin ({{\lambda }_{n}}z).} $

Используя соотношение

$\frac{{\partial \left( {r{{u}_{\varphi }}} \right)}}{{\partial r}} = \sum\limits_{n = 0}^\infty {\sum\limits_{j = 1}^\infty {{{C}_{{jn}}}\mu _{j}^{{\left( 1 \right)}}\frac{r}{R}{{J}_{0}}\left( {\mu _{j}^{{\left( 1 \right)}}\frac{r}{R}} \right)\cos \left( {{{\lambda }_{n}}z} \right)} } ,$

найдем из третьего уравнения системы (22) вертикальную компоненту скорости течения в вихре

(37)

${{u}_{z}}(r,z) = \sum\limits_{n = 0}^\infty {\sum\limits_{j = 1}^\infty {{{C}_{{jn}}}} \frac{{\mu _{j}^{{(1)}}}}{{{{k}_{{jn}}}R}}} {{J}_{0}}\left( {\mu _{j}^{{(1)}}\frac{r}{R}} \right)\cos ({{\lambda }_{n}}z) - \frac{{2{{\Omega }_{k}}}}{{{{k}_{{jn}}}}}.$

Аналогично задаче о сосредоточенном вихре с двумя компонентами скорости оставим в уравнениях (35)–(37) только первые слагаемые $(j = 1,n = 0)$. Тогда

${{\lambda }_{0}} = \frac{\pi }{{2H}},\,\,\,\,{{k}_{{10}}} = \sqrt {{{{\left( {\frac{{\mu _{1}^{{(1)}}}}{R}} \right)}}^{2}} + {{{\left( {\frac{\pi }{{2H}}} \right)}}^{2}}} .$

Для нахождения константы ${{C}_{{10}}},$ входящей в формулу для скорости ${{u}_{z}}\left( {r,z} \right),$ будем считать, что на верхней границе вихря вертикальная проекция скорости направлена вверх, а на земле скорость ${{u}_{z}}\left( {r,z} \right)$ равна нулю:

(38)

$z = 0,\,\,\,\,{{u}_{z}}(r,z = 0) = 0.$

При таких условиях константа составляет

(39)

${{C}_{{10}}} = {{\Omega }_{k}}R\frac{2}{{\mu _{1}^{{(1)}}}}\frac{1}{{{{J}_{0}}(\mu _{1}^{{(1)}})}}.$

Теперь зависимости всех компонент скорости течения от координат r, z в сосредоточенном вихре радиуса R имеют следующий вид:

(40)

$\begin{gathered} {{u}_{\varphi }}(r,z) = {{\Omega }_{k}}R\frac{2}{{\mu _{1}^{{(1)}}}}\frac{{{{J}_{1}}\left( {\mu _{1}^{{(1)}}\frac{r}{R}} \right)}}{{{{J}_{0}}(\mu _{1}^{{(1)}})}}\cos ({{\lambda }_{0}}z), \\ {{u}_{r}}(r,z) = {{\Omega }_{k}}R\frac{2}{{\mu _{1}^{{(1)}}}}\frac{{{{\lambda }_{0}}}}{{{{k}_{{10}}}}}\frac{{{{J}_{1}}\left( {\mu _{1}^{{(1)}}\frac{r}{R}} \right)}}{{{{J}_{0}}(\mu _{1}^{{(1)}})}}\sin ({{\lambda }_{0}}z), \\ {{u}_{z}}(r,z) = \frac{{2{{\Omega }_{k}}}}{{{{k}_{{10}}}}}\left[ {\frac{{{{J}_{0}}\left( {\mu _{1}^{{(1)}}\frac{r}{R}} \right)}}{{{{J}_{0}}(\mu _{1}^{{(1)}})}}\cos ({{\lambda }_{0}}z) - 1} \right]. \\ \end{gathered} $

Чтобы найти распределение давления в вихре, воспользуемся уравнением (3), из которого следует

(41)

$p(r,z) = \Pi - \rho \frac{{{{{\mathbf{u}}}^{2}}}}{2}.$

Находя квадрат скорости

$\begin{gathered} {{u}^{2}}(r,z) = {{({{\Omega }_{k}}R)}^{2}}\frac{4}{{\mu _{1}^{{{{{(1)}}^{2}}}}}}\frac{{J_{1}^{2}\left( {\mu _{1}^{{(1)}}\frac{r}{R}} \right)}}{{J_{0}^{2}(\mu _{1}^{{(1)}})}} \times \\ \times \,\,\left[ {{{{\cos }}^{2}}({{\lambda }_{0}}z) + \frac{{\lambda _{0}^{2}}}{{k_{{10}}^{2}}}{{{\sin }}^{2}}({{\lambda }_{0}}z)} \right] + \\ + \,\,4{{\left( {\frac{{{{\Omega }_{k}}}}{{{{k}_{{10}}}}}} \right)}^{2}}{{\left[ {\frac{{{{J}_{0}}\left( {\mu _{1}^{{(1)}}\frac{r}{R}} \right)}}{{{{J}_{0}}(\mu _{1}^{{(1)}})}}\cos ({{\lambda }_{0}}z) - 1} \right]}^{2}} \\ \end{gathered} $

и используя условие

(42)

$r = R,\,\,\,\,p(r,z) = {{p}_{0}},$

из (41) найдем константу

(43)

$\Pi (z) = {{p}_{0}} + 2\rho {{\left( {\frac{{{{\Omega }_{k}}}}{{{{k}_{{10}}}}}} \right)}^{2}}{{(\cos ({{\lambda }_{0}}z) - 1)}^{2}}.$

В результате распределение давления в сосредоточенном вихре выглядит следующим образом:

(44)

$\begin{gathered} p(r,z) = {{p}_{0}} - \rho {{({{\Omega }_{k}}R)}^{2}}\frac{2}{{\mu _{1}^{{{{{(1)}}^{2}}}}}}\frac{{J_{1}^{2}\left( {\mu _{1}^{{(1)}}\frac{r}{R}} \right)}}{{J_{0}^{2}(\mu _{1}^{{(1)}})}} \times \\ \times \,\,\left[ {{{{\cos }}^{2}}({{\lambda }_{0}}z) + \frac{{\lambda _{0}^{2}}}{{k_{{10}}^{2}}}{{{\sin }}^{2}}({{\lambda }_{0}}z)} \right] - 2\rho {{\left( {\frac{{{{\Omega }_{k}}}}{{{{k}_{{10}}}}}} \right)}^{2}} \times \\ \times \,\,\left\{ {{{{\left[ {\frac{{{{J}_{0}}\left( {\mu _{1}^{{(1)}}\frac{r}{R}} \right)}}{{{{J}_{0}}\left( {\mu _{1}^{{(1)}}} \right)}}\cos ({{\lambda }_{0}}z) - 1} \right]}}^{2}} - {{{(\cos ({{\lambda }_{0}}z) - 1)}}^{2}}} \right\}. \\ \end{gathered} $

Для построения графиков проведем обезразмеривание:

$\tilde {u} = \frac{{uk}}{{{{\Omega }_{k}}}},\,\,\,\,\tilde {\Omega } = \frac{\Omega }{{{{\Omega }_{k}}}},\,\,\,\,\xi = \frac{r}{R},\,\,\,\,\tilde {p} = \frac{p}{{{{p}_{0}}}}.$

Тогда профиль скорости будет совпадать с профилем завихренности. На рис. 6, 7 показаны распределения безразмерных скоростей, завихренностей и давления по радиусу вихря при $H = 1000{\text{ м }}{\text{.}}$

Рис. 6.

Распределение радиальной (1), угловой (2) и вертикальной (3) компонент скорости и завихренности при $z = {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}.$

Рис. 7.

Распределение безразмерного давления на высотах z = 0.1 (1), 0.5 (2), 1 (3) для вихря с тремя компонентами скорости и для вихря с двумя компонентами скорости (4).

3. СИСТЕМА СОСРЕДОТОЧЕННЫХ ВИХРЕЙ

Очевидно, что рассмотренные выше решения, в которых выполняются условия (1), являются частными. Представляет интерес использование полученных выше стационарных распределений для построения полных решений нелинейного уравнения движения и анализа различных механизмов генерации вихрей, приводящих к стационарным (квазистационарным) вихрям рассмотренного выше типа. Только в этом случае сосредоточенные образования, обладающие распределенной завихренностью (спиральностью $S = [\nabla \times {\mathbf{V}}] \cdot {{\mathbf{V}} \mathord{\left/ {\vphantom {{\mathbf{V}} 2}} \right. \kern-0em} 2}$) и циклоническим распределением давления, могут представлять интерес для физики атмосферы и различных технических приложений.

Если характерное число Маха рассматриваемого течения существенно меньше единицы, а число Рейнольдса $\operatorname{Re} = {{{{u}_{c}}R} \mathord{\left/ {\vphantom {{{{u}_{c}}R} \eta }} \right. \kern-0em} \eta }$ велико, решение нелинейной, нестационарной системы уравнений

Здесь ${{u}_{c}}$ – характерная скорость задачи, $\eta $ – коэффициент кинематической вязкости, $R$ – радиус сосредоточенного вихря. Функция ${{{\mathbf{u}}}_{0}}(r)$ является решением, полученным из условия $(\nabla \times {{{\mathbf{u}}}_{0}} - 2{{{\mathbf{\Omega }}}_{c}}) \times {{{\mathbf{u}}}_{0}} = 0$ и $\left( {\nabla \times {{{\mathbf{u}}}_{0}} - 2{{{\mathbf{\Omega }}}_{c}}} \right) = k{{{\mathbf{u}}}_{0}}.$ В этом случае для функции ${{{\mathbf{u}}}_{1}}$ с учетом неравенства $\varepsilon \ll 1$ приходим к линейному уравнению

Среди других задач, в которых решения, полученные в разделах 1, 2, могут оказаться полезными, остановимся на процессе воздействия электромагнитным полем круговой поляризации ${\mathbf{E}}{\kern 1pt} \exp (i\omega t)$ микроволнового диапазона частот $\omega $ на влажный воздух или поверхность воды. Проведем анализ таких процессов в рамках стандартной системы уравнений сплошной среды

Здесь ${\mathbf{F}} = {\mathbf{j}} \times {\mathbf{B}}$ – сила Ампера; ${\mathbf{g}}$ – сила тяжести; $J(E,\omega )$ – тепловыделение от внешнего микроволнового излучения; ${\mathbf{j}}$ – плотность электрического тока; ${\mathbf{B}}$ – магнитное поле Земли и кругового тока электромагнитной волны; ${{\varepsilon }_{0}},\,\,{{\mu }_{0}}$ – диэлектрическая и магнитная проницаемости соответственно; $\varepsilon {\text{'}}(r)$ – относительная диэлектрическая проницаемость среды.

Эта система может решаться только численно с начальными условиями, задаваемыми решениями, полученными в разделах 1, 2, как для одиночного вихря, так и для системы вихрей, расположенных на плоскости $P = P(\rho ,T),$ с учетом известных подходов [14–16].

В чем же состоит преимущество использования электромагнитной волны круговой поляризации в микроволновом диапазоне частот для генерации сосредоточенных вихрей? Пучки электромагнитной волны заданной конфигурации могут быть созданы именно в нужном месте и в установленное время посредством генераторов СВЧ-излучения, расположенных на самолетах или спутниках. Вихри создаются при воздействии пучка СВЧ и (или) лазерного излучения на поверхность влажного воздуха или воды, которые хорошо поглощают это излучение. Искусственно созданная посредством СВЧ-излучения система вихрей может быть использована для создания препятствий на пути распространения торнадо. Проблеме воздействия на вихри посвящена обширная литература [1, 14] и здесь она детально не обсуждается.

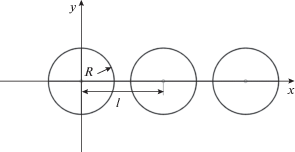
Далее рассмотрим более подробно, как решения, полученные в цилиндрической системе координат для одиночного стационарного сосредоточенного вихря, могут быть использованы для системы цилиндрических вихрей на плоскости. Если за пределами вихря радиуса $R$ все свойства среды остаются постоянными, то решения для сосредоточенного вихря, свойства которого изменяются в области $\left[ {0 \leqslant r \leqslant R} \right],$ полученные в разделе 1, могут быть использованы для любого сосредоточенного вихря радиуса $R$ в точке ${{x}_{j}},{{y}_{j}}$ плоскости $x{\kern 1pt} - {\kern 1pt} y,$ заменой в полученных решениях r на $0 \leqslant r = \sqrt {{{{(x - {{x}_{y}})}}^{2}} + {{{(y - {{y}_{j}})}}^{2}}} \leqslant R.$ Такое решение можно обобщить на систему $n$ сосредоточенных вихрей, расположенных в точках ${{x}_{j}},{{y}_{j}},$ $j = 1,2, \ldots ,n.$ Таким образом, если существует механизм, позволяющий создать сосредоточенный вихрь радиуса R, то возникает возможность создания системы вихрей, распределенных заранее заданным образом [17].

Одним из способов генерации системы вихрей может быть искусственное или естественное образование в некоторый момент времени локальных областей испарения влаги. Дальнейшая временная динамика вихрей может быть получена из численного решения системы уравнений (58), в котором внешний источник создается за счет поглощения сосредоточенного электромагнитного излучения. На рис. 8 и 9 показаны возможные конфигурации из сосредоточенных вихрей в точках ${{x}_{j}},{{y}_{j}}$ плоскости $x{\kern 1pt} - {\kern 1pt} y.$

Рис. 8.

Система сосредоточенных вихрей одинакового радиуса, расположенных линейно.

Рис. 9.

Следы от системы вихрей разного диаметра, расположенных в горизонтальной плоскости.

Стационарная система сосредоточенных невзаимодействующих между собой вихрей является неустойчивой, поскольку на границе вихря существует разрыв угловой скорости – развивается неустойчивость Кельвина–Гельмгольца. Если систему таких линейных вихрей (рис. 8) удается создать внешним воздействием, то после его прекращения она из-за неустойчивости Кельвина–Гельмгольца превращается в своеобразную “сильно турбулентную воздушную стену”, оказывающую препятствие в продвижении торнадо.

Создаваемая посредством электромагнитного излучения система сосредоточенных вихрей может быть расположена на пути продвижения торнадо и приводить к его разрушению в результате преобразования в серию более мелких вихрей, затухающих за счет вязкости и трения о поверхность земли. Электромагнитное поле позволяет создать серию вихрей вблизи от места формирования торнадо сразу после его зарождения. Поскольку торнадо еще не успевает набрать полную мощность, то можно обойтись достижимыми в настоящее время мощностями генераторов электромагнитного излучения, работающими в импульсных режимах. Воздействие электромагнитным излучением на грозовое материнское облако позволит разрушать его до появления торнадо [18, 19].

ЗАКЛЮЧЕНИЕ

1. С помощью намеченного в работе [8] подхода к решению задачи о вихре, в котором направление вектора завихренности и скорости течения совпадают по направлению, проведен детальный анализ характеристик течений в стационарном сосредоточенном вихре в цилиндрической системе координат с двумя компонентами скорости.

2. Найдены распределения давлений в стационарном сосредоточенном вихре с учетом силы Кориолиса и без нее. Установлены условия, при которых вихрь является циклоническим.

3. В цилиндрической системе координат построено новое решение задачи о течении в стационарном сосредоточенном вихре в цилиндрической системе координат с тремя компонентами вектора скорости.

4. Исследованы возможности получения вихрей, в которых направление вектора завихренности и скорости течения совпадают по направлению, в численных расчетах уравнений Навье–Стокса.

5. Обсуждаются способы генерации одиночного вихря или системы таких вихрей в природе путем воздействии электромагнитной волны круговой поляризации и микроволнового диапазона частот на поверхность влажного воздуха или воды.

6. Анализируются возможности использования системы искусственно созданных вихрей данного типа в качестве препятствий для перемещения торнадо и его разрушения на ранней стадии формирования.