Теплофизика высоких температур, 2019, T. 57, № 4, стр. 501-508
Проводимость неидеальной полностью ионизованной плазмы: сравнение результатов расчета методом молекулярной динамики и модельного подхода
А. Л. Хомкин 1, *, А. С. Шумихин 1, **
1 Объединенный институт высоких температур РАН
Москва, Россия
* E-mail: alhomkin@mail.ru
** E-mail: shum_ac@mail.ru
Поступила в редакцию 20.09.2018
После доработки 07.12.2018
Принята к публикации 27.03.2019
Аннотация
Рассмотрены новые результаты расчетов проводимости неидеальной полностью ионизованной плазмы, выполненных методом молекулярной динамики. Для их описания использована сформулированная ранее модель о наличии столкновительных комплексов и квазисвязанных состояний в неидеальной полностью ионизованной плазме. Рассчитаны концентрации квазисостояний, и определено их влияние на проводимость. Фиксируется удовлетворительное согласие численных и модельных расчетов проводимости плазмы.
ВВЕДЕНИЕ
Проводимость “неидеальной плазмы” – активно обсуждаемая научная проблема 70-х годов прошедшего столетия. Результаты многочисленных экспериментов, выполненных в десятке лабораторий у нас в стране и за рубежом, а также предлагаемых теорий обобщены и представлены в монографии [1]. Полученные на первом этапе экспериментальные результаты не выявили ярко выраженных эффектов в области газоплазменных состояний. С ростом параметра неидеальности проводимость немного уменьшалась, оставаясь меньше значений теоретических расчетов, а затем просматривалась тенденция к ее небольшому росту. Разумная коррекция кулоновского логарифма позволяла добиться удовлетворительного согласия с экспериментом при умеренных значениях параметра неидеальности. Были предложены модели для описания ее поведения с ростом параметра неидеальности [1], но они не получили широкого распространения. Надо отметить, что точность результатов для “полностью ионизованной” неидеальной плазмы была и остается невысокой. И в этом нет вины экспериментаторов, как правило, гарантирующих достаточно высокую точность своих измерений. Дело заключается в том, что в экспериментах измерялась проводимость плазмы низкотемпературной и, как правило, частично ионизованной, где идут столкновения электронов проводимости с атомами, ионами и электронами. Всех же интересовала “кулоновская” составляющая проводимости, обусловленная столкновениями электронов лишь с ионами и электронами. Именно здесь в теории возникал известный кулоновский логарифм и существовали классические результаты для полностью ионизованной плазмы, полученные Спитцером [2], Ландау [3] и рядом других авторов [4]. Коррекция этих результатов и поиск новых эффектов при переходе к плазме неидеальной, когда кулоновский логарифм уменьшался, и была одной из целей экспериментов. Но оказалось, что выделить из проводимости плазмы с небольшой степенью ионизации “кулоновскую” составляющую является не простой задачей. В ранних работах эта процедура строилась на предположении, что общее “сопротивление” плазмы, обусловленное столкновениями электронов с атомами и ионами, складывается из соответствующих им “сопротивлений” атомарной и ионной компонент. На этом была основана “аддитивная” расчетная формула [5]. Вычислив “сопротивление” атомарной компоненты и вычитая ее из полного сопротивления, можно было оценить “сопротивление” заряженной. Проверка погрешности этой процедуры, выполненная на основе численного решения уравнения Больцмана, показала, что она значительна и составляет величину порядка пятидесяти процентов [6]. Это заметно превышало погрешность измерений полной проводимости. Результатом данного обстоятельства явился довольно сильный разброс выдаваемой различными экспериментальными группами “кулоновской” составляющей проводимости неидеальной плазмы. Кроме того, исследования плотности состояний неидеальной атомарной плазмы [7] показали, что сама схема разделения электронных состояний лишь на две группы – “свободные” и “связанные” – требует уточнения. Оказалось, что между ними лежат квазисвязанные состояния и столкновительные комплексы [8], вклад которых в проводимость необходимо также учитывать. Наличие таких промежуточных состояний делало неопределенным само понятие “кулоновской” составляющей проводимости. В термодинамике наличие упомянутых промежуточных квазисостояний порождало многочисленные способы расчета статистической суммы атома [9].
Развитие численных методов в последнее время вновь привлекло внимание к проблеме проводимости неидеальной плазмы. В недавних численных экспериментах [10, 11] удалось получить проводимость той самой неидеальной “полностью ионизованной” плазмы, правда приготовленной искусственно, тем или иным способом. Кавычки здесь поставлены на том основании, что в плазме даже при отсутствии сильно связанных атомов всегда имеются атомы возбужденные, которые через область квазисостояний непрерывно переходят в состояния “свободных”.
Рассмотрим две работы. Это, прежде всего, работа Нормана Г.Э. и Морозова И.В. [10], а также работа Боброва А.А., Зеленера Б.В. и др. [11]. В этих работах методом молекулярной динамики (ММД) выполнен численный расчет проводимости и ряда других динамических характеристик неидеальной плазмы. Для определения проводимости рассчитывался коррелятор скоростей электронов. Это, безусловно, новый подход и шаг вперед, поскольку впервые можно было не обращаться к уравнению Больцмана, использование которого для неидеальной плазмы также вызывало сомнения [1].
Правда, использование классического по сути ММД для кулоновских систем сталкивается с давно обсуждаемой и до конца не решенной проблемой расходимости вклада конфигураций, возникающих при сближении электрона и иона и отсутствии состояния равновесия для классической системы точечных зарядов. Только при квантовом рассмотрении в теории появляется расстояние наименьшего сближения электрона с ионом – боровский радиус ${{a}_{0}}.$ В уравнении Больцмана эта проблема решается использованием резерфордовского квантового сечения рассеяния. Вторая проблема, возникающая при расчете проводимости плазмы, – дальнодействие кулоновского потенциала. В уравнении Больцмана для разреженной плазмы она решается введением максимального прицельного параметра рассеяния, равного дебаевскому радиусу, что в итоге и приводит к кулоновскому логарифму.
Проблема малых расстояний при использовании ММД в упомянутых выше работах решается по-разному. В [10] выбирается псевдопотенциал того или иного вида: конечного на малых расстояниях и совпадающего с кулоновским – на больших. В [11] рассмотрена ультрахолодная плазма ридберговских атомов, рекомбинация которой происходит значительно медленнее, чем в плазме обычной. Коррелятор скоростей измеряется на участке релаксации к равновесию, когда рекомбинационный поток еще не достиг глубоко лежащих связанных состояний. Важно, что в обеих работах в качестве конечного результата представлена проводимость “полностью” ионизованной неидеальной плазмы с учетом всех столкновений.
Заметим, что главным достижением Спитцера, по мнению авторов, являлся учет межэлектронных ударов и их влияния на проводимость, а отнюдь не кулоновский логарифм. Расчет спитцеровского множителя γE = 0.582 – достаточно сложная и нетривиальная задача. Величина этого множителя для кулоновского потенциала пересчитывалась в [4], а для muffin-tin-потенциала получена в [12]. Интересно проследить, учитывает ли методика расчета проводимости через коррелятор скоростей межэлектронные удары.
В настоящей работе результаты ММД [10, 11] рассматриваются как результаты эксперимента (численного) по измерению проводимости модельных кулоновских систем, состоящих из взаимодействующих Ne “электронов” и Ni “ионов”, находящихся в объеме V при температуре T, в которых тем или иным способом исключены “атомы” и столкновения с ними. Для дальнейшего введем полные плотности частиц ${{n}_{{e,i}}} = {{{{N}_{{e,i}}}} \mathord{\left/ {\vphantom {{{{N}_{{e,i}}}} V}} \right. \kern-0em} V}$ и обратную температуру $\quad\beta = {1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}.$ Будем считать, что данные численных расчетов с некоторыми оговорками дают ту самую “кулоновскую” составляющую проводимости неидеальной плазмы, поискам которой и были посвящены эксперименты 1970-х.
ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ИДЕАЛЬНОЙ ПЛАЗМЫ. ОСНОВНЫЕ СООТНОШЕНИЯ
В конце 1950-х годов в связи с исследованиями проблемы реализации управляемой термоядерной реакции возникла современная физика высокотемпературной плазмы. Существовала и традиционная физика плазмы электрических разрядов и т.д., которую сейчас принято называть физикой низкотемпературной плазмы. Что же разделяет эти два направления? Один из вариантов: высокотемпературная плазма, у которой $T > 100{\kern 1pt} 000$ К, и, соответственно, плазма низкотемпературная, если $T < 100{\kern 1pt} 000$ К. Предложим несколько иной критерий, возможно спорный. Разделим плазму по характеру взаимодействия зарядов. Высокотемпературная плазма – это плазма, где имеют место коллективные эффекты и работают основные предположения дебаевской теории. В такой плазме дебаевский радиус ${{R}_{{\text{D}}}} = {{\left( {4\pi \beta {{e}^{2}}\left( {{{n}_{e}} + {{n}_{i}}} \right)} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$ существенно превосходит размер ионной ячейки Вигнера–Зейтца (ВЗ) ${{R}_{i}} = {{\left( {{3 \mathord{\left/ {\vphantom {3 {\left( {4\pi {{n}_{i}}} \right)}}} \right. \kern-0em} {\left( {4\pi {{n}_{i}}} \right)}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{\kern 1pt} {\text{:}}$
Критерий (1) соответствует плазме, где энергия взаимодействия пробного электрона с ближайшими к нему зарядами разных знаков, находящихся приблизительно на одинаковом расстоянии от пробного заряда, компенсируется. В результате энергия его взаимодействия с плазмой определяется взаимодействием с эффективным зарядом, находящимся на дебаевском расстоянии, что является следствием поляризации плазмы этим пробным зарядом. Данной проблеме посвящены сотни работ. Проводимость и другие кинетические характеристики именно такой плазмы были рассчитаны в серии работ Спитцера и обобщены в монографии [2]. Оригинальный способ решения уравнения Больцмана для определения проводимости предложен Ландау [3]. Заметим, что во всех подходах центральное место занимает решение проблемы дальнодействия кулоновского потенциала путем обрезания транспортного сечения рассеяния электрона на ионе, расходящегося при больших прицельных параметрах.
Для кулоновского потенциала $u(r) = {{ - {{e}^{2}}} \mathord{\left/ {\vphantom {{ - {{e}^{2}}} {r\quad}}} \right. \kern-0em} {r\quad}}$ транспортное сечение рассеяния электрона со скоростью $\text{v}$ на покоящемся ионе имеет вид (здесь и в дальнейшем будем рассматривать водородную или однозарядную плазму)
 транспортное сечение рассеяния также вычисляется до конца:
транспортное сечение рассеяния также вычисляется до конца:
Эти достаточно известные формулы для транспортных сечений приведены, чтобы показать их трансформацию при переходе к расчетным формулам. Спитцер получил свои соотношения для плазмы высокотемпературной, в которой под знаком логарифма были использованы упрощения (${{b}_{{{\text{max}}}}} \cong {{R}_{{\text{D}}}}$ и ${{b}_{0}} \cong {{\beta {{e}^{2}}} \mathord{\left/ {\vphantom {{\beta {{e}^{2}}} 3}} \right. \kern-0em} 3}$), исключившие логарифмическую зависимость сечения от скорости.
В результате упрощений ${\text{ln}}{{\left[ {1 + {{{\left( {\frac{{{{b}_{{{\text{max}}}}}}}{{{{b}_{0}}}}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ → → ${\text{ln}}{{\left[ {1 + {{{\left( {\frac{{3{{R}_{{\text{D}}}}}}{{\beta {{e}^{2}}}}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ → ${\text{ln}}{{\left[ {1 + {{{\left( {\frac{3}{{\Gamma }}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ → ${\text{ln}}\left( {\frac{3}{{\Gamma }}} \right)$ приходим к выражению кулоновского логарифма
которое находим у Спитцера [2] и Ландау [3]. При этом Спитцер рассматривал только электронную экранировку, и в радиусе Дебая учитывалась только электронная плотность. Поэтому, строго говоря, спитцеровскому варианту соответствует величина ${\text{ln}}\left( {\frac{{3\sqrt 2 }}{{\Gamma }}} \right).$ Еще раз подчеркнем, что эти результаты получены для высокотемпературной, термоядерной плазмы, в которой ${1 \mathord{\left/ {\vphantom {1 {\Gamma }}} \right. \kern-0em} {\Gamma }} \gg 1.$ В (2) ${\Gamma } = {{\beta {{e}^{2}}} \mathord{\left/ {\vphantom {{\beta {{e}^{2}}} {{{R}_{{\text{D}}}}}}} \right. \kern-0em} {{{R}_{{\text{D}}}}}} = \beta {{e}^{2}}\sqrt {4\pi \beta {{e}^{2}}\left( {{{n}_{e}} + {{n}_{i}}} \right)} $ – параметр кулоновской неидеальности. Критерий (1), записанный через параметр ${\Gamma ,}$ приводит к неравенству ${\Gamma } < {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}.$При исследовании термодинамических и переносных свойств неидеальной плазмы, как правило низкотемпературной [1], были достигнуты большие значения параметра ${\Gamma } \cong 4{\kern 1pt} --{\kern 1pt} 5.$ В термодинамике в этой области ожидалось появление “плазменного фазового перехода” [1], а в проводимости по Спитцеру (2) формально происходила смена знака кулоновского логарифма, что могло свидетельствовать о существовании интересных эффектов.
При анализе различных соотношений для проводимости $\sigma $ полностью ионизованной плазмы можно использовать выражение
(3)
$\sigma = {{{{\sigma }_{0}}{{\gamma }_{E}}\left( \Gamma \right)} \mathord{\left/ {\vphantom {{{{\sigma }_{0}}{{\gamma }_{E}}\left( \Gamma \right)} {\Lambda \left( \Gamma \right),}}} \right. \kern-0em} {\Lambda \left( \Gamma \right),}}$(4)
$C = \frac{{{{\sigma }_{0}}{{\gamma }_{E}}}}{{{{\omega }_{p}}}} = \frac{{0.836}}{{\Gamma }} = {\;}\frac{{0.341}}{{{{\gamma }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}},$ПЛОТНОСТЬ ЭЛЕКТРОННЫХ СОСТОЯНИЙ И СОСТАВ ПЛАЗМЫ
Систематические теоретические исследования плотности электронных состояний в неидеальной атомарной (состоящей из электронов, ионов и атомов) плазме и рассмотрение известной ее расходимости при нулевых энергиях были начаты в [15] и продолжены в [7, 8]. В результате получена плотность состояний, конечная при нулевых энергиях электрона и приводящая к точным асимптотическим разложениям термодинамических функций по степеням активности [1]. В явном виде была продемонстрирована компенсация (с ненулевым остатком) части состояний дискретного и непрерывного спектров в конечных результатах. На основе анализа полученной плотности состояний электрона в неидеальной атомарной плазме введены понятия атомов (А), возбужденных атомов (ВА), квазисвязанных состояний (КС) и столкновительных комплексов (СК), найдены их концентрации [8]. Рассмотрение велось в большом каноническом ансамбле. В серии работ (см. [16]) было выполнено численное моделирование для модельной кулоновской системы и впервые получено распределение электронов по энергиям в области положительных и отрицательных энергий. Главное внимание уделялось исследованию процессов рекомбинации.
В работе [17] на основе теоретических подходов [7, 8] рассчитывались плотности состояний и функции распределения электронов по энергиям для кулоновской модели “с полочкой”. Выполнено сравнение теоретических результатов с результатами, полученными численным моделированием. Обсуждались особенности распределения электронов по отрицательным энергиям в “модели с полочкой” и в реальной плазме. Проведенное сравнение полностью подтвердило предложенную классификацию переходных состояний и показало их слабую зависимость от положения полочки при ее достаточной глубине. Воспользуемся этим результатом при сравнении с результатами численных экспериментов [10, 11].
Приведем ряд полезных соотношений из [17]. Для атомарной, невырожденной, водородоподобной плазмы в большом каноническом ансамбле получены разложения концентрации ядер $n = {{n}_{i}} = {{n}_{e}}$ по степеням активностей $z = {{z}_{e}} = {{z}_{i}}{\text{:}}$
(5)
$n = z\left( {1 + \frac{\alpha }{2} + z\frac{{{{g}_{a}}}}{2}\lambda _{e}^{3}\exp \left( {\beta {\text{Ry}}} \right)} \right).$В (5) ${{g}_{a}},\quad\,{{\lambda }_{e}},\quad\,{\text{Ry}}$ – статистический вес атома в приближении Планка–Ларкина, тепловая длина волны Де-Бройля и потенциал ионизации атома водорода соответственно. Параметр неидеальности в большом каноническом ансамбле имеет вид $\alpha = \beta {{e}^{2}}\sqrt {8\pi \beta {{e}^{2}}z} .$ Если исключить из рассмотрения атомы, приходим к уравнению Ликальтера [18], связывающему концентрации ядер и активности через соответствующие параметры неидеальности:
Решение этого уравнения позволяет найти зависимость $\alpha \left( \Gamma \right)$, которая необходима для расчета “состава” полностью ионизованной, неидеальной плазмы.
В [7, 8] было получено разложение полной концентрации ядер (без учета связанных состояний) по степеням активности $z$ на основе плотности состояний электрона в поле ближайшего иона:
(7)
$n = z\left( {1 + \frac{1}{{2 \times {{3}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{2}{3}} \right){{\alpha }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + \frac{1}{{4 \times {{3}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{1}{3}} \right){{\alpha }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}} \right),$Отличительной чертой квазисостояний является то, что внутри ячейки ВЗ умещается лишь часть траектории изолированной пары. Для состояний с положительной относительной энергией это часть гиперболы в момент столкновения (столкновительные комплексы). Сюда же можно отнести и движение по параболе при нулевой относительной энергии. Квазисвязанные состояния и высоковозбужденные атомы соответствуют отрезкам эллиптических траекторий. В [7, 8] предположено, что электрон в таких состояниях (траектории не замкнуты) может давать вклад в проводимость, но отличный от вклада “свободных” электронов.
Для дальнейшего понадобятся относительные плотности идеально газовых, “свободных”, состояний ${{x}^{0}} = {{{{n}^{0}}} \mathord{\left/ {\vphantom {{{{n}^{0}}} n}} \right. \kern-0em} n}$ и квазисостояний $x* = {{n{\kern 1pt} {\text{*}}} \mathord{\left/ {\vphantom {{n{\kern 1pt} {\text{*}}} n}} \right. \kern-0em} n}.$ Эти соотношения рассчитываются по формуле Саха для полностью ионизованной плазмы:
(8)
${{x}^{0}} = {{\left( {1 + \frac{1}{{2 \times {{3}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{2}{3}} \right){{\alpha }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + \frac{1}{{4 \times {{3}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{1}{3}} \right){{\alpha }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}} \right)}^{{ - 1}}},$(9)
$x* = \frac{{\frac{1}{{2 \times {{3}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{2}{3}} \right){{\alpha }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + \frac{1}{{4 \times {{3}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{1}{3}} \right){{\alpha }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}}}{{1 + \frac{1}{{2 \times {{3}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{2}{3}} \right){{\alpha }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + \frac{1}{{4 \times {{3}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{1}{3}} \right){{\alpha }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}}}.$Связь параметра $\alpha $ с ${\Gamma }$ можно найти из уравнения
(10)
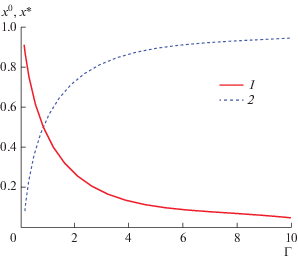
${{{\Gamma }}^{2}} = {{\alpha }^{2}}\left( {1 + \frac{1}{{2 \times {{3}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{2}{3}} \right){{\alpha }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + \frac{1}{{4 \times {{3}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{\Gamma }\left( {\frac{1}{3}} \right){{\alpha }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}} \right),$Рис. 1.
Зависимости $\alpha \left( \Gamma \right),$ полученные решением уравнений: 1 – (10), 2 – (6).

Имея связь активности с полной концентрацией, можно рассчитать “состав” полностью ионизованной плазмы (8), (9) в зависимости от полной плотности $n$. Результаты представлены на рис. 2.
Рис. 1 и 2 показывают, что полностью ионизованная неидеальная плазма состоит по рассматриваемой модели из двух групп частиц. Первая группа – это частицы, двигающиеся по прямолинейным траекториям. Их можно назвать “свободными”. Длина пробега определяется традиционно, и вклад в проводимость можно рассчитывать по соотношению (3), умножив его на отношение ${{{{n}_{0}}} \mathord{\left/ {\vphantom {{{{n}_{0}}} n}} \right. \kern-0em} n}.$ Тем самым просто изменяется число носителей тока. При этом, как показано в [8], число кулоновских рассеивателей не меняется. Вторая группа – электроны, находящиеся в квазисостояниях. Их вклад в проводимость оценен в [7, 8].
ЭФФЕКТЫ НЕИДЕАЛЬНОСТИ И ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ НЕИДЕАЛЬНОЙ ПЛАЗМЫ
Любые отклонения от идеально газовых расчетов принято относить к “эффектам неидеальности”. Но любому “эффекту неидеальности” можно сопоставить определенный вид взаимодействия частиц. Например, в нейтральных газах слабое взаимодействие между частицами приводит к появлению в расчетных формулах второго вириального коэффициента. В [4] показано, что второй вириальный коэффициент обусловлен столкновениями частиц и его можно функционально связать с временем столкновения частиц или временем пролета области взаимодействия. В идеальном газе, когда взаимодействие мало, реализуются ломаные траектории движения, состоящие из прямолинейных участков между столкновениями частиц. С ростом плотности длина свободного пробега уменьшается и становится сравнимой с размером области взаимодействия. Вклад взаимодействия частиц, пребывающих в этой области (столкновительные комплексы), и приводит к вириальным поправкам. Если взаимодействие достаточно сильное (велика глубина ямы), то главным эффектом неидеальности следует считать образование связанных состояний, когда частицы, рекомбинируя, образуют новую стабильную частицу. Для заряженных частиц картина полностью аналогична, хотя главные эффекты неидеальности в ансамбле заряженных частиц различны для высоко- и низкотемпературной плазмы. В высокотемпературной плазме главную роль играют дальнодействие кулоновского потенциала и, как следствие, коллективный характер поведения электронной плотности. Главным параметром является дебаевский радиус. Атомы практически отсутствуют из-за высокой температуры. В низкотемпературной плазме ситуация обратная. Главный эффект неидеальности – образование атомов и парный характер экранировки. Можно вообще обойтись без дебаевской модели и дебаевского радиуса. Возникают два характерных размера: боровский радиус (связанные состояния) и радиус ячейки Вигнера–Зейтца свободного иона – радиус парной экранировки. Взаимодействия “свободных” частиц, обусловленные столкновениями, проявляют себя через квазисостояния – состояния, переходные от связанных к свободным. Если тем или иным способом исключить связанные состояния, то остаются два типа состояний: свободные и квазисостояния.
На траектории электрона проводимости можно выделить два характерных участка: пробег между столкновениями (прямая линия) и пролет областей взаимодействия (куски гипербол, парабол и эллипсов). Они будут различаться временем пролета этих участков и зависимостью этого времени от плотности. Вероятности пребывания в том или ином состоянии будут пропорциональны плотности соответствующих состояний. В качестве времени свободного пробега для первой группы состояний возьмем величину, даваемую формулой Спитцера, но с улучшенным кулоновским логарифмом, а для вклада квазисостояний воспользуемся формулой Друде, приняв в качестве времени переноса импульса время пролета резерфордовского сечения рассеяния. По существу это повторение рассуждений, приведенных в [7, 8] для расчета полной проводимости
где(12)
${{\tau }_{0}} = \frac{{0.591}}{{\Lambda \left( \Gamma \right)}}\quad\frac{{\sqrt {\beta m} }}{{n{{{(\beta {{e}^{2}})}}^{2}}}},$(13)
$\begin{gathered} \sigma {\kern 1pt} * = n{\text{*}}\frac{{{{e}^{2}}}}{m}\tau * = \\ = {{\sigma }_{0}}{{\gamma }_{E}}0.24\alpha \left( {\frac{{\Gamma \left( {\frac{2}{3}} \right)}}{{2 \times {{3}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{\alpha }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + \frac{{\Gamma \left( {\frac{1}{3}} \right)}}{{4 \times {{3}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{\alpha }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}} \right), \\ \tau {\kern 1pt} * = \frac{{\beta {{e}^{2}}}}{{{{\text{v}}_{t}}}}\frac{{\sqrt {8\pi } }}{\alpha }. \\ \end{gathered} $СРАВНЕНИЕ С ДАННЫМИ ММД И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
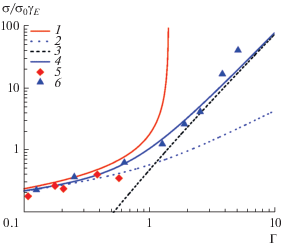
На рис. 3, 4 приведено сравнение результатов расчета по данной модели с [10, 11]. Результаты представлены в безразмерном виде. Видно, что использование кулоновского логарифма ${\text{ln}}{{\left[ {1 + {{{\left( {\frac{3}{{\Gamma }}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ позволяет описать, по крайней мере, данные моделирования [11] и часть данных [10].
Рис. 3.
Зависимость безразмерной проводимости полностью ионизованной плазмы от параметра неидеальности Γ; расчет по (3): 1 – ${\text{ln}}\left( {\frac{3}{{\Gamma }}} \right),$ 2 – ${\text{ln}}{{\left[ {1 + {{{\left( {\frac{3}{{\Gamma }}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ и методом молекулярной динамики: 3 – [11], 4 – [10].

На рис. 4 приведены результаты расчета проводимости по модели [7, 8]: вклад “свободных” и квазисостояний, а также их суммарное значение. Достаточно прозрачно видна смена механизма переноса. В неидеальной плазме практически исчезают пролеты по прямолинейным траекториям. Им на смену приходят траектории “силовые”, связанные с движением в поле кулоновского центра. Близкая интерпретация была предложена еще в [7, 8], но разброс экспериментальных данных помешал в то время сделать однозначный и надежный вывод. Данные численных экспериментов дополняют имеющиеся экспериментальные результаты в области высоких значений параметра неидеальности и позволяют сделать вывод о смене механизма переноса более убедительным.
ЗАКЛЮЧЕНИЕ
Проведенное сравнение результатов модельных и численных расчетов подтвердило ранее высказанные соображения о характере переноса в неидеальной полностью ионизованной плазме. Прямолинейные пролеты, характерные для плазмы идеальной, постепенно переходят в пролеты “силовые” в поле действия ближайшего иона. Можно с достаточной степенью уверенности утверждать, что в неидеальной плазме процессы переноса во многом идентичны процессам переноса в газах неидеальных, но нейтральных. Привлечение специфических “плазменных” эффектов, характерных исключительно для плазменного состояния (коллективные колебания, например), не требуется.
Авторы благодарят участников семинара Теоретического отдела им. Л.М. Бибермана ОИВТ РАН за активное и конструктивное обсуждение работы.
Список литературы
Фортов В.Е., Храпак А.Г., Якубов И.Т. Физика неидеальной плазмы. М.: Физматлит, 2010.
Спитцер Л. Физика полностью ионизованного газа / Под ред. Левина М.Л. М.: Мир, 1965.
Ландау Л.Д. Кинетическое уравнение в случае кулоновского взаимодействия // ЖЭТФ. 1937. Т. 7. С. 203.
Кинетические процессы в газах и плазме / Под ред. Хохштима А. М.: Атомиздат, 1971.
Митчнер М., Кругер Ч. Частично ионизованные газы. М.: Мир, 1976.
Муленко И.А., Хомкин А.Л. Кинетические коэффициенты неидеальной низкотемпературной плазмы. Препринт № 1-326. М.: ИВТАН, 1991.
Воробьев В.С., Хомкин А.Л. Столкновительные комплексы в плазме и их влияние на электропроводность // Физика плазмы. 1977. Т. 3. С. 885.
Воробьев В.С., Хомкин А.Л. Электрон-ионные коррелированные пары в плазме и их влияние на электропроводность // ТВТ. 1977. Т. 15. № 1. С. 188.
Кудрин Л.П. Статистическая физика плазмы. М.: Атомиздат, 1974.
Норман Г.Э., Морозов И.В. Столкновения и плазменные волны в неидеальной плазме // ЖЭТФ. 2005. Т. 127. С. 412.
Zelener B.B., Zelener B.V., Manykin E.A., Bronin S.Y., Bobrov A.A. Self-diffusion and Conductivity in an Ultracold Strongly Coupled Plasma. Calculation by the Method of Molecular Dynamics // J. Phys.: Conf. Ser. 2018. V. 946. P. 012126.
Муленко И.А., Хомкин А.Л. Решение уравнения Больцмана для полностью ионизованной плазмы с короткодействующим потенциалом взаимодействия между зарядами // ТВТ. 1991. Т. 29. № 6. С. 1234.
Очерки физики и химии низкотемпературной плазмы / Под ред. Полака Л.С. М.: Наука, 1971.
Дихтер И.Я., Зейгарник В.А. Уравнение состояния и проводимость цезиевой плазмы при давлениях 50–500 атм // ДАН СССР. 1976. Т. 227. № 3. С. 656.
Воробьев В.С., Хомкин А.Л. Приближение ближайшего соседа в термодинамике кулоновских систем и плазмы // Теор. и матем. физика. 1976. Т. 26. С. 364.
Майоров С.А., Ткачев A.Н., Яковленко С.И. Метастабильная переохлажденная плазма // УФН. 1994. Т. 164. С. 297.
Хомкин А.Л., Шумихин А.С. Распределение электронов по энергиям в неидеальных кулоновских системах: теория и результаты численного эксперимента // ТВТ. 2016. Т. 54. № 6. С. 851.
Ликальтер А.А. Взаимодействие атомов с электронами и ионами в плазме // ЖЭТФ. 1969. Т. 56. № 1. С. 240.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур