Теплофизика высоких температур, 2019, T. 57, № 5, стр. 755-763
Численное моделирование имплозионного процесса в цилиндрическом резервуаре
И. В. Моренко *
Институт механики и машиностроения
ФИЦ Казанский научный центр РАН
г. Казань, Россия
* E-mail: morenko@imm.knc.ru
Поступила в редакцию 10.10.2018
После доработки 14.11.2018
Принята к публикации 25.12.2018
Аннотация
Представлены результаты численного исследования имплозии сферической газовой полости в цилиндрическом резервуаре, заполненном жидкостью. Под влиянием перепада давления жидкость приходит в движение, и газовая полость начинает схлопываться. Математическое моделирование нестационарного неизотермического турбулентного движения сжимаемой жидкости основано на методе объема жидкости. Основное внимание сфокусировано на генерации волн давления в жидкости в процессе имплозии. Исследование выполнено при изменении начального давления в газовой полости. Показано, насколько начальное давление в газовой полости влияет на пиковое давление, регистрируемое в контрольной точке, и время, за которое оно достигается. Получена аппроксимационная формула для расчета пикового давления сферической волны сжатия.
ВВЕДЕНИЕ
Исследование имплозионного процесса, сопровождающегося ростом плотности, давления и температуры вещества, актуально в связи с появлением и развитием волновых технологий во многих отраслях промышленности. В медицине внедряется техника ударно-волновой терапии при опухолевых и инфекционных заболеваниях. Широко используется в настоящее время такой малоинвазивный метод лечения, как литотрипсия. В материаловедении сходящиеся к четко определенному фокусу ударные волны позволяют синтезировать новые материалы с нужными характеристиками. В нефтедобывающей промышленности технология гидроимпульсной скважинной обработки с применением имплозионной установки позволяет улучшать фильтрационные характеристики призабойной зоны пласта.
Впервые схлопывание сферической полости в несжимаемой жидкости исследовано Релеем в 1917 г. [1]. В частности, разработана математическая модель для расчета радиуса пузырька в процессе его сжатия. Позднее, в 1952 г., в [2] было предложено использовать имплозионное сигнализирующее устройство для измерения морских глубин. Задачей о схлопывании сферической полости в сжимаемой и несжимаемой жидкости занимались Я.Б. Зельдович [3], К. Хантер [4], Е.И. Забабахин [5], К.В. Брушлинский [6], А.Н. Крайко [7] и другие. В [4] построено автомодельное решение для течения после схлопывания в случае сферической симметрии. В [5] обнаружено два режима захлопывания пустой полости в вязкой жидкости: быстрое захлопывание с неограниченно возрастающей скоростью и относительно медленное захлопывание.
В последние годы активно ведутся исследования динамики маленьких паровых пузырьков, радиус которых составляет порядка 50–500 мкм [8–21]. При сильном сжатии газа в пузырьке достигаются высокие значения плотности, давления и температуры. Интерес к исследованию коллапса маленького пузырька обусловлен возможностью наблюдения таких явлений, как сонолюминисценция и нейтронная эмиссия [8]. В перечисленных выше работах предложены эффективные физико-математические модели, отличающиеся количеством учитываемых физических эффектов, и развиты вычислительные алгоритмы. В целом представленные результаты дают весьма полную картину процессов как в количественном, так и качественном отношениях. Однако данные работы ориентированы в основном на паровые пузырьки, где существенную роль играют фазовые переходы на межфазной поверхности. Поэтому данные работы не были направлены на изучение волновых процессов в системе.
Однако, если полость заполнена неконденсирующимся газом, ситуация кардинально меняется и волновые процессы могут выйти на первый план. При исследовании динамики воздушной полости относительно большого радиуса (порядка 0.01–0.1 м) основное внимание обычно уделяется не процессам внутри воздушной полости, а распространению волн в окружающей жидкости [22]. Генерируемый импульс давления при сжатии газа воздействует на смежные структуры. Понимание механики имплозии имеет важное значение при проектировании подводных сооружений, трубопроводов и гидрооборудования.
Как правило, в физических экспериментах имплозионные камеры представляют собой тонкостенные стеклянные сферы [22] и цилиндрические оболочки из металла [23–25] или композитных материалов [26].
Анализ публикаций показывает, что, несмотря на большое число работ, посвященных схлопыванию паровых пузырей, распространение волн в жидкости во время имплозионного процесса большой газовой полости, заполненной неконденсирующимся газом, до сих пор остается малоизученным.
Данная работа посвящена численному моделированию имплозионного процесса, инициированного перепадом давления в сферической газовой полости и окружающей ее жидкости, а также оценке влияния начального давления в газовой полости на волны разрежения и сжатия в жидкости и другие параметры.
ПОСТАНОВКА ЗАДАЧИ
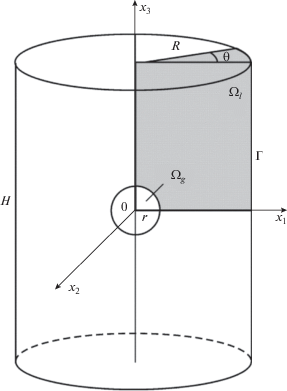
В настоящей работе для численного моделирования имплозионного процесса геометрические параметры сферической воздушной полости, цилиндрического резервуара и теплофизические свойства сред устанавливаются такими, как в экспериментальной работе [22]. В [22] эксперименты проводились в сосуде высокого давления (рис. 1). Резервуар цилиндрической формы радиусом $R$ = = 0.76 м и высотой $H = 3.65$ м заполнен водой. Гидростатическое давление составляет $P_{l}^{0}$ = = 6.996 МПа. На оси резервуара размещается тонкостенный стеклянный шар радиусом $r$ = = 0.0381 м. Три датчика давления закрепляются на расстоянии 0.1016 м от центра сферы. Исходное давление в области, занятой воздухом, составляет $P_{g}^{0}$ = 0.1013 МПа. В начальный момент времени стеклянный шар разрушается. Под влиянием перепада давления жидкость приходит в движение, и полость начинает схлопываться.
В общем случае при моделировании имплозионного процесса нужно решать сопряженные задачи об упруго-пластической деформации или разрушении оболочки камеры низкого давления и аэрогидродинамическую задачу о сжатии газовой полости и распространении волн разрежения и сжатия в двухфазной среде. Отметим, что решение задачи в полной постановке представляет большие трудности. В данной работе полагается, что стеклянная сфера разрушается мгновенно, и задача о разрушении оболочки камеры низкого давления не рассматривается. Кроме того, на межфазной границе не учитываются возможные испарение жидкости и конденсация пара.
В качестве расчетной области $\Omega = {{\Omega }_{l}} \cup {{\Omega }_{g}}$ выбран цилиндрический сектор с угловым размером $\theta = 5^\circ $ (рис. 1). Центр декартовой прямоугольной системы координат ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ размещается в центре газовой полости, ось $0{{x}_{3}}$ совпадает с осью цилиндрического резервуара. Газом заполнена подобласть ${{\Omega }_{g}},$ в подобласти ${{\Omega }_{l}}$ находится жидкость.
Как известно [27], модели, основанные на эйлеровом континуальном представлении, в настоящее время получили широкое распространение для описания различных классов двухфазных потоков [28–31], в том числе и для течений с подвижными границами [32]. Для расчета нестационарного движения жидкости со свободной поверхностью используется метод объема жидкости (volume of fluid) [33], согласно которому течение среды моделируется единым набором уравнений движения, энергии для всех фаз.
Рассматривается двухфазная среда, которая состоит из жидкой и газовой фаз. Обозначим через $\alpha $ объемную долю жидкой фазы. Если контрольный объем занят жидкостью, то $\alpha = 1,$ если газом – $\alpha = 0,$ если через контрольный объем проходит фазовая граница, то $0 < \alpha < 1.$
Плотность $\rho $ и динамический коэффициент вязкости $\mu $ среды рассчитываются по соответствующим значениям жидкости (индекс $l$) и газа (индекс $g$) с использованием маркерной функции $\alpha {\text{:}}$
Уравнения состояния газа и жидкости записываются в виде
(1)
${{\rho }_{g}} = {p \mathord{\left/ {\vphantom {p {{{R}_{g}}T,}}} \right. \kern-0em} {{{R}_{g}}T,}}\,\,\,\,{{\rho }_{l}} = {{\rho }_{{l0}}} + {{{{p}_{l}}} \mathord{\left/ {\vphantom {{{{p}_{l}}} {{{R}_{l}}T,}}} \right. \kern-0em} {{{R}_{l}}T,}}$Для описания нестационарного неизотермического турбулентного движения вязкой сжимаемой жидкости записывается следующая система уравнений.
Уравнение неразрывности –
(2)
$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {{u}_{i}}} \right)}}{{\partial {{x}_{i}}}} = 0.$Уравнение количества движения –
(3)
$\begin{gathered} \frac{{\partial \left( {\rho {{u}_{i}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {{u}_{i}}{{u}_{j}}} \right)}}{{\partial {{x}_{j}}}} = - \frac{{\partial p}}{{\partial {{x}_{i}}}} + \\ + \,\,\frac{\partial }{{\partial {{x}_{j}}}}\left[ {{{\mu }_{{{\text{eff}}}}}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}} - \frac{2}{3}\frac{{\partial {{u}_{k}}}}{{\partial {{x}_{k}}}}{{\delta }_{{ij}}}} \right)} \right] + \sigma \kappa \frac{{\partial \alpha }}{{\partial {{x}_{i}}}}. \\ \end{gathered} $Здесь ${{u}_{i}}$ – компонента осредненного вектора скорости ${\mathbf{u}};$ $t$ – время; $p$ – давление, ${{\mu }_{{{\text{eff}}}}} = \mu + {{\mu }_{T}}$ – эффективная вязкость; ${{\mu }_{T}}$ – турбулентная, или вихревая вязкость; ${{\delta }_{{ij}}}$ – символ Кронекера; $\kappa = - \nabla \cdot {\mathbf{n}}$ – кривизна свободной поверхности; ${\mathbf{n}} = {{\nabla \alpha } \mathord{\left/ {\vphantom {{\nabla \alpha } {\left| {\nabla \alpha } \right|}}} \right. \kern-0em} {\left| {\nabla \alpha } \right|}}$ – единичная нормаль к поверхности раздела фаз; $\sigma $ – коэффициент поверхностного натяжения.
Для определения положения свободной поверхности записывается уравнение конвективного переноса
(4)
$\frac{{\partial \alpha }}{{\partial t}} + \frac{{\partial \left( {\alpha {{u}_{i}}} \right)}}{{\partial {{x}_{i}}}} + \frac{{\partial \left( {\left( {1 - \alpha } \right)\alpha {{u}_{{r,i}}}} \right)}}{{\partial {{x}_{i}}}} = - \frac{\alpha }{{{{\rho }_{l}}}}\frac{{D{{\rho }_{l}}}}{{Dt}},$Уравнение сохранения энергии –
(5)
$\frac{{\partial \left( {\rho {{c}_{p}}T} \right)}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{i}}}}\left( {\rho {{c}_{p}}T{{u}_{i}}} \right) = \frac{{Dp}}{{Dt}} + \frac{\partial }{{\partial {{x}_{i}}}}\left( {{{\lambda }_{{{\text{eff}}}}}\frac{{\partial T}}{{\partial {{x}_{i}}}}} \right),$По повторяющимся индексам предполагается суммирование. Уравнения (1)–(5) дополняются моделью замыкания, начальными и граничными условиями.
Моделирование турбулентности осуществляется на основе хорошо апробированной [34] зональной модели Ментера [35]. Модель Ментера SST включает уравнения для транспорта кинетической энергии турбулентности $k$ и скорости диссипации турбулентной энергии $\omega {\kern 1pt} {\text{:}}$
(6)
$\begin{gathered} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {{u}_{j}}k} \right)}}{{\partial {{x}_{j}}}} = P{\kern 1pt} {\text{*}} - \\ - \,\,\beta {\text{*}}\rho \omega k + \frac{\partial }{{\partial {{x}_{j}}}}\left[ {\left( {\mu + {{\sigma }_{k}}{{\mu }_{T}}} \right)\frac{{\partial k}}{{\partial {{x}_{j}}}}} \right], \\ \end{gathered} $(7)
$\begin{gathered} \frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {{u}_{j}}\omega } \right)}}{{\partial {{x}_{j}}}} = \frac{{{{\gamma }_{\omega }}}}{{{{\nu }_{T}}}}P - {{\beta }_{\omega }}\rho {{\omega }^{2}} + \\ + \,\,\frac{\partial }{{\partial {{x}_{j}}}}\left[ {\left( {\mu + {{\sigma }_{\omega }}{{\mu }_{T}}} \right)\frac{{\partial \omega }}{{\partial {{x}_{j}}}}} \right] + 2\left( {1 - {{F}_{1}}} \right)\rho \frac{{{{\sigma }_{{\omega 2}}}}}{\omega }\frac{{\partial k}}{{\partial {{x}_{j}}}}\frac{{\partial \omega }}{{\partial {{x}_{j}}}}. \\ \end{gathered} $В уравнениях (6), (7) используются следующие обозначения для вспомогательных соотношений и коэффициентов замыкания:
$P{\kern 1pt} * = \min \left( {P,20\beta {\text{*}}\omega k} \right),$ $P = {{\tau }_{{ij}}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}},$ тензор вязких напряжений ${{\tau }_{{ij}}} = 2{{\mu }_{T}}{{S}_{{ij}}} - \frac{2}{3}\rho k{{\delta }_{{ij}}},$ тензор скоростей деформации ${{S}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right).$ Коэффициент турбулентной вязкости ${{\mu }_{T}} = \frac{{\rho {{a}_{1}}k}}{{\max \left[ {{{a}_{1}}\omega ,\Omega {{F}_{2}}} \right]}},$ $\Omega = \sqrt {2{{W}_{{ij}}}{{W}_{{ij}}}} ,$ ${{W}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} - \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right),$ ${{F}_{2}} = \operatorname{th} \left( {\arg _{2}^{2}} \right),$ ${{\arg }_{2}} = \max \left( {2\frac{{\sqrt k }}{{\beta {\text{*}}\omega d}},\frac{{500\nu }}{{{{d}^{2}}\omega }}} \right).$
Функция переключения ${{F}_{1}}$ имеет вид ${{F}_{1}} = \operatorname{th} \left( {\arg _{1}^{4}} \right),$ где arg1 = min$\left[ {\max \left( {2\frac{{\sqrt k }}{{\beta {\text{*}}\omega d}},\frac{{500\nu }}{{{{d}^{2}}\omega }}} \right)} \right.,$ $\left. {\frac{{4{{\sigma }_{{\omega 2}}}k}}{{C{{D}_{{k\omega }}}{{d}^{2}}}}} \right],$ $C{{D}_{{k\omega }}}$ = $\max \left( {2{{\sigma }_{{\omega 2}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {{x}_{j}}}}\frac{{\partial \omega }}{{\partial {{x}_{j}}}},{{{10}}^{{ - 20}}}} \right),$ $d$ – расстояние от узла сетки до стенки. Константы ${{\gamma }_{\omega }},$ ${{\beta }_{\omega }},$ ${{\sigma }_{\omega }}$ рассчитываются по формулам ${{\gamma }_{\omega }} = {{F}_{1}}{{\gamma }_{{\omega 1}}} + \left( {1 - {{F}_{1}}} \right){{\gamma }_{{\omega 2}}},$ ${{\beta }_{\omega }} = {{F}_{1}}{{\beta }_{{\omega 1}}} + \left( {1 - {{F}_{1}}} \right){{\beta }_{{\omega 2}}},$ σω = = ${{F}_{1}}{{\sigma }_{{\omega 1}}} + \left( {1 - {{F}_{1}}} \right){{\sigma }_{{\omega 2}}};$ ${{\gamma }_{1}} = \frac{{{{\beta }_{1}}}}{{\beta {\text{*}}}} - \frac{{{{\sigma }_{{\omega 1}}}{{\kappa }^{{*2}}}}}{{\sqrt {\beta {\text{*}}} }},$ ${{\gamma }_{2}} = \frac{{{{\beta }_{2}}}}{{\beta {\text{*}}}}$ – ‒ $\frac{{{{\sigma }_{{\omega 2}}}{{\kappa }^{{*2}}}}}{{\sqrt {\beta {\text{*}}} }}.$ Константы модели: ${{\sigma }_{{k1}}} = 0.85,$ ${{\sigma }_{{k2}}} = 1.0,$ ${{\sigma }_{{\omega 1}}} = 0.5,$ ${{\sigma }_{{\omega 2}}} = 0.856,$ ${{\beta }_{1}} = 0.075,$ ${{\beta }_{2}} = 0.0828,$ $\beta * = 0.09,$ $\kappa * = 0.41,$ ${{a}_{1}} = 0.31.$
Начальные и граничные условия задаются следующим образом. В начальный момент времени $t = 0$ значения компонент скорости равны нулю ${\mathbf{u}} = 0,$ движение отсутствует, температура сред $T = {{T}^{0}}.$ В области, занятой жидкостью ${{\Omega }_{l}}{\text{:}}$ $\alpha = 1,$ давление считается однородным и равным $P = P_{l}^{0},$ а в области ${{\Omega }_{g}},$ заполненной газом: $\alpha = 0,$ $P = P_{g}^{0}.$
На поверхности резервуара $\Gamma $ записывается условие прилипания: ${{\left. {\mathbf{u}} \right|}_{\Gamma }} = 0,$ ${{\left. {\frac{{\partial p}}{{\partial n}}} \right|}_{{\Gamma }}} = 0,$ ${{\left. {\frac{{\partial \alpha }}{{\partial n}}} \right|}_{{\Gamma }}} = 0,$ ${{\left. T \right|}_{{\Gamma }}} = {{T}^{0}},$ ${{\left. k \right|}_{{\Gamma }}} = 0,$ ${{\left. \omega \right|}_{{\Gamma }}} = 10\frac{{6\nu }}{{{{\beta }_{1}}d_{1}^{2}}},$ где ${{\beta }_{1}} = 0.075,$ ${{d}_{1}}$ – пристеночный шаг, $n$ – единичная нормаль. На гранях цилиндрического сектора ${{{\Gamma }}_{s}}$ ставятся условия: ${{\left. {\frac{{\partial {{u}_{i}}}}{{\partial n}}} \right|}_{{{{{\Gamma }}_{S}}}}} = 0,$ ${{\left. {\frac{{\partial p}}{{\partial n}}} \right|}_{{{{{\Gamma }}_{S}}}}} = 0,$ ${{\left. {\frac{{\partial \alpha }}{{\partial n}}} \right|}_{{{{{\Gamma }}_{S}}}}} = 0,$ ${{\left. {\frac{{\partial T}}{{\partial n}}} \right|}_{{{{{\Gamma }}_{S}}}}} = 0,$ ${{\left. {\frac{{\partial k}}{{\partial n}}} \right|}_{{{{{\Gamma }}_{S}}}}} = 0,$ ${{\left. {\frac{{\partial \omega }}{{\partial n}}} \right|}_{{{{{\Gamma }}_{S}}}}} = 0.$
Решение поставленной задачи (1)–(7) осуществляется на гексаэдральной сетке методом конечных объемов с помощью открытой интегрируемой платформы для численного моделирования задач механики сплошных сред OpenFOAM11 с лицензией GNU GPL. При помощи метода Гаусса интегралы по контрольному объему сводятся к поверхностным. Дискретные значения скорости и давления рассчитываются в центрах ячеек сетки. Для дискретизации производной по времени используется схема Эйлера. При решении системы уравнений для давления применяется метод сопряженных градиентов PCG c многосеточным алгебро-геометрическим предобусловливателем GAMG. Для сглаживания предобусловливателя используется метод Гауса–Зейделя. При решении уравнений для скорости – метод бисопряженных градиентов. Шаг по времени $\Delta t$ подбирается в процессе вычислений таким образом, чтобы число Куранта ${\text{Co}}$ для всех ячеек расчетной области не превышало 0.01. Число Куранта ячейки ${\text{Co}} = {{\left( {\Delta t\left| u \right|} \right)} \mathord{\left/ {\vphantom {{\left( {\Delta t\left| u \right|} \right)} {\Delta x}}} \right. \kern-0em} {\Delta x}}$ определяется по величине скорости жидкости через ячейку $\left| u \right|,$ размеру ячейки в направлении скорости $\Delta x$.
РЕЗУЛЬТАТЫ РАСЧЕТОВ
Задаются следующие теплофизические свойства газа: коэффициент кинематической вязкости ${{\nu }_{g}} = 1.46 \times {{10}^{{ - 5}}}$ м2/с, удельная теплоемкость ${{c}_{{pg}}}$ = 1006 Дж/(кг К), ${{\lambda }_{g}} = 0.024$ Вт/(м К), а также свойства жидкости: ${{\rho }_{{l0}}} = {{10}^{3}}$ кг/м3, ${{\nu }_{l}} = {{10}^{{ - 6}}}$ м2/с, ${{c}_{{pl}}}$ = 4182 Дж/(кг К), ${{\lambda }_{l}} = 0.6$ Вт/(м К). Кроме того, задаются ${{R}_{g}} = 287$ Дж/(кг К), ${{R}_{l}} = 3000$ Дж/(кг К), $\sigma = 0.07$ Н/м. До начального момента времени $t = 0$ давление газа в области низкого давления считается однородным и равным $P_{g}^{0} = 0.1013$ МПа. Давление жидкости составляет $P_{l}^{0} = 6.996$ МПа; температура ${{T}^{0}} = 300$ К.
Под влиянием перепада давления жидкость приходит в движение, и полость начинает схлопываться. Эволюцию поля давления иллюстрирует рис. 2. Сходящаяся волна сжимает газовую полость. Уменьшение объема воздушной полости сопровождается ростом давления, плотности и температуры газа.
В то же время в жидкости формируется сферическая волна разрежения, которая движется в радиальном направлении от границы раздела сред к стенкам резервуара (рис. 2: $t$ = 0.15, 0.35 мс).
В момент времени $t$ = 0.423 мс, когда радиус воздушной полости достигает минимального значения, жидкость внезапно останавливается, генерируется импульс давления, который распространяется в окружающую жидкость. По окончании фазы сжатия воздушной полости начинается фаза расширения.
Сферическая волна сжатия движется в направлении из центра воздушной области к стенкам резервуара (рис. 2: $t$ = 0.55, 0.75, 0.95, 1.15 мс). Следует отметить, что при этом максимальное давление значительно превышает начальное гидростатическое $P_{l}^{0}.$ По мере движения волны от центра к периферии максимальное значение давления уменьшается. Достигнув стенки, волна сжатия отражается от нее ($t = 1.7$ мс).
Отметим, что за первым следует второй цикл имплозионного процесса. Давление вновь понижается, и затем наблюдается еще одна волна сжатия. Однако наиболее интересные эффекты происходят во время первого цикла сжатия–расширения воздушной полости. Вторичные пульсации являются менее интенсивными. Амплитуда колебаний термодинамических параметров уменьшается. В конце процесса система жидкость–газ приходит в гидростатическое равновесие.
Результаты моделирования показали, что процесс имплозии характеризуется широким диапазоном изменения давления, плотности, температуры газа и малыми интервалами времени. Установлено, что длительность типичного события имплозии составляет порядка миллисекунд.
Для верификации численного решения задачи оценивается влияние числа разбиений расчетной области на локальные параметры в контрольной точке, которая расположена на таком же расстоянии (0.1016 м) от центра сферы, что и датчики давления в физическом эксперименте [22]. Число разбиений области в радиальном, осевом и тангенциальном направлениях для различных сеток составляет ${{M}_{1}} = 100 \times 200 \times 1,$ ${{M}_{2}} = 200 \times 300 \times 1$ и ${{M}_{3}} = 250 \times 340 \times 1.$ Результаты численных исследований сеточной сходимости представлены в табл. 1. Здесь ${{P}_{{\min }}},$ ${{P}_{{\max }}}$ – минимальное и максимальное давление в контрольной точке, $\Delta t = {{t}_{2}} - {{t}_{1}}$ – временнóй интервал между моментами времени ${{t}_{1}}$ и ${{t}_{2}},$ в которые в контрольной точке регистрируются минимальное и максимальное давление.
Таблица 1.
Сеточная сходимость
| Сетка | ${{P}_{{{\text{min}}}}},$ МПа | ${{P}_{{{\text{max}}}}},$ МПа | $\Delta t,$ мс |
|---|---|---|---|
| ${{M}_{1}}$ | 4.432 | 18.47 | 0.440 |
| ${{M}_{2}}$ | 4.433 | 23.74 | 0.443 |
| ${{M}_{3}}$ | 4.433 | 24.42 | 0.445 |
Представленные в табл. 1 локальные расчетные параметры, полученные на сетке ${{M}_{2}},$ отличаются менее чем на 3% от соответствующих, полученных на сетке ${{M}_{3}}.$ Для дальнейших расчетов выбрана сетка ${{M}_{3}}.$
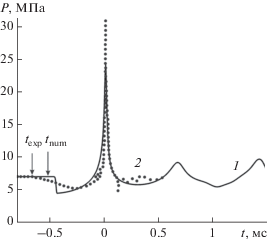
Для оценки достоверности результатов настоящей работы в ходе численного расчета дополнительно выводится давление в контрольной точке (рис. 3). Заметим, что время на оси абсцисс смещено таким образом, чтобы пиковые значения давления совпадали. На рис. 3 через ${{t}_{{{\text{exp}}}}},$ ${{t}_{{{\text{num}}}}}$ обозначены моменты начала имплозии соответственно в физическом и численном экспериментах. Видно, как в течение фазы сжатия воздушной полости давление жидкости снижается, в контрольной точке регистрируется волна разрежения. Длительность действия волны разрежения, наблюдаемая в эксперименте [22], больше, чем расчетная, а падение давления на начальном этапе происходит более плавно. Различие обусловлено тем обстоятельством, что при численном моделировании не учитывается время разрушения тонкостенной стеклянной сферы.
Рис. 3.
Давление в контрольной точке на расстоянии 0.1016 м от центра воздушной полости с течением времени: 1 – расчет, 2 – эксперимент [22].
Для сравнения в табл. 2 приведены данные эксперимента [22] и результаты численных расчетов других авторов, выполненных с помощью программных комплексов AERO-F [36] и DYSMAS [22]. Полученные значения давлений ${{P}_{{\min }}},$ ${{P}_{{\max }}},$ а также интервала $\Delta t$ лучше согласуются с численными результатами работы [36].
Численный эксперимент в отличие от физического позволяет получить не только давление в контрольной точке, но и проанализировать распространение волн разрежения и сжатия, движение межфазной границы и другие параметры.
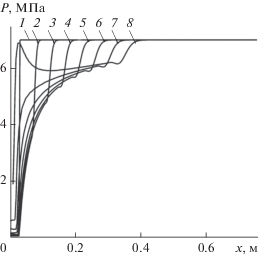
На рис. 4 показано распределение давления вдоль оси $0{{x}_{1}}$ в разные моменты времени в течение первой фазы процесса, когда происходит сжатие газовой полости. Видно, как в жидкости волна разрежения движется от межфазной границы к стенке резервуара. Фронт волны с течением времени становится менее крутым.
Рис. 4.
Давление вдоль оси $0{{x}_{1}}$ в разные моменты времени: 1 – $t = 0.00$ мс, 2 – 0.05, 3 – 0.10, 4 – 0.15, 5 – 0.20, 6 – 0.25, 7 – 0.30, 8 – 0.35.
Движение волны сжатия во время второй фазы процесса демонстрирует рис. 5. Видно, что максимальные значения давления при движении волны убывают. По мере распространения сферической волны сжатия увеличивается ее поверхность и количество вовлеченного в движение вещества, амплитуда волны падает. Кроме того, часть энергии волнового движения расходуется на нагревание слоев среды, через которые она прошла [3]. Следует заметить, что фронт волны с течением времени становится более широким и менее крутым.
Рис. 5.
Давление вдоль оси $0{{x}_{1}}$ в разные моменты времени: 1 – $t = 0.40$ мс, 2 – 0.45, 3 – 0.50, 4 – 0.55, 5 – 0.60, 6 – 0.65, 7 – 0.70, 8 – 0.75, 9 – 0.80, 10 – 0.85, 11 – 0.90.
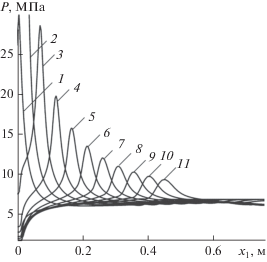
Обозначим через ${x \mathord{\left/ {\vphantom {x r}} \right. \kern-0em} r}$ безразмерное расстояние от центра воздушной полости. Тогда для расчета пика давления в зависимости от ${x \mathord{\left/ {\vphantom {x r}} \right. \kern-0em} r}$ предлагается аппроксимационная формула
(8)
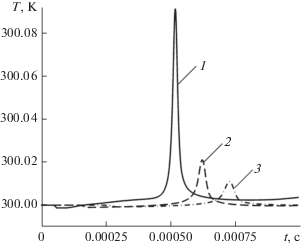
$P = 37.9 \times {{10}^{6}}{{\left( {{x \mathord{\left/ {\vphantom {x r}} \right. \kern-0em} r}} \right)}^{{ - 0.6}}}.$Повышение температуры жидкости в точках, расположенных на различном удалении $L$ от центра полости, иллюстрирует рис. 6. Нагрев среды регистрируется в период прохождения фронта волны сжатия. Показано, что чем больше расстояние от центра полости, тем меньше изменение температуры.
Рис. 6.
Изменение температуры $T$ в точках, расположенных на расстоянии $L$ от центра полости с течением времени: 1 – $L = 0.1$ м, 2 – 0.2, 3 – 0.3.
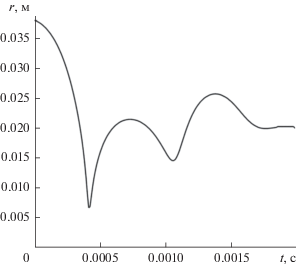
Изменение радиуса воздушной полости в ходе эксперимента показано на рис. 7. Отметим, что форма межфазной границы определяется изоповерхностью $\alpha = 0.5.$ Расчетным путем установлено, что минимальный радиус газового пузыря ${{r}_{{\min }}} = {\text{ }}6.6$ мм (17.3% от исходного значения) наблюдается через 0.420 мс после начала имплозионного процесса. За первыми сжатиями–расширениями сфероидальной структуры обычно следует ряд радиальных отскоков с меньшей амплитудой и с последующим затуханием колебаний. Как правило, в процессе имплозии газовая полость теряет сферичность, наблюдается деформация межфазной границы. Нарушение сферичности газовой полости может быть обусловлено разными факторами, в том числе мелкомасштабными возмущениями поля скорости вследствие турбулентных пульсаций, а также наличием стенки цилиндрического резервуара, вызывающей сферическую асимметрию поля скорости, распределения давления.
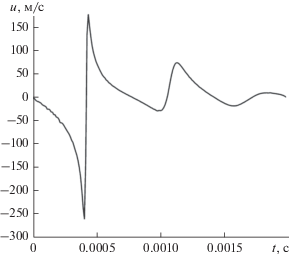
Для анализа динамики воздушной полости отслеживается также скорость точки, расположенной на межфазной границе жидкость–газ (рис. 8). На стадии сжатия газовой полости происходит ускоренное движение межфазной границы к ее центру. Максимальное значение скорости составило 266.6 м/с. После остановки жидкости вектор скорости границы раздела между жидкостью и газом меняет направление. Последующее увеличение радиуса полости сопровождается уменьшением скорости ее границы от 170.5 м/с до нуля. Вторичный цикл расширения–сжатия газовой области проходит с меньшей амплитудой скорости.
Рис. 8.
Изменение радиальной скорости контрольной точки, расположенной на межфазной границе с течением времени.
Далее приводятся результаты теоретического исследования влияния начального давления в газовой полости на основные параметры имплозионного процесса. Исследование выполнено при изменении начального давления в газовой полости от 0.05 до 0.5 МПа при прочих фиксированных параметрах.
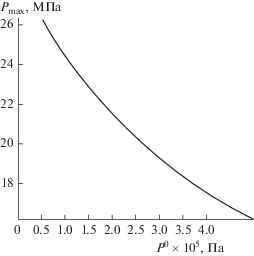
Установлено, что увеличение начального давления воздуха в имплозионной камере с 0.05 до 0.5 МПа уменьшает пиковое давление ${{P}_{{\max }}}$ в контрольной точке на 38% (рис. 9) и увеличивает время ${{t}_{2}},$ за которое оно достигается, на 6%; а также увеличивается на 6% значение минимального давления ${{P}_{{\min }}},$ регистрируемого в контрольной точке.
Рис. 9.
Влияние начального давления $P_{g}^{0}$ в воздушной полости на максимальное давление ${{P}_{{\max }}}$ в контрольной точке.
Обнаружено, что исходное давление газа в сферической полости влияет и на степень сжатия газа в момент внезапной остановки жидкости. Так, в момент максимального сжатия воздушной полости ее радиус составляет 15% при 0.05 МПа и 27% от начального при 0.5 МПа.
ЗАКЛЮЧЕНИЕ
Предложена математическая модель для описания инициированной перепадом давления имплозии, учитывающая наличие двух фаз, сжимаемость газа и жидкости, нестационарность, теплообмен, турбулентность и другие факторы.
Показано, что скорость межфазной границы достигает максимального значения в конце фазы сжатия воздушной полости; в процессе имплозии нарушается сферичность воздушной полости; фронт волны сжатия в жидкости с течением времени становится более широким и менее крутым. По мере распространения сферической волны сжатия пиковое значение давления уменьшается по закону (8).
Установлено, что увеличение начального давления воздуха в сферической полости с 0.05 до 0.5 МПа уменьшает пиковое давление в контрольной точке на 38% и увеличивает время, за которое оно достигается, на 6%, а также увеличивает радиус воздушной полости в момент максимального сжатия с 15% на 27% от начального значения.
Список литературы
Rayleigh L. On the Pressure Developed in a Liquid During the Collapse of a Spherical Cavity // Phil. Mag. 1917. V. 34. № 200. P. 94.
Isaacs J.D., Maxwell A.E. The Ball-breaker, a Deep Water Bottom Signalling Device // J. Marine Res. 1952. V. 11. P. 63.
Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука, 1966. 688 с.
Hunter C. On the Collapse of an Empty Cavity in Water // J. Fluid Mech. 1960. V. 8. № 2. P. 241.
Забабахин Е.И., Забабахин И.Е. Явления неограниченной кумуляции. М.: Наука, 1988. 171 с.
Брушлинский К.В., Каждан Я.М. Об автомодельных решениях некоторых задач газовой динамики // Успехи мат. наук. 1963. Т. 18. Вып. 2. С. 3.
Крайко А.Н. Быстрое цилиндрически и сферически симметричное сильное сжатие идеального газа // ПММ. 2007. Т. 71. Вып. 5. С. 744.
Аганин A.A., Халитова Т.Ф. Деформация ударной волны при сильном сжатии несферических пузырьков // ТВТ. 2015. Т. 53. № 6. С. 923.
Киселев А.Б. О динамическом сжатии (расширении) сферической полости в вязкой несжимаемой жидкости. Задача Забабахина // ПФиМ. 2014. № 6. С. 15.
Нигматулин Р.И., Аганин А.А., Топорков Д.Ю., Ильгамов М.А. Образование сходящихся ударных волн в пузырьке при его сжатии // ДАН. 2014. Т. 458. № 3. С. 282.
Нигматулин Р.И., Хабеев Н.С. Динамика паровых пузырьков // Изв. АН СССР. МЖГ. 1975. № 3. С. 59.
Десятов А.В., Ильмов Д.Н., Черкасов С.Г. Теоретическое исследование режимов сжатия сферического парового пузырька на основе упрощенной модели // ТВТ. 2007. Т. 45. № 6. С. 917.
Hyunik Yang, Desyatov A.V., Cherkasov S.G., McConnell D.B. On the Fulfillment of the Energy Conservation Law in Mathematical Models of Evolution of Single Spherical Bubble // Int. J. Heat Mass Transfer. 2008. V. 51. P. 3623.
Hyunik Yang, Desyatov A.V., Cherkasov S.G., Il’mov D.N., McConnell D.B. Numerical Simulation of Compression of the Single Spherical Vapor Bubble on a Basis of the Uniform Model // Int. J. Heat Mass Transfer. 2008. V. 51. P. 3615.
Десятов А.В., Ильмов Д.Н., Черкасов С.Г. Математическое моделирование эволюции одиночного сферического парового пузырька при его сжатии внешним давлением // ТВТ. 2008. Т. 46. № 1. С. 92.
Desyatov A.V., Il’mov D.N., Kubyshkin A.P., Cherkasov S.G. Mathematical Simulation of the Compression Process of a Vapor Bubble at a Pressure Increase in the Surrounding Liquid // J. Eng. Thermophys. 2008. V. 17. № 4. P. 300.
Десятов А.В., Ильмов Д.Н., Черкасов С.Г. Некоторые гидродинамические особенности эволюции одиночного сферического пузырька в режиме конечного сжатия // Изв. РАН. МЖГ. 2009. № 2. С. 92.
Десятов А.В., Ильмов Д.Н., Кубышкин А.П., Черкасов С.Г. Математическое моделирование эволюции одиночного сферического парового пузырька на основе гомобарической модели // ТВТ. 2011. Т. 49. № 3. С. 436.
Ильмов Д.Н., Черкасов С.Г. Теплофизические процессы при сжатии парового пузырька в жидком углеводороде на основе гомобарической модели // ТВТ. 2012. Т. 50. № 5. С. 676.
Багров В.В., Десятов А.В., Казанцева Н.Н. и др. Вода: эффекты и технологии / Под ред. Десятова А.В. М.: ООО НИЦ “Инженер”; ООО “Онико-М”, 2010. 488 с.
Avdeev A.A. Bubble Systems. Springer Int. Publ., 2016. 466 p.
Turner S.E. Underwater Implosion of Glass Spheres // J. Acoust. Soc. Am. 2007. V. 121. № 2. P. 844.
Shukla A., Gupta S., Matos H., LeBlanc J.M. Dynamic Collapse of Underwater Metallic Structures – Recent Investigations: Contributions after the 2011 Murray Lecture // Exp. Mech. 2018. V. 58. P. 387.
Ikeda C.M., Wilkerling J., Duncan J.H. The Implosion of Cylindrical Shell Structures in a High-pressure Water Environment // Proc. R. Soc. Math. Phys. Eng. Sci. 2013. V. 469. № 2160. P. 20130443.
Farhat C., Wang K.G., Main A., Kyriakides S., Lee L.-H., Ravi-Chandar K., Belytschko T. Dynamic Implosion of Underwater Cylindrical Shells: Experiments and Computations // Int. J. Solids Struct. 2013. V. 50. P. 2943.
Pinto M., Shukla A. Dynamic Collapse Mode Evolution in Carbon Composite Tubes // Extreme Mech. Lett. 2015. V. 3. P. 55.
Вараксин А.Ю. Гидрогазодинамика и теплофизика двухфазных потоков: проблемы и достижения (обзор) // ТВТ. 2013. Т. 51. № 3. С. 421.
Нигматулин Р.И. Динамика многофазных сред. Ч. 1. М.: Наука, 1987. 464 с.
Губайдуллин Д.А., Снигерев Б.А. Численное моделирование турбулентного восходящего потока газожидкостной пузырьковой смеси в вертикальной трубе. Сравнение с экспериментом // ТВТ. 2018. Т. 56. № 1. С. 61.
Вараксин А.Ю. Обтекание тел дисперсными газовыми потоками // ТВТ. 2018. Т. 56. № 2. С. 282.
Pakhomov M.A., Terekhov V.I. Enhancement of an Impingement Heat Transfer between Turbulent Mist Jet and Flat Surface // Int. J. Heat Mass Transfer. 2010. V. 53. P. 3156.
Ferrer P.J.M., Causon D.M., Qian L., Mingham C.G., Ma Z.H. A Multi-region Coupling Scheme for Compressible and Incompressible Flow Solvers for Two-phase Flow in a Numerical Wave Tank // Comput. Fluids. 2016. V. 125. P. 116.
Hirt C.W., Nichols B.D. Volume of Fluid (VOF). Methods for the Dynamics of Free Boundaries // J. Comput. Phys. 1981. № 39. P. 201.
Morenko I.V., Fedyaev V.L. Influence of Turbulence Intensity and Turbulence Length Scale on the Drag, Lift, and Heat Transfer of a Circular Cylinder // China Ocean Eng. 2017. V. 31. № 3. P. 357.
Menter F.R. Two-equation Eddy Viscosity Turbulence Models for Engineering Applications // AIAA J. 1994. V. 32. № 8. P. 1598.
Farhat C., Rallu A., Shankaran S. A Higher-order Generalized Ghost Fluid Method for the Poor for the Three-dimensional Two-phase Flow Computation of Underwater Implosions // J. Comput. Phys. 2008. V. 227. P. 7674.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур