Теплофизика высоких температур, 2019, T. 57, № 5, стр. 748-754
Особенности устойчивости и акустических свойств перегретой жидкости с газовыми зародышами при повышении давления
В. Ш. Шагапов 1, М. Н. Галимзянов 1, *, И. И. Вдовенко 1, 2
1 Институт механики им. Р.Р. Мавлютова УФИЦ РАН
г. Уфа, Башкортостан, Россия
2 Башкирский государственный университет
г. Уфа, Башкортостан, Россия
* E-mail: monk@anrb.ru
Поступила в редакцию 21.01.2019
После доработки 07.05.2019
Принята к публикации 16.05.2019
Аннотация
Изучена динамика слабых гармонических возмущений в перегретой водовоздушной пузырьковой среде, когда в пузырьках помимо водяного пара присутствует инертный газ, не участвующий в фазовых переходах. Проанализированы карты зон устойчивости рассмотренных систем в зависимости от степени перегрева жидкости на плоскости объемное содержание–радиус пузырьков с повышением равновесного давления от 0.1 до 10 МПа. Исследованы влияние начального перегрева (от сотых долей до одного градуса) и повышения давления на дисперсию гармонических волн, а также зависимость инкремента от радиуса пузырьков для неустойчивых систем.
ВВЕДЕНИЕ
Из литературы известно, что физико-химические свойства жидкостей в метастабильном состоянии в основном определяются наличием в их составе различных включений, например газовых пузырьков или твердых частиц [1]. Задачами распространения малых возмущений в жидкости с пузырьками занимались многие авторы [2–9]. В дальнейшем в двумерной постановке были получены критерии усиления и гашения волн давления в пузырьковых и пенных структурах [10–14]. В работах [15–17] исследовались вопросы роста паровых пузырьков в перегретой жидкости и проблемы ее устойчивости. В обзорной работе [18] рассмотрены проблемы и особенности изучения течений сплошной среды, содержащей дисперсную примесь в виде твердых частиц, капель или пузырей. Приведены основные характеристики двухфазных течений и методы их моделирования. В [19–21] представлены результаты исследований по акустическому воздействию на многофракционные смеси жидкости с парогазовыми и газовыми пузырьками различных размеров и разного состава с фазовыми превращениями. Определены критерии, приводящие как к уменьшению, так и к увеличению коэффициента затухания в низкочастотной области.
В настоящей работе, которая дополняет и расширяет результаты, ранее полученные в [22–25], рассмотрены особенности распространения звука и развития неустойчивости в перегретой жидкости, содержащей газовые зародыши, в зависимости от степени ее перегрева, определяемой как $\Delta {{T}_{0}} = {{T}_{0}} - {{T}_{s}}({{p}_{0}}).$
Отметим, если в жидкости газовые зародыши отсутствуют, то состояние равновесия парогазожидкостной системы определяется тремя параметрами, в качестве которых можно взять, например, объемное содержание пузырьков ${{\alpha }_{0}},$ их радиус ${{a}_{0}}$ и давление в жидкой фазе ${{p}_{0}}$ (вместо давления можно использовать температуру ${{T}_{0}}$). При наличии в системе газовых зародышей ее состояние определяется четырьмя параметрами (например, ${{\alpha }_{0}},$ ${{a}_{0}},$ ${{p}_{0}},$ ${{T}_{0}}$).
ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ УРАВНЕНИЯ
Пусть в жидкости, находящейся при температуре ${{T}_{0}}$ и давлении ${{p}_{0}},$ имеются сферические пузырьки радиусом ${{a}_{0}},$ которые содержат пар и нерастворимый в жидкой фазе газ. При состояниях, достаточно далеких от критического, имеет место следующее условие: ${{p}_{{\upsilon 0}}} = {{p}_{s}}({{T}_{0}}),$ согласно [1]. Рассмотрим распространение малых возмущений в парогазовой смеси в плоскоодномерном и односкоростном приближении.
Поставленная задача описывается уравнениями (1)–(12) из [23]. Основная методика расчета также приведена в [23]. Далее везде используется терминология и обозначения, принятые в [23]. Решение задачи будем искать в виде затухающей бегущей волны
Вывод уравнения (1) показан в [23].
Пренебрегая сжимаемостью жидкости (${{C}_{p}} \to \infty $) и слагаемым ${{{{k}_{0}}{{\alpha }_{0}}} \mathord{\left/ {\vphantom {{{{k}_{0}}{{\alpha }_{0}}} \beta }} \right. \kern-0em} \beta }$ по сравнению с единицей, из дисперсионного уравнения (1) при $\omega \to 0$ можно получить следующую формулу для равновесной скорости звука:
(2)
${{C}_{e}} = \sqrt {\frac{{{{p}_{{g0}}}}}{{\rho _{{\ell 0}}^{0}{{\alpha }_{0}}}}((1 - {{k}_{0}}){{H}_{a}} + {{k}_{0}}{{\alpha }_{0}}{\gamma \mathord{\left/ {\vphantom {\gamma \beta }} \right. \kern-0em} \beta }) - \frac{2}{3}\frac{\sigma }{{{{a}_{0}}\rho _{{\ell 0}}^{0}{{\alpha }_{0}}}}} ,$Для частных случаев (2σ/(a0p0) $ \ll $ 1), когда ${{k}_{0}} = 0$ и ${{k}_{0}} = 1$ (2), будем иметь формулы Мэллока [6] и Ландау [27] соответственно
Из формулы (2) следует, что если в полученном выражении второе слагаемое, связанное с капиллярными силами на межфазной поверхности, превышает первое слагаемое, то равновесная скорость ${{C}_{e}}$ – мнимая. А это в свою очередь означает [8], что когда параметры жидкости с газовыми зародышами удовлетворяют такому условию, то состояния такой системы неустойчивы. В противном случае состояния системы устойчивые. Приравнивая к нулю (2), получим условие для параметров, определяющих границу устойчивых и неустойчивых состояний. Это условие можно привести к виду
(3)
${{p}_{{g0}}}((1 - {{k}_{0}}){{H}_{a}} + {{k}_{0}}{{\alpha }_{0}}{\gamma \mathord{\left/ {\vphantom {\gamma \beta }} \right. \kern-0em} \beta }) = \frac{2}{3}\frac{\sigma }{{{{a}_{0}}}}.$Отметим, что данное условие совпадает с аналогичным, полученным в рамках равновесной схемы рассмотрения системы жидкость–парогазовые пузырьки [16].
Для удобства выполнения численных расчетов, уравнение (3) разрешим относительно объемного содержания пузырьков. Тогда будем иметь
(4)
${{\alpha }_{0}} = {{\alpha }_{*}},\,\,\,\,{{\alpha }_{*}} = \left( {\frac{2}{3}\frac{\sigma }{{{{p}_{{g0}}}{{a}_{0}}}} - (1 - {{k}_{0}}){{H}_{a}}} \right){\beta \mathord{\left/ {\vphantom {\beta {{{k}_{0}}\gamma }}} \right. \kern-0em} {{{k}_{0}}\gamma }}.$В случае отсутствия газа в пузырьках (${{k}_{0}} = 1$) получим
(5)
${{\alpha }_{*}} = \frac{2}{3}\frac{\sigma }{{\rho _{{\ell 0}}^{0}{{a}_{0}}C_{L}^{2}}},\,\,\,\,{{C}_{L}} = \frac{{\rho _{{g0}}^{0}}}{{\rho _{{\upsilon 0}}^{0}}}\frac{L}{{\sqrt {{{c}_{\ell }}{{T}_{0}}} }}.$Здесь ${{C}_{L}}$ – скорость звука по Ландау [27].
Поскольку $(1 - {{k}_{0}}){{H}_{a}}{{p}_{{g0}}} = {{p}_{{a0}}},$ формулу (4) с учетом (1) из [23] можно привести к виду
(6)
${{\alpha }_{*}} = \left( {\Delta {{p}_{\upsilon }} - \frac{{4\sigma }}{{3{{a}_{0}}}}} \right)\frac{\beta }{{{{k}_{0}}\gamma {{P}_{{g0}}}}},\,\,\,\,\Delta {{p}_{\upsilon }} = {{p}_{s}}({{T}_{0}}) - {{p}_{0}}.$На основе уравнения Клапейрона–Клаузиуса (8) из [23] в линейном приближении перепад давления $\,\Delta {{p}_{\upsilon }}$ можно выразить через перегрев жидкости $\Delta {{T}_{0}}$ как
Подставляя $\,\Delta {{p}_{\upsilon }}$ из (7) в (6), получим(8)
${{\alpha }_{*}} = \left( {\frac{{\rho _{{\upsilon 0}}^{0}L}}{{{{T}_{0}}}}\Delta {{T}_{0}} - \frac{{4\sigma }}{{3{{a}_{0}}}}} \right)\frac{\beta }{{{{k}_{0}}\gamma {{p}_{{g0}}}}}.$При этом масса газового зародыша определяется как
Для неустойчивых состояний (когда область значений ${{а}_{0}}$ и ${{\alpha }_{0}}$ на рис. 1 для соответствующего перегрева $\Delta {{T}_{0}}$ расположена правее представленных сплошных линий, а также левее пунктирных) дисперсионное состояние (1), рассмотренное как уравнение для $\omega $ при заданных $K > 0$ (так же как и в случае пузырьковой парожидкостной среды), имеет решение вида $\omega = \omega {\kern 1pt} 'i,$ причем $\omega {\kern 1pt} ' > 0$ [8]. Зависимость $\omega {\kern 1pt} ' = \omega {\kern 1pt} '(K)$ при этом монотонно возрастающая, имеющая асимптоту $\omega {\kern 1pt} ' = \omega _{\infty }^{'}$ при $K \to \infty .$ Для анализа темпа неустойчивости наибольший интерес представляет это предельное значение инкремента. Пренебрегая сжимае-мостью жидкости (${{C}_{e}} \to \infty $), для определения инкремента получим следующее уравнение:
Рис. 1.
Линии, определяющие на плоскости (${{\alpha }_{0}},$ $\,{{a}_{0}}$) границу раздела устойчивых и неустойчивых состояний перегретой воды с паровоздушными пузырьками.

Здесь выражение для $\psi (\omega _{\infty }^{'})$ определяется из (1) при соответствующей замене $ - i\omega $ на $\omega _{\infty }^{'}.$
В случае чисто паровых пузырьков (${{p}_{{g0}}} = {{p}_{{\upsilon 0}}},$ ${{p}_{{\upsilon 0}}} = {{p}_{s}}({{T}_{0}}),$ ${{k}_{0}} = 1$) выражение для $Q$ из (1) записывается как
где $\beta = (\gamma - 1)\frac{{\rho _{{\ell 0}}^{0}{{c}_{1}}}}{{\rho _{{\upsilon 0}}^{0}{{c}_{\upsilon }}}}{{\left( {\frac{{{{c}_{\upsilon }}{{T}_{0}}}}{L}} \right)}^{2}},$ $\rho _{{\upsilon 0}}^{0} = \frac{{{{p}_{{\upsilon 0}}}}}{{{{B}_{\upsilon }}{{T}_{0}}}},$ pυ0 = $ = {{p}_{0}} + \frac{{2\sigma }}{{{{a}_{0}}}},$ ${{T}_{0}} = {{T}_{s}}({{p}_{{\upsilon 0}}}).$РЕЗУЛЬТАТЫ РАСЧЕТОВ
На основе уравнения (1) и его следствия (2) выполнены численные расчеты для воды с паровоздушными пузырьками. В качестве значений физических и теплофизических параметров использованы данные из справочника [28]. Линии 1, 2 и 3 на рисунках (за исключением рис. 1–4) соответствуют следующим значениям статического давления: ${{p}_{0}} = 0.1,$ 1 и 10 МПа. Один, два и три штриха обозначают перегрев $\Delta {{T}_{0}} = {{10}^{{ - 2}}},$ ${{10}^{{ - 1}}}$ и $1$ К.
Рис. 2.
Дисперсионные кривые при различных значениях p0 при ${{\alpha }_{0}} = {{10}^{{ - 3}}},$ ${{a}_{0}} = {{10}^{{ - 6}}}$ м, $\Delta {{T}_{0}} = {{10}^{{ - 1}}}$ К.

Рис. 3.
Зависимость фазовой скорости и коэффициента затухания от частоты возмущения при трех значениях степени перегрева (${{\alpha }_{0}} = {{10}^{{ - 3}}},$ ${{a}_{0}} = {{10}^{{ - 6}}}$ м, ${{p}_{0}} = 1$ МПа).
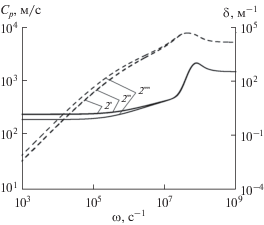
Рис. 4.
Зависимость фазовой скорости и коэффициента затухания от частоты возмущения при ${{\alpha }_{0}} = {{10}^{{ - 3}}},$ $\Delta {{T}_{0}} = 1$ К, ${{p}_{0}} = 1$ МПа и различных значениях радиуса пузырьков: 1 – ${{a}_{0}} = {{10}^{{ - 6}}},$ 2 – $2.62 \times {{10}^{{ - 6}}},$ 3 – $5.04 \times {{10}^{{ - 4}}},$ 4 – ${{10}^{{ - 3}}}$ м.

На рис. 1 представлены линии, полученные на основе (4) (или (8)), определяющие на плоскости (${{\alpha }_{0}},$ ${{a}_{0}}$) границу раздела устойчивых и неустойчивых состояний перегретой воды с паровоздушными пузырьками, находящимися при p0 (${{T}_{s}}({{p}_{0}}) = 373,$ $453$, $584$ К). Эти линии состоят из двух участков: восходящего (сплошные линии) и нисходящего (пунктирные линии). На восходящем участке соответствующая массовая концентрация ${{k}_{0}}$ пара растет. Причем при ${{p}_{0}} = 1$ и 10 МПа для всех трех значений перегревов достигается ${{k}_{0}} = 1$ (на графиках эти положения отмечены точками). Для случая ${{p}_{0}} = 1$ МПа при $\Delta {{T}_{0}} = 1$ К для объемных содержаний пузырьков, не превышающих 10% (${{\alpha }_{0}} \leqslant 0.1$), k0 не достигает единицы. На нисходящем участке массовая концентрация пара сохраняет свое постоянное значение (${{k}_{0}} = 1$). Таким образом, эти участки кривых соответствуют пароводяной пузырьковой системе. Данный участок (пунктирная линия) описывается формулой (5). Зоны вне кривых соответствуют устойчивым, а внутри – неустойчивым состояниям. В случае чисто паровых пузырьков линии, описываемые формулой (5), полностью определяют границу между устойчивыми (справа от кривых) и неустойчивыми (слева) состояниями. Этот случай изучен в работе [8]. Объемное содержание парогазовых пузырьков слабо влияет на характер кривых, определяющих границу устойчивости (рис. 1). Левые границы, изображенные сплошными линиями, для всех значений перегревов крутые, почти вертикальные линии. Зоны, находящиеся левее пунктирных линий, соответствуют неустойчивым состояниям парожидкостных пузырьковых систем. Следовательно, наличие газа в пузырьках расширяет зону устойчивости перегретой жидкости. Чем меньше перегрев, тем правее смещается сплошная линия, определяющая границу между устойчивыми и неустойчивыми состояниями. Поэтому чем меньше перегрев, тем больше зона устойчивости.
На рис. 2 показаны зависимости фазовой скорости и коэффициента затухания от частоты возмущения для устойчивых парогазовых и паровых систем, иллюстрирующие влияние статического давления. Для равновесного радиуса пузырьков принято значение ${{a}_{0}} = {{10}^{{ - 6}}}$ м, для степени перегрева $\Delta {{T}_{0}} = {{10}^{{ - 1}}}$ К. При таком перегреве массовое содержание пара при ${{p}_{0}} = 0.1,$ $1$ и $10$ МПа составляет k0 = 0.349, 0.891, 0.998 соответственно. Для низкочастотного диапазона ($\omega \leqslant {{\omega }_{R}},$ ωR = $ = a_{0}^{{ - 1}}\sqrt {{{3\gamma {{p}_{0}}} \mathord{\left/ {\vphantom {{3\gamma {{p}_{0}}} {\rho _{{\ell 0}}^{0}}}} \right. \kern-0em} {\rho _{{\ell 0}}^{0}}}} $ – миннаэртовская частота собственных колебаний пузырьков) наблюдается сравнительно слабое влияние изменения давления от 0.1 до 10 МПа на величину фазовой скорости, но значение коэффициента затухания при этом возрастает примерно в десять раз.
Что касается кривых для ${{p}_{0}} = 10$ МПа, когда пузырьки становятся почти чисто паровыми, в области низких частот наблюдается сильное уменьшение фазовой скорости. Для этого диапазона частот скорость звука приближается к значению, определяемому формулой Ландау. Кроме того, здесь наблюдается аномальное повышение (более чем на два порядка) величины коэффициента затухания.
На рис. 3 показаны зависимости фазовой скорости и коэффициента затухания от частоты возмущения для устойчивых парогазовых и паровых систем, иллюстрирующие влияние перегрева системы ($\Delta {{T}_{0}} = {{10}^{{ - 2}}},$ ${{10}^{{ - 1}}}$ и $1$ К). Значение равновесного радиуса пузырьков принято ${{a}_{0}} = {{10}^{{ - 6}}}$ м при ${{p}_{0}} = 1$ МПа. Для рассмотренных значений ΔT0 массовые содержания пара составляют k0 = 0.889, 0.891, 0.916. Видно, что для перегревов $\Delta {{T}_{0}} = {{10}^{{ - 2}}}$ и ${{10}^{{ - 1}}}$ К дисперсионные кривые практически совпадают. При увеличении перегрева до $\Delta {{T}_{0}} = 1$ К при низких частотах ($\omega \leqslant {{\omega }_{R}}$) фазовая скорость несколько снижается, а коэффициент затухания возрастает в несколько раз. Это связано с увеличением роли фазовых переходов при росте массового содержания пара в пузырьках.
На рис. 4 проиллюстрирован характер дисперсионных зависимостей при дискретном изменении равновесного радиуса ${{a}_{0}}$ для $\Delta {{T}_{0}} = 1$ К. В данном случае ${{p}_{0}} = 1$ МПа, а объемное содержание пузырьков ${{\alpha }_{0}} = {{10}^{{ - 3}}}.$ Линии 1–4 соответствуют следующим значениям радиуса пузырьков: ${{a}_{0}} = {{10}^{{ - 6}}},$ $2.62 \times {{10}^{{ - 6}}},$ $5.04 \times {{10}^{{ - 4}}}$ и ${{10}^{{ - 3}}}$ м. Причем промежуточные значения радиуса соответствуют равновесным радиусам $a_{0}^{{(m)}}$ и $a_{0}^{{(M)}},$ расположенным на левой и правой границах области устойчивости. Графики указывают на аномально сильное увеличение коэффициента затухания с приближением ${{a}_{0}}$ к значениям $a_{0}^{{(m)}}.$ Для низкочастотной области увеличение радиуса в два раза приводит к росту коэффициента затухания на 2–3 порядка. Фазовая скорость при этом снижается в несколько раз. Что касается кривых 3 и 4, соответствующих парожидкостным системам, то при низких частотах ($\omega \leqslant {{\omega }_{R}}$) наблюдается сравнительно небольшое различие для фазовых скоростей. Для этого диапазона частот температурные перепады внутри пузырьков реализуются в тонких слоях вблизи межфазной поверхности (в основном объеме пузырьков пар в них ведет себя как адиабатический газ). Поэтому в плане определения фазовой скорости массообмен между пузырьком и жидкостью не играет заметной роли. Но коэффициент затухания, как видно из рисунков, отличается примерно в два раза.
На рис. 5 представлена зависимость равновесной скорости звука от радиуса пузырьков ${{a}_{0}}$ при различных значениях перегрева $\Delta {{T}_{0}}$ для ${{p}_{0}} = 1$ МПа и ${{\alpha }_{0}} = {{10}^{{ - 3}}}.$ Для рассматриваемых задач радиус пузырьков меняется от 10–6 до 10–2 м. Картина состоит из двух частей. Левые ветви кривых, соответствующие парогазожидкостной смеси, показывают монотонное снижение равновесной скорости до нулевого значения, когда радиусы пузырьков увеличиваются и достигают границы между устойчивыми и неустойчивыми состояниями системы для соответствующих значений $\Delta {{T}_{0}}.$ Значения радиусов для принятых значений перегрева равны соответственно ${{a}_{0}} = 3.6 \times {{10}^{{ - 4}}},$ $2.8 \times {{10}^{{ - 5}}}$ и $2.7 \times {{10}^{{ - 6}}}$ м. Таким образом, чем больше $\Delta {{T}_{0}},$ тем уже становится зона устойчивости и, следовательно, раньше (с ростом радиуса $a_{0}^{{}}$) достигается нулевое значение равновесной скорости. Далее, начиная со значения ${{a}_{0}} = a_{0}^{{(m)}},$ следует промежуток, где равновесная скорость формально становится мнимой, и поэтому для значений ${{a}_{0}}$ из этого промежутка смесь неустойчива. Но при некотором ${{a}_{0}} = a_{0}^{{(M)}}$ находящаяся на правой границе устойчивости равновесная скорость растет с нулевого значения. Для этого участка смесь представляет собой чисто парожидкостную пузырьковую систему. Значения радиуса $a_{0}^{{(M)}}$ для всех трех перегревов очень близки и его величину можно определить, разрешая относительно радиуса ${{a}_{0}}{\text{:}}$
Рис. 5.
Зависимость равновесной скорости звука от радиуса пузырьков ${{a}_{0}}$ при различных значениях перегрева $\Delta {{T}_{0}}$ для ${{p}_{0}} = 1$ МПа и ${{\alpha }_{0}} = {{10}^{{ - 3}}}.$

Для более перегретой жидкости с парогазовыми пузырьками графики (левый пучок кривых на рис. 5) для равновесной скорости расположены ниже. Это также связано с увеличением массовой доли пара в пузырьках, которое приводит к тому, что упругость парогазовой смеси в пузырьках в плане определения равновесной скорости полностью определяется эффектами фазовых переходов. За счет них парциальное давление пара в пузырьках меняется очень слабо. Следовательно, общая упругость парогазовой смеси в пузырьках в основном определяется парциальным давлением.
На рис. 6 представлена зависимость инкремента $\omega _{\infty }^{'}$ от радиуса ${{a}_{0}}$ для ${{p}_{0}} = 1$ и 10 МПа (линии 2 и 3 соответственно). Для объемного содержания пузырьков принято ${{\alpha }_{0}} = {{10}^{{ - 4}}}.$ Радиус пузырьков меняется от $a_{0}^{{(m)}}$ до $a_{0}^{{(M)}}.$ При увеличении радиуса пузырьков от значения на левой до значения на правой границе зон устойчивости величина инкремента растет от нуля до максимального значения, затем монотонно снижается до нуля. При этом максимальное значение инкремента, которое достигается при максимально возможном радиусе парогазовых пузырьков (точки – пересечения сплошных и штриховых линий на рис. 6), который, согласно (1), реализуется при ${{p}_{{g0}}} = 0$ (${{k}_{0}} = 1$) и определяется как
(9)
$a_{0}^{{(*)}} \simeq \frac{{2\sigma }}{{\Delta {{p}_{\upsilon }}}},\,\,\,\,\Delta {{p}_{\upsilon }} = {{p}_{s}}({{T}_{0}}) - {{p}_{0}}.$(10)
$a_{0}^{{\left( * \right)}} \simeq \frac{{2\sigma }}{{\rho _{{\upsilon 0}}^{0}L}}\frac{{{{T}_{0}}}}{{\Delta {{T}_{0}}}}.$Рис. 6.
Зависимость $\omega {\kern 1pt} '$ от ${{a}_{0}}$ при различных значениях перегрева $\Delta {{T}_{0}}{\text{:}}$ обозначения как на рис. 1.

При дальнейшем росте $a_{0}^{{}}$ (от $a_{0}^{{(*)}}$) из представленных графиков следует, что $\omega _{\infty }^{'}$ монотонно снижается до нуля (это участок кривых изображен пунктирными линиями). На этом промежутке изменения равновесного радиуса пузырьки чисто паровые, и поэтому соответствующий текущему значению радиуса пузырьков перегрев жидкости должен соответствовать расчетам по (9) (или (10)). Кроме того, как следует из рис. 6, зависимость инкремента от радиуса для всех перегревов ложится на одну кривую. Отметим, что для радиусов, не превышающих $a_{0}^{{(*)}},$ когда газ в пузырьках отсутствует, соответствующие инкременты также лежат на пунктирных линиях на участках, расположенных выше отмеченных жирными точками.
ЗАКЛЮЧЕНИЕ
На основе аналитических и численных расчетов построены карты зон устойчивости в области (${{a}_{0}},$ $\alpha $) пузырьковой парогазожидкостной смеси в зависимости от величины перегрева жидкости $\Delta {{T}_{0}}.$ Установлено, что наличие нерастворимого газа в пузырьках существенно расширяет зону значений объемного содержания ${{\alpha }_{0}}$ и радиуса ${{a}_{0}}$ пузырьков на плоскости (${{a}_{0}},$ $\alpha $). С ростом статического давления ${{p}_{0}}$ зона устойчивости, где чисто парожидкостная система расширяется, а зона устойчивости, где в пузырьках присутствует газ, при одних и тех же перегревах $\Delta {{T}_{0}}$ сужается.
Рассмотрено влияние перегрева жидкости $\Delta {{T}_{0}}$ на величину фазовой скорости и коэффициент затухания, когда система находится в устойчивом состоянии. Установлено, что для мелкодисперсной смеси (при ${{a}_{0}} = {{10}^{{ - 6}}}$ м) в зоне устойчивости перегрева несущественно влияет на изменение фазовой скорости и коэффициента затухания, что связано с достаточно высокой концентрацией инертного газа в пузырьках. Декремент затухания в устойчивой области меняется не более чем в два раза.
Результаты, полученные в данной работе, уточняют и дополняют исследования в [29].
Работа авторов В.Ш. Шагапова и М.Н. Галимзянова поддержана средствами государственного бюджета по госзаданию на 2019–2022 годы (№ 0246-2019-0052). Работа И.И. Вдовенко частично поддержана грантом РФФИ (№ 17-41-020582-р_а).
Список литературы
Нигматулин Р.И. Динамика многофазных сред. Т. 1, 2. М.: Наука, 1987.
Fox F.E., Curley S.R., Larson G.S. Phase Velocity and Absorption Measurements in Water Containing Air Bubbles // J. Acoust. Soc. Amer. 1955. V. 27. Iss. 3. P. 534.
Silberman E. Sound Velocity and Attenuation in Bubbly Mixture Measured in Standing Wave Tubes // J. Acoust. Soc. Amer. 1957. V. 29. Iss. 8. P. 925.
Кедринский В.К. Распространение возмущений в жидкости, содержащей пузырьки газа // ПМТФ. 1968. № 4. С. 29.
Van Wijngaarden L. One-dimensional Flow of Liquids Containing Small Gas Bubbles // Ins. Annu. Rev. Fluid Mech. 1972. V. 4. P. 369.
Накоряков В.Е., Шрейбер И.Р. Распространение малых возмущений в парожидкостной смеси // Проблемы теплофизики и физической гидродинамики. Новосибирск, 1974. С. 161.
Кутателадзе С.С., Накоряков В.Е. Тепломассообмен и волны в газожидкостных системах. Новосибирск: Наука, 1984. 301 с.
Шагапов В.Ш., Вахитова Н.К. О распространении малых возмущений в парожидкостных пузырьковых средах // ПМТФ. 1984. № 5. С. 34.
Шагапов В.Ш. Об устойчивости пузырьковых газожидкостных сред // ПММ. 1986. Т. 50. № 3. С. 516.
Нигматулин Р.И., Шагапов В.Ш., Гималтдинов И.К., Галимзянов М.Н. Двумерные волны давления в жидкости, содержащей пузырьковые зоны // ДАН. 2001. Т. 378. № 6. С. 763.
Шагапов В.Ш., Гималтдинов И.К., Галимзянов М.Н. Двумерные волны давления в жидкости, содержащей пузырьки // МЖГ. 2002. № 2. С. 139.
Болотнова Р.Х., Галимзянов М.Н., Агишева У.О. Моделирование процессов взаимодействия сильных ударных волн в газожидкостных смесях // Изв. вузов. Поволжский регион. Физ.-матем. науки. 2011. № 2. С. 3.
Агишева У.О., Болотнова Р.Х., Бузина В.А., Галимзянов М.Н. Параметрический анализ режимов ударно-волнового воздействия на газожидкостные среды // МЖГ. 2013. № 2. С. 15.
Агишева У.О. Воздействие ударных волн на пузырьковые и пенные структуры в двумерных осесимметричных объемах // Вестн. Башкирск. ун-та. 2013. Т. 18. № 3. С. 640.
Carey V.P. Thermodynamic Analysis of the Intrinsic Stability of Superheated Liquid in a Micromechanical Actuator with Elastic Walls // Microscale Thermophys. Eng. 2000. V. 4. Iss. 2. P. 109.
Шагапов В.Ш., Коледин В.В., Вахитова Н.К. Об устойчивости перегретой жидкости, содержащей парогазовые зародыши // ПМТФ. 2013.Т. 54. № 5. С. 64.
Коледин В.В., Шагапов В.Ш. К динамике роста паровых пузырьков в перегретой жидкости // ПММ. 2013. Т. 77. № 5. С. 754.
Вараксин А.Ю. Гидрогазодинамика и теплофизика двухфазных потоков: проблемы и достижения (обзор) // ТВТ. 2013. Т. 51. № 3. С. 421.
Губайдуллин Д.А., Никифоров А.А. Акустические возмущения в смеси жидкости с пузырьками пара и газа // ТВТ. 2010. Т. 48. № 2. С. 188.
Губайдуллин Д.А., Никифоров А.А., Гафиятов Р.Н. Акустические волны в двухфракционных пузырьковых жидкостях с фазовыми превращениями // ТВТ. 2012. Т. 50. № 2. С. 269.
Губайдуллин Д.А., Никифоров А.А., Гафиятов Р.Н. Акустические волны в многофракционных пузырьковых жидкостях // ТВТ. 2015. Т. 53. № 2. С. 250.
Шагапов В.Ш., Галимзянов М.Н., Вдовенко И.И., Хабеев Н.С. Особенности распространения звука в теплой воде с воздушными пузырьками // ИФЖ. 2018. Т. 91. № 4. С. 912.
Шагапов В.Ш., Галимзянов М.Н., Вдовенко И.И. Особенности отражения и прохождения акустических волн на границе «чистой» и пузырьковой жидкости при прямом их падении // ТВТ. 2019. Т. 57. № 2. С. 284.
Шагапов В.Ш., Галимзянов М.Н., Вдовенко И.И. Особенности отражения и прохождения акустических волн на границе “чистой” и пузырьковой жидкости при “косом” их падении // ТВТ. 2019. Т. 57. № 3. С. 464.
Agisheva U.O., Vdovenko I.I., Galimzyanov M.N. Acoustic Waves in a Superheated Liquid with a Gas Nuclei // J. Phys.: Conf. Ser. 2019. V. 1158. 022007.
Нигматулин Р.И., Шагапов В.Ш., Вахитова Н.К. Проявление сжимаемости несущей фазы при распространении волны в пузырьковой среде // Докл. АН СССР. 1989. Т. 304. № 5. С. 1077.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Физматлит, 2006. 736 с.
Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. 2-е изд. М.: Наука, 1972. 720 с.
Шагапов В.Ш., Галимзянов М.Н., Вдовенко И.И. Акустика и устойчивость перегретой жидкости с газовыми зародышами // ПМТФ. 2019. Т. 60. № 3. С. 1.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур





