Теплофизика высоких температур, 2019, T. 57, № 5, стр. 727-733

Условие существования оптимальной толщины стенки, разделяющей две различные среды при локальном тепловом воздействии

П. А. Власов^*

Московский государственный технический университет им. Н.Э. Баумана (национальный исследовательский университет)
Москва, Россия

^* E-mail: pvlx@mail.ru

Поступила в редакцию 05.04.2018
После доработки 15.12.2018
Принята к публикации 27.03.2019

DOI: 10.1134/S0040364419040240

Полный текст (PDF)

Аннотация

С использованием интегрального преобразования Ганкеля нулевого порядка решена задача об определении достаточных условий существования оптимальной толщины ортотропной разделительной стенки, обе поверхности которой участвуют в теплообмене с внешними средами, обладающими постоянными температурами, а одна из них также находится под воздействием стационарного осесимметричного теплового потока с интенсивностью гауссовского типа. В качестве критерия оптимальности использовано требование минимизации температуры наиболее нагретой точки объекта исследований. Получено достаточное условие в виде неравенства, устанавливающего связь между теплофизическими характеристиками ортотропного материала стенки и параметрами внешнего теплового воздействия. С использованием вычислительного эксперимента установлена достаточная точность полученного условия.

ВВЕДЕНИЕ

В математической теории теплопроводности [1–5] особое место занимают задачи, посвященные управлению тепловым состоянием конструкций [6, 7], а также разработке и оптимизации их тепловой защиты [8–10]. Среди множества возможных направлений повышения эффективности теплозащиты можно выделить направление, связанное с подбором геометрических характеристик защищаемого объекта при условии неизменности теплофизических характеристик его материала и внешнего теплового воздействия. В 1970 вышла в некотором смысле базовая работа [9], посвященная этому направлению. В ней получено достаточное условие существования оптимальной толщины стенки, которая с одной стороны омывается средой постоянной температуры с постоянным же коэффициентом теплоотдачи, а с другой – подвержена локальному нагреву тепловым потоком с интенсивностью гауссовского типа. В качестве критерия оптимальности использовалось минимальное по толщине стенки значение установившейся температуры наиболее нагретой точки на поверхности стенки.

Работа [9] привела к появлению серии работ [10–14], посвященных обобщению рассмотренной задачи. Указанные обобщения можно условно разделить на два направления, первое из которых связано с модификацией допущений о теплофизических свойствах материала стенки [10–13], а второе – с изменением предположений о характере внешнего теплового воздействия на рассматриваемую стенку [12–14]. При этом во всех указанных работах использовался сходный критерий оптимальности, минимизирующий установившуюся температуру либо в наиболее нагретой точке стенки, либо в наиболее нагретой точке на ее защищаемой поверхности.

В [10] принято допущение о различии коэффициентов теплопроводности материала стенки в осевом и тангенциальном направлениях; в [12, 13] предполагалось наличие теплозащитного покрытия на поверхности стенки, которая подвержена воздействию теплового потока, а в [11] рассматривался случай, когда материал стенки обладает анизотропией свойств общего вида.

Модификация предположений о характере внешнего теплового воздействия заключалась в рассмотрении осесимметричных потоков (гауссовского типа или кольцевых постоянной интенсивности), функционирующих в импульсно-периодических режимах [12–14], при этом в [13, 14] предполагался теплообмен со средой не только на защищаемой поверхности стенки, но и на той ее поверхности, которая подвержена воздействию теплового потока.

Среди множества неисследованных на сегодняшний день сочетаний внешнего теплового воздействия и предположений о теплофизических характеристиках материала разделительной стенки для рассмотрения в настоящей работе выбран случай ортотропной стенки, разделяющей две различные среды. Одна из поверхностей стенки также подвержена воздействию постоянного во времени теплового потока с интенсивностью гауссовского типа. Основная цель проведенных исследований заключается в получении достаточного условия существования оптимальной толщины стенки, подверженной указанному тепловому воздействию.

ИСХОДНЫЕ ДОПУЩЕНИЯ И МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Для достижения основной цели исследования при построении исходной математической модели для определения стационарного температурного поля в фиксированной декартовой системе координат Oxyz предполагалось:

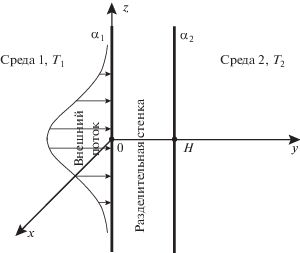
1) объект исследований моделируется ортотропной разделительной стенкой двух различных сред постоянной толщины H (рис. 1), одну из поверхностей которой будем называть внешней, а другую – внутренней;

Рис. 1.

Схема анализируемой системы.

2) внешняя поверхность стенки подвержена локальному нагреву тепловым потоком, который реализуется по закону Ньютона с постоянными коэффициентами теплоотдачи [1–5], при этом и внешняя, и внутренняя поверхности стенки участвуют в теплообмене с внешними средами, обладающими постоянными температурами;

3) коэффициент теплоотдачи на внешней (внутренней) стороне стенки равен α₁ (α₂), а температура среды – T₁ (T₂);

4) тепловой поток, воздействующий на внешнюю поверхность y = 0 объекта исследований в направлении оси Oy декартовой системы координат, является осесимметричным и обладает интенсивностью гауссовского типа [9] с определяющими параметрами Q₀ и K:

$Q(x,z) = \frac{{{{Q}_{0}}{{K}^{2}}}}{\pi }\exp [ - {{K}^{2}}({{x}^{2}} + {{z}^{2}})];$

5) главные оси тензора теплопроводности совпадают с направлениями осей используемой системы координат Oxyz, при этом коэффициенты теплопроводности в направлениях Ox и Oz совпадают;

6) температура среды на внешней поверхности стенки выше температуры среды с внутренней ее стороны (T₁ > T₂).

Допущения 1−5 позволяют представить исходную математическую модель для определения стационарного температурного поля объекта исследований в виде краевой задачи для уравнения в частных производных эллиптического типа

(1)

$\begin{gathered} \frac{\mu }{\rho }\frac{\partial }{{\partial \rho }}\left( {\rho \frac{{\partial \theta }}{{\partial \rho }}} \right) + \frac{{{{\partial }^{2}}\theta }}{{\partial {{y}^{2}}}} = 0,\,\,\,\,\rho > 0,\,\,\,\,0 < y < H, \\ {{\left. {\frac{{\partial \theta }}{{\partial y}}} \right|}_{{y = 0 + 0}}} = - \frac{{{{Q}_{0}}{{K}^{2}}}}{\pi }\exp \left( { - {{K}^{2}}{{\rho }^{2}}} \right) + Bi{{\left. {\left[ {\theta - \bar {\theta }} \right]} \right|}_{{y = 0 + 0}}}, \\ {{\left. {\frac{{\partial \theta }}{{\partial y}}} \right|}_{{y = H - 0}}} = - m{\text{Bi}}{{\left. \theta \right|}_{{y = H - 0}}}, \\ \end{gathered} $

при записи которой использованы следующие обозначения:

$\begin{gathered} \theta = \frac{{T - {{T}_{2}}}}{{{{T}_{2}}}},\,\,\,\,\mu = \frac{{{{\lambda }_{{11}}}}}{{{{\lambda }_{{22}}}}},\,\,\,\,\rho = \sqrt {{{x}^{2}} + {{z}^{2}}} , \\ x = \frac{X}{l},\,\,\,\,y = \frac{Y}{l},\,\,\,\,z = \frac{Z}{l},\,\,\,\,H = \frac{h}{l},\,\,\,\,m = \frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}}}}, \\ {\text{Bi}} = \frac{{{{\alpha }_{1}}l}}{{{{\lambda }_{{22}}}}},\,\,\,\,\bar {\theta } = \frac{{{{T}_{1}} - {{T}_{2}}}}{{{{T}_{2}}}}, \\ \end{gathered} $

где λ₁₁ − коэффициент теплопроводности материала стенки вдоль осей Ox и Oz, λ₂₂–коэффициент теплопроводности вдоль оси Oy, l − используемая единица масштаба пространственных переменных X, Y, Z (при проведении вычислительных экспериментов использовалось значение l = = 100 мм). При этом с учетом допущения 6 безразмерная константа $\bar {\theta } > 0.$

ТЕМПЕРАТУРНОЕ ПОЛЕ

Согласно сделанным допущениям, все определяющие параметры модели (1) обладают симметрией относительно оси Oy, поэтому в силу очевидных физических соображений можно считать, что искомое решение соответствующей задачи зависит лишь от пространственных переменных ρ и y. Кроме того, анализ задачи (1) позволяет сделать вывод о том, что искомое температурное поле θ(ρ, y) имеет аддитивную структуру

(2)

$\theta = {{\theta }_{1}} + {{\theta }_{2}},$

где функционал θ₁(ρ, y) является решением задачи

(3)

$\begin{gathered} \frac{\mu }{\rho }\frac{\partial }{{\partial \rho }}\left( {\rho \frac{{\partial {{\theta }_{1}}}}{{\partial \rho }}} \right) + \frac{{{{\partial }^{2}}{{\theta }_{1}}}}{{\partial {{y}^{2}}}} = 0,\,\,\,\,\rho > 0,\,\,\,\,0 < y < H, \\ {{\left. {\frac{{\partial {{\theta }_{1}}}}{{\partial y}}} \right|}_{{y = 0 + 0}}} = Bi{{\left. {\left[ {{{\theta }_{1}} - \bar {\theta }} \right]} \right|}_{{y = 0 + 0}}}, \\ {{\left. {\frac{{\partial {{\theta }_{1}}}}{{\partial y}}} \right|}_{{y = H - 0}}} = - m{\text{Bi}}{{\left. {{{\theta }_{1}}} \right|}_{{y = H - 0}}}, \\ \end{gathered} $

а функционал θ₂(ρ, y) соответственно является решением задачи

(4)

$\begin{gathered} \frac{\mu }{\rho }\frac{\partial }{{\partial \rho }}\left( {\rho \frac{{\partial {{\theta }_{2}}}}{{\partial \rho }}} \right) + \frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{y}^{2}}}} = 0,\,\,\,\,\rho > 0,\,\,\,0 < y < H, \\ {{\left. {\frac{{\partial {{\theta }_{2}}}}{{\partial y}}} \right|}_{{y = 0 + 0}}} = - \frac{{{{Q}_{0}}{{K}^{2}}}}{\pi }\exp \left( { - {{K}^{2}}{{\rho }^{2}}} \right) + Bi{{\left. {{{\theta }_{2}}} \right|}_{{y = 0 + 0}}}, \\ {{\left. {\frac{{\partial {{\theta }_{2}}}}{{\partial y}}} \right|}_{{y = H - 0}}} = - m{\text{Bi}}{{\left. {{{\theta }_{2}}} \right|}_{{y = H - 0}}}, \\ {{\left. {{{\theta }_{2}}(\rho ,y)} \right|}_{{y \in [0;H]}}} \in {{L}^{2}}[0, + \infty ), \\ \end{gathered} $

последнее условие которой показывает, что при каждом фиксированном значении $y \in [0,H]$ функция θ₂(ρ, y) интегрируема с квадратом по $\rho \in [0, + \infty ).$ С физической точки зрения декомпозиция задачи (1) означает, что искомое температурное поле θ(ρ, y) является суперпозицией полей θ₁(ρ, y) и θ₂(ρ, y), первое из которых описывает температурное состояние объекта исследований в случае его нагрева средой с температурой $\bar {\theta }$ с внешней стороны и охлаждения средой с нулевой температурой с внутренней стороны. Функционал θ₂(ρ, y) описывает температурное состояние объекта исследований в случае его нагрева тепловым потоком гауссовского типа с внешней стороны и охлаждения средой с внутренней.

Физическая интерпретация модели (3) также позволяет сделать вывод о том, что функционал θ₁ фактически не зависит от переменной ρ, т.е. θ₁(ρ, y) ≡ θ₁(y), поэтому он является решением краевой задачи

$\begin{gathered} \frac{{{{d}^{2}}{{\theta }_{1}}}}{{d{{y}^{2}}}} = 0,\,\,\,\,0 < y < H,\,\,\,\,{{\left. {\frac{{d{{\theta }_{1}}}}{{dy}}} \right|}_{{y = 0}}} = {\text{Bi}}\left[ {{{\theta }_{1}}(0) - \bar {\theta }} \right], \\ {\kern 1pt} {{\left. {\frac{{d{{\theta }_{1}}}}{{dy}}} \right|}_{{y = H}}} = - m{\text{Bi}}{{\theta }_{1}}(H) \\ \end{gathered} $

для обыкновенного линейного дифференциального уравнения второго порядка и может быть найден стандартными методами [15]:

(5)

${{\theta }_{1}}(\rho ,y) = \frac{{\bar {\theta }}}{{m{\text{Bi}}H + m + 1}}\left[ { - m\operatorname{Bi} y + mBiH + 1} \right].$

Для решения задачи (4) заметим, что, согласно ее последнему условию, при каждом фиксированном значении $y \in [0,H]$ функционал θ₂(ρ, y) как скалярная функция пространственной переменной ρ является оригиналом интегрального преобразования Ганкеля нулевого порядка [16], задаваемого парой операторов:

(6)

${{H}_{0}}[\centerdot ] \equiv \int\limits_0^\infty {\centerdot \,{{J}_{0}}(p\rho ){\kern 1pt} \rho d\rho } ,\,\,\,\,H_{0}^{{ - 1}}[\centerdot ] \equiv \int\limits_0^\infty {\centerdot \,{{J}_{0}}(p\rho ){\kern 1pt} p{\kern 1pt} dp,} $

где J₀ − функция Бесселя нулевого порядка [15]. Полагая

$\Theta (p,y) \triangleq {{H}_{0}}[{{\theta }_{2}}(\rho ,y)],$

с использованием стандартных свойств интегрального преобразования Ганкеля [16] и соответствующих ему таблиц “оригинал–изображение” [17] в пространстве изображений интегрального преобразования (6) представим задачу (4) в виде

(7)

$\begin{gathered} \frac{{{{d}^{2}}\Theta }}{{d{{y}^{2}}}} - \mu {{p}^{2}}\Theta = 0,\,\,\,\,0 < y < H, \\ {{\left. {\frac{{d\Theta }}{{dy}}} \right|}_{{y = 0}}} = - \frac{{{{Q}_{0}}}}{{2\pi }}\exp \left( { - \frac{{{{p}^{2}}}}{{4{{K}^{2}}}}} \right) + Bi{{\left. \Theta \right|}_{{y = 0}}}, \\ {{\left. {\frac{{d\Theta }}{{dy}}} \right|}_{{y = H}}} = - m{\text{Bi}}{{\left. \Theta \right|}_{{y = H}}}. \\ \end{gathered} $

Задача (7) является краевой задачей для обыкновенного линейного дифференциального уравнения второго порядка, решение которой также может быть найдено с использованием стандартных методов [15]:

(8)

$\begin{gathered} \Theta (p,y) = \frac{1}{{2\pi }}\frac{{{{Q}_{0}}\exp \left( {{{ - {{p}^{2}}} \mathord{\left/ {\vphantom {{ - {{p}^{2}}} {4{{K}^{2}}}}} \right. \kern-0em} {4{{K}^{2}}}}} \right)}}{{{\text{Bi}}p\sqrt \mu (m + 1){\text{ch}}\left( {p\sqrt \mu H} \right) + \left( {m{\text{B}}{{{\text{i}}}^{2}} + {{p}^{2}}\mu } \right){\text{sh}}\left( {p\sqrt \mu H} \right)}} \times \\ \\ \times \,\,\left\{ {\left[ {p\sqrt \mu \operatorname{ch} \left( {p\sqrt \mu H} \right) + m\operatorname{Bi} \operatorname{sh} \left( {p\sqrt \mu H} \right)} \right]\operatorname{ch} \left( {p\sqrt \mu y} \right) - } \right. \\ - \,\,\left. {\left[ {p\sqrt \mu \operatorname{sh} \left( {p\sqrt \mu H} \right) + m\operatorname{Bi} \,ch\left( {p\sqrt \mu H} \right)} \right]\operatorname{sh} \left( {p\sqrt \mu y} \right)} \right\}. \\ \end{gathered} $

Применяя к (8) обратное преобразование Ганкеля нулевого порядка (6), получаем искомое решение задачи (4):

(9)

$\begin{gathered} {{\theta }_{2}}(\rho ,y) = \frac{{{{Q}_{0}}}}{{2\pi }}\mathop \smallint \limits_0^\infty \frac{{p\exp \left( {{{ - {{p}^{2}}} \mathord{\left/ {\vphantom {{ - {{p}^{2}}} {4{{K}^{2}}}}} \right. \kern-0em} {4{{K}^{2}}}}} \right){{J}_{0}}(p\rho )}}{{\operatorname{Bi} p\sqrt \mu (m + 1)ch\left( {p\sqrt \mu H} \right) + \left( {m{\text{B}}{{{\text{i}}}^{2}} + {{p}^{2}}\mu } \right)\operatorname{sh} \left( {p\sqrt \mu H} \right)}} \times \\ \times \,\,\left\{ {\left[ {p\sqrt \mu \operatorname{ch} \left( {p\sqrt \mu H} \right) + m\operatorname{Bi} \operatorname{sh} \left( {p\sqrt \mu H} \right)} \right]\operatorname{ch} \left( {p\sqrt \mu y} \right) - } \right. \\ {\kern 1pt} - \,\,\left. {\left[ {p\sqrt \mu sh\left( {p\sqrt \mu H} \right) + m\operatorname{Bi} \,ch\left( {p\sqrt \mu H} \right)} \right]sh\left( {p\sqrt \mu y} \right)} \right\}dp. \\ \end{gathered} $

Таким образом, принимая во внимание соотношения (2), (5), (9), можно утверждать, что решение исходной задачи (1), определяющее стационарное температурное поле объекта исследований, найдено.

УСЛОВИЯ ОПТИМАЛЬНОСТИ

Согласно исходным предположениям о структуре тензора теплопроводности рассматриваемой ортотропной стенки, а также о характере теплового потока и соотношении температур среды на внешней и внутренней ее поверхностях, можно утверждать, что наиболее нагретой точкой объекта исследований является точка с декартовыми координатами (0, 0, 0). В соответствии с (2), (5), (9) значение температурного поля в этой точке составляет

(10)

${{\theta }_{0}}(H) \triangleq \theta {\kern 1pt} (0,0,0) = {{\theta }_{1}}(H) + {{\theta }_{2}}(H),$

где

(11)

$\begin{gathered} {{\theta }_{1}}(H) \triangleq {{\left. {{{\theta }_{1}}} \right|}_{{\rho = 0,\,y = 0}}} = \left( {1 - \frac{m}{{m\operatorname{Bi} H + m + 1}}} \right)\bar {\theta }, \\ {{\theta }_{2}}(H) \triangleq {{\left. {{{\theta }_{2}}} \right|}_{{\rho = 0,\,y = 0}}} = \frac{{{{Q}_{0}}}}{{2\pi }}\int\limits_0^\infty {\frac{{p\exp \left( {{{ - {{p}^{2}}} \mathord{\left/ {\vphantom {{ - {{p}^{2}}} {4{{K}^{2}}}}} \right. \kern-0em} {4{{K}^{2}}}}} \right)\left[ {p\sqrt \mu \operatorname{ch} \left( {p\sqrt \mu H} \right) + m\operatorname{Bi} \operatorname{sh} \left( {p\sqrt \mu H} \right)} \right]}}{{\operatorname{Bi} p\sqrt \mu (m + 1)ch\left( {p\sqrt \mu H} \right) + \left( {m{{{\operatorname{Bi} }}^{2}} + {{p}^{2}}\mu } \right)\operatorname{sh} \left( {p\sqrt \mu H} \right)}}{\kern 1pt} {\kern 1pt} dp} . \\ \end{gathered} $

Для нахождения условий существования толщины H_opt рассматриваемой ортотропной стенки, которая удовлетворяет сформулированному выше критерию оптимальности (минимальная температура наиболее нагретой точки), воспользуемся тем, что достаточным условием существования глобального минимума непрерывно дифференцируемой на $[0,\, + {\kern 1pt} \infty )$ функции θ₀(H) является одновременное выполнение условий

(12)

$\begin{gathered} \mathop {\lim }\limits_{H \to 0 + 0} \frac{{d{{\theta }_{0}}(H)}}{{dH}} < 0, \\ \left( {\exists \tilde {H} > 0} \right)\left( {\forall H > \tilde {H}} \right)\left( {\frac{{d{{\theta }_{0}}(H)}}{{dH}} > 0} \right). \\ \end{gathered} $

Не останавливаясь на обосновании возможности дифференцирования по параметру под знаком интеграла, заметим, что с использованием соотношений (10), (11) и известных свойств гиперболических функций [18] можно записать

(13)

$\begin{gathered} \frac{{d{{\theta }_{0}}(H)}}{{dH}} = \frac{{{{m}^{2}}\operatorname{Bi} }}{{{{{\left( {m\operatorname{Bi} H + m + 1} \right)}}^{2}}}}\bar {\theta } + \frac{{{{Q}_{0}}\mu }}{{2\pi }}\int\limits_0^\infty {\exp \left( {{{ - {{p}^{2}}} \mathord{\left/ {\vphantom {{ - {{p}^{2}}} {4{{K}^{2}}}}} \right. \kern-0em} {4{{K}^{2}}}}} \right)} \times \\ \times \,\,\frac{{{{p}^{3}}\left( {{{m}^{2}}{{{\operatorname{Bi} }}^{2}} - {{p}^{2}}\mu } \right){\kern 1pt} {\kern 1pt} dp}}{{{{{\left[ {p\sqrt \mu \operatorname{Bi} (m + 1)ch\left( {p\sqrt \mu H} \right) + \left( {m{{{\operatorname{Bi} }}^{2}}\, + {{p}^{2}}\mu } \right)\operatorname{sh} \left( {p\sqrt \mu H} \right)} \right]}}^{{{\kern 1pt} 2}}}}}. \\ \end{gathered} $

Из полученного соотношения следует

$\begin{gathered} \mathop {\lim }\limits_{H \to 0 + 0} \frac{{d{{\theta }_{0}}(H)}}{{dH}} = \frac{{{{m}^{2}}\operatorname{Bi} \bar {\theta }}}{{{{{(m + 1)}}^{2}}}} + \frac{{{{Q}_{0}}}}{{2\pi {{{\operatorname{Bi} }}^{2}}{{{(m + 1)}}^{2}}}} \times \\ \times \,\,\int\limits_0^\infty {p\left( {{{m}^{2}}{{{\operatorname{Bi} }}^{2}} - {{p}^{2}}\mu } \right)\exp \left( {{{ - {{p}^{2}}} \mathord{\left/ {\vphantom {{ - {{p}^{2}}} {4{{K}^{2}}}}} \right. \kern-0em} {4{{K}^{2}}}}} \right){\kern 1pt} dp} = \\ = \frac{{{{m}^{2}}\operatorname{Bi} \bar {\theta }}}{{{{{(m + 1)}}^{2}}}} + \frac{{{{Q}_{0}}{{K}^{2}}}}{{2\pi {{{\operatorname{Bi} }}^{2}}{{{(m + 1)}}^{2}}}}\left[ {2{{m}^{2}}{{{\operatorname{Bi} }}^{2}} - 8\mu {{K}^{2}}} \right], \\ \end{gathered} $

где для вычисления несобственного интеграла использована стандартная техника сведения его к интегралу Пуассона [18, 19]. Таким образом, для обеспечения первого из условий (12) достаточно выполнения неравенства

$\frac{{{{m}^{2}}\operatorname{Bi} \bar {\theta }}}{{{{{(m + 1)}}^{2}}}} + \frac{{{{Q}_{0}}{{K}^{2}}}}{{2\pi {{{\operatorname{Bi} }}^{2}}{{{(m + 1)}}^{2}}}}\left[ {2{{m}^{2}}{{{\operatorname{Bi} }}^{2}} - 8\mu {{K}^{2}}} \right] < 0$

или эквивалентного ему неравенства

(14)

$\mu > \frac{{{{m}^{2}}{{{\operatorname{Bi} }}^{2}}}}{{4{{K}^{2}}}}\left[ {1 + \frac{{\pi \bar {\theta }\operatorname{Bi} }}{{{{Q}_{0}}{{K}^{2}}}}} \right].$

Чтобы сформулировать достаточные условия выполнения второго из соотношений (12), заметим, что из равенства (13) при $H \to + \infty $ следует

(15)

$\frac{{d{{\theta }_{0}}(H)}}{{dH}}\sim \,\frac{{\bar {\theta }}}{{\operatorname{Bi} {{H}^{2}}}} + \frac{{2\mu {{Q}_{0}}I(H)}}{\pi },$

где интеграл

$\begin{gathered} I(H) \triangleq \int\limits_0^\infty {\exp \left( { - 2pH\sqrt \mu } \right)\exp \left( { - \frac{{{{p}^{2}}}}{{4{{K}^{2}}}}} \right)} \times \\ \times \,\,\frac{{{{p}^{3}}\left( {{{m}^{2}}{{{\operatorname{Bi} }}^{2}} - {{p}^{2}}\mu } \right){\kern 1pt} {\kern 1pt} dp}}{{{{{\left[ {p\sqrt \mu \operatorname{Bi} \left( {m + 1} \right) + \left( {m{{{\operatorname{Bi} }}^{2}} + {{p}^{2}}\mu } \right)} \right]}}^{{\,2}}}}} \\ \end{gathered} $

заменой переменной интегрирования $t = p\sqrt \mu $ приводится к виду

$\begin{gathered} I(H) = \frac{1}{{{{\mu }^{2}}}}\int\limits_0^\infty {\exp \left( { - 2Ht} \right)\exp } \left( { - \frac{{{{t}^{2}}}}{{4\mu {{K}^{2}}}}} \right) \times \\ \times \,\,\frac{{{{t}^{3}}\left( {m\operatorname{Bi} - t} \right)\,dt}}{{{{{\left( {t + \operatorname{Bi} } \right)}}^{2}}\left( {t + m\operatorname{Bi} } \right)}}. \\ \end{gathered} $

Из цепочки соотношений

следует, что при $H \to + \infty $ функция I(H) имеет не менее чем четвертый порядок малости относительно ${1 \mathord{\left/ {\vphantom {1 H}} \right. \kern-0em} H},$ поэтому при достаточно больших значениях H знак производной ${{d{{\theta }_{0}}(H)} \mathord{\left/ {\vphantom {{d{{\theta }_{0}}(H)} {dH}}} \right. \kern-0em} {dH}}$ совпадает со знаком первого слагаемого в правой части (15), имеющего относительно ${1 \mathord{\left/ {\vphantom {1 H}} \right. \kern-0em} H}$ лишь второй порядок малости. Это означает, что второе из условий (12) выполняется всегда вне зависимости от значений определяющих параметров задачи.

Таким образом, неравенство (14) задает достаточное условие существования оптимальной толщины ортотропной стенки, обе стороны которой участвуют в теплообмене с внешней средой, а одна из сторон еще и подвержена нагреву осесимметричным тепловым потоком с интенсивностью гауссовского типа.

ЗАКЛЮЧЕНИЕ

Анализ неравенства (14), связывающего теплофизические характеристики ортотропного материала стенки и характеристики внешнего теплового воздействия, позволяет сделать следующие выводы о влиянии определяющих параметров задачи на существование оптимальной толщины рассматриваемой стенки:

1) увеличение параметра μ, характеризующееся более интенсивным переносом в радиальном направлении тепловой энергии от окрестности наиболее нагретой точки стенки к ее периферии, ассоциируется с существованием рассматриваемой оптимальной толщины;

2) увеличение параметра Q₀, означающее рост суммарной мощности теплового потока, воздействующего на внешнюю поверхность стенки, и увеличение параметра К, характерное для высокой концентрации потока в окрестности наиболее нагретой точки стенки, также ассоциируются с существованием ее оптимальной толщины;

3) увеличение параметров m, Bi, $\bar {\theta }$, характеризующее рост интенсивности теплообмена со средой как на внешней, так и на внутренней поверхностях объекта исследований, напротив, приводит к тому, что значения H_opt толщины рассматриваемой стенки, удовлетворяющего сформулированному критерию оптимальности, не существует;

4) теплообмен со средой на внешней поверхности объекта исследований, представляющий одно из существенных отличий настоящей работы от [11], оказывает такое же влияние на существование оптимальной толщины стенки, как и теплообмен со средой на ее внутренней поверхности: его интенсификация ассоциируется с тем, что оптимального значения толщины не существует;

5) два вида теплового воздействия – нагрев потоком и теплообмен со средой по закону Ньютона, рассмотренные в настоящей работе, оказывают противоположное влияние на существование оптимального значения толщины рассматриваемой стенки: рост интенсивности теплового потока ассоциируется с существованием такого значения, а интенсификация теплообмена со средой как на внешней, так и на внутренней поверхностях объекта исследований – с его отсутствием;

6) выводы 1–4 допускают понятную физическую интерпретацию и в известной мере согласуются с аналогичными выводами [9–14].

Дадим физическую интерпретацию полученных результатов. Так, анализ выражения (11) для θ₁(H) показывает, что в отсутствие воздействия теплового потока на внешнюю поверхность стенки рост ее толщины Н приводит к монотонному росту температуры наиболее нагретой точки – оптимальное значение толщины не существует. С физической точки зрения это означает, что увеличение толщины стенки приводит к снижению интенсивности процесса теплопередачи от ее внешней стороны к внутренней, что сопровождается аккумулированием тепловой энергии материалом стенки и, как следствие, ростом температуры наиболее нагретой точки. Характерно, что интенсивность этого процесса переноса тепловой энергии не изменяется в радиальном направлении при удалении от оси Oy и во всех областях пластины теплопередача происходит лишь в направлении этой оси – анизотропия свойств материала не оказывает влияния на процесс.

При наличии в этой системе теплового потока гауссовского типа, воздействующего на внешнюю поверхность пластины, внешнее тепловое воздействие становится неравномерным, вследствие чего в материале пластины возникает теплоперенос в радиальном направлении. Если этот процесс достаточно интенсивен, то значимая часть тепловой энергии будет отводиться от наиболее нагретой точки объекта исследований к его периферии. При этом рост толщины пластины будет сопровождаться ростом ее теплоемкости, что ассоциируется со снижением температуры наиболее нагретой точки.

Таким образом, толщина H пластины играет в изучаемом процессе двоякую роль: ее рост, с одной стороны, нивелирует воздействие теплового потока, а с другой – подчеркивает воздействие нагрева средой. По этой причине в некоторых условиях можно ожидать существования таких значений толщины стенки, при которых два этих процесса будут уравновешивать друг друга, что будет сопровождаться минимизацией температуры ее наиболее нагретой точки.

Указанные условия могут сформироваться в случае достаточно интенсивного переноса тепловой энергии к периферии системы, что, с одной стороны, ассоциируется с ростом параметра μ, а с другой – с увеличением коэффициента фокусировки К, сопровождающимся ростом степени неравномерности теплового воздействия внешнего потока. Эти результаты полностью соответствуют выводам 1–4 о влиянии определяющих параметров задачи на существование оптимальной толщины рассматриваемой стенки и подтверждаются приведенными ниже результатами вычислительных экспериментов.

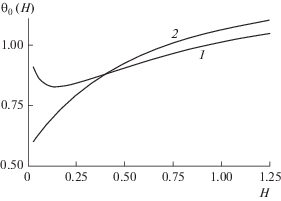
Для анализа качества условия (14) была проведена серия вычислительных экспериментов, результаты которых позволяют утверждать, что это достаточное условие является довольно точным (“почти необходимым”), т.е. его невыполнение приводит к тому, что оптимального значения толщины рассматриваемой стенки не существует. На рис. 2 приведены некоторые результаты расчетов зависимости температуры θ₀ наиболее нагретой точки стенки от ее толщины H для Q₀ = π, K = 2, $\bar {\theta } = 1$. При этом кривая 1 построена для значений Bi = 1, µ = 2, m = 2 (условие (14) выполнено), а кривая 2 – для Bi = 2, µ = 1.5, m = 2.5 (условие (14) не выполнено).

Рис. 2.

Зависимость нормированной температуры θ₀ наиболее нагретой точки стенки от ее нормированной толщины H в случае существования оптимального значения толщины (1) и ее отсутствия (2).

Таким образом, для ортотропной разделительной стенки двух различных сред, одна из поверхностей которой подвержена локальному нагреву внешним тепловым потоком с интенсивностью гауссовского типа, впервые получено достаточное условие существования оптимальной толщины, проведено качественное и количественное исследование влияния определяющих параметров задачи на существование такой толщины, с использованием вычислительного эксперимента установлена точность сформулированного достаточного условия. Полученные результаты могут быть использованы при проектировании и оптимизации элементов тепловой защиты конструкций.

Список литературы

Карслоу Е., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 488 с.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М.: Высшая школа, 2001. 550 с.
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М.: URSS, 2012. 653 с.
Формалев В.Ф. Теплопроводность анизотропных тел. Аналитические методы решения задач. М.: Физматлит, 2014. 312 с.
Бутковский А.Г., Малый С.А., Андреев Ю.Н. Оптимальное управление нагревом металлов. М.: Металлургия, 1972. 439 с.
Егоров А.И. Оптимальное управление нестационарными тепловыми и диффузионными процессами. М.: Наука, 1978. 463 с.
Зарубин В.С. Расчет и оптимизация теплоизоляции. М.: Энергоатомиздат, 1991. 192 с.
Зарубин В.С. Оптимальная толщина охлаждаемой стенки, подверженной местному нагреву // Изв. вузов. Машиностроение. 1970. № 10. С. 18.
Зарубин В.С., Котович А.В., Кувыркин Г.Н. Оптимальная толщина анизотропного покрытия на охлаждаемой стенке при локальном внешнем нагреве // Изв. РАН. Энергетика. 2014. № 5. С. 45.
Аттетков А.В., Власов П.А., Волков И.К. Условие существования оптимальной толщины охлаждаемой стенки, подверженной локальному тепловому воздействию // ТВТ. 2018. Т. 56. № 3. С. 407.
Аттетков А.В., Волков И.К., Тверская Е.С. Оптимальная толщина охлаждаемой стенки с покрытием, подверженной импульсно-периодическому нагреву // ИФЖ. 2001. Т. 74. № 6. С. 82.
Аттетков А.В., Волков И.К., Тверская Е.С. Оптимальная толщина охлаждаемой стенки с покрытием при локальном импульсно-периодическом нагреве // ТВТ. 2005. Т. 43. № 3. С. 466.
Аттетков А.В., Волков И.К., Тверская Е.С. Оптимальная толщина охлаждаемой стенки при локальном импульсно-периодическом нагреве // ИФЖ. 2005. Т. 78. № 2. С. 16.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969. 424 с.
Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. М.: Изд-во МГТУ им. Н.Э. Баумана, 1996. 228 с.
Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. Преобразования Фурье, Лапласа, Меллина. М.: Наука, 1969. 344 с.
Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. М.: Наука; Физматлит, 1998. 608 с.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. 1108 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал