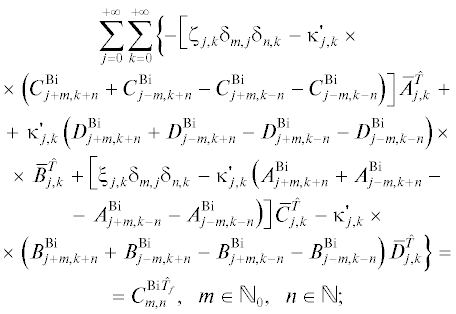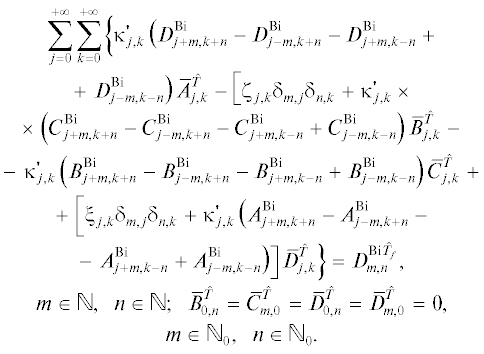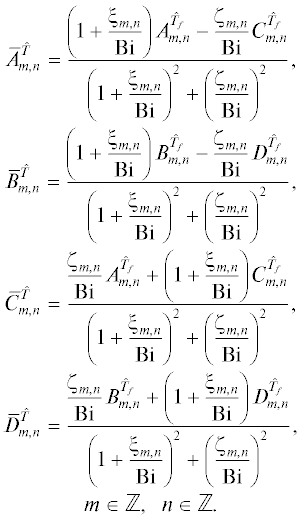1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 57, № 5, 2019

Теплофизика высоких температур, 2019, T. 57, № 5, стр. 713-726

Колебания температуры полупространства при пространственно-неоднородных условиях теплообмена

М. И. Супельняк *

Калужский филиал Московского государственного технического университета им. Н.Э. Баумана
Калуга, Россия

* E-mail: max2901@mail.ru

Поступила в редакцию 12.03.2019
После доработки 15.05.2019
Принята к публикации 16.05.2019

Полный текст (PDF)

Аннотация

Рассмотрена нестационарная двумерная задача теплопроводности без начального условия для полупространства при граничных условиях I, II и III рода. Предполагается, что краевые функции, в том числе коэффициент теплоотдачи, являются периодическими функциями времени и пространственной переменной. Найдены циклические решения задачи в виде двойных тригонометрических рядов Фурье. На ряде конкретных примеров показано применение полученных зависимостей. Исследованы условия, при которых возможно использование квазиодномерных решений.

ВВЕДЕНИЕ

На практике часто встречаются задачи, связанные с циклическим изменением температуры элементов и деталей конструкций. К ним относятся рабочие лопатки газовых турбин, элементы двигателей внутреннего сгорания, насадки регенеративных теплообменных аппаратов, стены зданий и сооружений и т.д. Известно [1], что с удалением от твердой поверхности вглубь тела колебания температуры затухают. При достаточно высокой частоте процесса затухание колебаний температуры с увеличением глубины происходит так интенсивно, что они оказываются существенными лишь в тонком поверхностном слое тела, называемом термическим. В таких случаях для исследования тепловых волн обычно используется модель полупространства, для которого решается нестационарная одномерная задача теплопроводности. В тех задачах, где необходимо учесть влияние кривизны поверхности твердого тела на колебания температуры в термическом слое, решается нестационарная одномерная задача теплопроводности для цилиндра, шара, пространства с цилиндрическим каналом или пространства со сферической полостью. Классические решения одномерных циклических задач теплопроводности приведены в [2].

Колебания температуры вызывают в твердом теле термоциклические напряжения, которые могут достигать больших величин и влиять на его прочность. При малых колебаниях температуры термоциклические напряжения являются упругими, поэтому они могут привести к многоцикловому усталостному разрушению материала. Упругие термические напряжения определяются из решения задачи термоупругости, в рамках которой интегрируются уравнения теории теплопроводности и теории упругости. Строго говоря, поле температуры не только влияет на напряженно-деформированное состояние, но и само зависит от его изменения, однако обычно эффект связанности мал и влиянием напряженно-деформированного состояния на поле температуры можно пренебречь. Также обычно не учитываются инерционные эффекты. В таком случае термические напряжения определяются из решения несвязанной квазистатической задачи термоупругости. Поскольку в такой постановке задача теплопроводности решается независимо от задачи теории упругости, то для расчета термических напряжений необходимо первоначально определить поле температуры.

Современные исследования волновых процессов теплопроводности [3–8] связаны с использованием более совершенных моделей переноса теплоты в твердом теле. В то же время остается ряд нерешенных актуальных вопросов, которые могут быть исследованы в рамках классической феноменологии Фурье. В частности, до конца не изучено, при каких условиях допустимо использовать одномерные модели для расчета колебаний температуры и термоциклических напряжений в термическом слое. Открытыми остаются вопросы о влиянии пространственной неоднородности кривизны поверхности тела, определяющей его форму, и условий теплообмена на поверхности тела на колебания температуры в термическом слое. Для их разрешения целесообразно использовать такие модельные задачи теплопроводности, которые позволяют наиболее просто учесть указанные факторы и получить удобные для расчетных исследований аналитические решения. Поскольку рассматриваемые процессы являются многомерными, то простейшая задача теплопроводности, пригодная для их изучения, должна быть двумерной. Влияние пространственной неоднородности условий теплообмена на колебания температуры удобно исследовать на примере тел, имеющих постоянную кривизну поверхности. Такими телами являются полупространство, цилиндр и пространство с цилиндрическим каналом. Одномерные колебания температуры в указанных областях, имеющие место при зависящих только от времени условиях теплообмена, хорошо изучены [2]. Приняв, что условия теплообмена также изменяются вдоль поверхности, получим интересующие нас постановки задач теплопроводности. В представленной работе ищется решение соответствующей задачи теплопроводности для полупространства. Полученное решение может оказаться полезным для дальнейших исследований термоциклических напряжений в полупространстве и найти применение, например, при расчете многоцикловой термоусталостной прочности рабочих лопаток газовых турбин на участках с малой кривизной поверхности. Возможная область применения результатов работы не ограничивается только расчетами термоциклических напряжений, поскольку с периодическим изменением температуры деталей во времени в условиях пространственно неоднородного циклического теплообмена с жидкой средой связана работа двигателей внутреннего сгорания и регенеративных теплообменных аппаратов, на показатели эффективности которых могут влиять колебания температуры деталей.

Поскольку интерес представляют установившиеся колебания температуры полупространства, то будем определять его поле температуры из решения краевой задачи теплопроводности без начального условия. Теплообмен на поверхности полупространства опишем при помощи граничного условия I, II или III рода. Чтобы учесть пространственную неоднородность условий теплообмена на колебания температуры, примем, что краевые функции являются периодическими функциями пространственной переменной и времени. В таком случае установившееся поле температуры будет периодической функцией пространственной переменной и времени, что позволит представить его в виде двойного тригонометрического ряда Фурье.

В граничном условии III рода учтем зависимость коэффициента теплоотдачи от пространственной переменной и времени, которая имеет место в действительности [9]. Следует заметить, что аналитическое решение задач с переменной теплоотдачей вызывает существенные сложности математического характера. В [9, 10] дан обзор методов приближенного аналитического решения задач подобного рода. Исследуемая проблема отличается от задач, рассмотренных в [9, 10], тем, что для нее можно получить точное решение дифференциального уравнения теплопроводности в виде ряда Фурье по собственным функциям. Это позволяет в конечном итоге вывести бесконечную систему линейных алгебраических уравнений с бесчисленным множеством неизвестных для нахождения постоянных интегрирования. Подобного рода задача рассматривалась в статье [11], где искалось стационарное поле температуры в кольце при частном виде зависимости коэффициента теплоотдачи от полярного угла. Наиболее широко указанный метод применялся в работах Р.С. Минасяна, который получил решения стационарных двумерных задач теплопроводности в неподвижных [12–16] и движущихся [17, 18] областях при зависимости коэффициента теплоотдачи от одной из пространственных переменных и нестационарных одномерных задач теплопроводности при зависимости коэффициента теплоотдачи от времени [19–21]. В рассматриваемом случае, когда коэффициент теплоотдачи зависит не от одной, а от двух переменных, общая методика решения будет такой же, как и в цитируемых работах.

Прежде чем перейти к непосредственному решению задачи, укажем работы, в которых также исследовались двумерные циклические задачи теплопроводности с переменным коэффициентом теплоотдачи. В монографии [22] с помощью конечных интегральных преобразований найдены приближенные решения для полей температуры пластины и цилиндра конечной длины. Коэффициент теплоотдачи считался кусочно-постоянной функцией времени, а температура жидкости на каждом интервале времени, где теплоотдача не менялась, задавалась отдельной функцией пространственной переменной. В работах [23, 24] исследовалось двумерное поле температуры пластины и цилиндра неограниченной длины. Температура жидкости принималась постоянной, коэффициент теплоотдачи считался функцией от линейной комбинации времени и пространственной переменной. Заменой переменных задача теплопроводности сводилась к одномерной, решение которой представлялось в виде совокупности бегущих волн. Для частных случаев теплоотдачи получены приближенные решения. Для простейшего поля температуры определен соответствующий ему переменный коэффициент теплоотдачи.

Недостатком указанных работ применительно к рассматриваемой задаче является то, что в них приведены частные случаи теплоотдачи, а найденные приближенные решения имеют ограниченную общность. Кроме того, при проведении исследований авторы преследовали цели, отличные от тех, что поставлены в представленной работе.

РЕШЕНИЕ ЗАДАЧИ

Поле температуры полупространства, не зависящее от начального условия, определяется из решения уравнения теплопроводности

(1)
$\begin{gathered} \frac{{\partial T}}{{\partial t}} = a\left( {\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}T}}{{\partial {{y}^{2}}}}} \right){\text{,}} \\ x > 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,t > - \infty {\text{.}} \\ \end{gathered} $
Здесь $T = T\left( {x,y,t} \right)$ – температура полупространства, К; x, y – пространственные координаты, м; t – время, с; a – коэффициент температуропроводности, м2/с. Интерес представляет поле температуры, периодическое по координате y и времени t. Оно должно удовлетворять условию периодичности
$\begin{gathered} T\left( {x,y + l,t} \right) = T\left( {x,y,t + \mathcal{T}} \right) = T\left( {x,y,t} \right){\text{,}} \\ x > 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,t > - \infty {\text{,}} \\ \end{gathered} $
где $l$ – пространственный период поля температуры, м; $\mathcal{T}$ – период цикла изменения температуры, c. На бесконечном удалении от поверхности полупространства температура должна подчиняться условию
$\mathop {\lim }\limits_{x \to + \infty } \frac{{\partial T}}{{\partial x}} = 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,t > - \infty {\text{,}}$
при котором
$\mathop {\lim }\limits_{x \to + \infty } \left( { - \lambda \int\limits_y^{y + l} {\frac{{\partial T}}{{\partial x}}} dy} \right) = 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,t > - \infty {\text{,}}$
т.е. обеспечивается равенство нулю теплового потока через плоскость, параллельную поверхности полупространства и бесконечно от нее удаленную. Здесь $\lambda $ – коэффициент теплопроводности, Вт/(м К). На поверхности полупространства температура должна подчиняться одному из трех граничных условий: граничному условию I рода
$T\left( {0,y,t} \right) = {{T}_{w}}{\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,t > - \infty {\text{;}}$
граничному условию II рода
$\lambda \frac{{\partial T\left( {0,y,t} \right)}}{{\partial x}} = {{q}_{w}}{\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,{\text{ }}t > - \infty {\text{;}}$
граничному условию III рода
$\begin{gathered} \lambda \frac{{\partial T\left( {0,y,t} \right)}}{{\partial x}} = \alpha \left[ {T\left( {0,y,t} \right) - {{T}_{f}}} \right]{\text{,}} \\ - \infty < y < + \infty {\text{,}}\,\,\,\,{\text{ }}t > - \infty {\text{.}} \\ \end{gathered} $
Здесь ${{T}_{w}} = {{T}_{w}}\left( {y,t} \right)$ – температура поверхности полупространства, К; ${{q}_{w}} = {{q}_{w}}\left( {y,t} \right)$ – плотность теплового потока на поверхности полупространства в направлении ее внешней нормали, Вт/м2; $\alpha = \alpha \left( {y,t} \right) > 0$ – коэффициент теплоотдачи, Вт/(м2 К); ${{T}_{f}} = {{T}_{f}}\left( {y,t} \right)$ – температура жидкой среды, К. Краевые функции, согласно постановке задачи, являются ограниченными и периодическими:
$\begin{gathered} {{T}_{w}}\left( {y + l,t} \right) = {{T}_{w}}\left( {y,t + \mathcal{T}} \right) = {{T}_{w}}\left( {y,t} \right){\text{,}} \\ - \infty < y < + \infty {\text{,}}\,\,\,\,{\text{ }}t > - \infty {\text{;}}\,\,\,\,{{q}_{w}}\left( {y + l,t} \right) = \\ = {{q}_{w}}\left( {y,t + \mathcal{T}} \right) = {{q}_{w}}\left( {y,t} \right){\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,t > - \infty {\text{;}} \\ {{T}_{f}}\left( {y + l,t} \right) = {{T}_{f}}\left( {y,t + \mathcal{T}} \right) = {{T}_{f}}\left( {y,t} \right){\text{,}} \\ - \infty < y < + \infty {\text{,}}\,\,\,\,{\text{ }}t > - \infty {\text{;}}\,\,\,\,\alpha \left( {y + l,t} \right) = \alpha \left( {y,t + \mathcal{T}} \right) = \\ = \alpha \left( {y,t} \right){\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,t > - \infty {\text{.}} \\ \end{gathered} $
Помимо этого функция ${{q}_{w}}$ удовлетворяет условию
$\int\limits_t^{t + \mathcal{T}} {\int\limits_y^{y + l} {{{q}_{w}}} } dydt = 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < y < + \infty {\text{,}}\,\,\,\,t > - \infty {\text{,}}$
согласно которому количество теплоты, подводимое к полупространству за период цикла $\mathcal{T},$ равно нулю.

Для удобства перейдем к безразмерным переменным. Введем безразмерные пространственные координаты $\hat {x} = {x \mathord{\left/ {\vphantom {x \chi }} \right. \kern-0em} \chi }{\text{,}}$ $\hat {y} = {{2\pi y} \mathord{\left/ {\vphantom {{2\pi y} {l;}}} \right. \kern-0em} {l;}}$ безразмерное время $\hat {t} = \omega t;$ параметр двумерности $\hat {l} = {l \mathord{\left/ {\vphantom {l {\left( {2\pi \chi } \right)}}} \right. \kern-0em} {\left( {2\pi \chi } \right)}};$ безразмерную температуру поверхности полупространства ${{\hat {T}}_{w}} = {{{{T}_{w}}} \mathord{\left/ {\vphantom {{{{T}_{w}}} {\Delta T_{w}^{*}}}} \right. \kern-0em} {\Delta T_{w}^{*}}};$ безразмерную плотность теплового потока на поверхности полупространства ${{\hat {q}}_{w}} = {{{{q}_{w}}} \mathord{\left/ {\vphantom {{{{q}_{w}}} {\Delta q_{w}^{*}}}} \right. \kern-0em} {\Delta q_{w}^{*}}};$ безразмерную температуру жидкости ${{\hat {T}}_{f}} = {{{{T}_{f}}} \mathord{\left/ {\vphantom {{{{T}_{f}}} {\Delta T_{f}^{*}}}} \right. \kern-0em} {\Delta T_{f}^{*}}};$ критерий Био ${\text{Bi}} = {{\alpha \chi } \mathord{\left/ {\vphantom {{\alpha \chi } \lambda }} \right. \kern-0em} \lambda };$ безразмерную температуру полупространства при граничном условии I рода $\hat {T} = {T \mathord{\left/ {\vphantom {T {\Delta T_{w}^{*}}}} \right. \kern-0em} {\Delta T_{w}^{*}}};$ безразмерную температуру полупространства при граничном условии II рода $\hat {T} = {{\lambda T} \mathord{\left/ {\vphantom {{\lambda T} {\left( {\chi \Delta q_{w}^{*}} \right)}}} \right. \kern-0em} {\left( {\chi \Delta q_{w}^{*}} \right)}};$ безразмерную температуру полупространства при граничном условии III рода $\hat {T} = {T \mathord{\left/ {\vphantom {T {\Delta T_{f}^{*}}}} \right. \kern-0em} {\Delta T_{f}^{*}}}.$ Здесь $\chi = \sqrt {{a \mathord{\left/ {\vphantom {a \omega }} \right. \kern-0em} \omega }} $ – характерный линейный размер тепловой волны, м; $\omega = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \mathcal{T}}} \right. \kern-0em} \mathcal{T}}$ – круговая частота, рад/с; $\Delta T_{w}^{*},$ $\Delta T_{f}^{*}$ – характерные размахи колебаний температуры поверхности и жидкости, К; $\Delta q_{w}^{*}$ – характерный размах колебаний плотности теплового потока, Вт/м2. Задача (1)–(6) в безразмерном виде примет следующий вид:

$\begin{gathered} \frac{{\partial{ \hat {T}}}}{{\partial{ \hat {t}}}} = \frac{{{{\partial }^{2}}\hat {T}}}{{\partial {{{\hat {x}}}^{2}}}} + \frac{1}{{{{{\hat {l}}}^{2}}}}\frac{{{{\partial }^{2}}\hat {T}}}{{\partial {{{\hat {y}}}^{2}}}}{\text{,}}\,\,\,\,\hat {x} > 0{\text{,}} \\ - \infty < \hat {y} < + \infty {\text{,\;}}\,\,\,\,\hat {t} > - \infty {\text{;}} \\ \end{gathered} $
$\begin{gathered} \hat {T}\left( {\hat {x},\hat {y} + 2\pi ,\hat {t}} \right) = \hat {T}\left( {\hat {x},\hat {y},\hat {t} + 2\pi } \right) = \hat {T}\left( {\hat {x},\hat {y},\hat {t}} \right){\text{,}} \\ \hat {x} > 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < \hat {y} < + \infty {\text{,}}\,\,\,\,\hat {t} > - \infty {\text{;}} \\ \end{gathered} $
$\mathop {\lim }\limits_{\hat {x} \to + \infty } \frac{{\partial{ \hat {T}}}}{{\partial{ \hat {x}}}} = 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < \hat {y} < + \infty {\text{,}}\,\,\,\,\hat {t} > - \infty {\text{;}}$
$\hat {T}\left( {0,\hat {y},\hat {t}} \right) = {{\hat {T}}_{w}}{\text{,}}\,\,\,\, - {\kern 1pt} \infty < \hat {y} < + \infty {\text{,}}\,\,\,\,\hat {t} > - \infty {\text{;}}$
$\frac{{\partial{ \hat {T}}\left( {0,\hat {y},\hat {t}} \right)}}{{\partial{ \hat {x}}}} = {{\hat {q}}_{w}}{\text{,}}\,\,\,\, - {\kern 1pt} \infty < \hat {y} < + \infty {\text{,}}\,\,\,\,{\text{ }}\hat {t} > - \infty {\text{;}}$
$\begin{gathered} \frac{{\partial{ \hat {T}}\left( {0,\hat {y},\hat {t}} \right)}}{{\partial{ \hat {x}}}} = {\text{Bi}}\left[ {\hat {T}\left( {0,\hat {y},\hat {t}} \right) - {{{\hat {T}}}_{f}}} \right]{\text{,}} \\ - \infty < \hat {y} < + \infty {\text{,}}\,\,\,\,\hat {t} > - \infty {\text{.}} \\ \end{gathered} $
Приведем основные обозначения, которые будем использовать в дальнейшем, на примере функции $f = f\left( {\hat {y},\hat {t}} \right),$ периодической по $\hat {y}$ и $\hat {t}$ с периодами $2\pi {\text{:}}$
$\begin{gathered} f\left( {\hat {y} + 2\pi ,\hat {t}} \right) = f\left( {\hat {y},\hat {t} + 2\pi } \right) = f\left( {\hat {y},\hat {t}} \right){\text{,}} \\ - \infty < \hat {y} < + \infty {\text{,\;}}\,\,\,\,\hat {t} > - \infty {\text{.}} \\ \end{gathered} $
Введем следующие осредненные значения f:
$\begin{gathered} \left[\kern-0.15em\left[ f \right]\kern-0.15em\right] = \frac{1}{{2\pi }}\int\limits_0^{2{\pi }} {fd\hat {y}} {\text{,}}\,\,\,\,\left\langle f \right\rangle = \frac{1}{{2\pi }}\int\limits_0^{2{\pi }} {fd\hat {t}} {\text{,}} \\ \left\langle {\left[\kern-0.15em\left[ f \right]\kern-0.15em\right]} \right\rangle = \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {fd\hat {y}d\hat {t}} } . \\ \end{gathered} $
Под размахом колебаний $f$ будем понимать функцию
$\Delta {\kern 1pt} f = \mathop {\max }\limits_{0 \leqslant \hat {t} < 2\pi } f - \mathop {\min }\limits_{0 \leqslant \hat {t} < 2\pi } f{\text{.}}$
Комплексную форму двойного тригонометрического ряда Фурье функции $f$ запишем в виде
$f = \sum\limits_{m = - \infty }^{m = + \infty } {\sum\limits_{n = - \infty }^{n = + \infty } {\mathcal{C}_{{m,n}}^{f}} } {{e}^{{i\left( {m\hat {y} + n\hat {t}} \right)}}}{\text{,}}$
где $i = \sqrt { - 1} ;$
$\mathcal{C}_{{m,n}}^{f} = \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {f{{e}^{{ - i\left( {m\hat {y} + n\hat {t}} \right)}}}} } d\hat {y}d\hat {t}{\text{.}}$
Вещественная форма двойного тригонометрического ряда Фурье функции $f$ имеет вид
$\begin{gathered} f = \frac{{A_{{0,0}}^{f}}}{4} + \frac{1}{2}\sum\limits_{m = 1}^{ + \infty } {\left[ {A_{{m,0}}^{f}\cos \left( {m\hat {y}} \right) + B_{{m,0}}^{f}\sin \left( {m\hat {y}} \right)} \right]} + \\ + \,\,\frac{1}{2}\sum\limits_{n = 1}^{ + \infty } {\left[ {A_{{0,n}}^{f}\cos \left( {n\hat {t}} \right) + C_{{0,n}}^{f}\sin \left( {n\hat {t}} \right)} \right]} + \\ + \,\,\sum\limits_{m = 1}^{ + \infty } {\sum\limits_{n = 1}^{ + \infty } {\left[ {A_{{m,n}}^{f}\cos \left( {m\hat {y}} \right)\cos \left( {n\hat {t}} \right) + } \right.} } \\ + \,\,B_{{m,n}}^{f}\sin \left( {m\hat {y}} \right)\cos \left( {n\hat {t}} \right) + C_{{m,n}}^{f}\cos \left( {m\hat {y}} \right)\sin \left( {n\hat {t}} \right) + \\ \left. { + \,\,D_{{m,n}}^{f}\sin \left( {m\hat {y}} \right)\sin \left( {n\hat {t}} \right)} \right]{\text{,}} \\ \end{gathered} $
где

$\begin{gathered} A_{{m,n}}^{f} = \frac{1}{{{{\pi }^{2}}}}\int\limits_0^{2{\pi }} {\int\limits_0^{2{\pi }} f } \cos \left( {m\hat {y}} \right)\cos \left( {n\hat {t}} \right)d\hat {y}d\hat {t}{\text{,}} \\ B_{{m,n}}^{f} = \frac{1}{{{{\pi }^{2}}}}\int\limits_0^{2{\pi }} {\int\limits_0^{2{\pi }} f } \sin \left( {m\hat {y}} \right)\cos \left( {n\hat {t}} \right)d\hat {y}d\hat {t}{\text{,}} \\ C_{{m,n}}^{f} = \frac{1}{{{{\pi }^{2}}}}\mathop \smallint \limits_0^{2{\pi }} \mathop \smallint \limits_0^{2{\pi }} f\cos \left( {m\hat {y}} \right)\sin \left( {n\hat {t}} \right)d\hat {y}d\hat {t}{\text{,}} \\ D_{{m,n}}^{f} = \frac{1}{{{{\pi }^{2}}}}\int\limits_0^{2{\pi }} {\int\limits_0^{2{\pi }} f } \sin \left( {m\hat {y}} \right)\sin \left( {n\hat {t}} \right)d\hat {y}d\hat {t}{\text{.}} \\ \end{gathered} $

Из приведенных соотношений следует, что

$\begin{gathered} \mathcal{C}_{{m,n}}^{f} = \frac{{A_{{m,n}}^{f} - iB_{{m,n}}^{f} - iC_{{m,n}}^{f} - D_{{m,n}}^{f}}}{4}{\text{,}} \\ B_{{0,n}}^{f} = C_{{m,0}}^{f} = D_{{0,n}}^{f} = D_{{m,0}}^{f} = 0{\text{,}} \\ A_{{m,n}}^{f} = A_{{ - m,n}}^{f} = A_{{m, - n}}^{f} = A_{{ - m, - n}}^{f}{\text{,}} \\ B_{{m,n}}^{f} = - B_{{ - m,n}}^{f} = B_{{m, - n}}^{f} = - B_{{ - m, - n}}^{f}{\text{,}} \\ C_{{m,n}}^{f} = C_{{ - m,n}}^{f} = - C_{{m, - n}}^{f} = - C_{{ - m, - n}}^{f}{\text{,}} \\ D_{{m,n}}^{f} = - D_{{ - m,n}}^{f} = - D_{{m, - n}}^{f} = D_{{ - m, - n}}^{f}{\text{,}} \\ A_{{m,n}}^{f} = 2\operatorname{Re} \left( {\mathcal{C}_{{m,n}}^{f} + \mathcal{C}_{{ - m,n}}^{f}} \right) = 2\operatorname{Re} \left( {\mathcal{C}_{{m,n}}^{f} + \mathcal{C}_{{m, - n}}^{f}} \right){\text{,}} \\ \end{gathered} $
$\begin{gathered} B_{{m,n}}^{f} = - 2{\text{Im}}\left( {\mathcal{C}_{{m,n}}^{f} - \mathcal{C}_{{ - m,n}}^{f}} \right) = - 2{\text{Im}}\left( {\mathcal{C}_{{m,n}}^{f} + \mathcal{C}_{{m, - n}}^{f}} \right){\text{,}} \\ C_{{m,n}}^{f} = - 2{\text{Im}}\left( {\mathcal{C}_{{m,n}}^{f} + \mathcal{C}_{{ - m,n}}^{f}} \right) = - 2{\text{Im}}\left( {\mathcal{C}_{{m,n}}^{f} - \mathcal{C}_{{m, - n}}^{f}} \right){\text{,}} \\ D_{{m,n}}^{f} = - 2\operatorname{Re} \left( {\mathcal{C}_{{m,n}}^{f} - \mathcal{C}_{{ - m,n}}^{f}} \right) = - 2\operatorname{Re} \left( {\mathcal{C}_{{m,n}}^{f} - \mathcal{C}_{{m, - n}}^{f}} \right){\text{,}} \\ m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $
Здесь $\mathbb{Z}$ – множество целых чисел.

Решение (7)–(12) будем искать в виде ряда

$\hat {T} = \sum\limits_{m = - \infty }^{m = + \infty } {\sum\limits_{n = - \infty }^{n = + \infty } {\mathcal{C}_{{m,n}}^{{\hat {T}}}} } {{e}^{{i\left( {m\hat {y} + n\hat {t}} \right)}}}{\text{.}}$

В таком случае задача сводится к отысканию коэффициентов $\mathcal{C}_{{m,n}}^{{\hat {T}}} = \mathcal{C}_{{m,n}}^{{\hat {T}}}\left( {\hat {x}} \right),$ которые определяются из решения краевой задачи

$\begin{gathered} \frac{{{{d}^{2}}\mathcal{C}_{{m,n}}^{{\hat {T}}}}}{{d{{{\hat {x}}}^{2}}}} - \left( {\frac{{{{m}^{2}}}}{{{{{\hat {l}}}^{2}}}} + in} \right)\mathcal{C}_{{m,n}}^{{\hat {T}}} = 0{\text{,}} \\ \hat {x} > 0{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{;}} \\ \end{gathered} $
$\mathop {\lim }\limits_{\hat {x} \to + \infty } \frac{{d\mathcal{C}_{{m,n}}^{{\hat {T}}}}}{{d\hat {x}}} = 0{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{;}}$
$\mathcal{C}_{{m,n}}^{{\hat {T}}}\left( 0 \right) = \mathcal{C}_{{m,n}}^{{{{{\hat {T}}}_{w}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{;}}$
$\frac{{d\mathcal{C}_{{m,n}}^{{\hat {T}}}\left( 0 \right)}}{{d\hat {x}}} = \mathcal{C}_{{m,n}}^{{{{{\hat {q}}}_{w}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{;}}$
$\begin{gathered} \frac{{d\mathcal{C}_{{m,n}}^{{\hat {T}}}\left( 0 \right)}}{{d\hat {x}}} = \sum\limits_{j = - \infty }^{j = + \infty } {\sum\limits_{k = - \infty }^{k = + \infty } {\mathcal{C}_{{m - j,n - k}}^{{{\text{Bi}}}}} } \mathcal{C}_{{j,k}}^{{\hat {T}}}\left( 0 \right) - \mathcal{C}_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}} \\ m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $

Решение (14)–(18) имеет вид

$\begin{gathered} \mathcal{C}_{{m,n}}^{{\hat {T}}} = \bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}}{{e}^{{ - \left( {{{\xi }_{{m,n}}} + i{{\zeta }_{{m,n}}}} \right)\hat {x}}}}{\text{,}} \\ \hat {x} \geqslant 0{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $

Здесь

$\begin{gathered} {{\xi }_{{m,n}}} = \frac{1}{{\sqrt 2 }}{{\left[ {{{{\left( {\frac{{{{m}^{4}}}}{{{{{\hat {l}}}^{4}}}} + {{n}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \frac{{{{m}^{2}}}}{{{{{\hat {l}}}^{2}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{;}} \\ {{\zeta }_{{m,n}}} = \frac{{{\text{sign}}n}}{{\sqrt 2 }}{{\left[ {{{{\left( {\frac{{{{m}^{4}}}}{{{{{\hat {l}}}^{4}}}} + {{n}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - \frac{{{{m}^{2}}}}{{{{{\hat {l}}}^{2}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{;}} \\ \end{gathered} $
при граничном условии (16)
$\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} = \mathcal{C}_{{m,n}}^{{{{{\hat {T}}}_{w}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{;}}$
при граничном условии (17)
$\begin{gathered} \bar {\mathcal{C}}_{{0,0}}^{{\hat {T}}} = \left\langle {\left[\kern-0.15em\left[ {\hat {T}} \right]\kern-0.15em\right]} \right\rangle {\text{;}}\,\,\,\,\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} = {{ - \mathcal{C}_{{m,n}}^{{{{{\hat {q}}}_{w}}}}} \mathord{\left/ {\vphantom {{ - \mathcal{C}_{{m,n}}^{{{{{\hat {q}}}_{w}}}}} {\left( {{{\xi }_{{m,n}}} + i{{\zeta }_{{m,n}}}} \right)}}} \right. \kern-0em} {\left( {{{\xi }_{{m,n}}} + i{{\zeta }_{{m,n}}}} \right)}}{\text{,}} \\ m \in \mathbb{Z}{\text{,\;}}\,\,\,\,\left| m \right| + \left| n \right| \in \mathbb{N}{\text{;}} \\ \end{gathered} $
при граничном условии (18) коэффициенты $\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}},$ $m \in \mathbb{Z}{\text{,}}$ $n \in \mathbb{Z}{\text{,}}$ удовлетворяют бесконечной системе линейных алгебраических уравнений с бесчисленным множеством неизвестных

$\begin{gathered} \sum\limits_{j = - \infty }^{j = + \infty } {\sum\limits_{k = - \infty }^{k = + \infty } {\left[ {\left( {{{\xi }_{{j,k}}} + i{{\zeta }_{{j,k}}}} \right){{\delta }_{{m,j}}}{{\delta }_{{n,k}}} + \mathcal{C}_{{m - j,n - k}}^{{{\text{Bi}}}}} \right]{\kern 1pt} } } \bar {\mathcal{C}}_{{j,k}}^{{\hat {T}}} = \\ = \mathcal{C}_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $

Здесь $\mathbb{N}$ – множество натуральных чисел, ${{\delta }_{{m,n}}}$ – символ Кронекера:

${{\delta }_{{m,n}}} = \left\{ {\begin{array}{*{20}{l}} {1{\text{,\;если\;}}m = n{\text{;}}} \\ {0{\text{,\;если\;}}m \ne n{\text{.}}} \end{array}} \right.$

Система (19) может быть решена приближенно методом последовательных приближений или методом редукции [25]. При решении методом редукции считаем, что

$\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} = 0{\text{,}}\,\,\,\,\left| m \right| > m*{\text{,}}\,\,\,\,\left| n \right| > n*{\text{,}}$
где $m* \in \mathbb{N},$ $n* \in \mathbb{N}.$ В таком случае вместо (19) получаем усеченную систему

$\begin{gathered} \sum\limits_{j = - m*}^{j = m*} {\sum\limits_{k = - n*}^{k = n*} {\left[ {\left( {{{\xi }_{{j,k}}} + i{{\zeta }_{{j,k}}}} \right){{\delta }_{{m,j}}}{{\delta }_{{n,k}}} + \mathcal{C}_{{m - j,n - k}}^{{{\text{Bi}}}}} \right]} } {\kern 1pt} \bar {\mathcal{C}}_{{j,k}}^{{\hat {T}}} = \\ = \mathcal{C}_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}}\,\,\,\,m = \overline { - m*,m{\text{*}}} {\text{,}}\,\,\,\,n = \overline { - n*,n{\text{*}}} {\text{.}} \\ \end{gathered} $

В частных случаях система уравнений (19) упрощается. При ${\text{Bi}} = {\text{Bi}}\left( {\hat {y}} \right)$ имеем

$\mathcal{C}_{{m,n}}^{{{\text{Bi}}}} = 0{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| n \right| \in \mathbb{N}{\text{,}}$
поэтому (19) принимает вид

$\begin{gathered} \sum\limits_{j = - \infty }^{j = + \infty } {\left[ {\left( {{{\xi }_{{j,n}}} + i{{\zeta }_{{j,n}}}} \right){{\delta }_{{m,j}}} + \mathcal{C}_{{m - j,0}}^{{{\text{Bi}}}}} \right]} {\kern 1pt} \bar {\mathcal{C}}_{{j,n}}^{{\hat {T}}} = \mathcal{C}_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}} \\ m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $

Таким образом, коэффициенты $\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}}$ с различными номерами $n$ определяются независимо друг от друга. При ${\text{Bi}} = {\text{Bi}}\left( {\hat {t}} \right)$ имеем

$\mathcal{C}_{{m,n}}^{{{\text{Bi}}}} = 0{\text{,}}\,\,\,\,\left| m \right| \in \mathbb{N}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{,}}$
поэтому (19) запишется как
$\begin{gathered} \sum\limits_{k = - \infty }^{k = + \infty } {\left[ {\left( {{{\xi }_{{m,k}}} + i{{\zeta }_{{m,k}}}} \right){{\delta }_{{n,k}}} + \mathcal{C}_{{0,n - k}}^{{{\text{Bi}}}}} \right]} {\kern 1pt} \bar {\mathcal{C}}_{{m,k}}^{{\hat {T}}} = \mathcal{C}_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}} \\ m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $
Таким образом, коэффициенты $\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}}$ с различными номерами $m$ определяются независимо друг от друга. При ${\text{Bi}} = {\text{const}}$ имеем
$\mathcal{C}_{{0,0}}^{{{\text{Bi}}}} = {\text{Bi;}}\,\,\,\,\mathcal{C}_{{m,n}}^{{{\text{Bi}}}} = 0{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| m \right| + \left| n \right| \in \mathbb{N}{\text{,}}$
что позволяет получить решение (19) в аналитически замкнутом виде
$\begin{gathered} \bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} = {{\mathcal{C}_{{m,n}}^{{{{{\hat {T}}}_{f}}}}} \mathord{\left/ {\vphantom {{\mathcal{C}_{{m,n}}^{{{{{\hat {T}}}_{f}}}}} {\left( {1 + \frac{{{{\xi }_{{m,n}}}}}{{{\text{Bi}}}} + i\frac{{{{\zeta }_{{m,n}}}}}{{{\text{Bi}}}}} \right)}}} \right. \kern-0em} {\left( {1 + \frac{{{{\xi }_{{m,n}}}}}{{{\text{Bi}}}} + i\frac{{{{\zeta }_{{m,n}}}}}{{{\text{Bi}}}}} \right)}}{\text{,}} \\ m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $
Из полученного решения задачи следует, что $\left\langle {\left[\kern-0.15em\left[ {\hat {T}} \right]\kern-0.15em\right]} \right\rangle = {\text{const}}{\text{.}}$ Постановка задачи теплопроводности с граничным условием (17) не допускает непосредственного определения величины $\left\langle {\left[\kern-0.15em\left[ {\hat {T}} \right]\kern-0.15em\right]} \right\rangle ,$ поэтому в случае необходимости нахождения $\left\langle {\left[\kern-0.15em\left[ {\hat {T}} \right]\kern-0.15em\right]} \right\rangle $ следует привлекать дополнительные сведения. Часто на практике интерес представляет не поле безразмерной температуры $\hat {T},$ а его переменная составляющая
${\hat {\theta }} = \hat {T} - \left\langle {\left[\kern-0.15em\left[ {\hat {T}} \right]\kern-0.15em\right]} \right\rangle {\text{,}}$
у которой $\left\langle {\left[\kern-0.15em\left[ {{\hat {\theta }}} \right]\kern-0.15em\right]} \right\rangle = 0.$ В ряде случаев внимание заслуживает только колебательная составляющая поля безразмерной температуры
$\hat {\vartheta } = \hat {T} - \left\langle {\hat {T}} \right\rangle {\text{,}}$
у которой $\left\langle {\hat {\vartheta }} \right\rangle = 0.$ Очевидно, что
$\begin{gathered} \mathcal{C}_{{0,0}}^{{{\hat {\theta }}}} = 0{\text{;}}\,\,\,\,\mathcal{C}_{{m,n}}^{{{\hat {\theta }}}} = \mathcal{C}_{{m,n}}^{{\hat {T}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| m \right| + \left| n \right| \in \mathbb{N}{\text{;}} \\ \mathcal{C}_{{m,0}}^{{\hat {\vartheta }}} = 0{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{;}}\,\,\,\,\mathcal{C}_{{m,n}}^{{\hat {\vartheta }}} = \mathcal{C}_{{m,n}}^{{\hat {T}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| n \right| \in \mathbb{N}{\text{.}} \\ \end{gathered} $
Обычно ${\hat {\theta }}$ используется для расчета переменных термических напряжений, а $\hat {\vartheta }$ – для расчета термоциклических напряжений. В последнем случае стационарные напряжения, вызванные изменением $\left\langle {\hat {T}} \right\rangle $ по $\hat {y},$ интереса не представляют. При решении задач теплопроводности с граничными условиями I и III рода удобно также вместо $\hat {T},$ ${{\hat {T}}_{w}}$ и ${{\hat {T}}_{f}}$ использовать безразмерные избыточные температуры

$\begin{gathered} {\hat {\Theta }} = \hat {T} - \left\langle {\left[\kern-0.15em\left[ {{{{\hat {T}}}_{w}}} \right]\kern-0.15em\right]} \right\rangle {\text{,}}\,\,\,\,{{{{\hat {\Theta }}}}_{w}} = {{{\hat {T}}}_{w}} - \left\langle {\left[\kern-0.15em\left[ {{{{\hat {T}}}_{w}}} \right]\kern-0.15em\right]} \right\rangle {\text{,}} \\ {\hat {\Theta }} = \hat {T} - \left\langle {\left[\kern-0.15em\left[ {{{{\hat {T}}}_{f}}} \right]\kern-0.15em\right]} \right\rangle {\text{,}}\,\,\,\,{{{{\hat {\Theta }}}}_{f}} = {{{\hat {T}}}_{f}} - \left\langle {\left[\kern-0.15em\left[ {{{{\hat {T}}}_{f}}} \right]\kern-0.15em\right]} \right\rangle {\text{.}} \\ \end{gathered} $

Очевидно, что

$\begin{gathered} \mathcal{C}_{{0,0}}^{{{\hat {\Theta }}}} = \left\langle {\left[\kern-0.15em\left[ {{\hat {\Theta }}} \right]\kern-0.15em\right]} \right\rangle {\text{;}}\,\,\,\,\mathcal{C}_{{m,n}}^{{{\hat {\Theta }}}} = \mathcal{C}_{{m,n}}^{{\hat {T}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| m \right| + \left| n \right| \in \mathbb{N}{\text{;}} \\ \mathcal{C}_{{m,0}}^{{{{{{\hat {\Theta }}}}_{w}}}} = 0{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{;}}\,\,\,\,\mathcal{C}_{{m,n}}^{{{{{{\hat {\Theta }}}}_{w}}}} = \mathcal{C}_{{m,n}}^{{{{{\hat {T}}}_{w}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| n \right| \in \mathbb{N}{\text{;}} \\ \mathcal{C}_{{m,0}}^{{{{{{\hat {\Theta }}}}_{f}}}} = 0{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{;}}\,\,\,\,\mathcal{C}_{{m,n}}^{{{{{{\hat {\Theta }}}}_{f}}}} = \mathcal{C}_{{m,n}}^{{{{{\hat {T}}}_{f}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| n \right| \in \mathbb{N}{\text{,}} \\ \end{gathered} $
причем для ${\text{Bi}} = {\text{var}}$ в граничном условии III рода в общем случае $\left\langle {\left[\kern-0.15em\left[ {{\hat {\Theta }}} \right]\kern-0.15em\right]} \right\rangle \ne 0.$

Полученные соотношения могут быть использованы и в частных случаях, когда поле температуры стационарное или одномерное. Если краевые функции являются стационарными, то приходим к стационарному полю температуры, для которого решение (13) принимает вид

$\hat {T} = \sum\limits_{m = - \infty }^{m = + \infty } {\mathcal{C}_{{m,0}}^{{\hat {T}}}{{e}^{{im\hat {y}}}}} {\text{.}}$

Если краевые функции не зависят от пространственной координаты $\hat {y},$ то получаем одномерное поле температуры, для которого решение (13) имеет вид

$\hat {T} = \sum\limits_{n = - \infty }^{n = + \infty } {\mathcal{C}_{{0,n}}^{{\hat {T}}}{{e}^{{in\hat {t}}}}} {\text{.}}$

Перейдем к действительной форме ряда Фурье в (13), которую можно представить в виде

$\begin{gathered} \hat {T} = \sum\limits_{m = 0}^{ + \infty } {\sum\limits_{n = 0}^{ + \infty } {{{\kappa }_{{m,n}}}} } \left[ {A_{{m,n}}^{{\hat {T}}}\cos \left( {m\hat {y}} \right)\cos \left( {n\hat {t}} \right)} \right. + \\ + \,\,B_{{m,n}}^{{\hat {T}}}\sin \left( {m\hat {y}} \right)\cos \left( {n\hat {t}} \right) + C_{{m,n}}^{{\hat {T}}}\cos \left( {m\hat {y}} \right)\sin \left( {n\hat {t}} \right) + \\ \left. { + \,\,D_{{m,n}}^{{\hat {T}}}\sin \left( {m\hat {y}} \right)\sin \left( {n\hat {t}} \right)} \right]{\text{,}} \\ \end{gathered} $
где

${{\kappa }_{{m,n}}} = {{\bar {\kappa }}_{m}}{{\bar {\kappa }}_{n}};\,\,\,\,{{\bar {\kappa }}_{j}} = {{\left( {1 + {{\delta }_{{0,j}}}} \right)}^{{ - 1}}}.$

Чтобы получить коэффициенты ряда, примем, что

$\begin{gathered} \bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} = \frac{{\bar {A}_{{m,n}}^{{\hat {T}}} - i\bar {B}_{{m,n}}^{{\hat {T}}} - i\bar {C}_{{m,n}}^{{\hat {T}}} - \bar {D}_{{m,n}}^{{\hat {T}}}}}{4}{\text{,}} \\ \bar {B}_{{0,n}}^{{\hat {T}}} = \bar {C}_{{m,0}}^{{\hat {T}}} = \bar {D}_{{0,n}}^{{\hat {T}}} = \bar {D}_{{m,0}}^{{\hat {T}}} = 0{\text{,}} \\ \bar {A}_{{m,n}}^{{\hat {T}}} = \bar {A}_{{ - m,n}}^{{\hat {T}}} = \bar {A}_{{m, - n}}^{{\hat {T}}} = \bar {A}_{{ - m, - n}}^{{\hat {T}}}{\text{,}} \\ \bar {B}_{{m,n}}^{{\hat {T}}} = - \bar {B}_{{ - m,n}}^{{\hat {T}}} = \bar {B}_{{m, - n}}^{{\hat {T}}} = - \bar {B}_{{ - m, - n}}^{{\hat {T}}}{\text{,}} \\ \bar {C}_{{m,n}}^{{\hat {T}}} = \bar {C}_{{ - m,n}}^{{\hat {T}}} = - \bar {C}_{{m, - n}}^{{\hat {T}}} = - \bar {C}_{{ - m, - n}}^{{\hat {T}}}{\text{,}} \\ \bar {D}_{{m,n}}^{{\hat {T}}} = - \bar {D}_{{ - m,n}}^{{\hat {T}}} = - \bar {D}_{{m, - n}}^{{\hat {T}}} = \bar {D}_{{ - m, - n}}^{{\hat {T}}}{\text{.}} \\ \end{gathered} $

Тогда с учетом зависимостей

$\begin{gathered} {{\xi }_{{m,n}}} = {{\xi }_{{ - m,n}}} = {{\xi }_{{m, - n}}} = {{\xi }_{{ - m, - n}}},\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{;}} \\ {{\zeta }_{{m,n}}} = {{\zeta }_{{ - m,n}}} = - {{\zeta }_{{m, - n}}} = - {{\zeta }_{{ - m, - n}}},\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{,}} \\ \end{gathered} $
получим
где

$\begin{gathered} \bar {A}_{{m,n}}^{{\hat {T}}} = 2\operatorname{Re} \left( {\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} + \bar {\mathcal{C}}_{{ - m,n}}^{{\hat {T}}}} \right) = 2\operatorname{Re} \left( {\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} + \bar {\mathcal{C}}_{{m, - n}}^{{\hat {T}}}} \right){\text{,}} \\ \bar {B}_{{m,n}}^{{\hat {T}}} = - 2{\text{Im}}\left( {\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} - \bar {\mathcal{C}}_{{ - m,n}}^{{\hat {T}}}} \right) = - 2{\text{Im}}\left( {\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} + \bar {\mathcal{C}}_{{m, - n}}^{{\hat {T}}}} \right){\text{,}} \\ \bar {C}_{{m,n}}^{{\hat {T}}} = - 2{\text{Im}}\left( {\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} + \bar {\mathcal{C}}_{{ - m,n}}^{{\hat {T}}}} \right) = - 2{\text{Im}}\left( {\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} - \bar {\mathcal{C}}_{{m, - n}}^{{\hat {T}}}} \right){\text{,}} \\ \bar {D}_{{m,n}}^{{\hat {T}}} = - 2\operatorname{Re} \left( {\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} - \bar {\mathcal{C}}_{{ - m,n}}^{{\hat {T}}}} \right) = - 2\operatorname{Re} \left( {\bar {\mathcal{C}}_{{m,n}}^{{\hat {T}}} - \bar {\mathcal{C}}_{{m, - n}}^{{\hat {T}}}} \right){\text{,}} \\ m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $

При граничном условии (16)

$\begin{gathered} \bar {A}_{{m,n}}^{{\hat {T}}} = A_{{m,n}}^{{{{{\hat {T}}}_{w}}}}{\text{,}}\,\,\,\,\bar {B}_{{m,n}}^{{\hat {T}}} = B_{{m,n}}^{{{{{\hat {T}}}_{w}}}}{\text{,}}\,\,\,\,\bar {C}_{{m,n}}^{{\hat {T}}} = C_{{m,n}}^{{{{{\hat {T}}}_{w}}}}{\text{,}} \\ \bar {D}_{{m,n}}^{{\hat {T}}} = D_{{m,n}}^{{{{{\hat {T}}}_{w}}}}{\text{,}}\,\,\,\,m \in \mathbb{Z}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{.}} \\ \end{gathered} $

При граничном условии (17)

$\begin{gathered} \bar {A}_{{0,0}}^{{\hat {T}}} = 4\left\langle {\left[\kern-0.15em\left[ {\hat {T}} \right]\kern-0.15em\right]} \right\rangle {\text{;}}\,\,\,\,\bar {A}_{{m,n}}^{{\hat {T}}} = - \frac{{{{\xi }_{{m,n}}}A_{{m,n}}^{{{{{\hat {q}}}_{w}}}} - {{\zeta }_{{m,n}}}C_{{m,n}}^{{{{{\hat {q}}}_{w}}}}}}{{\xi _{{m,n}}^{2} + \zeta _{{m,n}}^{2}}}{\text{,}} \\ \bar {B}_{{m,n}}^{{\hat {T}}} = - \frac{{{{\xi }_{{m,n}}}B_{{m,n}}^{{{{{\hat {q}}}_{w}}}} - {{\zeta }_{{m,n}}}D_{{m,n}}^{{{{{\hat {q}}}_{w}}}}}}{{\xi _{{m,n}}^{2} + \zeta _{{m,n}}^{2}}}{\text{,}}\,\,\,\,\bar {C}_{{m,n}}^{{\hat {T}}} = \\ = - \frac{{{{\zeta }_{{m,n}}}A_{{m,n}}^{{{{{\hat {q}}}_{w}}}} + {{\xi }_{{m,n}}}C_{{m,n}}^{{{{{\hat {q}}}_{w}}}}}}{{\xi _{{m,n}}^{2} + \zeta _{{m,n}}^{2}}}{\text{,}}\,\,\,\,\bar {D}_{{m,n}}^{{\hat {T}}} = - \frac{{{{\zeta }_{{m,n}}}B_{{m,n}}^{{{{{\hat {q}}}_{w}}}} + {{\xi }_{{m,n}}}D_{{m,n}}^{{{{{\hat {q}}}_{w}}}}}}{{\xi _{{m,n}}^{2} + \zeta _{{m,n}}^{2}}}{\text{,}} \\ m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| m \right| + \left| n \right| \in \mathbb{N}{\text{.}} \\ \end{gathered} $

При граничном условии (18) постоянные интегрирования удовлетворяют бесконечной системе линейных алгебраических уравнений с бесчисленным множеством неизвестных

Здесь

${{\mathbb{N}}_{0}} = \mathbb{N} \cup \left\{ 0 \right\}{\text{;}}\,\,\,\,\kappa _{{j,k}}^{'} = {{{{\kappa }_{{j,k}}}} \mathord{\left/ {\vphantom {{{{\kappa }_{{j,k}}}} 4}} \right. \kern-0em} 4}{\text{.}}$

При ${\text{Bi}} = {\text{Bi}}\left( {\hat {y}} \right)$ имеем

$\begin{gathered} A_{{m,n}}^{{{\text{Bi}}}} = B_{{m,n}}^{{{\text{Bi}}}} = C_{{m,n}}^{{{\text{Bi}}}} = D_{{m,n}}^{{{\text{Bi}}}} = C_{{m,0}}^{{{\text{Bi}}}} = D_{{m,0}}^{{{\text{Bi}}}} = 0{\text{,}} \\ m \in \mathbb{Z}{\text{,}}\,\,\,\,\left| n \right| \in \mathbb{N}{\text{,}} \\ \end{gathered} $
что приводит к системе уравнений

$\begin{gathered} \sum\limits_{j = 0}^{ + \infty } {\left\{ {\left[ {{{\xi }_{{j,n}}}{{\delta }_{{m,j}}} + \bar {\kappa }_{j}^{'}\left( {A_{{j + m,0}}^{{{\text{Bi}}}} + A_{{j - m,0}}^{{{\text{Bi}}}}} \right)} \right]} \right.} \bar {A}_{{j,n}}^{{\hat {T}}} + \\ + \,\,\left. {\bar {\kappa }_{j}^{'}\left( {B_{{j + m,0}}^{{{\text{Bi}}}} + B_{{j - m,0}}^{{{\text{Bi}}}}} \right)\bar {B}_{{j,n}}^{{\hat {T}}} + {{\zeta }_{{j,n}}}{{\delta }_{{m,j}}}\bar {C}_{{j,n}}^{{\hat {T}}}} \right\} = \\ = A_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}}\,\,\,\,m \in {{\mathbb{N}}_{0}}{\text{,}}\,\,\,\,n \in {{\mathbb{N}}_{0}}{\text{;}} \\ \end{gathered} $
$\begin{gathered} \sum\limits_{j = 0}^{ + \infty } {\left\{ {\bar {\kappa }_{j}^{'}\left( {B_{{j + m,0}}^{{{\text{Bi}}}} - B_{{j - m,0}}^{{{\text{Bi}}}}} \right)} \right.} \bar {A}_{{j,n}}^{{\hat {T}}} + \\ + \,\,\left[ {{{\xi }_{{j,n}}}{{\delta }_{{m,j}}} - \bar {\kappa }_{j}^{'}\left( {A_{{j + m,0}}^{{{\text{Bi}}}} - A_{{j - m,0}}^{{{\text{Bi}}}}} \right)} \right]\bar {B}_{{j,n}}^{{\hat {T}}} + \\ \left. { + \,\,{{\zeta }_{{j,n}}}{{\delta }_{{m,j}}}\bar {D}_{{j,n}}^{{\hat {T}}}} \right\} = B_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}}\,\,\,\,m \in \mathbb{N}{\text{,}}\,\,\,\,n \in {{\mathbb{N}}_{0}}{\text{;}} \\ \sum\limits_{j = 0}^{ + \infty } {\left\{ { - {{\zeta }_{{j,n}}}{{\delta }_{{m,j}}}\bar {A}_{{j,n}}^{{\hat {T}}} + } \right.} \left[ {{{\xi }_{{j,n}}}{{\delta }_{{m,j}}} + \bar {\kappa }_{j}^{'}\left( {A_{{j + m,0}}^{{{\text{Bi}}}} + A_{{j - m,0}}^{{{\text{Bi}}}}} \right)} \right] \times \\ \times \,\,\bar {C}_{{j,n}}^{{\hat {T}}} + \bar {\kappa }_{j}^{'}\left. {\left( {B_{{j + m,0}}^{{{\text{Bi}}}} + B_{{j - m,0}}^{{{\text{Bi}}}}} \right)\bar {D}_{{j,n}}^{{\hat {T}}}} \right\} = C_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}} \\ m \in {{\mathbb{N}}_{0}}{\text{,}}\,\,\,\,n \in \mathbb{N}{\text{;}} \\ \end{gathered} $
$\begin{gathered} \sum\limits_{j = 0}^{ + \infty } {\left\{ { - {{\zeta }_{{j,n}}}{{\delta }_{{m,j}}}\bar {B}_{{j,n}}^{{\hat {T}}} + \bar {\kappa }_{j}^{'}} \right.} \left( {B_{{j + m,0}}^{{{\text{Bi}}}} - B_{{j - m,0}}^{{{\text{Bi}}}}} \right)\bar {C}_{{j,n}}^{{\hat {T}}} + \\ \left. { + \,\,\left[ {{{\xi }_{{j,n}}}{{\delta }_{{m,j}}} - \bar {\kappa }_{j}^{'}\left( {A_{{j + m,0}}^{{{\text{Bi}}}} - A_{{j - m,0}}^{{{\text{Bi}}}}} \right)} \right]\bar {D}_{{j,n}}^{{\hat {T}}}} \right\} = \\ = D_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}}\,\,\,\,m \in \mathbb{N}{\text{,}}\,\,\,\,n \in \mathbb{N}{\text{;}}\,\,\,\,\bar {B}_{{0,n}}^{{\hat {T}}} = \bar {C}_{{m,0}}^{{\hat {T}}} = \bar {D}_{{0,n}}^{{\hat {T}}} = \\ = \bar {D}_{{m,0}}^{{\hat {T}}} = 0{\text{,}}\,\,\,\,m \in {{\mathbb{N}}_{0}}{\text{,}}\,\,\,\,n \in {{\mathbb{N}}_{0}}{\text{.}} \\ \end{gathered} $

Здесь

$\bar {\kappa }_{j}^{'} = {{{{{\bar {\kappa }}}_{j}}} \mathord{\left/ {\vphantom {{{{{\bar {\kappa }}}_{j}}} 4}} \right. \kern-0em} 4}{\text{.}}$

При ${\text{Bi}} = {\text{Bi}}\left( {\hat {t}} \right)$ получаем

$\begin{gathered} A_{{m,n}}^{{{\text{Bi}}}} = B_{{m,n}}^{{{\text{Bi}}}} = C_{{m,n}}^{{{\text{Bi}}}} = D_{{m,n}}^{{{\text{Bi}}}} = B_{{0,n}}^{{{\text{Bi}}}} = D_{{0,n}}^{{{\text{Bi}}}} = 0{\text{,}} \\ \left| m \right| \in \mathbb{N}{\text{,}}\,\,\,\,n \in \mathbb{Z}{\text{,}} \\ \end{gathered} $
что дает следующую систему уравнений:

$\begin{gathered} \sum\limits_{k = 0}^{ + \infty } {\left\{ {\left[ {{{\xi }_{{m,k}}}{{\delta }_{{n,k}}} + \bar {\kappa }_{k}^{'}\left( {A_{{0,k + n}}^{{{\text{Bi}}}} + A_{{0,k - n}}^{{{\text{Bi}}}}} \right)} \right]\bar {A}_{{m,k}}^{{\hat {T}}} + } \right.} \\ \left. { + \,\,\left[ {{{\zeta }_{{m,k}}}{{\delta }_{{n,k}}} + \bar {\kappa }_{k}^{'}\left( {C_{{0,k + n}}^{{{\text{Bi}}}} + C_{{0,k - n}}^{{{\text{Bi}}}}} \right)} \right]\bar {C}_{{m,k}}^{{\hat {T}}}} \right\} = \\ = A_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}}\,\,\,\,m \in {{\mathbb{N}}_{0}}{\text{,}}\,\,\,\,n \in {{\mathbb{N}}_{0}}{\text{;}} \\ \end{gathered} $
$\begin{gathered} \sum\limits_{k = 0}^{ + \infty } {\left\{ {\left[ {{{\xi }_{{m,k}}}{{\delta }_{{n,k}}} + \bar {\kappa }_{k}^{'}\left( {A_{{0,k + n}}^{{{\text{Bi}}}} + A_{{0,k - n}}^{{{\text{Bi}}}}} \right)} \right]\bar {B}_{{m,k}}^{{\hat {T}}} + } \right.} \\ \left. { + \,\,\left[ {{{\zeta }_{{m,k}}}{{\delta }_{{n,k}}} + \bar {\kappa }_{k}^{'}\left( {C_{{0,k + n}}^{{{\text{Bi}}}} + C_{{0,k - n}}^{{{\text{Bi}}}}} \right)} \right]\bar {D}_{{m,k}}^{{\hat {T}}}} \right\} = B_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}} \\ m \in \mathbb{N}{\text{,}}\,\,\,\,n \in {{\mathbb{N}}_{0}}{\text{;}} \\ \sum\limits_{k = 0}^{ + \infty } {\left\{ { - \left[ {{{\zeta }_{{m,k}}}{{\delta }_{{n,k}}} - \bar {\kappa }_{k}^{'}\left( {C_{{0,k + n}}^{{{\text{Bi}}}} - C_{{0,k - n}}^{{{\text{Bi}}}}} \right)} \right]\bar {A}_{{m,k}}^{{\hat {T}}} + } \right.} \\ \left. { + \,\,\left[ {{{\xi }_{{m,k}}}{{\delta }_{{n,k}}} - \bar {\kappa }_{k}^{'}\left( {A_{{0,k + n}}^{{{\text{Bi}}}} - A_{{0,k - n}}^{{{\text{Bi}}}}} \right)} \right]\bar {C}_{{m,k}}^{{\hat {T}}}} \right\} = C_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}} \\ m \in {{\mathbb{N}}_{0}}{\text{,}}\,\,\,\,n \in \mathbb{N}{\text{;}} \\ \end{gathered} $
$\begin{gathered} \sum\limits_{k = 0}^{ + \infty } {\left\{ { - \left[ {{{\zeta }_{{m,k}}}{{\delta }_{{n,k}}} - \bar {\kappa }_{k}^{'}\left( {C_{{0,k + n}}^{{{\text{Bi}}}} - C_{{0,k - n}}^{{{\text{Bi}}}}} \right)} \right]\bar {B}_{{m,k}}^{{\hat {T}}} + } \right.} \\ \left. { + \,\,\left[ {{{\xi }_{{m,k}}}{{\delta }_{{n,k}}} - \bar {\kappa }_{k}^{'}\left( {A_{{0,k + n}}^{{{\text{Bi}}}} - A_{{0,k - n}}^{{{\text{Bi}}}}} \right)} \right]\bar {D}_{{m,k}}^{{\hat {T}}}} \right\} = D_{{m,n}}^{{{\text{Bi}}{{{\hat {T}}}_{f}}}}{\text{,}} \\ m \in \mathbb{N}{\text{,}}\,\,\,\,n \in \mathbb{N}{\text{;}}\,\,\,\,\bar {B}_{{0,n}}^{{\hat {T}}} = \bar {C}_{{m,0}}^{{\hat {T}}} = \bar {D}_{{0,n}}^{{\hat {T}}} = \bar {D}_{{m,0}}^{{\hat {T}}} = 0{\text{,}} \\ m \in {{\mathbb{N}}_{0}}{\text{,}}\,\,\,\,n \in {{\mathbb{N}}_{0}}{\text{.}} \\ \end{gathered} $

При ${\text{Bi}} = {\text{const}}$ имеем

Некоторые свойства решения (7)–(12) можно установить без его непосредственного нахождения. Для этого достаточно учесть, что $\hat {T}$ и все ее производные являются ограниченными функциями. Осуществив в (7) предельный переход при $\hat {l} \to + \infty ,$ получим одномерное дифференциальное уравнение

$\frac{{\partial{ \hat {T}}}}{{\partial{ \hat {t}}}} = \frac{{{{\partial }^{2}}\hat {T}}}{{\partial {{{\hat {x}}}^{2}}}}{\text{,}}\,\,\,\,\hat {x} > 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < \hat {y} < + \infty {\text{,}}\,\,\,\,\hat {t} > - \infty {\text{.}}$

В этом случае $\hat {T}$ определяется из решения квазиодномерной краевой задачи, в которой краевые функции зависят от второй пространственной переменной $\hat {y}.$ Следует иметь в виду, что решение квазиодномерной задачи теплопроводности в некоторых случаях приводит к парадоксальному результату

$\mathop {\lim }\limits_{\hat {x} \to + \infty } \frac{{\partial{ \hat {T}}}}{{\partial{ \hat {y}}}} \ne 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < \hat {y} < + \infty {\text{,}}\,\,\,\,\hat {t} > - \infty {\text{,}}$
невозможность которого следует из полученных точных зависимостей для двумерного процесса. В действительности для любого сколь угодно большого параметра $\hat {l}$ в полупространстве всегда найдется такое достаточно большое значение $\hat {x},$ при котором начнет проявляться существенная двумерность $\hat {T},$ исключающая возможность существования указанного выше парадокса. Из найденных точных решений следует, что при $\hat {l} \gg 1$ квазиодномерное решение справедливо в области $0 \leqslant \hat {x} \ll {{\hat {l}}^{2}},$ где оно дает малую погрешность.

Умножив (7) на ${{\hat {l}}^{2}}$ и осуществив предельный переход при $\hat {l} \to 0,$ получим дифференциальное уравнение

$\frac{{{{\partial }^{2}}\hat {T}}}{{\partial {{{\hat {y}}}^{2}}}} = 0{\text{,}}\,\,\,\,\hat {x} > 0{\text{,}}\,\,\,\, - {\kern 1pt} \infty < \hat {y} < + \infty {\text{,}}\,\,\,\,\hat {t} > - \infty {\text{.}}$

Отсюда с учетом (8) легко установить, что $\hat {T} = \hat {T}\left( {\hat {x},\hat {t}} \right).$ Таким образом, имеем

(20)
$\begin{gathered} \mathop {\lim }\limits_{\hat {l} \to 0} \hat {T} = \mathop {\lim }\limits_{\hat {l} \to 0} \left[\kern-0.15em\left[ {\hat {T}} \right]\kern-0.15em\right]{\text{,}}\,\,\,\,\hat {x} > 0{\text{,}} \\ - {\kern 1pt} \infty < \hat {y} < + \infty {\text{,\;}}\,\,\,\,\hat {t} > - \infty {\text{.}} \\ \end{gathered} $

Для нахождения краевой задачи, соответствующей $\hat {l} \to 0,$ осредним (7)–(12) по $\hat {y}$ на периоде $2\pi ,$ приняв во внимание условие периодичности по $\hat {y}$ (8), и выполним предельный переход при $\hat {l} \to 0.$ Учитывая (20), получим одномерную краевую задачу

$\begin{gathered} \frac{{\partial{ \hat {T}}}}{{\partial{ \hat {t}}}} = \frac{{{{\partial }^{2}}\hat {T}}}{{\partial {{{\hat {x}}}^{2}}}}{\text{,}}\,\,\,\,\hat {x} > 0{\text{,}}\,\,\,\,\hat {t} > - \infty {\text{;}}\,\,\,\,\hat {T}\left( {\hat {x},\hat {t} + 2\pi } \right) = \\ = \hat {T}\left( {\hat {x},\hat {t}} \right){\text{,}}\,\,\,\,\hat {x} > 0{\text{,}}\,\,\,\,\hat {t} > - \infty {\text{;}}\,\,\,\,\mathop {\lim }\limits_{\hat {x} \to + \infty } \frac{{\partial{ \hat {T}}}}{{\partial{ \hat {x}}}} = 0{\text{,}} \\ \hat {t} > - \infty {\text{;}} \\ \end{gathered} $
$\begin{gathered} \hat {T}\left( {0,\hat {t}} \right) = \left[\kern-0.15em\left[ {{{{\hat {T}}}_{w}}} \right]\kern-0.15em\right]{\text{,}}\,\,\,\,\hat {t} > - \infty {\text{;}}\,\,\,\,\frac{{\partial{ \hat {T}}\left( {0,\hat {t}} \right)}}{{\partial{ \hat {x}}}} = \left[\kern-0.15em\left[ {{{{\hat {q}}}_{w}}} \right]\kern-0.15em\right]{\text{,}}\,\,\,\,\hat {t} > - \infty {\text{;}} \\ \frac{{\partial{ \hat {T}}\left( {0,\hat {t}} \right)}}{{\partial{ \hat {x}}}} = \left[\kern-0.15em\left[ {{\text{Bi}}} \right]\kern-0.15em\right]\hat {T}\left( {0,\hat {t}} \right) - \left[\kern-0.15em\left[ {{\text{Bi}}{{{\hat {T}}}_{f}}} \right]\kern-0.15em\right]{\text{,}}\,\,\,\,\hat {t} > - \infty {\text{.}} \\ \end{gathered} $

Отсюда следует, что при $0 < \hat {l} \ll 1$ поле температуры близко к одномерному.

ПРИМЕРЫ

Используем полученные зависимости для нахождения переменной составляющей поля температуры для ряда простых краевых функций и сопоставим точные решения ${\hat {\theta }}$ с квазиодномерными ${\hat {\theta }}{\kern 1pt} {\text{'}}{\text{.}}$ Для краевой функции

${{{\hat {\Theta }}}_{w}} = \frac{1}{2}\cos \left( {\hat {t} - \hat {y}} \right)$
в граничном условии I рода имеем

$\begin{gathered} {\hat {\theta }} = \frac{1}{2}{{{\text{e}}}^{{ - \xi \hat {x}}}}\cos \left( {\hat {t} - \hat {y} - \zeta \hat {x}} \right){\text{,}}\,\,\,\,\Delta {\hat {\theta }} = {{{\text{e}}}^{{ - \xi \hat {x}}}}{\text{;}} \\ {\hat {\theta }}{\kern 1pt} {\text{'}} = \frac{1}{2}{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}\cos \left( {\hat {t} - \hat {y} - {{\hat {x}} \mathord{\left/ {\vphantom {{\hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}} \right){\text{,}}\,\,\,\,\Delta {\hat {\theta }}{\kern 1pt} {\text{'}} = {{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}{\text{.}} \\ \end{gathered} $

Для краевой функции

${{{\hat {\Theta }}}_{w}} = \frac{1}{2}\cos \hat {y}\cos \hat {t}$
в граничном условии I рода

$\begin{gathered} {\hat {\theta }} = \frac{1}{2}{{{\text{e}}}^{{ - \xi \hat {x}}}}\cos \hat {y}\cos \left( {\hat {t} - \zeta \hat {x}} \right){\text{,}}\,\,\,\,\Delta {\hat {\theta }} = {{{\text{e}}}^{{ - \xi \hat {x}}}}\cos \hat {y}{\text{;}} \\ {\hat {\theta }}{\kern 1pt} {\text{'}} = \frac{1}{2}{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}\cos \hat {y}\cos \left( {\hat {t} - {{\hat {x}} \mathord{\left/ {\vphantom {{\hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}} \right){\text{,}} \\ \Delta {\hat {\theta }}{\kern 1pt} {\text{'}} = {{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}\cos \hat {y}{\text{.}} \\ \end{gathered} $

Для краевой функции

${{\hat {q}}_{w}} = \frac{1}{2}\cos \left( {\hat {t} - \hat {y}} \right)$
в граничном условии II рода имеем

$\begin{gathered} {\hat {\theta }} = - \frac{1}{2}\frac{{{{e}^{{ - \xi \hat {x}}}}}}{{\sqrt {{{\xi }^{2}} + {{\zeta }^{2}}} }}\cos \left( {\hat {t} - \hat {y} - \zeta \hat {x} - \hat {\tau }} \right){\text{,}} \\ \Delta {\hat {\theta }} = \frac{{{{e}^{{ - \xi \hat {x}}}}}}{{\sqrt {{{\xi }^{2}} + {{\zeta }^{2}}} }}{\text{;}}\,\,\,\,{\hat {\theta }}{\kern 1pt} {\text{'}} = - \frac{1}{2}{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}} \times \\ \times \,\,\cos \left( {\hat {t} - \hat {y} - {{\hat {x}} \mathord{\left/ {\vphantom {{\hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }} - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}} \right){\text{,}}\,\,\,\,\Delta {\hat {\theta }}{\kern 1pt} {\text{'}} = {{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}{\text{.}} \\ \end{gathered} $

Для краевой функции

${{\hat {q}}_{w}} = \frac{1}{2}\cos \hat {y}\cos \hat {t}$
в граничном условии II рода

$\begin{gathered} {\hat {\theta }} = - \frac{1}{2}\frac{{{{{\text{e}}}^{{ - \xi \hat {x}}}}}}{{\sqrt {{{\xi }^{2}} + {{\zeta }^{2}}} }}\cos \hat {y}\cos \left( {\hat {t} - \zeta \hat {x} - \hat {\tau }} \right){\text{,}} \\ \Delta {\hat {\theta }} = \frac{{{{{\text{e}}}^{{ - \xi \hat {x}}}}\cos \hat {y}}}{{\sqrt {{{\xi }^{2}} + {{\zeta }^{2}}} }}{\text{,}}\,\,\,\,{\hat {\theta }}{\kern 1pt} {\text{'}} = - \frac{1}{2}{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}\cos \hat {y} \times \\ \times \,\,\cos \left( {\hat {t} - {{\hat {x}} \mathord{\left/ {\vphantom {{\hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }} - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}} \right){\text{,}}\,\,\,\,\Delta {\hat {\theta }}{\kern 1pt} {\text{'}} = {{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}\cos \hat {y}{\text{.}} \\ \end{gathered} $

Для краевых функций

${\text{Bi}} = {\text{const,}}\,\,\,\,{{{\hat {\Theta }}}_{f}} = \frac{1}{2}\cos \left( {\hat {t} - \hat {y}} \right)$
в граничном условии III рода имеем

$\begin{gathered} {\hat {\theta }} = \frac{1}{2}\frac{{{{{\text{e}}}^{{ - \xi \hat {x}}}}}}{{{{{\left( {1 + \frac{{2\xi }}{{{\text{Bi}}}} + \frac{{{{\xi }^{2}} + {{\zeta }^{2}}}}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\cos \left( {\hat {t} - \hat {y} - \zeta \hat {x} - \hat {\tau }} \right){\text{,}} \\ \Delta {\hat {\theta }} = \frac{{{{{\text{e}}}^{{ - \xi \hat {x}}}}}}{{{{{\left( {1 + \frac{{2\xi }}{{{\text{Bi}}}} + \frac{{{{\xi }^{2}} + {{\zeta }^{2}}}}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\kern 1pt} {\text{;}}\,\,\,\,{\hat {\theta }}{\kern 1pt} {\text{'}} = \frac{1}{2}\frac{{{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}}}{{{{{\left( {1 + \frac{{\sqrt 2 }}{{{\text{Bi}}}} + \frac{1}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \times \\ \times \,\,\cos \left( {\hat {t} - \hat {y} - {{\hat {x}} \mathord{\left/ {\vphantom {{\hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }} - \hat {\tau }{\kern 1pt} {\text{'}}} \right){\text{,}}\,\,\,\,\Delta {\hat {\theta }}{\kern 1pt} {\text{'}} = \frac{{{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}}}{{{{{\left( {1 + \frac{{\sqrt 2 }}{{{\text{Bi}}}} + \frac{1}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\text{.}} \\ \end{gathered} $

Для краевых функций

${\text{Bi}} = {\text{const,}}\,\,\,\,{{{\hat {\Theta }}}_{f}} = \frac{1}{2}\cos \hat {y}\cos \hat {t}$
в граничном условии III рода

$\begin{gathered} {\hat {\theta }} = \frac{1}{2}\frac{{{{{\text{e}}}^{{ - \xi \hat {x}}}}}}{{{{{\left( {1 + \frac{{2\xi }}{{{\text{Bi}}}} + \frac{{{{\xi }^{2}} + {{\zeta }^{2}}}}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\cos \hat {y}\cos \left( {\hat {t} - \zeta \hat {x} - \hat {\tau }} \right){\text{,}} \\ \Delta {\hat {\theta }} = \frac{{{{{\text{e}}}^{{ - \xi \hat {x}}}}\cos \hat {y}}}{{{{{\left( {1 + \frac{{2\xi }}{{{\text{Bi}}}} + \frac{{{{\xi }^{2}} + {{\zeta }^{2}}}}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\text{;}} \\ {\hat {\theta }}{\kern 1pt} {\text{'}} = \frac{1}{2}\frac{{{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}}}{{{{{\left( {1 + \frac{{\sqrt 2 }}{{{\text{Bi}}}} + \frac{1}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\cos \hat {y}\cos \left( {\hat {t} - {{\hat {x}} \mathord{\left/ {\vphantom {{\hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }} - \hat {\tau }{\kern 1pt} {\text{'}}} \right){\text{,}} \\ \Delta {\hat {\theta }}{\kern 1pt} {\text{'}} = \frac{{{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}\cos \hat {y}}}{{{{{\left( {1 + \frac{{\sqrt 2 }}{{{\text{Bi}}}} + \frac{1}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\text{.}} \\ \end{gathered} $

Здесь

$\begin{gathered} \xi \equiv {{\xi }_{{1,1}}} = \sqrt {\frac{{\sqrt {1 + {1 \mathord{\left/ {\vphantom {1 {{{{\hat {l}}}^{4}}}}} \right. \kern-0em} {{{{\hat {l}}}^{4}}}}} + {1 \mathord{\left/ {\vphantom {1 {{{{\hat {l}}}^{2}}}}} \right. \kern-0em} {{{{\hat {l}}}^{2}}}}}}{2}} {\text{,}} \\ \zeta \equiv {{\zeta }_{{1,1}}} = \sqrt {\frac{{\sqrt {1 + {1 \mathord{\left/ {\vphantom {1 {{{{\hat {l}}}^{4}}}}} \right. \kern-0em} {{{{\hat {l}}}^{4}}}}} - {1 \mathord{\left/ {\vphantom {1 {{{{\hat {l}}}^{2}}}}} \right. \kern-0em} {{{{\hat {l}}}^{2}}}}}}{2}} {\text{;}} \\ \end{gathered} $
для граничного условия II рода

$\hat {\tau } = {\text{arctg}}\left( {{\zeta \mathord{\left/ {\vphantom {\zeta \xi }} \right. \kern-0em} \xi }} \right){\text{;}}$

для граничного условия III рода

$\hat {\tau } = {\text{arctg}}\left( {\frac{\zeta }{{\xi + {\text{Bi}}}}} \right){\text{,}}\,\,\,\,\hat {\tau }{\kern 1pt} {\text{'}} = {\text{arctg}}\left( {\frac{1}{{1 + {\text{Bi}}\sqrt 2 }}} \right){\text{.}}$

Из сравнения точных решений с квазиодномерными следует, что они имеют одинаковую структуру и различаются лишь значениями коэффициентов $\xi $ и ζ. Коэффициент $\xi $ определяет интенсивность уменьшения размаха колебаний температуры с ростом $\hat {x},$ а коэффициент $\zeta $ – запаздывание колебаний температуры на различных глубинах. От коэффициентов $\xi $ и $\zeta $ также зависит размах колебаний температуры при граничных условиях II и III рода и сдвиг фаз между колебаниями температуры на поверхности тела и колебаниями краевых функций ${{\hat {q}}_{w}}$ и ${{\hat {T}}_{f}}.$

Рассмотрим поведение решений при малых и больших параметрах $\hat {l}.$ При $\hat {l} \gg 1$ имеем

$\begin{gathered} \xi \approx \frac{1}{{\sqrt 2 }}\left( {1 + \frac{1}{{2{{{\hat {l}}}^{2}}}}} \right){\text{,}}\,\,\,\,\zeta \approx \frac{1}{{\sqrt 2 }}\left( {1 - \frac{1}{{2{{{\hat {l}}}^{2}}}}} \right){\text{,}} \\ \frac{{\Delta {\hat {\theta }}}}{{\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}}} \approx \exp \left( { - \frac{{\hat {x}}}{{2{{{\hat {l}}}^{2}}\sqrt 2 }}} \right){\text{,}}\,\,\,\,\frac{{\hat {x}}}{{\sqrt 2 }} - \zeta \hat {x} \approx \frac{{\hat {x}}}{{2{{{\hat {l}}}^{2}}\sqrt 2 }}{\text{,}} \\ {\text{arctg}}\left( {{\zeta \mathord{\left/ {\vphantom {\zeta \xi }} \right. \kern-0em} \xi }} \right) \approx {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}{\text{,}}\,\,\,\,{\text{arctg}}\left( {\frac{\zeta }{{\xi + {\text{Bi}}}}} \right) \approx {\text{arctg}}\left( {\frac{1}{{1 + {\text{Bi}}\sqrt 2 }}} \right){\text{.}} \\ \end{gathered} $

Отсюда следует, что при $0 < \hat {x} \ll {{\hat {l}}^{2}}$ квазиодномерные решения мало отличаются от точных. При $\hat {l} \to + \infty $ точные решения совпадают с квазиодномерными, поскольку

$\mathop {\lim }\limits_{\hat {l} \to + \infty } \xi = \mathop {\lim }\limits_{\hat {l} \to + \infty } \zeta = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}{\text{.}}$

При $0 < \hat {l} \ll 1$

$\xi \approx {1 \mathord{\left/ {\vphantom {1 {\hat {l}{\text{,}}}}} \right. \kern-0em} {\hat {l}{\text{,}}}}\,\,\,\,\zeta \approx {{\hat {l}} \mathord{\left/ {\vphantom {{\hat {l}} 2}} \right. \kern-0em} 2}{\text{,}}$
поэтому $\left| {{\hat {\theta }}} \right| \ll 1.$ В предельном случае находим
$\mathop {\lim }\limits_{\hat {l} \to 0} {\hat {\theta }} = 0{\text{,}}$
что согласуется с результатами проведенного ранее общего анализа, поскольку для рассмотренных краевых функций

$\left[\kern-0.15em\left[ {{{{{\hat {\Theta }}}}_{w}}} \right]\kern-0.15em\right] = \left[\kern-0.15em\left[ {{{{\hat {q}}}_{w}}} \right]\kern-0.15em\right] = \left[\kern-0.15em\left[ {{{{{\hat {\Theta }}}}_{f}}} \right]\kern-0.15em\right] = 0.$

В таком случае ${\hat {\theta }}$ удовлетворяет краевым задачам для однородного дифференциального уравнения с однородными граничными условиями, которые имеют лишь тривиальное решение.

С помощью полученных решений можно показать, что вблизи поверхности квазиодномерное решение дает приемлемые для практики результаты даже при $\hat {l} > 1,$ поскольку обычно интерес представляют колебания температуры на поверхности полупространства, где возникают наибольшие термоциклические напряжения. Для этого запишем отношение ${{\Delta {\hat {\theta }}} \mathord{\left/ {\vphantom {{\Delta {\hat {\theta }}} {\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}}}} \right. \kern-0em} {\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}}}$ в виде

${{\Delta {\hat {\theta }}} \mathord{\left/ {\vphantom {{\Delta {\hat {\theta }}} {\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}}}} \right. \kern-0em} {\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}}} = \eta \mu ,$
где

$\eta = \sqrt {\frac{{{\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}\sqrt 2 + 1}}{{{\text{B}}{{{\text{i}}}^{2}} + 2\xi {\text{Bi}} + {{\xi }^{2}} + {{\zeta }^{2}}}}} {\text{,}}\,\,\,\,\mu = {{{\text{e}}}^{{ - \left( {\xi - {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}} \right)\hat {x}}}}{\text{.}}$

Граничному условию I рода соответствует ${\text{Bi}} \to + \infty ,$ граничному условию II рода – ${\text{Bi}} = 0,$ граничному условию III рода – ${\text{Bi}} > 0.$ На рис. 1 и 2 показано поведение ${\eta }$ и $\mu $ с увеличением $\hat {l}.$ Из них следует, что уже при $\hat {l} = 2$ квазиодномерное решение позволяет определить размах колебаний на поверхности полупространства с погрешностью менее $5\% $, что вполне приемлемо для практических целей.

Рис. 1.

Зависимость ${\eta }$ от $\hat {l}$ при различных значениях ${\text{Bi:}}$ 1 – ${\text{Bi}} = 0,$ 2 – 0.1, 3 – 1, 4 – 10.

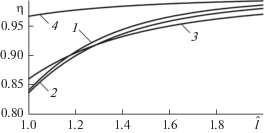
Рис. 2.

Зависимость ${\mu }$ от $\hat {x}$ при различных значениях $\hat {l}{\text{:}}$ 1 – $\hat {l} = 1,$ 2 – 2, 3 – 3.

На примере граничного условия III рода рассмотрим более сложные краевые функции и проверим допустимость использования квазиодномерных решений для $\hat {l} > 1.$ В качестве первого примера представим краевые функции

${\text{Bi}} = {\text{const,}}\,\,\,\,{{{\hat {\Theta }}}_{f}} = \frac{1}{2}{\text{sign}}\left( {\cos \hat {y}} \right)\cos \hat {t}{\text{.}}$

Последней функции соответствует ряд Фурье

${{{\hat {\Theta }}}_{f}} = \sum\limits_{m = 1}^{ + \infty } {\frac{2}{{\pi m}}} \sin \left( {\frac{{\pi m}}{2}} \right)\cos \left( {m\hat {y}} \right)\cos \hat {t}{\text{.}}$

Указанным краевым функциям соответствуют

$\begin{gathered} {\hat {\theta }} = \sum\limits_{m = 1}^{ + \infty } {\left[ {A_{{m,1}}^{{\hat {T}}}\cos \left( {m\hat {y}} \right){\kern 1pt} \cos \left( {\hat {t}} \right) + C_{{m,1}}^{{\hat {T}}}\cos \left( {m\hat {y}} \right){\kern 1pt} \sin \left( {\hat {t}} \right)} \right]} {\text{,}} \\ \Delta {\hat {\theta }} = 2{\kern 1pt} \sqrt {{{{\left\{ {\sum\limits_{m = 1}^{ + \infty } {\left[ {A_{{m,1}}^{{\hat {T}}}\cos {\kern 1pt} \left( {m\hat {y}} \right)} \right]} } \right\}}}^{2}} + {{{\left\{ {\sum\limits_{m = 1}^{ + \infty } {\left[ {C_{{m,1}}^{{\hat {T}}}\cos {\kern 1pt} \left( {m\hat {y}} \right)} \right]} } \right\}}}^{2}}} {\text{;}} \\ {\hat {\theta }}{\kern 1pt} {\text{'}} = \frac{1}{2}\frac{{{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}}}{{{{{\left( {1 + \frac{{\sqrt 2 }}{{{\text{Bi}}}} + \frac{1}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\kern 1pt} {\text{sign}}{\kern 1pt} \left( {\cos \hat {y}} \right){\kern 1pt} \cos {\kern 1pt} \left( {\hat {t} - {{\hat {x}} \mathord{\left/ {\vphantom {{\hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }} - {\hat {\tau }}{\kern 1pt} {\text{'}}} \right){\kern 1pt} {\text{,\;}} \\ \Delta {\hat {\theta }}{\kern 1pt} {\text{'}} = \frac{{{{{\text{e}}}^{{{{ - \hat {x}} \mathord{\left/ {\vphantom {{ - \hat {x}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}}}}}}{{{{{\left( {1 + \frac{{\sqrt 2 }}{{{\text{Bi}}}} + \frac{1}{{{\text{B}}{{{\text{i}}}^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\text{.}} \\ \end{gathered} $

Здесь

$\begin{gathered} A_{{m,1}}^{{\hat {T}}} = \frac{2}{{\pi m}}\sin \left( {\frac{{\pi m}}{2}} \right){{{\text{e}}}^{{ - {{\xi }_{{m,1}}}\hat {x}}}} \times \\ \times \,\,\frac{{\left( {1 + \frac{{{{\xi }_{{m,1}}}}}{{{\text{Bi}}}}} \right)\cos \left( {{{\zeta }_{{m,1}}}\hat {x}} \right) - \frac{{{{\zeta }_{{m,1}}}}}{{{\text{Bi}}}}\sin \left( {{{\zeta }_{{m,1}}}\hat {x}} \right)}}{{{{{\left( {1 + \frac{{{{\xi }_{{m,1}}}}}{{{\text{Bi}}}}} \right)}}^{2}} + {{{\left( {\frac{{{{\zeta }_{{m,1}}}}}{{{\text{Bi}}}}} \right)}}^{2}}}}{\text{,}}\,\,\,\,m \in \mathbb{N}{\text{;}} \\ C_{{m,1}}^{{\hat {T}}} = \frac{2}{{\pi m}}\sin \left( {\frac{{\pi m}}{2}} \right){{{\text{e}}}^{{ - {{\xi }_{{m,1}}}\hat {x}}}} \times \\ \times \,\,\frac{{\frac{{{{\zeta }_{{m,1}}}}}{{{\text{Bi}}}}\cos \left( {{{\zeta }_{{m,1}}}\hat {x}} \right) + \left( {1 + \frac{{{{\xi }_{{m,1}}}}}{{{\text{Bi}}}}} \right)\sin \left( {{{\zeta }_{{m,1}}}\hat {x}} \right)}}{{{{{\left( {1 + \frac{{{{\xi }_{{m,1}}}}}{{{\text{Bi}}}}} \right)}}^{2}} + {{{\left( {\frac{{{{\zeta }_{{m,1}}}}}{{{\text{Bi}}}}} \right)}}^{2}}}}{\text{,}}\,\,\,\,m \in \mathbb{N}{\text{;}} \\ {\hat {\tau }}{\kern 1pt} {\text{'}} = {\text{arctg}}\left( {\frac{1}{{1 + {\text{Bi}}\sqrt 2 }}} \right){\text{.}} \\ \end{gathered} $

Следует заметить, что в рассматриваемом случае функция $\Delta \hat {\theta } = \Delta \hat {\theta }\left( {\hat {y}} \right)$ имеет период $\pi .$ На рис. 3–5 показано изменение $\Delta {\hat {\theta }}$ по координате $\hat {y}$ на различных глубинах $\hat {x}$ в зависимости от величины $\hat {l}.$ Там же приведены соответствующие значения $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}{\text{.}}$ Из представленных результатов следует, что наиболее заметно двумерность поля температуры проявляется в окрестности точек, имеющих те же координаты

$\hat {y} = \left( {2k + 1} \right){\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}{\text{,}}\,\,\,\,k \in \mathbb{Z}{\text{,}}$
что и точки на поверхности полупространства, в которых происходит резкое изменение условий теплообмена. С увеличением координаты $\hat {x}$ двумерность поля температуры проявляется сильнее. При $\hat {l} = 1$ влияние неоднородности условий теплообмена на поле температуры заметно во всех точках полупространства. При $\hat {l} > 1$ в слое $0 \leqslant \hat {x} < \hat {l}$ возникают зоны, в которых квазиодномерное решение мало отличается от точного, причем с ростом $\hat {l}$ они расширяются. Достаточно наглядным интегральным параметром, характеризующим влияние $\hat {l}$ на поле температуры, является $\left[\kern-0.15em\left[ {\Delta {\hat {\theta }}} \right]\kern-0.15em\right],$ поскольку $\left[\kern-0.15em\left[ {\Delta {\hat {\theta }}} \right]\kern-0.15em\right] \to \Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ при $\hat {l} \to \infty .$ На рис. 6–8 сопоставлено изменение $\left[\kern-0.15em\left[ {\Delta {\hat {\theta }}} \right]\kern-0.15em\right]$ и $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ по глубине $\hat {x}$ при различных значениях ${\text{Bi}}$ и $\hat {l}.$ Из них следует, что при $\hat {l} = 5$ разница между $\left[\kern-0.15em\left[ {\Delta {\hat {\theta }}} \right]\kern-0.15em\right]$ и $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ мала.

Рис. 3.

Зависимости $\Delta {\hat {\theta }}$ (сплошные линии) и $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ (штриховые линии) от $\hat {y}$ при $\hat {l} = 1,$ ${\text{Bi}} = 1,$ ${{{\hat {\Theta }}}_{f}} = 0.5{\text{sign}}\left( {\cos \hat {y}} \right)\cos \hat {t}$ на глубинах $\hat {x}{\text{:}}$ 1 – $\hat {x} = 0,$ 2 – 1, 3 – $2.$

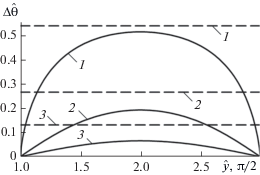
Рис. 4.

Зависимости $\Delta {\hat {\theta }}$ (сплошные линии) и $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ (штриховые линии) от $\hat {y}$ при $\hat {l} = 2,$ ${\text{Bi}} = 1,$ ${{{\hat {\Theta }}}_{f}} = 0.5{\text{sign}}\left( {\cos \hat {y}} \right)\cos \hat {t}$ на глубинах $\hat {x}{\text{:}}$ 1 – $\hat {x} = 0,$ 2 – 1, 3 – $2.$

Рис. 5.

Зависимости $\Delta {\hat {\theta }}$ (сплошные линии) и $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ (штриховые линии) от $\hat {y}$ при $\hat {l} = 5,$ ${\text{Bi}} = 1,$ ${{{\hat {\Theta }}}_{f}} = 0.5{\text{sign}}\left( {\cos \hat {y}} \right)\cos \hat {t}$ на глубинах $\hat {x}{\text{:}}$ 1 – $\hat {x} = 0,$ 2 – 1, 3 – 2.

Рис. 6.

Зависимости $\left[\kern-0.15em\left[ {\Delta {\hat {\theta }}} \right]\kern-0.15em\right]$ (сплошные линии) и $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ (штриховые линии) от $\hat {x}$ при ${\text{Bi}} = 0.1,$ ${{{\hat {\Theta }}}_{f}} = 0.5{\text{sign}}\left( {\cos \hat {y}} \right)\cos \hat {t}$ и различных $\hat {l}{\text{:}}$ 1 – $\hat {l} = 1,$ 2 – 2, 3 – $5.$

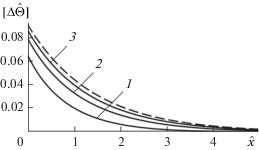
Рис. 7.

Зависимости $\left[\kern-0.15em\left[ {\Delta {\hat {\theta }}} \right]\kern-0.15em\right]$ (сплошные линии) и $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ (штриховые линии) от $\hat {x}$ при ${\text{Bi}} = 1,$ ${{{\hat {\Theta }}}_{f}} = 0.5{\text{sign}}\left( {\cos \hat {y}} \right)\cos \hat {t}$ и различных $\hat {l}{\text{:}}$ 1 – $\hat {l} = 1,$ 2 – $2$, 3 – $5$.

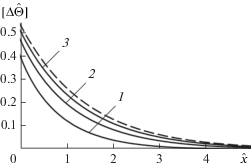
Рис. 8.

Зависимости $\left[\kern-0.15em\left[ {\Delta {\hat {\theta }}} \right]\kern-0.15em\right]$ (сплошные линии) и $\Delta {\hat {\theta }}{\kern 1pt} {\text{'}}$ (штриховые линии) от $\hat {x}$ при ${\text{Bi}} = 10,$ ${{{\hat {\Theta }}}_{f}} = 0.5{\text{sign}}\left( {\cos \hat {y}} \right)\cos \hat {t}$ и различных $\hat {l}{\text{:}}$ 1 – $\hat {l} = 1,$ 2 – 2, 3 – $5.$

В качестве второго примера рассмотрим краевые функции

${\text{Bi}} = 1 + \cos \hat {y}\cos \hat {t}{\text{,}}\,\,\,\,{{{\hat {\Theta }}}_{f}} = \frac{1}{2}\cos \hat {t}{\text{,}}$
при которых пространственная неоднородность теплообмена на поверхности тела вызвана зависимостью теплоотдачи от пространственной координаты $y.$ В данном случае критерием, характеризующим влияние пространственной неоднородности условий теплообмена на поле температуры, является отношение

${{\Delta {\text{Bi}}} \mathord{\left/ {\vphantom {{\Delta {\text{Bi}}} {\left\langle {\left[\kern-0.15em\left[ {{\text{Bi}}} \right]\kern-0.15em\right]} \right\rangle }}} \right. \kern-0em} {\left\langle {\left[\kern-0.15em\left[ {{\text{Bi}}} \right]\kern-0.15em\right]} \right\rangle }} = 2\cos \hat {y}{\text{.}}$

Приближенное решение задачи получено в виде

$\begin{gathered} {\hat {\Theta }} = \sum\limits_{m = 0}^{m*} {\sum\limits_{n = 0}^{n{\text{*}}} {{{\kappa }_{{m,n}}}} } \left[ {A_{{m,n}}^{{{\hat {\Theta }}}}\cos \left( {m\hat {y}} \right)\cos \left( {n\hat {t}} \right)} \right. + \\ + \,\,\left. {C_{{m,n}}^{{{\hat {\Theta }}}}\cos \left( {m\hat {y}} \right)\sin \left( {n\hat {t}} \right)} \right]{\text{,}} \\ \end{gathered} $
причем в ходе расчетов установлено, что при $m* = n* = 10$ его можно считать точным. Коэффициенты ряда Фурье приближенного квазиодномерного решения
${\hat {\Theta }}{\kern 1pt} {\text{'}} = \mathop \sum \limits_{n = 0}^{n*} {{\kappa }_{{0,n}}}\left[ {A_{{0,n}}^{{{\hat {\Theta }}}}\cos \left( {n\hat {t}} \right) + C_{{0,n}}^{{{\hat {\Theta }}}}\sin \left( {n\hat {t}} \right)} \right]$
определялись для локальных краевых функций, соответствующих фиксированному значению $\hat {y}.$ В ходе расчетов установлено, что в рассматриваемом случае функция $\Delta {\hat {\Theta }} = \Delta {\hat {\Theta }}\left( {\hat {y}} \right)$ имеет период $\pi .$ Результаты расчетов колебаний температуры и размаха колебаний температуры на поверхности полупространства по найденным зависимостям приведены на рис. 9–12. Из приведенных результатов следует, что сильнее всего влияние пространственной неоднородности условий теплообмена проявляется в окрестности точек, имеющих координаты
$\hat {y} = k\pi {\text{,}}\,\,\,\,k \in \mathbb{Z}{\text{,}}$
при которых ${{\Delta {\text{Bi}}} \mathord{\left/ {\vphantom {{\Delta {\text{Bi}}} {\left\langle {\left[\kern-0.15em\left[ {{\text{Bi}}} \right]\kern-0.15em\right]} \right\rangle }}} \right. \kern-0em} {\left\langle {\left[\kern-0.15em\left[ {{\text{Bi}}} \right]\kern-0.15em\right]} \right\rangle }}$ принимает экстремальные значения. В точках, имеющих координаты
$\hat {y} = \left( {2k + 1} \right){\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}{\text{,}}\,\,\,\,k \in \mathbb{Z}{\text{,}}$
при которых ${{\Delta {\text{Bi}}} \mathord{\left/ {\vphantom {{\Delta {\text{Bi}}} {\left\langle {\left[\kern-0.15em\left[ {{\text{Bi}}} \right]\kern-0.15em\right]} \right\rangle }}} \right. \kern-0em} {\left\langle {\left[\kern-0.15em\left[ {{\text{Bi}}} \right]\kern-0.15em\right]} \right\rangle }} = 0,$ двумерное решение мало отличается от квазиодномерного, соответствующего стационарной теплоотдаче, уже при $\hat {l} = 1.$ С возрастанием $\hat {l}$ разница между ${\hat {\Theta }}$ и ${\hat {\Theta }}{\kern 1pt} {\text{',}}$ как и следует ожидать, уменьшается. При определении $\Delta {{{\hat {\Theta }}}_{w}}$ при $\hat {l} = 10$ квазиодномерное решение обеспечивает приемлемую для практических расчетов погрешность менее $5\% $ для всех значений $\hat {y}.$

Рис. 9.

Зависимости ${{{\hat {\Theta }}}_{w}}$ (сплошные линии) и ${\hat {\Theta }}_{w}^{'}$ (штриховые линии) от $\hat {t}$ при $\hat {l} = 1,$ $~{\text{Bi}} = 1 + \cos \hat {y}\cos \hat {t},$ ${{{\hat {\Theta }}}_{f}} = 0.5\cos \hat {t}$ и различных $\hat {y}{\text{:}}$ 1 – $\hat {y} = 0,$ 2 – ${{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2},$ 3 – ${\pi }{\text{.}}$

Рис. 10.

Зависимости ${{{\hat {\Theta }}}_{w}}$ (сплошные линии) и ${\hat {\Theta }}_{w}^{'}$ (штриховые линии) от $\hat {t}$ при $\hat {l} = 10,$ ${\text{Bi}} = 1 + \cos \hat {y}\cos \hat {t},$ ${{{\hat {\Theta }}}_{f}} = 0.5\cos \hat {t}$ и различных $\hat {y}{\text{:}}$ 1 – $\hat {y} = 0,$ 2 – ${{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2},$ 3 – ${\pi }{\text{.}}$

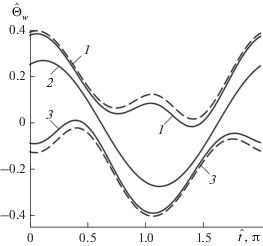
Рис. 11.

Зависимости $\Delta {\hat {\Theta }}$ (сплошные линии) и $\Delta {\hat {\Theta }}{\kern 1pt} {\text{'}}$ (штриховые линии) от $\hat {y}~$при $\hat {l} = 1,$ ${\text{Bi}} = 1 + \cos \hat {y}\cos \hat {t},$ ${{{\hat {\Theta }}}_{f}} = 0.5\cos \hat {t}$ на глубинах $\hat {x}{\text{:}}$ 1 – $\hat {x} = 0,$ 2 – 1, 3 – $2.$

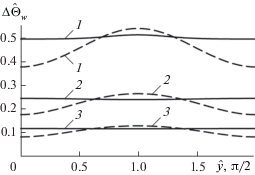
Рис. 12.

Зависимости $\Delta {\hat {\Theta }}$ (сплошные линии) и $\Delta {\hat {\Theta }}{\kern 1pt} {\text{'}}$ (штриховые линии) от $\hat {y}~$ при $\hat {l} = 10,$ ${\text{Bi}} = 1 + \cos \hat {y}\cos \hat {t},$ ${{{\hat {\Theta }}}_{f}} = 0.5\cos \hat {t}$ на глубинах $\hat {x}{\text{:}}$ 1 – $\hat {x} = 0,$ 2 – 1, 3 – $2.$

ЗАКЛЮЧЕНИЕ

С помощью найденных решений двумерной циклической задачи теплопроводности для полупространства показано, что основным критерием, определяющим возможность использования квазиодномерного решения, является $\hat {l}.$ Установлено, что при $\hat {l} \geqslant 10$ квазиодномерное решение обеспечивает приемлемую для практики точность в области $0 \leqslant \hat {x} \ll {{\hat {l}}^{2}}$ для любых значений $\hat {y},$ а в некоторых случаях квазиодномерное решение может быть использовано для расчета размаха колебаний температуры на поверхности полупространства уже при $\hat {l} > 1.$

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-31-00090.

Список литературы

  1. Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.

  2. Карслоу Г., Егер Д. Теплопроводность твердых тел. Пер. с. англ. М.: Наука, 1964. 488 с.

  3. Шашков А.Г., Бубнов В.А., Яновский С.Ю. Волновые явления теплопроводности: Системно-структурный подход. М.: Едиториал УРСС, 2004. 296 с.

  4. Wang L., Zhou X., Wei X. Heat Conduction: Mathematical Models and Analytical Solutions. Berlin: Springer–Verlag, 2008. 515 p.

  5. Карташов Э.М. Аналитические решения гиперболических моделей теплопроводности // ИФЖ. 2014. Т. 87. № 5. С. 1072.

  6. Карташов Э.М. Математические модели теплопроводности с двухфазным запаздыванием // ИФЖ. 2016. Т. 89. № 2. С. 338.

  7. Кудинов В.А., Кудинов И.В. Получение и анализ точного аналитического решения гиперболического уравнения теплопроводности для плоской стенки // ТВТ. 2012. Т. 50. № 1. С. 118.

  8. Кудинов В.А., Кудинов И.В. Исследование теплопроводности с учетом конечной скорости распространения теплоты // ТВТ. 2013. Т. 51. № 2. С. 301.

  9. Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М.: Высшая школа, 2001. 550 с.

  10. Карташов Э.М. Теплопроводность при переменном во времени относительном коэффициенте теплообмена // Изв. РАН. Энергетика. 2015. № 2. С. 138.

  11. Поляков А.Ф. Температурное поле в кольце с источником тепла и переменными граничными условиями третьего рода // ТВТ. 1968. Т. 6. № 3. С. 558.

  12. Минасян Р.С. О плоском установившемся течении тепла в составном цилиндре при наличии теплообмена с двумя различными окружающими средами // Докл. АН АрмССР. 1964. Т. 39. № 5. С. 257.

  13. Минасян Р.С. Об одной смешанной граничной задаче теплопроводности для полого составного цилиндра // Тепло- и массоперенос. Т. 8. Вопросы теории тепло- и массопереноса. Минск: Наука и техника, 1968. С. 205.

  14. Минасян Р.С. О смешанной граничной задаче теплопроводности для цилиндра конечной длины // Докл. АН АрмССР. 1986. Т. 82. № 5. С. 210.

  15. Минасян Р.С. Смешанная граничная задача теплопроводности для полого цилиндра конечной длины // Докл. АН АрмССР. 1986. Т. 83. № 4. С. 180.

  16. Минасян Р.С. О смешанной граничной задаче теплопроводимости для шара // Докл. АН АрмССР. 1978. Т. 67. № 3. С. 132.

  17. Минасян Р.С. Смешанная граничная задача теплопроводности для вращающегося цилиндра // Докл. АН АрмССР. 1984. Т. 78. № 1. С. 28.

  18. Минасян Р.С. О смешанной граничной задаче теплопроводности для составного цилиндра // Докл. АН АрмССР. 1985. Т. 80. № 5. С. 210.

  19. Минасян Р.С. Об одной задаче периодического течения тепла в бесконечном цилиндре // Докл. АН АрмССР. 1969. Т. 48. № 1. С. 3.

  20. Минасян Р.С. Об одной периодической задаче теплопроводности в полом бесконечном цилиндре // ИФЖ. 1969. Т. 17. № 5. С. 880.

  21. Минасян Р.С. Об одной задаче распространения тепла в полном шаре, заполненном хорошо перемешиваемой жидкостью // Докл. АН АрмССР. 1977. Т. 64. № 4. С. 202.

  22. Кирсанов Ю.А. Циклические тепловые процессы и теория теплопроводности в регенеративных воздухоподогревателях. М.: Физматлит, 2007. 240 с.

  23. Zudin Y.B. Theory of Periodic Conjugate Heat Transfer. Heidelberg–Dordrecht–London–N.Y.: Springer, 2016. 301 p.

  24. Зудин Ю.Б., Уртенов Д.С. Теплопроводность с периодическим (по поверхности и по времени) коэффициентом теплоотдачи // Изв. РАН. Энергетика. 2017. № 5. С. 121.

  25. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. М.–Л.: Физматлит, 1962. 708 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал