Теплофизика высоких температур, 2019, T. 57, № 5, стр. 742-747

ВВЕДЕНИЕ

Подводный старт ракет сопровождается процессами интенсивного истечения горячих продуктов сгорания топлива двигателя в воду и тепломассообменом горячего газа с жидкостью. Это происходит при запуске маршевого двигателя в затопленной водой шахте, при запуске твердотопливного газогенератора в воду, а также в процессах, сопутствующих старту, – при разгерметизации шахтного объема в момент выхода из него кормы или при послестартовом затоплении объема шахты водой. В результате возникает сложная, существенно нестационарная картина взаимодействия горячих струй газа с водой. Кроме того, для уменьшения гидродинамических нагрузок на ракету при старте с движущейся подводной лодки могут применяться различные устройства, обеспечивающие двухфазное обтекание ракеты на подводном участке траектории, например газогенераторы наддува газовой каверны. Эти особенности обтекания оказывают влияние на изменение давления как у корпуса ракеты, так и в шахте, что требуется учитывать при расчете гидродинамических нагрузок и кинематических параметров движения ракеты на шахтном участке. Более плотная компоновка ракеты и элементов стартовой системы в ограниченном объеме шахты подводной лодки, усложнение геометрии трактов приводят к локальным неравномерностям газодинамического и теплового воздействий. В течение многих лет в АО “ГРЦ Макеева” проводятся расчетно-теоретические и экспериментальные исследования подводного старта ракет и сопутствующих ему процессов, в частности, при запуске двигателя в затопленную водой шахту. Истечение газа создает интенсивную циркуляцию жидкости, которая в свою очередь воздействует на всплывающие пузыри и газожидкостные структуры [1–5]. Области знаний, связанные с исследованием нестационарных двухфазных потоков с учетом тепломассобмена, являются в настоящее время актуальными, и им посвящены работы многих авторов [6–8].

Целью настоящего исследования является создание математической модели процессов тепломассообмена горячих газовых струй с жидкостью при подводном старте ракет, проведение валидации и верификации разработанного метода математического моделирования.

МЕТОД РАСЧЕТА ГИДРОДИНАМИЧЕСКОЙ ЗАДАЧИ

С учетом полученных результатов исследования физических процессов и тепломассообмена двухфазных потоков выполнено математическое моделирование гидродинамических процессов. Решение получается численным интегрированием системы дифференциальных уравнений.

Для расчета турбулентных течений используются методы на основе осредненных по Рейнольдсу уравнений Навье–Стокса. При этом уравнения движения относительно осредненных параметров течения с использованием дивергенции тензора рейнольдсовых напряжений записываются следующим образом:

Наличие межфазовых членов при осреднении по Рейнольдсу и в модели турбулентности не учитывается из-за их малости. В математической модели учитывалась сила поверхностного натяжения на межфазной границе путем добавления в правую часть уравнения движения объемной силы

где $\sigma $ – коэффициент поверхностного натяжения, задается таблично в зависимости от температуры жидкости; $k = - {\text{div}}~{\mathbf{n}}$ – локальная кривизна контактной границы; ${\mathbf{n}} = \frac{{{\text{grad}}~\alpha }}{{\left| {{\text{grad}}~\alpha } \right|}}$ – нормаль к контактной границе.

Уравнения Навье–Стокса дополняются дифференциальными уравнениями неразрывности и энергии [9]. Решается двухмерная задача.

Граничные условия: на твердых стенках модели и шахты – условия прилипания $\upsilon = 0;$ на твердых стенках – условия постоянной температуры (280 К). Начальные условия ($t = 0$): в момент прорыва мембраны сопла в его критическом сечении – неподвижная граница раздела фаз газ–жидкость.

Уравнения стандартной модели турбулентности k–ε записываются следующим образом:

при этом используются следующие замыкающие соотношения: ${{\mu }_{{{\text{turb}}}}} = \rho {{C}_{\mu }}\frac{{{{k}^{2}}}}{\varepsilon }$ – турбулентная вязкость; ${{G}_{k}} = {{\mu }_{{{\text{turb}}}}}{{S}^{2}} \equiv 2{{\mu }_{{{\text{turb}}}}}{{S}_{{ij}}}{{S}_{{ji}}}$ $ \equiv {\kern 1pt} {\kern 1pt} {\kern 1pt} \,{\kern 1pt} {\kern 1pt} \frac{1}{2}{{\mu }_{{{\text{turb}}}}}$ × × ${{\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right)}^{2}}$ – генерация турбулентности; ${{C}_{{1\varepsilon }}},~{{C}_{{2\varepsilon }}},~{{C}_{\mu }},~{{\sigma }_{k}},{{\sigma }_{\varepsilon }}$ – константы модели.

Для замыкания системы также предполагается, что парогазовая смесь является совершенным газом, а жидкость – несжимаемая. Наличие межфазовых членов при этом не учитывается из-за их малости.

Для моделирования течений с переменной по времени конфигурацией двухмерной расчетной области используются динамические и перестраиваемые сеточные модели, при этом уравнение сохранения обобщенного скаляра $\varphi $ в интегральной форме формулируется для контрольного объема, границы которого перемещаются следующим образом [9]:

Здесь $\rho $ – плотность, u – вектор скорости потока, ${{{\mathbf{u}}}_{g}}$ – скорость перемещения сеточной области, D – коэффициент диффузии, ${{S}_{\varphi }}$ – источниковый член для $\varphi ,$ A – вектор площади граней контрольного объема, $\partial V$ указывает на интегрирование по поверхности контрольного объема V. Расчетная область со временем не изменяется.

Источниковый член в уравнении энергии – это теплота межфазового взаимодействия $\int_V {\left[ {r\dot {m} + \dot {m}\left( {H\left( {{{P}_{{\text{Г}}}}{{T}_{{\text{Г}}}}} \right) - H\left( {{{P}_{{\text{Г}}}}{{T}_{{\text{Ж}}}}} \right)} \right)} \right]} {\kern 1pt} dV,$ где $\dot {m}$ – массовая скорость парообразования на единицу объема.

В эйлеровых алгоритмах для дискретизации уравнений движения среды используется, как правило, неподвижная расчетная сетка (в ряде случаев сетка может быть деформируемой в определенных пределах, например для учета перемещения твердых границ). При этом межфазная граница перемещается по сетке, и для определения ее положения нужны специальные методики.

В литературе также используется деление алгоритмов на interface capturing и interface tracking (устоявшихся русских терминов нет) в зависимости от способа определения положения контактной поверхности. К первой группе относят эйлеровы подходы, в которых положение межфазной границы восстанавливается по получаемому объемному распределению так называемых маркеров (возможно использование дискретных маркеров-частиц или непрерывных маркеров-функций). В методах второй группы граница раздела непосредственно отслеживается связанными с ней поверхностными маркерами (дискретными или непрерывными) или узлами расчетной сетки.

Среди вышеуказанных методов в настоящее время предпочтение отдается использованию непрерывных маркеров-функций. Поскольку положение границы раздела при этом явно не отслеживается, для ее реконструкции применяют специальные методики. Обычно за границу раздела принимают изоповерхность среднего значения используемого маркера-функции, хотя применяют и более сложные методики.

Методы, использующие маркер-функцию, можно считать наиболее эффективными на сегодняшний день методами решения задач о течении жидкости со свободной поверхностью. Под эффективностью в данном случае понимается не только оптимальное соотношение между точностью алгоритма и временем решения задачи, но и возможность моделировать разнообразные сложные течения (в том числе трехмерные, со слиянием и разделением объемов, с учетом сил поверхностного натяжения, кавитацией и т.п.). В качестве примера таких течений можно назвать разрушение струи, движение крупных пузырей в жидкости, движение жидкости после обрушения дамбы, обтекание полностью или не полностью погруженных тел и пр.

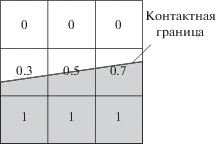
Широко используемым в настоящее время является метод VOF (Volume-of-Fluid), в котором в качестве маркера-функции используется объемная доля жидкости в ячейке расчетной сетки α: при α = 1 – ячейка заполнена жидкостью, при α = 0 – ячейка пуста. Межфазной границе соответствует изоповерхность α = 0.5 (рис. 1). Данный подход был предложен в работе [10] и имеет несколько разновидностей, отличающихся способом определения маркера-функции и/или способом задания граничных условий на границе раздела (метод псевдоконцентраций [11], метод скалярного уравнения [12] и др.). Эволюция маркера-функции описывается в общем виде уравнением переноса

где t – временнáя координата, ${{x}_{i}}$ – i-я пространственная координата, ${{u}_{i}}$ – скорость в направлении i-й пространственной координаты. Неустойчивость на границе раздела фаз при разных скоростях фаз в рассматриваемом случае не учитывается, используется алгоритм определения координат свободных границ раздела фаз.

В литературе имеется множество примеров успешного применения метода VOF для решения самых разнообразных задач. Косвенно о достоинствах метода VOF свидетельствует тот факт, что именно этот подход применяется для решения задач со свободной поверхностью в таких известных коммерческих CFD-пакетах, как ANSYS Fluent, Star-CD, CFX, Flow-3D и др.

В настоящей работе использовалась так называемая “одножидкостная” разновидность метода VOF, в которой уравнения сохранения массы и количества движения системы жидкость–газ формулируются как для сплошной среды с объемными характеристиками, выражаемыми через объемную долю жидкости (или газа) (маркер-функцию) следующим образом:

Здесь p – давление, ${\mathbf{g}}$ – ускорение свободного падения, индексы “ж” и “г” относятся к жидкости и газу соответственно, $\mu $ – динамическая вязкость.

Тензор вязких напряжений находится при этом как

где ${\mathbf{I}}$ – единичная матрица.

МЕТОДЫ РАСЧЕТА ТЕПЛОМАССООБМЕНА

Температура поверхности испарения должна определяться из решения правильно поставленной краевой задачи. Такой подход является академически строгим, но вычислительно затратным вследствие необходимости явного моделирования тепломассообмена с учетом затрат на теплоту испарения–конденсации и сопряженные процессы. Также численная модель такого процесса довольно часто бывает вычислительно неустойчивой. В данной статье предлагается упрощенная методика, по которой тепловой поток между ячейками, соседними с теми, в которых маркер-функция равен нулю, уточняется исходя из решения описанной задачи теплообмена.

Процессы тепломассообмена в двухфазных потоках осуществляются на границе раздела фаз газ–жидкость. Переносимая теплота газового потока конвекцией подводится к границе жидкости, что приводит к испарению части жидкости с ее поверхности в окружающую среду, а часть переносится посредством теплопроводности внутрь жидкости. Удельный тепловой поток вследствие конвекции находится согласно уравнению Ньютона $q = {{\alpha }_{t}}\left( {{{T}_{{\text{г}}}} - {{T}_{\omega }}} \right).$ Зависимости скоростей переноса теплоты от свойств фаз и параметров течения представляется в расчете коэффициентом теплоотдачи ${{\alpha }_{t}} = \frac{\lambda }{d}{\text{N}}{{{\text{u}}}_{P}}$ с использованием модели Томиямы [13, 14]

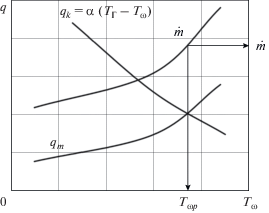
Здесь $\operatorname{Re} _{q}^{{}} = \frac{{\upsilon {{\rho }_{q}}d}}{{{{\mu }_{q}}}}$ – число Рейнольдса, вычисленное по характерному линейному размеру d кольцевого зазора и относительной скорости $u = \left| {{{{\bar {u}}}_{P}} - {{{\bar {u}}}_{q}}} \right|,$ ${\text{Pr}}$ – число Прандтля для q-й фазы ${\text{Pr}} = {{{{С}_{{pq}}}{{{\mu }}_{q}}} \mathord{\left/ {\vphantom {{{{С}_{{pq}}}{{{\mu }}_{q}}} {{{\lambda }_{q}}}}} \right. \kern-0em} {{{\lambda }_{q}}}},$ ${{С}_{{pq}}}$ – удельная теплоемкость фазы q, ${{\mu }_{q}}$ – динамическая вязкость, ${{\lambda }_{q}}$ – коэффициент теплопроводности, ${{\rho }_{q}}$ – плотность q-й фазы.

Для расчетной оценки массового потока пара необходимо знать температуру поверхности испарения. Значение этой температуры можно найти только после выполнения теплового расчета. Поэтому расчет массового парового потока приходится выполнять для нескольких значений температуры поверхности жидкости ${{T}_{{\omega }}},$ меньших температуры насыщения при заданном давлении газа. Условие теплового баланса на границе раздела фаз позволяет выявить равновесное состояние системы и отвечающие ему значения $\dot {m}$ и ${{T}_{{\omega }}}.$ Обозначим плотность теплового потока $~{{q}_{k}},$ поступающего от внешней среды к поверхности испарения путем конвекции:

плотность потока ${{q}_{m}},$ расходуемого на испарение и подогрев жидкости до равновесной температуры испарения (первое слагаемое правой части), и потока, отводимого внутрь жидкости (второе слагаемое правой части), [15, 16]: Здесь $r~$ – удельная теплота парообразования; $\lambda ~$ – коэффициент теплопроводности жидкости; $\delta ~$ – толщина пограничного слоя; $H\left( {{{p}_{{\text{г}}}}{{T}_{{\text{г}}}}} \right),$ $H\left( {{{p}_{{\text{г}}}}{{T}_{\omega }}} \right)~$ – полные энтальпии фаз, которые можно выразить в общем виде: где ${{T}_{r}}$ – опорная температура, $H\left( {{{T}_{r}}} \right)$ – энтальпия стандартного состояния при ${{T}_{r}}.$

При соблюдении теплового баланса $\left( {{{q}_{k}} = {{q}_{m}}} \right)$ и принятой модели фазового перехода (1), (2) рассчитаем равновесные значения ${{T}_{\omega }}$ и $\dot {m}$. Модель фазового перехода качественно иллюстрируется графиками на рис. 2.

При соприкосновении пара с поверхностью, температура которой меньше температуры насыщения, для определения ${{T}_{\omega }}$ и $\dot {m}$ в условиях конденсации перегретого пара используются также условия теплового баланса и модель (1), (2).

Таким образом, в модели теплового фазового перехода процесс массопередачи при испарении–конденсации полностью обусловливается процессами межфазовой теплопередачи и общим тепловым балансом [17, 18]. Для установления границ раздела фаз (газ–жидкость) и газодинамических параметров образующейся парогазовой смеси необходимо решить гидрогазодинамическую задачу.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Экспериментальные исследования выполнены на вертикальном гидрогазодинамическом стенде (рис. 3), состоящем из моделей ракеты 1, затопленной водой шахты 2, обтюратора, частично перекрывающего кольцевой зазор 3, порохового аккумулятора давления 4 (ПАД). Стенд оснащен датчиками давления и температуры среды 5. Длина модели ракеты составляет 1050 мм, диаметр – 200 мм, длина модели шахты – 1250 мм и диаметр – 230 мм. Весь процесс испытания на стенде можно условно разделить на отдельные стадии: включение порохового аккумулятора давления и последующий прорыв мембраны сопла, истечение горячих продуктов сгорания пороха в затопленный водой задонный объем, сопровождающееся повышением донного давления и процессами интенсивного тепломассообмена горячих газовых струй с жидкостью. Массовый расход в ПАД составлял 0.4 кг/с при прорыве мембраны и достигал значения 1.1 кг/с в момент выхода модели из шахты.

Основные параметры ПАД: температура горения – 2250 К, газовая постоянная – 373 Дж/(кг К), коэффициент адиабаты k = 1.25, С_р = 780 Дж/(кг К) [19].

Стенд оснащен датчиками давления и температуры в камере сгорания порохового аккумулятора давления и на поверхностях моделей ракеты и шахты.

РЕЗУЛЬТАТЫ РАСЧЕТОВ И СРАВНЕНИЕ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

Расчетная область представляет собой задонное пространство, кольцевой зазор и прилегающую к срезу шахты область жидкости. При этом на срезе сопла порохового аккумулятора давления заданы массовый расход и температура газовых продуктов сгорания пороха, рассчитанные по теории изоэнтропических течений с использованием замеренных при испытании давления и температуры среды в камере сгорания ПАД. Моделирование производилось со следующими настройками: для обеспечения точности и сходимости расчета исследовалось влияние параметров сеточной модели на результаты расчета. В расчетах использовалась сеточная модель с гексаэдрическими ячейками, измельченными в зоне пограничного слоя на твердых стенках. Общее количество ячеек в модели ∼3 × 10⁶, характерный размер ячейки в зоне двухфазного течения варьировалась от 2 до 10 мм, толщина первой пристенной ячейки – 0.5 мм, количество слоев – 10, коэффициент роста толщины слоя – 1.2. При указанных параметрах сеточной модели и характерных скоростях течения вариацией шага по времени обеспечивалось число Куранта не более 50, что гарантировало устойчивость расчета. Указанные размеры ячеек в пограничном слое при характерных скоростях течения обеспечивали величину параметра у⁺ не более 10, что допустимо при использовании в k–ε-модели турбулентности.

В силу осевой симметрии течения расчетная область представляет собой меридиональную плоскость от оси симметрии до границы. Выявлено также, что численное решение зависит от используемого линейного размера в критерии Рейнольдса. Наилучшее соответствие результатов расчетов с экспериментальными данными получилось при использовании в качестве линейного размера диаметра критического сечения сопла ПАД. Сходимость численного метода к точному решению исходной краевой задачи подтверждена расчетами с уменьшением размеров сетки. Верификация и валидация разработанного метода проводились сравнением результатов расчета с экспериментальными данными.

Сравнение представлено на рис. 4 в виде графиков зависимостей безразмерной температуры газовой среды T/T₀ и безразмерного давления Р/Р₀ в задонной области в зависимости от безразмерного времени, рассчитываемого по формуле

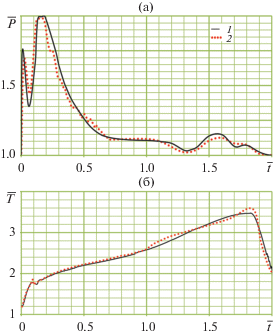
Здесь T₀ – начальная температура стенки, Р₀ – гидростатическое давление на верхнем срезе шахты, L – длина модели. Видно, что в целом результаты расчетов удовлетворительно согласуются с данными экспериментов.

ЗАКЛЮЧЕНИЕ

Разработана математическая модель процессов тепломассообмена горячих газовых струй с жидкостью при подводном старте ракет. На основе разработанной модели создана программа расчета тепловых и газодинамических процессов при старте. Валидация и верификация выполнены с помощью экспериментальных данных. Получено удовлетворительное согласие.