Теплофизика высоких температур, 2019, T. 57, № 5, стр. 651-659

ВВЕДЕНИЕ

Знание термодинамических свойств плазменных сред при высоких температурах и давлениях необходимо в различных областях экспериментальной и теоретической физики. В частности, такая потребность возникает при исследовании космических объектов, в экспериментах по ударному сжатию, при ядерных взрывах и т.д. [1]. Кроме того, электроны в металлах, электроны и дырки в полупроводниках даже при “обычных” температурах и давлениях могут демонстрировать поведение, в значительной степени аналогичное поведению плазменных сред в экстремальных состояниях [2]. Особый интерес представляют пороговые энергии и константы скоростей химических и ядерных реакций, необходимые при изучении процессов горения, детонации, термоядерного синтеза при высоких давлениях [3].

Однако при исследованиях веществ в экстремальных условиях возникают определенные трудности. Во-первых, эксперимент в этом случае является сложным и дорогостоящим мероприятием; зачастую он вовсе неосуществим при современном уровне развития науки и техники. Во-вторых, такие системы в большинстве случаев являются квантовыми и сильнонеидеальными, так что различные аналитические подходы и модели, основанные на теории возмущений, неприменимы ввиду отсутствия физических параметров малости. Поэтому при исследовании таких систем на первое место выходит численное моделирование, позволяющее проводить расчеты различных термодинамических и кинетических свойств кулоновских систем, исходя из первых принципов.

Одними из наиболее мощных численных подходов к моделированию термодинамических свойств сильнонеидеальных квантовых систем являются методы Монте-Карло, основанные на интегралах по траекториям. Стандартные подходы [4–6] используют представление статистической суммы и термодинамических величин в виде интегралов по путям в координатном пространстве. Однако эти подходы не позволяют проводить вычисления средних значений произвольных квантовых операторов, зависящих от импульсов и координат частиц. Тем более, эти методы не могут быть использованы для расчета кинетических и транспортных свойств вещества.

Предложенная Вигнером формулировка квантовой механики [7] позволяет особенно просто анализировать физические величины, зависящие от импульсов и координат частиц. Этот формализм основан на квантовой функции распределения в фазовом пространстве, называемой функцией Вигнера и определяющейся как преобразование Фурье матрицы плотности:

Среднее значение произвольного оператора $\hat {A} = A(\hat {p},\hat {q})$ по ансамблю, определяемому матрицей плотности ρ(q, q'), может быть вычислено по формуле:

Здесь функция импульсов и координат A(p, q), которая ставится в соответствие оператору, называется его символом Вейля:

причем S – общее число координат системы. Формула (2) аналогична хорошо известной формуле для среднего по ансамблю в классической статистике. При этом функция Вигнера является квантовым аналогом функции распределения в фазовом пространстве, а символ Вейля – аналогом усредняемой классической величины.

Несмотря на то что вигнеровская формулировка квантовой механики появилась в 30-х годах XX века, только в последние два десятилетия ее стали применять для изучения квантовомеханических систем. В работе [8] было предложено обобщение функции Вигнера на одночастичную систему с релятивистской динамикой и получено соответствующее уравнение временной эволюции. На основе [8] разработан метод, позволяющий численно моделировать временную эволюцию функции Вигнера для релятивистской частицы во внешнем поле, и исследована динамика релятивистского гармонического осциллятора [9, 10]. В [11] в рамках вигнеровского формализма исследована динамика микроканонического ансамбля фермионов с кулоновским взаимодействием. Однако использованный метод пригоден только для небольших систем с числом частиц порядка десяти. В работах [12, 13] с помощью вигнеровского подхода проведено квазиклассическое исследование модели кварк-глюонной плазмы. Получено уравнение состояния, пространственные и временны́е корреляционные функции, а также вычислены некоторые транспортные коэффициенты.

В работе [14] предложено использовать функцию Вигнера для расчета термодинамических свойств и равновесных функций распределения по импульсам. Для этого было получено следующее представление функции Вигнера для канонического ансамбля в виде интеграла по траекториям:

где символ P обозначает всевозможные перестановки тождественных частиц, q(τ) = λz(τ) + (1 – τ)× × (q – ξ/2) + τP(q + ξ/2). Это выражение непосредственно непригодно для расчетов на ЭВМ, так как преобразование Фурье технически невозможно из-за большой размерности интеграла (3N). Для преодоления этой проблемы предложены приближенные методы LAPIMC и HAPIMC, основанные на разложении потенциальной энергии в степенной ряд по ξ. С их помощью проведены расчеты функций распределения по импульсам водородной и электрон-дырочной плазмы [14–16]. Кроме того, предложен “одноимпульсный” подход и метод SMPIMC [17], позволяющий свести задачу к одномерному преобразованию Фурье. Этот метод испытан на простейших одночастичных системах.

Основная цель данной работы заключалась в обобщении “одноимпульсного” подхода на многочастичные системы, разработке метода SMPIMC для двухкомпонентных фермионных систем и расчете термодинамических свойств и парных корреляционных функций сильнонеидеальной водородной плазмы с умеренным вырождением.

“ОДНОИМПУЛЬСНАЯ” ФУНКЦИЯ ВИГНЕРА

Рассмотрим какой-либо многочастичный оператор, который можно представить в виде суммы одинаковых одночастичных операторов, зависящих от импульсов частиц: $\hat {A} = \sum {a\left( {{{{{\mathbf{\hat {p}}}}}_{a}}} \right)} $ (сумма берется по номерам частиц a). В частности, такую структуру имеет оператор кинетической энергии системы. Так как все частицы одного сорта в условиях термодинамического равновесия тождественны, то среднее значение оператора Â может быть выражено через среднее значение какого-либо одночастичного оператора, например для первой частицы: $\left\langle {\hat {A}} \right\rangle = \int {dpdq} Na\left( {{{p}_{1}}} \right)W\left( {p,q} \right).$

Теперь рассмотрим многочастичный оператор, зависящий только от координат всех частиц и инвариантный относительно их перестановок: $\hat {B} = B\left( {{{{\hat {q}}}_{1}},{{{\hat {q}}}_{2}}, \ldots ,{{{\hat {q}}}_{N}}} \right).$ В частности, таким оператором является оператор потенциальной энергии системы. Среднее значение такого оператора может быть вычислено следующим образом: $\left\langle {\hat {B}} \right\rangle = \int {dpdqB\left( {{{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{N}}} \right)} {\kern 1pt} W\left( {p,q} \right),$ причем зависимость функции Вигнера от импульса в этом случае не требуется вовсе.

Таким образом, для вычисления операторов вида $\hat {T} = \sum {a\left( {{{{\hat {p}}}_{a}}} \right) + B\left( {{{{\hat {q}}}_{1}},{{{\hat {q}}}_{2}}, \ldots ,{{{\hat {q}}}_{N}}} \right)} $ достаточно знать “одноимпульсную” функцию Вигнера:

т.е. функцию Вигнера, проинтегрированную по импульсам всех частиц, кроме одной. Среднее значение оператора $\hat {T}$ вычисляется при этом по формуле: С другой стороны, импульсы всех частиц входят в определение функции Вигнера (1) только через преобразование Фурье. Поэтому интегрирование функции Вигнера по импульсам ${{p}_{2}},{{p}_{3}}, \ldots ,{{p}_{N}}$ приводит к появлению дельта-функций от переменных ξ, в результате чего имеем где ρ_SM обозначает “одноимпульсную” матрицу плотности

Выражение (4) представляет собой трехмерное преобразование Фурье от недиагональных элементов матрицы плотности, которое в принципе может быть выполнено численно с помощью ЭВМ. Если интересоваться физическими величинами и функциями распределения, зависящими от абсолютных значений импульсов, можно упростить задачу еще больше и свести ее к одномерному преобразованию Фурье. Так как “одноимпульсная” матрица плотности ρ_SM в силу изотропности зависит только от абсолютной величины импульса, то, выбирая ось Z в направлении импульса и переходя к сферическим координатам, получаем

Таким образом, при вычислении средних значений величин и функций распределения, зависящих от абсолютных значений импульсов, “одноимпульсная” функция Вигнера может быть получена с помощью одномерного синусного преобразования Фурье.

В данной работе рассматриваются только системы, состоящие из фермионов со спином 1/2, так что упростим выражение для ρ_SM, собрав все перестановки тождественных частиц в определители соответствующих матриц. Прежде всего, заметим, что в вырожденной системе среднее расстояние между частицами не превышает тепловой длины волны де Бройля λ, в результате чего траектории, представляющие частицы, сильно “перепутаны” друг с другом. Из-за этого потенциальная энергия U(q(τ)) для различных перестановок не должна сильно отличаться от таковой для тождественной перестановки:

где n обозначает плотность частиц. В случае же, когда система вырождена слабо, обменное взаимодействие мало и вклад перестановок в потенциальную энергию также оказывается незначительным. В обоих случаях перестановки не связаны с потенциальной энергией и в формуле (3) могут быть собраны в определитель матрицы N_σ × N_σ: где a, b обозначают номера частиц с проекцией спина σ, причем ξ_a, ξ_b равны нулю при a ≠ 1 и b ≠ 1.

Таким образом, “одноимпульсная” функция Вигнера может быть получена с помощью одномерного преобразования Фурье (5) “одноимпульсной” матрицы плотности, которая представляется интегралом по траекториям:

Каждому значению проекции спина σ соответствует свой детерминант ${{D}_{\sigma }}\left( {\xi ;q} \right).$ При этом зависимость от переменной ξ содержится как в детерминантах, так и в потенциальном слагаемом под экспонентой. Если система содержит фермионы разных сортов, то каждому сорту будут соответствовать 2s + 1 определителей (6), по одному на каждое значение проекции спина.

ЧИСЛЕННЫЙ МЕТОД SMPIMC

Разработанный авторами в [17] метод SMPIMC (Single Momentum Path Integral Monte Carlo), основанный на “одноимпульсной” функции Вигнера, может быть использован для расчета термодинамических свойств неидеальных систем, состоящих из фермионов разных сортов. Рассмотрим алгоритм этого метода, для краткости ограничиваясь случаем однокомпонентной системы, состоящей из фермионов со спином 1/2. На многокомпонентную систему все рассуждения распространяются непосредственно, и там, где это необходимо, будут даны соответствующие указания.

Представим выражение (7) для “одноимпульсной” матрицы плотности ρ_SM в дискретизованной форме:

Каждая траектория z(τ) приближенно представляется замкнутой ломаной линией с M звеньями, причем вершины z^m являются 3N-мерными координатами, по которым берется 3N(M–1)-кратный интеграл. При достаточно большом M это выражение аппроксимирует (7) с точностью O(M^–2).

В “одноимпульсном” подходе основной интерес представляют одночастичная функция распределения по импульсам F(|p|) и средние значения операторов “одноимпульсного” вида. Обозначим через f(ξ) “одноимпульсную” матрицу плотности ρ_SM, проинтегрированную по координатам всех частиц.

Тогда F(|p|) может быть вычислена как синусное преобразование Фурье от f(ξ):

Среднее значение части оператора $\hat {T},$ зависящей от импульса, может быть вычислено усреднением одночастичного оператора a(p) с функцией распределения F(|p|). Среднее значение части $\hat {T},$ зависящей от координат, может быть вычислено ее усреднением с матрицей плотности ρ_SM, проинтегрированной по ξ.

Таким образом, вычисление средних значений операторов, а также функций распределения по импульсам и координатам сводится к вычислению многомерных интегралов следующего вида:

Здесь Ω – многомерная область интегрирования, x – совокупность координат ξ, q, z¹, z², …, z^M–1, P(x) = |ρ_SM| – неотрицательная функция, имеющая смысл плотности вероятности, w(x) = = sign(ρ_SM) – знакопеременная весовая функция, f(x) – усредняемая величина. Для вычисления таких интегралов может быть использована процедура Монте-Карло, основанная на оценке подынтегральных выражений на случайных выборках конфигураций, распределенных с плотностью P(x). Такие выборки получаются с помощью алгоритма Метрополиса [18] в результате марковского процесса.

Таким образом, общая схема алгоритма метода SMPIMC такова.

1. Задается начальная конфигурация системы x = x₀. N частиц размещаются случайным образом по всему объему V так, чтобы распределение их координат q_a было равновероятным. Траектории, представляющие частицы, стянуты в точки, так что ${\mathbf{z}}_{a}^{m}$ = 0. Фурье-координата равна нулю, ξ = 0.

2. Случайным образом выбирается шаг: а) с вероятностью P_q – изменение координаты одной из частиц, б) с вероятностью P_z – деформация траектории, представляющей одну из частиц, в) с вероятностью P_ξ – изменение фурье-переменной.

3. В случае шагов а и б случайным образом выбирается частица с номером a с вероятностью 1/N.

4. С вероятностями g(q → q'), g(z → z'), g(ξ → ξ') соответственно изменяется состояние частицы a: x → x'.

5. Состояние x' принимается с вероятностью $A\left( {x \to x{\kern 1pt} '} \right) = \min \left( {1,\frac{{P\left( {x{\kern 1pt} '} \right)}}{{P\left( x \right)}}} \right)$ в качестве x либо отклоняется.

6. Пункты 2–5 повторяются до тех пор, пока не получится последовательность из N_MC0 + N_MC конфигураций x.

7. Первые N_MC0 конфигураций отбрасываются, чтобы результат не зависел от выбора начальной конфигурации x₀.

8. Требуемые физические величины вычисляются усреднением соответствующих выражений по N_MC конфигурациям.

Вероятности g(q → q'), g(z → z'), g(ξ → ξ') изменения состояния частицы (пункт 4):

где i = (x, y, z), Δ_q, Δ_z, Δ_ξ – постоянные положительные параметры, подбираемые так, чтобы доля принятых конфигураций составляла от 20 до 50%. Вероятности шагов P_q, P_z, и P_ξ выбираются из тех же соображений.

Так как существующие ЭВМ позволяют моделировать лишь системы с относительно малым (N < 10³) числом частиц при числе звеньев траекторий M ~ 10², то при заданной плотности n = N/V приходится существенно ограничивать объем и рассматривать системы с размерами, не превышающими среднее межчастичное расстояние более чем на порядок. Из-за этого существенную роль начинают играть поверхностные эффекты, связанные с тем, что значительная доля частиц находится у границы и менее эффективно взаимодействует с остальной системой. Чтобы практически исключить влияние нежелательных поверхностных эффектов, на систему накладываются периодические граничные условия. При шагах, изменяющих координаты частиц q и траектории z, а также при расчете координатных частей операторов и корреляционных функций в качестве координат q_a берется координата частицы в основной ячейке. Каждая частица взаимодействует только с ближайшими образами других частиц. При шагах, изменяющих переменную Фурье ξ, используется более сложная процедура наложения периодических граничных условий. В этом случае берутся координаты q_– и q₊, лежащие в основной ячейке Монте-Карло, и вычисляется их разность, которая может превысить размеры ячейки. В этом случае в качестве ξ применяется образ q₊–q_–, лежащий в основной ячейке.

РАСЧЕТ ТЕРМОДИНАМИЧЕСКИХ СВОЙСТВ ВОДОРОДНОЙ ПЛАЗМЫ

Водородная плазма состоит из электронов и протонов со спином 1/2, взаимодействующих по закону Кулона. Электроны обладают массой m_e и отрицательным зарядом –e, протоны – массой m_p ≈ 1836m_e и положительным зарядом +e. Числа частиц каждого сорта обозначим N_e и N_p, причем в силу электронейтральности N_e = N_p = N/2. Гамильтониан такой системы имеет вид

В водородной плазме имеется несколько масштабов длин, соотношения между которыми определяют ее термодинамические свойства. Радиус Вигнера–Зейца характеризует среднее межчастичное расстояние. Длина Ландау $l = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {kT}}} \right. \kern-0em} {kT}}$ определяет расстояние между частицами, на котором их взаимная потенциальная энергия равна кинетической энергии. Средние тепловые длины волн де Бройля ${{\lambda }_{e}} = \sqrt {\frac{{2\pi {{\hbar }^{2}}}}{{{{m}_{e}}kT}}} $ и ${{\lambda }_{p}} = \sqrt {\frac{{2\pi {{\hbar }^{2}}}}{{{{m}_{p}}kT}}} $ характеризуют квантовые размеры частиц. Боровский радиус a₀ определяет размеры связанных состояний. На практике удобно использовать безразмерные комбинации этих характерных длин: параметр Бракнера r_s = d/a₀, параметры вырождения электронов χ_e = n_e$\lambda _{e}^{3}$ и протонов χ_p = n_e$\lambda _{p}^{3},$ а также параметр неидеальности $\Gamma = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {dkT}}} \right. \kern-0em} {dkT}}.$

При моделировании методами PIMC вместо истинно кулоновского потенциала следует использовать специальные псевдопотенциалы, учитывающие квантовые эффекты при r_ab < a₀. Одним из наиболее известных псевдопотенциалов такого рода является потенциал Кельбга [19], зависящий от температуры:

где ${{\lambda }_{{ab}}} = {{\left( {\lambda _{a}^{{ - 1}} + \lambda _{b}^{{ - 1}}} \right)} \mathord{\left/ {\vphantom {{\left( {\lambda _{a}^{{ - 1}} + \lambda _{b}^{{ - 1}}} \right)} {\sqrt {2\pi } }}} \right. \kern-0em} {\sqrt {2\pi } }}.$ Заметим, что потенциал Кельбга конечен при r_ab = 0, что является следствием принципа неопределенности Гейзенберга для основного состояния атома водорода.

Функции распределения по импульсам. Прежде всего, были рассчитаны функции распределения по импульсам электронов и протонов в условиях, когда плазма сильнонеидеальна (0.8 ≤ Γ ≤ 2.0) и слабо или умеренно вырождена (0.3 ≤ χ_e ≤ 5.0). В этом случае волновые функции электронов в значительной степени перекрываются, так как d сопоставимо с λ_e, что приводит к существенной делокализации электронов и сильной ионизации системы [20].

Если бы межчастичное взаимодействие отсутствовало, то импульсы электронов и протонов описывались бы распределениями Ферми и Максвелла соответственно. Однако кулоновское притяжение электронов и протонов может формировать состояния, близкие к связанным, и несколько ограничивать доступный электронам объем. В силу принципа неопределенности Гейзенберга это приводит к росту неопределенности в значении импульсов и, следовательно, может изменить равновесные функции распределения [3].

На рис. 1 представлены функции распределения по импульсам электронов в водородной плазме при Γ = 0.8 (рис. 1а) и Γ = 1.2 (рис. 1б) и различных вырождениях. Несмотря на то что плазма в данных условиях является сильнонеидеальной, функция распределения электронов с большой точностью совпадает с распределением Ферми. Протоны при этом остаются максвелловскими. Расчеты методом SMPIMC показывают, что такое поведение сохраняется вплоть до Γ = 3.0.

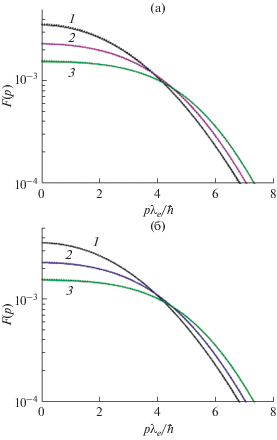
Метод SMPIMC не позволяет исследовать “хвосты” функций распределения по импульсам из-за сильного влияния периодических граничных условий на точность преобразования Фурье, так что надежный расчет возможен лишь в двух порядках по ${{F\left( {\left| p \right|} \right)} \mathord{\left/ {\vphantom {{F\left( {\left| p \right|} \right)} {F\left( 0 \right)}}} \right. \kern-0em} {F\left( 0 \right)}}.$ Тем не менее полученные результаты позволяют сделать важный вывод: в сильноионизованной водородной плазме импульсы электронов с большой точностью удовлетворяют распределению Ферми. Поэтому при расчете термодинамических величин, нечувствительных к “хвостам” функции распределения, можно использовать распределение Ферми. Таковыми являются, например, давление, средняя кинетическая и полная энергии и т.д. Это подтверждается, в частности, расчетами функции распределения в [15]: отклонения от распределения Ферми в водородной плазме наблюдаются лишь при ${{F\left( {\left| p \right|} \right)} \mathord{\left/ {\vphantom {{F\left( {\left| p \right|} \right)} {F\left( 0 \right)}}} \right. \kern-0em} {F\left( 0 \right)}} < {{10}^{4}}.$

Внутренняя энергия и давление. Полная внутренняя энергия рассчитывалась как сумма средней кинетической и потенциальной энергий: $E = \left\langle {\hat {K}} \right\rangle + \left\langle {\hat {U}} \right\rangle .$ Давление вычислялось через среднюю кинетическую энергию и вириал сил:

где F_ab – сила кулоновского взаимодействия между частицами a и b. Как было показано выше, электроны с большой точностью подчиняются распределению Ферми, в то время как протоны являются максвелловскими. Поэтому средние кинетические энергии электронов и протонов с большой точностью равны соответствующим энергиям в идеальном газе.

На рис. 2а показана полная внутренняя энергия, приходящаяся на одну частицу в водородной плазме, при различных значениях Γ и χ_e. Во-первых, внутренняя энергия уменьшается при увеличении Γ, так как усиливается притяжение между электронами и протонами. Во-вторых, с ростом вырождения внутренняя энергия увеличивается, так как обменное отталкивание усиливается, в то время как кулоновское притяжение ослабевает. В-третьих, при значительном вырождении E является практически линейной функцией χ_e, однако при слабом вырождении эта зависимость более резкая, что связано с образованием связанных состояний в данной области состояний. При этом статистическая погрешность метода SMPIMC резко возрастает, что не позволяет продвинуться в область меньших вырождений. Для сравнения на рисунке также приведены результаты расчета полной внутренней энергии методом DPIMC [5], в пределах статистических ошибок согласующиеся с расчетами SMPIMC.

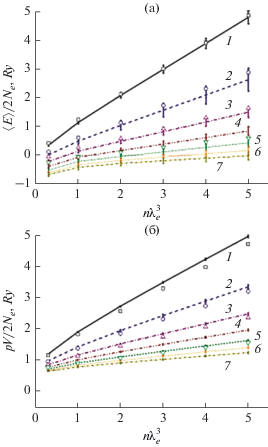
На рис. 2б показано давление в водородной плазме, умноженное на объем и отнесенное к одной частице при различных значениях Γ и χ_e. Как и внутренняя энергия, давление уменьшается при увеличении Γ из-за притяжения между электронами и протонами и возрастает при увеличении χ_e из-за обменного взаимодействия. При значительном вырождении pV является почти линейной функцией χ_e, а при слабом вырождении эта зависимость значительно более резкая из-за возникновения связанных состояний. Для сравнения на рисунке также приведены результаты расчета давления методом DPIMC [5], причем результаты SMPIMC несколько превышают результаты DPIMC, особенно при больших Γ.

Наконец, вычисленные значения полной внутренней энергии и давления представлены в таблице (с указанием статистической ошибки). В каждой ячейке верхнее число – полная внутренняя энергия, приходящаяся на одну частицу, а нижнее – давление, умноженное на объем и отнесенное к числу частиц. Отрицательное значение давления, полученное при Γ = 2.0 и χ_e = 0.8, объясняется, по всей видимости, погрешностью метода. Результаты, собранные в таблице, подтверждают и расширяют результаты, полученные методом DPIMC в работе [5].

Парные корреляционные функции. Парные корреляционные функции g_ab(r) определяют вероятность обнаружить частицы сортов a и b на расстоянии r друг от друга. Если частицы не взаимодействуют, то соответствующие корреляционные функции тождественно равны единице. Неравенство g_ab(r) > 1 говорит о преимущественном притяжении, g_ab(r) < 1 – о преимущественном отталкивании частиц на данном расстоянии.

На рис. 3а представлены парные корреляционные функции в слабовырожденной водородной плазме при Γ = 1.0 и χ_e = 0.3. Корреляционная функция g_ep резко возрастает на малых расстояниях из-за кулоновского притяжения; для наглядности ее масштаб был уменьшен в 25 раз. В то же время корреляционные функции g_ee и g_pp спадают при r ≤ 7a₀ из-за кулоновского и обменного отталкивания. Заметим, что g_ee, в отличие от g_pp, не обращается в нуль на малых расстояниях благодаря квантовому туннелированию электронов с противоположными спинами.

На рис. 3б представлены парные корреляционные функции в водородной плазме при том же значении Γ, но при значительно большем вырождении χ_e = 4.0. Качественно характер пространственных корреляций между частицами не изменился. Однако теперь вероятность сближения электрона и протона существенно ниже из-за нелокальности электронов, чей характерный размер λ_e ≈ 2.5a₀ превосходит область корреляций.

На рис. 4а представлены парные корреляционные функции в водородной плазме при существенно большем параметре неидеальности Γ = 2.0 и χ_e = 1.0. Несмотря на вырождение, функция g_ep на малых расстояниях оказывается существенно больше, чем в случае Γ = 1.0, χ_e = 0.3. Кроме того, функция g_pp имеет максимум при r ≈ 2a₀, что свидетельствует об образовании связанных состояний протон-протон, а именно – молекулярных ионов H₂ [20].

На рис. 4б представлены парные корреляционные функции при том же значении Γ, однако при большем вырождении χ_e = 2.0. Видно, что вероятность сближения протонов и электронов существенно уменьшилась из-за большей нелокальности последних. Кроме того, отсутствуют признаки связанных состояний “протон–протон”: функция g_pp монотонно возрастает от нуля до единицы.

Свидетельством того, что в плазме присутствуют неионизованные атомы водорода, является локальный максимум функции g_epr² на расстоянии порядка a₀ [20]. На рис. 5 показаны функции g_epr² для всех условий, рассмотренных выше. В случаях Γ = 1.0, χ_e = 0.3 и Γ = 2.0, χ_e = 1.0 наблюдается отчетливый пик при 1.0 ≤ r/a₀ ≤ 2.5, что свидетельствует о наличии в плазме атомов водорода. Однако при большем вырождении он существенно уменьшается (Γ = 2.0, χ_e = 2.0), пока не исчезнет вовсе (Γ = 1.0, χ_e = 4.0). Причина этого заключается в том, что при увеличении плотности плазмы волновые функции электронов, находящихся в соседних атомах, начинают перекрываться, в результате чего электрон получает возможность покинуть атом благодаря квантовому туннелированию (эффект Мотта, или ионизация давлением). Отметим, что убывание функции g_epr² в случае Γ = 1.0, χ_e = 4.0 является граничным эффектом и не содержит физического смысла.

ЗАКЛЮЧЕНИЕ

Проведено обобщение подхода, основанного на “одноимпульсной” функции Вигнера [17], на многочастичные фермионные системы. На его основе разработан численный метод SMPIMC, позволяющий рассчитывать различные термодинамические величины, средние значения операторов, функции распределения по импульсам и парные корреляционные функции для сильнонеидеальных многокомпонентных систем фермионов с умеренным вырождением. С помощью этого метода рассчитаны функции распределения по импульсам, внутренняя энергия и давление, а также парные корреляционные функции водородной плазмы в условиях Γ ≤ 2.0, χ_e ≤ 5.0. Представленные данные подтверждают и дополняют результаты, полученные другими методами.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 18-32-00282).