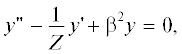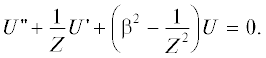Теплофизика высоких температур, 2019, T. 57, № 5, стр. 790-792
Аналитический расчет нестационарного температурного поля плоского тела при переменном коэффициенте теплопроводности
Ю. В. Видин 1, В. С. Злобин 1, *
1 Сибирский федеральный университет
г. Красноярск, Россия
* E-mail: zlobinsfu@mail.ru
Поступила в редакцию 24.10.2018
После доработки 11.03.2019
Принята к публикации 27.03.2019
Аннотация
Получены аналитические формулы, описывающие нестационарное температурное поле в неоднородных конструкциях. На практике такие конструкции наиболее часто являются многослойными, что осложняет в математическом отношении получение решения, приемлемого для практических расчетов. Особенностью данной задачи является существенная зависимость коэффициента теплопроводности от пространственной координаты. В случае, когда эта зависимость носит экспоненциальный характер, удается получить строгое аналитическое решение.
Известно, что расчет нестационарных температурных полей в многослойных конструкциях является в математическом отношении чрезвычайно сложным [1–5]. Причем с увеличением числа слоев трудности определения изменения температуры в каждом элементе существенно возрастают. Однако в тех случаях, когда характер поведения теплофизических свойств материалов неоднородной системы, в частности коэффициентов теплопроводности, может быть аппроксимирован некоторой монотонной функцией пространственной координаты, удается получить сравнительно приемлемые в инженерном отношении расчетные зависимости. Такой подход может быть проиллюстрирован на примере следующей задачи:
(1)
$\frac{{\partial \vartheta }}{{\partial {\text{Fo}}}} = \frac{\partial }{{\partial X}}\left[ {\lambda \left( X \right)\frac{{\partial \vartheta }}{{\partial X}}} \right],$(2)
$\begin{gathered} {\text{0}} \leqslant {\text{Fo}} < \infty ,\,\,\,{\text{0}} \leqslant X \leqslant {\text{1,}}\,\,\,\,{\text{0}} \leqslant \vartheta \left( {X{\text{,Fo}}} \right) \leqslant {\text{1}}, \\ \frac{{\partial \vartheta }}{{\partial X}} = {\text{0}}\,\,\,\,{\text{при }}X = {\text{0,}} \\ \end{gathered} $(3)
$\frac{{\partial \vartheta }}{{\partial X}} = - {\text{Bi}}\vartheta \,\,\,\,{\text{при }}X = 1{\text{,}}$Здесь использована общепринятая форма представления зависимых и независимых величин в безразмерном виде [6].
Предположим, что функцию $\lambda = \lambda \left( X \right)$ можно аппроксимировать экспонентой
где постоянный коэффициент $a \geqslant 0.$ Когда $a = 0,$ строгое решение задачи (1)–(4) широко известно [6, 7]. Следовательно, более интересным является случай $a > 0.$Для определения собственных функций и собственных значений поставленной задачи (1)–(4) с учетом ограничения (5) необходимо провести исследование соответствующего обыкновенного дифференциального уравнения, дополненного заданными краевыми условиями
После выполнения операции дифференцирования уравнение (6) принимает вид
Введем новую пространственную координату $Z$
Тогда зависимость (9) преобразуется в выражение
гдеИспользуя подстановку
приводим дифференциальное уравнение (11) к видуПолученное уравнение (13) относится к классу уравнений Бесселя [8, 9]. Его общее решение
где ${{J}_{1}}\left( {\beta Z} \right)$ и ${{Y}_{1}}\left( {\beta Z} \right)$ являются соответственно функциями Бесселя первого и второго рода первого порядка. Подробные таблицы значений этих функций приведены во многих справочных пособиях, например [8–12].С учетом (10), (12) и (14) искомый интеграл уравнения (9) может быть записан в виде
Таким образом, общее аналитическое решение уравнения (9) удается выразить как произведение элементарной показательной функции и специальных функций Бесселя.
Постоянная интегрирования $B$ определяется на основе условия симметрии искомого температурного поля (7):
где ${{J}_{0}}\left( \beta \right)$ и ${{Y}_{0}}\left( \beta \right)$ – также функции Бесселя соответственно первого и второго рода, но нулевого порядка.Итак, полное аналитическое решение дифференциального уравнения (9) с учетом (15) запишется в виде
(16)
$y = A{{{\text{e}}}^{{\frac{{ax}}{{\text{2}}}}}}\left[ {{{Y}_{0}}\left( \beta \right){{J}_{1}}\left( {\beta {{{\text{e}}}^{{\frac{{ax}}{{\text{2}}}}}}} \right) - {{J}_{0}}\left( \beta \right){{Y}_{1}}\left( {\beta {{{\text{e}}}^{{\frac{{ax}}{{\text{2}}}}}}} \right)} \right],$Комплекс в квадратных скобках в правой части (16) следует рассматривать как собственную функцию исследуемой задачи, т.е.
(17)
${{K}_{n}}\left( X \right) = {{Y}_{0}}\left( {{{\beta }_{n}}} \right){{J}_{1}}\left( {{{\beta }_{n}}{{{\text{e}}}^{{\frac{{ax}}{2}}}}} \right) - {{J}_{0}}\left( {{{\beta }_{n}}} \right){{Y}_{1}}\left( {{{\beta }_{n}}{{{\text{e}}}^{{\frac{{ax}}{2}}}}} \right).$(18)
$\frac{{{{Y}_{0}}\left( \beta \right){{J}_{1}}\left( {K\beta } \right) - {{J}_{0}}\left( \beta \right){{Y}_{1}}\left( {K\beta } \right)}}{{{{Y}_{0}}\left( \beta \right){{J}_{0}}\left( {K\beta } \right) - {{J}_{0}}\left( \beta \right){{Y}_{0}}\left( {K\beta } \right)}} = - \frac{{aK\beta }}{{2{\text{Bi}}}},$При $a \to 0$ зависимость (18) вырождается в соотношение
При этом нужно использовать асимптотические формулы [11] для функций ${{J}_{0}}\left( X \right),$ ${{J}_{1}}\left( X \right),$ ${{Y}_{0}}\left( X \right),$ ${{Y}_{1}}\left( X \right),$ справедливые при больших значениях X.Первые шесть корней ${{\mu }_{n}}$ уравнения (19) для разных значений числа ${\text{Bi}}$ (от 0 до $\infty $) даны в монографии [6]. Корни ${{\mu }_{n}},$ удовлетворяющие уравнению (19), можно рассматривать как максимально предельные по отношению к собственным значениям, определяемым по зависимости (18) при одинаковых величинах ${\text{Bi}}$. При ${\text{Bi}} = {\text{0}}$ граничное условие (3) трансформируется в условие второго рода, и формула (18) принимает вид
(20)
$\frac{{{{J}_{0}}\left( \beta \right)}}{{{{Y}_{0}}\left( \beta \right)}} = \frac{{{{J}_{0}}\left( {K\beta } \right)}}{{{{Y}_{0}}\left( {K\beta } \right)}}.$(21)
$\frac{{{{J}_{0}}\left( \beta \right)}}{{{{Y}_{0}}\left( \beta \right)}} = \frac{{{{J}_{1}}\left( {K\beta } \right)}}{{{{Y}_{1}}\left( {K\beta } \right)}}.$Если воспользоваться рекомендуемыми в справочном пособии [10] аппроксимационными зависимостями для функций Бесселя, входящими в соотношения (20) и (21), то удается составить квадратные алгебраические уравнения соответственно следующего вида:
Таким образом, корни уравнения (20), начиная с n = 2, рассчитываются по формуле
(22)
${{\beta }_{n}} = \frac{{\left( {n - 1} \right)\pi }}{{2\left( {K - 1} \right)}} + \sqrt {\frac{{{{{\left( {n - 1} \right)}}^{2}}{{\pi }^{2}}}}{{4{{{\left( {K - 1} \right)}}^{2}}}} - \frac{{0.125}}{K}} ,$(23)
${{\beta }_{n}} = \frac{{\left( {2n - 1} \right)\pi }}{{4\left( {K - 1} \right)}} + \sqrt {\frac{{{{{\left( {2n - 1} \right)}}^{2}}{{\pi }^{2}}}}{{16{{{\left( {K - 1} \right)}}^{2}}}} - \frac{{0.125\left( {K + 3} \right)}}{{K\left( {K - 1} \right)}}} .$В таблице приведены значения первых трех корней ${{\beta }_{n}}$ характеристического уравнения (18) для ряда чисел ${\text{Bi}}$ и трех величин параметра $a$ (1.0, 0.5 и 0.2), полученных численным методом. При этом расчеты для ${\text{Bi}} = {\text{0}}$ и ${\text{Bi}} \to \infty $ были проведены по формулам (22) и (23).
Таблица 1.
Значения первых трех корней характеристического уравнения (18)
| ${\text{Bi}}$ | $a = 1.0$ $K = 1.6487$ | $a = 0.5$ $K = 1.2840$ | $a = 0.2$ $K = 1.1052$ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ${{\beta }_{1}}$ | ${{\beta }_{2}}$ | ${{\beta }_{3}}$ | ${{\beta }_{1}}$ | ${{\beta }_{2}}$ | ${{\beta }_{3}}$ | ${{\beta }_{1}}$ | ${{\beta }_{2}}$ | ${{\beta }_{3}}$ | |
| 0 | 0 | 4.8277 | 9.6778 | 0 | 11.0520 | 22.1172 | 0 | 29.8678 | 59.7412 |
| 0.5 | 0.8053 | 5.0128 | 9.7732 | 2.0530 | 11.5236 | 22.3618 | 5.9331 | 31.2331 | 60.4512 |
| 1.0 | 1.0750 | 5.1792 | 9.8659 | 2.7238 | 11.9442 | 22.5985 | 7.8381 | 32.4448 | 61.1369 |
| 5.0 | 1.7332 | 6.0109 | 10.4765 | 4.2809 | 13.8596 | 24.1199 | 12.1132 | 38.0858 | 65.4699 |
| 10.0 | 1.9255 | 6.4452 | 10.9455 | 4.7063 | 14.9372 | 25.2197 | 13.2314 | 40.6983 | 68.4777 |
| 25.0 | 2.0709 | 6.8472 | 11.5064 | 5.0180 | 15.7978 | 26.4495 | 14.0348 | 42.9252 | 71.7043 |
| 50.0 | 2.1257 | 7.0110 | 11.7671 | 5.1331 | 16.1380 | 26.9950 | 14.3280 | 43.7901 | 73.0970 |
| 100.0 | 2.1543 | 7.0984 | 11.9110 | 5.1928 | 16.3174 | 27.2910 | 14.4796 | 44.2433 | 73.8453 |
| 500.0 | 2.1779 | 7.1706 | 12.0313 | 5.2418 | 16.4649 | 27.5364 | 14.5034 | 44.6147 | 74.4632 |
| 1000.0 | 2.1790 | 7.1738 | 12.0367 | 5.2480 | 16.4836 | 27.5676 | 14.6190 | 44.6616 | 74.5414 |
| $\infty $ | 2.1839 | 7.1890 | 12.0619 | 5.2507 | 16.5022 | 27.5987 | 14.6341 | 44.7086 | 74.6197 |
Таким образом, окончательное аналитическое решение задачи (1)–(4) с учетом условия (5) принимает вид
(24)
$\vartheta \left( {X,{\text{Fo}}} \right) = {{{\text{e}}}^{{\frac{{ax}}{2}}}}\sum\limits_{n = 1}^\infty {{{A}_{n}}{{K}_{n}}\left( X \right)\exp \left( { - \mu _{n}^{2}{\text{Fo}}} \right)} ,$Список литературы
Видин Ю.В. Инженерные методы расчета процессов теплопереноса. Красноярск: Изд-во Красноярск. политех. ин-та, 1974. 144 с.
Иванов В.В., Видин Ю.В., Колесник В.А. Процессы прогрева многослойных тел лучисто-конвективным теплом. Ростов-на-Дону: Изд-во Ростовск. ун-та, 1990. 159 с.
Видин Ю.В., Иванов В.В., Казаков Р.В. Инженерные методы расчета задач теплообмена. Красноярск: СФУ, 2014. 167 с.
Видин Ю.В., Злобин В.С., Иванов Д.И. Нестационарный теплоперенос в неоднородных конструкциях криволинейной конфигурации. Красноярск: СФУ, 2016. 167 с.
Беляев Н.М., Рядно А.А. Методы нестационарной теплопроводности. М.: Высшая школа, 1978. 328 с.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Карслоу Г.С., Егер Д.К. Теплопроводность твердых тел. М.: Наука, 1964. 487 с.
Ватсон Г.Н. Теория бесселевых функций. Т. 1, 2. М.: Изд-во иностр. лит., 1949.
Янке Е., Эмде Ф., Лёш Ф. Специальные функции. М.: Наука, 1977. 342 с.
Справочник по специальным функциям / Под ред. Абрамовиц М., Стиган И. М.: Наука, 1979. 890 с.
Сегал Б.И., Семендяев К.А. Пятизначные математические таблицы. 3-е изд. М.: Гос. изд-во физ.-мат. лит., 1962. 464 с.
Чистова Э.А. Таблицы функций Бесселя от действительного аргумента и интегралов от них. М.: Изд-во АН СССР, 1958. 524 с.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур