Теплофизика высоких температур, 2019, T. 57, № 6, стр. 898-908

ВВЕДЕНИЕ

При создании гиперзвуковых летательных аппаратов (ГЛА) актуальным является проведение исследований, связанных с созданием систем тепловой защиты от аэродинамического нагрева. Температура некоторых участков тела при полете может достигать 2500–3000 К [1, 2]. Известно много различных методов пассивной, активной и комбинированной тепловой защиты [1–9].

Отметим один из перспективных способов активной тепловой защиты, основанной на термоэмиссионном методе [8, 9]. Данный метод позволяет преобразовать тепловую энергию, полученную при нагреве оболочки ГЛА, непосредственно в электрическую. При этом испарение тепловых электронов с эмиттера сопровождается понижением температуры последнего [10]. В системе тепловой защиты, основанной на термоэмиссионном методе, протекают множество взаимосвязанных процессов [10]: эмиссионных, электрических, плазменных, тепловых, адсорбционных и др. Экспериментальные исследования термоэмиссионных установок довольно сложны и дорогостоящи [11, 12], поэтому уделяется большое внимание математическому моделированию протекающих в них процессов [10, 13–18]. В данной работе представлена и исследована модель активной термоэмиссионной тепловой защиты (АТЭТЗ). Показано, что выбором параметров защиты возможно существенно уменьшить температуру ее конструкций.

ПОСТАНОВКА ЗАДАЧИ

Пусть имеется многоэлементная конструкция из электрогенерирующих элементов (ЭГЭ) и у каждого из них есть своя зона влияния с характерным размером ${{L}_{k}}.$ С целью упрощения анализа рассмотрим один ЭГЭ, представляющий собой слоеный коаксиальный аксиально симметричный цилиндр с небольшой долей конусности. На рис. 1 схематично представлены слои активной защиты для фиксированного аксиального угла со своей зоной влияния и характерным поперечным размером ${{L}_{k}} = {{s}_{k}} - {{s}_{A}}.$ Исследуем задачу о теплообмене внутри типичного ЭГЭ, под которым будем понимать составную область с теплоизолированной стенкой при $s = {{s}_{A}}$ $0 \leqslant n \leqslant {{L}_{2}}$ (кроме коллектора ${{L}_{4}} \leqslant n \leqslant {{L}_{5}}$) и $s = {{s}_{k}}$ ${{L}_{5}} < n \leqslant {{L}_{8}}$ (кроме эмиттера ${{L}_{2}} \leqslant n \leqslant {{L}_{3}}$). Координата n направлена от поверхности в глубь оболочки (см. рис. 1), где слой 1 – внешняя поверхность оболочки: сплав молибдена с вольфрамом [19]; слой 2 – эмиттерная изоляция из карбида циркония; слой 3 включает изолятор 2, эмиттер из вольфрама 3 и вольфрамовый токоввод 3; слой 4 состоит из молибденового токовывода 4, коллектора из молибдена 4 и изолятора 5; 5, 7 – емкость теплоносителя из $A{{l}_{2}}{{O}_{3}}$; 6 – охлаждающий теплоноситель (воздух или гелий); 8 – потребитель электрической энергии (электрическая нагрузка); эмиттер 3 и коллектор 4 составляют термоэмиссионный элемент, через d обозначена величина межэлектродного зазора (МЭЗ); ${{L}_{j}},$ j = 1–8 – расстояния от начала координат по n областей 1–3, зазора, областей 4–7; ${{\delta }_{j}},$ j = 1–7 – толщины областей 1–7 на рис. 1.

Исследование характеристик ЭГЭ основывается на вольт-амперных характеристиках (ВАХ) изотермического термоэмиссионного преобразователя (ТЭП) [10–13, 15], которые в свою очередь являются интегральными характеристиками многообразных процессов в МЭЗ и на электродах [10, 14, 15] и определяются переносом частиц и энергии в плазме, ионизационными, адсорбционными и другими процессами.

При создании математических моделей одной из проблем является выбор их типов: нестационарные, стационарные, эмпирические и т.д. Характерное время тепловых процессов составляет ${{\tau }_{T}}$ ~ 5–50 с и определяется теплофизическими свойствами используемых материалов, размерами конструкционных элементов, условиями охлаждения, уровнем тока, проходящего через электроды. В изотермическом ТЭП в зависимости от соотношения величины межэлектродного зазора и длины свободного пробега частиц плазмы, характера ионизационных процессов в МЭЗ может реализоваться вакуумный или плазменные (квазивакуумный, прямопролетный, диффузионный, дуговой) режимы работы [10]. Для осуществления плазменных режимов в МЭЗ вводят атомы цезия, которые, во-первых, за счет ионизации образуют плазму и, во-вторых, за счет адсорбции на электродах значительно увеличивают их эмиссионную способность [10, 17]. Характерное время, определяемое адсорбцией-десорбцией атомов цезия на электродах, найденное из оценок [17], составляет ${{\tau }_{a}}$ ~ ${{10}^{{ - 5}}}$−${{10}^{{ - 1}}}$ с. Характерное время плазменных процессов в МЭЗ ТЭП в дуговом режиме работы определяется временем релаксации возмущений плотности плазмы и составляет ${{\tau }_{п}}$ ~ ${{10}^{{ - 6}}}$−${{10}^{{ - 3}}}$ с [18], а время установления электрических характеристик много меньше, чем для плотности плазмы ${{\tau }_{э}} \ll {{\tau }_{п}}.$ Таким образом, в интервале времени 5–50 с тепловые процессы будем рассматривать в нестационарной постановке, а остальные процессы в МЭЗ и, соответственно, ВАХ изотермического ТЭП – в квазистационарном приближении.

Для исследования процессов в АТЭТЗ необходимо решать самосогласованную задачу, состоящую из электрической и тепловой моделей. В результате ее решения получим распределения потенциальных, токовых, тепловых и других полей конструкции защиты.

Рассмотрим математическую формулировку электрической модели. В связи с тем, что по электродам течет постоянный ток и толщина электродов невелика, ограничимся одномерной моделью по координате s.

Падение потенциала по эмиттеру и коллектору при прохождении токов через поперечное сечение электродов в естественной системе координат определяется уравнениями

где n и s – нормальная и продольная составляющие естественной системы координат; θ − угол конусности; ${{\xi }_{i}},$ i = 1, 2 – коэффициенты электропроводности эмиттера и коллектора; ${{S}_{1}} = 2\pi {{\delta }_{3}}({{{{R}_{1}} + {{\delta }_{3}}} \mathord{\left/ {\vphantom {{{{R}_{1}} + {{\delta }_{3}}} 2}} \right. \kern-0em} 2}),$ ${{S}_{2}} = 2\pi {{\delta }_{4}}({{{{R}_{2}} - {{\delta }_{4}}} \mathord{\left/ {\vphantom {{{{R}_{2}} - {{\delta }_{4}}} 2}} \right. \kern-0em} 2})$ – площади поперечных сечений эмиттера и коллектора; ${{R}_{{{\kern 1pt} 1}}} = {{R}_{N}} - {{L}_{3}}$ – внутренний радиус эмиттера; ${{R}_{2}} = {{R}_{N}} - {{L}_{4}}$ – внешний радиус коллектора; ${{R}_{N}}$ − радиус сферического затупления.

Для малых углов конусности $\theta \leqslant 5^\circ $ (sin θ < 0.1) распределение потенциала по длине электродов примет вид [10, 13]

Если на участке эмиттера и коллектора плотность эмиссионного тока считать постоянной, то изменение силы тока эмиттера и коллектора вследствие термоэмиссии [10, 13] составляет

где $J = J({{T}_{{2,4}}},{{T}_{{1,3}}},\Delta V)$ – ВАХ изотермического ТЭП; ${{T}_{{2,4}}},{{T}_{{1,3}}}$ – температуры внешней поверхности коллектора и внутренней поверхности эмиттера; $\Delta V$ – разность напряжения между эмиттером и коллектором. Отметим, что ВАХ изотермического ТЭП зависят также от величины МЭЗ, давления насыщенных паров цезия, работы выхода эмиттера и коллектора. Из уравнений (2) следует, что в любом сечении электродов, перпендикулярном оси s, выполняется соотношение где ${{I}_{1}}(s)$ = $2\pi {{R}_{1}}\int_{{{s}_{1}}}^s {J({{T}_{{2,4}}},{{T}_{{1,3}}},\Delta V)ds} $ – сила тока, текущего по эмиттеру; ${{I}_{R}}$ – сила тока внешней цепи; ${{I}_{2}}(s)$ = $2\pi {{R}_{1}}\int_s^{{{s}_{2}}} {J({{T}_{{2,4}}},{{T}_{{1,3}}},\Delta V)ds} $ – сила тока, текущего по коллектору.

Комбинируя уравнения (1) и (2), запишем, как в [13], дифференциальное уравнение для разности потенциалов между электродами ЭГЭ

которое определяет условия генерации плотности тока в межэлектродном зазоре в каждой точке по координате s. В отличие от [13] в данной работе рассмотрен общий случай: коллектор не эквипотенциален и электропроводность электродов и коммутационных деталей зависит от их температуры.

Условимся, что потенциал эмиттера в точке $s = {{s}_{1}}$ равен ${{V}_{1}}(s = {{s}_{1}}) = 0,$ а потенциал коллектора – ${{V}_{2}}(s = {{s}_{1}})$ = ${{V}_{1}}(s = {{s}_{2}}) + {{U}_{{Ec}}}$ + ${{U}_{R}} + {{U}_{{Cc}}}.$ При этом

– падение напряжения на эмиттере; ${{U}_{{Ec}}},$ ${{U}_{{Cc}}}$ – падение напряжения на коммутационной детали эмиттера и коллектора; ${{U}_{R}}$ – падение напряжения на нагрузке ЭГЭ. Тогда начальное условие для уравнения (3) запишется в виде

При прохождении тока через электроды и коммутационные детали выделяется джоулево тепло. При значительной силе тока оно заметным образом влияет на тепловой баланс (поле температур) конструкции АТЭТЗ.

Джоулево тепловыделение коммутационных деталей эмиттера и коллектора вычисляется как

Погонное джоулево тепловыделение эмиттера и коллектора находится как

Объемное джоулево тепловыделение эмиттера и коллектора, являющееся источником тепла в уравнении теплопроводности для соответствующего электрода, запишется как

Для нахождения прототипов ГЛА, на которых может быть оправдана установка АТЭТЗ, желательно найти уровень тепловых потоков, снимаемых с внешней открытой оболочки эмиттера (область 3 на рис. 1) и внешней поверхности коллектора (область 4 на рис. 1) за счет электронного охлаждения и процессов излучения. Кроме того, надо знать высокоэнтальпийные потоки от аэродинамического нагрева внешней части тугоплавкого металла (область 1 на рис. 1). Тепловые потоки для внешних открытых частей областей 3 и 4 имеют вид [10, 13]

где k – постоянная Больцмана; e – заряд электрона; σ – постоянная Стефана–Больцмана; ${{\lambda }_{{{\text{Cs}}}}}$ – коэффициент теплопроводности паров цезия в межэлектродном зазоре; ${{\varphi }_{j}},$ j = 1, 2 – работа выхода материалов эмиттера и коллектора; ${{\varepsilon }_{s}}$ – приведенная излучательная способность поверхности эмиттера и коллектора. Нижние индексы 1 и 2 в левой части формул (9) и (10) отвечают параметрам эмиттера и коллектора, Cs – парам цезия, $Ec,$ $Cc$ – коммутационным деталям эмиттера и коллектора, R – внешней цепи; верхний индекс V – объемное джоулево тепловыделение эмиттера и коллектора, A – граница сопряжения сфера–конус на рис. 1, k – конечное значение по координате s, * – характерная величина.

При постановке тепловой модели задачи сделаем следующие допущения:

1) число Рейнольдса в набегающем гиперзвуковом потоке воздуха достаточно велико $\left( {{{{\operatorname{Re} }}_{\infty }} \gg 1} \right),$ и в окрестности поверхности тела сформировался пограничный слой (ПС);

2) воздух на внешней границе ПС находится в состоянии термохимического равновесия, явления переноса в ПС рассматриваются при упрощающих предположениях о равенстве коэффициентов диффузии; число Льюиса Le = 1;

3) тепловое состояние конической части оболочки (рис. 1) определяется из решения (двухмерного по пространству) нестационарного уравнения сохранения энергии.

На основании допущений 1–3 задача расчета характеристик теплообмена при использовании естественных координат с учетом (7) сводится к решению системы уравнений [3] при ${{s}_{A}} < s < {{s}_{k}}$

где $r = ({{R}_{N}} - n)\cos \theta $ + $(s - {{s}_{A}})\sin \theta ;$ t – время; ${{c}_{{Pj}}},$ ${{\lambda }_{j}},$ ${{\rho }_{j}},$ j = 1–7 – коэффициенты удельной теплоемкости, теплопроводности и плотность слоев конструкций АТЭТЗ.

Систему уравнений (12)–(17) необходимо решать с учетом следующих начальных и граничных условий.

Начальные условия:

На обтекаемой внешней поверхности оболочки (n = 0):

на поверхности третьего слоя – изолятора (n = ${{L}_{3}},$ ${{s}_{A}} \leqslant s \leqslant {{s}_{1}}$) – выставляется условие теплообмена по закону Ньютона и учитывается отвод тепла от излучения поверхности карбида циркония на поверхности третьего слоя – эмиттера (n = ${{L}_{3}}$) – согласно первой формулы (8): на поверхности третьего слоя – эмиттера (n = ${{L}_{3}},$ ${{s}_{2}} \leqslant s \leqslant {{s}_{k}}$) – выставляется граничное условие третьего рода и учитывается отвод тепла от излучения поверхности вольфрама на внешней поверхности четвертого слоя – коллектора (n = ${{L}_{4}},$ ${{s}_{A}} \leqslant s < {{s}_{1}}$) – имеет место теплообмен по закону Ньютона на внешней поверхности четвертого слоя – коллектора (n = ${{L}_{4}},$ ${{s}_{1}} \leqslant s < {{s}_{2}}$) – из второй формулы (8): на внешней поверхности четвертого слоя – изолятора $A{{l}_{2}}{{O}_{3}}$ (n = ${{L}_{4}},$ ${{s}_{2}} \leqslant s \leqslant {{s}_{k}}$) – имеет место граничное условие третьего рода на поверхности седьмого слоя – подложке (n = ${{L}_{8}}$) – выставляется условие теплообмена по закону Ньютона На линиях сопряжения n = ${{L}_{j}},$ j = 1, 2 и n = ${{L}_{i}},$ i = 5–7 выписываются условия идеального контакта и равенства температур На левом $s = {{s}_{A}}$ торце слоев 1–3 и правом $s = {{s}_{k}}$ торце слоев 1, 2, 4–7 имеет место условие тепловой изоляции на левом $s = {{s}_{A}}$ торце четвертого слоя осуществляется теплообмен по закону Ньютона на правом $s = {{s}_{k}}$ торце катода выставляется граничное условие третьего рода и учитывается отвод тепла излучением с поверхности вольфрама на линиях сопряжения $s = {{s}_{1}}$ областей 2, 3 на эмиттере и $s = {{s}_{2}}$ областей 4, 5 на коллекторе имеет место условие идеального контакта и равенства температур где ${{T}_{0}}$ − начальная температура тела составной оболочки; ${{\varepsilon }_{i}},$ i = 1, 2 – излучательная способность поверхности сплава (Мо + W) и ZrC; ${{T}_{{1*}}},$ ${{T}_{{2*}}}$ − характерные температуры воздушной среды вблизи торца эмиттера при $s = {{s}_{A}}$ и коллектора при $s = {{s}_{k}};$ δ, ${{\Delta }_{1}},$ ${{\Delta }_{2}}$ − коэффициенты теплоотдачи составной конструкции с внешней средой.

Эффективность АТЭТЗ оценивается как по степени снижения температуры ее конструкций, так и традиционным способом – коэффициентом полезного действия (КПД) ЭГЭ преобразования тепловой энергии в электрическую [13]. Отметим, что оцениваемый КПД ЭГЭ – это нестационарная величина, существующая только во время полета ГЛА в атмосфере, т.е. когда существуют значительные по величине температурные поля конструкций АТЭТЗ.

КПД ЭГЭ вычисляется для эмиттера как отношение полезной электрической мощности ${{G}_{M}} = {{U}_{R}}{{I}_{R}}$ к общим энергетическим затратам, которые включают общую тепловую мощность ${{Q}_{\Sigma }}$ и суммарную генерируемую электрическую мощность ${{G}_{\Sigma }}{\text{:}}$

Общая тепловая мощность эмиттера содержит четыре составляющие (см. формулы (9)–(11)):

Суммарная генерируемая электрическая мощность ЭГЭ включает нагрев электродов и их коммутационных деталей за счет джоулева тепловыделения (формулы (5), (6)) и полезную электрическую мощность

МЕТОД РАСЧЕТА И ИСХОДНЫЕ ДАННЫЕ

На каждом шаге по времени при известных распределениях температур эмиттера, коллектора и коммутационных деталях электродов решение задачи Коши (3), (4) определяет распределение тока и потенциала по эмиттеру, коллектору и коммутационным деталям электродов ЭГЭ в рабочей точке на ВАХ электрогенерирующего элемента на основе ВАХ изотермического ТЭП. Задача Коши решается итерационным численным методом [20] до тех пор, пока не выполнится условие

где $\Delta {{V}_{{i + 1}}}(s),$ $\Delta {{V}_{i}}(s)$ – i + 1-я и i-я итерации распределения $\Delta V = \Delta V(s),$ ${{\varepsilon }_{{\Delta V}}}$ – заданная точность расчета. В условии, представленном выше, использована евклидова норма. Для расчета определенных интегралов в электрической части задачи и расчета КПД использован метод трапеций [20].

Краевая задача (12)–(31) решена численно локально-одномерным методом расщепления [21]. Использована неявная, абсолютно устойчивая, монотонная разностная схема с суммарной погрешностью аппроксимации О(τ + $H_{n}^{2}$ + $H_{s}^{2}$), где ${{H}_{n}}$ − максимальный шаг по пространству вдоль координаты $n$ (${{H}_{n}}$ = max ${{H}_{i}},$ i = 1–7), ${{H}_{s}}$ − шаг по пространству вдоль координаты $s$, τ − шаг по времени. Для проверки программы численного расчета в теле использовалась последовательность сгущающихся сеток по пространству ${{H}_{1}}$ = 2 × ${{10}^{{ - 4}}}$ м, ${{H}_{2}}$ = ${{10}^{{ - 4}}}$ м, ${{H}_{3}}$ = ${{10}^{{ - 4}}}$ м, ${{H}_{j}}$ = ${{10}^{{ - 4}}}$ м, j = 4–7; ${{H}_{s}}$ = = ${{10}^{{ - 2}}}$ м и бралось ${{h}_{{s1}}}$ = 2${{H}_{s}},$ ${{h}_{{s2}}}$ = ${{H}_{s}},$ ${{h}_{{s3}}}$ = ${{{{H}_{s}}} \mathord{\left/ {\vphantom {{{{H}_{s}}} 2}} \right. \kern-0em} 2},$ ${{h}_{{s4}}}$ = ${{{{H}_{s}}} \mathord{\left/ {\vphantom {{{{H}_{s}}} 4}} \right. \kern-0em} 4};$ ${{h}_{{1i}}}$ = 2${{H}_{{1i}}},$ ${{h}_{{2i}}}$ = ${{H}_{{1i}}},$ ${{h}_{{3i}}}$ = ${{{{H}_{{1i}}}} \mathord{\left/ {\vphantom {{{{H}_{{1i}}}} 2}} \right. \kern-0em} 2},$ ${{h}_{{4i}}}$ = = ${{{{H}_{{1i}}}} \mathord{\left/ {\vphantom {{{{H}_{{1i}}}} 4}} \right. \kern-0em} 4},$ i = 1–7. Фиксировалась температура слоев ${{T}_{{1,i}}},$ i = 1–3; ${{T}_{{2,j}}},$ j = 4–7 по глубине и ширине тела в различные моменты времени. Во всех вариантах задача решалась с переменным шагом по времени, который выбирался из условия заданной точности, одинаковой для всех шагов по пространству. Различие относительной погрешности по температуре падало и к моменту времени t = ${{t}_{z}}$ составляло ${{\psi }_{1}}$ = 8.4%, ${{\psi }_{2}}$ = 4.5%, ${{\psi }_{3}}$ = 2.24%. Ниже результаты расчета получены для шагов по пространству ${{h}_{{3i}}} = {{{{H}_{{1,i}}}} \mathord{\left/ {\vphantom {{{{H}_{{1,i}}}} 2}} \right. \kern-0em} 2},$ i = 1–7, ${{h}_{{s3}}}$ = ${{{{H}_{s}}} \mathord{\left/ {\vphantom {{{{H}_{s}}} 2}} \right. \kern-0em} 2}.$

Важным элементом электрической модели ЭГЭ являются ВАХ изотермического ТЭП, которые определяют диапазон генерируемого тока элемента. Для расчета ВАХ ТЭП использовался алгоритм [14], модификация которого в [15] состояла в аппроксимации характеристик в области плотностей токов $J \leqslant 6$ А/${{м}^{2}}$. Это позволило приближенно описать диффузионную ветвь ВАХ и автоматизировать расчеты вплоть до напряжения холостого хода. Данный алгоритм расчета ВАХ изотермического ТЭП использовался для исследования характеристик распределенных термоэмиссионных систем [11, 15, 16, 22, 23], где получено удовлетворительное согласие модельных и экспериментальных ВАХ распределенных термоэмиссионных систем. Отметим, что моделировалась только обратная ветвь ВАХ ТЭП, т.е. не моделировались явления поджига дуги.

В данной работе рассчитывалось семейство ВАХ изотермического ТЭП (рис. 1) для величины МЭЗ $d = 2.5 \times {{10}^{{ - 4}}}$ м и давления насыщенных паров цезия ${{p}_{{Cs}}}$ = 666.61 Па (${{p}_{{Cs}}}$ = 5 мм рт. ст.). Это соответствует температуре резервуара с цезием ${{T}_{{Cs}}}$ = 606.9 К. Температура эмиттера изменялась в диапазоне $1400 \leqslant {{T}_{1}} \leqslant 2300$ К, коллектора – $600 \leqslant {{T}_{2}} \leqslant 2400$ К, напряжение между электродами: $ - 0.4 \leqslant \Delta V \leqslant 1.6$ В. Работы выхода электродов представлялись в виде кривых Рейзора [24], т.е. в виде соотношений ${{\varphi }_{i}}$ = ${{\varphi }_{i}}({{{{T}_{i}}} \mathord{\left/ {\vphantom {{{{T}_{i}}} {{{T}_{{Cs}}}}}} \right. \kern-0em} {{{T}_{{Cs}}}}}),$ i = 1, 2. Для эмиттера задавалась кривая Рейзора, соответствующая вакуумной работе выхода материала электрода (монокристалл W(110)) $\varphi _{1}^{0}$ = 5.0 эВ [25, 26]. Для коллектора задавалась кривая Рейзора, соответствующая Mo ($\varphi _{2}^{0}$ = 4.32 эВ). Кривая Рейзора эмиттера и температура резервуара с цезием выбирались таким образом, чтобы в диапазоне температур эмиттера $1400 \leqslant {{T}_{1}} \leqslant 2300$ К его эмиссионная плотность тока соответствовала диапазону $J\sim {{10}^{5}}{\kern 1pt} - {\kern 1pt} {{10}^{6}}$ А/${{м}^{2}}$, т.е. плотностям тока, когда существенен эффект термоэмиссионного охлаждения.

Отметим, что кривая Рейзора эмиттера в область больших значений ${{{{T}_{1}}} \mathord{\left/ {\vphantom {{{{T}_{1}}} {{{T}_{{Cs}}}}}} \right. \kern-0em} {{{T}_{{Cs}}}}}$ и коллектора в области малых значений ${{{{T}_{2}}} \mathord{\left/ {\vphantom {{{{T}_{2}}} {{{T}_{{Cs}}}}}} \right. \kern-0em} {{{T}_{{Cs}}}}}$ выходят на насыщение. Такое поведение кривой Рейзора коллектора приводит к тому, что ВАХ ТЭП перестают изменяться для ${{T}_{2}}$ ≤ 700 К. Для используемого в данной работе семейства ВАХ изотермического ТЭП область насыщения для кривой Рейзора эмиттера не достигалась.

Коэффициент теплопроводности паров цезия в (11) принимался равным ${{\lambda }_{{Cs}}}$ = $1.65$ × × ${{10}^{{ - 4}}}\sqrt T $ Вт/(м К) [13, 14].

Как отмечалось выше, коэффициенты электропроводности электродов ЭГЭ зависят от температуры:

Брались экспериментальные результаты из [27] и находилась их линейная аппроксимация: для эмиттера – ${{\xi }_{{10}}}$ = $3.82 \times {{10}^{{ - 8}}}$ Ом м, ${{\xi }_{{i\alpha }}}$ = = $8.14 \times {{10}^{{ - 3}}}$ 1/К и для коллектора – ${{\xi }_{{20}}}$ = = $3.284 \times {{10}^{{ - 8}}}$ Ом м, ${{\xi }_{{i\alpha }}}$ = $9.0138 \times {{10}^{{ - 3}}}$ 1/К. Формулы справедливы для диапазона 350 ≤ T ≤ 2500 К.

При низких температурах эмиттера и коллектора дуговой режим работы ТЭП может отсутствовать. При повышении температур эмиттера и коллектора дуговые вольт-амперные характеристики ТЭП существенно сдвинуты в непреобразовательную область и электронное охлаждение электродов неэффективно. Поэтому в данной статье на начальном интервале по времени велся расчет только с использованием тепловой части модели, а электрическая модель могла подключаться при температурах эмиттера ${{T}_{{{{L}_{3}}}}} \geqslant 1350{\kern 1pt} - {\kern 1pt} 1400$ К и температурах коллектора ${{T}_{{{{L}_{4}}}}} \geqslant 350{\kern 1pt} - {\kern 1pt} 400$ К. Исследования показали, что в диапазоне ${{T}_{{{{L}_{3}}}}} \approx 1350{\kern 1pt} - {\kern 1pt} 1700$ K момент подключения к расчету электрической модели слабо влияет на процессы в АТЭТЗ. Поэтому дальнейшие исследования проводились для ${{T}_{{L_{3}^{*}}}} = 1700$ K.

Для расчета конвективного теплового потока из газовой фазы на конической части тела ${{q}_{w}}$ использовались формулы [28] для пространственного случая при турбулентном режиме течения в ПС:

где ${{{v}}_{\infty }}$ − скорость набегающего потока, h − энтальпия, ${{M}_{\infty }}$ − число Маха, c_i, i = 1, 2 − постоянные. Индексы: w отвечает параметрам внешней границы тела первого слоя; e и e0 − величинам на внешней границе ПС и в точке торможения тела; ∞ − величинам набегающего газового потока на бесконечности; черта вверху − безразмерным параметрам; z − времени окончания теплового воздействия; ef − эффективной величине; 0 − начальной величине; m − максимальному значению.

Расчеты обтекания конуса с углом полураствора $\theta = 5^\circ $ потоком химически равновесного воздуха проводились для следующих условий, которые соответствуют высоте полета: ${{H}_{\infty }} = 3.0 \times {{10}^{4}}$ м, ${{h}_{{e0}}} = 5.92 \times {{10}^{6}}$ Дж/кг, ${{{v}}_{\infty }}$ = 3.36 × ${{10}^{3}}$ м/с, ${{P}_{\infty }}$ = = 1.197 × ${{10}^{3}}$ Н/м², ${{\rho }_{\infty }}$ = 1.84 × ${{10}^{{ - 2}}}$ кг/м³, ${{g}_{\infty }}$ = = 9.73 м/с², ${{M}_{\infty }}$ = 13.07, а безразмерное давление $\bar {p} = {{{{P}_{e}}} \mathord{\left/ {\vphantom {{{{P}_{e}}} {{{P}_{{e0}}}}}} \right. \kern-0em} {{{P}_{{e0}}}}}$ и эффективный показатель адиабаты ${{\gamma }_{{{\text{ef}}}}}$ определялись согласно [29].

Расстояния слоев оболочки вглубь по n (излучательные способности эмиттера, коллектора), их толщины, плотности, а также некоторые входные данные в уравнениях (11), (19), (20), (22), (23) даны в таблице. Теплофизические характеристики первого слоя отвечают сплаву молибден–вольфрам (${{\rho }_{1}} = 11{\kern 1pt} 600\,\,{{кг} \mathord{\left/ {\vphantom {{кг} {{{м}^{3}}}}} \right. \kern-0em} {{{м}^{3}}}}$) в соотношении (83.5% Мо + + 16.5% W) и приведены в [19]. Этот сплав не подвержен коррозии и используется в соплах реактивных двигателей при температурах больше 3000 К. Теплофизические характеристики третьего слоя (эмиттер на рис. 1) отвечают вольфраму, второго слоя – карбиду циркония, четвертого слоя (коллектор на рис. 1) – молибдену, пятого и седьмого слоев (подложка) – $A{{l}_{2}}{{O}_{3}}$ и взяты из [30, 31], а шестого слоя (гелия, воздушной среды) даны в [31, 32]. Приводимые ниже результаты получены при ${{T}_{0}}$ = 273 К.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РЕШЕНИЯ И ИХ АНАЛИЗ

На рис. 2, 3 приведены зависимости температур внешней поверхности тела ${{T}_{w}}$ и эмиттера ${{T}_{{{{L}_{3}}}}}$ вдоль оболочки по s. Кривые 1–5 на рис. 2, 3 отвечают следующим моментам времени t: 1 – 20 с, 2 – 25 с, 3 – 30 с, 4 – 40 с, 5 – $t = {{t}_{z}}$ (${{t}_{z}}$ = 60 с соответствует стационарному режиму процесса нагрева тела) и получены для опорного режима прогрева, когда в шестом слое составной оболочки (см. рис. 1) в качестве теплоносителя используется воздух. На рис. 2, 3 штриховые кривые отвечают варианту отсутствия термоэмиссионного охлаждения (ТЭО) эмиттера в те же самые моменты времени. Видно, что наличие ТЭО снижает максимальную температуру поверхности оболочки ${{T}_{w}}$ на 170 при t = 30 с, а температура поверхности эмиттера уменьшается на некоторых участках траектории на 166–223 К. Уменьшение температуры внешней оболочки, связанное с электронным охлаждением катода, качественно согласуется с данными [10].

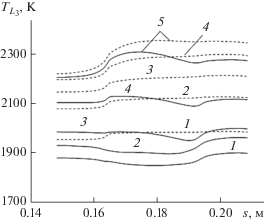
Отметим также, что в области больших величин плотности эмиссионного тока J (рис. 4) распределения внешней температуры поверхности ${{T}_{w}},$ эмиттера ${{T}_{{{{L}_{3}}}}}$ имеют вогнутость (сплошные кривые 1–3 на рис. 2, 3), а распределение температуры поверхности коллектора ${{T}_{{{{L}_{4}}}}}$ – выпуклость (рис. 5) в области действия ТЭО, при этом максимальная температура анода достигает ${{T}_{{{{L}_{4}}}}}$ = 1992 К для $t = {{t}_{z}}.$

Если в качестве теплоносителя в шестом слое взять гелий с начальной температурой ${{T}_{2}}({{\delta }_{6}})$ = 200 К, теплофизические характеристики которого известны [31], то максимальная температура поверхности коллектора (штриховые кривые на рис. 5) не превышает ${{T}_{{{{L}_{4}}}}}$ = 1522 К, а эмиттера – ${{T}_{{{{L}_{3}}}}}$ = 2140 К при $t = {{t}_{z}}.$ Как известно [1], теплоноситель гелий оказывается более эффективным с точки зрения тепловой защиты.

Для практики представляет интерес величина температуры внутренней стенки ${{T}_{{{{L}_{8}}}}}$ конструкции для коллектора. На рис. 6 сплошные кривые отвечают распределению температуры по глубине n в центре тела ($s{\text{*}} = {{({{L}_{k}} - {{s}_{A}})} \mathord{\left/ {\vphantom {{({{L}_{k}} - {{s}_{A}})} 2}} \right. \kern-0em} 2}$) для опорного режима прогрева, штриховые – теплоносителю гелию в те же самые моменты времени. Оказалось, что температура внутренней стенки подложки увеличилась незначительно в момент $t = {{t}_{z}}$ до ${{T}_{{{{L}_{8}}}}}$ = 288 К.

На рис. 4 даны распределения плотности эмиссионного тока J (сплошные кривые) и силы тока ${{I}_{1}}$ (штриховые кривые), текущего по эмиттеру в области 3 для воздушного теплоносителя в шестом слое (см. рис. 1) вдоль координаты s в те же самые моменты времени. Из сравнения рис. 3 и 4 видно, что наибольший эффект охлаждения эмиттера на траектории отвечает максимальным значениям J и ${{I}_{1}}$ при t = 25−30 с.

Важным моментом исследований процессов в АТЭТЗ является выбор рабочей точки на ВАХ ЭГЭ. Эффективность АТЭТЗ прямо пропорциональна силе тока ЭГЭ. Поэтому рабочая точка на ВАХ ЭГЭ выбиралась в области максимальной мощности. Фиксировалось напряжение на нагрузке (на выходе ЭГЭ) ${{U}_{R}} = 0.06$ В и сохранялось в течение времени полета ГЛА. На рис. 7 представлены ампер-секундные характеристики ЭГЭ (кривые 1) для разных типов теплоносителя. Обе кривые имеют подобную ассиметричную форму с максимумом в районе t = 20–25 с. Асимметричность формы характеристики ЭГЭ объясняется как различной чувствительностью ВАХ ТЭП по отношению к температуре эмиттера, так и разной скоростью нарастания последней. При ${{T}_{{{{L}_{3}}}}} \geqslant 2100$ К крутизна характеристик ТЭП и скорость нарастания температуры эмиттера ЭГЭ (кривые 2) заметно уменьшаются, поэтому правая часть характеристик ЭГЭ более пологая. Кроме этого, ампер-секундная характеристика ЭГЭ с гелиевым охлаждением имеет большее значение максимума, чем характеристика ЭГЭ с воздушным охлаждением, что объясняется уменьшением на 200–500 K температуры коллектора (рис. 5).

Эффективность АТЭТЗ также оценивалась с помощью коэффициентов неравномерности распределений ее параметров, т.е. оценки однородности условий работы разных частей электродов ЭГЭ. Например, для температуры эмиттера коэффициент неравномерности рассчитывался как [11, 13] ${{k}_{{{{T}_{1}}}}}$ = ${{{{T}_{{1\max }}}} \mathord{\left/ {\vphantom {{{{T}_{{1\max }}}} {\left[ {{{{({{s}_{2}} - {{s}_{1}})}}^{{ - 1}}}\int_{{{s}_{1}}}^{{{s}_{2}}} {{{T}_{1}}(s)ds} } \right]}}} \right. \kern-0em} {\left[ {{{{({{s}_{2}} - {{s}_{1}})}}^{{ - 1}}}\int_{{{s}_{1}}}^{{{s}_{2}}} {{{T}_{1}}(s)ds} } \right]}}.$

Коэффициенты неравномерности остальных распределенных параметров АТЭТЗ находились аналогичным образом. Исследования показали, что наиболее сильно изменяется коэффициент ${{k}_{J}},$ характеризующий неравномерность распределения плотности тока по сечениям ЭГЭ. Так, в интервале времени полета ГЛА 20−60 с он изменяется более чем в четыре раза – от 1.09 до 4.6. Как следствие, согласно выражениям (9), (10), аналогично изменяются коэффициенты неравномерности плотностей тепловых потоков электронных составляющих с эмиттера и на коллектор. Коэффициенты неравномерности остальных распределений параметров АТЭТЗ меняются в пределах 10%. Таким образом, для выбранной длины электродов неравномерность параметров ЭГЭ оказывается существенной, что влияет на эффективность тепловой защиты.

КПД ЭГЭ (32) уменьшается в процессе полета ГЛА от η = 1.6% при $t = 20$ с до η = 0.48% при $t = {{t}_{z}}.$ Представляет отдельный интерес модельное исследование влияния параметров ЭГЭ на генерацию им электрической энергии в составе АТЭТЗ.

ЗАКЛЮЧЕНИЕ

Разработана математическая модель активной термоэмиссионной тепловой защиты при высокотемпературном обтекании многослойной коаксиальной оболочки. Обнаружено понижение температуры поверхности оболочки и температуры поверхности эмиттера в результате тепловой эмиссии электронов с поверхности эмиттера. Исследовано влияние типа теплоносителя на режимы теплообмена в многослойной оболочке. Результаты численных расчетов качественно согласуются с известными данными [10].

Статья написана при поддержке фонда Д.И. Мен-делеева (грант № 8.2.15.2018).