Теплофизика высоких температур, 2020, T. 58, № 1, стр. 81-90
Редуцирование полной системы уравнений химической кинетики для течений многокомпонентных высокотемпературных газов на основе метода частичного локального равновесия
К. Э. Сон *
Московский физико-технический институт
Москва, Россия
* E-mail: kson@mail.ru
Поступила в редакцию 25.06.2018
После доработки 15.08.2019
Принята к публикации 22.10.2019
Аннотация
Представлен метод редуцирования полной системы уравнений химической кинетики от большого числа уравнений к конечному их числу, которые можно решить, используя доступные вычислительные средства без заметной потери точности, например, для моделирования химических реакций горения. В работе приведены теория и примеры применения метода частичного локального химического равновесия с целью расчетов и моделирования до- и сверхзвуковых потоков реагирующих сред для редуцирования кинетических схем полных химических реакций при неполном локальном химическом равновесии.
ВВЕДЕНИЕ
Математическое описание и численное моделирование течений высокотемпературных газов в задачах входа летательных (ЛА) и космических аппаратов в атмосферу Земли и других планет при учете конечных скоростей химических реакций представляет сложную многомасштабную задачу вследствие того, что химические реакции имеют разные временны́е масштабы, охватывающие более десяти порядков, а турбулентное движение вводит дополнительные пространственные и временны́е масштабы. Интегрирование уравнений химической кинетики сильно затруднено из-за их чрезмерной жесткости, обусловленной большим диапазоном временны́х масштабов.
Математическое моделирование течений высокотемпературных газов и горения может быть значительно упрощено, если использовать временнóе разделение масштабов в предположении, что быстрые реакции, обычно связанные с промежуточными радикалами и компонентами, находятся в локальном равновесии. Теория упрощения транспортных процессов при наличии полного химического равновесия или в предположении о локальном химическом равновесии (ЛХР) впервые была введена Иевлевым В.М. и Соном Э.Е. [1–5]. Расчеты коэффициентов переноса в модели ЛХР выполнены в работах [6–8].
Позже этот подход для случая частичного локального химического равновесия (ЧЛХР) (Partial Local Chemical Equilibrium) использовался в работах [9–11]. В этом методе на основе анализа кинетических процессов в качестве независимых переменных выбираются компоненты, наиболее медленно изменяющиеся в потоке реагирующего газа. Концентрации остальных компонентов определяются на основе минимизации потенциала Гиббса смеси при дополнительных ограничениях. Это позволяет получить общий набор дифференциально-алгебраических уравнений (ДАУ), которые применимы к любой системе, в которой можно выделить быстрые и медленные реакции.
В данной работе показано, как дифференциально-алгебраическая формулировка ЧЛХР может быть выведена из первых принципов в виде расширения вычисления химического равновесия посредством минимизации свободной энергии. Далее метод ЧЛХР используется для уменьшения сложности механизма горения и расчета скорости горения предварительно перемешанной смеси метана с воздухом при различных величинах обогащенности смеси, давлений и температур.
Турбулентное горение является существенно многомасштабной проблемой. Одновременно может происходить большое количество химических реакций (сотни или даже тысячи), имеющих широкий диапазон временны́х масштабов: от 10–15 до 10–2 с. В то же время химические вещества транспортируются потоком газа, что требует использования дополнительных пространственных и временны́х масштабов, связанных с диффузионными и конвективными процессами, которые в турбулентном потоке также охватывают широкий спектр, как правило, по меньшей мере в шесть порядков: от временны́х и пространственных тейлоровских и колмогоровских масштабов до масштабов, связанных с масштабами в энергетическом интервале, т.е. с физическими размерами каналов, пограничных слоев и т.п. Таким образом, математическое моделирование процессов горения является сложной проблемой, принципиальной для большого класса задач гидродинамики реагирующих сред, и требует поиска методов решения.
Химическая кинетика описывает динамическую эволюцию химической системы с помощью набора уравнений кинетики для всех компонентов и радикалов, а также всех возможных элементарных реакций. Такие всеобъемлющие механизмы часто включают очень большое количество компонентов и реакций, например, для горения метана отдельные кинетические схемы могут включать около 60 компонентов и 400 реакций. При рассмотрении более высоких углеводородов, т.е. с увеличением количества атомов углерода в составе топлива, сложность возрастает. Опыт решения задач химической кинетики с большим числом уравнений показывает, что не всегда увеличение числа уравнений приводит к лучшему согласованию теории и эксперимента. Это связано с тем, что чем большее количество уравнений химической кинетики принимается во внимание, тем большее количество неопределенных величин (константы скоростей прямых и обратных реакций, сечения элементарных процессов и др.) возникает в моделях. Кроме того, есть понятие превышения точности, связанное с наличием погрешностей численного решения, неточностью постановки задачи, граничными и начальными данными, неопределенностями в моделях турбулентности, учетом влияния химических реакций на турбулентность и обратного влияния турбулентности на химические реакции, вследствие чего включение большого числа уравнений химической кинетики должно быть обосновано и соразмерно с решаемой задачей и ее численной реализацией.
Основным принципом разделения по временны́м масштабам является то, что динамику системы на характерных гидродинамических временах можно описать кинетикой компонентов, связанных с “медленными” временны́ми масштабами. В то же время нужен способ учета влияния компонентов, быстро приходящих в равновесие. Традиционный подход к механизмам разделения на быстрые и медленные компоненты заключается в изучении детальных механизмов реакций, их скоростей и оценке характерных времен установления частичного равновесия отдельных компонентов и реакций. Эта кропотливая процедура должна выполняться индивидуально для каждого механизма реакции и решаемой проблемы в целом. Существуют некоторые математические методы, в которых делаются попытки систематического разделения задач на разных временны́х масштабах [7].
В методе ЛХР система уравнений многокомпонентной реагирующей смеси сводится к уравнениям для концентраций химических элементов, число которых существенно меньше числа компонентов, существующих в смеси. Например, в смеси, соответствующей пограничному слою у ЛА в плотных слоях атмосферы, к компонентам, содержащим азот и кислород, добавляются компоненты углеродного теплозащитного покрытия. Поэтому на основе химических элементов O, N и C возникает большое число (десятки) компонентов (N2, O2, NO, NO2, N2O, CO2, CO, …). Концентрации компонентов затем вычисляются решением уравнений химического равновесия или путем минимизации свободной энергии Гиббса локально в каждой точке по заданным термодинамическим параметрам, например давлению и температуре и элементному составу смеси (заданным постоянным количествам ядер химических элементов, находящихся в различных атомарных и молекулярных соединениях), для которых решаются транспортные уравнения совместно с уравнениями гидродинамики (непрерывности, движения, энергии электромагнитного поля).
До сих пор в литературе в основном рассматривались два предельных случая: замороженные течения или локально химически равновесные. В случае наличия химических реакций, протекающих с конечной скоростью, эти два предельных случая соответствуют бесконечно большим или бесконечно малым числам Дамкеллера (отношение характерных времен диффузии и химических реакций). Случаи эти практически никогда не выполняются, а точное решение уравнений гидродинамики с учетом всех известных химических реакций оказывается слишком сложным.
Целью настоящей работы является рассмотрение промежуточного случая, когда полного локального химического равновесия в многокомпонентной смеси нет, но можно выделить отдельные компоненты, концентрации которых медленно изменяются в потоке, а концентрации остальных компонентов определяются быстрыми реакциями, вследствие чего данные компоненты находятся в локальном равновесии с медленными компонентами. Этот случай назван частичным локальным химическим равновесием. Условия применимости ЧЛХР много шире, чем полного ЛХР, так как оно может применяться для описания существенно неравновесных потоков и его использование определяется возможностями компьютеров или суперкомпьютеров. Такой подход частично использовался в [8], а его обоснование представлено в настоящей работе. Компоненты, которые входят в число медленных и для которых требуется решение отдельных транспортных уравнений, будем называть “базовыми”. Определение концентраций остальных, небазовых, компонентов представляет отдельную сложную задачу, и ее решение может быть получено на основе минимизации потенциала Гиббса, где в качестве независимых переменных используются давление, температура (или другие термодинамические переменные) и концентрации базовых компонентов. Необходимо при этом показать, что полученные решения имеют пределы “замороженных” и полностью локально-равновесных течений и являются однозначными.
В случае ЧЛХР строгой теории, по-видимому, построить нельзя, так как оно соответствует неравновесному состянию, в котором энтропия (или другой термодинамический потенциал, определяющий равновесное состояние и устойчивость термодинамической системы [11]) может не достигать экстремума. Тогда в независимых переменных (отдельных базисных компонентов), выбираемых на основе уравнений химической кинетики, а не термодинамики, минимум потенциала Гиббса будет соответствовать неравновесному состоянию, где энтропия может не достигать экстремума, что может привести, например, к нарушению закона действующих масс для реакций с участием базисных компонентов. В режиме ЧЛХР динамическая эволюция системы определяется кинетикой видов, связанных с более медленными временны́ми шкалами, кинетически контролируемыми, в то время как концентрации остальных компонентов вычисляются с помощью минимизации свободной энергии Гиббса смеси при дополнительных ограничениях на заданные локальные концентрации базовых компонентов. В пределах уменьшения числа базовых компонентов до полного числа компонентов или до нуля получаются пределы химически равновесных или замороженных течений. Этот метод позволяет найти общий набор ДАУ, применимых к любой системе, в которой можно выделить быстрые и медленные реакции. В данной работе показано, как дифференциально-алгебраическая формулировка ЧЛХР может быть выведена из первых принципов в виде расширения вычисления химического равновесия посредством минимизации свободной энергии. Далее ЧЛХР используется для уменьшения сложного механизма горения и расчета скорости горения предварительно перемешанной смеси метана с воздухом при различных величинах обогащенности смеси, давлений и температур. В результате такого подхода динамическая эволюция многокомпонентной смеси регулируется кинетикой базовых компонентов. Этот подход фактически является основой для редуцирования полной системы уравнений химической кинетики к любому конкретному случаю в зависимости от характерных гидродинамических времен задачи.
1. МЕТОД ЧАСТИЧНОГО ЛОКАЛЬНОГО ХИМИЧЕСКОГО РАВНОВЕСИЯ
Транспортное уравнение для i-го компонента в многокомпонентной реагирующей смеси из N компонентов с r = 1 … NR независимыми реакциями имеет вид [4]
(1)
$\rho \left( {\frac{{\partial {{c}_{j}}}}{{\partial t}} + {\mathbf{u}}\nabla {{c}_{j}}} \right) = - \nabla {{{\mathbf{i}}}_{j}} + \rho {{\dot {c}}_{j}},$(2)
$\begin{gathered} {{c}_{j}} = \frac{{\dot {1}}}{\rho }{{m}_{j}}{{{\dot {n}}}_{j}},\,\,\,\,{{{\dot {n}}}_{j}} \equiv \frac{{d{{n}_{j}}}}{{dt}} = \\ = \sum\limits_{r = 1}^{{{N}_{R}}} {{{{v}}_{{jr}}}} {{{\dot {R}}}_{r}}\mathop {\left( {{{n}_{1}},{{n}_{2}}, \ldots ,{{n}_{N}},T,p} \right)}\limits^ ,\,\,\,\,j = {\text{1}} \ldots N. \\ \end{gathered} $Таким образом, динамическая эволюция многокомпонентной реагирующей смеси описывается системой дифференциальных уравнений в частных производных (1), (2), которая является частью полной системы [4], куда входят уравнения непрерывности, движения, энергии, уравнения состояния и электродинамические уравнения, если имеется ионизация, выражения для потоков компонентов Онсагера, включая потоки массы, тепла, замыкающие уравнения, начальные и граничные условия [4].
Метод ЛХР относится к случаю, когда при высоких температурах и давлениях в каждой точке устанавливается локальное термодинамическое равновесие, при котором состав определяется локальными параметрами – давлением p, температурой T и концентрациями химических элементов вне зависимости от того, в каких атомах или молекулах они представлены, например, ядра химического элемента N могут находиться в атомном состоянии N или в молекулах N2, NO, NO2 и т.д. В этом случае вместо уравнений для большого числа компонентов можно использовать только уравнения для химических элементов, число которых во много раз меньше числа компонентов. Например, для задач входа ЛА в атмосферу Земли, где из химических элементов присутствуют кислород, азот и углерод, число компонентов может составлять несколько десятков, а число химических элементов всего три, из них независимых – два.
Метод ЧЛХР основан на немного другом принципе: на анализе скоростей химических реакций и выделении базисных компонентов, которые эволюционируют наиболее медленно, за времена, сравнимые с характерными газодинамическими временами. Для их выбора необходим кинетический анализ химических процессов. Например, при низких температурах вещество находится в молекулярном состоянии, в воздухе при температурах менее 2000 К основными (базисными) компонентами являются молекулы азота N2 и кислорода O2. Можно считать, что остальные компоненты быстро рекомбинируют в молекулы, тогда запишем
(3)
$\widetilde {{{n}_{b}}} = \sum\limits_{j = 1}^N {{{u}_{{bj}}}{{n}_{j}}} ,\,\,\,\,b = {\text{1}}, \ldots ,{{N}_{B}},$1.1. Уравнения гидродинамики и транспортные уравнения для базисных компонентов. Поскольку введены новые базисные компоненты, то уравнения гидродинамики должны быть представлены через базисные уравнения.
В уравнении неразрывности
плотность представлена через базисные компоненты по уравнениям где ${\mathbf{u}} = \sum\nolimits_i {{{c}_{i}}{{{\mathbf{u}}}_{i}}} $ – гидродинамическая скорость.Система транспортных уравнений для концентраций базисных компонентов следует из (1) суммированием с учетом (3):
(4)
$\rho \left[ {\frac{{\partial \widetilde {{{c}_{\alpha }}}}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right)\widetilde {{{c}_{b}}}} \right] = - \nabla \cdot \widetilde {{{{\mathbf{i}}}_{b}}} + \mathop {\widetilde {{{c}_{b}}}}\limits^ ,$Таким образом, число транспортных уравнений сводится к системе с меньшим числом уравнений для основных базисных компонентов (4).
Уравнения для небазисных компонентов имеют вид уравнений, выражающих законы действующих масс при заданных концентрациях базисных компонентов:
Приведенные алгебраические уравнения выведены из физического принципа, в соответствии с которым такие виды компонентов можно считать временно находящимися в равновесном состоянии, так как временны́е масштабы, связанные с ними, очень малы по сравнению с масштабами для ведущих компонентов. Состояние такого равновесия ограничено концентрациями базисных компонентов и поэтому может быть названо “частичным локально химическим равновесием”. Подобно тому, как равновесие химической реакции в замкнутой системе при фиксированной температуре может быть вычислено за счет минимизации свободной энергии Гельмгольца, а при фиксированных температуре и давлении – по свободной энергии Гиббса, можно определить еще одно условие равновесия при фиксированных температуре, давлении и концентрации ведущих видов. В качестве примера рассмотрим систему CH4–O2 и ограничимся O2. Тогда все атомы О будут встречаться в виде O2, однако атомы C и H могут принимать любую форму, благоприятную в этих условиях (CH3, H, C2, H4 и т.д.). Динамическая эволюция системы является, таким образом, последовательностью таких состояний с ограниченным равновесием.
При рассмотрении химически реагирующих систем важным этапом является выбор кинетически контролируемых компонентов, находящихся в равновесии. Здесь, однако, не будет рассматриваться эта важная проблема. Выбор должен быть основан на кинетических критериях, описывающих эволюцию системы с учетом определенного выбора компонентов, находящихся в равновесии. Одним из основных преимуществ ЧЛХР является то, что разработанные уравнения будут иметь одинаковую общую форму независимо от выбора компонентов.
Уравнения движения и энергии также могут быть выражены через базисные концентрации
(5)
$\begin{gathered} \rho \left[ {\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}}} \right] = - \nabla p + \nabla \cdot \sigma + \\ + \,\,\rho {\mathbf{g}} + \rho _{e}^{*}{\mathbf{E}} + {\mathbf{j}} \times {\mathbf{B}}, \\ \end{gathered} $(6)
$\begin{gathered} \rho \left[ {\frac{{\partial h}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right)h} \right] = \left[ {\frac{{\partial p}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right)p} \right] - \\ - \,\,\nabla \cdot {\mathbf{q}} + {\mathbf{S}} \cdot {\mathbf{\sigma }} + {\mathbf{j}} \cdot {\mathbf{E}}, \\ \end{gathered} $1.2. Минимизация энергии Гиббса. Поскольку представление системы через базисные компоненты отличается от представления в рамках полного термодинамического равновесия, необходимо рассмотреть выражения для термодинамических функций в состоянии частичного локального химического равновесия.
Химическое равновесие может быть рассчитано двумя способами, которые физически эквивалентны. Один – метод расчета прямых и обратных реакций, константы скоростей которых связаны константами равновесия, основан на решении всех уравнений, возникающих в результате наступления равновесия в каждой реакции. В основе метода лежат законы действующих масс. Второй метод основан на втором законе термодинамики – максимуме энтропии в состоянии термодинамического равновесия. В замкнутой системе при фиксированных температуре и давлении имеет место экстремум термодинамического потенциала Гиббса. На его минимизации основан вывод уравнений ЧЛХР. Это относится не только к течениям с химическими реакциями, где давление и температура постоянны, но и к произвольному течению, так как в общую систему уравнений входят транспортные уравнения для базисных компонентов. Также в систему входят уравнение для энтальпии, через которую определяется температура, и уравнение непрерывности, которое может быть преобразовано в уравнение для давления, поэтому можно считать заданными температуру, давление и концентрации базисных компонентов. Энтальпия и давление имеют вид
где $H_{j}^{0} = f(T)$ в Дж/кмоль – энтальпия на одну частицу компонента k и уравнение состояния или выражение для давления где газовая постоянная смесиТермодинамический потенциал Гиббса G для смеси химических компонентов вычисляется как
где µj – химический потенциал компонента j$\mu _{j}^{0}$ – химический потенциал чистого компонента при стандартном давлении p0, Дж/кмоль; ${{p}_{j}}$ – парциальное давление; ${{R}_{0}} = 8314$ – универсальная газовая постоянная, Дж/(кмоль К). Отсюда получаем(8)
$\begin{gathered} {{\mu }_{j}} = \mu _{j}^{0} + {{R}_{0}}T{\text{ln}}\frac{{{{n}_{j}}}}{n} + {{R}_{0}}T{\text{ln}}\frac{p}{{{{p}_{0}}}} = \\ = \mu _{j}^{0} + {{R}_{0}}T{\text{ln}}{{x}_{j}} + {{R}_{0}}T{\text{ln}}\frac{p}{{{{p}_{0}}}}, \\ \end{gathered} $Для неидеальных газов из статистической физики [4] следует выражение для химического потенциала для газа с внутренними степенями свободы
где kB – постоянная Больцмана, zj – статистическая сумма частицы компонента j для идеального газаУсловием минимума свободной энергии Гиббса является
с учетом ограничений, выражающих сохранение элементов.Таким образом, вычисление концентраций небазисных компонентов в состоянии локального химического и термодинамического равновесия в подсистеме небазисных компонентов, быстро релаксирующих к локальному термодинамическому равновесию, сводится к решению задачи определения экстремума, которое может быть получено методом множителей Лагранжа. Определим удельный термодинамический потенциал Гиббса с учетом фиксированных концентраций базисных компонентов:
(9)
$\begin{gathered} {{g}_{{LCE}}} = g + \sum\limits_{b = 1}^{{{N}_{b}}} {{{\lambda }_{b}}} \left( {\widetilde {{{n}_{b}}} - \sum\limits_{j = 1}^N {{{u}_{{bj}}}{{n}_{j}}} } \right) = \\ = \sum\limits_{j = 1}^N {{{\mu }_{j}}{{n}_{j}}} + \sum\limits_{b = 1}^{{{N}_{B}}} {{{\lambda }_{b}}} \left( {\widetilde {{{n}_{b}}} - \sum\limits_{j = 1}^N {{{u}_{{bj}}}{{n}_{j}}} } \right), \\ \end{gathered} $Чтобы найти состав в равновесии, нужно вычислить экстремумы этой функции:
Подставляя формулы (7) и (8) в уравнение (9) и (10), записываем Вместе с (8) получаем(11)
$\mu _{j}^{0} + {{R}_{0}}T\left( {\ln {{x}_{j}} + \ln \frac{p}{{{{p}_{0}}}}} \right) = \sum\limits_{b = 1}^{{{N}_{B}}} {{{\lambda }_{b}}{{u}_{{bj}}}} .$Аналогично рассмотрим метод Лагранжа для случая фиксированных базисных компонентов, добавляя ограничения, которые определены уравнениями (3). Это означает, что некоторые компоненты (или их линейные комбинации) должны сохранять определенную фиксированную величину. Если ограничены только отдельные компоненты, то операция эквивалентна стандартной минимизации свободной энергии Гиббса, выполняемой на подмножестве всей системы, исключая атомы, участвующие в ограниченных компонентах.
Из уравнений (4), (5), (11) следуют уравнения для решения задач методом ЧЛХР. Для вычислений нужно знать только компоненты, связанные с медленными временны́ми масштабами, температуру, давление, остальные переменные являются внутренними.
Для всех этих переменных необходимо поставить граничные и начальные условия для температуры, давления и базисных компонентов, а также для множителей Лагранжа.
2. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА ЧЛХР
В задачах для реагирующих течений уравнения ЧЛХР представляют систему уравнений переноса для базисных компонентов, связанных с медленными временны́ми масштабами, с химическими реакциями, а небазисные компоненты вычисляются через алгебраические уравнения частичного локального термодинамического и химического равновесия, которые должны выполняться локально, в каждой точке.
Система уравнений с множителями Лагранжа может быть преобразована к виду, содержащему производные от множителей Лагранжа, если из (11) выразить концентрации через химические потенциалы.
Эти уравнения имеют вид
(12)
$n_{j}^{{\text{*}}} = n\frac{p}{{{{p}_{0}}}}{\text{exp}}\left( {\frac{{ - \mu _{j}^{0}}}{{RT}}} \right){\text{exp}}\left[ {\sum\limits_{b = 1}^{{{N}_{B}}} {\left( {{{u}_{{bj}}}{{\lambda }_{b}}} \right)} } \right].$(13)
$\begin{gathered} \frac{{\partial n_{j}^{*}}}{{\partial {{\lambda }_{b}}}} = u_{{bj}}^{e}n_{j}^{{\text{*}}}\,\,\,\,\left( {j = 1, \ldots N - {{N}_{B}}} \right), \\ b = {\text{1}}, \ldots ,{{N}_{B}};\,\,\,\,\frac{{\partial n_{j}^{{\text{*}}}}}{{\partial T}} = \frac{1}{T}\left( {\frac{{H_{j}^{0}}}{{{{R}_{0}}T}} - 1} \right)n_{j}^{{\text{*}}}, \\ j = {\text{1}}, \ldots ,N;\,\,\,\,\frac{{\partial n_{j}^{{\text{*}}}}}{{\partial \rho }} = - \frac{1}{\rho }n_{j}^{{\text{*}}},\,\,\,\,j = {\text{1}}, \ldots ,N. \\ \end{gathered} $Подставляя в уравнение (4), получаем
(14)
$\frac{{d{{n}_{b}}}}{{dt}} = \frac{{d{{n}_{b}}}}{{dp}}\frac{{dp}}{{dt}} + \frac{{d{{n}_{b}}}}{{dT}}\frac{{dT}}{{dt}} + \sum\limits_{c = 1}^{{{N}_{B}}} {\frac{{d{{n}_{b}}}}{{d{{\lambda }_{c}}}}\frac{{d{{\lambda }_{c}}}}{{dt}}} .$С учетом (13) уравнения (14) можно обратить и выразить субстанциальные производные от множителей Лагранжа через производные по времени, и далее через транспортные уравнения для базисных компонентов
3. ГОРЕНИЕ МЕТАНА
В гиперзвуковых летательных аппаратах (ГЛА) активного действия с прямоточным или гиперзвуковым воздушно-реактивным двигателем используются водородные или углеводородные топлива. Наиболее изученным является горение метана – основного компонента бытового газа, поэтому рассмотрим особенности горения на примере метана, а затем горение водорода. Ключевой проблемой создания активных ГЛА является сверхзвуковое турбулентное горение – крайне сложный и малоизученный процесс [12–14].
Метан представляет собой газообразное химическое соединение с химической формулой CH4. Это самый простой представитель алканов. Другие названия этой группы органических соединений: предельные, насыщенные или парафиновые углеводороды. Они характеризуются наличием простой связи между атомами углерода в молекуле, а все остальные валентности каждого углеродного атома насыщены атомами водорода. Для алканов наиболее важной реакцией является горение. Они горят с образованием газообразной двуокиси углерода и паров воды. В результате выделяется огромное количество химической энергии, которая превращается в тепловую или электрическую. Метан является горючим веществом и основным компонентом природного газа, что и делает его привлекательным топливом. В основе широкого использования природного ископаемого лежит реакция горения метана. Поскольку он в нормальных условиях является газом, его трудно транспортировать на дальние расстояния от источника, поэтому часто его предварительно сжижают. Процесс горения заключается в реакции между метаном и кислородом, т.е. в окислении простейшего алкана. В результате образуются двуокись углерода, вода и много энергии. Горение метана происходит в одностадийной реакции и может быть описано брутто-реакцией
(15)
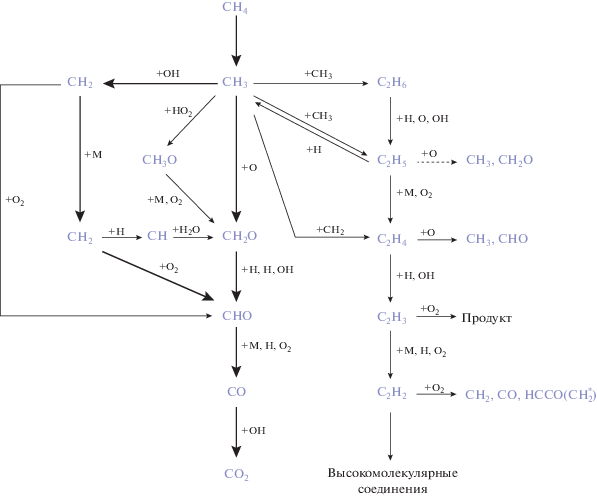
$\begin{gathered} {\text{C}}{{{\text{H}}}_{4}}~\left( {\text{г}} \right) + 2{{{\text{O}}}_{2}}~\left( {\text{г}} \right) \to {\text{C}}{{{\text{O}}}_{2}}~\left( {\text{г}} \right) + \\ + \,\,2{{{\text{H}}}_{2}}{\text{O}}~\left( {{\text{пар}}} \right) + 891~\,\,{\text{кДж}}, \\ \end{gathered} $Однако реакция (15) на самом деле содержит значительное количество разветвленных цепных реакций (рис. 1), часть из которых обрывается. В настоящее время существуют и продолжают разрабатываться кинетические схемы горения различных веществ, однако метан занимает одну из лидирующих позиций. Наиболее широко применимой является схема окисления метана, представленная в механизме GRI-Mech.3.0 (рис. 2) [15], разработанном в университете Беркли (США). Она содержит 53 компонента, входящих в 325 реакций. Поскольку такое большое количество компонентов не может быть использовано в расчетах, были предприняты попытки создания редуцированных баз данных реакций. Для метана одной из наиболее употребительных является база данных К. Лоy и Т. Лу (C.K. Law и T.F. Lu, 15 компонентов и 12 реакций, 2008 г.), и по рекомендации профессора К. Лоу для моделирования в данной работе используется эта база данных.
Рис. 2.
Скорость ламинарного горения метана в воздухе в зависимости от коэффициента избытка топлива: 1 – GRIMech 3.0, 2 – GRIMech 2.11, 3 – LU19 (из GRIMech 3.0), 4 – Lu13 (из GRIMech 2.11).
Данная схема была верифицирована на большом количестве экспериментальных данных и в настоящее время является одной из наиболее полных, используемых в моделировании. Изучение продуктов промежуточных реакций дает возможность исследовать общую структуру пламени, динамику фронта, оценить условия (границы) воспламенения и перехода к детонации. Понимание кинетики горения также способствует созданию технических устройств с повышенной эффективностью сгорания топлива, позволяет оптимизировать и снизить долю вредных выбросов (чистое горение) и может использоваться для создания новых комбинированных и альтернативных видов топлива.
В процессе окисления происходит наработка различных радикалов: H, OH, CH, CH2, HCO, CO2, CO. Одним из наиболее важных, определяющих кинетику процессов горения, является химически активный радикал – гидроксил OH. Разветвленные цепные реакции с наработкой возбужденных радикалов OH способствуют лавинообразному размножению частиц, что сопровождается выделением большого количества энергии, проявляющимся в высвечивании. Таким образом, гидроксил определяет положение фронта пламени, соответствующего области с наибольшей интенсивностью выделения энергии, т.е. максимально высокой температурой. В работе [16] показано, что OH не проникает в зоны “холодных реагентов”. По местоположению радикалов OH можно судить о динамике положения и структуре фронта горения. Гидроксил ОН, вместе с тем, быстро исчезает, поскольку является реагентом в реакциях образования воды. Для детектирования компонентов OH, как и других промежуточных реагентов, используется неинвазивный метод лазерной индуцированной флуоресценции. При определенном составе диагностического оборудования измерения флуоресценции OH могут позволить определить не только положение фронта пламени, но и распределение температуры и концентрации частиц OH. На основе таких экспериментальных данных проводят верификацию численных расчетов и кинетических схем, описанных выше.
Для расчетов скорости ламинарного пламени использован модуль скорости пламени в пакете CHEMKIN 4.0, предоставленном Л. Бромбергом (МИТ, США). Предпринята попытка использовать полный механизм GRI-PRF, но он был слишком велик для кода CHEMKIN (хотя более поздняя версия пакета CHEMKIN 4.0.2 решает эту проблему), поэтому применялась укороченная схема Лоу [16].
Расчеты выполнены для горения метана в воздухе с учетом термодинамических, транспортных процессов и плазмохимических реакций, используемых при моделировании из GRI 3.011.
4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Рассмотрим свободно распространяющееся одномерное предварительно перемешанное ламинарное пламя постоянного давления с одинаковой диффузией и числами Льюиса, равными единице. В этих условиях управляющие уравнения принимают известную форму:
Результаты расчета для разных давлений для пламени CH4 в широком диапазоне коэффициентов избытка топлива показаны на рис. 3, на рис. 4 – результаты расчета в зависимости от температуры. Рассчитанные скорости горения как функции коэффициента избытка топлива для метанового пламени в сравнении с результатами для полной модели представлены на рис. 5. Получено хорошее согласие для “бедного” пламени.
Рис. 3.
Скорость ламинарного горения метана при различных значениях коэффициента избытка топлива и давления: 1 – 0.5 атм, 2 – 1, 3 – 5, 4 – 10, 5 – 20.
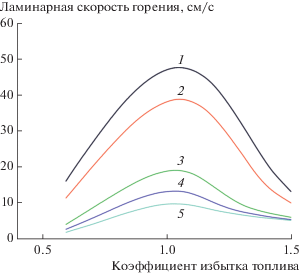
Рис. 4.
Скорость ламинарного горения метана в воздухе в зависимости от температуры при различных давлениях: 1 – 1 бар, 2 – 10, 3 – 30.
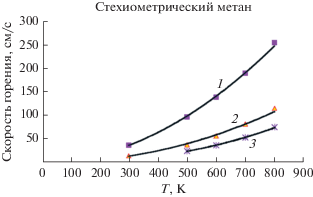
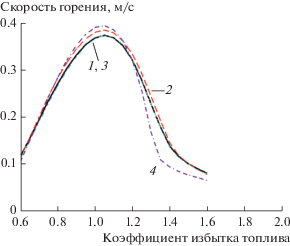
Рис. 5.
Зависимость скорости горения стехиометрической смеси CH4 и воздуха для перемешанной смеси от коэффициента избытка топлива: 1 – полная модель, 2 – метод ЧЛХР (GRIMech3.0).
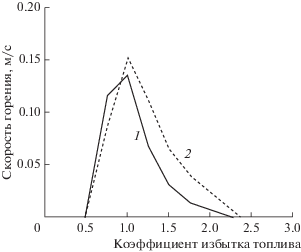
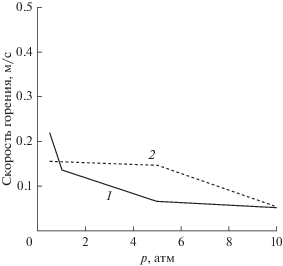
Некоторое несоответствие существует для богатой смеси. Результаты для разных давлений для пламени CH4 также показаны на рис. 6. При повышенном давлении расхождение является более значительным. Следственно, для получения количественного согласия в данном диапазоне могут потребоваться дополнительные изменения в модели.
ЗАКЛЮЧЕНИЕ
В работе представлен метод ЧЛХР и показаны результаты для скорости горения ламинарного предварительно перемешанного пламени. ЧЛХР обеспечивает строгую основу для создания редуцированных кинетических схем. Главным преимуществом является то, что общая дифференциально-алгебраическая система уравнений описывает редуцированный механизм независимо от выбора кинетически контролируемых и равновесных компонентов. Данный метод после валидации и верификации может значительно облегчить исследование редуцированных механизмов химических реакций.
Работа выполнена при поддержке гранта РНФ № 19-49-02031.
Список литературы
Иевлев В.М., Сон Э.Е. Теплофизические свойства водорода и щелочных металлов в газофазном ядерном реакторе. Научно-технический отчет. М.: НИИ тепловых процессов, 1967.
Иевлев В.М. Турбулентное движение высокотемпературных сплошных сред. М.: Наука, 1975.
Иевлев В.М., Сон Э.Е. Теплофизические свойства плазмы. М.: МФТИ, 1975.
Сон Э.Е. Физическая механика. М.: МФТИ, 1975.
Иевлев В.М., Сон Э.Е. Гидродинамическое описание высокотемпературных сред: Уч. пособ. Долгопрудный: Изд-во МФТИ, 1977.
Павлов Г.А., Сон Э.Е. Транспортные процессы в приближении локального химического равновесия // ПМТФ. 1975. № 6. С. 51.
Кучеренко В.И., Павлов Г.А., Сон Э.Е. Эффективные коэффициенты переноса в плазме в приближении локального термодинамического равновесия // ТВТ. 1976. Т. 14. № 5. С. 921.
Кучеренко В.И., Павлов Г.А., Грязнов В.К. и др. Теплофизические свойства плазмы смеси гелия с водородом в интервале температур 2800–3000 К и давлений 1–100 атм. Препринт. Черноголовка: ОИХФ РАН, 1978.
Keck I.C. Rate-controlled Constrained-equilibrium Theory of Chemical Reactions in Complex Systems // Prog. Energy Combust. Sci. 1990. V. 16. P. 125.
Keck I.C., Gillespie D. Rate-controlled Partial-equilibrium Method for Treating Reacting Gas Mixtures // Combust. Flame. 1971. V. 17. P. 237.
Колесников А.Ф., Тирский Г.А. Уравнения гидродинамики для частично ионизованных многокомпонентных смесей газов с коэффициентами переноса в высших приближениях. В сб.: Молекулярная газодинамика. М.: Наука, 1982. С. 20.
Shetinkov E., Shcherbina Y., Spiridonov V. Turbulent Combustion of Gaseous Mixtures // Astronautica Acta. Great Britain. 1979. V. 15. № 63. P. 597.
Щетинков Е.С. О кусочно-одномерных моделях сверхзвукового горения и псевдоскачка в каналах // ФГВ. 1973. № 4. С. 473.
Son E., Son K. Introduction to Mechanics Continuum Media. M.: MIPT Publ., 2012. P. 340.
Lafferty J., Coblish J., Marineau E. et al. The Hypervelocity Wind Tunnel; Continued Excellence through Improvement and Modernization // AIAA 2015-1340.
Law C. Combustion Physics. Cambridge University Press, 2006.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур