Теплофизика высоких температур, 2020, T. 58, № 2, стр. 275-286
Течение двухфазной парокапельной смеси в канале переменного сечения при наличии фазовых превращений
1 Южно-Казахстанский государственный университет им. М. Ауэзова
г. Шымкент, Казахстан
2 Институт математики и математического моделирования
г. Алматы, Казахстан
* E-mail: tulegen_amanbaev@mail.ru
Поступила в редакцию 25.06.2019
После доработки 08.10.2019
Принята к публикации 22.10.2019
Аннотация
В квазиодномерной постановке исследованы особенности течения двухфазной парокапельной среды в сопле Лаваля с учетом фазовых превращений. Изучено влияние определяющих параметров (концентрации и диаметра дисперсных капель и т.п.) на движение смеси в широком диапазоне их изменения. Расчеты проведены как в докритическом, так и в критическом режимах истечения смеси. Рассмотрен характер поведения двухфазной смеси при различных типах критического режима течения. Проанализировано влияние определяющих параметров на критический (максимальный) расход смеси.
ВВЕДЕНИЕ
Многофазные (или гетерогенные), в частности двухфазные, системы встречаются в различных областях современной техники. При этом течение таких сред в большинстве случаев сопровождается тепло- и массообменными процессами. Исследование данных течений является одной из актуальных проблем динамики и теплофизики многофазных систем [1–4]. Большое значение имеет изучение движений в различных каналах, в частности переменного сечения (например, типа сопла Лаваля). Такие течения часто встречаются в различных теплоэнергетических и теплообменных [5, 6], а также других [7, 8] установках. Течение двухфазных смесей газа с инертными частицами в соплах исследовано достаточно подробно [9–14]. В [10] рассмотрено двухфазное течение в соплах при больших числах Рейнольдса с учетом взаимного влияния газа и твердых частиц, а также взаимодействия частиц со стенками канала. Работа [11] посвящена исследованию газокапельного течения (без фазовых переходов) в сопле при больших концентрациях дисперсной фазы. Построена методика расчета двумерных дозвуковых двухфазных течений в соплах.
Течение газокапельных смесей в каналах при наличии фазовых превращений исследовано в [2, 15–18]. В частности, в [15] получен ряд элементарных соотношений для расчета критических (максимальных) расходов двухфазного потока в каналах постоянного сечения. В [2, 16] на основе анализа уравнений квазиодномерного движения двухфазной парокапельной смеси показано, что в зависимости от начальных значений определяющих параметров в сопле Лаваля могут реализоваться два типа критического режима истечения, в которых расход смеси достигает максимальной величины.
Возросшее использование различных каналов, в том числе переменного сечения, требует более детального изучения особенностей поведения двухфазных газокапельных смесей в таких каналах. В частности, к настоящему времени недостаточно исследовано влияние различных определяющих параметров (размеров дисперсных капель, их концентрации и т.п.) на течение двухфазной парокапельной среды в соплах, в том числе при наличии межфазных превращений (испарения, конденсации). Актуальность данного вопроса возрастает в связи с бурным развитием в последние годы перспективных способов получения ультра- и нанодисперсных порошков с заданными характеристиками в соплах и расширяющихся каналах за счет процессов зародышеобразования и конденсации [19–21]. При этом особый интерес представляет изучение влияния определяющих параметров на течение двухфазной смеси в соплах в критическом режиме (так как в этом режиме, как указано выше, реализуется максимальный расход смеси). Также вызывает интерес вопрос, связанный с переходом течения из одного типа критического режима в другой (этот вопрос еще не изучен).
Цель настоящей работы – исследование течения двухфазной парокапельной среды в канале переменного сечения (типа сопла Лаваля) при наличии межфазных превращений и установление особенностей поведения парокапельной среды в зависимости от определяющих параметров в докритическом и критическом режимах.
УРАВНЕНИЯ ДВИЖЕНИЯ И ЗАМЫКАЮЩИЕ СООТНОШЕНИЯ
Основные допущения. Наряду с главными допущениями, обычно принимаемыми для описания движения гетерогенных сред, примем дополнительно следующие (характерные для газовзвесей) допущения [1]: вязкость и теплопроводность фаз проявляются лишь в процессах межфазного взаимодействия и не проявляются в макроскопическом переносе импульса и энергии; плотность газовой (несущей) фазы много меньше плотности вещества конденсированной (дисперсной) фазы; дисперсные капли не деформируются, не дробятся и не коагулируют; межфазные превращения (испарение, конденсация), из-за которых размеры капель меняются, происходят на линии насыщения; при этом конденсированная фаза локально-монодисперсна (т.е. в каждом элементарном объеме дисперсные капли имеют одинаковый, свойственный этому объему размер); для более детального описания процесса фазовых превращений используется трехтемпературная схема межфазного теплообмена, которая учитывает отличие температуры межфазной поверхности от средних температур отдельных фаз (данная схема подробно рассмотрена в [1]); внешние массовые силы, трение со стенкой канала и поток тепла извне отсутствуют; давление на срезе сопла совпадает с противодавлением во внешней среде (расчетный режим); задача рассматривается в квазиодномерном приближении, когда поперечными градиентами параметров среды можно пренебречь.
В приведенных далее уравнениях нижние индексы 1, 2 отвечают параметрам несущей и дисперсной фаз, а индекс s – параметрам среды в состоянии насыщения.
Уравнения движения. В рамках механики многофазных сред с учетом принятых допущений стационарное движение двухфазной парокапельной среды в канале переменного сечения в квазиодномерном приближении описывается следующей системой уравнений [2]:
(1)
$\frac{{d{{m}_{{{\kern 1pt} 1}}}}}{{dx}} = {{J}_{{21}}},\,\,\,\,\frac{{d{{m}_{2}}}}{{dx}} = - {{J}_{{21}}},\,\,\,\,\frac{{dn{{{v}}_{2}}S}}{{dx}} = 0,$(2)
$\begin{gathered} {{m}_{1}}\frac{{d{{{v}}_{1}}}}{{dx}} = - {{\alpha }_{1}}S\frac{{dp}}{{dx}} + {{F}_{{21}}} + {{J}_{{21}}}({{{v}}_{2}} - {{{v}}_{1}}), \\ {{m}_{2}}\frac{{d{{{v}}_{2}}}}{{dx}} = - {{\alpha }_{2}}S\frac{{dp}}{{dx}} - {{F}_{{21}}}, \\ \end{gathered} $(3)
$\begin{gathered} {{m}_{1}}\frac{{d{{i}_{1}}}}{{dx}} = {{\alpha }_{1}}{{{v}}_{1}}S\frac{{dp}}{{dx}} + {{J}_{{21}}}\left[ {\frac{{{{{({{{v}}_{2}} - {{{v}}_{1}})}}^{2}}}}{2} + {{i}_{{1s}}} - {{i}_{1}}} \right] + \\ + \,\,{{F}_{{21}}}({{{v}}_{2}} - {{{v}}_{1}}) - {{Q}_{{1\Sigma }}}, \\ \end{gathered} $(4)
${{m}_{2}}\frac{{d{{i}_{2}}}}{{dx}} = {{\alpha }_{2}}{{{v}}_{2}}S\frac{{dp}}{{dx}} - {{J}_{{21}}}({{i}_{{2s}}} - {{i}_{2}}) - {{Q}_{{2\Sigma }}},$(5)
$\begin{gathered} {{\alpha }_{1}} + {{\alpha }_{2}} = 1,\,\,\,\,n = {{6{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{6{{\alpha }_{2}}} {(\pi {{d}^{3}})}}} \right. \kern-0em} {(\pi {{d}^{3}})}},\,\,\,\,{{m}_{k}} = {{\rho }_{k}}{{{v}}_{k}}S, \\ {{\rho }_{k}} = \rho _{k}^{^\circ }{{\alpha }_{k}},\,\,\,\,k = {\text{1}},{\text{2}}. \\ \end{gathered} $Здесь $\rho _{k}^{^\circ },$ ${{\rho }_{k}},$ ${{\alpha }_{k}},$ ${{{v}}_{k}},$ ${{i}_{k}}$ – истинные и приведенные плотности, объемные содержания, скорости и энтальпии несущей (k = 1) и дисперсной (k = 2) фаз; p, n, d – давление в газе, концентрация и диаметр капель; x, S(x) – продольная координата и площадь поперечного сечения канала; ${{i}_{{1s}}},$ ${{i}_{{2s}}}$ – энтальпии фаз в состоянии насыщения; J21, F21, Q1Σ, Q2Σ – соответственно интенсивности фазовых превращений, силового взаимодействия между несущей и дисперсной фазами, а также интенсивности оттока тепла от газа и дисперсных капель к межфазной поверхности (так называемой Σ-фазе [1]) на единице длины канала. Уравнения (1) – это уравнения неразрывности фаз и уравнение сохранения числа дисперсных капель; (2) – уравнения сохранения импульсов фаз; (3), (4) – уравнения сохранения энтальпий фаз. Заметим, что при записи уравнений сохранения энтальпий фаз использована трехтемпературная схема [1, 2], когда температура межфазной поверхности отличается от температур газа и основной массы капли.
Уравнения состояния. Для замыкания системы (1)–(5) необходимо привлечь термодинамические уравнения состояния фаз. При этом газ будем считать калорически совершенным с постоянной теплоемкостью, а капли – несжимаемыми. Тогда имеем [1]
(6)
$\begin{gathered} p = \rho _{1}^{^\circ }R{{T}_{1}},\,\,\,\,{{i}_{1}} = {{i}_{{10}}} + {{c}_{1}}({{T}_{1}} - {{T}_{0}}), \\ {{i}_{2}} = {{i}_{{20}}} + {{c}_{2}}({{T}_{2}} - {{T}_{0}}) + {{(p - {{p}_{0}}{\text{)}}} \mathord{\left/ {\vphantom {{(p - {{p}_{0}}{\text{)}}} {\rho _{{\text{2}}}^{^\circ }}}} \right. \kern-0em} {\rho _{{\text{2}}}^{^\circ }}}, \\ \rho _{2}^{^\circ },{{c}_{1}},{{c}_{2}},R = {\text{const}}, \\ \end{gathered} $(7)
$\begin{gathered} l(p) = l({{p}_{0}}) - ({{c}_{2}} - {{c}_{1}})({{T}_{s}}(p) - {{T}_{s}}({{p}_{0}})) - \\ - \,(p - {{p}_{0}}){\text{/}}\rho _{2}^{^\circ }. \\ \end{gathered} $(8)
${{T}_{s}}(p) = \frac{{T^\circ }}{{\ln ({{p^\circ } \mathord{\left/ {\vphantom {{p^\circ } p}} \right. \kern-0em} p})}}.$Таким образом, если задать формулы, определяющие интенсивности межфазных массообмена J21, силового взаимодействия F21 и теплообмена Q1Σ, Q2Σ, то получим замкнутую систему уравнений двухскоростного и двухтемпературного течения газокапельной среды.
Интенсивности межфазного взаимодействия. Для интенсивностей межфазного взаимодействия J21, F21, Q1Σ, Q2Σ имеются очевидные соотношения
(9)
$\begin{gathered} {{J}_{{21}}} = Sn{{j}_{{21}}},\,\,\,\,{{F}_{{21}}} = Sn{{f}_{{\mu }}},\,\,\,\,{{Q}_{{1\Sigma }}} = Sn{{q}_{{1\Sigma }}}, \\ {{Q}_{{2\Sigma }}} = Sn{{q}_{{2\Sigma }}}. \\ \end{gathered} $(10)
$\begin{gathered} {{f}_{{\mu }}} = \left( {{{\pi {{d}^{2}}} \mathord{\left/ {\vphantom {{\pi {{d}^{2}}} 8}} \right. \kern-0em} 8}} \right)\rho _{1}^{^\circ }{{C}_{{\mu }}}{{w}_{{12}}}({{{v}}_{2}} - {{{v}}_{1}}),\,\,\,\,{{w}_{{12}}} = \left| {{{{v}}_{1}} - {{{v}}_{2}}} \right|, \\ {{q}_{{1\Sigma }}} = \pi d{{\lambda }_{{{\kern 1pt} 1}}}N{{u}_{1}}({{T}_{1}} - {{T}_{\Sigma }}), \\ {{q}_{{2\Sigma }}} = \pi d{{\lambda }_{2}}N{{u}_{2}}({{T}_{2}} - {{T}_{\Sigma }}). \\ \end{gathered} $(11)
$\begin{gathered} {{C}_{{\mu }}} = C_{{\mu }}^{^\circ }{{\psi }_{M}},\,\,\,\,C_{{\mu }}^{^\circ } = \frac{{24}}{{{{{\operatorname{Re} }}_{{12}}}}} + \frac{{4.4}}{{\operatorname{Re} _{{12}}^{{0.5}}}} + 0.42, \\ {{\psi }_{M}} = 1 + \exp \left( { - \frac{{0.427}}{{M_{{12}}^{{4.63}}}}} \right), \\ {\text{N}}{{{\text{u}}}_{1}} = 2 + 0.6{\text{Re}}_{{{\text{12}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{\text{Pr}}_{{\text{1}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}, \\ {\text{N}}{{{\text{u}}}_{2}} \cong 10,\,\,\,\,{{\operatorname{Re} }_{{12}}} = \frac{{\rho _{1}^{^\circ }d{{w}_{{12}}}}}{{{{\mu }_{1}}}},\,\,\,\,{{M}_{{12}}} = \frac{{{{w}_{{12}}}}}{{{{a}_{1}}}},\,\,\,\,{{\Pr }_{1}} = \frac{{{{\mu }_{1}}{{c}_{1}}}}{{{{\lambda }_{1}}}}, \\ \end{gathered} $Будем считать, что на межфазной границе выполняются условия фазового равновесия [1]
Эти условия позволяют определять интенсивность фазовых переходов при заданных интенсивностях теплообмена
или Таким образом, система уравнений (1)–(5) с замыкающими соотношениями (6)–(13) представляет собой замкнутую систему относительно неизвестных переменных ${{m}_{1}},$ ${{m}_{2}},$ ${{{v}}_{1}},$ ${{{v}}_{2}},$ p, n, d, ${{T}_{1}},$ ${{T}_{2}}.$ПЕРВЫЕ ИНТЕГРАЛЫ
Складывая оба уравнения масс фаз (1) получим интеграл массы или расхода смеси
Из третьего уравнения системы (1) следует соотношение, устанавливающее закон сохранения числа капель
Сложение уравнений импульсов (2) для несущей и дисперсной фаз дает
Отсюда, проинтегрировав левую часть от 0 до x и используя очевидное равенство Sdp/dx = = d(Sp)/dx – pdS/dx, нетрудно получить следующее уравнение, отражающее закон сохранения полного импульса потока смеси вдоль канала:
(16)
$\begin{gathered} {{m}_{1}}{{{v}}_{1}} + {{m}_{2}}{{{v}}_{2}} + pS = \\ = ({{m}_{{10}}}{{{v}}_{{10}}} + {{m}_{{20}}}{{{v}}_{{20}}} + {{p}_{0}}{{S}_{0}}) + \int\limits_0^x {p\left( {\frac{{dS}}{{dx}}} \right)dx} , \\ \end{gathered} $Имеет место также и интеграл энергии смеси
(17)
${{m}_{1}}\left( {{{i}_{1}} + \frac{{{v}_{1}^{2}}}{2}} \right) + {{m}_{2}}\left( {{{i}_{2}} + \frac{{{v}_{2}^{2}}}{2}} \right) = const.$Постоянные в правых частях соотношений (14), (15), (17) определяются по значениям параметров среды в некотором фиксированном состоянии (например, на входе в канал). Установленные первые интегралы (14)–(17) можно использовать, в частности, для проверки решений, полученных расчетным путем.
КРИТИЧЕСКИЙ РЕЖИМ ТЕЧЕНИЯ
Комбинируя уравнения системы (1)–(5) с учетом уравнений состояния (6) можно получить, аналогично [2, 16], уравнение отдельно для давления, которое имеет вид
(18)
$\,\,\,\,\,\,\,\,\,\frac{{dp}}{{dx}} = \frac{{{{\gamma }_{1}}p}}{{{{\alpha }_{1}}}}{{{\text{M}}}^{2}}\frac{{\eta + \zeta }}{{1 - {{{\text{M}}}^{2}}}},\,$В общем случае вследствие большого количества возможных значений параметров, входящих в уравнения, выяснить заранее расположение критического сечения затруднительно (оно определяется в ходе численного решения задачи). Анализ практически важных случаев критических течений двухфазных сред проведен в [2, 16]. В частности, отмечено, что при выполнении определенных условий непрерывный переход через характеристическую скорость звука ${{a}_{f}}$ происходит в расширяющейся части канала. Соответствующая точка с продольной координатой ${{x}_{*}}$ является в плоскости xp особой точкой типа седло, а решение дифференциального уравнения (18) в случае критического режима – сепаратрисой семейства интегральных кривых этого уравнения.
Для заданных параметров торможения и заданного канала в [16] установлены два возможных случая критического режима истечения. Первый – если в процессе интегрирования системы дифференциальных уравнений особая точка находится в пределах рассматриваемого канала длиной L:
(19)
$\begin{gathered} x = {{x}_{*}}\,\,\,\,(0 < {{x}_{*}} \leqslant L){\text{:}}\,\,\,\,\eta + \zeta = 0, \\ {{{v}}_{1}} = {{a}_{f}},\,\,\,\,\frac{{dp}}{{dx}} = \frac{0}{0}. \\ \end{gathered} $Данный случай относится к описанному выше типу критического течения. Второй случай – когда в пределах сопла особая точка не реализуется (или особая точка формально находится вне канала) и характеристическая скорость достигается несущей фазой на выходе из канала. При этом на выходе градиент давления, согласно (18), стремится к бесконечности
(20)
$x = L{\text{:}}\,\,~\,\,\eta + \zeta < 0,\,\,\,\,{{{v}}_{1}} = {{a}_{f}},\,\,\,\,\frac{{dp}}{{dx}} = - \infty .$Реализация того или иного типа критического режима зависит от значений определяющих параметров на входе в сопло (см. ниже).
РАСЧЕТ ПО РАВНОВЕСНОЙ СХЕМЕ
Интересно рассмотреть для сравнения предельную схему термодинамически равновесной смеси, когда скорости и температуры фаз совпадают ${{{v}}_{1}} = {{{v}}_{2}} = {v},$ ${{T}_{1}} = {{T}_{2}} = T.$ При наличии фазовых превращений температура такой среды равна температуре насыщения $T = {{T}_{s}}.$ Поскольку уменьшение размера капель при фиксированных прочих параметрах приводит к ускорению межфазных релаксационных процессов, стремящихся выравнивать скорости и температуры фаз, то для краткости данную схему обозначают условно как “d = 0” [1]. Известно, что если использовать равновесную схему разреженной газовзвеси без фазовых переходов (когда массовые доли компонентов смеси постоянны), то газодинамические расчеты проводятся обычным образом по классическим уравнениям газовой динамики совершенного газа, имеющего эффективные теплофизические параметры [1]. Однако при наличии фазовых переходов массовые доли составляющих смеси не остаются постоянными. В этом случае расчет течения в рамках предельной равновесной схемы значительно сложнее, чем при отсутствии фазовых переходов. Приведем вкратце один из возможных способов расчета течений по равновесной схеме в канале переменного сечения при наличии фазовых переходов. С этой целью запишем уравнение движения равновесной смеси, которое получается сложением уравнений импульсов отдельных составляющих (2):
Очевидно, согласно интегралу массы (14):
Уравнение состояния несущей среды (6) приведем к виду
где температура насыщения ${{T}_{s}}$ есть функция от давления p, удовлетворяющая уравнению Клапейрона–Клаузиуса (или при выполнении определенных условий выражаемая, например, формулой (8)). Из интеграла энергии (17) с учетом интеграла массы (22) и выражений для энтальпий фаз (6) определяется расход газа ${{m}_{1}}$ как функция p, v, ${{T}_{s}}(p),$ подставляя которую в (23) получим квадратное относительно v уравнениеЗдесь a, c – функции, зависящие только от давления p, а b – от p и S. Анализ показал, что действительным течениям соответствует корень данного уравнения со знаком “плюс” перед радикалом. Уравнение (24) позволяет выразить скорость v через давление p и площадь поперечного сечения канала S.
Далее продифференцируем уравнение (24) по x. Имеем
(25)
$(2a{v} + b)\frac{{d{v}}}{{dx}} + (a{\kern 1pt} '{{{v}}^{2}} + b{\kern 1pt} '{v} + c{\kern 1pt} ')\frac{{dp}}{{dx}} = - {v}pl(p)\frac{{dS}}{{dx}},$(26)
$\left[ {(a{\kern 1pt} '{{{v}}^{2}} + b{\kern 1pt} '{v} + c{\kern 1pt} ') - \frac{S}{m}(2a{v} + b)} \right]\frac{{dp}}{{dx}} = - {v}pl(p)\frac{{dS}}{{dx}}.$Зная распределение давления, нетрудно рассчитать и другие характеристики потока (скорость, температуру, состав смеси и т.п.).
В случае критического течения множитель перед dp/dx в уравнении (26) должен обратиться в нуль в минимальном сечении, где dS/dx = 0:
В этом уравнении значения всех параметров соответствуют минимальному сечению канала. Минимальный положительный корень данного квадратного относительно v уравнения (анализ показал, что оно имеет по крайней мере один положительный корень) и есть характеристическая скорость, непрерывный переход через которую осуществляется в горле сопла. Отметим, что в рамках равновесной схемы наличие фазовых переходов не влияет на положение критического сечения, которое совпадает в данном случае с минимальным сечением.
Ниже обсуждаются некоторые результаты расчетов течения двухфазной газокапельной смеси в канале переменного сечения при наличии фазовых превращений.
ПОСТАНОВКА ЗАДАЧИ И РЕЗУЛЬТАТЫ РАСЧЕТОВ
Постановка задачи. В качестве примера рассмотрим течение двухфазной парокапельной смеси в сопле Лаваля, безразмерная площадь поперечного сечения которого задается соотношением [23]
Результаты расчетов контролировались по выполнению первых интегралов уравнений движения двухфазной смеси (14)–(17). Расчеты по построенной модели при отсутствии дисперсной фазы (${{\bar {\rho }}_{{20}}} = 0$) практически полностью совпали с результатами, следующими из известных изэнтропических формул для одномерного стационарного течения идеального газа [25]. Кроме того, адекватность математической модели проверялась сравнением результатов расчета с известными экспериментальными данными по истечению двухфазной парокапельной смеси в соплах [26], которое показало хорошее их согласие (рис. 1). Отметим, что в данном случае имеет место критическое течение второго типа, когда градиент давления в выходном сечении канала стремится к –∞ (см. выше).
Рис. 1.
Сравнение расчетного (линия) и экспериментального [26] (точки) распределения давления вдоль сопла при начальном массовом расходном паросодержании ${{{{{\bar {m}}}_{{10}}}} \mathord{\left/ {\vphantom {{{{{\bar {m}}}_{{10}}}} {{{{\bar {m}}}_{0}}}}} \right. \kern-0em} {{{{\bar {m}}}_{0}}}} = 0.17.$

В процессе численного решения задачи в случае критического течения для заданных массового содержания и размера капель путем подбора отыскивалось значение скорости на входе, при котором выполнялось одно из критических условий (19), (20). При этом в окрестности критического сечения (особой точки) значения давления и других параметров, градиенты которых вдоль оси x терпят разрыв, определялись экстраполяцией в критическое сечение.
В представленных ниже рисунках скорости несущей и дисперсной фаз ${{{v}}_{1}},$ ${{{v}}_{2}}$ отнесены к скорости звука в газе на входе в сопло ${{a}_{{10}}},$ плотность дисперсной фазы ${{\rho }_{2}}$ – к начальной плотности несущей фазы ${{\rho }_{{10}}},$ массовые расходы газовой фазы и всей смеси в целом ${{m}_{1}},$ $m$ – к характерной величине ${{\rho }_{{10}}}{{a}_{{10}}}{{S}_{0}},$ а остальные параметры – к соответствующим их значениям на входе в сопло. Безразмерные параметры потока отмечены верхней чертой (кроме числа Маха М). Сплошные и пунктирные линии отвечают параметрам газа и капель. Для сравнения штриховыми кривыми показаны параметры газа при отсутствии дисперсной фазы, а штрихпунктирными кривыми – параметры смеси, рассчитанные по равновесной схеме “d = 0” (см. выше).
Докритическое течение смеси. На рис. 2 представлены результаты расчетов докритического (везде M < 1) течения двухфазной парокапельной среды при скорости ${{{\bar {v}}}_{0}}$ = 0.2, относительном массовом содержании капель ${{\bar {\rho }}_{{20}}} = 1$ и их диаметре d0 = 20 мкм на входе в сопло. Видно, что давление $\bar {p}$ и плотность ${{\bar {\rho }}_{1}}$ газа в суживающейся части сопла уменьшаются, а в расширяющейся части, наоборот, увеличиваются (рис. 2а). Причем наличие дисперсных капель приводит к заметному падению давления и плотности газа по всей длине канала. Такое поведение ${{\bar {\rho }}_{1}}$ и $\bar {p}$ объясняется тем, что, как показал анализ уравнения для давления (18), наличие дисперсной фазы приводит к уменьшению отрицательного градиента давления в начальной части канала (до минимального сечения) из-за интенсивного межфазного взаимодействия. Это обстоятельство в свою очередь приводит к дополнительному ускорению газовой фазы (несмотря на тормозящий эффект дисперсных капель). В результате при наличии капель плотность пара падает быстрее, чем при их отсутствии.
Рис. 2.
Распределения давления газа и плотностей (а), скоростей (б), температур (в) фаз вдоль канала в докритическом режиме при ${{{\bar {v}}}_{0}}$ = 0.2, ${{\bar {\rho }}_{{20}}} = 1,$ d0 = 20 мкм: сплошные линии – параметры несущей фазы (газа), пунктирные – параметры дисперсной фазы (капель), штрихпунктирные – расчеты при отсутствии дисперсной фазы (${{\bar {\rho }}_{{20}}}$ = 0), штрихпунктирные – расчеты по равновесной схеме “d = 0”.
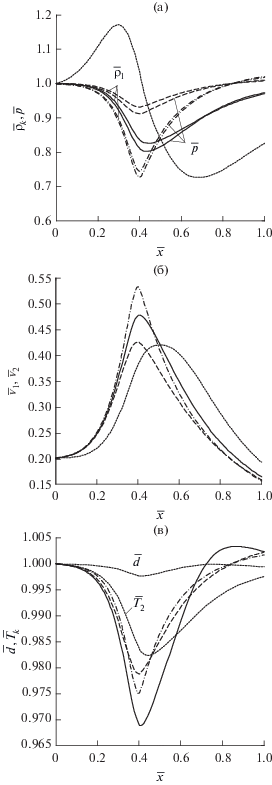
Плотность дисперсной фазы ${{\bar {\rho }}_{2}}$ сначала растет, затем уменьшается, а потом снова увеличивается. Объясняется такое поведение ${{\bar {\rho }}_{2}}$ тем, что на плотность конденсированной фазы влияют два основных фактора: сужение (или расширение) трубки тока дисперсной фазы, приводящее соответственно к росту (или падению) концентрации капель, а также ускорение (или торможение) капель в канале из-за силового взаимодействия с несущим газом, которое способствует уменьшению (или увеличению) плотности дисперсной фазы. В зависимости от того, какой из этих факторов преобладает, величина ${{\bar {\rho }}_{2}}$ может увеличиваться или уменьшаться вдоль канала. Например, как видно на рис. 2а, до точки $\bar {x} \cong 0.3$ преобладает фактор сужения канала, и поэтому, несмотря на ускорение капель (вследствие взаимодействия с ускоряющимся газом) плотность дисперсной фазы растет. В средней зоне сопла 0.3 $ \lesssim $ $\bar {x}$ $ \lesssim $ 0.65 плотность ${{\bar {\rho }}_{2}}$ уменьшается, так как здесь преобладает фактор ускорения капель. Ближе к выходу из сопла 0.65 $ \lesssim $ $\bar {x}$ $ \lesssim $ 1 плотность капель увеличивается из-за торможения (несмотря на расширение канала, способствующее падению концентрации капель). Необходимо заметить, что на плотности газа и капель могут влиять также межфазные превращения, однако, как показали расчеты, в рассматриваемом диапазоне варьирования определяющих параметров они не вносят каких-нибудь существенных вкладов в процесс изменения плотностей фаз.
Скорость пара ${{{\bar {v}}}_{1}}$ в сужающейся части канала увеличивается более чем в два раза и существенно уменьшается в расширяющейся части сопла (рис. 2б). Причем, как видно на рисунке, наличие дисперсной фазы в смеси приводит к увеличению скорости газа (объяснение этому эффекту дано выше). Скорость дисперсной фазы ${{{\bar {v}}}_{2}}$ ведет себя, подобно скорости несущей фазы, немонотонно. Вначале (при $\bar {x}$ $ \lesssim $ 0.5) дисперсные капли, увлекаясь ускоряющимся потоком газа, приобретают значительную скорость (более чем в два раза превышающую скорость на входе в сопло), затем, когда газ начинает тормозиться, их скорость также падает, оставаясь при этом больше скорости газа. В этой зоне ($\bar {x}$ $ \gtrsim $ 0.5) дисперсная фаза отдает обратно несущей фазе приобретенный в начальном участке импульс.
На рис. 2в показаны распределения температур несущей и дисперсной фаз, а также характер изменения диаметра капель из-за фазовых превращений. Заметно, что по мере движения смеси процесс межфазного массообмена меняет свое направление: сначала идет испарение капель, затем за минимальным сечением – конденсация пара. Отметим, что при диаметре капель d0 = 20 мкм распределение температур дисперсной фазы ${{\bar {T}}_{2}}$ достаточно слабо отличается от температуры насыщения ${{\bar {T}}_{s}},$ так что в рассматриваемом случае фазовые переходы происходят практически в режиме насыщения жидкой фазы ${{\bar {T}}_{2}} \cong {{\bar {T}}_{s}}$ (в связи с этим, чтобы не загромождать рисунок, распределение температуры насыщения опущено). Температура пара несколько меньше, чем при отсутствии капель (за исключением зоны ближе к концу сопла $\bar {x}$ $ \gtrsim $ 0.6), что связано с дополнительным ускорением газа при наличии дисперсных капель (см. рис. 2б). Отметим, что до точки $\bar {x}$ $ \lesssim $ 0.6 температура капель выше, чем температура пара ${{\bar {T}}_{1}} < {{\bar {T}}_{2}},$ а далее имеет место обратное соотношение ${{\bar {T}}_{1}} > {{\bar {T}}_{2}}.$
Как видно на представленных выше рисунках, при заданных значениях ${{{\bar {v}}}_{0}},$ ${{\bar {\rho }}_{{20}}},$ d0 максимумы и минимумы изучаемых параметров достигаются чуть далее минимального сечения ${{\bar {x}}_{{\min (S)}}} = 0.4$ рассматриваемого канала. Расчеты показали, что увеличение массовой концентрации капель (в диапазоне, отвечающем докритическому течению) в смеси приводит к увеличению скорости, уменьшению давления, плотности и температуры газа. При этом фазовые превращения не сильно влияют на характер течения двухфазной смеси в канале.
Критический режим истечения. Особый интерес представляет изучение течения двухфазной среды в критическом режиме, когда массовый расход смеси достигает максимального значения. На рис. 3 представлены распределения числа Маха, определенного по характеристической скорости звука $M = {{{{{v}}_{1}}} \mathord{\left/ {\vphantom {{{{{v}}_{1}}} {{{a}_{f}}}}} \right. \kern-0em} {{{a}_{f}}}},$ давления и температуры фаз при начальной массовой концентрации капель ${{\bar {\rho }}_{{20}}}$ = 1 и их диаметре d0 = 20 мкм в случае критического режима первого типа (удовлетворяющего условию (19)). Число Маха для предельной схемы “d = 0” рассчитано по эффективной (равновесной) скорости смеси [1]. При данных значениях ${{\bar {\rho }}_{{20}}}$ и d0 имеют место, как и в случае идеального газа, два вида течения за критическим сечением: первый – дозвуковой (соответствующие параметры обозначены верхним знаком “–”), второй – сверхзвуковой (отвечает знак “+”). Видно, что при наличии дисперсной фазы критическое сечение $\bar {x} = \bar {x}{\text{*}}$ смещается в сторону расширяющейся части сопла ($\bar {x}* \cong 0.544$). В случае критического сверхзвукового течения наличие капель приводит к уменьшению числа Маха и увеличению давления, а в случае критического дозвукового течения – наоборот, к увеличению числа Маха и уменьшению давления по всей длине канала. Заметим, что в сверхзвуковом режиме капли испаряются на всем протяжении канала, в то время как в дозвуковом режиме происходит смена направления фазового перехода в пределах сопла: сначала идет испарение капель, затем – конденсация пара (диаметр капель меняется достаточно слабо, поэтому, чтобы не загромождать рисунок, он не приводится).
Рис. 3.
Распределения числа Маха (а), давления (б) и температур фаз (в) вдоль канала в критическом режиме первого типа при ${{\bar {\rho }}_{{20}}} = 1,$ d0 = 20 мкм: обозначения – как на рис. 2.

Рис. 4 иллюстрирует зависимость положения критического сечения $\bar {x}{\text{*}}$ от массового содержания дисперсной фазы. При увеличении массового содержания дисперсной фазы в смеси ${{\bar {\rho }}_{{20}}}$ критическое сечение перемещается в сторону выхода из канала, и при некотором значении ${{\bar {\rho }}_{{20}}} = \bar {\rho }_{{20}}^{*}$ оно окажется на срезе сопла $\bar {x}{\text{*}} = 1.$ Очевидно, в этом случае течение становится дозвуковым (за исключением конца канала $\bar {x}$ = 1, где M = 1). Данную ситуацию можно рассматривать как крайнее состояние, при котором еще имеет место критический режим первого типа, соответствующий условию (19). Дальнейший рост величины ${{\bar {\rho }}_{{20}}}$ приводит к переходу течения в критический режим второго типа, когда выполняется условие (20). Так что течение при ${{\bar {\rho }}_{{20}}} = \bar {\rho }_{{20}}^{*}$ можно рассматривать как переходный режим между критическими режимами первого и второго типов. Как показали расчеты, с ростом начального размера капель характерное значение $\bar {\rho }_{{20}}^{*},$ приводящее к предельному критическому течению первого типа, описанному выше, также увеличивается. В частности, для двухфазной смеси с каплями диаметром d0 = = 20 мкм ситуация $\bar {x}{\text{*}} = 1$ наступает при $\bar {\rho }_{{20}}^{*}$ = 3, а с каплями диаметром d0 = 50 мкм – при $\bar {\rho }_{{20}}^{*}$ = 3.5. Поведение параметров смеси в случае предельного критического течения (переходного режима), получающегося при ${{\bar {\rho }}_{{20}}} = \bar {\rho }_{{20}}^{*} = 3$ и d0 = 20 мкм, продемонстрировано на рис. 5.
Рис. 4.
Зависимость положения критического сечения в случае критического режима первого типа от массовой концентрации капель: 1 – d0 = 20 мкм, 2 – 50 мкм.
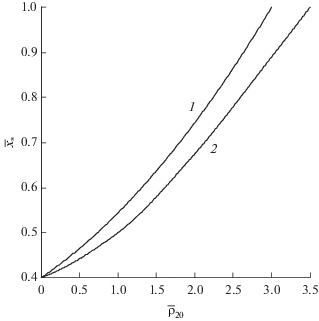
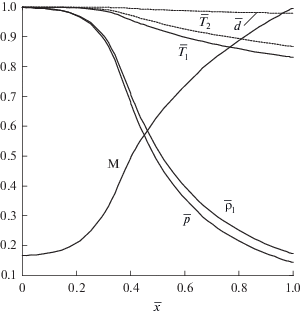
Рис. 5.
Распределение параметров смеси вдоль канала в характерной ситуации $\bar {x}* = 1,$ соответствующей значениям определяющих параметров ${{\bar {\rho }}_{{20}}} = 3,$ d0 = 20 мкм (переходный режим).
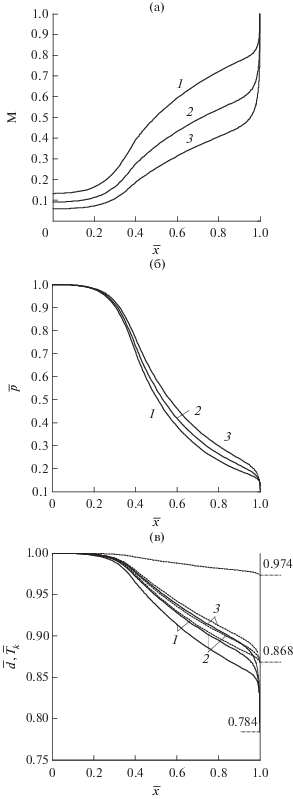
На рис. 6 представлены распределения числа Маха, давления и температур фаз вдоль канала в случае критического режима второго типа (удовлетворяющего условию (20)) при d0 = 20 мкм и разных значениях массовой концентрации дисперсной фазы на входе. С ростом ${{\bar {\rho }}_{{20}}}$ число Маха уменьшается, а давление и температура пара повышаются. Диаметр капель вдоль канала уменьшается, что свидетельствует об испарении жидкой фазы. Причем изменение ${{\bar {\rho }}_{{20}}}$ от 5 до 20 достаточно слабо влияет на поведение диаметра капель (в связи с этим распределение $\bar {d}$ показано одной и той же кривой, соответствующей случаю ${{\bar {\rho }}_{{20}}}$ = 20). Характер поведения числа Маха, давления и температур фаз показывает, что для них можно выделить зоны медленного, умеренного и быстрого изменения. Отметим, что варьирование ${{\bar {\rho }}_{{20}}}$ в рассматриваемом диапазоне не сильно влияет на распределения давления и температур фаз вдоль сопла (хотя и приводит к незначительным их увеличениям). Температура несущей фазы на выходе из сопла уменьшается с ростом массовой концентрации капель и при ${{\bar {\rho }}_{{20}}}$ = 20 достигает 0.784. Температура дисперсной фазы на выходе при разных ${{\bar {\rho }}_{{20}}}$ примерно одинакова и равна 0.868. Давление на срезе сопла равняется 0.1, а диаметр капель – 0.974.
Рис. 6.
Распределения числа Маха (а), давления (б) и температур фаз (в) в критическом режиме второго типа при d0 = 20 мкм и разных массовых содержаниях дисперсной фазы на входе: 1 – ${{\bar {\rho }}_{{20}}} = 5,$ 2 – 10, 3 – 20.
Зависимость характерной скорости среды на входе ${\bar {v}}_{0}^{*},$ при которой наступает критический режим истечения, от массовой концентрации дисперсной фазы показана на рис. 7. Вдоль кривой левее и правее вертикальной черточки реализуются критические режимы соответственно первого и второго типов. Область ниже каждой из кривых (${{{\bar {v}}}_{0}} < {\bar {v}}_{0}^{*}$) отвечает докритическим течениям, а область выше (${{{\bar {v}}}_{0}} > {\bar {v}}_{0}^{*}$) – физически нереализующимся течениям. Видно, что с ростом ${{\bar {\rho }}_{{20}}}$ характерная скорость ${\bar {v}}_{0}^{*},$ соответствующая критическому режиму, уменьшается. Причем увеличение начального размера капель приводит к росту величины ${\bar {v}}_{0}^{*}.$ Очевидно, штрихпунктирная кривая, отвечающая предельной равновесной схеме “d = 0”, устанавливает нижнюю границу зависимости ${\bar {v}}_{0}^{*}$ от ${{\bar {\rho }}_{{20}}}$ при уменьшении начального размера капель.
Рис. 7.
Зависимость характерной скорости на входе в сопло, при которой реализуется критический режим течения, от массового содержания дисперсной фазы: 1 – d0 = 20 мкм, 2 – 50 мкм, штрихпунктирная кривая – равновесная схема “d = 0”.

Зависимость полного расхода смеси в критическом режиме $\bar {m}{\text{*}}$ от массового содержания дисперсной фазы изображена на рис. 8. Как и на предыдущем рисунке, части кривых левее и правее вертикальной черточки соответствуют критическим режимам первого и второго типов. Видно, что с ростом ${{\bar {\rho }}_{{20}}}$ критический расход $\bar {m}{\text{*}}$ увеличивается (хотя при этом критическая скорость ${\bar {v}}_{0}^{*},$ судя по рис. 7, уменьшается), причем в случае критического режима второго типа величина $\bar {m}{\text{*}}$ больше, чем в режиме первого типа, несмотря на то что второй тип критического режима возникает при меньших значениях скорости ${\bar {v}}_{0}^{*}.$ Увеличение начального размера капель приводит к повышению критического расхода. Очевидно, на каждой из кривых реализуется максимальный расход смеси $\bar {m}$ = $\bar {m}{\text{*,}}$ соответствующий заданным значениям ${{\bar {\rho }}_{{20}}}$ и d0, область ниже кривых отвечает меньшим расходам смеси $\bar {m}$ < $\bar {m}*,$ а область выше – нереализуемым расходам (здесь $\bar {m}$ > $\bar {m}*,$ что невозможно). Необходимо отметить, что штрихпунктирная кривая (“d = 0”) ограничивает снизу зависимость $\bar {m}{\text{*}}$(${{\bar {\rho }}_{{20}}}$) при уменьшении начального размера капель дисперсной фазы.
ЗАКЛЮЧЕНИЕ
В рамках квазиодномерной модели установлены некоторые важные особенности течения двухфазной парокапельной среды в канале переменного сечения типа сопла Лаваля при наличии межфазных превращений. Получена формула для полного импульса потока смеси, показывающая, что в суживающейся части сопла полный импульс уменьшается, а в расширяющейся части, наоборот, увеличивается. Представлен способ расчета предельной термодинамически равновесной смеси (когда скорости и температуры фаз совпадают) с учетом переменного фазового состава.
Проведены расчеты в докритическом и критическом режимах течения смеси. Обнаружено, что в докритическом режиме при наличии дисперсных капель, несмотря на их тормозящий эффект, поток газа в канале ускоряется. Дано объяснение такому поведению газового потока. С увеличением массовой концентрации капель давление, температура и плотность газа уменьшаются, а скорость, наоборот, увеличивается. Установлено, что в докритическом режиме течения в пределах сопла имеет место смена направления фазовых переходов: вначале происходит испарение капель, а затем, в расширяющейся части канала – конденсация пара.
В случае критического потока первого типа (когда критическое сечение, где число Маха равно единице, а градиент давления дает неопределенность вида 0/0, возникает в пределах сопла) получены зависимости положения критического сечения от определяющих параметров смеси. Обнаружено, что при увеличении массовой концентрации капель или уменьшении их размера критическое сечение смещается в расширяющуюся часть канала. При этом возникает характерная ситуация (в рамках критического режима первого типа), когда критическое сечение достигает выходного сечения канала. Данная ситуация рассматривается как условная граница перехода между критическими режимами первого и второго (когда число Маха достигает значения единицы на выходе из сопла, а градиент давления при этом стремится к бесконечности) типов (переходный режим). Приведены результаты расчетов в установленном переходном режиме.
Выявлено, что в случаях критического сверхзвукового течения и критического течения второго типа происходит испарение капель по всей длине канала. Показано, что критический расход смеси увеличивается с ростом массовой концентрации дисперсной фазы и диаметра капель на входе в сопло.
Работа выполнена при поддержке Министерства образования и науки Республики Казахстан (грант № BR05236656).
Список литературы
Нигматулин Р.И. Динамика многофазных сред. Т. 1. М.: Наука, 1987. 464 с.
Нигматулин Р.И. Динамика многофазных сред. Т. 2. М.: Наука, 1987. 360 с.
Ивандаев А.И., Кутушев А.Г., Нигматулин Р.И. Газовая динамика многофазных сред // Итоги науки и техники. Сер. МЖГ. Т. 16. М.: ВИНИТИ, 1981. С. 209.
Morel C. Mathematical Modeling of Disperse Two-phase Flows. Switzerland: Springer Int. Publ., 2015. 350 p.
Леонтьев А.И., Лущик В.Г., Решмин А.И. Теплообмен в конических расширяющихся каналах // ТВТ. 2016. Т. 54. № 2. С. 287.
Лущик В.Г., Решмин А.И. Интенсификация теплообмена в плоском безотрывном диффузоре // ТВТ. 2018. Т. 56. № 5. С. 589.
Девисилов В.А., Шарай Е.Ю. Сепарация частиц в кольцевом конфузорном канале с внутренней вращающейся проницаемой перегородкой // ТВТ. 2018. Т. 56. № 4. С. 597.
Арбеков А.Н. Экспериментальное исследование влияния тангенциального закрученного вдува на эффективность диффузора // ТВТ. 2016. Т. 54. № 6. С. 934.
Агрест Э.М., Крайко А.Н. Двухслойная квазиодномерная модель для расчета течения смеси газа с инородными частицами в соплах // Изв. АН СССР. МЖГ. 1969. № 3. С. 64.
Ветлуцкий В.Н., Ганимедов В.Л., Мучная М.И. Исследование потока газа с твердыми частицами в сверхзвуковом сопле // ПМТФ. 2005. Т. 46. № 6. С. 65.
Лепешинский И.А., Яковлев А.А., Моллесон Г.В., Воронецкий А.В., Онес В.И., Ципенко А.В. Численное и экспериментальное исследование газокапельного течения в сопле с большими концентрациями дисперсной фазы // Матем. моделирование. 2002. Т. 14. № 7. С. 121.
Веревкин А.А., Циркунов Ю.М. Течение дисперсной примеси в сопле Лаваля и рабочей секции двухфазной гиперзвуковой ударной трубы // ПМТФ. 2008. Т. 49. № 5. С. 102.
Маслов Б.Я., Стернин Л.Е., Шрайбер А.А. Численное исследование особенностей двухфазного течения с коагуляцией и дроблением частиц в осесимметричных соплах Лаваля // Изв. АН СССР. МЖГ. 1982. № 3. С. 145.
Васенин И.М., Архипов В.А., Бутов В.Г., Глазунов А.А., Трофимов В.Ф. Газовая динамика двухфазных течений в соплах. Томск: Изд-во Томского ун-та, 1986. 264 с.
Ивандаев А.И., Нигматулин Р.И. К элементарной теории критических (максимальных) расходов двухфазных смесей // ТВТ. 1972. Т. 10. № 5. С. 1055.
Нигматулин Б.И., Сопленков К.И. К элементарной теории критического (максимального) расхода двухфазной смеси в каналах переменного сечения // ТВТ. 1978. Т. 16. № 2. С. 370.
Галимзянов М.Н., Лепихин С.А. Истечение двухфазной смеси через сопло с учетом фазовых переходов // Вестн. Самарск. ГУ. Естественнонаучная серия. 2010. № 2. С. 96.
Арсланова С.Н., Баянов Р.И., Тукмаков А.Л., Тонконог В.Г. Течение парокапельной смеси метана в канале переменного сечения // ИФЖ. 2017. Т. 90. № 2. С. 299.
Горбунов В.Н., Муслаев А.В., Пирумов У.Г., Розовский П.В. Неравновесная конденсация паров металла в смеси с инертным газом при расширении в соплах установок для генерации кластерных пучков // Изв. РАН. МЖГ. 1995. № 3. С. 80.
Пирумов У.Г. Перспективные методы получения ультрадисперсных частиц в высокоскоростных потоках // Проблемы машиностроения и надежности. 1996. № 1. С. 94.
Zhang Y., Erkey C. Preparation of Supported Metallic Nanoparticles Using Supercritical Fluids: a Review // J. Supercrit. Fluids. 2006. V. 38. P. 252.
Yuen M.C., Chen L.W. Heat-transfer Measurements of Evaporating Liquid Droplets // Int. J. Heat Mass Transfer. 1978. V. 21. № 5. P. 537.
Чусов С.И. Типовой расчет по курсу “Гидрогазодинамика” // 2015. https://docplayer.ru/58847682
Вукалович М.П., Ривкин С.Л., Александров А.А. Таблицы теплофизических свойств воды и водяного пара. М.: Изд-во стандартов, 1969. 654 с.
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1987. 840 с.
Циклаури Г.В., Данилин В.С., Селезнев Л.И. Адиабатные двухфазные течения. М.: Атомиздат, 1973. 212 с.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур



