Теплофизика высоких температур, 2020, T. 58, № 3, стр. 412-418

ВВЕДЕНИЕ

Теплозащитные композиционные материалы (КМ) в условиях аэродинамического нагрева сверх- и гиперзвуковых летательных аппаратов (ЛА) подвергаются фазовым превращениям, а именно разложению связующих (пиролизу) КМ с образованием газовой компоненты и пористого остатка, через который пиролизные газы фильтруются и вдуваются в высокотемпературный пограничный слой, уносу массы с наружной границы ЛА под действием высоких температур и касательных напряжений в пограничном слое, а также различным гетерогенным и гомогенным химическим реакциям внутри КМ. При проектировании тепловой защиты, изготовляемой из теплозащитных КМ, необходимо прежде всего определять массовую скорость разложения связующих КМ с учетом эндотермического эффекта, массовую и линейную скорости движения зоны пиролиза, массовую и линейную скорости фильтрации газов через пористый остаток с учетом конвективного охлаждения, а также тепловой эффект вдува в температурный пограничный слой. Все эти процессы происходят под действием высоких температур и тепловых потоков от пограничного слоя к телу параллельно с тепломассопереносом внутри КМ.

Для каждого теплозащитного КМ до настоящего времени разрабатывается своя физико-математическая модель разложения связующих с учетом их химического состава, возможных химических реакций как между химическими элементами пиролизного газа (гомогенные реакции), так и реакции между пиролизными газами и коксовым остатком КМ (гетерогенные реакции). При тепловом проектировании другого КМ необходимо разрабатывать свою физико-химическую и тепловую модель. Такой путь проектирования тепловой защиты бесперспективен.

Поскольку моделирование тепломассопереноса в теплозащитных КМ является комплексной проблемой, то необходимо взаимосвязанно рассматривать модели разложения связующих, фильтрации, прогрева с учетом подвижной зоны пиролиза и фильтрации, вдува в пограничный слой и многие другие проблемы для большинства теплозащитных КМ.

Задачи прогрева с учетом подвижных границ фазовых превращений рассматривались в работах [1–3], модели разложения связующих в [1–6], неизотермическая фильтрация в [7, 8], теплопроводность в составных телах в [9–13].

В данной работе в математической модели тепломассопереноса в КМ идентифицирован и использован новый универсальный закон разложения связующих КМ на основе известных паспортных данных для каждого теплозащитного КМ о температурах и плотностях начала и окончания разложения связующих. Поскольку данный закон использует общие паспортные характеристики КМ, то он носит универсальный характер и пригоден для большинства теплозащитных КМ. В работе идентифицированный закон использован для математического моделирования тепломассопереноса в теплозащитных КМ с учетом всех физико-химических превращений, включая определение скорости движения зоны пиролиза под действием баланса тепловых потоков в окрестности этой зоны.

ИДЕНТИФИКАЦИЯ УНИВЕРСАЛЬНОГО ЗАКОНА РАЗЛОЖЕНИЯ СВЯЗУЮЩИХ ТЕПЛОЗАЩИТНЫХ КМ

Рассмотрим температуры ${{T}_{b}},$ ${{T}_{e}}$ и плотности ${{\rho }_{b}},$ ${{\rho }_{e}}$ начала и окончания разложения связующих теплозащитных КМ в зоне пиролиза, ограниченной границами начала ${{x}_{b}}$ и окончания ${{x}_{e}},$ причем ${{T}_{e}} > {{T}_{b}},$ ${{\rho }_{b}} > {{\rho }_{e}},$ т.е. имеют место следующие границы изменения температур и плотностей в зоне пиролиза: $x \in \left[ {{{x}_{e}},{{x}_{b}}} \right]{\kern 1pt} :$ $T \in \left[ {{{T}_{b}},{{T}_{e}}} \right],$ $\rho \in \left[ {{{\rho }_{e}},{{\rho }_{b}}} \right].$

Известно [5], что уменьшение плотности связующего КМ, а следовательно, и всего КМ, описывается обыкновенным дифференциальным уравнением первого порядка с учетом движения зоны пиролиза $x \in \left[ {{{x}_{e}},{{x}_{b}}} \right]$ со скоростью $\dot {x}\left( t \right){\kern 1pt} :$

где $E$ – энергия активации реакций разложения, $\bar {R}$ – газовая постоянная смеси газов.

Интегрируя это уравнение, получим

где $A$ – неизвестная постоянная интегрирования, постоянная $B = {E \mathord{\left/ {\vphantom {E {\bar {R}}}} \right. \kern-0em} {\bar {R}}}$ также считается неизвестной.

Для нахождения $A$ и $B$ используем две пары экспериментальных данных ${{T}_{b}},$ ${{T}_{e}},$ ${{\rho }_{e}},$ ${{\rho }_{b}},$ которые являются паспортными данными каждого теплозащитного КМ. Подставляя их в (2) вначале для $x = {{x}_{b}},$ а затем для $x = {{x}_{e}},$ получим систему уравнений для определения $A$ и $B$

откуда

Подставляя (5) и (6) в (2) и используя равенства ${{t}_{e}} = {{{{x}_{e}}} \mathord{\left/ {\vphantom {{{{x}_{e}}} {\dot {x}\left( t \right)}}} \right. \kern-0em} {\dot {x}\left( t \right)}},$ ${{t}_{b}} = {{{{x}_{b}}} \mathord{\left/ {\vphantom {{{{x}_{b}}} {\dot {x}\left( t \right)}}} \right. \kern-0em} {\dot {x}\left( t \right)}},$ получим

Формула (7) является искомой зависимостью плотности КМ в зоне пиролиза $x \in \left[ {{{x}_{e}},{{x}_{b}}} \right]$ от переменной $x\left( t \right)$ и температуры $T\left( x \right).$

Считая распределение температур квазистационарным (стационарным в каждый момент времени), находим его из решения задачи

Среднюю скорость изменения плотности $\dot {\rho }\left( t \right)$ можно принять пропорциональной линейной скорости движения $\dot {x}\left( t \right),$ т.е.

Решением задачи (8)–(10) будет функция

где a = λ/(cρ) – температуропроводность в зоне пиролиза, $Q{\kern 1pt} *$ – тепловой эффект разложения связующего КМ. Линейная скорость $\dot {x}\left( t \right)$ движения зоны пиролиза при решении комплексной задачи тепломассопереноса определяется из баланса тепловых потоков, подводимых к этой зоне и отводимых от нее.

ПОСТАНОВКА ЗАДАЧИ О ТЕПЛОМАССОПЕРЕНОСЕ В ТЕПЛОЗАЩИТНОМ КМ

При моделировании тепломассопереноса в КМ используются следующие допущения:

– зона разложения (пиролиза) связующего возникает сразу после приложения тепловых потоков к наружной границе $x = 0;$

– для нахождения скорости движения узкой зоны пиролиза последняя заменяется подвижной границей $x{\kern 1pt} *\left( t \right)$ с температурой $T* = {{\left( {{{T}_{b}} + {{T}_{e}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{b}} + {{T}_{e}}} \right)} 2}} \right. \kern-0em} 2},$ а после определения температур в областях $x \in \left[ {0;x{\kern 1pt} *\left( t \right)} \right]$ и $x \in \left[ {x{\kern 1pt} *\left( t \right);\infty } \right]$ зона пиролиза реализуется интерполяцией по температурам ${{T}_{b}}$ и ${{T}_{e}},$ причем ${{T}_{b}} > {{T}_{e}};$

– полубесконечное тело заменяется конечным $x \in \left[ {0;l} \right],$ где $l$ – расстояние, на котором температура не превышает 1% сверх начальной температуры;

– в пористом коксовом остатке $x \in \left[ {0;x{\kern 1pt} *\left( t \right)} \right]$ реакции разложения отсутствуют так же, как и в области $x > x{\kern 1pt} *\left( t \right),$ не затронутой разложением.

С учетом этих допущений комплексная физико-математическая модель представлена следующим образом:

зафиксируем границу $x{\kern 1pt} *\left( t \right)$ фазовых превращений введением параметра ${{x}_{f}};$

баланс тепловых потоков на наружной границе с учетом вдува пиролизных газов

уравнение теплопроводности в коксовом остатке 2 с учетом фильтрации температура подвижной границы фазовых превращений, разделяющей фазы 2 и 1, уравнение теплопроводности в области 1, не затронутой фазовыми превращениями, баланс тепловых потоков на подвижной границе фазовых превращений с учетом массовой скорости $\dot {m}\left( t \right)$ с эндотермическим эффектом $Q{\kern 1pt} *$В соотношениях (13)–(19) ${{q}_{w}}$ – плотность теплового потока на границе $x = 0,$ $a$ – температуропроводность, ${{T}_{0}}$ – начальная температура. Они предназначены для определения следующих функций: ${{T}_{2}}\left( {x,t} \right),$ $0 < x < {{x}_{f}},$ ${{T}_{1}}\left( {x,t} \right),$ $x \in \left[ {{{x}_{f}},\infty } \right],$ $\dot {m},$ $x = {{x}_{f}}$ и ${{\dot {x}}_{f}} = {{\dot {m}} \mathord{\left/ {\vphantom {{\dot {m}} {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}}.$

В уравнениях газообразования в зоне пиролиза связующих КМ $\rho \left( x \right)$ определяется законом (7);

где ${{\rho }_{g}}$ – плотность газов;

плотность торможения газов в зоне пиролиза ${{x}_{e}} < x < {{x}_{b}}$

давление торможения в зоне пиролиза

где ${{\bar {R}}_{g}}$ – усредненная газовая постоянная смеси, $\bar {T}$ – усредненная температура в зоне пиролиза, определяемая по формуле (12);

уравнение фильтрации в пористой среде

нелинейный закон фильтрации [3] где $k$ – коэффициент проницаемости пористой среды; ${{\mu }_{g}}$ – динамическая вязкость газа; $\Pi $ – пористость; ${{\operatorname{Re} }_{d}}$ – фильтрационное число Рейнольдса, определяемое по толщине капилляра $d.$

МЕТОД РЕШЕНИЯ

Метод решения задачи (7)–(24) содержит следующие пункты.

1. Расчет начинается с момента достижения границей $x = 0$ температуры $T\left( {0,t} \right) > T{\kern 1pt} *$ = = ${{\left( {{{T}_{b}} + {{T}_{e}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{b}} + {{T}_{e}}} \right)} {2,}}} \right. \kern-0em} {2,}}$ в соответствии с чем интерполяцией полученного распределения температур определяется координата $x{\kern 1pt} *\left( t \right)$ границы фазовых превращений. Граница $x{\kern 1pt} *$ фиксируется введением параметра ${{x}_{f}}{\kern 1pt} :$ $x* = {{x}_{f}}.$

2. Решается задача теплопроводности в пористом коксовом остатке ${{T}_{2}}\left( {x,t} \right),$ $0 < x < {{x}_{f}}.$

3. Решается задача теплопроводности в области, не затронутой разложением T₁T₂ связующего, ${{T}_{1}}\left( {x,t} \right),$ ${{x}_{f}} < x < \infty .$

4. Определяется тепловой поток на границе $x = {{x}_{f}}$ со стороны пористой области 2.

5. Определяется тепловой поток на границе $x = {{x}_{f}}$ со стороны области 1.

6. Находится массовая $\dot {m}$ и линейная $\dot {x}* = {{\dot {x}}_{f}} = {{\dot {m}} \mathord{\left/ {\vphantom {{\dot {m}} {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}}$ скорости движения границы фазовых превращений из условия (19).

7. Определяется зона пиролиза ${{x}_{e}} < x < {{x}_{b}}$ интерполяцией из равенств_{${{T}_{1}}\left( {{{x}_{b}}} \right) = {{T}_{b}}$ и${{T}_{2}}\left( {{{x}_{e}}} \right) = {{T}_{e}}.$}

8. В этой зоне определяются плотность газовой компоненты ${{\rho }_{g}}\left( x \right),$ плотности торможения ${{\rho }_{{g0}}}$ и давления торможения ${{p}_{{g0}}}.$

9. Формулируется и решается задача распределения давления пиролизных газов и вдува в пограничный слой.

10. По распределению давления устанавливается распределение скорости фильтрации ${{{v}}_{g}}\left( x \right)$ и включения ее в задачу теплопроводности в пористой области 2 с учетом фильтрации.

Распределение температур ${{T}_{2}}\left( {x,t} \right)$ в пористой области $x \in \left[ {0;{{x}_{f}}} \right]$ получим из решения задачи (13)–(15), сделав предварительно подстановку [2]:

Получим

где $\vartheta = \sqrt {{{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {\pi t}}} \right. \kern-0em} {\pi t}}} .$

Распределение температуры ${{T}_{1}}\left( {x,t} \right)$ в области $\left[ {{{x}_{f}},\infty } \right]$ получим из решения задачи (16)–(18)

Поскольку аргументы функций ошибок ${\text{erf}}\left( {\frac{{{{x}_{f}}}}{{2\sqrt {{{a}_{2}}{{t}_{f}}} }}} \right),$ ${\text{erf}}\left( {\frac{{{{x}_{f}}}}{{2\sqrt {{{a}_{1}}{{t}_{f}}} }}} \right)$ в функциях (26), (27) должны быть безразмерными, то уместно предположить, что ${{x}_{f}}$ пропорциональна $\sqrt {{{a}_{1}}{{t}_{f}}} {\kern 1pt} :$Коэффициент пропорциональности $\chi $ определяется из условия (19) подстановкой в него функций (26), (27), в которых положено $x = {{x}_{f}}.$ В результате получаем следующее трансцендентное уравнение относительно коэффициента $\chi {\kern 1pt} :$где $\bar {V} = \frac{1}{{{{{v}}_{g}}}}\sqrt {{{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} t}} \right. \kern-0em} t}} = {{{{{v}}_{T}}} \mathord{\left/ {\vphantom {{{{{v}}_{T}}} {{{{v}}_{g}}}}} \right. \kern-0em} {{{{v}}_{g}}}},$ $\bar {c} = {{{{c}_{2}}{{\rho }_{2}}} \mathord{\left/ {\vphantom {{{{c}_{2}}{{\rho }_{2}}} {{{{\left( {{{c}_{p}}\rho } \right)}}_{g}}.}}} \right. \kern-0em} {{{{\left( {{{c}_{p}}\rho } \right)}}_{g}}.}}$

В (29) ${{{v}}_{T}} = \sqrt {{{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} t}} \right. \kern-0em} t}} $ – скорость температурного фронта [3] в пористой области (ее можно принять как скорость движения фронта с температурой T *), а отношение $\bar {V} = {{{{{v}}_{T}}} \mathord{\left/ {\vphantom {{{{{v}}_{T}}} {{{{v}}_{g}}}}} \right. \kern-0em} {{{{v}}_{g}}}}$ характеризует отношение скорости температурного фронта к скорости фильтрации пиролизных газов и является критерием уменьшения скорости прогрева от скорости фильтрации газов.

Уравнение (29) решается численно. Полученное значение $\chi $ подставляется в (26)–(28), из этих функций находится распределение температур в областях 2 и 1 и значение $x{\kern 1pt} *\left( t \right){\kern 1pt} :$

Образование зоны пиролиза и гидродинамических характеристик фильтрации. Вначале фиксируется зона пиролиза ${{x}_{e}} < x < {{x}_{b}}$ интерполяцией температурного профиля (30) по температуре ${{T}_{b}}{\kern 1pt} :$ ${{T}_{2}}\left( {{{x}_{b}},t} \right) = {{T}_{b}}$ и температурного профиля (31) по температуре ${{T}_{e}}{\kern 1pt} :$ ${{T}_{1}}\left( {{{x}_{e}},t} \right) = {{T}_{e}}.$ В этой зоне по закону (7) определяется плотность $\rho \left( {x\left( t \right)} \right)$ КМ, распределение плотности ${{\rho }_{g}}\left( x \right),$ плотность торможения ${{\rho }_{{g0}}}$ и давления торможения пиролизных газов по соотношениям (20)–(22). Принимая давление торможения в зоне пиролиза и давление ${{p}_{{gw}}}$ в газодинамическом потоке на границе $x = 0$ в качестве граничных условий для уравнения фильтрации, сформированного из уравнений (23), (24) и уравнения состояния

получим задачу фильтрации относительно давления фильтрации ${{p}_{g}}\left( {x,t} \right){\kern 1pt} :$ Полагая в пористом остатке распределение температуры ${{T}_{2}}\left( {x,t} \right)$ приближенно линейным (это видно ниже по результатам расчетов) получим из решения задачи (33)–(35) с учетом (36) квадратичную зависимость давления фильтрации ${{p}_{g}}\left( x \right)$ в пористом остатке где ${{p}_{{gw}}}$ – давление на границе тела $x = 0,$ ${{p}_{{g0}}}$ – давление торможения в зоне пиролиза.

Подставляя давление ${{p}_{g}}\left( {x,t} \right)$ в закон фильтрации (24), получим распределение скорости ${{{v}}_{g}}\left( x \right)$ фильтрации, а из уравнения состояния (32) – плотности ${{\rho }_{g}}\left( {x,t} \right).$ Произведение ${{\rho }_{g}}{{{v}}_{g}}$ теперь можно включить в уравнение теплопроводности (14) относительно ${{T}_{2}}\left( {x,t} \right).$

Таким образом, получены распределения температур в пористом остатке ${{T}_{2}}\left( {x,t} \right)$ (30), в зоне пиролиза (12), в области 1, не затронутой разложением связующего, ${{T}_{1}}\left( {x,t} \right)$ (31), координаты подвижной средней линии $x{\kern 1pt} *\left( t \right)$ в соотношениях (29), (28), распределение плотностей КМ в зоне пиролиза (7) и газа (20), распределение давления и скорости фильтрации (37) и (24).

АНАЛИЗ РЕЗУЛЬТАТОВ ЧИСЛЕННОГО РЕШЕНИЯ

Ниже приводятся некоторые результаты расчетов, полученных с помощью формул (7), (28)–(31), (37).

На рис. 1 приведена температура КМ в зоне разложения связующего, а на рис. 2 – графики изменения плотности $\rho \left( x \right)$ КМ и плотности пиролизных газов для следующих входных данных: ${{T}_{e}} = 1000\,{\text{K}},$ ${{T}_{b}} = 500\,{\text{K,}}$ ${{\rho }_{e}} = 1100$ кг/м³, ${{\rho }_{b}} = $ = 1400 кг/м³, x_e = 0.002 м, x_b = 0.004 м, $\dot {x}$ = 0.00012 м/с, $Q{\kern 1pt} * = 800$ Дж/кг, $a = {{10}^{{ - 7}}}$ м²/с, λ = 0.1 Вт/(м К). Из рис. 1 видна значительная вогнутость температурного профиля в зоне пиролиза, что объясняется большим значением стокового члена ${{\dot {\rho }Q{\text{*}}} \mathord{\left/ {\vphantom {{\dot {\rho }Q{\text{*}}} \lambda }} \right. \kern-0em} \lambda }$ в формуле (12), так как ${{\dot {\rho }Q{\kern 1pt} *} \mathord{\left/ {\vphantom {{\dot {\rho }Q{\kern 1pt} *} {(\rho {{c}_{p}})}}} \right. \kern-0em} {(\rho {{c}_{p}})}}$ = $\dot {\rho }Q{\kern 1pt} *{a \mathord{\left/ {\vphantom {a \lambda }} \right. \kern-0em} \lambda }.$

Распределение плотности $\rho \left( x \right)$ КМ на рис. 2 получено в соответствии с законом (7) разложения связующего КМ. Это распределение имеет точку перегиба, т.е. в окрестности высоких температур – в левой части кривой, $\frac{{{{d}^{2}}\rho }}{{d{{x}^{2}}}} > 0,$ тогда как в правой – $\frac{{{{d}^{2}}\rho }}{{d{{x}^{2}}}} < 0.$ При этом на концах графика $\frac{{d\rho }}{{dx}} \ne 0,$ т.е. образование газовой компоненты происходит скачком. Там же нанесено изменение плотности пиролизных газов ${{\rho }_{g}}\left( x \right),$ причем сумма ординат зависимостей $\rho \left( x \right)$ и ${{\rho }_{g}}\left( x \right)$ в любой точке $x$ равна 1400, т.е. плотности КМ, не затронутого фазовыми превращениями.

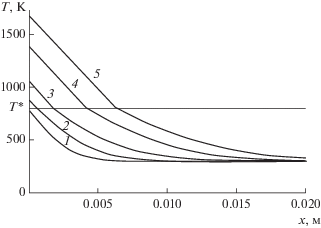
На рис. 3 приведены распределения температур в различные моменты времени, рассчитанные по формулам (28), (29)–(31). Рисунок одновременно иллюстрирует положение координаты $x{\kern 1pt} *\left( t \right)$ в точках излома кривых и скорость движения зоны пиролиза $x \in \left[ {{{x}_{e}},{{x}_{b}}} \right],$ в середине которой находится точка $x{\kern 1pt} *\left( t \right).$ Как и предполагалось выше, линейность температурных профилей в пористом остатке 2 (кривые выше прямой $T{\kern 1pt} *$) подтвердилась. Резкий излом кривых в точках $x{\kern 1pt} *\left( t \right)$ объясняется значительным эндотермическим разложением связующего КМ ($Q{\kern 1pt} * = 800$ Дж/кг).

На рис. 4 приведены результаты расчетов распределения давления фильтрации ${{p}_{g}}\left( {x,t} \right)$ по формуле (37) в зависимости от времени. Кривые в каждый момент времени имеют параболический вид, причем из этого рисунка также видна скорость движения границы $x{\kern 1pt} *\left( t \right)$ в точках $x_{1}^{{\text{*}}},$ $x_{2}^{{\text{*}}},$ $x_{3}^{{\text{*}}}.$ В этих точках давление равно давлению торможения газов в зоне пиролиза ~4.7 × 10⁷ Па, а на левой границе $x = 0$ давление принималось равным атмосферному ${{10}^{5}}$ Па.

ЗАКЛЮЧЕНИЕ

1. На основе идентифицированного универсального закона разложения связующих КМ аналитически решена задача о тепломассопереносе в теплозащитных КМ, подверженных интенсивному аэродинамическому нагреву летательных аппаратов. Закон применим к большинству теплозащитных КМ.

2. На основе баланса тепловых потоков в зоне пиролиза связующих КМ получено замкнутое трансцендентное соотношение для определения скорости движения и координат зоны фазовых превращений. Для этого использованы аналитические зависимости нестационарных температур в пористом коксовом остатке и в области, не затронутой разложением связующего КМ.

3. Получены плотность торможения в зоне пиролиза (скорость ~0) и давление торможения, выведено уравнение фильтрации для пористой области на основе уравнений неразрывности, нелинейного закона фильтрации и уравнения состояния. Для этого уравнения поставлена и аналитически решена задача фильтрации и вдува пиролизных газов, причем граничными условиями являются давление торможения в зоне пиролиза и давление газодинамического потока на наружной границе.

Работа выполнена при поддержке Российского научного фонда (проект № 16-19-10 340).