1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 58, № 3, 2020

Теплофизика высоких температур, 2020, T. 58, № 3, стр. 323-326

Плазменная частота, параболические траектории и проводимость неидеальной полностью ионизованной плазмы

А. Л. Хомкин 1, *, А. С. Шумихин 1, **

1 Объединенный институт высоких температур РАН
Москва, Россия

* E-mail: alhomkin@mail.ru
** E-mail: shum_ac@mail.ru

Поступила в редакцию 05.11.2019
После доработки 08.12.2019
Принята к публикации 24.12.2019

Полный текст (PDF)

Аннотация

Рассчитана проводимость неидеальной полностью ионизованной плазмы в предположении, что прямолинейные участки траектории электрона отсутствуют. Траектория состоит из кусочков параболических траекторий, лежащих внутри ячейки Вигнера–Зейтца. Проводимость в таком приближении пропорциональна плазменной частоте и близка к экспериментально измеренной проводимости плотной плазмы цезия.

ВВЕДЕНИЕ

При обсуждении проблемы проводимости “неидеальной плазмы” в 70-х гг. прошедшего столетия было высказано много интересных идей и предложены многочисленные “универсальные” расчетные формулы [1]. В настоящей заметке обращается внимание на гипотезу о существовании предельной проводимости полностью ионизованной неидеальной плазмы, высказанную в работе Асиновского Э.И. и Валуева А.А. [2]. Насколько известно авторам, в этой работе впервые было введено понятие “предельной” проводимости сильно неидеальной плазмы:

(1)
${{\sigma }_{l}} = \frac{{{{\omega }_{p}}}}{{4\pi }}.$

В (1) ${{\omega }_{p}} = \sqrt {{{4\pi {{e}^{2}}{{n}_{e}}} \mathord{\left/ {\vphantom {{4\pi {{e}^{2}}{{n}_{e}}} m}} \right. \kern-0em} m}} $ – плазменная частота, выраженная через концентрацию ${{n}_{e}},$ заряд $e$ и массу $m$ электронов. Большинство экспериментов не подтверждали это предположение. Лишь экспериментальные данные, полученные Дихтер И.Я. и Зейгарником В.А. в плотных парах цезия [3] при их экстраполяции, указывали на (1). В указанных экспериментах была получена достаточно плотная плазма с практически полной ионизацией и отсутствием влияния столкновений электронов с атомами, что отличало эти эксперименты от большинства других. Подчеркнем, что именно анализ экспериментальных данных [3] привел авторов [2] к соотношению (1). При этом следует отметить, что (1) совершенно не соответствует классической картине процессов переноса в газах и плазме, которая предполагает движение частицы по прямолинейной траектории, прерываемой случайными, мгновенными столкновениями. Проводимость полностью ионизованной плазмы при этом практически не зависит от плотности (число носителей равно числу рассеивателей). К сожалению, совокупность всех экспериментальных данных и их точность не позволяли сделать окончательных выводов о существовании тех или иных “эффектов” неидеальности.

Отметим еще один важный для дальнейшего эффект. Еще в работах [4, 5] было обращено внимание на возрастающую роль в процессах переноса состояний рассеяния – столкновительных комплексов при увеличении плотности атомарных газов.

В связи с прогрессом вычислительной техники исследователи вновь обратили внимание на переносные и другие динамические свойства полностью ионизованной неидеальной плазмы. Метод молекулярной динамики (ММД) позволил получить [6, 7] проводимость неидеальной “полностью ионизованной” классической плазмы. В [8] с использованием ММД выполнено комплексное исследование переносных свойств одно- и многократно ионизованной неидеальной классической плазмы. Рассчитаны электронный и ионный корреляторы скоростей и токов. Выполнены расчеты коэффициентов диффузии и проводимости, которые позволяют получить ряд новых аналитических результатов.

В [9] найдены поправки к проводимости идеальной плазмы, учитывающие существование электрон-ионных столкновительных комплексов. Их экстраполяция в область больших неидеальностей качественно соответствовала результатам [6] и указывала на возрастание роли пролета электроном области собственно столкновения.

В настоящей работе выполнен расчет коррелятора скоростей, коэффициента диффузии, частоты столкновений и проводимости сильно неидеальной плазмы, в предположении, что траектория электрона представляет собой последовательность параболических траекторий, лежащих внутри ячейки Вигнера–Зейтца (ВЗ). Предполагается, что прямолинейные участки траектории вообще отсутствуют. Получены соотношения, связывающие плазменную частоту и скорость электрона на пересечении параболической траектории электрона с границей ячейки ВЗ. Рассчитанная в рамках модели проводимость сильно неидеальной плазмы подтверждает гипотезу Асиновского Э.И. и Валуева А.А. [2] и коррелирует с асимптотикой результатов Дихтер И.Я. и Зейгарника В.А. [3].

ОСНОВНЫЕ СООТНОШЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

Рассмотрим полностью ионизованную плазму, состоящую из ${{N}_{e}}$ электронов и ${{N}_{i}}$ ионов, находящихся в объеме $V,$ при температуре $kT = {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }{\text{.}}$ Соответствующие плотности частиц ${{n}_{{e,i}}} = {{{{N}_{{e,i}}}} \mathord{\left/ {\vphantom {{{{N}_{{e,i}}}} V}} \right. \kern-0em} V}.$ Определим необходимые для дальнейшего радиус ячейки Вигнера–Зейтца ${{R}_{{{\text{WZ}}}}}$ и маделунговский параметр неидеальности ${\Gamma :}$

${{R}_{{{\text{WZ}}}}} = {{\left( {\frac{3}{{4\pi {{n}_{i}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},\,\,\,\,{\Gamma } = \frac{{\beta {{e}^{2}}}}{{{{R}_{{{\text{WZ}}}}}}},$
а также дебаевский радиус ${{R}_{{\text{D}}}}$ и дебаевский параметр неидеальности ${{{\Gamma }}_{{\text{D}}}}{\text{:}}$

$\begin{gathered} {{R}_{{\text{D}}}} = {{\left( {\frac{1}{{4\pi \beta {{e}^{2}}\left( {{{n}_{e}} + {{n}_{i}}} \right)}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{{\Gamma }}_{{\text{D}}}} = {{\beta {{e}^{2}}} \mathord{\left/ {\vphantom {{\beta {{e}^{2}}} {{{R}_{{\text{D}}}}}}} \right. \kern-0em} {{{R}_{{\text{D}}}}}} = \beta {{e}^{2}}\sqrt {4\pi \beta {{e}^{2}}\left( {{{n}_{e}} + {{n}_{i}}} \right)} {\kern 1pt} . \\ \end{gathered} $

При математическом моделировании нет необходимости решать достаточно сложное кинетическое уравнение Больцмана, тем более что оно получено для идеального газа. Уже в [10] с использованием ММД рассчитывается коррелятор скорости, который определяется через скалярное произведение начальной и текущей скоростей частицы:

$K = \int\limits_0^\infty {\left\langle {{\mathbf{V}}\left( 0 \right){\mathbf{V}}\left( t \right)} \right\rangle dt} .$

Физический смысл этой величины легко получить в приближении ближайшего соседа, считая, что после усреднения скорость частицы близка к тепловой ${{V}_{T}}.$ Скорость частицы будет равна начальной при условии, что она не столкнется с иной частицей. Для этого необходимо, чтобы в объеме ${v} = Q{{V}_{T}}t$ не было других частиц ($Q$ – сечение рассеяния). Вероятность такого события определяется формулой Пуассона $\omega = \exp \left( { - n{v}} \right)$ = = ${\text{exp}}\left( { - n{{V}_{T}}Qt} \right)$ или $\omega = {\text{exp}}\left( {{{ - t} \mathord{\left/ {\vphantom {{ - t} \tau }} \right. \kern-0em} \tau }} \right),$ где $\tau = {1 \mathord{\left/ {\vphantom {1 {n{{V}_{T}}Q}}} \right. \kern-0em} {n{{V}_{T}}Q}}$ – время свободного пробега. После усреднения по скоростям получим коррелятор

$K = V_{T}^{2}\tau {\text{.}}$

Вводя длину пробега $l = {1 \mathord{\left/ {\vphantom {1 {nQ}}} \right. \kern-0em} {nQ}},$ для коррелятора можно получить соотношение

$K = {{V}_{T}}l.$

Теория линейного отклика позволяет связать коррелятор скоростей $K$ и коэффициенты переноса, такие как проводимость $\sigma = {{{{n}_{e}}{{e}^{2}}K} \mathord{\left/ {\vphantom {{{{n}_{e}}{{e}^{2}}K} {3T}}} \right. \kern-0em} {3T}}$ и коэффициент диффузии $D = {K \mathord{\left/ {\vphantom {K 3}} \right. \kern-0em} 3}.$

Рассчитаем коррелятор скоростей для сильно неидеальной полностью ионизованной плазмы в рамках следующих предположений:

1. Участки прямолинейного свободного движения электрона отсутствуют. Траектория электрона состоит из участков траекторий внутри ячейки Вигнера–Зейтца (рис. 1). Электрон взаимодействует только с ближайшим к нему ионом.

Рис. 1.

Траектория пролета электроном ячейки Вигнера–Зейтца по параболической траектории: ${{R}_{i}}$ – радиус ячейки ВЗ, ${{V}_{i}}$ – скорость электрона на границе ячейки ВЗ при влете в нее.

2. Траекторией пролета электрона внутри ячейки ВЗ является парабола.

3. При переходе из ячейки в ячейку электрон “забывает” свою скорость. Считаем, что учет корреляции скоростей при переходах из ячейки в ячейку приведет к численному коэффициенту, близкому к единице.

ПАРАБОЛИЧЕСКАЯ ТРАЕКТОРИЯ

Параметры параболической траектории пролета в кулоновском потенциале хорошо известны. Для частицы с энергией $E$ и моментом импульса $M$ в [11] приведено решение кеплеровой задачи для всех траекторий: эллипса, гиперболы и параболы. Координаты траекторий получены в неявном виде, в частности для параболы через параметры ${\eta }$ и $p = {{{{M}^{2}}} \mathord{\left/ {\vphantom {{{{M}^{2}}} {m{{e}^{2}}}}} \right. \kern-0em} {m{{e}^{2}}}}.$

Траектория электрона $R\left( t \right)$ описываетcя параметрически:

$R = \frac{p}{2}\left( {1 + {{\eta }^{2}}} \right),\,\,\,\,~t = \sqrt {\frac{{m{{p}^{3}}}}{{{{e}^{2}}}}} \frac{\eta }{2}\left( {1 + \frac{{{{\eta }^{3}}}}{2}} \right).$

Для декартовых координат имеем

$X = \frac{p}{2}\left( {1 - {{\eta }^{2}}} \right)~,\,\,\,\,~Y = p\eta {\text{.}}$

Параметр ${\eta }$ “пробегает” значения от $ - \infty $ до $ + \infty .$ На параболе полная энергия частицы равна нулю:

$\frac{{mV_{i}^{2}}}{2} = \frac{{{{e}^{2}}}}{{{{R}_{i}}}},$
а момент импульса
$M = m{{V}_{i}}{{R}_{i}}{\text{sin}}\varphi {\text{,}}$
где $\varphi $ – угол между вектором скорости ${{V}_{i}}$ и радиус-вектором ${{R}_{i}}.$ Для записи коррелятора понадобятся декартовы координаты скорости электрона вдоль траектории:

$\begin{gathered} {{V}_{x}}\left( \eta \right) = \frac{{\partial X}}{{\partial t}} = \frac{{\partial X}}{{\partial \eta }}~\frac{{\partial \eta }}{{\partial t}} = - p\eta \frac{{\partial \eta }}{{\partial t}}, \\ {{V}_{y}}\left( \eta \right) = \frac{{\partial Y}}{{\partial t}} = \frac{{\partial Y}}{{\partial \eta }}~\frac{{\partial \eta }}{{\partial t}} = p\frac{{\partial \eta }}{{\partial t}}, \\ \frac{{\partial \eta }}{{\partial t}} = 2\sqrt {\frac{{{{e}^{2}}}}{{m{{p}^{3}}}}} ~\frac{1}{{\left( {1 + {{\eta }^{2}}} \right)}}. \\ \end{gathered} $

КОРРЕЛЯТОР СКОРОСТЕЙ И КОЭФФИЦИЕНТЫ ПЕРЕНОСА

Траектории пролета ячейки ВЗ по параболе отличаются только углом $\varphi ,$ по нему и проведем усреднение. От интегрирования по времени перейдем к интегрированию по $\eta {\text{:}}$

(2)
$\begin{gathered} K = \frac{2}{\pi }\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\int\limits_{ - {{{\eta }}_{i}}}^{{{{\eta }}_{i}}} {\left[ {{{V}_{x}}\left( { - {{\eta }_{i}}} \right){{V}_{x}}\left( {\eta } \right) + {{V}_{y}}\left( { - {{{\eta }}_{i}}} \right){{V}_{y}}\left( {\eta } \right)} \right]d{\eta }d\varphi = } } \\ = \frac{2}{\pi }\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\int\limits_{ - {{{\eta }}_{i}}}^{{{{\eta }}_{i}}} {\left[ {{{V}_{y}}\left( { - {{\eta }_{i}}} \right){{V}_{y}}\left( \eta \right)} \right]d\eta d\varphi {\text{\;}}} } = \\ = \frac{2}{\pi }\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\left[ {4\sqrt {\frac{{{{e}^{2}}p}}{m}} {\text{arctg}}\left( {\sqrt {\frac{1}{{{\text{si}}{{{\text{n}}}^{2}}\varphi }} - 1} } \right)} \right]d\varphi } = {{V}_{i}}{{R}_{i}}{{K}_{0}}, \\ \end{gathered} $
где ${{K}_{0}} = 1.029$ – константа. Интегрирование X-компоненты скорости дает нуль. Соответственно, для коэффициента диффузии имеем $D = {K \mathord{\left/ {\vphantom {K 3}} \right. \kern-0em} 3}$ = $0.343{{V}_{i}}{{R}_{i}}$ – то же выражение (2), но с другой константой ${{K}_{D}} = 0.343.$ Предполагая экспоненциальный характер зависимости от времени, для времени “пробега” $\tau $ получаем
$\tau = \frac{K}{{V_{i}^{2}}} = 1.028~\frac{{{{R}_{i}}}}{{{{V}_{i}}}}.$
Плазменная частота, выраженная через скорость электрона на границе ячейки ВЗ и ее радиус, не зависит от расчета коррелятора и определяется соотношением:
${{\omega }_{p}} = \sqrt {\frac{3}{2}} ~\frac{{{{V}_{i}}}}{{{{R}_{i}}}},\,\,\,\,{{\omega }_{p}}\tau = 1.26.$
Для проводимости, используя общее соотношение
$\sigma = \frac{{\omega _{p}^{2}}}{{4\pi }}\tau {\text{,}}$
получим выражение, практически совпадающее с предложенным в работе [2]:

$\sigma = \frac{{{{\omega }_{P}}}}{{4\pi }}~\left( {{{\omega }_{P}}\tau } \right) = \frac{{{{\omega }_{p}}}}{{4\pi }}~1.26.$

СРАВНЕНИЕ С ЧИСЛЕННЫМ И ФИЗИЧЕСКИМ ЭКСПЕРИМЕНТАМИ И ОБСУЖДЕНИЕ

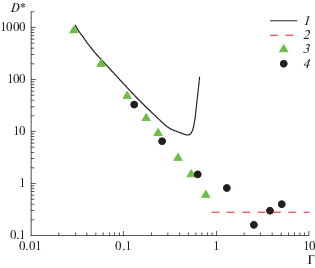
На рис. 2 и 3 представлено сравнение полученных результатов с данными численных расчетов и эксперимента для проводимости σ и коэффициента диффузии D. Данные по проводимости и коэффициенту диффузии, полученные в [6], дополнены результатами [8] и представлены в безразмерном виде $\sigma * = {\sigma \mathord{\left/ {\vphantom {\sigma {{{\omega }_{p}}}}} \right. \kern-0em} {{{\omega }_{p}}}}.$ В данной работе получено $\sigma * = {{1.26} \mathord{\left/ {\vphantom {{1.26} {4\pi }}} \right. \kern-0em} {4\pi }}$ = $0.103,$ $D* = \frac{D}{{{{\omega }_{p}}~R_{i}^{2}}}$ = = $\frac{{0.343}}{{\sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} }} = 0.28.$

Рис. 2.

Зависимость безразмерной проводимости полностью ионизованной плазмы от параметра неидеальности Γ: 1 – расчет по формуле Спитцера–Ландау (см. [8]), 2 – настоящая работа, 3 – [8], 4 – [6], 5 – эксперимент [3].

Рис. 3.

Безразмерный коэффициент диффузии: 1–4 – то же, что на рис. 2.

На рис. 2 хорошо виден участок падения проводимости при ${\Gamma } < 1.$ Здесь численные данные ММД [6] и [8] практически совпадают. Давно замечено, что проводимость в этой области описывается минимальной, причем теоретически оправданной, коррекцией кулоновского логарифма [9]. При ${\Gamma } > 1$ имеются расчеты только [6] и по данной модели. Их расхождение связано, по-видимому, с тем, что в [6] кулоновский потенциал скорректирован в начале координат. Если это потенциал “с полочкой”, то ее влияние будет заметно именно при больших значениях параметра ${\Gamma }$ (размер ячейки ВЗ сравнивается с размером “полочки”). Не сомневаясь в правильности расчетов, их все же следует рассматривать как модельные, которые зависят от конкретной процедуры коррекции кулоновского потенциала в начале координат. Полученная в данной работе проводимость (назовем ее “столкновительной”) качественно совпадает с численными данными и соответствует асимптотике экспериментальных данных [3]. Другие экспериментальные данные, рассмотренные в [8], не приводятся, так как точность процедуры извлечения проводимости “полностью ионизованной” плазмы из измеренной проводимости “частично ионизованной” плазмы инертных газов и особенно воздуха невелика. Данные по коэффициенту диффузии (рис. 3) только подтверждают сделанные выводы.

ЗАКЛЮЧЕНИЕ

Выполнен модельный расчет коррелятора скорости электрона в плотной классической плазме. Предположено, что траектория электрона состоит из кусочков параболических траекторий, лежащих внутри ячеек Вигнера–Зейтца. Прямолинейные участки пролета отсутствуют. С использованием полученного коррелятора рассчитаны коэффициент диффузии и проводимость. Оказалось, что рассчитанная таким образом проводимость пропорциональна плазменной частоте и практически совпадает с предельной проводимостью, предложенной в работе [2], и асимптотикой экспериментальных данных [3].

Список литературы

  1. Фортов В.Е., Храпак А.Г., Якубов И.Т. Физика неидеальной плазмы. М.: Физматлит, 2010.

  2. Асиновский Э.И., Валуев А.А. Электропроводность и характерные частоты в неидеальной плазме // ТВТ. 1980. Т. 18. № 6. С. 1318.

  3. Дихтер И.Я., Зейгарник В.А. Уравнение состояния и проводимость цезиевой плазмы при давлениях 50–500 атм // ДАН СССР. 1976. Т. 227. № 3. С. 656.

  4. Смит Ф. Рассмотрение химических реакций в высокотемпературных газах в рамках теории столкновений. В сб.: Кинетические процессы в газах и плазме / Под ред. Хохштима А. М.: Атомиздат, 1972. С. 277.

  5. Kim S., Ross J. Viscosity of Moderately Dense Gases // J. Chem. Phys. 1965. T. 42. C. 263.

  6. Норман Г.Э., Морозов И.В. Столкновения и плазменные волны в неидеальной плазме // ЖЭТФ. 2005. Т. 127. С. 412.

  7. Zelener B.B., Zelener B.V., Manykin E.A., Bronin S.Y., Bobrov A.A. Self-diffusion and Conductivity in an Ultracold Strongly Coupled Plasma. Calculation by the Method of Molecular Dynamics // J. Phys.: Conf. Ser. 2018. V. 946. P. 012126.

  8. Bobrov A.A., Bunkov A.M., Bronin S.Y., Klyarfeld A.B., Zelener B.B., Zelener B.V. Conductivity and Diffusion Coefficients in Fully Ionized Strongly Coupled Plasma: Method of Molecular Dynamics // Phys. Plasmas. 2019. V. 26. P. 082102.

  9. Хомкин А.Л., Шумихин А.С. Проводимость неидеальной полностью ионизованной плазмы: сравнение результатов расчета методом молекулярной динамики и модельного подхода // ТВТ. 2019. Т. 57. № 4. С. 501.

  10. Валуев А.А. О колебаниях электронов в неидеальной плазме // ТВТ. 1977. Т. 15. № 6. С. 1143.

  11. Ландау Л.Д., Лифшиц Е.М. Механика. М.: Физматлит, 2004. С. 51.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал