Теплофизика высоких температур, 2020, T. 58, № 4, стр. 563-583

ОГЛАВЛЕНИЕ

Введение

1. Солитон, общие сведения

    1.1. Линейная теория, дисперсионное соотношение

    1.2. Нелинейная теория, уравнение КдВ

    1.3. Нелинейная теория, псевдопотенциал Сагдеева

2. Плазменные токи, индуцированные ионно-акустическими солитонами

    2.1. Вывод и анализ уравнения для токов

    2.2. Группа солитонов

    2.3. Одночастичное приближение

    2.4. Ионно-акустические солитоны. Учет захваченных электронов

3. Электронно- и пыле-акустическая моды

    3.1. Электронно-акустические солитоны

    3.2. Пыле-акустические солитоны. Эксперимент

    3.3. Пыле-акустические солитоны. Теория

Заключение

Список литературы

ВВЕДЕНИЕ

Солитон – уединенная нелинейная волна, существующая благодаря балансу нелинейности и дисперсии [1]. Впервые уединенные волны описаны Джоном Скотом Расселом [2, 3], наблюдавшим их на поверхности водного канала, связывающего Эдинбург с Глазго в 1834 г. “Я наблюдал движение баржи, которую быстро двигала вдоль узкого канала пара лошадей. Вдруг баржа остановилась — баржа, но не масса воды в канале, увлеченная ее движением. Она собралась у носа судна в состоянии сильного волнения, затем внезапно оторвалась от него, покатившись вперед с большой скоростью и принимая форму одиночного, ярко выраженного возвышения, плавного и округлого, которое продолжало двигаться вдоль канала, как казалось, не изменяя своей формы и не уменьшая скорости. Я последовал за ним на лошади и, догнав, обнаружил его движущимся со скоростью восемь или девять миль в час и сохранившим свою первоначальную форму: 30 футов в длину, фут в ширину и полфута в высоту. Его высота постепенно уменьшалась, так что, проскакав милю или две, я потерял его из виду в волнах канала”. Рассел также указывал на инвариантность солитонов относительно столкновений друг с другом. Открытие Рассела имело прикладное значение и использовалось для оптимизации формы судов. Фундаментальная значимость данного явления обнаружилась позднее. Теоретическую модель, описывающую указанный феномен, построили Кортевег и де Вриз [4] спустя 50 лет после открытия Рассела. Ключевое уравнение модели в настоящее время носит название “КдВ-уравнение” в их честь. Позже в теории солитонов появились уравнения синус-Гордона, Хироты, Захарова, нелинейное уравнение Шредингера [1, 5–8] и др. Термином “солитон” стали описывать широкий класс нелинейных волн не только на поверхности воды, но и в плазме, оптических волокнах, нелинейных электрических линиях, механических системах и др. Феномен солитона заключается в том, что его энергия локализована в узкой области пространства. Классическая солитонная теория является консервативной. Она описывает эволюцию начального локального импульсного возмущения исходной нелинейной среды в один или несколько солитонов. При этом энергия системы (первый интеграл движения) остается постоянной. Более того, классические КдВ-солитоны имеют бесконечно много интегралов движения. В большинстве экспериментальных работ (начиная с наблюдений Рассела) солитоны возбуждались искусственно. В то же время в космических экспериментах наблюдались самовозбуждаемые плазменные солитонные структуры, для описания которых использовалась классическая теория [9–14]. Иногда для описания самовозбуждаемых солитонов пользуются термином и концепцией “автосолитон” [15]. В последнее время также активно развивается теория диссипативных солитонов, которая обобщает классическую теорию на случай термодинамически открытых систем¹¹ [16–18]. Такая концепция рассматривает волны как результат самоорганизации. Диссипативные силы F_dis играют важную роль в процессах эволюции открытых систем. Солитон называется слабо-диссипативным в случае выполнения условия F_dis$ \ll $ F_main, где под обозначением F_main скрыты основные силы, участвующие в формировании волны. В противном случае солитоны сильно-диссипативные. Формализм новой концепции основан на уравнении Гинзбурга–Ландау [19]. При этом некоторые свойства слабо-диссипативных солитонов можно анализировать и в рамках классической теории [20–22].

К настоящему времени основные свойства солитонов исследованы как теоретически, так и экспериментально. Можно с уверенностью утверждать, что солитон является каноническим объектом нелинейной волновой физики, по аналогии с гармоническими волнами в линейной теории. Действительно, распад начального импульса на последовательность солитонов в нелинейной среде аналогичен распаду импульса на гармонические составляющие в линейном случае. Плоские солитоны (нелинейный случай) и гармонические волны (линейный случай) могут стационарно распространяться в пространстве без изменения формы, скорости и других параметров. Вместе с тем необходимо признать, что свойства нелинейных объектов намного разнообразнее. Поэтому физику солитонов нельзя считать завершенной.

Открытым является вопрос о роли солитонов в генерации плазменных токов и ускорении заряженных частиц. Обсуждению этой проблемы посвятим данный обзор. Ограничимся рассмотрением только солитонов акустического типа, к которым относятся ионно-, электронно- и пыле-акустические солитоны. Как оказалось, ионно- и электронно-акустические нелинейные волны и солитоны часто встречаются в магнитосфере Земли [9–14]. Электрические поля и потоки заряженных частиц, по-видимому, являются источником энергии волн. О наличии в магнитосфере областей втекающих и вытекающих токов с большой населенностью солитонами сообщалось в [9, 10]. На связь электрических полей солитонов с электрическими полями и токами в магнитосфере Земли указывалось в [23]. В экспериментальной работе [9] обсуждался вопрос о структуре плазменных токов в магнитосфере на временны́х и пространственных масштабах солитонов, однако временнóе разрешение токоизмерительных приборов на спутниках позволяло измерить только средние значения токов (электрические поля при этом измерялись намного точнее). Соответствующие теоретические модели, создаваемые для интерпретации экспериментов, построены для анализа электрических полей, потенциалов или концентраций заряженных частиц, но не токов. И лишь в последние годы появились количественные теоретические модели, раскрывающие роль солитонов в генерации плазменных токов [24–28]. Термин “солитонный токовый механизм” впервые был предложен в работе [25] для описания феномена плазменных токов, индуцируемых солитонами. Термин “солитонные токи” появился в работе [22]. Указанные модели теоретически предсказывают новое свойство солитонов – односторонний перенос вещества. Этот результат является довольно неожиданным, поскольку классическая волновая теория предсказывает перенос энергии, но не массы. Односторонний перенос заряженных частиц приводит к возникновению токов со значительной постоянной составляющей, индуцируемых в плазме солитонами.

1. СОЛИТОН, ОБЩИЕ СВЕДЕНИЯ

Основные методы анализа волновых процессов в плазме можно разделить на две группы: методы магнитной гидродинамики (МГД-теория) и методы плазменной кинетики [29]. МГД-модели оперируют такими макропараметрами плазмы, как скорость потоков заряженных частиц, их концентрации, давление и т.д. Кинетическое описание плазмы основано на анализе функций распределения частиц. Кинетическая теория является более общей, а основные уравнения МГД-формализма могут быть получены на ее основе. Однако в большинстве случаев анализ солитонов проводится на основе МГД-уравнений.

1.1. Линейная теория, дисперсионное соотношение. Ограничимся изучением только одномерных волн. Начнем анализ с рассмотрения ионно-акустической моды (в русскоязычной литературе чаще используется термин ионно-звуковая мода, но для общности будем пользоваться термином “ионно-акустическая”). Рассмотрим простую МГД-модель двухкомпонентной бесстолкновительной плазмы, содержащей электроны и однозарядные ионы. Будем считать, что в невозмущенном состоянии заряженные частицы находятся в равновесном состоянии и описываются распределением Максвелла.

Уравнения движения и непрерывности для ионов, а также распределение Больцмана для электронов и уравнение Пуассона представим в виде [30]

где υ_i, m_i, n_i, T_i – соответственно скорость, масса, концентрация и температура ионной популяции; n_e, T_e – концентрация и температура электронов; n₀ = n_0e = n_0i – невозмущенная концентрация электронов и ионов; e – элементарный заряд. Потенциал φ соответствует электростатическому полю $E = {{ - \partial \varphi } \mathord{\left/ {\vphantom {{ - \partial \varphi } {\partial x}}} \right. \kern-0em} {\partial x}}$. В уравнении движения (1) учитываются сила электростатического поля (первый член справа) и сила давления (второй член), силы трения полагаем равными нулю.

В линейном приближении будем считать, что величины ${{\upsilon }_{i}},~{{n}_{e}},{{n}_{i}},~\varphi $ можно представить в виде $\psi = {{\psi }_{0}} + {{\psi }_{1}}$, ${{\psi }_{0}}$ – невозмущенное значение величин, ${{\psi }_{1}} = {{\hat {\psi }}_{1}}{\text{exp}}\left( { - {\text{i}}\omega t~ + {\text{\;i}}kx} \right)$ – малая гармоническая составляющая. Причем ${{\upsilon }_{{0i}}} = 0$, ${{\varphi }_{0}} = 0$, но ${{n}_{{0i}}} = {{n}_{{0e}}} = {{n}_{0}} \ne 0$. С учетом наших допущений, пренебрегая членами второго и более высоких порядков, перепишем систему (1)–(4) в виде

Продифференцировав выражение (5) по x, а выражение (6) по t и скомбинировав полученные выражения, можно получить

где V_Ti = (T_i/m_i)^1/2 – тепловая скорость ионов. Теперь комбинируя (7)–(9) и учитывая, что фазовая скорость ионного звука значительно превышает тепловую скорость ионов (${\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k} \gg {{V}_{{Ti}}}$), а также то, что для гармонических возмущений $\frac{\partial }{{\partial t}} \to - i\omega {\kern 1pt} ,$ $\frac{\partial }{{\partial x}} \to ik,$ получим где ${{\lambda }_{{\text{D}}}} = {{\lambda }_{{{\text{De}}}}} = \sqrt {{{{{\varepsilon }_{0}}{{T}_{e}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}{{T}_{e}}} {{{e}^{2}}{{n}_{0}}}}} \right. \kern-0em} {{{e}^{2}}{{n}_{0}}}}} $ – радиус Дебая, ${{\omega }_{i}} = \sqrt {{{{{e}^{2}}{{n}_{0}}} \mathord{\left/ {\vphantom {{{{e}^{2}}{{n}_{0}}} {{{m}_{i}}{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{m}_{i}}{{\varepsilon }_{0}}}}} $ – ионная плазменная частота. Учитывая, что ${{C}_{i}} = {{\omega }_{{pi}}}{{\lambda }_{{\text{D}}}}$, где ${{C}_{i}} = \sqrt {{{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}} $ – ионно-акустическая скорость, запишем окончательно дисперсионное соотношение для ионного звука в виде

На рис. 1 представлен характерный вид дисперсионного соотношения для акустических мод в плазме.

Фазовая скорость ионно-акустических волн уменьшается с ростом их частоты. Существование солитонов неразрывно связано с этим их свойством. Отметим, что с точностью до масштабов аналогичная дисперсия свойственна электронно- и пыле-акустическим волнам.

1.2. Нелинейная теория, уравнение КдВ. Как известно, существование солитонов возможно благодаря взаимной компенсации влияния нелинейных и дисперсионных эффектов на профиль волны [1]. На рис. 2 схематически отображена эволюция возмущения в нелинейной среде. Нелинейность среды вызывает рождение высших гармоник при эволюции начального возмущения $({{\omega }_{1}},{{\omega }_{2}}\,\, \ldots \,\,~{{\omega }_{n}}$), $({{k}_{1}},{{k}_{2}}\,\, \ldots ~\,\,{{k}_{n}}$). Кроме того, появляются биения гармоник $(\omega = {{\omega }_{1}} + {{\omega }_{2}}$), $(k = {{k}_{1}} + {{k}_{2}})$. Повышение доли высокочастотных составляющих в спектре волны приводит к укручению фронта волны (рис. 2). Нелинейность стремится “опрокинуть” волну. Как показано в предыдущем пункте, наличие дисперсии акустического типа приводит к тому, что высшие составляющие спектра начинают “отставать” от переднего фронта волны, перемещаясь ближе к центру. Таким образом, дисперсия останавливает укручение волны и стабилизирует ее форму.

Самым известным уравнением, описывающим феномен уединенных волн, является уравнение КдВ. Его можно получить из системы (1)–(4) методом конечных возмущений (reductive perturbation method) [28]. Кроме того, можно воспользоваться дисперсионным уравнением, выполнив обратное преобразование $ - i\omega \to \frac{\partial }{{\partial t}}$, $ik \to \frac{\partial }{{\partial x}}.$ Для простоты положим С_i = 1, $a = {{\lambda }_{{\text{D}}}}~{\text{,}}$ тогда уравнение (10) можно записать в виде

Применяя операторы к функции ψ, которая может быть интерпретирована как возмущение концентрации, скорости заряженных частиц или потенциала, получим из (11)

Решение уравнения (12) можно, согласно [7, 8], записать в виде функции Эйри:

Решение представляет собой движущийся с нормализованной скоростью с = 1 максимум функции ψ и дисперсионный “хвост” позади него. Далее необходимо учесть нелинейную зависимость скорости распространения возмущения ψ от значения ψ

Тогда (12) можно переписать в виде

Полагая $\xi \to x - t$, $\tau \to t,$ окончательно получим КдВ-уравнение для ψ

Данное односолитонное решение может быть записано в виде

где ψ₀= V/с – 1, V – скорость движения солитона относительно лабораторной системы отсчета. Амплитуда солитонов растет с увеличением скорости, при этом их ширина уменьшается. Существенный вклад в развитие теории классических солитонов внесли авторы [1] и др. Эти исследователи построили численные модели для исследования свойств солитонов, установили инвариантность солитонов относительно столкновений, развили метод обратной задачи рассеяния, который позволил получить и исследовать аналитические солитонные решения КдВ-уравнения. В работах [31, 32] получены аналитические неконсервативные решения КдВ-уравнения для случая слабой диссипации. Созданный метод получил название “метод анализа солитонов с флуктуациями параметров” (soliton perturbation analysis). Этот метод лег в основу теоретических моделей, описывающих диссипативные солитоны [20, 21]. Уравнение КдВ можно считать каноническим уравнением нелинейной волновой физики. Методы его анализа позволяют изучать эволюцию волн. Нужно, однако, помнить, что уравнение КдВ является приближенным и с увеличением амплитуды солитонов степень его применимости уменьшается.

1.3. Нелинейная теория, псевдопотенциал Сагдеева. Метод псевдопотенциала Сагдеева состоит в преобразовании системы (1)–(4) к единственному уравнению Пуассона и получении из него уравнения для псевдопотенциала (аналога потенциала в механике). Такой подход требует намного меньше допущений, нежели формализм КдВ, однако позволяет получить только стационарные решения, соответствующие волнам, прошедшим все стадии эволюции.

Поскольку ионный звук может существовать при условии T_e $ \gg $ T_i, то сначала рассмотрим более простой и наглядный случай T_i = 0. В этом случае ионы будут называться “холодными”, а в правой части уравнения (1) останется только первый член (сила давления ионов обращается в нуль).

Будем искать стационарные решения системы (1)–(4). Для этого введем новую переменную $S = {{(x - Vt)} \mathord{\left/ {\vphantom {{(x - Vt)} {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}$, где V – установившаяся скорость солитона. Введем также нормировку для концентраций заряженных частиц и электрического потенциала ${{N}_{i}} = {{{{n}_{i}}} \mathord{\left/ {\vphantom {{{{n}_{i}}} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$, ${{N}_{e}} = {{{{n}_{e}}} \mathord{\left/ {\vphantom {{{{n}_{e}}} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$, $\Phi = {{e\varphi } \mathord{\left/ {\vphantom {{e\varphi } {{{T}_{e}}}}} \right. \kern-0em} {{{T}_{e}}}}$. Уравнение (2) после замены переменных и однократного интегрирования можно переписать в виде

Однократное интегрирование (1) в новых переменных и с учетом выражения (13) приводит к уравнению для ионной концентрации ${\text{M}}_{i}^{2}{\kern 1pt} (1 - N_{i}^{2})$ + $2\Phi N_{i}^{2} = 0$, решение которого имеет вид: где ${{{\text{M}}}_{i}} = {V \mathord{\left/ {\vphantom {V {{{C}_{i}}}}} \right. \kern-0em} {{{C}_{i}}}}$ – число Маха. Величина N_i остается действительной при $\Phi < {{{\text{M}}_{i}^{2}} \mathord{\left/ {\vphantom {{{\text{M}}_{i}^{2}} 2}} \right. \kern-0em} 2}$. При ${{T}_{i}} \ne 0$, вводя новый параметр ${{\sigma }_{i}} = {{{{T}_{i}}} \mathord{\left/ {\vphantom {{{{T}_{i}}} {{{T}_{e}}}}} \right. \kern-0em} {{{T}_{e}}}}$ и следуя [33], можно получить выражения для N_i: где ${{y}_{i}} = {\text{arch}}({\text{M}}_{i}^{2} + 3{{\sigma }_{i}} - {{2\Phi )} \mathord{\left/ {\vphantom {{2\Phi )} {\sqrt {12{{\sigma }_{i}}{\text{M}}_{i}^{2}} }}} \right. \kern-0em} {\sqrt {12{{\sigma }_{i}}{\text{M}}_{i}^{2}} }}.$

С учетом нормировок уравнение (3) перепишем в виде N_e = exp(Φ). Теперь можно записать нормированное уравнение Пуассона (4) следующим образом:

Уравнение (15) автономно, и одним из его решений выступает профиль солитона Φ(S). Солитоны являются одним из классов решений уравнения (15). Однократное интегрирование (15) дает явный вид псевдопотенциала Сагдеева U(Φ):

При T_i = 0 получим

При ${{T}_{i}} \ne 0$ псевдопотенциал также может быть найден в явном виде, согласно [33]. Солитонные решения с положительной полярностью потенциала уравнения (16) существуют при выполнении условий: где Φ₀ – амплитуда солитона:

Форма классического псевдопотенциала Сагдеева представлена на рис. 3.

Форма псевдопотенциала U(Φ) при M_i > 1 характерна для солитонов с положительной полярностью потенциала, при этом амплитуда солитонов растет с увеличением скорости. При M_i < 1 псевдопотенциал соответствует периодической волне, которая является гармонической для малых амплитуд. Таким образом, псевдопотенциал содержит в себе как линейную, так и нелинейную задачи. Комбинируя уравнения (16), (17), можно получить уравнение для профиля солитона Φ(S):

Впрочем, уравнение (18) содержит неберущийся интеграл, поэтому в явном виде зависимость Φ (S) найти не удается. Однако это можно сделать либо численно, например методом Рунге–Кутты, либо приближенно, полагая амплитуду солитона малой. На рис. 3б представлены численные решения уравнения (18), соответствующие графикам псевдопотенциала, отображенным на рис. 3a. В случае малых амплитуд (|Φ| $ \ll $ 1) можно разложить правую часть уравнения (17) в ряд по степеням Φ :

где А_i – коэффициенты разложения в ряд Тейлора функции U(Φ). В выражении (19) учтено, что $U(0) = {{\partial U(0)} \mathord{\left/ {\vphantom {{\partial U(0)} {\partial \Phi }}} \right. \kern-0em} {\partial \Phi }} = 0$, поэтому А₀ = 0 и А₁ = 0. Для нашей простой модели ${{A}_{2}} = \frac{1}{{2{\text{M}}_{i}^{2}}} - \frac{1}{2}$, A₃ = $ = \frac{1}{{2{\text{M}}_{i}^{4}}} - \frac{1}{6}$. Аналитическим решением уравнения (19) является уже известная функция Здесь Φ₀= –А₂/А₃ – амплитуда солитона. Результаты сравнения двух методов представлены на рис. 4, где отображены зависимость амплитуды и ширины ионно-акустических солитонов от числа Маха. Для определения ширины солитона по уровню Φ₀/exp(1) использовалась как приближенная $\Delta = \frac{{{\text{arch}}\left( {\sqrt {{\text{exp}}\left( 1 \right)} } \right)}}{{\sqrt {{{ - {{A}_{2}}} \mathord{\left/ {\vphantom {{ - {{A}_{2}}} 8}} \right. \kern-0em} 8}} }},$ так и точная $\Delta = 2\int_{{{{{\Phi }_{0}}} \mathord{\left/ {\vphantom {{{{\Phi }_{0}}} e}} \right. \kern-0em} e}}^{{{\Phi }_{0}}} {\frac{2}{{\sqrt { - 2U(\Phi )} }}} {\kern 1pt} d\Phi $ формулы. Точный результат рассчитывался численно.

Из рис. 4 видно, что результаты обоих методов хорошо согласуются для небольших амплитуд |Φ₀| < 0.2. При больших амплитудах стоит пользоваться численными методами решения уравнений (15), (17). Различные профили ионно-акустического солитона представлены на рис. 5. Профили являются стандартными для исследуемого типа волн, в дальнейшем они понадобятся нам при выводе и анализе уравнений для плазменных токов.

2. ПЛАЗМЕННЫЕ ТОКИ, ИНДУЦИРОВАННЫЕ ИОННО-АКУСТИЧЕСКИМИ СОЛИТОНАМИ

2.1 Вывод и анализ уравнения для токов. Профиль потенциала (рис. 5a) свидетельствует о наличии ненулевого электрического заряда внутри солитона. При этом потенциал солитона отличен от нуля в некоторой локальной области пространства, но быстро падает до нуля по мере удаления от центра солитона. Теорема Гаусса позволяет рассчитать заряд, зная профиль потенциала или электрического поля. Согласно теореме, суммарный поток напряженности поля через поверхность, ограничивающую заряд, пропорциональна этому заряду. Электрическое поле, а следовательно, и его поток быстро стремятся к нулю по мере удаления от центра солитона (рис. 5a), это значит, что суммарный электрический заряд классического солитона оказывается равным нулю. Нормированную плотность этого заряда можно представить как ρ = N_i – N_e, в виде графика она отображена на вкладке к рис. 5б. В определенном смысле солитон представляет собой движущуюся квазичастицу с нетривиальной зарядовой структурой. Возникает закономерный вопрос, будет ли солитон формировать ток и какими свойствами обладает этот ток. Ответ на этот вопрос был дан в работе [24] в рамках МГД-формализма. Задача была сведена к анализу движения заряженных частиц, формирующих солитон. Посвятим этот параграф обсуждению этой темы.

Рассмотрим сначала ионный ток, индуцируемый ионно-акустическими солитонами. Под действием электрического поля солитона изначально покоящиеся ионы приобретут скорость, которую в неподвижной системе координат можно выразить, используя уравнение непрерывности (2):

Профили скорости ионного потока представлены на рис. 6а. Далее по известной формуле ${{j}_{i}} = e{{n}_{i}}{{\upsilon }_{i}}$ найдем выражение для плотности ионного тока

Нормируя (22) на $e{{n}_{0}}{{C}_{i}}$, получим окончательное выражение для нормированной плотности ионного тока [24] Из (23) следует, что плотность ионного тока отлична от нуля при условии ${{N}_{i}} \ne 1$, которое выполняется только внутри солитона (рис. 5б). Профили плотности ионного тока (зависимость J_i(X)) для разных моментов времени τ представлены на рис. 6б. Здесь и далее $X = {x \mathord{\left/ {\vphantom {x {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}$, $\tau = t{{\omega }_{i}}$. Проанализируем полученные профили солитона. Из рис. 5б видно, что ионная концентрация в электрическом поле солитона положительной полярности повышена по сравнению с невозмущенным состоянием. Следовательно, в соответствии с (21) нормированная ионная скорость ${{{{\upsilon }_{i}}} \mathord{\left/ {\vphantom {{{{\upsilon }_{i}}} {{{C}_{i}}}}} \right. \kern-0em} {{{C}_{i}}}}$ будет положительной, т.е. она будет иметь направление, совпадающее с направлением движения солитона (рис. 6a). Этот результат согласуется с результатами модели [34], где система уравнений (1)–(4) решалась относительно переменной ${{\upsilon }_{i}}$ (токи в [34] не анализировались). Таким образом, поле ионно-акустического солитона положительной полярности осуществляет перенос ионов только в направлении движения солитона. Результатом переноса заряженных частиц является импульс плотности ионного тока J_i, имеющего направление, совпадающее с направлением ${{\upsilon }_{i}}$ (рис. 6б). Другими словами, ионно-акустические солитоны должны возбуждать в плазме однополярные импульсы ионного тока. В модели с двумя электронными популяциями разной температуры, предложенной в [35], возможно существование ионно-акустических солитонов отрицательной полярности. Этому случаю будут соответствовать уменьшение нормированной концентрации ионов по сравнению с невозмущенной (${{N}_{i}} < 1$) и, согласно (23), противоположная направленность ионного тока.

Возбуждение плазменных токов – важное свойство солитонов акустического типа. Для описания свойств таких токов будем использовать термин “солитонные токи”, предложенный в [22].

Поскольку тепловая скорость электронов в плазме значительно превышает ионно-акустическую скорость, полагалось, что электроны стационарно распределены в поле солитона, согласно уравнению Больцмана (3). В таком приближении найти электронный ток нельзя. Отметим однако, что практический интерес представляют токи отдельных популяций, которые регистрируются в виде электронных и ионных пучков различной плотности, энергии и т.д. Электронный ток, индуцируемый солитонами, можно найти в рамках МГД-модели, учитывающей электроны, захваченные солитоном (раздел 2.4).

Рассмотрим основные свойства солитонных токов. Начнем с расчета длительности однополярных импульсов тока. Это важно с прикладной точки зрения для оценки необходимого временнóго разрешения экспериментального оборудования. Определим длительность импульса тока χ_i как время, в течение которого выполняется условие $J > {{{{J}_{0}}} \mathord{\left/ {\vphantom {{{{J}_{0}}} {\exp (1)}}} \right. \kern-0em} {\exp (1)}}$, где J₀ – амплитуда импульса. Зависимость длительности импульса ионного тока от числа Маха M_i для ионно-акустических солитонов нетрудно рассчитать, используя уравнения (23), (14), (20) в виде [24]:

где $B = 1 + \frac{1}{{\exp (1)}}\left( {\frac{{{{{\text{M}}}_{i}}}}{{\sqrt {{\text{M}}_{i}^{2} - 2{{\Phi }_{0}}} }} - 1} \right).$ Зависимость χ_i(Φ₀) можно представить в параметрическом виде, комбинируя (24) с выражением для амплитуды Φ₀= –A₂/A₃ (коэффициенты A₂, A₃ являются функциями M_i). График χ_i(Φ₀) приведен на рис. 7.

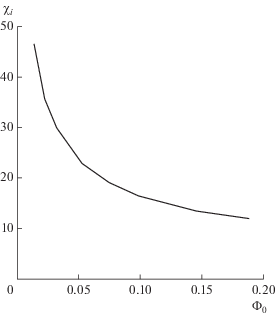
Из анализа рис. 7 видно, что χ_i уменьшается с ростом амплитуды солитонов, что связано с уменьшением их ширины и, следовательно, времени воздействия солитона на ионы. Из рис. 7 также следует, что ${{\chi }_{i}} \sim 10$ при Φ₀ = 0.2. Длительность импульсов тока становится еще меньше для солитонов с большей амплитудой (численное интегрирование (17) позволяет получить солитонные решения с амплитудой Φ₀ ~ 1, см. рис. 4). Таким образом, для экспериментальной регистрации солитонных токов необходимы приборы с временны́м разрешением порядка $\omega _{i}^{{ - 1}}$ [24]. В противном случае измеряется интегральное значение тока, которое может ошибочно приписываться несуществующим пучкам заряженных частиц.

Зная скорость частиц в электрическом поле солитона, можно оценить еще один важный, экспериментально определяемый параметр – кинетическую энергию частиц W в сравнении с их тепловой энергией. Этот параметр связан с функцией распределения по скоростям для ионов. Запишем простое выражение для нормированной кинетической энергии [24]:

Здесь υ_imax – максимальное значение $\left| {{{\upsilon }_{i}}} \right|$. В соответствии с рис. 6a υ_imax/C_i = 0.2, тогда $W = {{0.02} \mathord{\left/ {\vphantom {{0.02} {{{\sigma }_{i}}}}} \right. \kern-0em} {{{\sigma }_{i}}}}$, где ${{\sigma }_{i}} = {{{{T}_{i}}} \mathord{\left/ {\vphantom {{{{T}_{i}}} {{{T}_{e}}}}} \right. \kern-0em} {{{T}_{e}}}}$. Условие существования ионно-акустических солитонов T_e $ \gg $ T_i приводит к ${{\sigma }_{i}} \ll 1$. Полагая ${{\sigma }_{i}} = 0.01$, получим W = 2. Для солитонов большей амплитуды Φ₀ ~ 1 (соответствующие решения можно получить при численном интегрировании (17)) величина W может возрасти еще на порядок. Таким образом, кинетическая энергия ионов в импульсах солитонных токов на порядок превысит тепловую энергию ионов. При низком временнóм разрешении приборов эта энергия может быть ошибочно приписана несуществующим пучкам ионов.

2.2. Группа солитонов. При низком временнóм разрешении приборов импульс тока, возбуждаемый одним солитоном, может остаться незарегистрированным. Однако солитоноподобные структуры в космической плазме часто регистрируются большими каскадами, насчитывающими десятки последовательно движущихся уединенных волн [9, 10]. В этом случае интегральный электрический ток может быть значительным и измеряется даже приборами с низким временны́м разрешением. Смоделируем группу ионно-акустических солитонов, состоящую из множества объектов. На рис. 8 представлено численное решение (15) для группы из десяти солитонов. Среднее значение ионного тока для рассмотренного примера равно

Здесь τ_max= 710. В соответствии с нормировкой тока, принятой в (23), такой же ток соответствует пучку ионов с концентрацией n_b = 0.026n_0i, движущихся с околозвуковой скоростью υ_bi ≈ С_i, плотность ионного тока при этом равна ${{j}_{b}} \approx 0.026e{{n}_{{0i}}}{{C}_{i}}$.

Электрические токи в плазме часто связаны с пучками заряженных частиц. Известно, что волны, в том числе и солитоны, могут усиливаться в присутствии пучков заряженных частиц [36, 37]. Представленные здесь результаты свидетельствуют о том, что и сами солитоны могут вносить вклад в регистрируемые электрические токи, отличительной чертой которых является импульсный характер. В работе [24] был предположен новый нелинейный механизм трансформации тока в плазме, когда под действием пучка заряженных частиц в плазме возбуждаются солитоны, которые в свою очередь возбуждают солитонные токи. При этом характер тока претерпевает существенное изменение – постоянный ток пучка может трансформироваться в пульсирующий ток солитонов (или их суперпозицию).

Как упоминалось выше, модель, в которой электроны подчиняются распределению Больцмана, непригодна для анализа электронных токов, возбуждаемых ионно-звуковыми солитонами. Эта задача была впервые решена в работе [25] в рамках МГД-модели плазмы с учетом захваченных электронов.

2.3. Одночастичное приближение. Уравнение движения является одним из основных в системе МГД-уравнений, где оно имеет эйлерову форму и описывает движение малого объема вещества. Использование МГД-уравнений позволяет построить самосогласованные модели линейных волн и солитонов в плазме. Однако движение отдельных частиц МГД-уравнения не описывают. Для анализа траекторий отдельных частиц в поле солитонов в работах [22, 24] было использовано одночастичное приближение. Суть такого подхода состоит в анализе уравнения движения в лагранжевой форме для отдельной заряженной частицы в электрическом поле солитона. Рассмотрим этот метод подробнее.

Будем считать, что на ионы действует только электрическое поле солитона, пренебрежем силой давления (считая T_i = 0) и другими силами. В этом случае одномерное уравнение движения заряженной частицы можно записать в виде [24]

где $E(x,t) = {{ - d\varphi } \mathord{\left/ {\vphantom {{ - d\varphi } {dx}}} \right. \kern-0em} {dx}}$ – электрическое поле солитона. Воспользуемся введенными ранее безразмерными переменными X = x/λ_D, τ = tω_i, Φ = eφ/T_e, S = X – M_iτ и преобразуем (26) к виду Функцию Ф(X, t) можно получить в явном виде, подставив S = X – M_iτ в (20). Положим в (27) начальную скорость ионов равной нулю, пренебрегая их распределением по скоростям. Это можно сделать, поскольку для существования ионно-акустических солитонов необходимо выполнение условия V_Ti $ \ll $ C_i. Начальное положение иона будем считать равным нулю, в то время как начальное положение солитона примем равным X_Sol = –40. Решение (27) с указанными начальными условиями для M_i = 1.05, описывающее траекторию иона, представлено на рис. 9.

В результате взаимодействия с солитоном меняется положение иона в пространстве. При этом скорость иона после взаимодействия остается равной нулю (рис. 9б). Отметим, что максимальные значения нормированной скорости ${{{{\upsilon }_{i}}} \mathord{\left/ {\vphantom {{{{\upsilon }_{i}}} {{{C}_{i}}}}} \right. \kern-0em} {{{C}_{i}}}}$, полученные разными методами и представленные на рис. 6а и 9б, хорошо согласуются. Стоит отметить, что скорости ${{{{\upsilon }_{i}}} \mathord{\left/ {\vphantom {{{{\upsilon }_{i}}} {{{C}_{i}}}}} \right. \kern-0em} {{{C}_{i}}}}$ и ${{dX} \mathord{\left/ {\vphantom {{dX} {d\tau }}} \right. \kern-0em} {d\tau }}$ нетождественны, первая описывает МГД-скорость потока частиц, а вторая – скорость отдельных частиц. На практике для всей совокупности ионов рассмотренная ситуация будет соответствовать движущемуся вместе с солитоном импульсу ионного тока положительной полярности.

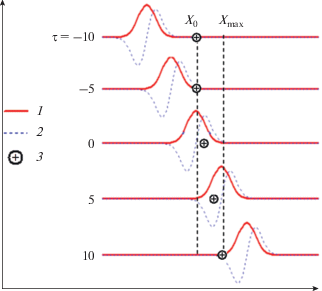
Поэтапно процесс переноса иона полем солитона проиллюстрирован на рис. 10. При τ = –5, ион попадает в область положительного поля и начинает ускоряться в положительном направлении за счет энергии солитона. Масса иона велика, и он не может приобрести достаточную скорость, чтобы опередить солитон²², поэтому при τ = 2 область отрицательного поля солитона догоняет ион и замедляет его до начальной скорости (в данном случае равной нулю). При этом ион возвращает приобретенную энергию солитону. Вместе с тем положение иона в пространстве меняется в соответствии с тем, как показано на рис. 9a.

Дистанцию переноса определим как L = X_max– X₀, где X₀, X_max – начальное и конечное положения иона. С одной стороны, с ростом амплитуды солитонов дистанция переноса должна расти, но, с другой стороны, увеличение амплитуды приводит к уменьшению ширины солитонов (рис. 4б), а следовательно, и времени воздействия поля солитона на ионы. Зависимость L(Φ₀) представлена на рис. 11, из которого видно, что один солитон с амплитудой Φ₀ > 0.05 переносит ионы на расстояние в несколько λ_D.

Одночастичное приближение позволяет рассчитать траектории, скорости и фазовые траектории отдельных ионов. В рассматриваемом случае однородной плазмы с “холодными” ионами все характеристики ионов можно считать равными, кроме начального положения. Обозначим траекторию i-го иона f_i(τ), тогда легко показать, что траектория j-го иона, начальное положение которого отличается на ΔX, может быть записана в виде   f_j(τ) = f_i(τ − M_i/ΔX) + ΔX. На рис. 12a отображены траектории частиц, взаимодействующих с ионно-акустическим солитоном, начальное положение частиц отличается на единицу: X₀₁ = 0, X₀₂ = 1, …, X₀₂₀ = 20. Как видно, траектории частиц подобны, но сдвинуты в пространстве. В случае солитонов докритической амплитуды траектории соседних частиц не пересекаются [22]. Зная траектории частиц, можно с использованием методов статистической физики рассчитать макропараметры плазмы, такие как концентрация и скорость ионного потока, плотность ионного тока и др. В определенном смысле одначастичное приближение можно считать кинетическим приближением. В рассматриваемом случае (“холодных” ионов) задача упрощается, поскольку начальная скорость ионов равна нулю, при этом нет необходимости проводить интегрирование по функциям распределения.

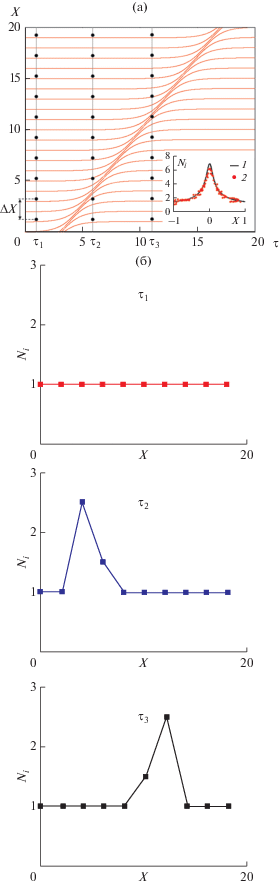
Рассмотрим простейший метод определения профиля ионной концентрации N_i. Зафиксируем несколько моментов времени τ₁, τ₂, τ₃, как показано на рис. 12a. Далее разобьем ось X на равные отрезки ΔX. Очевидно, что количество траекторий внутри каждого отрезка ΔX будет равно количеству частиц $N_{i}^{*}$ в нем. Если полученный профиль нормировать на невозмущенное значение $N_{i}^{*}$ (вдали от солитона), то он совпадет с профилем, полученным по формуле (14). Профили N_i(X) для выделенных моментов времени τ₁ – τ₃ отображены на рис. 12б. На вкладке к рис. 12а отображен профиль N_i(X), рассчитанный по указанной методике для M_i = 1.45 и большого числа ионов. На этом же рисунке представлен этот же профиль, рассчитанный в соответствии с аналитической МГД-формулой (14). Оба профиля хорошо согласуются, что свидетельствует о справедливости одночастичного приближения. Такой упрощенный кинетический подход может оказаться весьма полезным инструментом анализа солитонов в более сложных моделях [20, 21].

Далее с использованием одночастичного приближения рассчитаем среднюю плотность ионного тока, возбуждаемого группой солитонов в ситуации, представленной на рис. 8. Согласно рис. 11, ионно-акустический солитон с амплитудой Φ₀ ≈ 0.2 переносит ионы на расстояние L ≈ ≈ 2λ_D. Десять солитонов за время τ = 710 переместят ионы на расстояние 10L. Поскольку в движении участвуют все ионы, можно записать для среднего значения плотности ионного тока следующую оценку:

Здесь k – количество солитонов в группе, множитель в скобках учитывает нормировку L и τ. Для указанных параметров получим значение $\overline {{{j}_{i}}} \approx 0.028e{{n}_{{0i}}}{{C}_{i}}$, или $\overline {{{J}_{i}}} \approx 0.028$ после нормировки на $e{{n}_{{0i}}}{{C}_{i}}$ (принятой ранее для формулы (23)). Полученное значение хорошо согласуется со значением плотности тока (25), рассчитанным в рамках МГД-теории.

Одночастичное приближение не является самосогласованным. В правой части (26) можно использовать любую зависимость E(x, t). Так, например, можно исследовать влияние на заряженные частицы поля ленгмюровского солитона, определяемого решением нелинейного уравнения Шредингера, поля двойных слоев, поля монохроматической волны и др. Кроме того, начальную скорость частиц в (26), (27) можно задать произвольно, в соответствии, например, с распределением Максвелла.

2.4. Ионно-акустические солитоны. Учет захваченных электронов. Как показано в [38], корректный анализ ионно-акустических солитонов требует учета захваченных электронов. Согласно [38, 39], ионно-акустический солитон с положительной полярностью потенциала является для электронов потенциальной ямой, в которой часть из них совершает финитное (колебательное) движение. Такие электроны считаются захваченными, они двигаются вместе с солитоном. Второй тип электронов называется “пролетные”, они находятся в яме конечное время. Эти две группы электронов формируются из однородного равновесного электронного фона. В процессе формирования солитона часть электронов захватывается его потенциалом, формируя захваченную фракцию. Захват прекращается с окончанием эволюции волны. Электроны, которые не были захвачены солитоном, остаются свободными. Согласно [38, 39], установившееся распределение для электронов можно записать в виде

Или с учетом принятых ранее нормировок

Здесь erf – функция ошибок, первое слагаемое в правой части выражений (29), (30) описывает концентрацию пролетных электронов, а второе – концентрацию захваченных. Остальные МГД-уравнения полностью совпадают с уравнениями (1), (2), (4). Уравнение Пуассона с учетом (30) можно переписать в виде

Псевдопотенциал Сагдеева получим однократным интегрированием (31) по Φ :

где А – константа интегрирования. При A = A₀ = = ${\text{M}}_{i}^{2} + 1$, что соответствует условию dФ/dX = 0 при Ф = 0, решением (32) является ионно-акустический солитон. Профили солитона как результат численного решения (32) представлены на рис. 13 для M_i = 1.5 [25].

Солитону соответствует повышение концентраций N_i, N_e (рис. 13б), при этом ${{N}_{i}} \ne {{N}_{e}}$ внутри солитона. Ионная скорость определяется по формуле (21). Профиль ионной скорости υ_i(X)/C_i в поле солитона представлен на рис. 13a, из которого видно, что υ_i(X)/C_i > 0. Это хорошо согласуется с результатами простой МГД-модели (см. рис. 6а). Плотность ионного тока в этой модели описывается уже использованной ранее формулой (23). Однако в модели, учитывающей захваченные электроны, представляется возможным рассчитать электронные токи, возбуждаемые ионно-акустическим солитоном. В моделях [38, 39] пролетные частицы приходят из бесконечности, причем эти потоки из –∞ и +∞ равны, их суммарный ток равен нулю. Следовательно, ненулевой электронный ток определяется только захваченными частицами. Поскольку захваченные электроны движутся вместе с солитоном, то плотность электронного тока можно выразить, умножив концентрацию захваченных электронов (второе слагаемое в правой части (29)) на скорость движения солитона и на заряд электрона: ${{j}_{e}} = 2{{n}_{0}}eV\sqrt {{{e\varphi } \mathord{\left/ {\vphantom {{e\varphi } {\pi {{T}_{e}}}}} \right. \kern-0em} {\pi {{T}_{e}}}}} $, или с учетом нормировки на en₀C_i:

Профиль J_e(X) отображен на рис. 13a, из которого очевидна пространственная локализованность и однополярный импульсный характер J_e(X). В [40] можно найти выражение для плотности электронного тока, полученное из уравнений Власова–Пуассона. Приведенное в [25] выражение (33) содержит меньше параметров, что упрощает его практическое использование.

Как видно из рис. 13а, профили плотности электронного и ионного токов подобны. На первый взгляд, они отличаются лишь количественно, однако механизмы возникновения и распространения токов различаются принципиально [25]. Действительно, ионные токи в рассмотренном случае (так же как и в модели с больцмановскими электронами) обусловлены инертностью ионов в электрическом поле солитона. Причиной электронных токов является захват электронов потенциальной ямой солитона, движущегося в пространстве. Другими словами, ионно-акустический солитон подобен контейнеру для переноса электронов. Как показано в предыдущем параграфе, каждый ион переносится солитоном на конечное расстояние в направлении его движения. Электроны же захватываются в области формирования солитона и сопровождают его до распада [38, 39].

Рассмотрим такие параметры, как ширина Δ_J и длительность χ токовых импульсов. Очевидно, что величины Δ_J и χ, с учетом нормировки соответственно на λ_D и $\omega _{i}^{{ - 1}}$, оказываются связанными простым соотношением ${{\Delta }_{J}} = {{{\text{M}}}_{i}}\chi $. Из анализа численных решений (32) с учетом формул для токов (23), (33) следует, что Δ_J и χ монотонно убывают с ростом амплитуды солитонов. Соответствующие графики приведены на рис. 14, из которого видно, что для солитонов большой амплитуды Φ₀ = 3 имеем Δ_Ji = 0.9, Δ_Je = 7.3, χ_i = = 0.36, χ_e = 2.9 (индексы i, e соответствуют ионной и электронной популяции). Для экспериментальной регистрации структуры таких токовых импульсов разрешение приборов должно быть как минимум в несколько раз меньше указанных величин.

Рассмотрим теперь среднее значение (постоянную составляющую) плотности электронного и ионного токов, генерируемых каскадом солитонов. Численное решение (32) для М_i = 1.5, А = А₀ + + 6.7 × 10^–12, описывающее токи, индуцированные каскадом из 5 солитонов, представлено на рис. 15а.

Анализ в рамках новой модели, как видно из рис. 15, свидетельствует о том, что каскад солитонов возбуждает не только пульсирующие ионные токи, но и электронные токи такого же характера. При этом и электронные и ионные токи имеют существенные постоянные составляющие $\overline {{{J}_{e}}} $, $\overline {{{J}_{i}}} $, которые важно отличать от токов пучков в экспериментах. Надежная регистрация плазменных токов часто связана с трудностями экспериментального характера, с уменьшением временны́х масштабов эта проблема становится еще более актуальной. Проанализируем постоянную составляющую солитонных токов, которая будет зависеть от Φ₀ и частоты следования солитонов v. Зависимость величин $\overline {{{J}_{e}}} $, $\overline {{{J}_{i}}} $ от v будет, очевидно, пропорциональной, а их зависимость от Φ₀ при постоянной v представлена на рис. 15б. Как видно, $\overline {{{J}_{e}}} $ и $\overline {{{J}_{i}}} $ являются величинами одного порядка, но при этом $\overline {{{J}_{e}}} > \overline {{{J}_{i}}} $ для ионно-акустических солитонов любых амплитуд Φ₀. В работе [41] показано, что число захваченных электронов может быть меньше, чем следует из [38, 39], следовательно, соотношение между $\overline {{{J}_{e}}} $ и $\overline {{{J}_{i}}} $ может варьироваться.

В этом параграфе рассмотрены токи, индуцируемые ионно-акустическими солитонами большой амплитуды Φ₀ ~ 1. Соответствующие решения получены численным интегрированием уравнения (32). В параграфе 2.2 использовался метод малых амплитуд, справедливый при ${{{\Phi }}_{0}} \lesssim $ 0.1. Поэтому средние токи в случае, приведенном на рис. 8, на порядок меньше, чем токи, представленные на рис. 15. Такое отличие связано с ограничением методов, используемых в параграфе 2.2.

3. ЭЛЕКТРОННО- И ПЫЛЕ-АКУСТИЧЕСКАЯ МОДЫ

Электронно- и пыле-акустическая плазменные моды во многом подобны ионно-акустической моде. Указанные моды отличаются характерными частотами. Частоты в свою очередь определяются массой соответствующей плазменной популяции, ее зарядом и концентрацией. Рассмотрим некоторые свойства плазменных токов, индуцируемых электронно- и пыле-акустическими солитонами.

3.1. Электронно-акустические солитоны. Анализ электронно-акустических солитонов будет выполнен в рамках трехкомпонентной модели с горячим электронным фоном, популяцией холодных электронов и неподвижными однозарядными ионами [42, 43]. Для холодной электронной компоненты запишем уравнения движения и непрерывности, для горячей – распределение Больцмана, дополним систему уравнением Пуассона, считая ионную концентрацию постоянной (${{n}_{i}} \equiv {{n}_{0}}$):

Здесь m_e – масса электрона, индексы ec, eh относятся соответственно к холодной и горячей электронным популяциям, T_ec = 0. Взаимосвязь невозмущенных электронных концентраций n_0eh, n_0ec определяется принципом квазинейтральности: ${{n}_{0}} - {{n}_{{0eh}}} - {{n}_{{0ec}}} = 0$. Следуя рассуждениям главы 2, систему (34)–(37) можно свести к уравнению Пуассона в виде где Здесь $\Phi = {{e\varphi } \mathord{\left/ {\vphantom {{e\varphi } {{{T}_{{eh}}}}}} \right. \kern-0em} {{{T}_{{eh}}}}},$ $\delta = {{{{n}_{{0eh}}}} \mathord{\left/ {\vphantom {{{{n}_{{0eh}}}} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$, ${{{\text{M}}}_{e}} = {V \mathord{\left/ {\vphantom {V {{{C}_{e}}}}} \right. \kern-0em} {{{C}_{e}}}}$, ${{C}_{e}} = \sqrt {{{{{T}_{{eh}}}{{n}_{{0ec}}}} \mathord{\left/ {\vphantom {{{{T}_{{eh}}}{{n}_{{0ec}}}} {{{m}_{e}}{{n}_{{0eh}}}}}} \right. \kern-0em} {{{m}_{e}}{{n}_{{0eh}}}}}} $ – электронно-акустическая скорость. Временны́е и пространственные переменные нормированы на $\omega _{{ec}}^{{ - 1}}$ и ${{\lambda }_{{\text{D}}}} = \sqrt {{{{{\varepsilon }_{0}}{{T}_{{eh}}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}{{T}_{{eh}}}} {{{e}^{2}}{{n}_{0}}}}} \right. \kern-0em} {{{e}^{2}}{{n}_{0}}}}} $, где ${{\omega }_{{ec}}} = \sqrt {{{{{e}^{2}}{{n}_{{0ec}}}} \mathord{\left/ {\vphantom {{{{e}^{2}}{{n}_{{0ec}}}} {{{m}_{e}}{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{m}_{e}}{{\varepsilon }_{0}}}}} $ – электронная плазменная частота для холодной электронной популяции. Солитонные решения (38) можно представить в виде (20) с учетом ${{A}_{1}} = \frac{\delta }{2}\left( {\frac{1}{{{\text{M}}_{e}^{2}}} - 1} \right),$ ${{A}_{2}} = \frac{\delta }{2}\left( {\frac{1}{{{\text{M}}_{e}^{4}(1 - \delta )}} + \frac{1}{3}} \right).$ Электронный ток, обусловленный движением холодных электронов в поле электронно-акустических солитонов, нормированный на $ - e{{n}_{{0ec}}}{{C}_{e}},$ нетрудно выразить в виде

Расчет плотности тока горячих электронов выходит за рамки данной работы. Ионный ток равен нулю вследствие неподвижности ионов.

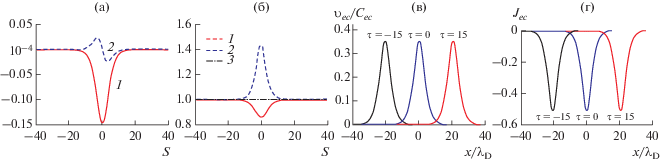
Возмущение потенциала, электрического поля и концентраций заряженных частиц для электронно-акустического солитона, а также скорость и плотность тока холодных электронов представлены на рис. 16. Очевидно, что электронно-акустические солитоны также генерируют однополярные импульсы тока в плазме, при этом отрицательной полярности потенциала соответствует отрицательная полярность импульсов тока холодных электронов.

Длительность импульсов электронного тока по аналогии с (24) можно записать в виде

где $\gamma = \frac{\delta }{{\delta - 1}}$, $B = 1 + \frac{1}{{\exp (1)}}\left( {\frac{{{{{\text{M}}}_{e}}}}{{\sqrt {{\text{M}}_{e}^{2} - 2\gamma {{\Phi }_{0}}} }} - 1} \right).$ График зависимости длительности электронного тока от амплитуды солитона представлен на рис. 17. Зависимость χ_e(Φ₀) подобна зависимости χ_i(Φ₀), которая представлена на рис. 7, однако с учетом нормировок, принятых для формул (23) и (40), при прочих равных параметрах токи, возбуждаемые электронно-акустическими солитонами, будут больше по сравнению с токами, возбуждаемыми ионно-акустическими солитонами.

3.2. Пыле-акустические солитоны. Эксперимент. Пылевой плазмой называется ионизированный газ, содержащий заряженные маркочастицы. Свойства пылевой плазмы довольно подробно описаны в [44, 45]. Наличие в плазме относительно тяжелой заряженной компоненты существенно обогащает разнообразие волновых процессов. В частности, появляется пыле-акустическая мода, свойства которой определяются инерцией пылевых частиц. Частоты соответствующих колебаний располагаются в удобном для наблюдений диапазоне 10–100 Гц. Для наблюдения пыле-акустических процессов можно использовать относительно доступное оптическое оборудование, что делает пылевую плазму удобным инструментом для проведения фундаментальных исследований в области коллективных явлений. Теория пыле-акустических солитонов впервые описана в [46] и развита в [47], где в рамках МГД-модели получены уравнения, описывающие уединенные волны. В работах [48, 49] представлены результаты экспериментальных исследований пыле-акустических солитонов, возбуждаемых электрическими импульсами, которые подавались на сетку или проволоку. В работе [26] экспериментально и теоретически изучена эволюция самовозбуждаемого пыле-акустического солитона от рождения до “опрокидывания” в пылевом облаке страты тлеющего разряда. Экспериментально подтвержден эффект одностороннего переноса частиц электрическим полем пыле-акустического солитона. Рассмотрим подробнее последнюю работу.

Эксперимент, описанный в [26], проводился в вертикальной стеклянной газоразрядной трубке. Схема экспериментальной установки приведена на рис. 18.

В качестве буферного газа в настоящих экспериментах использовался неон при давлении 0.085–0.125 Торр, ток составлял I = 0.6 мА при напряжении U = 1.27 кВ. Инжекция пылевых частиц осуществлялась с помощью механического инжектора, расположенного в верхней части. Для формирования плазменно-пылевого облака использовались монодисперсные частицы меламин-формальдегида диаметром d_p = 4.25 ± 0.09 мкм. Пылевая плазма формировалась в стратах тлеющего разряда, наблюдения проводились в самой нижней из них. Диаметр пылевого облака составлял ~8 мм с межчастичным расстоянием L = = 300 мкм. Видеорегистрация проводилась с частотой f_c = 100–500 кадр/с. Подсветка пылевой структуры осуществлялась с помощью “лазерного ножа” мощностью W = 0.1 мВт. В результате пыле-акустической неустойчивости в пылевом облаке самостоятельно возбуждалась уединенная пыле-акустическая волна, распространяющаяся вниз, как показано на рис. 19. Процесс повторялся с частотой f ≈ 3 Гц.

Скорость перемещения волны плотности V составляла от 4.5 × 10^–2 до 5 × 10^–2 м/с, что примерно в 1.5–2 раза превышает значение пыле-акустической скорости. Сверхзвуковое движение свойственно нелинейным волнам и солитонам. Величина δN_d возрастала при движении волны сверху вниз. Механизм усиления волны, по мнению авторов [26], связан с силой ионного увлечения.

Все пылевые частицы можно разделить на три части. Частицы в верхней части облака локализованы и формируют структуру, близкую к кристаллу; ближе к середине пылевого облака частицы участвуют в зарождении пыле-акустической волны и формируют солитон. Их характерное смещение относительно положения равновесия при взаимодействии с волной составляет несколько межчастичных расстояний (рис. 19, частица № 1 и № 2); начиная с определенного момента наблюдается “опрокидывание” солитона и формирование многопотоковости (эта фаза эволюции солитона исследовалась в [22]). Ускоренные волной частицы (рис. 19, частица № 3) достигают нижней границы пылевого облака и выбрасываются за его границы. Динамика выбранных пылевых частиц характерна для большинства частиц из соответствующего горизонтального слоя.

На рис. 20 отображены траектории выделенных частиц № 1, № 2, № 3, а также зависимость их скорости от координаты. Из рис. 19 и 20а видно, что внутри солитона пылевые частицы перемещаются преимущественно в направлении движения волны. Присутствует также некоторое обратное движение, которое авторы [26] связывали с силами, стремящимися восстановить первоначальную форму пылевого облака. При этом частицы №№ 1, 2 перемещаются на конечное расстояние порядка десяти радиусов Дебая. Частица № 3 ускоряется солитоном и перемещается вниз до нижней границы облака.

Частицы, расположенные ниже (с большим значением начального положения x₀), ускоряются до бóльших скоростей, нежели частицы, расположенные вверху, что связано с ростом амплитуды солитона, движущегося сверху вниз. Частица № 3 и другие частицы из этого горизонтального слоя, а также частицы, расположенные ниже, захватываются волной, перемещаются до нижней границы облака и выбрасываются за границы области стационарного расположения пыли, что в теории солитонов называется многопотоковым движением и соответствует “опрокидыванию” солитона [26]. Более подробнее распад пыле-акустического солитона исследован в [22].

По мнению авторов [26], перенос “вниз” индуцируется солитоном, а перенос “вверх” обусловлен балансом основных сил, формирующих облако.

3.3. Пыле-акустические солитоны. Теория. Пылевая плазма тлеющего разряда является неоднородной. Строгое математическое описание реальных волновых процессов в таких системах – задача нетривиальная. В работе [26] для описания эксперимента использовалась простая одномерная МГД-модель пылевой плазмы с постоянным отрицательным зарядом пылевых частиц [47].

Будем считать, что на пылевую частицу в невозмущенном состоянии действует электрическая сила F_E = ZeЕ, которая компенсирует силу тяжести mg и силу ионного увлечения F_i. Пыле-акустическая скорость в общем случае определяется выражением [47]

где Z = |q_d/e|, q_d – заряд пылевых частиц; n_0e, n_0i, n_0d – начальные концентрации электронов, ионов и пылевых частиц; T_e, T_i – электронная и ионная температуры; m_d – масса пылевых частиц. В эксперименте [26] указаны следующие параметры плазмы: Z = 10⁴, n_0e = 10¹⁴ м^–3, n_0d = 5 × 10¹⁰ м^–3, T_e = 1.3 × 10⁵ К, T_i = 300 К, m_d = 5 × 10^–14 кг. В таком случае С_d = 2.6 × 10^–2 м/с. Полученное значение согласуется с экспериментально измеренным значением скорости солитона V с учетом сверхзвукового распространения нелинейных волн. Систему МГД-уравнений согласно [26] можно записать в виде где β = T_e/T_i, Φ = eφ/$C_{d}^{2}{{m}_{d}}$ – нормированный потенциал, υ_d – скорость пылевой фракции, δ₁ = = n_0e/Zn_0d, δ₂ = n_0i/Zn_0d, (из условия квазинейтральности δ₁ – δ₂ + 1 = 0). Действуя как и ранее, вводя переменную $S = {{\left( {x - Vt} \right)} \mathord{\left/ {\vphantom {{\left( {x - Vt} \right)} {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}} = X - {{{\text{M}}}_{d}}\tau $, где ${{\lambda }_{{\text{D}}}} = \sqrt {{{{{\varepsilon }_{0}}{{T}_{e}}{{T}_{i}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}{{T}_{e}}{{T}_{i}}} {{{e}^{2}}}}} \right. \kern-0em} {{{e}^{2}}}}\left( {{{n}_{{0e}}}{{T}_{i}} + {{n}_{{0i}}}{{T}_{e}}} \right)} $ – радиус Дебая [47], а M_d = V/C_d – число Маха, получим из уравнений (41), (42)

Для связи концентрации частиц используем уравнение Пуассона в безразмерном виде

Для определения параметров движения пылевых частиц в солитоне воспользуемся разработанным ранее одночастичным приближением (параграф 2.3).

Результаты численного решения (43) при Z = = 10⁴, β = 427, δ₁ = 0.2 отображены на рис. 21 для разных значений М_d и, соответственно, разных амплитуд. Одночастичное приближение использовалось для поиска зависимостей X(τ) и U_d(X), где U_d(X) – скорость пылевых частиц, нормированная на C_d. Профиль солитона соответствует повышению концентрации пыли, что согласуется с результатами эксперимента. Значения скорости пылевых частиц, полученные экспериментально (рис. 20б) и теоретически (рис. 21в) хорошо согласуются, причем в обоих случаях с ростом амплитуды солитона растет скорость частиц внутри него. Из рис. 21 также следует, что максимум скорости частиц соответствует максимуму концентрации. Хорошее согласие эксперимента и теории имеется также при анализе перемещения пыли в поле солитона (рис. 20a и 21б).

ЗАКЛЮЧЕНИЕ

В обзоре рассмотрено свойство солитонов акустического типа возбуждать электрические токи в плазме. Это свойство состоит в том, что солитоны осуществляют односторонний перенос заряженных частиц, в результате чего появляются однополярные импульсы электрического тока. Как оказалось, токи, индуцированные солитонами, существенны по величине и их необходимо учитывать в общей динамике плазмы. Механизм возбуждения токов получил название “солитонный токовый механизм” [25], а термин “солитонные токи” впервые появился в [22]. Значение солитонных токов еще больше возрастает, когда имеется не единичная волна, а группа солитонов, последовательно движущихся в плазме. В этом часто реализуемом на практике случае солитонные токи сравнимы по величине с плазменными токами пучков заряженных частиц. Для регистрации импульсов солитонных токов необходимо временнóе разрешение менее периода ионной плазменной частоты (электронной, ионной, пылевой для ионно-, электронно- и пыле-акустических солитонов соответственно). При недостатке разрешения измеряется только постоянная составляющая солитонных токов, а сами токи могут ошибочно интерпретироваться несуществующими пучками заряженных частиц. Уверенно измерить параметры солитонных токов можно в пылевой плазме, где характерная пылевая плазменная частота составляет единицы–сотни герц.

Рассмотрим вопрос отсутствия затухания солитонов при генерации токов. В соответствии с рис. 9 и 10 начальное и конечное положение заряженной частицы меняется при взаимодействии с солитонами, в то время как начальная и конечная скорости этой частицы равны (рис. 9б). Поскольку в самосогласованном движении участвует большое количество частиц, часть из которых ускоряется, а часть – замедляется, то общий баланс энергии сохраняется, и при отсутствии столкновений солитон не затухает. Следовательно, солитоны не передают энергию заряженным частицам, а обмениваются ею с ними, участвуя в адиабатическом движении. Таким образом, можно предположить, что перенос заряженных частиц присущ солитонам любой амплитуды и является их фундаментальным свойством.

Следует отметить задачи, которые еще требуют решения. Формулу для энергии солитонов (см., например, [20]) тоже необходимо пересмотреть и учесть энергию упорядоченного движения заряженных частиц. Важным остается вопрос о функции распредления плазменных популяций в присутствии солитонов. Также полезно учесть диссипативные силы и силы, их компенсирующие в случае стационарного распространения солитонов в термодинамически открытых системах.