Теплофизика высоких температур, 2020, T. 58, № 6, стр. 856-859

ВВЕДЕНИЕ

В работе [1] сообщается об обнаружении нового физического эффекта, состоящего в увеличении высоты столба жидкости в капилляре при касании газоразрядной плазмой мениска жидкости и названного плазменным капиллярным эффектом. По данным [1], высота столба жидкости (30%-ного водного раствора медного купороса) увеличивается скачкообразно в момент искрового разряда в промежутке между игольчатым электродом и мениском жидкости, инициированного однократным высоковольтным наносекундным импульсом, и далее высота столба не изменяется, по меньшей мере, в течение нескольких часов. По мнению авторов [1], причиной подъема жидкости является электризация мениска искровым разрядом, которая приводит к увеличению смачиваемости стенок капилляра жидкостью. Однако этот вывод сделан на основе только качественного обсуждения результатов собственных наблюдений и похожих экспериментов, описанных в ряде других работ, ссылки на которые приведены в [1]. Поэтому в данной работе ставится цель обосновать предложенный в [1] механизм плазменного капиллярного эффекта на основе простой математической модели.

МОДЕЛЬ

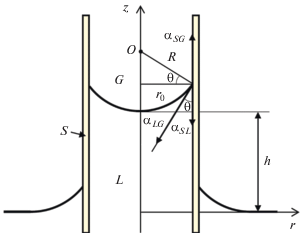
Рассматривается трехфазная система “жидкость–твердое тело (капилляр)–газ”, ограниченная стенками цилиндрического капилляра. Считается, что жидкость смачивает капилляр. В связи с этим реализуется капиллярный эффект, состоящий в поднятии жидкости в капилляре относительно основного уровня жидкости в широком сосуде, в который опущен капилляр (рис. 1).

Дополнительно учитывается, что искривленная поверхность жидкости в капилляре может быть заряжена электричеством. Мениск рассматривается в приближении заряженной поверхности “идеального” жидкого проводника, внутри которого электрическим полем пренебрегается. Применимость такого упрощенного представления наэлектризованной жидкости (воды и водных растворов) в электростатике обосновывается ее “большой” диэлектрической проницаемостью, в электрогидродинамике заряженных поверхностей – быстрой релаксацией зарядов [2]. Тогда электрическое поле со стороны газа перпендикулярно к мениску в любой его точке. В противном случае, как показывает опыт, возникает движение жидкости [2]. Равенство нулю тангенциальной составляющей поля на мениске происходит за счет обеспечивающего его эквипотенциальность распределения электрических зарядов. Такое электрическое поле приводит к перепаду электрического давления, который для вогнутого мениска эквивалентен увеличению поверхностного натяжения жидкости, вследствие чего высота столба жидкости в капилляре может увеличиться.

Стационарное устойчивое состояние рассматриваемой системы “жидкость–капилляр–газ” соответствует минимуму ее энергии, которая слагается из поверхностной энергии, потенциальной энергии столба жидкости в капилляре в однородном поле тяготения и энергии взаимодействия электрических зарядов, расположенных на эквипотенциальном мениске:

где α – коэффициент поверхностного натяжения на контактной границе с площадью $A$ двух фаз, обозначенных нижними индексами L – жидкость, S – капилляр, G – газ (рис. 1); $m$ – масса столба жидкости в капилляре; ${{h}_{{{\kern 1pt} C}}}$ – высота центра тяжести столба жидкости относительно основного уровня жидкости в широком сосуде; $q$, $C$ – сторонний электрический заряд и электроемкость мениска.

В осесимметричном приближении мениска задача минимизации энергии упрощается, если учесть в (1) условия механического равновесия вершины мениска и общей линии соприкосновения трех фаз на стенке капилляра. Для незаряженного мениска эти условия выражаются соответственно формулой Лапласа – равенства капиллярного и гидростатического давлений в вершине мениска, главные радиусы кривизны которого одинаковы, и формулой Юнга – баланса касательных к стенке капилляра составляющих сил, действующих на единичный элемент контактной линии, со стороны трех межфазных поверхностей (рис. 1). Для заряженного мениска формула Лапласа дополняется учетом электрического давления, поэтому условия механического равновесия записываются в виде

Здесь ρ – плотность жидкости (плотностью газа по сравнению с ρ пренебрегается); $h$, $R$ – высота и радиус кривизны мениска в его вершине; σ₀ – поверхностная плотность электрического заряда в вершине мениска; θ – краевой угол (рис. 1).

Видно из (2), что наличие электричества на мениске эквивалентно увеличению коэффициента поверхностного натяжения в вершине. Для оценки порядка доли увеличения ${{\alpha }_{{LG}}}$ в зависимости от электрического заряда мениск принимается полусферическим с однородным распределением $q$ на его поверхности. Тогда доля $\gamma = {{R\sigma _{0}^{2}} \mathord{\left/ {\vphantom {{R\sigma _{0}^{2}} {(4{{\varepsilon }_{0}}{\kern 1pt} {{\alpha }_{{LG}}})}}} \right. \kern-0em} {(4{{\varepsilon }_{0}}{\kern 1pt} {{\alpha }_{{LG}}})}}$ = = ${{{{q}^{2}}} \mathord{\left/ {\vphantom {{{{q}^{2}}} {(16{{\pi }^{2}}{{\varepsilon }_{0}}r_{0}^{3}{\kern 1pt} {{\alpha }_{{LG}}})}}} \right. \kern-0em} {(16{{\pi }^{2}}{{\varepsilon }_{0}}r_{0}^{3}{\kern 1pt} {{\alpha }_{{LG}}})}}$ есть отношение характерных значений электрической и поверхностной энергий заряженной полусферы, ${{r}_{0}}$ – радиус капилляра. Например, для воды в капилляре с радиусом 1 мм получается $\gamma $ ~ ${{({{10}^{9}}q)}^{2}}$, т.е. при $q$ = 1 нКл ${{\alpha }_{{LG}}}$ увеличивается (эффективно) вдвое. Поэтому далее, чтобы избежать необходимой при строгом подходе самосогласованной постановки механической и электростатической задач для столба жидкости в капилляре, электризация мениска полагается малой настолько, что вкладом электрического давления можно пренебречь в (2) и считать, что для вершины мениска $Rh = {{a}^{2}}$, $a = \sqrt {{{2{{\alpha }_{{LG}}}} \mathord{\left/ {\vphantom {{2{{\alpha }_{{LG}}}} {g{\kern 1pt} \rho }}} \right. \kern-0em} {g{\kern 1pt} \rho }}} $ – капиллярная постоянная. Формула Юнга используется для исключения ${{\alpha }_{{SG}}} - {{\alpha }_{{SL}}}$ из (1) заменой на ${{\alpha }_{{LG}}}\cos {{\theta }_{Y}}$, где θ_Y – краевой угол в случае незаряженного мениска, аналогично теории электросмачиваемости на диэлектрике (см., например, [3]). В этом случае наличие электричества на мениске учитывается только в выражении энергии (1) для рассматриваемой системы, минимум которой реализуется при некотором краевом угле θ, отличном от θ_Y.

Дальнейшее упрощение модели состоит в аппроксимации мениска сферическим сегментом, приемлемость которого обсуждается ниже. Тогда с учетом геометрических формул для неизменного радиуса кривизны $R = {{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {\cos \theta }}} \right. \kern-0em} {\cos \theta }}$ сферического сегмента, площадей межфазных поверхностей ${{A}_{{LG}}} = 2\pi {\kern 1pt} R{\kern 1pt} {{h}_{0}}$, ${{A}_{{SL}}} = 2\pi {\kern 1pt} {{r}_{0}}H$, ${{A}_{{SG}}} = {{A}_{0}} - {{A}_{{SL}}}$ (h₀ = $ = R{\kern 1pt} (1 - \sin \theta )$ – высота сегмента, $H = h + {{h}_{0}}$, ${{A}_{0}}$ – площадь внутренней поверхности капилляра), высоты ${{h}_{{{\kern 1pt} C}}}$ центра тяжести на оси осесимметричного однородного ($\rho = {\text{const}}$) столба жидкости как центра тяжести его объема $V$ из формулы $V{{h}_{C}} = {{\pi {\kern 1pt} r_{0}^{2}{{H}^{2}}} \mathord{\left/ {\vphantom {{\pi {\kern 1pt} r_{0}^{2}{{H}^{2}}} 2}} \right. \kern-0em} 2}$ – ${{V}_{0}}(h + R - {{\pi {\kern 1pt} r_{0}^{4}} \mathord{\left/ {\vphantom {{\pi {\kern 1pt} r_{0}^{4}} {4{{V}_{0}}}}} \right. \kern-0em} {4{{V}_{0}}}})$ (где V₀ = $ = \pi {\kern 1pt} h_{0}^{2}(R - {{{{h}_{0}}} \mathord{\left/ {\vphantom {{{{h}_{0}}} 3}} \right. \kern-0em} 3})$ – объем шарового сегмента) и формулы для электроемкости $C = 4{{\varepsilon }_{0}}R\,\, \times $ $ \times \,\,({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \theta + \cos \theta )$ сферического сегмента [4] выражение энергии (1) сводится к зависимости $E$ от краевого угла θ в виде

Здесь $E{\kern 1pt} ' = {{(E - {{\alpha }_{{SG}}}{{A}_{0}})} \mathord{\left/ {\vphantom {{(E - {{\alpha }_{{SG}}}{{A}_{0}})} {({{\alpha }_{{LG}}}\pi {\kern 1pt} r_{0}^{2})}}} \right. \kern-0em} {({{\alpha }_{{LG}}}\pi {\kern 1pt} r_{0}^{2})}}$ – переменная часть безразмерной энергии рассматриваемой системы; $b = {{({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} a}} \right. \kern-0em} a})}^{2}}$ = ${{\rho {\kern 1pt} g{\kern 1pt} r_{0}^{2}} \mathord{\left/ {\vphantom {{\rho {\kern 1pt} g{\kern 1pt} r_{0}^{2}} {(2{\kern 1pt} {{\alpha }_{{LG}}})}}} \right. \kern-0em} {(2{\kern 1pt} {{\alpha }_{{LG}}})}}$ – квадрат отношения радиуса капилляра к капиллярной постоянной или отношение потенциальной энергии ${{\rho {\kern 1pt} g{\kern 1pt} \pi {\kern 1pt} r_{0}^{4}} \mathord{\left/ {\vphantom {{\rho {\kern 1pt} g{\kern 1pt} \pi {\kern 1pt} r_{0}^{4}} 2}} \right. \kern-0em} 2}$ прямого кругового цилиндрического столбика жидкости с одинаковыми радиусом и высотой, равными ${{r}_{0}}$, в поле тяготения к поверхностной энергии ${{\alpha }_{{LG}}}{\kern 1pt} \pi {\kern 1pt} r_{0}^{2}$ его верхнего основания (отметим, что $b$ в два раза меньше числа Бонда).

Таким образом, задача минимизации энергии (1) сводится к поиску краевого угла θ, соответствующего минимуму функции (3).

АНАЛИЗ

В случае $b \ll 1$ выражение (3) для энергии заметно упрощается:

а ее минимум реализуется при краевом угле θ, удовлетворяющем уравнению

Видно, что θ_Y является корнем этого уравнения только для незаряженного мениска. Это означает, что приближение мениска сферическим сегментом является приемлемым при одновременном соблюдении двух условий: $b \ll 1$ и $\gamma = 0$. В частности, известная формула Жюрена ${{r}_{0}}h = {{a}^{2}}\cos {{\theta }_{Y}}$, получаемая для сферического мениска из условий механического равновесия вершины незаряженного мениска и общей линии соприкосновения трех фаз на стенке капилляра, строго говоря, не согласовывается с условием минимальности энергии (1) столба жидкости в капилляре в стационарном состоянии для сферического мениска. Тогда в качестве апостериорной оценки приемлемости аппроксимации незаряженного мениска сферическим сегментом принимается близость значения θ, соответствующего минимуму (3), к θ_Y.

Минимизация (4) в отличие от аналогичной задачи для (3) является двухпараметрической, поэтому трансцендентное уравнение (5) решается численно в интервале $\theta \in (0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2})$ при фиксированном краевом угле θ_Y для набора значений параметра $\gamma {\kern 1pt} b$. Результаты расчета приводятся на рис. 2.

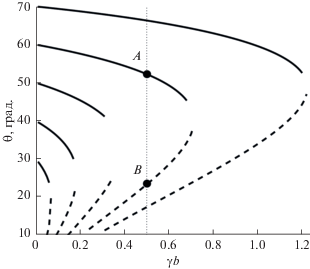
Видно из рис. 2, что существуют наборы значений параметров, при которых реализуются два экстремальных по энергии состояния трехфазной системы: устойчивые с минимумом энергии (например, состояние А – θ = 52° при $\gamma {\kern 1pt} b$ = 0.5 и θ_Y = = 60°) и неустойчивые с максимумом энергии (состояние В – θ = 23° для тех же $\gamma {\kern 1pt} b$ и θ_Y).

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Численная оценка влияния электризации мениска на высоту жидкости в капилляре проводится по экспериментальным данным [1], где до электризации мениска высота 30%-ного водного раствора медного купороса составляла примерно 6 мм в капилляре радиусом 0.85 мм, а после разрядного импульса она скачком увеличивалась на 0.5–3 мм. Коэффициент ${{\alpha }_{{LG}}}$ принимается равным 74 мН/м по данным [5]. Тогда $b$ ≈ 0.06, а краевой угол, соответствующий высоте столба до электризации, по формуле Жюрена θ_Y = 64°. Результаты расчета этих данных по формуле (3) представлены на рис. 3 в виде зависимостей $\theta (E{\kern 1pt} ')$ и $h(E{\kern 1pt} ')$ для двух значений заряда мениска.

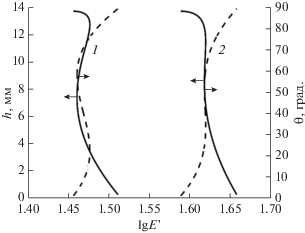
Расчет показывает, что минимуму $E{\kern 1pt} '$ трехфазной системы до электризации мениска соответствуют θ и $h$, которые практически совпадают с заданными из эксперимента значениями этих величин. Поэтому в рассматриваемом случае аппроксимация мениска сферическим сегментом приемлема.

При наличии заряда 0.5 нКл на мениске смачиваемость увеличивается: краевой угол уменьшается на 2°, а высота столба увеличивается на 0.5 мм. При этом в зависимости $E{\kern 1pt} '(\theta )$ (и $E{\kern 1pt} '(h)$ соответственно) реализуется дополнительный экстремум – локальный максимум, означающий возникновение при этих условиях второго стационарного, но неустойчивого, состояния системы. Энергия неустойчивого состояния превышает энергию устойчивого на 35%. Видно из рис. 3, что при увеличении заряда мениска до 0.8 нКл краевой угол устойчивого состояния системы становится равным 57°, высота – 7.4 мм, причем параметры устойчивого и неустойчивого состояний системы (экстремумы $E{\kern 1pt} '$) сближаются. Далее отмеченные тенденции сохраняются так, что при заряде 1 нКл θ = 51°, $h$ = 8.6 мм, а энергии состояний отличаются только на 0.3%. При $q$ > 1 нКл стационарных состояний у рассматриваемой системы уже нет.

Расчетная величина дополнительного подъема жидкости в капилляре на 2.8 мм за счет заряда на мениске согласуется с данными наблюдений [1].

Существование в рамках рассмотренной модели критического электрического заряда, при превышении которого система не имеет стационарных состояний, соответствует общей закономерности поведения заряженных поверхностей жидкостей – при существовании критического электрического поля поверхность становится неустойчивой [2]. Расчетный критический заряд не превышает заряда, падающего из плазмы на поверхность жидкости, который грубо оценивается как произведение длительности импульса на ток проводимости ∼10 А из осциллограммы тока разряда [1].

Наличием второго стационарного неустойчивого состояния можно объяснить, что в проведенных ранее [1] экспериментах регистрировалось только кратковременное увеличение смачиваемости за счет внесенного на мениск заряда в виде резких скачков высоты столба жидкости в моменты поступления импульсов тока.

ЗАКЛЮЧЕНИЕ

На основе простой математической модели стационарного состояния трехфазной системы “жидкость–капилляр–газ” продемонстрирована роль электризации мениска в механизме плазменного капиллярного эффекта. Результаты работы могут быть полезны при дальнейшей разработке теории плазменного капиллярного эффекта в рамках самосогласованной постановки механической и электростатической задач для столба жидкости в капилляре.