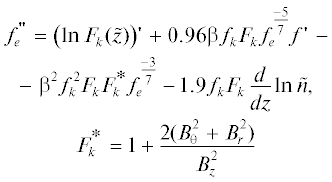Теплофизика высоких температур, 2020, T. 58, № 6, стр. 844-855
Математическая модель диффузной моды короткой сильноточной вакуумной дуги в аксиальном магнитном поле
Т. М. Сапронова 1, *, К. Н. Ульянов 1
1 Всероссийский электротехнический институт –
филиал ФГУП “Российский федеральный ядерный центр –
Всероссийский научно-исследовательский институт технической физики
им. акад. Е.И. Забабахина”
Москва, Россия
* E-mail: sapron0109@mail.ru
Поступила в редакцию 25.04.2019
После доработки 19.02.2020
Принята к публикации 10.03.2020
Аннотация
Развита теория диффузной моды аксиально-симметричной короткой сильноточной вакуумной дуги во внешнем аксиальном магнитном поле. Получено дифференциальное уравнение второго порядка в частных производных для линий уровней тока разряда (2D-модель). Сформулированы граничные условия на катодной и анодной границах плазмы. Решение этого уравнения с учетом уравнения баланса тепла для электронов и уравнения для концентрации плазмы позволяет определить зависимости линий тока от координат. С помощью этих линий по полученным аналитическим формулам могут быть рассчитаны компоненты плотности тока, магнитного поля, а также распределения температуры электронов и концентрации плазмы в разрядном промежутке. Предложена и обоснована (1.5D) математическая модель (jr $ \ll $ jz), которая существенно упрощает расчеты и имеет достаточно широкие пределы применимости. При проведении расчетов по этой модели использовался метод последовательных приближений, который обеспечил получение результатов с необходимой точностью. Рассчитаны распределения компонентов магнитного поля Br, Bθ, Bz, плотности тока (jr, jz, jθ), распределения температуры электронов и концентрации электронов и ионов в плазме вакуумной дуги.
ВВЕДЕНИЕ
В настоящей работе авторы рассматривают диффузную моду вакуумной дуги (ВД) с большим количеством катодных пятен, которая реализуется в аксиальном магнитном поле в разрядном промежутке с электродами из Cu50Cr50. Именно эта форма ВД с таким материалом электродов находит широкое практическое применение. Разработана математическая модель диффузной моды аксиально-симметричной короткой сильноточной вакуумной дуги во внешнем аксиальном магнитном поле B0 с учетом магнитных полей, создаваемых аксиальным током дуги (Bθ) и током Холла ($B_{z}^{{\text{H}}},B_{r}^{{\text{H}}}$). При отсутствии внешнего магнитного поля B0 плазма дуги под действием силы Ампера jzBθ поляризуется в поперечном току направлении, возникает большое радиальное электрическое поле Er и радиальное падение потенциала φ(r)–φ0. В теории сильноточных разрядов высокого давления (z-пинч) сила jzBθ компенсируется радиальным компонентом градиента давления [1]. В ВД низкой плотности (ne = Zni = 3.6 × 1020 м–3 для плотности тока разряда j = 107 А/м2) такая компенсация при больших токах невозможна [2]. Падение напряжения между центром и внешней границей R плазмы и электродов при jz = const имеет вид φ(R) – φ(0) = 17I В, где ток в килоамперах. Например, при I = 50 кА φ(R) – φ(0) = 850 В. Это значение на два порядка превышает как напряжение на плазме разряда, так и радиальную разность потенциалов, связанную с радиальным градиентом давления. Поэтому при B0 = 0 диффузная мода ВД может существовать только при небольших токах (до нескольких килоампер [3]), а сильноточная ВД при больших токах существует в контрагированной моде при гораздо более высоком давлении (порядка атмосферного). При наличии внешнего аксиального поля B0 ситуация меняется кардинальным образом. В плазме ВД реализуется режим протекания тока, при котором его линии наклонены относительно оси. Возникает радиальный ток jr, взаимодействие которого с полем Bθ генерирует азимутальный ток Холла jθ. При этом сила jθBz практически полностью уравновешивает силу jzBθ (пинч-эффект), величина радиального электрического поля снижается до значений, при которых возможен режим протекания большого тока с эквипотенциальным анодом. Таким образом, в сильноточной ВД с аксиальным магнитным полем действует принцип глубокой компенсации радиальных магнитных сил. Именно по этой причине математические модели диффузной моды аксиально-симметричной сильноточной ВД должны быть двумерными. Они должны учитывать три компоненты плотности тока (jr, jz, jθ), три компоненты магнитного поля (Br, Bz, Bθ) и две компоненты электрического поля (Er, Ez), компонента Eθ = 0. Такие модели были разработаны [2–9], они применялись для расчета различных режимов диффузной сильноточной ВД. Эти модели основаны на различных математических подходах, они по-разному учитывают влияние собственного магнитного поля тока ВД. Например, в [4, 5, 7, 8] в расчет принимались только Bθ и B0, магнитное поле тока Холла BH не учитывалось. В работах [2, 3] магнитное поле Холла учитывалось, однако не вполне корректно рассчитывалось анодное падение. В частности, для его определения использовалась формула Ленгмюра, область применимости которой ограниченна. В дальнейшем оказалось, что эта формула неприменима для анодного падения ВД [10].
При расчете параметров плазмы ВД для определения зависимости температуры электронов от координат необходимо использовать баланс энергии электронов. В настоящей работе показано, что в этом балансе коэффициенты теплопроводности и электропроводности для электронов зависят от магнитного поля. Наличие аксиального (продольного) поля B0 и поперечных полей Br и Bθ существенным образом влияет как на эти коэффициенты, так и на распределения температуры электронов в разрядном промежутке. Рост B0 увеличивает значения коэффициентов теплопроводности и электропроводности, а увеличение поперечных полей Br и Bθ уменьшают эти коэффициенты. В опубликованных работах этот фактор не принимается во внимание.
В настоящей работе для плазмы короткой сильноточной ВД разработаны две математические модели (2D и 1.5D), которые позволяют произвести расчет параметров плазмы ВД. Получены распределения компонентов плотности тока, магнитного поля, концентрации и распределения электронной температуры в плазме ВД с учетом зависимости коэффициентов теплопроводности и электропроводности от компонентов магнитного поля.
2D МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Рассмотрим ВД с большим количеством катодных пятен в аксиальном магнитном поле. Из катодных пятен в направлении анода вылетают струи полностью ионизованной плазмы с широким угловым распределением [5, 6]. При движении к аноду происходит пересечение струй отдельных факелов. На некотором (небольшом) расстоянии от катода находится стартовая плоскость, начиная с которой плазму можно рассматривать как однородную сплошную среду. В промежутке катод–стартовая плоскость плазма дискретна. Стартовая плоскость является катодной границей плазмы. На этой границе имеется круговая область, из которой в направлении анода истекает плазма, состоящая из электронов и быстрых катодных ионов со средним зарядом Z . Поскольку ток ионов ВД на порядок меньше тока электронов, то при расчете магнитных полей пренебрегаем ионным током.
Рассмотрим движение электронов в цилиндрической системе координат во внешнем магнитном поле Bz с учетом магнитных полей, создаваемых током дуги I. Ось z направлена к аноду, система координат (r, θ, z) – правая. Уравнение движения электронов в магнитогидродинамическом приближении имеет вид [1]
(1)
$m{{n}_{e}}\frac{{d{{V}_{{e\alpha }}}}}{{dt}} = - \frac{{\partial {{p}_{e}}}}{{\partial {{x}_{\alpha }}}} - e{{n}_{e}}\left( {{{E}_{\alpha }} + \frac{1}{c}{{{\left[ {{{{\bar {V}}}_{e}}\bar {B}} \right]}}_{\alpha }}} \right) + \frac{{{{j}_{{e\alpha }}}}}{\sigma }.$Здесь Ve – скорость, pe – давление, ne – концентрация электронов, σ – электропроводность плазмы. Электроны в плазме замагничены, ларморовский радиус электронов на два–три порядка меньше характерных размеров плазмы, поэтому в (1) можно пренебречь [1] инерцией электронов (левой частью (1)). Тогда для компонентов электрического поля Eα имеем
Поскольку Eθ = 0, то можно записать выражение для плотности тока Холла
Параметр Холла в замагниченной плазме ВД βH = Bzσ/cene = ωeτei $ \gg $ 1. Исключая jθ из выражений для Еr и Еz, имеем
(2)
${{E}_{r}} = \frac{{{{j}_{r}}}}{\sigma }\left( {1 + \beta _{{\text{H}}}^{2}} \right) - \frac{{{{j}_{z}}}}{\sigma }\left( {{{\beta }_{{\text{H}}}}\frac{{{{B}_{\theta }}}}{{{{B}_{z}}}} + \beta _{{\text{H}}}^{2}\frac{{{{B}_{r}}}}{{{{B}_{z}}}}} \right) - \frac{1}{{e{{n}_{e}}}}\frac{{\partial {{p}_{e}}}}{{\partial r}},$(3)
${{E}_{z}} = \frac{{{{j}_{z}}}}{\sigma }\left( {1 + \beta _{{\text{H}}}^{2}\frac{{B_{r}^{2}}}{{B_{z}^{2}}}} \right) + \frac{{{{j}_{r}}}}{\sigma }\left( {{{\beta }_{{\text{H}}}}\frac{{{{B}_{\theta }}}}{{{{B}_{z}}}} - \beta _{{\text{H}}}^{2}\frac{{{{B}_{r}}}}{{{{B}_{z}}}}} \right) - \frac{1}{{e{{n}_{e}}}}{\kern 1pt} \frac{{\partial {{p}_{e}}}}{{\partial z}}.$Введем новую переменную I – ток вакуумной дуги:
Дифференцируя (4) по r и учитывая непрерывность линий тока div j = 0, получим выражения для jr и jz:
(5)
${{j}_{r}} = - \frac{1}{{2\pi r}}\frac{{\partial I}}{{\partial z}},\,\,\,\,{{j}_{z}} = \frac{1}{{2\pi r}}\frac{{\partial I}}{{\partial r}}.$Из уравнений (2) и (3) можно исключить jr , jz и получить выражения для Еr и Еz , в которые входят только ток I(r, z) и давление электронов pe. Имеем
(6)
$\begin{gathered} {{E}_{r}} = - \frac{{1 + \beta _{{\text{H}}}^{2}}}{{2\pi \sigma r}}\frac{{\partial I}}{{\partial z}} - \\ - \,\,\frac{{{{\beta }_{{\text{H}}}}}}{{2\pi \sigma r}}\left( { - \frac{{{{B}_{\theta }}}}{{{{B}_{z}}}} + {{\beta }_{{\text{H}}}}\frac{{{{B}_{r}}}}{{{{B}_{z}}}}} \right)\frac{{\partial I}}{{\partial r}} - \frac{1}{{e{{n}_{e}}}}\frac{{\partial {{p}_{e}}}}{{\partial r}}, \\ \end{gathered} $(7)
$\begin{gathered} {{E}_{z}} = \frac{1}{{2\pi \sigma r}}\left( {1 + \beta _{{\text{H}}}^{2}\frac{{B_{r}^{2}}}{{B_{z}^{2}}}} \right)\frac{{\partial I}}{{\partial r}} + \\ + \,\,\frac{{{{\beta }_{{\text{H}}}}}}{{2\pi \sigma r}}\left( {\frac{{{{B}_{\theta }}}}{{{{B}_{z}}}} + {{\beta }_{{\text{H}}}}\frac{{{{B}_{r}}}}{{{{B}_{z}}}}} \right)\frac{{\partial I}}{{\partial z}} - \frac{1}{{e{{n}_{e}}}}\frac{{\partial {{p}_{e}}}}{{\partial z}}. \\ \end{gathered} $Используем уравнение rot E = 0
Продифференцируем (6) по z, (7) по r, приравняем производные и получим уравнение второго порядка в частных производных для определения линий уровня тока I(r, z). Перейдем к безразмерным переменным $\tilde {I} = {I \mathord{\left/ {\vphantom {I {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}},$ $\tilde {r} = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R},$ $\tilde {z} = {z \mathord{\left/ {\vphantom {z L}} \right. \kern-0em} L}$, где R – радиус электродов, L – расстояние между ними. Значение I0 задается произвольно, например I0 = 40 кА. Тогда
(8)
$\begin{gathered} {{a}_{1}}\frac{{{{\partial }^{2}}\tilde {I}}}{{\partial {{{\tilde {z}}}^{2}}}} + {{a}_{2}}\frac{{{{\partial }^{2}}\tilde {I}}}{{\partial {{{\tilde {r}}}^{2}}}} + {{a}_{3}}\frac{{{{\partial }^{2}}\tilde {I}}}{{\partial{ \tilde {r}}\partial{ \tilde {z}}}} + \frac{{\partial{ \tilde {I}}}}{{\partial{ \tilde {r}}}}\left( {\frac{{\partial {{a}_{2}}}}{{\partial{ \tilde {r}}}} + \frac{{\partial {{b}_{2}}}}{{\partial{ \tilde {z}}}}} \right) + \\ + \,\,\frac{1}{{\tilde {r}}}\left( {{{b}_{1}}\frac{{\partial{ \tilde {I}}}}{{\partial{ \tilde {z}}}} - {{a}_{2}}\frac{{\partial{ \tilde {I}}}}{{\partial{ \tilde {r}}}}} \right) + \frac{{\partial{ \tilde {I}}}}{{\partial{ \tilde {z}}}}\left( { - \frac{{\partial {{b}_{1}}}}{{\partial{ \tilde {r}}}} + \frac{{\partial {{a}_{1}}}}{{\partial{ \tilde {z}}}}} \right) + \\ + \,\,c\tilde {r}\left( {\frac{{\partial {{{\tilde {T}}}_{e}}}}{{\partial{ \tilde {z}}}}\frac{{\partial {{p}_{e}}}}{{\partial{ \tilde {r}}}} - \frac{{\partial {{{\tilde {T}}}_{e}}}}{{\partial{ \tilde {r}}}}\frac{{\partial {{p}_{e}}}}{{\partial{ \tilde {z}}}}} \right) = 0, \\ \end{gathered} $Граничные условия для уравнения (8) задаются на катодной и анодной границах плазмы. Катодную границу можно считать эквипотенциальной, поскольку все катодные факелы идентичны (токи в них одинаковые). Такое граничное условие применяется во всех ранее опубликованных теоретических работах. Поэтому φ(0) = 0, Er(0) = 0. На анодной границе плазмы потенциал φпл(L) = = φa – Ua. На катодной границе необходимо задать распределения тока jr(r, 0), jz(r, 0). Следует отметить, что радиальные электрические силы и силы, связанные с радиальным градиентом электрического давления, на два порядка меньше радиальных магнитных сил jθBz и jzBθ [11]. В этом случае между компонентами плотности тока jr и jz имеет место соотношение
Зависимость Ez(z) определяется формулой (3). Таким образом, в плоскости z = 0 задается распределение jz(r, 0). После этого из (8) в заданном магнитном поле Bz(r, z) и Br(r, z) в промежутке находятся распределения линий уровня тока, распределения плотности тока (5), электрического поля Е(r, z) и потенциала, а также распределение концентрации плазмы. При этом распределение потенциала на аноде может зависеть от координаты r. Полученные зависимости магнитных полей от тока I(r, z), а также от тока Холла jθ(r, z) позволяют рассчитать распределения новых магнитных полей Br, Bz, Bθ в промежутке. С этим распределением полей расчет повторяется. Решение находится методом последовательных приближений. Распределение jz(r) изменяется до тех пор, пока потенциал на аноде не перестанет зависеть от координаты, а распределение параметров плазмы и магнитных полей установятся. При наличии внешнего магнитного поля Br и Bz линии тока наклонены к оси. Взаимодействие jr с Bz и jz с Br приводит к появлению тока Холла jθ, выражение для которого может быть записано в виде
(9)
$\begin{gathered} {{j}_{\theta }} = {{j}_{{z{\text{ср}}}}}f(r)\left( {\frac{{{{B}_{\theta }}}}{{{{B}_{z}}}} + \frac{{{{B}_{r}}}}{{{{B}_{z}}{{\beta }_{{\text{H}}}}}}} \right){{\left( {1 + \beta _{{\text{H}}}^{{ - 2}}} \right)}^{{ - 1}}}, \\ {{B}_{\theta }} = - \frac{{{{\mu }_{0}}I}}{{\pi R\tilde {r}}}\int\limits_0^{\tilde {r}} {f(\tilde {r})\tilde {r}d\tilde {r}} ,\,\,\,\,{{j}_{{z{\text{ср}}}}} = \frac{I}{{\pi {{R}^{2}}}}. \\ \end{gathered} $Для расчета компонентов магнитного поля тока Холла $B_{r}^{{\text{Н}}}$ и $B_{z}^{{\text{Н}}}$ плазма ВД разбивается на кольца равноотстоящими цилиндрическими поверхностями вокруг оси z и равноотстоящими параллельными плоскостями, перпендикулярными оси z. По этим кольцам течет ток Холла. В плоскости r, z образуется система из M × N прямоугольников, каждый из которых является сечением кольца. При достаточно большом числе колец плотность азимутального тока в каждом из них можно считать постоянной, а сами кольца тонкими. Для азимутального тока каждого кольца можно записать Iθik = jθikhrhz, где hr = Δr и hz = Δz – радиальный и аксиальный размеры кольца. Для компонентов $B_{r}^{{\text{Н}}}$ и $B_{z}^{{\text{Н}}}$ магнитного поля тонкого кольца используем известные аналитические формулы [12]
(10)
$\begin{gathered} B_{{zik}}^{{\text{H}}}({{r}_{p}},{{z}_{p}}) = \frac{1}{{2\pi }}\frac{{{{\mu }_{0}}{{I}_{{\theta ik}}}}}{{\sqrt {{{{({{r}_{p}} + {{r}_{{ik}}})}}^{2}} + {{{({{z}_{p}} - {{z}_{i}})}}^{2}}} }} \times \\ \times \,\,\left[ {K(q) + \frac{{r_{{ik}}^{2} - r_{p}^{2} - {{{({{z}_{p}} - {{z}_{i}})}}^{2}}}}{{{{{({{r}_{{ik}}} - {{r}_{p}})}}^{2}} + {{{({{z}_{p}} - {{z}_{i}})}}^{2}}}}E(q)} \right], \\ \end{gathered} $(11)
$\begin{gathered} B_{{rik}}^{{\text{H}}}({{r}_{p}},{{z}_{p}}) = \frac{{{{z}_{p}} - {{z}_{i}}}}{{2\pi {{r}_{p}}}}\frac{{{{\mu }_{0}}{{I}_{{\theta ik}}}}}{{\sqrt {{{{({{r}_{p}} + {{r}_{{ik}}})}}^{2}} + {{{({{z}_{p}} - {{z}_{i}})}}^{2}}} }} \times \\ \times \,\,\left[ { - K(q) + \frac{{r_{{ik}}^{2} + r_{p}^{2} + {{{({{z}_{p}} - {{z}_{i}})}}^{2}}}}{{{{{({{r}_{{ik}}} - {{r}_{p}})}}^{2}} + {{{({{z}_{p}} - {{z}_{i}})}}^{2}}}}E(q)} \right], \\ \end{gathered} $(12)
$\begin{gathered} {{I}_{{\theta ik}}} = {{j}_{\theta }}({{r}_{k}},{{r}_{i}}){{h}_{r}}{{h}_{z}}, \\ K(q) = \int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{{(1 - q{{{\sin }}^{2}}\theta )}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}} d\theta , \\ E(q) = \int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{{(1 - q{{{\sin }}^{2}}\theta )}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} d\theta , \\ q = \frac{{4{{r}_{{ik}}}{{r}_{p}}}}{{{{{({{r}_{{ik}}} + {{r}_{p}})}}^{2}} + {{{({{z}_{p}} - {{z}_{i}})}}^{2}}}}. \\ \end{gathered} $1.5D МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Рассмотрим более простую модель, в которой jr $ \ll $ jz. В этой модели магнитные поля имеют три компонента Br, Bz, Bθ, зависящие от r, z. Поле Bz является суммой внешнего аксиального магнитного поля и магнитного поля тока Холла, поле Br создается током Холла. Поле Bθ создается азимутальным током дуги. Линии уровня плотности тока в такой модели практически параллельны оси z, угол наклона этих линий к оси δ $ \ll $ 1. Связь между плотностью тока j и jz при jr $ \ll $ jz определяется соотношением j = jz(1 + ${{j_{r}^{2}} \mathord{\left/ {\vphantom {{j_{r}^{2}} {j_{z}^{2}}}} \right. \kern-0em} {j_{z}^{2}}}$)1/2 ≈ jz(1 + $0.5{{j_{r}^{2}} \mathord{\left/ {\vphantom {{j_{r}^{2}} {j_{z}^{2}}}} \right. \kern-0em} {j_{z}^{2}}}$). В результатах расчетов максимальное значение отношения jr/jz меньше 0.135, тогда отношение jz/j больше 0.99. Отметим, что линии тока практически параллельны оси z. Таким образом, в 1.5D-модели можно принять, что j = jz, и считать плотность тока не зависящей от z. В такой модели расчет распределения плотности тока по радиусу существенно упрощается, поскольку это распределение не будет зависеть от z. Разобьем плазму ВД в плоскости (r, z) на клетки таким же образом, как при расчете магнитного поля тока Холла. Индекс k нумерует клетки по r, индекс i – по z. Тогда, интегрируя электрическое поле Ezk по z и учитывая анодное падение Ua, получим напряжение U0 между катодной границей плазмы и анодом:
(13)
$\begin{gathered} {{E}_{{zk}}} = E_{{zk}}^{\sigma } - \frac{1}{{e{{n}_{e}}}}\frac{{\partial {{p}_{e}}}}{{\partial z}},\,\,\,\,E_{{zk}}^{\sigma } = - \frac{{{{j}_{{{\text{ср}}}}}{{f}_{k}}}}{{\sigma (0)t_{e}^{{\frac{3}{2}}}}}F, \\ {{F}_{\kappa }} = 1 + \frac{{B_{{\theta \kappa }}^{2}(z) + B_{{r\kappa }}^{2}(z)}}{{B_{{z\kappa }}^{2}(z)}}\frac{{\beta _{{\text{H}}}^{2}}}{{1 + \beta _{{\text{H}}}^{2}}}, \\ {{U}_{0}} = \varphi (L) - \varphi (0) = \int\limits_0^L {E_{{zk}}^{\sigma }(z)dz} + {{U}_{a}} + \\ + \,\,\frac{{\kappa ({{T}_{e}}(z) - {{T}_{e}}(0))}}{e} + Un,{\text{ }}Un = \int\limits_0^z {\frac{{\kappa {{T}_{e}}(z)}}{e}\ln {{n}_{e}}dz} , \\ \end{gathered} $(14)
$\begin{gathered} {{U}_{0}} = E{\text{*}}{{h}_{z}}{{f}_{k}}\sum\limits_{i = 1}^{nz} {{{F}_{{ki}}}(z){{{({{t}_{{eki}}}(z))}}^{{\frac{{ - 3}}{2}}}} + } \\ + \,\,{{U}_{{ak}}} + \frac{{k{{T}_{e}}(0)}}{e}\left( {{{t}_{{ek}}}(1) - 1} \right) + Un, \\ {{\omega }_{e}} = \frac{{e{{B}_{z}}}}{{mc}} = 1.76 \times {{10}^{7}}{{B}_{z}}, \\ {{\tau }_{{ei}}} = \frac{{3.5 \times {{{10}}^{4}}}}{{{{(\lambda } \mathord{\left/ {\vphantom {{(\lambda } {10)}}} \right. \kern-0em} {10)}}}}\frac{{{{{({{T}_{e}}(0)eВ)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{{{Z}_{i}}{{n}_{e}}}}t_{e}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}},\,\,\,\,{{f}_{k}} = \frac{{{{j}_{z}}({{r}_{k}})}}{{{{j}_{{{\text{ср}}}}}}} \\ E* = \frac{I}{{\pi {{R}^{2}}\sigma (0)}} = \frac{{{{j}_{{{\text{ср}}}}}}}{{\sigma (0)}},\,\,\,\,{{U}_{k}} = {{U}_{0}}\,\,{\text{при}}\,\,{{f}_{k}} = {{f}_{0}}. \\ \end{gathered} $Отметим, что первый член в правой части (14) – это омическое падение напряжения на плазме, второй член – анодное падение, третий и четвертый члены получены при интегрировании по z члена с градиентом давления. При этом учтено, что
Второй член в правой части не вносит существенного вклада в U0, поскольку скорость потока быстрых ионов, движущихся от стартовой плоскости к аноду, мало меняется. Тем не менее в расчетах этот член будет учитываться.
Функция fk(r), подбираемая с учетом выполнения условия U0 = сonst, является отношением плотности тока при заданном k к средней плотности тока jср. В уравнение (14) входит анодное падение Ua, которое зависит от отношения направленной скорости электронов v0 к тепловой vТ на анодной границе плазмы, температуры электронов на катодной (Те(0)) и анодной (Те(0)tek(1)) границах плазмы. Таким образом, одновременно с решением (14) необходимо для каждого значения fk(r) решать уравнение баланса энергии электронов, вычислять анодное падение, относительную электронную температуру tek(1), а также относительную концентрацию плазмы $\tilde {n} = {{n(L)} \mathord{\left/ {\vphantom {{n(L)} {n(0)}}} \right. \kern-0em} {n(0)}}$ на анодной границе.
ОТРИЦАТЕЛЬНОЕ АНОДНОЕ ПАДЕНИЕ
Теория отрицательного анодного падения развита в [10]. При малых отношениях направленной скорости к тепловой v0/vT ≈ 10–2 отрицательное анодное падение согласуется с рассчитанным по формуле Ленгмюра Ua = –(κTe/e) ln(v0/vT), которая ранее использовалась для расчета Ua всеми авторами. При v0/vT ≥ 0.1 различие существенно. Показано, что с ростом v0/vT значение Ua монотонно приближается к нулю, оставаясь отрицательным. Для расчета Ua в [10] получены аналитические выражения. Результаты расчетов ηa = eφa/κTe приведены в табл. 1. Там же для сравнения представлены значения ηL, рассчитанные по формуле Ленгмюра. Отметим, что ηL = 0 при v0/vT = 0.25, а при больших значениях v0/vT анодное падение становится положительным (в этом случае формулой Ленгмюра пользоваться нельзя). При расчете Ua были использованы значения ηa, приведенные в табл. 1.
Таблица 1.
Зависимость анодного падения ηa и ηL от параметра v0/vT
| v0/vT | 0.005 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| ηa | –3.93 | –3.25 | –2.6 | –2.22 | –1.96 | –1.76 | –1.61 | –1.48 | –1.37 | –1.27 |
| ηL | –3.91 | –3.21 | –2.52 | –2.12 | –1.83 | –1.61 | –1.43 | –1.27 | –1.14 | –1.02 |
| v0/vT | 0.1 | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| ηa | –1.19 | –0.698 | –0.564 | –0.466 | –0.331 | –0.245 | –0.188 | –0.148 | –0.119 | –0.098 |
| ηL | –0.909 | –0.223 | 0 | – | – | – | – | – | – | – |
Анодное падение для паров меди может быть рассчитано по формулам
Для меди доля ионного тока γ = 0.08.
БАЛАНС ЭНЕРГИИ ЭЛЕКТРОНОВ В МАГНИТНОМ ПОЛЕ
Запишем баланс энергии в виде баланса тепла [1]
(15)
$\frac{3}{2}{{n}_{e}}{{V}_{e}}\frac{{d\kappa {{T}_{e}}}}{{dz}} + {{n}_{e}}\kappa T\frac{{d{{V}_{e}}}}{{dz}} = - \frac{{d{{q}_{e}}}}{{dz}} + {{Q}_{e}}.$Отношение ${{W}_{{{\text{el}}}}}$ к джоулеву нагреву j2/σ(0) = = 3γ2κTe/(1 + γ)2mi$V_{i}^{2}$ = 3 × 10–4 (при εi = 70 эВ, κTe = 3 эВ). В выражении для ${{Q}_{e}}$ пренебрежем упругими потерями. В балансе тепла для электронов учитывались джоулев нагрев электронов при столкновении с ионами, конвективный перенос тепла на анод, а также перенос тепла электронной теплопроводностью на катодную границу плазмы. При записи баланса тепла предполагалось, что j = jz, пренебрегалось поперечной теплопроводностью. В рассматриваемой задаче ${{\kappa }_{{e \bot }}}$/${{\kappa }_{{e\parallel }}}$ = = F(r, z)$\beta _{{\text{H}}}^{{ - 2}}$ $ \ll $ 1. Расчеты показали, что при внешнем аксиальном магнитном поле B0 = 2.5 мТл/кА и конфигурации плазмы R = 6 см, L = 3 см максимальное значение этого отношения – 0.01, а минимальное – 10–4.
В магнитном поле, имеющем продольную составляющую Bz, поперечные составляющие Bθ и Br, выражение для электропроводности имеет вид σe = σ(0)$t_{e}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}$F–1. С учетом закона Видемана–Франца, связывающего коэффициенты теплопроводности $\kappa _{e}^{*}$ и электропроводности σe для полностью ионизованной плазмы соотношением $\kappa _{e}^{*}$/σe = (4κ2Te)/e2, коэффициент теплопроводности может быть записан в виде $\kappa _{e}^{*}$ = $\kappa {\text{*}}\left( 0 \right)t_{e}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}{{F}^{{ - 1}}}$, где κ*(0) – коэффициент теплопроводности на нижней границе плазмы при te(0) = 1. Таким образом, оба коэффициента зависят от отношения суммы квадратов поперечных полей к квадрату продольного поля.
Перейдем к безразмерным переменным:
Нормировочные коэффициенты Te(0) и d можно выбирать произвольно. Для функции ${{f}_{e}}(z)$ получим нелинейное дифференциальное уравнение второго порядка
с граничными условиями ${{f}_{e}}(0) = {2 \mathord{\left/ {\vphantom {2 7}} \right. \kern-0em} 7}$, $f_{e}^{'}(1) = 0$. Здесь(17)
$\begin{gathered} {{t}_{e}} = {{\left( {\frac{7}{2}{{f}_{e}}} \right)}^{{\frac{2}{7}}}},\,\,\,\,\beta = \frac{{{{j}_{{{\text{ср}}}}}L}}{{j{\text{*}}d}}, \\ j* = {{\left( {\frac{7}{2}} \right)}^{{\frac{3}{{14}}}}}{{\left( {\frac{{\sigma (0)\kappa {\text{*}}(0){{T}_{e}}(0)}}{{{{d}^{2}}}}} \right)}^{{\frac{1}{2}}}}. \\ \end{gathered} $РАСПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ ИОНОВ В ПЛАЗМЕ ВД
Распределение концентрации ионов находится из уравнения движения [1]
(18)
$\begin{gathered} {{m}_{i}}{{n}_{i}}{{v}_{i}}\frac{{d{{v}_{i}}}}{{dz}} = - \frac{{d{{p}_{i}}}}{{dz}} - eZ{{n}_{i}}\left( {{{E}_{z}} + {{{\left[ {{{{\bar {v}}}_{i}}\bar {B}} \right]}}_{z}}} \right) + {{R}_{{ie}}}, \\ {{R}_{{ie}}} = - {{R}_{{ei}}} = {{ - e{{n}_{e}}{{j}_{e}}} \mathord{\left/ {\vphantom {{ - e{{n}_{e}}{{j}_{e}}} {{{\sigma }_{e}}.}}} \right. \kern-0em} {{{\sigma }_{e}}.}} \\ \end{gathered} $Электрическое поле в плазме Ez имеет вид (13). Подставив Ez в уравнение (18), получим
(19)
$\begin{gathered} {{m}_{i}}{{n}_{i}}{{v}_{i}}\frac{{d{{v}_{i}}}}{{dz}} = - \frac{{d({{p}_{i}} + {{p}_{e}})}}{{dz}} - \\ - \,\,eZ{{n}_{i}}E{\text{*}}t_{e}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}{{f}_{k}}\left( {{{F}_{k}}({{r}_{k}},z) - 1} \right). \\ \end{gathered} $Оценим tа для ионов меди (me/mi = 10–5, Vi = 1.5 × × 106 см/с, κTe(0) = 3 эВ, κTi(0) = 0.2 эВ). При L = = 1 см tа = 1.3, при L = 3 см tа = 1.9. Таким образом, температура ионов на аноде на порядок меньше температуры электронов, и давлением ионов можно пренебречь.
Введем безразмерные переменные ${{\tilde {n}}_{i}} = {{{{n}_{i}}} \mathord{\left/ {\vphantom {{{{n}_{i}}} {{{n}_{i}}}}} \right. \kern-0em} {{{n}_{i}}}}(0),$ ${{\tilde {v}}_{{iz}}} = {{{{v}_{{iz}}}} \mathord{\left/ {\vphantom {{{{v}_{{iz}}}} {{{v}_{{iz}}}(0)}}} \right. \kern-0em} {{{v}_{{iz}}}(0)}},$ $\tilde {z} = {z \mathord{\left/ {\vphantom {z L}} \right. \kern-0em} L}.$ Для ${{\tilde {n}}_{{iz}}}$ получим
(20)
$\begin{gathered} \frac{{d{{{\tilde {n}}}_{i}}}}{{d\tilde {z}}} = \tilde {n}_{i}^{3}\left( {{{a}_{1}}\frac{{d{{t}_{e}}}}{{d\tilde {z}}} + {{a}_{2}}t_{e}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}\left( {F(r,\tilde {z}) - 1} \right)} \right){{\left( {1 - {{a}_{1}}{{t}_{e}}\tilde {n}_{i}^{2}} \right)}^{{ - 1}}}, \\ {{a}_{1}} = \frac{{\kappa Z{{T}_{e}}(0)}}{{{{m}_{i}}v_{i}^{2}(0)}},\,\,\,\,{{a}_{2}} = \frac{{eZE{\text{*}}L}}{{{{m}_{i}}v_{i}^{2}(0)}}. \\ \end{gathered} $РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
При проведении расчетов предполагалось, что в плазме ВД средний заряд иона меди Z = 1.8. Энергия электронов на катодной границе плазмы κTe(0) = 3 эВ, энергия ионов εi(0) = 70 эВ. Для заданных значений тока дуги I и однородного аксиального магнитного поля B0 c использованием 1.5D-модели подбиралось распределение jzk(r) = = fk jср. Задавалось значение f0 для k = 0, после чего рассчитывалось напряжение U0 с помощью уравнения (14). При этом вычислялось анодное падение и решались уравнение баланса энергии электронов (16) для определения te(r, z) и уравнение (20) для определения $\tilde {n}(r,z)$. Первый расчет проводился в поле B0 без учета магнитного поля тока Холла при $\tilde {n} = 1$. На оси Br = Bθ = 0, поэтому F0i = 1. Такие расчеты проводились для всех значений k, после чего определялись зависимости fk(r), $\tilde {n}(r,z)$, te(r, z) и вычислялся интеграл в (14). Затем производился расчет Bθ и jθ по (9), а также расчет компонентов магнитного поля тока Холла по (10)–(12). Поскольку первое значение f0 задавалось произвольно, то значение интеграла отличалось от 0.5. Таким образом, в первом приближении определены $B_{z}^{{\text{Н}}}$ и $B_{r}^{{\text{Н}}}$. Следующее приближение f(r) рассчитывается с тем же значением f0 с учетом всех компонентов магнитного поля и с полученными значениями $\tilde {n}(r,z)$ и te(r, z). Определяется новое значение интеграла. Эта процедура повторяется пока значения $B_{z}^{{\text{Н}}}$, $B_{r}^{{\text{Н}}}$, f(r) не установятся. Расчеты повторялись до тех пор, пока интеграл не будет отличаться от 0.5 на две-три единицы в третьем знаке, а значения $\tilde {n}(r,z)$ и te(r, z) установятся. Для улучшения сходимости приближений использовался метод регуляризации А.Н. Тихонова. Применение метода последовательных приближений позволяет решать уравнения для te (16) и $\tilde {n}$ (20) независимо, поскольку при их решении в правой части использовались компоненты магнитного поля и значения $\tilde {n}(r,z)$ и te(r, z) из предыдущего приближения.
В обширной литературе по ВД широко используется приведенное магнитное поле, равное отношению B/I в единицах мТл/кА, поэтому ниже результаты расчетов магнитных полей приводятся в этих единицах. Расчеты были выполнены для трех значений приведенного внешнего аксиального магнитного поля B0 = 1.5, 2.5, 4.0 мТл/кА, двух конфигураций плазмы R = 6 см, L = 1, 3 см. Результаты расчетов приведены в табл. 2–6 и на рис. 1–8 при I = 40 кА.
Таблица 2.
Значения $B_{z}^{{\text{Н}}}$, мТл/кА
| k | i | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | –1.48 | –1.64 | –1.76 | –1.85 | –1.90 | –1.91 | –1.90 | –1.85 | –1.76 | –1.64 | –1.48 |
| 1 | –1.43 | –1.58 | –1.69 | –1.77 | –1.82 | –1.84 | –1.82 | –1.77 | –1.69 | –1.58 | –1.43 |
| 2 | –1.33 | –1.47 | –1.58 | –1.65 | –1.70 | –1.71 | –1.70 | –1.65 | –1.58 | –1.47 | –1.33 |
| 3 | –1.21 | –1.33 | –1.43 | –1.49 | –1.53 | –1.55 | –1.53 | –1.49 | –1.43 | –1.33 | –1.21 |
| 4 | –1.05 | –1.16 | –1.24 | –1.30 | –1.33 | –1.35 | –1.33 | –1.30 | –1.24 | –1.16 | –1.05 |
| 5 | –0.87 | –0.96 | –1.03 | –1.08 | –1.11 | –1.16 | –1.11 | –1.08 | –1.03 | –0.96 | –0.87 |
| 6 | –0.68 | –0.74 | –0.80 | –0.83 | –0.85 | –0.86 | –0.85 | –0.83 | –0.80 | –0.74 | –0.68 |
| 7 | –0.47 | –0.51 | –0.55 | –0.57 | –0.59 | –0.59 | –0.59 | –0.57 | –0.55 | –0.51 | –0.47 |
| 8 | –0.26 | –0.27 | –0.29 | –0.30 | –0.30 | –0.30 | –0.30 | –0.30 | –0.29 | –0.27 | –0.26 |
| 9 | –0.04 | –0.02 | 0.011 | 0.002 | 0.003 | 0.004 | 0.003 | 0.002 | 0.011 | –0.02 | –0.04 |
| 10 | 0.17 | 0.23 | 0.28 | 0.30 | 0.32 | 0.32 | 0.32 | 0.30 | 0.28 | 0.23 | 0.17 |
Таблица 3.
Значения $B_{r}^{{\text{Н}}}$, мТл/кА
| k | i | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0.15 | 0.13 | 0.09 | 0.06 | 0.03 | 0 | –0.03 | –0.06 | –0.09 | –0.13 | –0.15 |
| 2 | 0.27 | 0.22 | 0.17 | 0.11 | 0.06 | 0 | –0.06 | –0.11 | –0.17 | –0.22 | –0.27 |
| 3 | 0.37 | 0.31 | 0.23 | 0.15 | 0.08 | 0 | –0.08 | –0.15 | –0.23 | –0.31 | –0.37 |
| 4 | 0.45 | 0.37 | 0.28 | 0.19 | 0.09 | 0 | –0.09 | –0.19 | –0.28 | –0.37 | –0.45 |
| 5 | 0.51 | 0.42 | 0.32 | 0.21 | 0.10 | 0 | –0.10 | –0.21 | –0.32 | –0.42 | –0.51 |
| 6 | 0.54 | 0.45 | 0.34 | 0.23 | 0.11 | 0 | –0.11 | –0.23 | –0.34 | –0.45 | –0.54 |
| 7 | 0.55 | 0.46 | 0.35 | 0.23 | 0.12 | 0 | –0.12 | –0.23 | –0.35 | –0.46 | –0.55 |
| 8 | 0.53 | 0.44 | 0.33 | 0.22 | 0.11 | 0 | –0.11 | –0.22 | –0.33 | –0.44 | –0.53 |
| 9 | 0.46 | 0.38 | 0.29 | 0.19 | 0.1 | 0 | –0.1 | –0.19 | –0.29 | –0.38 | –0.46 |
| 10 | 0.33 | 0.28 | 0.21 | 0.14 | 0.07 | 0 | –0.07 | –0.14 | –0.21 | –0.28 | –0.33 |
Таблица 4.
Значения te(r, z)
| k | i | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 1 | 1.13 | 1.23 | 1.31 | 1.38 | 1.43 | 1.47 | 1.50 | 1.53 | 1.544 | 1.549 |
| 2 | 1 | 1.14 | 1.25 | 1.33 | 1.40 | 1.45 | 1.50 | 1.53 | 1.56 | 1.57 | 1.58 |
| 4 | 1 | 1.17 | 1.29 | 1.38 | 1.46 | 1.52 | 1.56 | 1.60 | 1.63 | 1.64 | 1.65 |
| 6 | 1 | 1.20 | 1.34 | 1.44 | 1.52 | 1.58 | 1.64 | 1.68 | 1.71 | 1.726 | 1.732 |
| 8 | 1 | 1.23 | 1.39 | 1.50 | 1.59 | 1.66 | 1.71 | 1.75 | 1.78 | 1.80 | 1.81 |
| 10 | 1 | 1.26 | 1.43 | 1.56 | 1.66 | 1.74 | 1.80 | 1.84 | 1.87 | 1.89 | 1.90 |
Таблица 5.
Значения te(1), ${{\tilde {n}}_{k}}(1)$, fk, ${{f}_{k}}{{\tilde {n}}_{k}}(1)$, Un/Up при L = 1 см
| k | 0 | 2 | 4 | 6 | 8 | 10 |
| te(1) | 1.19 | 1.21 | 1.22 | 1.26 | 1.28 | 1.30 |
| ${{\tilde {n}}_{k}}(1)$ | 1.0075 | 1.012 | 1.019 | 1.024 | 1.028 | 1.031 |
| fk | 1.82 | 1.65 | 1.31 | 1.04 | 0.83 | 0.66 |
| ${{f}_{k}}{{\tilde {n}}_{k}}(1)$ | 1.83 | 1.66 | 1.34 | 1.06 | 0.86 | 0.68 |
| Un/Up | 0.0079 | 0.012 | 0.020 | 0.025 | 0.029 | 0.031 |
Таблица 6.
Значения te(1), ${{\tilde {n}}_{k}}(1)$, fk, ${{f}_{k}}{{\tilde {n}}_{k}}(1)$, Un/Up при L = 3 см
| k | 0 | 2 | 4 | 6 | 8 | 10 |
| te(1) | 1.55 | 1.58 | 1.65 | 1.73 | 1.81 | 1.90 |
| ${{\tilde {n}}_{k}}(1)$ | 1.021 | 1.027 | 1.040 | 1.053 | 1.064 | 1.069 |
| fk | 1.63 | 1.55 | 1.35 | 1.10 | 0.85 | 0.62 |
| ${{f}_{k}}{{\tilde {n}}_{k}}(1)$ | 1.66 | 1.60 | 1.41 | 1.16 | 0.90 | 0.67 |
| Un/Up | 0.012 | 0.015 | 0.022 | 0.030 | 0.035 | 0.037 |
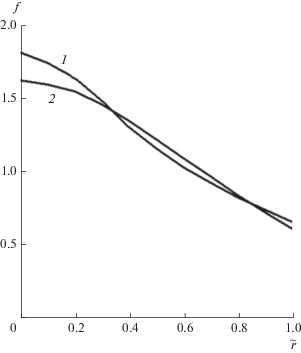
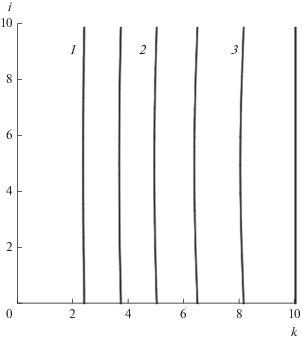
Рис. 7.
Линии уровней плотности тока j × 10–6А/м2 для B0 = 2.5 мТл/кА: –5.44 (1), –4.46 (2), –3.03 (3).
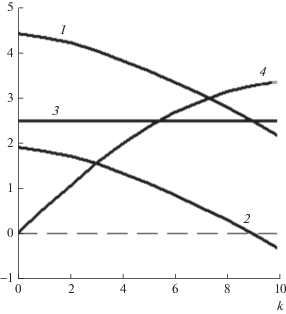
Значения приведенных магнитных полей Холла $B_{z}^{{\text{Н}}}$ и $B_{r}^{{\text{Н}}}$ для B0 = 2.5 мТл/кА представлены в табл. 2, 3 и на рис. 1. Отметим, что значение $B_{z}^{{\text{Н}}}$ на оси сопоставимо с B0, при увеличении r значения $B_{z}^{{\text{Н}}}$ уменьшаются. На краю $B_{z}^{{\text{Н}}}$ меняет знак, модуль Bz на краю меньше |B0|. Распределения |$B_{z}^{{\text{Н}}}$| по z более однородны, они имеют максимум в центре промежутка. Величина $B_{r}^{{\text{Н}}}$ в центре промежутка меняет знак, она монотонно уменьшается по z. Для каждого значения k кривая |$B_{r}^{{\text{Н}}}$| симметрична.
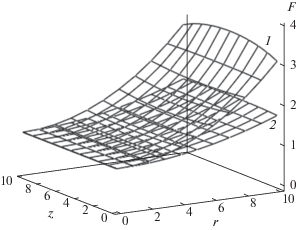
На рис. 1 приведены распределения компонентов магнитного поля для z = L/2 (i = 5). Отметим нелинейную зависимость Bθ(r), связанную с контракцией тока (f(r) ≠ 1), а также заметное влияние на зависимость Bz(r) магнитного поля тока Холла. В данном случае f0 = 1.63. При большей контракции кривая Bθ(r) может пройти через максимум. На рис. 2 представлены значения функции F(r, z), имеющей важное значение в теории ВД в магнитном поле.
Функция F(r, z) характеризует рост по r удельного сопротивления ρ плазмы в магнитном поле. Именно с этим фактом связана контракция электронного тока: на краю (по r) промежутка ρ больше, поэтому для выполнения условия эквипотенциальности анода с ростом r должна уменьшаться плотность тока.
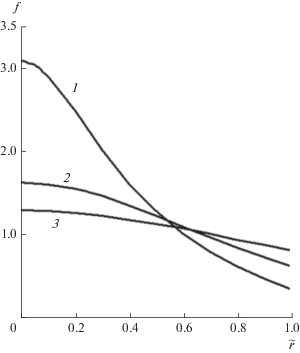
На рис. 3 представлены зависимости f(r) для трех значений внешнего магнитного поля B0. С ростом B0 уменьшается контракция тока и удельное сопротивление плазмы (функция F(r, z)). На рис. 4 показаны аналогичные зависимости для двух значений L.
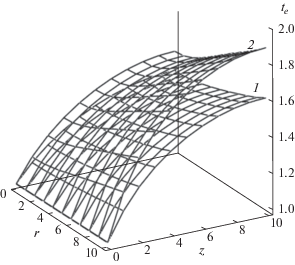
В табл. 4 приведены значения относительной электронной температуры (te(r, z)). Отметим, что скорость роста температуры с увеличением z существенно уменьшается. Это связано с тем фактом, что при увеличении температуры уменьшается интенсивность нагрева ( j 2/σ) и увеличивается коэффициент электронной теплопроводности. При этом часть тепла отводится в направлении катодной границы плазмы. Рост температуры по r связан с нагревом электронов током Холла.
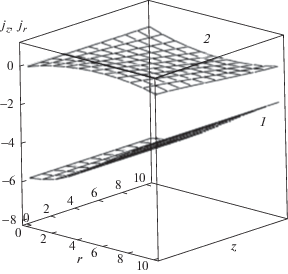
На рис. 5 представлены поверхности значений te(r, z) для двух B0. С ростом B0 нагрев электронов уменьшается, что в первую очередь связано с уменьшением степени контракции тока. Результаты расчетов позволяют проверить возможность использования 1.5D-модели, применимость которой ограничена условием jr $ \ll $ jz. На рис. 6 приведены поверхности зависимостей jr(r, z) и jz(r, z). Видно, что jr $ \ll $ jz. На рис. 7 приведены линии уровней плотности тока j. Они параллельны оси z. Это полностью соответствует 1.5D-модели. В ВД сила радиального сжатия jzBθ уравновешена силой jθBz. ВД – это короткая дуга в движущемся с большой скоростью потоке плазмы. Время пролета ионами промежутка L – порядка 10–6 с. Форму плазменной границы определяют радиальные магнитные силы, она совпадает с линиями тока на рис. 7.
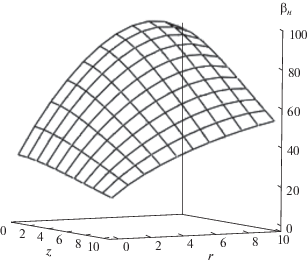
На рис. 8 приведены значения параметра Холла βH(r, z). Поскольку температура электронов существенно увеличивается по z, то βH(z) растет. Таким образом, 1.5D-модель вполне пригодна для расчета параметров плазмы и распределения плотности тока, если jr $ \ll $ jz. Если jr и jz сравнимы, то необходимо воспользоваться гораздо более сложной 2D-моделью.
В табл. 5 и 6 приведены результаты расчетов с учетом $\tilde {n}(\tilde {r},\tilde {z})$ распределений на анодной границе температуры электронов te(1), концентрации ионов ${{\tilde {n}}_{i}}(1)$, функции fk, концентрации плазмы, произведения ${{f}_{k}}{{\tilde {n}}_{k}}(1)$. Приведено также отношение доли напряжения Un, связанного с учетом влияния $\ln \tilde {n}$ (формулы (13), (16)) к напряжению на плазме Up. Это отношение характеризует степень влияния $\tilde {n}(\tilde {r},\tilde {z})$ на распределение $f(\tilde {r})$. Если пренебречь этим влиянием и считать ${{\tilde {n}}_{i}} = 1$, то функцию $f(\tilde {r})$ следует увеличить в (1 + Un/Up) раза, снова скорректировать расчет, который уменьшит расхождение точного и приближенного (${{\tilde {n}}_{i}} = 1$) расчетов. Таким образом, в рассмотренных случаях распределение концентрации плазмы практически не влияет на распределение плотности тока.
ЗАКЛЮЧЕНИЕ
Обратим внимание на тот факт, что плазма ВД полностью ионизована. Кулоновская электропроводность и теплопроводность плазмы без магнитного поля зависят только от температуры электронов и не зависят от концентрации плазмы. В магнитном поле обе эти величины зависят от магнитного поля через функцию $F = 1 + \frac{{B_{\theta }^{2}(z) + B_{r}^{2}(z)}}{{B_{z}^{2}(z)}}\frac{{\beta _{{\text{H}}}^{2}}}{{1 + \beta _{{\text{H}}}^{2}}}$, где ${{\beta }_{{\text{H}}}}$ – параметр Холла. Параметр Холла ${{\beta }_{{\text{H}}}}$ включает концентрацию электронов. Значение ${{\beta }_{{\text{H}}}}$ в диффузной вакуумной дуге много больше единицы, поэтому множитель $\beta _{{\text{H}}}^{2}$/(1 + $\beta _{{\text{H}}}^{2}$) можно считать равным единице. Функция Fk, полученная с учетом глубокой компенсации аксиальных и радиальных магнитных сил, зависит от отношения суммы квадратов поперечных полей Bθ и Br к квадрату Bz. Она определяет распределения плотности тока, компонентов магнитного поля тока дуги и температуры электронов. Для практических целей при разработке устройств, использующих диффузную форму ВД с аксиальным магнитным полем (например, в вакуумных дугогасительных камерах), можно эффективно применять предложенную в работе 1.5D-модель на стадии конструирования. С помощью расчетов обеспечивается необходимая степень однородности распределения плотности тока по аноду. При неоднородном распределении анод максимально нагревается в центре. При температуре Та > 1800 К с поверхности анода испаряются медленные атомы в предельно допустимом количестве, которые ионизуются в плазме ВД. Разряд переходит из диффузной моды в моду с анодным пятном. В этом режиме вакуумный выключатель перестает надежно отключать переменный ток. Чем более однородно распределение тока по поверхности анода, тем больший ток может отключить выключатель.
Целесообразно было бы сравнить результаты расчетов с экспериментом. Однако экспериментальные данные по распределению плотности тока в сильноточной ВД во внешнем однородном магнитном поле отсутствуют. Накопленные экспериментальные данные по отключающей способности (максимальному току отключения) вакуумных дугогасительных камер (ВДК) позволяют создавать в разрядном промежутке приведенное магнитное поле Bz > 3 мТл/кА. Считается, что в этом случае распределение плотности тока в плазме ВД близко к однородному. Этот факт согласуется с результатами расчетов, представленных в данной работе на рис. 3.
Для количественного сравнения рассчитанных распределений плотности тока с экспериментальными данными следует провести специальный эксперимент с разрядным промежутком, в котором секционированный анод состоит из системы концентрических колец. Внешнее однородное магнитное поле Bz должно создаваться с помощью катушек Гельмгольца. Ток через каждое кольцо можно измерять поясом Роговского. Одновременно можно проводить скоростную многокадровую фотосъемку катодных пятен (как это делалось в [15, 16]), обработка результатов которой позволяет определить распределение плотности пятен по поверхности катода. Поскольку токи в катодных пятнах одинаковы, то это распределение совпадает с распределением плотности тока на катоде. Такой эксперимент представляет несомненный научный и практический интерес.
Отметим также, что при конструировании ВДК индукторы, создающие магнитное поле Bz, Br, расположены внутри электродов. Магнитное поле Bz, как правило, заметно уменьшается с ростом r, а Br увеличивается. На краю электрода значение Br может превышать Bz. При этом линии тока сильно наклонены к оси, удельное сопротивление плазмы с ростом r резко возрастает. Эти факты могут привести к сильной контракции тока (f0$ \gg $ 1) на аноде. Для расчета распределения плотности тока в плазме с такими индукторами необходимо использовать 2D-модель.
В настоящее время возникла потребность разработки ВДК для электроэнергетики: генераторные выключатели на токи в несколько сотен кА, а также высоковольтные выключатели для напряжений 110 и 220 кВ. Для решения этих весьма сложных задач метод математического расчета распределений плотности тока на стадии разработки особенно эффективен.
Кратко сформулируем основные результаты работы.
1. Развита теория двухмерной аксиально-симметричной ВД, учитывающая магнитное поле, создаваемое током дуги (Bθ), магнитное поле тока Холла ($B_{z}^{{\text{Н}}}$, $B_{r}^{{\text{Н}}}$) и внешнее магнитное поле (Bz, Br). Для линий уровня тока получено дифференциальное уравнение второго порядка в частных производных (2D-модель), сформулированы нелинейные граничные условия.
2. В приближении jr $ \ll $ jz разработана более простая 1.5D-модель ВД. В этой модели магнитное поле имеет те же компоненты, что и в 2D-модели, однако угол наклона линий тока к оси δ $ \ll $ 1. Такую модель удобно использовать для расчетов на стадии конструирования вакуумных дугогасительных устройств для разработки конструкций с достаточно однородным распределением плотности тока j(r).
3. Для расчета распределения температуры электронов в плазме ВД получено интегро-дифференциальное уравнение, учитывающее зависимость коэффициентов теплопроводности и электропроводности от компонентов магнитного поля Br, Bθ и Bz. Для этих коэффициентов получены аналитические выражения. В уравнении учтено влияние распределения концентрации плазмы на температуру электронов.
4. Для различных значений внешнего аксиального магнитного поля и размеров плазмы рассчитаны распределения компонентов плотности тока ВД (jr, jθ, jz), магнитного поля тока Холла ($B_{z}^{{\text{Н}}}$, $B_{r}^{{\text{Н}}}$), азимутального магнитного поля Bθ, распределения электронной температуры te(r, z) и концентрации плазмы. Расчеты выполнены с учетом нелинейной зависимости анодного падения от плотности тока. Показано, что магнитное поле тока Холла $B_{z}^{{\text{Н}}}$, $B_{r}^{{\text{Н}}}$ сравнимо с внешним магнитным полем, оно влияет на зависимость j(r). Увеличение индукции внешнего магнитного поля Bz уменьшает контракцию электронного тока.
Список литературы
Брагинский С.И. Явления переноса в плазме. В кн.: Вопросы теории плазмы / Под ред. Леонтовича М.А. М.: Госатомиздат, 1963. Вып. 1. С. 183.
Лондер Я.И., Ульянов К.Н. Кризис течения быстрых ионов в сильноточном вакуумно-дуговом разряде // ТВТ. 2007. Т. 45. № 4. С. 499.
Schade E., Shmelev D. Numerical Simulation of High-current Vacuum Arcs with an External Axial Magnetic Fild (AMF) // IEEE Trans. Plasma Sci. 2003. V. 31. № 5. P. 890.
Лондер Я.И., Ульянов К.Н. Двумерная математическая модель короткой вакуумной дуги во внешнем магнитном поле // ТВТ. 2005. Т. 43. № 6. С. 845.
Лондер Я.И., Ульянов К.Н. Двумерная математическая модель короткой вакуумной дуги во внешнем магнитном поле. Результаты численных расчетов // ТВТ. 2006. Т. 44. № 1. С. 25.
Keidar M., Beilis I., Boxman R.L., Goldmith S. 2D Expansion of the Low-density Interelectrode Vacuum Arc Plasma Jet in an Axial Magnetic Fields // J. Phys. D: Appl. Phys. 1996. V. 26. P. 1973.
Beilis I., Keidar M., Boxman R.L., Goldmith S. Theoretical Study of Plasma Expansion in a Magnetic Field in a Disk Anode Vacuum Arc // J. Appl. Phys. 1998. V. 83. № 2. P. 709.
Wang L., Jia S., Shi Z., Rong M. MHD Simulation of Vacuum Arc under Different AMF // Proc. 21st Int. Symp. on Discharges and Electrical Insulation in Vacuum. Yalta. Crimea. 2004. P. 197.
Londer Y.I., Ulynov K.N. Model of Shot Vacuum Arc at Collision Free Motion of Ions // IEEE Trans. Plasma Sci. 2013. V. 41. № 8. P. 1996.
Лондер Я.И., Ульянов К.Н. Теория отрицательного анодного падения в разрядах низкого давления // ТВТ. 2013. Т. 51. № 1. С. 13.
Лондер Я.И., Ульянов К.Н. Теоретическое изучение влияния магнитного поля тока Холла на параметры сильноточного вакуумно-дугового разряда // ТВТ. 2008. Т. 46. № 2. С. 185.
Ландау Л.Д., Лившиц Е.М. Электродинамика сплошных сред. М.: Наука, 1992. С. 661.
Boxman R.L., Martin P., Sanders D. Handbook of Va-cuum Arc Sience and Technology. Ridge Park, USA: Noyes Publ., 1995.
Boxman R.L., Goldsmith S. Model of the Anode Region in a Uniform Multi-cathode-spot Vacuum Arc // J. Appl. Phys. 1983. V. 54. № 2. P. 592.
Прозоров Е.Ф., Ульянов К.Н., Федоров В.А., Лондер Я.И. Изучение процесса обрыва постоянного тока во внешнем неоднородном магнитном поле // ТВТ. 2011. Т. 49. № 5. С. 649.
Прозоров Е.Ф., Ульянов К.Н., Федоров В.А. Изучение динамики катодных пятен в вакуумно-дуговом разряде с кольцевыми электродами // ТВТ. 2013. Т. 51. № 2. С. 176.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур