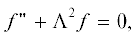Теплофизика высоких температур, 2020, T. 58, № 6, стр. 885-895

ВВЕДЕНИЕ

Различного типа волны, возникающие в неоднородной атмосфере Земли, начиная с работ Гельмгольца, Кельвина, Рэлея и Лэмба, широко обсуждаются в литературе [1–10]. Результаты, относящиеся к внутренним гравитационным волнам, подробно разобраны в [2]. Влияние вязкости и теплопроводности на распространение волн в атмосфере рассмотрено в [6] и [9], где исследование проводится для изотермической атмосферы. Основным механизмом, учтенным в перечисленных работах, приводящим к возникновению и распространению возмущений, является неоднородность по высоте исходного стационарного фона и наличие сдвига горизонтальной скорости среды [2].

В данной работе анализируются динамические процессы в сжимаемых средах, когда возникают спонтанные источники тепловыделения (поглощения) $Q(\rho ,P)$, отсутствующие в стационарной, неоднородной атмосфере Земли. Такими источниками могут быть: а) примеси, находящиеся в воздухе (газовая фаза) в виде твердых частичек (льда) и жидких капель воды, которые приводят к генерации фазовых переходов (испарение, конденсация, сублимация); б) тепловыделение от локальных электрических разрядов, вызывающих испарение влаги в разрядной стадии и ее конденсацию после окончания разряда. Подобные процессы возникают при протекании различного рода электрических разрядов включая молнии, когда протекание электрического тока приводит к джоулеву нагреву и испарению большого количества влаги. Источником рассматриваемых возмущений могут быть также микрометеориты, влетающие и сгорающие в плотных слоях атмосферы, или взрывы спутников, ракет и т.п.

Целью данной работы является анализ влияний спонтанных источников тепловыделения на распространение волн и устойчивость стационарного состояния среды и получение аналитических формул, позволяющих оценить времена развития неустойчивостей в рамках возмущений малой амплитуды. Представленная система уравнений позволяет также проводить численные расчеты динамики возмущений конечной амплитуды вихревых течений во влажном воздухе с учетом внутренних источников различного типа, наличия сдвига горизонтальной скорости среды, неколлинеарности стационарных профилей давления и плотности и более детально исследовать механизмы зарождения торнадо.

СТАЦИОНАРНЫЙ ФОН

Хорошо известно, что развитие возмущений зависит не только от источников, генерирующих эти возмущения, но и от вида стационарного фона, на котором они развиваются [3, 11]. Рассмотрим устойчивость плоского бесконечно протяженного слоя толщиной h, заполненного влажным воздухом, относительно трехмерных малых возмущений. В исходном стационарном состоянии профили давления, температуры и плотности неоднородны по высоте: ${{P}_{0}}\left( z \right),{{T}_{0}}\left( z \right),\mathop \rho \nolimits_0 \left( z \right)$. Исследование выполняется в декартовой системе координат: ось x направлена на восток, y – на север, z – к локальному зениту. В данном анализе рассматриваются длинноволновые возмущения, поэтому в пренебрежении вязкостью и теплопроводностью учитываются силы тяжести $\vec {g}\left( {0,0, - g} \right)$ и Кориолиса $\rho [{{{\mathbf{\Omega }}}_{C}} \times {\mathbf{v}}];{{{\mathbf{\Omega }}}_{C}}$ = $2{{{\mathbf{e}}}_{z}}{{\Omega }_{0}}\sin \left( \alpha \right)$. Здесь α – широтный угол, Ω₀ = 0.73 × 10^–4 рад/с – угловая скорость вращения Земли, e_z – единичный вектор вдоль вертикали к поверхности Земли.

В отличие от работы [10] стационарная среда считается неподвижной (не учитывается зависимость геопотенциала от координаты). Рассматривается специальный случай, когда в стационарном состоянии в среде выполняется силовое равновесие

а связь между плотностью и давлением зависит от вида протекающих в атмосфере процессов.

Процессы в атмосфере адиабатические S₀ = const. В этом случае при решении системы уравнений (1) можно воспользоваться связью $\frac{{{{P}_{0}}\left( z \right)}}{{{{P}_{0}}\left( 0 \right)}} = {{\left( {\frac{{\mathop \rho \nolimits_0 \left( z \right)}}{{\mathop \rho \nolimits_0 \left( 0 \right)}}} \right)}^{\gamma }}$. Тогда распределения давления, температуры и плотности по высоте описываются следующими уравнениями:

где g – ускорение силы тяжести, ${{S}_{0}}$ – энтропия, $\gamma $ – показатель адиабаты, ${{R}_{g}}$ – газовая постоянная влажного воздуха.

Процессы в неподвижной атмосфере не являются адиабатическими $\frac{{\partial {{S}_{{\mathbf{0}}}}}}{{\partial z}} \ne {\mathbf{0}}$. В этом случае считается, что выполняется условие равновесия (1), и из наблюдений известны распределения ${{T}_{0}}\left( z \right),$ ${{P}_{0}}\left( z \right),{{S}_{0}}\left( z \right)$.

Считается, что в начальный момент времени в неподвижной среде источники (стоки) тепловыделения $Q({{\rho }_{0}},{{P}_{0}}) = 0$ отсутствуют. Однако из-за того, что ${{\left( {\frac{{\partial Q}}{{\partial \rho }}} \right)}_{{{{P}_{0}}}}} \ne 0,$ ${{\left( {\frac{{\partial Q}}{{\partial P}}} \right)}_{{{{\rho }_{0}}}}} \ne 0$, при возникновении даже малых возмущений стационарного состояния эти источники оказывают влияние на состояние атмосферы.

СИСТЕМА УРАВНЕНИЙ ДЛЯ МАЛЫХ ВОЗМУЩЕНИЙ

При анализе устойчивости исходного стационарного состояния $\mathop f\nolimits_0 (z)$ зависимая переменная представляется в виде суммы

где ${{f}_{0}}\left( z \right)$ – известное стационарное значение, $f{\kern 1pt} '\left( {x,y,z,t} \right)$ – возмущения (далее знак ′ опускается). Без учета сдвига горизонтальной скорости течения исходя из общей системы уравнений сплошной среды и, ограничиваясь только линейными по возмущениям членами, получим следующую систему уравнений для возмущений: Если источники (стоки) тепловыделения $Q\left( {p,T} \right)$ зависят от давления и температуры, то их по-прежнему можно свести к форме, приведенной в (5), используя уравнение состояния (6).

Аналогично [6], выделяя в горизонтальной составляющей скорости потенциальную и вихревую компоненты, можно записать поток массы в следующем виде:

Здесь $\Phi \left( {x,y,z,t} \right),\Psi \left( {x,y,z,t} \right)$ – неизвестные функции, через которые, согласно (7), выражаются горизонтальные потоки массы.

Поиск решения системы уравнений (3)–(6) осуществляется с помощью представления зависимости каждой функции $F(x,y,z,t)$ от координат и времени в виде

Здесь ${{{\mathbf{r}}}_{ \bot }}(x,y,0);\,\,\,\,{{{\mathbf{k}}}_{ \bot }}\left( {{{k}_{x}},{{k}_{y}},0} \right);$ $ - \infty < {{k}_{x}} < \infty ,$ $ - \infty < {{k}_{y}} < \infty $ – координаты волнового вектора в горизонтальной плоскости Земли. Представление зависимости решения системы (3)–(6) от горизонтальных координат r в виде (8) – $\exp \left( {i{{{\mathbf{k}}}_{ \bot }} \cdot {{{\mathbf{r}}}_{ \bot }}} \right)$ означает использование периодических граничных условий по этим координатам. С помощью уравнения состояния (6) можно выразить возмущение температуры через возмущения давления и плотности. Затем, используя уравнения (3)–(5), выразить все остальные функции через $\zeta \left( z \right)$. Такой подход позволяет для длинноволновых возмущений свести анализ всей системы (3)–(5) к решению одного уравнения для функции $\zeta (z)$ (см. Приложение 1): где Уравнение (8) описывает ряд явлений в атмосфере планеты, не изучавшихся ранее с учетом спонтанных внутренних тепловыделений, отражаемых параметрами ${{\chi }_{p}},{{\chi }_{\rho }}$. С точностью до малого параметра $\frac{g}{{a_{s}^{2}F}}\frac{{\partial F}}{{\partial z}} \ll 1$ слагаемым $\hat {H}\zeta $ в (8) можно пренебречь, поэтому далее используется уравнение Здесь $F = \frac{{(\gamma - 1)a_{s}^{2}}}{{\gamma {{R}_{g}}}}\frac{{d{{S}_{0}}}}{{dz}}$, ${{\chi }_{\rho }} = \left[ {\frac{{1 - \gamma }}{{a_{s}^{2}}}{{{\left( {\frac{{\partial Q}}{{\partial \rho }}} \right)}}_{p}} - 1} \right],$ ${{\chi }_{p}} = \left[ {1 - \left( {\gamma - 1} \right){{{\left( {\frac{{\partial Q}}{{\partial P}}} \right)}}_{\rho }}} \right],$ ${{S}_{0}}$ – энтропия воздуха, $\mathop a\nolimits_s = \sqrt {{{R}_{g}}T} $ – скорость звука, $\gamma $ – показатель адиабаты, ${{R}_{g}}$ – газовая постоянная влажного воздуха. Граничные условия для уравнения (9) зависят от конкретной физической задачи.

Далее рассмотрим процессы в слое толщиной h, находящемся над твердой поверхностью. Когда нижняя граница непроницаема, а на верхней границе поток массы экстремален, уравнение (9) решается со следующими условиями:

В других режимах, когда на нижней границе слоя происходит интенсивное испарение влаги (например, поверхность океана), а верхняя граница непроницаема или возмущения на ней стремятся к нулю, граничные условия сводятся к следующим:

или где $b$ – коэффициент массообмена, учитывающий интенсивность образования потока массы на водной поверхности.

Для анализа устойчивости перейдем к безразмерным переменным:

и, опуская далее тильду над безразмерными переменными, перепишем уравнение (8) и граничные условия (10) в виде С заменой переменных $\zeta \left( z \right) = f\left( z \right)\exp \left( {\alpha z} \right)$ уравнения (12), (13) сводятся к где Функции $F,{{\chi }_{p}},{{\chi }_{\rho }}$ можно определить, используя данные наблюдений о состоянии атмосферы. Изменения по высоте профилей давления, температуры, плотности $\left( {{{P}_{0}}\left( z \right),{{T}_{0}}\left( z \right),{{\rho }_{0}}\left( z \right)} \right)$ и величин ${{\left( {\frac{{\partial Q}}{{\partial \rho }}} \right)}_{{{{P}_{0}}}}} \ne 0,$ ${{\left( {\frac{{\partial Q}}{{\partial P}}} \right)}_{{{{\rho }_{0}}}}} \ne 0$ зависят от состояния атмосферы Земли и могут иметь разные значения в различные сезоны и времена суток (Приложение 2). Для приближенных оценок можно воспользоваться либо уравнениями (2), либо усредненными по времени значениями (Приложение 2). В общем случае коэффициенты уравнения (12) ($a_{s}^{2} = {{R}_{g}}T(z)$, $F = \frac{{(\gamma - 1)a_{s}^{2}}}{{\gamma {{R}_{g}}}}\frac{{d{{S}_{0}}}}{{dz}},$ ${{\chi }_{\rho }},{{\chi }_{p}}$) и, следовательно, (14) зависят от координаты $z$. Однако при выполнении неравенства их в первом приближении можно принять постоянными. Если это неравенство не выполнено, то при аналитическом решении задачи слой $h$ разбивается на серию слоев $m$: $h = \sum\nolimits_{i = 1}^m {{{h}_{i}}} $, так чтобы внутри каждого слоя выполнялось условие

ДИСПЕРСИОННОЕ УРАВНЕНИЕ И АНАЛИЗ ЕГО КОРНЕЙ

Решение уравнения (14) представляется в виде

Из граничных условий (15) находим Используя соотношение (18), находим дисперсионное уравнение Учитывая, что в атмосфере Земли параметр ${{W}^{2}} = \frac{{\Omega _{C}^{2}a_{s}^{2}}}{{{{g}^{2}}}} \approx {{10}^{{ - 5}}}$ мал, удобно провести переопределение безразмерной частоты $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } = \frac{\omega }{g}{{\Omega }_{C}}{{a}_{s}}$ и далее использовать дисперсионное уравнение $D\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } ,k} \right)$ в виде Корни дисперсионного уравнения (16), зависящие от параметров задачи $\left( {k,{{\chi }_{p}},{{\chi }_{\rho }},F} \right)$ и определяющие поведение возмущений во времени, имеют простой вид

Данная формула позволяет описать целый ряд процессов, происходящих во влажной, неоднородной по высоте атмосфере, и может быть использована для анализа явлений в атмосферах других планет Солнечной системы. Подчеркнем еще раз, что в качестве внутренних источников теплоты могут выступать не только процессы фазовых переходов, но и поглощение или генерация излучения, джоулев нагрев (когда в слое может протекать электрический ток). Учет электрического тока существенен для анализа устойчивости грозового облака [9].

Изменяя безразмерные переменные (11), можно рассмотреть процессы с характерными временами, различающимися на четыре порядка.

Далее исследуем ряд частных случаев для характерных параметров атмосферы Земли (a_s ≈ ≈ 320 м/с, h = 7000 м).

Тепловыделение и неоднородность температуры и давления отсутствуют. Если тепловыделение $Q = 0\left( {{{\chi }_{p}} = 1,{{\chi }_{\rho }} = - 1} \right)$ и неоднородности температуры и давления отсутствуют $F = 0$, безразмерные коэффициенты в (17) принимают вид

В этом случае с учетом ${{W}^{2}} \approx {{10}^{{ - 5}}} \ll 1$ корни дисперсионного уравнения (17) записываются в виде

Первая мода колебания, записанная в размерном виде:

описывает акустические колебания воздуха в слое толщиной $h$ при наличии силы тяжести.

Вторая мода, записанная в размерном виде:

при выполнении неравенств ${{g}^{2}}a_{s}^{{ - 4}} \gg {{\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + \pi n} \right)}^{2}}{{h}^{{ - 2}}}$ и ${{k}^{2}} \gg {{g}^{2}}a_{s}^{{ - 4}}$ сводится к

Мода ω_2n описывает колебания однородного слоя воздуха как целого под воздействием сил Кориолиса.

Существование вращательной неустойчивости, отмеченной в [8]. При условиях $Q = 0$ $\left( {{{\chi }_{p}} = 1,{{\chi }_{\rho }} = - 1} \right)$ уравнение (9) сводится к уравнению (11) работы [8], если в нем пренебречь изменением скорости звука с высотой. Используя модельные представления о характере изменения скорости звука с высотой, автор [8] получил инкремент неустойчивости, названной вращательной:

Согласно [8] обнаруженная вращательная неустойчивость связана с изменением скорости звука с высотой, однако формулы (19) и (20) различаются только множителем $i$ и в (20) не входят какие-либо характеристики, связанные с изменением скорости звука. Следует отметить, что использованное автором выражение для скорости звука (см. формулу (2) работы [8]) отличается от стандартного термодинамического выражения ${{a}_{s}} = \sqrt {\mathop {\left( {\frac{{\partial P}}{{\partial \rho }}} \right)}\nolimits_{s = {\text{const}}} } = \sqrt {{{R}_{g}}T} $. В состоянии локального термодинамического равновесия скорость звука изменяется пропорционально $\sqrt {\mathop T\nolimits_0 (z)} $.

Если решить дифференциальное уравнение (11) работы [8], пренебрегая изменением скорости звука с высотой, то снова приходим к (19), демонстрирующей отсутствие вращательной неустойчивости, выявленной в [8].

Тепловыделения в неоднородной среде отсутствуют. В этом случае не учитывается тепловыделение, но принимаются во внимание неоднородность температуры и давления по высоте. С учетом характерных значений остальных безразмерных параметров корни дисперсионного уравнения (17) определяются выражением

При выполнении условий

корни уравнения (17) можно записать в удобном для дальнейшего анализа виде

Мода $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{3}^{2} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{2}$ аналогична соотношению (18) и представляет собой акустические колебания воздуха в слое толщиной $h$ при наличии силы тяжести. Мода $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{4}^{2}$ демонстрирует влияние силы Кориолиса на внутренние гравитационные волны и условия возникновения конвекции. В частных случаях $W = 0$ и ${{k}^{2}} \gg {{\alpha }^{2}} + {{\Lambda }^{2}}, - F < 0$ или $\frac{{d{{S}_{0}}}}{{dz}} > 0$ эта мода в размерной форме имеет вид

и описывает внутренние гравитационные волны-колебания Брента–Вяйсяля [2].

При условии

происходит нарастание возмущения – образуется неустойчивость, связанная с возникновением конвекции в атмосфере. Если данное неравенство записать в другом виде, то условие возникновения конвекции сводится к хорошо известному критерию Шварцшильда: С учетом силы Кориолиса $W \ne 0$ из (21) условие возникновения неустойчивости атмосферы в пространстве параметров $F,k,\Lambda ,W$ представляет собой поверхность (“нейтральную кривую”), отделяющую области устойчивости ${{W}^{2}}({{\alpha }^{2}} + {{\Lambda }^{2}})$ + $ + \,{{k}^{2}}F{\kern 1pt} {\kern 1pt} > {\kern 1pt} {\kern 1pt} 0$ от областей неустойчивости ${{W}^{2}}({{\alpha }^{2}} + {{\Lambda }^{2}}) + $ $ + \,\,{{k}^{2}}F < 0$: На рис. 1 в пространстве параметров задачи (k, F) показано поведение нейтральной кривой $k_{W}^{2}$ = $ = f\left( { - F} \right)$, получаемой из условия ${{\omega }^{2}}(k_{W}^{2}, - F) = 0$. При выполнении условий $Q = 0,$ ${{\chi }_{\rho }} = - 1,$ ${{\chi }_{P}} = 1,\,\,\tilde {F} \ne 0$ критические значения волнового числа $\mathop k\nolimits_{W{\text{cr}}} $ и величины ${{F}_{{{\text{cr}}}}}$ находятся из условия (22) и имеют вид Полученные здесь результаты хорошо демонстрируют влияние вращения атмосферы ($W \ne 0$) на возникновение конвекции в атмосфере. При $W \ne 0$ критерий Шварцшильда $F < 0$ остается необходимым, а достаточное условие принимает вид где При $W \to 0$и условие (23) сводится к критерию Шварцшильда.

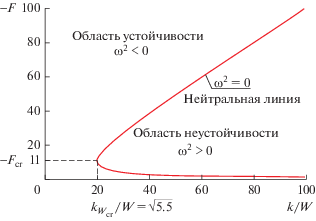
Из неравенств (23) следует, что во вращающейся атмосфере $W \ne 0$ при $k > {{k}_{{W{\text{cr}}}}}$ с ростом градиента температуры $\left| { - F} \right| > \left| { - {{F}_{{{\text{cr}}}}}} \right|$ происходит стабилизация конвективной неустойчивости (рис. 1).

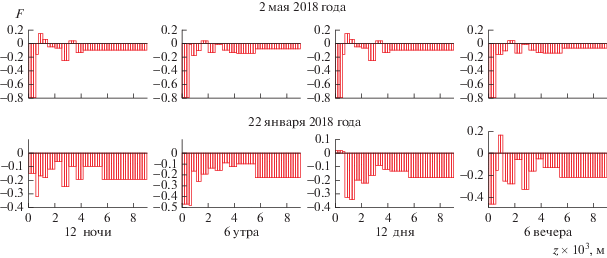
Данные об изменении параметра $F$ в реальной атмосфере, приведенные на рис. 2 (Приложение 2), показывают, что условия для возникновения конвективной неустойчивости [2], связанной с неоднородностью атмосферы $\left| { - F} \right| > \left| {{{F}_{{{\text{cr}}}}}} \right| \approx 20$, реализуются.

Учет вязкости $\eta = {\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0em} \rho }$ и теплопроводности $\chi = {\lambda \mathord{\left/ {\vphantom {\lambda {\rho {{c}_{v}}}}} \right. \kern-0em} {\rho {{c}_{v}}}}$ в системе уравнений (3)–(6) приведет к ограничению области неустойчивости ($\omega > 0$), изображенной на рис. 1, в диапазоне больших волновых чисел (малых длин волн) k > $ > \sqrt {\left| {\frac{{\gamma - 1}}{{\mathop R\nolimits_g \gamma }}\frac{{d{{S}_{0}}}}{{dz}}} \right|{g \mathord{\left/ {\vphantom {g {{{\eta }_{m}}}}} \right. \kern-0em} {{{\eta }_{m}}}}} $, где $\mathop \eta \nolimits_m = \max (\eta ,\chi )$.

Влияние тепловыделения и неоднородностей температуры и давления на устойчивость атмосферы. Рассмотрим более детально общий случай, в котором учитываются тепловыделения, связанные с появлением источников возмущений. Такие процессы возникают в атмосфере с неоднородностью температуры и давления по высоте при испарении или конденсации влаги, при джоулевом нагреве от электрического разряда. В таких процессах вклад источников тепловыделения удовлетворяет условию ${{Q(\mathop P\nolimits_0 ,\mathop \rho \nolimits_0 )} \mathord{\left/ {\vphantom {{Q(\mathop P\nolimits_0 ,\mathop \rho \nolimits_0 )} {\mathop T\nolimits_0 }}} \right. \kern-0em} {\mathop T\nolimits_0 }}\frac{{d{{S}_{0}}}}{{dz}}h = \varepsilon \ll 1$, и поэтому с точностью до малого параметра можно рассмотреть случай, когда в системе (1), определяющей исходные стационарные состояния ($\mathop P\nolimits_0 ,\mathop \rho \nolimits_0 ,\mathop T\nolimits_0 $), полагается $Q(\mathop P\nolimits_0 ,\mathop \rho \nolimits_0 ) = 0$, но в возмущениях ${{\left( {\frac{{\partial Q}}{{\partial \rho }}} \right)}_{{{{P}_{0}}}}} \ne 0,$ ${{\left( {\frac{{\partial Q}}{{\partial P}}} \right)}_{{{{\rho }_{0}}}}} \ne 0$. Анализ корней (17) дисперсионного уравнения (16) демонстрирует широкое разнообразие в поведении возмущений в атмосфере в зависимости от соотношения между параметрами задачи $W,F,{{\chi }_{\rho }},{{\chi }_{P}},k,\Lambda $.

В частном случае в данной задаче имеет место принцип смены устойчивости. При W = const в пятимерном пространстве параметров (F, χ_ρ, χ_P, k, Λ) существует поверхность, отделяющая области устойчивости от областей неустойчивости. Эта поверхность получается из условия

При Λ = const в двумерном пространстве (F, k) нейтральная кривая $ - F = f(k)$изображена на рис. 1.

Используя это условие и найденные корни уравнения (16), можно рассчитать границу возникновения неустойчивости атмосферы.

Чтобы кратко продемонстрировать влияние тепловыделений, можно рассмотреть более детально частный случай неподвижной атмосферы $W = 0$, когда источник зависит только от давления: ${{\left( {\frac{{\partial Q}}{{\partial \rho }}} \right)}_{{{{p}_{0}}}}} = 0,{{\chi }_{\rho }} = - 1,{{\left( {\frac{{\partial Q}}{{\partial P}}} \right)}_{{{{\rho }_{0}}}}} > 0,$ ${{\chi }_{p}} > 0$. В этом случае корни (17) дисперсионного уравнения (16) принимают вид

Если выполняются условия одна из мод является неустойчивой и возмущение нарастает с инкрементом При условии ${{\left[ { - \frac{1}{{{{\chi }_{p}}}}\left( {{{\alpha }^{2}} + {{\Lambda }^{2}} + {{k}^{2}}} \right)} \right]}^{2}} \gg \frac{{4{{k}^{2}}F}}{{{{\chi }_{p}}}}$ инкремент не зависит от переменной ${{\chi }_{p}}$: При условии ${{\left[ { - \frac{1}{{{{\chi }_{p}}}}\left( {{{\alpha }^{2}} + {{\Lambda }^{2}} + {{k}^{2}}} \right)} \right]}^{2}} < \frac{{4{{k}^{2}}F}}{{{{\chi }_{p}}}}$ эта мода является неустойчивой и возмущение нарастает с инкрементом: Для этого случая инкремент зависит от переменной ${{\chi }_{p}}$ и ее рост параметра приводит к снижению инкремента.

Другая мода уравнения (24) соответствует колебаниям с частотами:

Рассмотрим два других конкретных примера влияния тепловыделения на устойчивость неоднородной атмосферы.

1) ${{\left( {\frac{{\partial Q}}{{\partial \rho }}} \right)}_{{{{p}_{0}}}}} = 0,$ ${{\chi }_{\rho }} = - 1,$ ${{\left( {\frac{{\partial Q}}{{\partial P}}} \right)}_{{{{\rho }_{0}}}}} > 0$. Возмущения создаются находящимися в воздухе в виде твердых частичек (льда) и (или) жидких капель воды примесями. В этом случае источниками возмущений являются фазовые переходы (испарение, конденсация, сублимация) в атмосфере. В данном простейшем случае они могут быть представлены в виде

Здесь $f = \frac{{{{P}_{w}}}}{{{{P}_{{ws}}}}}$ – влажность воздуха; ${{P}_{w}}$ – давление водяных паров; ${{P}_{{ws}}}$ – давление насыщения водяных паров; $\rho $ – плотность влажного воздуха; ${{\rho }_{w}}$ – плотность паров воды; ${{h}_{{LG}}}$ – теплота парообразования (конденсации), Дж/кг; ${{R}_{g}}$ – газовая постоянная влажного воздуха, Дж/(кг К).

При

возникает неустойчивость, инкремент которой может быть определен из уравнения (25). Если наряду с неравенством (26) выполняются условия

то инкремент равен

При

для коротковолновых возмущений неустойчивость развивается очень быстро.

2) Источником возмущений является джоулев нагрев, генерируемый электрическим током атмосферного электрического разряда [11, 12].

В этом случае источник возмущений может быть представлен в виде

Здесь $\sigma (T,P)$ – электропроводность воздуха, $E = \sqrt {\frac{1}{\tau }\int_0^\tau {{{{(E(\tau {\kern 1pt} '))}}^{2}}d\tau {\kern 1pt} '} } $ – средняя напряженность электрического поля в разряде.

При развитии электрического разряда в атмосфере электропроводность воздуха возникает не только за счет ионизации атомов азота и кислорода, но и из-за наличия в воздухе фрагментов, содержащих щелочные металлы. В большинстве важных случаев

При электрическом разряде в атмосфере возникают возмущения, инкремент которых равен

Отметим, что случаи ${{\left( {\frac{{\partial Q}}{{\partial \rho }}} \right)}_{{{{p}_{0}}}}} < 0,$ ${{\chi }_{\rho }} < 0,$ ${{\left( {\frac{{\partial Q}}{{\partial P}}} \right)}_{{{{\rho }_{0}}}}} < 0$ и ${{\chi }_{p}} \to 0$ требуют специальных рассмотрений, которым посвящено отдельное исследование с использованием дисперсионного уравнения (16).

ЗАКЛЮЧЕНИЕ

Проведено исследование устойчивости двухфазного слоя влажного воздуха, находящегося над нагретой поверхностью суши или океана, с учетом внутренних источников тепловыделения, зависящих от давления и плотности.

Для малых трехмерных возмущений во вращающейся атмосфере получено дисперсионное уравнение, которое позволяет получить модифицированный критерий возникновения конвективной неустойчивости. Показано, что во вращающейся неоднородной атмосфере $W \ne 0$ при $k > {{k}_{{W{\text{cr}}}}}$ с ростом неоднородности – параметра $\left| { - F} \right| > \left| { - {{F}_{{{\text{cr}}}}}} \right| \approx 20$ – происходит стабилизация конвективной неустойчивости.

Полученное дисперсионное уравнение позволяет аналитически исследовать целый ряд частных явлений, хорошо фиксируемых экспериментами в лабораториях и наблюдаемых во вращающейся атмосфере. В частности, удается проследить совместные влияния неоднородности стационарного профиля атмосферы и различного рода тепловыделений на волны в атмосфере.

Получены условия возникновения неустойчивостей, в которых источником возмущений является джоулев нагрев, генерируемый током атмосферного электрического разряда в воздухе, или испарение и последующая конденсация влаги. Показано, что учет тепловыделения может приводить как к регистрации новых неустойчивостей, так и к модификации ранее известных.

Предложенная система уравнений позволяет выполнять численные расчеты динамики возмущений конечной амплитуды вихревых течений во влажном воздухе с учетом источников теплоты различной природы и более детально исследовать механизмы зарождения различного рода смерчей.