1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 59, № 1, 2021

Теплофизика высоких температур, 2021, T. 59, № 1, стр. 133-139

Влияние фазовых переходов на распространение акустических волн в многофракционных газовзвесях с полидисперсными включениями

Д. А. Губайдуллин 1, *, Р. Р. Зарипов 1, **

1 Институт механики и машиностроения – ОСП ФГБУН “Федеральный исследовательский центр КазНЦ РАН”
г. Казань, Россия

* E-mail: gubaidullin@imm.knc.ru
** E-mail: rinat_zaripov.imm@mail.ru

Поступила в редакцию 14.01.2020
После доработки 01.04.2020
Принята к публикации 18.06.2020

Полный текст (PDF)

Аннотация

Исследовано распространение акустических волн в многофракционных смесях газа с паром, каплями и твердыми частицами с учетом межфазного массообмена. Дисперсная фаза состоит из M + 1 фракций, различающихся размерами включений, функциями распределения включений по размерам и материалами. Представлена система интегродифференциальных уравнений движения многофракционной полидисперсной смеси. Получено дисперсионное соотношение, которое обобщает известные ранее соотношения. Построены зависимости относительной скорости звука и декремента затухания на определенной длине волны от безразмерной частоты возмущения с учетом межфазного массообмена. Проанализировано влияние межфазного тепломассообмена и трения фаз на декремент затухания.

ВВЕДЕНИЕ

Как известно, многофазные среды широко распространены в природе и технике, например, газокапельные смеси широко используются в энергетике. Неоднородность смеси может привести к некорректной оценке параметров среды. Возникает необходимость учитывать полидисперсность и многофракционность смеси, а также эффекты, связанные с теплообменом, массообменом и межфазным трением. Различные проблемы акустики парогазокапельных смесей рассмотрены в известных монографиях [1–3]. Некоторые проблемы в двухфазных потоках представлены в [4, 5]. Влияние фазовых превращений на распространение акустических волн ранее исследовано в работах [6–11]. Влияние полидисперсности состава парогазокапельной смеси на распространение малых возмущений рассмотрено в [12, 13]. В [14] в рамках монодисперсной модели изучено распространение акустических волн в многофракционных газовзвесях при наличии фазовых превращений. В работе [15] исследуется распространение акустических волн в газовзвесях с учетом полидисперсности и многофракциональности смеси, но без учета фазовых превращений.

В настоящей работе рассматривается наиболее общий случай распространения акустических волн в многофракционных полидисперсных газовзвесях с учетом межфазного тепломассообмена и трения фаз, когда каждая фракция капель и частиц разных материалов имеет свои функции распределения по размерам.

ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим движение парогазокапельной смеси с полидисперсными твердыми частицами в плоском и одномерном случаях. Будем считать, что дисперсная фаза состоит из M + 1 полидисперсных фракций. При этом одна фракция участвует в фазовых переходах, а M фракций не участвуют. Каждая из фракций имеет разные размеры включений и описывается своей функцией распределения включений по размерам. Объемное содержание несущей фазы ${{\alpha }_{1}}$ и каждой из фракций ${{\alpha }_{2}}$ определяется как

$\begin{gathered} {{\alpha }_{{2d}}} = \frac{4}{3}\pi \int\limits_{\vartriangle {{r}_{d}}} {N_{0}^{d}({{r}_{d}})r_{d}^{3}d{{r}_{d}}} ,\,\,\,\,{{\alpha }_{{2j}}} = \frac{4}{3}\pi \int\limits_{\vartriangle {{r}_{j}}} {N_{0}^{j}({{r}_{j}})r_{j}^{3}d{{r}_{j}}} , \\ {{\alpha }_{1}} + {{\alpha }_{{2d}}} + \sum\limits_{j = 1}^M {{{\alpha }_{{2j}}}} = 1,\,\,\,\,\Delta {{r}_{d}} = \left[ {r_{d}^{{\min }},r_{d}^{{\max }}} \right], \\ \Delta {{r}_{j}} = \left[ {r_{j}^{{\min }},r_{j}^{{\max }}} \right],\,\,\,\,j = \overline {1,M} . \\ \end{gathered} $
Здесь и далее нижний индекс 1 относится к несущей фазе, $2j$ – к дисперсной фазе $j$-й фракции. Для удобства индекс $d$ относится к каплям, $j$ ($j = \overline {1,M} $) – к твердым частицам, $N_{0}^{d}({{r}_{d}})$, $N_{0}^{j}({{r}_{j}})$ – функции распределения капель и твердых частиц $j$-й фракции по радиусам.

Основными характеристиками смеси являются следующие параметры:

$\begin{gathered} {{\rho }_{i}} = \rho _{i}^{0}{{\alpha }_{i}},\,\,\,\,{{k}_{i}} = {{{{\rho }_{i}}} \mathord{\left/ {\vphantom {{{{\rho }_{i}}} {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}},\,\,\,\,{{m}_{d}} = \frac{{{{\rho }_{{2d}}}}}{{{{\rho }_{1}}}}, \\ {{m}_{j}} = \frac{{{{\rho }_{{2j}}}}}{{{{\rho }_{1}}}},\,\,\,\,j = \overline {1,M} . \\ \end{gathered} $
Здесь ${{\rho }_{i}}$, $\rho _{i}^{0}$ – средняя и истинная плотности несущей фазы ($i = 1$), капель ($i = 2d$) и твердых частиц ($i = 2j$) соответственно; ${{k}_{i}}$ – начальные концентрации паровой ($i = V$) и газовой ($i = G$) компонент несущей фазы; ${{m}_{d}}$, ${{m}_{j}}$ – массовые содержания капель и твердых частиц $j$-й фракции.

Будем рассматривать малые возмущения параметров $\varphi = {{\varphi }_{0}} + \varphi {\kern 1pt} '$ (штрих вверху обозначает возмущение параметра, нижний индекс 0 – начальное невозмущенное состояние).

Линеаризованные уравнения сохранения массы для фаз записываются аналогично [2, 15] и с учетом M + 1 полидисперсных фракций принимают вид

(1)
$\begin{gathered} \frac{{\partial \rho _{1}^{'}}}{{\partial t}} + {{\rho }_{{10}}}\frac{{\partial v_{1}^{'}}}{{\partial x}} = - \int\limits_{\vartriangle {{r}_{d}}} {N_{0}^{d}({{r}_{d}}){{j}_{d}}d{{r}_{d}}} , \\ \frac{{\partial \rho _{V}^{'}}}{{\partial t}} + {{\rho }_{{V0}}}\frac{{\partial v_{1}^{'}}}{{\partial x}} = - \int\limits_{\vartriangle {{r}_{d}}} {N_{0}^{d}({{r}_{d}}){{j}_{d}}d{{r}_{d}}} , \\ \frac{{\partial \rho _{{2d}}^{'}}}{{\partial t}} + \int\limits_{\vartriangle {{r}_{d}}} {\frac{{\partial v_{{2d}}^{'}}}{{\partial x}}N_{0}^{d}({{r}_{d}})g_{0}^{d}({{r}_{d}})d{{r}_{d}}} = \int\limits_{\vartriangle {{r}_{d}}} {N_{0}^{d}({{r}_{d}}){{j}_{d}}d{{r}_{d}}} , \\ \frac{{\partial \rho _{{2j}}^{'}}}{{\partial t}} + \int\limits_{\vartriangle {{r}_{j}}} {\frac{{\partial v_{{2j}}^{'}}}{{\partial x}}N_{0}^{j}({{r}_{j}})g_{0}^{j}({{r}_{j}})d{{r}_{j}}} = 0,\,\,\,\,j = \overline {1,M} . \\ \end{gathered} $
Уравнение сохранения импульса с учетом $M + 1$ полидисперсных фракций твердых частиц записывается в следующем виде:
(2)
$\begin{gathered} {{\rho }_{{10}}}\frac{{\partial v_{1}^{'}}}{{\partial t}} + \frac{{\partial p_{1}^{'}}}{{\partial x}} + \int\limits_{\vartriangle {{r}_{d}}} {{{f}_{d}}N_{0}^{d}({{r}_{d}})d{{r}_{d}}} + \\ + \,\,\sum\limits_{j = 1}^M {\int\limits_{\vartriangle {{r}_{j}}} {{{f}_{j}}N_{0}^{j}({{r}_{j}})d{{r}_{j}}} } = 0, \\ g_{0}^{d}\left( {{{r}_{d}}} \right)\frac{{\partial v_{{2d}}^{'}}}{{\partial t}} = {{f}_{d}},\,\,\,\,g_{0}^{j}\left( {{{r}_{j}}} \right)\frac{{\partial v_{{2j}}^{'}}}{{\partial t}} = {{f}_{j}},\,\,\,\,j = \overline {1,M} . \\ \end{gathered} $
Уравнения внутренней энергии для несущей фазы, капель, частиц и их межфазной поверхности принимают вид [2, 15]
(3)
$\begin{gathered} {{\rho }_{{10}}}{{c}_{{p1}}}\frac{{\partial T_{1}^{'}}}{{\partial t}} - {{\alpha }_{{10}}}\frac{{\partial p}}{{\partial t}} + \int\limits_{\Delta {{r}_{d}}} {N_{0}^{d}({{r}_{d}}){{q}_{{1d}}}d{{r}_{d}}} + \\ + \,\,\sum\limits_{j = 1}^M {\int\limits_{\Delta {{r}_{j}}} {N_{0}^{j}({{r}_{j}}){{q}_{{1j}}}d{{r}_{j}}} } = 0, \\ g_{0}^{d}\left( {{{r}_{d}}} \right){{c}_{{p2d}}}\frac{{\partial T_{{2d}}^{'}}}{{\partial t}} = - {{q}_{{2d}}},\,\,\,\,g_{0}^{j}\left( {{{r}_{j}}} \right){{c}_{{p2j}}}\frac{{\partial T_{{2j}}^{'}}}{{\partial t}} = - {{q}_{{2j}}}, \\ j = \overline {1,M} ,\,\,\,\,{{q}_{{1d}}} + {{q}_{{2d}}} = - {{j}_{d}}{{l}_{0}}, \\ {{q}_{{1j}}} + {{q}_{{2j}}} = 0,\,\,\,\,j = \overline {1,M} . \\ \end{gathered} $
Уравнения состояния пара и газовой смеси удобно записать в следующем виде [2]:
(4)
$\begin{gathered} p_{V}^{'} = \frac{{C_{V}^{2}}}{{{{\gamma }_{V}}{{\alpha }_{{10}}}}}\rho _{V}^{'} + {{p}_{{V0}}}\frac{{T_{1}^{{\text{'}}}}}{{{{T}_{{10}}}}}, \\ p_{1}^{'} = \frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}(\rho _{1}^{'} + \Delta \bar {R}(\rho _{V}^{'} - {{k}_{V}}\rho _{1}^{'})) + \frac{{{{p}_{{10}}}}}{{{{T}_{{10}}}}}T_{1}^{'}, \\ \Delta \bar {R} = \frac{{{{R}_{V}} - {{R}_{G}}}}{{{{k}_{V}}{{R}_{V}} + {{k}_{G}}{{R}_{G}}}}. \\ \end{gathered} $
Анализ показывает, что при $\rho _{2}^{0} \gg \rho _{1}^{0}$ основными силами, действующими на индивидуальную частицу или каплю дисперсной фазы, являются силы Стокса и Бассэ [1, 2]. Тогда силу, действующую на каплю и частицу, можно определить как сумму этих двух сил:
(5)
$\begin{gathered} {{f}_{d}} = g_{0}^{d}\frac{{v_{1}^{'} - v_{{2d}}^{'}}}{{\tau _{{vd}}^{*}}},\,\,\,\,{{f}_{j}} = g_{0}^{j}\frac{{v_{1}^{'} - v_{{2j}}^{'}}}{{\tau _{{v2j}}^{*}}}, \\ j = \overline {1,M} ,\,\,\,\,\tau _{{vk}}^{*} = {{\tau }_{{vk}}}{{\left[ {1 - \frac{{1 - i}}{{\sqrt 2 }}\sqrt {\omega {{\tau }_{{\mu 1k}}}} } \right]}^{{ - 1}}}, \\ {{\tau }_{{vk}}} = \frac{2}{9}\frac{{\rho _{{2k}}^{0}r_{k}^{2}}}{{{{\mu }_{1}}}},\,\,\,\,{{\tau }_{{\mu 1k}}} = \frac{{\rho _{1}^{0}r_{k}^{2}}}{{{{\mu }_{1}}}},\,\,\,\,\,k = d,1,...M. \\ \end{gathered} $
Тепловые потоки $q$, а также интенсивность фазовых переходов ${{j}_{d}}$ определены соотношениями [2, 12]

(6)
$\begin{gathered} {{q}_{{1d}}} = g_{0}^{d}\frac{{{{c}_{{p1}}}}}{{{{m}_{d}}}}\frac{{T_{1}^{'} - T_{{\sum d}}^{'}}}{{\tau _{{T1d}}^{*}}},\,\,\,\,{{q}_{{2d}}} = g_{0}^{d}{{c}_{{p2d}}}\frac{{T_{{2d}}^{'} - T_{{\sum d}}^{'}}}{{\tau _{{T2d}}^{*}}}, \\ {{q}_{{1j}}} = g_{0}^{j}\frac{{{{c}_{{p1}}}}}{{{{m}_{j}}}}\frac{{T_{1}^{'} - T_{{\sum j}}^{'}}}{{\tau _{{T1j}}^{*}}},\,\,\,\,{{q}_{j}} = g_{0}^{j}{{c}_{{p2j}}}\frac{{T_{{2j}}^{'} - T_{{\sum j}}^{'}}}{{\tau _{{T2j}}^{*}}}, \\ j = \overline {1,M} ,\,\,\,\,{{j}_{d}} = g_{0}^{d}\frac{{m_{d}^{0}}}{{{{p}_{{10}}}}}\frac{{p_{V}^{'} - p_{{V\sum d}}^{'}}}{{\tau _{{k1d}}^{*}}} = \\ = g_{0}^{d}\frac{{m_{d}^{0}}}{{{{p}_{{10}}}}}\frac{{p_{{V\sum d}}^{'} - p_{{VS}}^{'}}}{{{{\tau }_{{\beta d}}}}},\,\,\,\,p_{{VS}}^{'} = T_{{\sum d}}^{'}{{l}_{0}}\frac{{\rho _{{V0}}^{0}}}{{{{T}_{{10}}}}}. \\ \end{gathered} $

Здесь

$\begin{gathered} \tau _{{T1k}}^{*} = \frac{1}{3}\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{{2k}}}}}\frac{{{{\tau }_{{\lambda 1k}}}}}{{1 + {{z}_{{1k}}}}}, \\ \tau _{{T2k}}^{*} = \frac{1}{3}{{\tau }_{{\lambda 2k}}}\frac{{3{{z}_{{2k}}} - (3 + z_{{2k}}^{2}){\text{th}}({{z}_{{2k}}})}}{{z_{{2k}}^{2}\left( {{\text{th}}({{z}_{{2k}}}) - {{z}_{{2k}}}} \right)}}, \\ {{z}_{{1k}}} = \frac{{1 - i}}{{\sqrt 2 }}\sqrt {\omega {{\tau }_{{\lambda 1k}}}} ,\,\,\,\,{{z}_{{2k}}} = \frac{{1 - i}}{{\sqrt 2 }}\sqrt {\omega {{\tau }_{{\lambda 2k}}}} , \\ {{\tau }_{{\lambda 1k}}} = \frac{{r_{k}^{2}\rho _{1}^{0}{{c}_{{p1}}}}}{{{{\lambda }_{1}}}},\,\,\,\,{{\tau }_{{\lambda 2k}}} = \frac{{r_{k}^{2}\rho _{{2k}}^{0}{{c}_{{p2k}}}}}{{{{\lambda }_{{2k}}}}},\,\,\,\,m_{k}^{0} = \frac{{\rho _{{10}}^{0}}}{{\rho _{{20k}}^{0}}}, \\ k = d,1,...M,\,\,\,\,{{\tau }_{{k1d}}} = \frac{1}{3}{{{\bar {R}}}_{v}}\left( {1 - {{k}_{{v}}}} \right)\frac{{{{\tau }_{d}}}}{{1 + y}}, \\ {{\tau }_{{\beta d}}} = \frac{1}{3}\frac{{\sqrt {2\pi } }}{{{{\gamma }_{V}}}}\frac{{{{\gamma }_{1}}{{C}_{V}}{{r}_{d}}}}{{\beta C_{1}^{2}}},\,\,\,\,{{\tau }_{d}} = \frac{{r_{d}^{2}}}{{{{D}_{1}}}},\,\,\,\,y = \frac{{1 - i}}{{\sqrt 2 }}\sqrt {\omega {{\tau }_{d}}} . \\ \end{gathered} $

В приведенных уравнениях приняты следующие обозначения: $C$ – скорость звука, ${{D}_{1}}$ – коэффициент диффузии, $R$ – газовая постоянная, ${{c}_{p}}$ – теплоемкость, $v$ – скорость, $p$ – давление, $g_{0}^{{}}$ – масса частицы или капли, ${{l}_{0}}$ – удельная теплота парообразования, $r$ – радиус включений, $\Delta r$ – диапазон изменения радиуса включений, T – температура, $t$ – время, $x$ – координата, $\alpha $ – объемное содержание, $\beta $ – коэффициент аккомодации, $\gamma $ – показатель адиабаты, $\lambda $ – коэффициент теплопроводности, $\mu $ – коэффициент динамической вязкости, $\omega $ – частота возмущений, ${{\tau }_{{v}}}$ – время релаксации скоростей фаз при квазистационарном обтекании частиц газом, ${{\tau }_{{\mu 1}}}$ – характерное время установления квазистационарного распределения скорости в газообразной фазе, ${{\tau }_{{\beta d}}}$ – характерное время выравнивания парциальных давлений пара на межфазной границе, $\tau _{{k1d}}^{*}$ – комплексное время релаксации парциального давления пара, ${{\tau }_{d}}$ – характерное время установления квазистационарного распределения концентрации пара, ${{\tau }_{{Tj}}}$ – время релаксации температуры в $j$-й фазе, ${{\tau }_{{\lambda 1k}}}$ – характерное время проникания возмущения температуры от поверхности частицы в $j$-фазу.

ДИСПЕРСИОННОЕ СООТНОШЕНИЕ

Решение системы уравнений (1)–(6) будем искать в виде прогрессивных волн для возмущений $\varphi {\kern 1pt} ' = \rho {\kern 1pt} ',p{\kern 1pt} ',T{\kern 1pt} {\kern 1pt} '$ [1]:

$\begin{gathered} \varphi {\kern 1pt} ' = {{A}_{\varphi }}\exp [i({{K}_{*}}x - \omega t)],\,\,\,\,{{K}_{*}} = K + i{{K}_{{{\text{**}}}}}, \\ {{C}_{p}} = {\omega \mathord{\left/ {\vphantom {\omega K}} \right. \kern-0em} K},\,\,\,\,\sigma = {{2\pi {{K}_{{{\text{**}}}}}} \mathord{\left/ {\vphantom {{2\pi {{K}_{{{\text{**}}}}}} {K.}}} \right. \kern-0em} {K.}} \\ \end{gathered} $
Здесь ${{K}_{*}}$ – комплексное волновое число, ${{K}_{{{\text{**}}}}}$ – линейный коэффициент затухания, ${{С}_{p}}$ – фазовая скорость, $\sigma $ – декремент затухания на длине волны, ${{A}_{\varphi }}$ – амплитуда.

Введем $v_{k}^{'} = \frac{{\partial \varphi _{k}^{'}}}{{\partial x}},\varphi _{k}^{'} = {{A}_{{\varphi k}}}{{e}^{{i({{K}_{*}}x - \omega t)}}}$ [12], тогда уравнения (1)–(6) примут вид

(7)
$\begin{gathered} - i\omega {{A}_{{\rho 1}}} - {{\rho }_{{10}}}K_{*}^{2}{{A}_{{\varphi 1}}} + \frac{{m_{d}^{0}\rho _{{20}}^{d}}}{{{{p}_{{10}}}}}{{\left\langle {\frac{{{{A}_{{pV}}} - {{A}_{{pV\sum d}}}}}{{\tau _{{k1d}}^{*}}}} \right\rangle }_{d}} = 0, \\ - i\omega {{A}_{{\rho V}}} - {{\rho }_{{V0}}}K_{*}^{2}{{A}_{{\varphi 1}}} + \frac{{m_{d}^{0}\rho _{{20}}^{d}}}{{{{p}_{{10}}}}}{{\left\langle {\frac{{{{A}_{{pV}}} - {{A}_{{pV\sum d}}}}}{{\tau _{{k1d}}^{*}}}} \right\rangle }_{d}} = 0, \\ \end{gathered} $
(8)
$\begin{gathered} - i\omega {{A}_{{\rho 2d}}} - \rho _{{20}}^{j}K_{*}^{2}{{\left\langle {{{A}_{{\varphi 2d}}}} \right\rangle }_{d}} = \frac{{m_{d}^{0}\rho _{{20}}^{d}}}{{{{p}_{{10}}}}}{{\left\langle {\frac{{{{A}_{{pV\sum d}}} - {{A}_{{pVS}}}}}{{{{\tau }_{{\beta d}}}}}} \right\rangle }_{d}}, \\ - i\omega {{A}_{{\rho 2j}}} - \rho _{{20}}^{j}K_{*}^{2}{{\left\langle {{{A}_{{\varphi 2j}}}} \right\rangle }_{j}} = 0,\,\,\,\,j = \overline {1,M,} \\ \omega {{K}_{*}}{{\rho }_{{10}}}{{A}_{{\varphi 1}}} + i{{K}_{*}}{{A}_{{p1}}} + i{{K}_{*}}\rho _{{20}}^{d}{{\left\langle {\frac{{{{A}_{{\varphi 1}}} - {{A}_{{\varphi 2d}}}}}{{\tau _{{vd}}^{*}}}} \right\rangle }_{d}} + \\ + \,\,i{{K}_{*}}\sum\limits_{j = 1}^M {\rho _{{20}}^{j}{{{\left\langle {\frac{{{{A}_{{\varphi 1}}} - {{A}_{{\varphi 2j}}}}}{{\tau _{{vj}}^{*}}}} \right\rangle }}_{j}}} = 0, \\ \end{gathered} $
(9)
$\begin{gathered} - i\omega {{A}_{{\varphi 2d}}} - \frac{{{{A}_{{\varphi 1}}} - {{A}_{{\varphi 2d}}}}}{{\tau _{{vd}}^{*}}} = 0, \\ - i\omega {{A}_{{\varphi 2j}}} - \frac{{{{A}_{{\varphi 1}}} - {{A}_{{\varphi 2j}}}}}{{\tau _{{vj}}^{*}}} = 0,\,\,\,\,j = \overline {1,M} , \\ \end{gathered} $
(10)
$\begin{gathered} - i\omega {{A}_{{T1}}} + \frac{{i\omega }}{{\rho _{{10}}^{0}{{c}_{{p1}}}}}{{A}_{{p1}}} + {{\left\langle {\frac{{{{A}_{{T1}}} - {{A}_{{T\sum d}}}}}{{\tau _{{T1d}}^{*}}}} \right\rangle }_{a}} + \\ + \,\,\sum\limits_{j = 1}^M {{{{\left\langle {\frac{{{{A}_{{T1}}} - {{A}_{{T\sum j}}}}}{{\tau _{{T1j}}^{*}}}} \right\rangle }}_{j}}} = 0, \\ \end{gathered} $
(11)
$\begin{gathered} - i\omega {{A}_{{T2d}}} + \frac{{{{A}_{{T2d}}} - {{A}_{{T\sum d}}}}}{{\tau _{{T2d}}^{*}}} = 0, \\ - i\omega {{A}_{{T2j}}} + \frac{{{{A}_{{T2j}}} - {{A}_{{T\sum j}}}}}{{\tau _{{T2j}}^{*}}} = 0,\,\,\,\,j = \overline {1,M} , \\ \end{gathered} $
(12)
$\begin{gathered} \frac{{{{c}_{{p1}}}}}{{{{m}_{d}}}}\frac{{{{A}_{{T1}}} - {{A}_{{T\sum d}}}}}{{\tau _{{T1d}}^{*}}} + {{c}_{{p2d}}}\frac{{{{A}_{{T2d}}} - {{A}_{{T\sum d}}}}}{{\tau _{{T2d}}^{*}}} + \\ + \,\,\frac{{m_{d}^{0}{{l}_{0}}}}{{{{p}_{{10}}}}}\frac{{{{A}_{{pV\sum d}}} - {{A}_{{pVS}}}}}{{{{\tau }_{{\beta d}}}}} = 0, \\ \end{gathered} $
(13)
$\begin{gathered} {{c}_{{p1}}}\frac{{{{A}_{{T1}}} - {{A}_{{T\sum j}}}}}{{\tau _{{T1j}}^{*}}} + {{m}_{j}}{{c}_{{p2j}}}\frac{{{{A}_{{T2j}}} - {{A}_{{T\sum j}}}}}{{\tau _{{T2j}}^{*}}} = 0, \\ j = \overline {1,M} , \\ \end{gathered} $
(14)
${{A}_{{pV}}} - \frac{{C_{V}^{2}}}{{{{\gamma }_{V}}{{\alpha }_{{10}}}}}{{A}_{{\rho V}}} - \frac{{{{p}_{{V0}}}}}{{{{T}_{{10}}}}}{{A}_{{T1}}} = 0,$
(15)
${{A}_{{p1}}} - \frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}\left[ {\left( {1 - \Delta \bar {R}{{k}_{{v}}}} \right){{A}_{{\rho 1}}} + \Delta \bar {R}{{A}_{{\rho V}}}} \right] - \frac{{{{p}_{{10}}}}}{{{{T}_{{10}}}}}{{A}_{{T1}}} = 0,$
(16)
$\begin{gathered} \frac{{{{A}_{{pV\sum d}}} - {{A}_{{pVS}}}}}{{{{\tau }_{{\beta d}}}}} = \frac{{{{A}_{{pV}}} - {{A}_{{pV\sum d}}}}}{{\tau _{{k1d}}^{*}}}, \\ {{A}_{{pVS}}} = \frac{{{{l}_{0}}\rho _{{V0}}^{0}}}{{{{T}_{{10}}}}}{{A}_{{T\sum d}}}, \\ \end{gathered} $
Здесь ${{\left\langle h \right\rangle }_{j}} = \frac{1}{{\rho _{{20}}^{j}}}\int_{\Delta {{r}_{j}}} {N_{0}^{j}({{r}_{j}})g_{0}^{j}({{r}_{j}})} {{h}_{j}}d{{r}_{j}}$ (j = d, 1, …, M) – оператор осреднения [2].

Выразив ${{A}_{{T2j}}}$ из второго уравнения (11) и подставив полученное выражение в (13), получим выражение для ${{A}_{{T\sum j}}}$:

(17)
${{A}_{{T\sum j}}} = \frac{{{{A}_{{T1}}}}}{{1 - {{e}_{{1j}}}{{t}_{{ej}}}}},\,\,\,\,j = \overline {1,M} ,$
где ${{e}_{{1j}}} = \frac{{{{c}_{{p2j}}}}}{{{{c}_{{p1}}}m_{j}^{0}}}\frac{1}{{1 - i\omega \tau _{{T2j}}^{*}}},$ ${{t}_{{ej}}} = {{m}_{j}}m_{j}^{0}i\omega \tau _{{T1j}}^{*}$ $j = \overline {1,M} .$

Далее из первого уравнения (11) находим ${{A}_{{T2d}}}$, а из первого уравнения (16) – ${{A}_{{pV\sum d}}}$. Тогда уравнение (12) с учетом полученных выражений для ${{A}_{{T2d}}}$ и ${{A}_{{pV\sum d}}}$ принимает вид

$\begin{gathered} \frac{{{{c}_{{p1}}}}}{{{{m}_{d}}}}\frac{{{{A}_{{T1}}} - {{A}_{{T\sum d}}}}}{{\tau _{{T1d}}^{*}}} + i\omega {{c}_{{p2d}}}\frac{1}{{1 - i\omega \tau _{{T2d}}^{*}}}{{A}_{{T\sum d}}} + \\ + \,\,\frac{{m_{d}^{0}{{l}_{0}}}}{{{{p}_{{10}}}}}\frac{{{{A}_{{pV}}} - {{A}_{{pVS}}}}}{{{{\tau }_{{\beta d}}} + \tau _{{k1d}}^{*}}} = 0. \\ \end{gathered} $
Дальше в данное уравнение подставляется выражение для ${{A}_{{pVS}}}$, и из второго уравнения (16) получается
(18)
$\begin{gathered} \frac{{{{A}_{{T1}}} - {{A}_{{T\sum d}}}}}{{{{t}_{{ed}}}}} + {{e}_{{1d}}}{{A}_{{T\sum d}}} + \\ + \,\,\frac{{{{l}_{0}}}}{{{{p}_{{10}}}{{c}_{{p1}}}}}\left( {{{A}_{{pV}}} - \frac{{{{l}_{0}}\rho _{{V0}}^{0}}}{{{{T}_{{10}}}}}{{A}_{{T\sum d}}}} \right)e = 0, \\ \end{gathered} $
где ${{e}_{{1d}}} = \frac{{{{c}_{{p2d}}}}}{{m_{d}^{0}{{c}_{{p1}}}}}\frac{1}{{1 - i\omega \tau _{{T2d}}^{*}}},$ $e = \frac{1}{{i\omega {\kern 1pt} ({{\tau }_{{\beta d}}} + \tau _{{k1d}}^{*})}},$ ted = $ = {{m}_{d}}m_{d}^{0}\tau _{{T1d}}^{*}i\omega $. Вводя обозначения Z = = ${{\left[ {1 - {{t}_{{ed}}}\left( {{{e}_{{1d}}} - eL} \right)} \right]}^{{ - 1}}}$ и $L = \frac{{\bar {l}_{0}^{2}\rho _{{V0}}^{0}}}{{{{c}_{{p1}}}{{p}_{{10}}}{{T}_{{10}}}}}$, из уравнения (18) получаем выражение для ${{A}_{{T\sum d}}}$:
(19)
${{A}_{{T\sum d}}} = Z\left( {{{A}_{{T1}}} + \frac{{{{l}_{0}}}}{{{{p}_{{10}}}{{c}_{{p1}}}}}e{{t}_{{ed}}}{{A}_{{pV}}}} \right).$
Из уравнений (8) и (9) находится значение ${{A}_{{p1}}}$:
(20)
${{A}_{{p1}}} = i\omega {{\rho }_{{10}}}{{A}_{{\varphi 1}}}V\left( \omega \right).$
Здесь
$\begin{gathered} V\left( \omega \right) = 1 + {{m}_{d}}{{\left\langle {\frac{1}{{1 - i\omega \tau _{{vd}}^{*}}}} \right\rangle }_{d}} + \sum\limits_{j = 1}^M {{{m}_{j}}{{{\left\langle {\frac{1}{{1 - i\omega \tau _{{vj}}^{*}}}} \right\rangle }}_{j}}} , \\ {{m}_{d}} = \frac{{\rho _{{20}}^{d}}}{{{{\rho }_{{10}}}}},\,\,\,\,{{m}_{j}} = \frac{{\rho _{{20}}^{j}}}{{{{\rho }_{{10}}}}},\,\,\,\,j = \overline {1,M} . \\ \end{gathered} $
Из уравнений (14) и (15) получим
$\begin{gathered} \frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}{{{\bar {R}}}_{v}}{{A}_{{\rho V}}} = {{A}_{{p1}}} - \frac{{{{p}_{{10}}}}}{{{{T}_{{10}}}}}{{A}_{{T1}}} + \\ + \,\,\frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}\frac{{K_{*}^{2}}}{{i\omega }}{{\rho }_{{10}}}\left( {1 - {{k}_{v}}{{{\bar {R}}}_{v}}} \right){{A}_{{\varphi 1}}}. \\ \end{gathered} $
В данное уравнение подставим выражение для ${{A}_{{p1}}}$ из (20) и получим следующее уравнение:
(21)
$\begin{gathered} \frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}{{{\bar {R}}}_{v}}{{A}_{{\rho V}}} = i\omega {{\rho }_{{10}}}{{A}_{{\varphi 1}}}V\left( \omega \right) - \frac{{{{p}_{{10}}}}}{{{{T}_{{10}}}}}{{A}_{{T1}}} + \\ + \,\,\frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}\frac{{K_{*}^{2}}}{{i\omega }}{{\rho }_{{10}}}\left( {1 - {{k}_{v}}{{{\bar {R}}}_{v}}} \right){{A}_{{\varphi 1}}}. \\ \end{gathered} $
При учете (17) и (20) уравнение (10) примет вид
(22)
$\begin{gathered} - i\omega {{A}_{{T1}}} - \frac{{{{\alpha }_{{10}}}}}{{{{c}_{{p1}}}}}{{\omega }^{2}}{{A}_{{\varphi 1}}}V\left( \omega \right) + {{\left\langle {\frac{{{{A}_{{T1}}} - {{A}_{{T\sum d}}}}}{{\tau _{{T1d}}^{*}}}} \right\rangle }_{d}} - \\ - \,\,i\omega \sum\limits_{j = 1}^M {{{{\left\langle {\frac{{{{m}_{{2j}}}{{e}_{{1j}}}}}{{1 - {{e}_{{1j}}}{{t}_{{ej}}}}}} \right\rangle }}_{j}}{{A}_{{T1}}}} = 0, \\ \end{gathered} $
где ${{m}_{{2j}}} = {{m}_{j}}m_{j}^{0},\,j = \overline {1,M} $.

Уравнение (7) с учетом (16) и (14) примет вид

(23)
$\begin{gathered} - i\omega {{A}_{{\rho V}}} - {{\rho }_{{V0}}}K_{*}^{2}{{A}_{{\varphi 1}}} + \frac{{{{m}_{d}}\rho _{{20}}^{d}}}{{{{p}_{{10}}}}} \times \\ \times \,\,{{\left\langle {\left( {\frac{{C_{1}^{2}{{{\bar {R}}}_{v}}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}{{A}_{{\rho V}}} + \frac{{{{p}_{{V0}}}}}{{{{T}_{{10}}}}}{{A}_{{T1}}} - \frac{{{{l}_{0}}\rho _{{V0}}^{0}}}{{{{T}_{{10}}}}}{{A}_{{T\sum d}}}} \right)i\omega e} \right\rangle }_{d}} = 0. \\ \end{gathered} $
Уравнение (19) при учете (14) запишем как
(24)
${{A}_{{T\sum d}}} = Z\left[ {{{A}_{{T1}}} + \frac{{{{l}_{0}}}}{{{{p}_{{10}}}{{c}_{{p1}}}}}e{{t}_{{ed}}}\left( {\frac{{C_{1}^{2}{{{\bar {R}}}_{v}}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}{{A}_{{\rho V}}} + \frac{{{{p}_{{V0}}}}}{{{{T}_{{10}}}}}{{A}_{{T1}}}} \right)} \right].$
Таким образом, получена система уравнений (21)–(24) с неизвестными ${{A}_{{T1}}},{{A}_{{\rho V}}},{{A}_{{\varphi 1}}}$. Исключая неизвестные из данной системы, найдем дисперсионное соотношение
(25)
${{\left( {\frac{{{{C}_{1}}{{K}_{*}}}}{\omega }} \right)}^{2}} = V(\omega )D(\omega ),$
где
$\begin{gathered} V\left( \omega \right) = 1 + {{m}_{d}}{{\left\langle {\frac{1}{{1 - i\omega \tau _{{vd}}^{*}}}} \right\rangle }_{d}} + \sum\limits_{j = 1}^M {{{m}_{j}}{{{\left\langle {\frac{1}{{1 - i\omega \tau _{{vj}}^{*}}}} \right\rangle }}_{j}}} , \\ D\left( \omega \right) = 1 + \left( {{{\gamma }_{1}} - 1} \right)\frac{{{{m}_{{2d}}}\left( {{{H}_{2}} - {{k}_{v}}{{{\bar {R}}}_{v}}{{\gamma }_{1}}\left( {{{{\bar {R}}}_{v}}{{{\bar {c}}}_{1}}{{H}_{3}} - 2{{{\bar {l}}}_{0}}{{H}_{1}}} \right) - {{M}_{{1d}}}\Lambda } \right) + \left( {1 - {{M}_{{1d}}}{{H}_{3}}} \right){{t}_{b}}}}{{1 + {{m}_{{2d}}}\left( {{{H}_{2}} - B{{H}_{3}} - {{M}_{{2d}}}\Lambda } \right) + \left( {1 - {{M}_{{2d}}}{{H}_{3}}} \right){{t}_{b}}}}, \\ \end{gathered} $
$\begin{gathered} \Lambda = LH_{1}^{2} + {{H}_{2}}{{H}_{3}},\,\,\,\,{{M}_{{1d}}} = {{{\bar {c}}}_{1}}{{m}_{{2d}}}{{{\bar {R}}}_{v}}\left( {{{\gamma }_{1}} - 1 + {{{\bar {R}}}_{v}}{{k}_{v}}} \right), \\ \,\,\,\,B = {{{\bar {R}}}_{v}}\left( {1 - {{{\bar {R}}}_{v}}{{k}_{v}}} \right), \\ {{H}_{i}} = {{\left\langle {{{h}_{i}}} \right\rangle }_{d}},\,\,\,\,i = 1{\kern 1pt} - {\kern 1pt} 3,\,\,\,\,{{h}_{1}} = eZ,\,\,\,\,\,{{h}_{2}} = \left( {{{e}_{{1d}}} - Le} \right)Z,\, \\ \,\,\,{{h}_{3}} = e\left( {1 - {{e}_{{1d}}}{{t}_{{ed}}}} \right)Z, \\ Z = {{\left[ {1 - {{t}_{{ed}}}\left( {{{e}_{{1d}}} - eL} \right)} \right]}^{{ - 1}}},\,\,\,\,{{e}_{{1d}}} = \frac{{{{c}_{{p2d}}}}}{{m_{d}^{0}{{c}_{{p1}}}}}\frac{1}{{1 - i\omega \tau _{{T2d}}^{*}}},\, \\ \,\,\,e = \frac{1}{{i\omega {\kern 1pt} ({{\tau }_{{\beta d}}} + \tau _{{k1d}}^{*})}}, \\ {{t}_{{ed}}} = {{m}_{d}}m_{d}^{0}\tau _{{T1d}}^{*}i\omega ,\,\,\,\,{{t}_{b}} = \sum\limits_{j = 1}^M {{{m}_{{2j}}}{{{\left\langle {\frac{{{{e}_{{1j}}}}}{{1 - {{e}_{{1j}}}{{t}_{{ej}}}}}} \right\rangle }}_{j}}} ,\, \\ \,\,\,L = {{\gamma }_{1}}({{\gamma }_{1}} - 1){{k}_{v}}\bar {l}_{0}^{2},\,\,\,\,{{{\bar {l}}}_{0}} = \frac{{{{l}_{0}}}}{{C_{1}^{2}}}. \\ \end{gathered} $
При отсутствии межфазного массообмена (${{k}_{{v}}} = 0$) соотношение (25) согласуется с соответствующим соотношением [15]. В случае, когда рассматривается двухфракционная парогазокапельная смесь ($j = 1$), соотношение (25) согласуется с [12].

РЕЗУЛЬТАТЫ РАСЧЕТОВ

На рис. 1 представлено сравнение зависимостей относительной скорости звука ${{{{С}_{p}}} \mathord{\left/ {\vphantom {{{{С}_{p}}} {{{C}_{1}}}}} \right. \kern-0em} {{{C}_{1}}}}$ и декремента затухания на длине волны $\sigma $ от безразмерной частоты возмущений ${{\Omega }_{{3,1}}}$ для смеси газа с паром, каплями воды, частицами песка и алюминия с учетом и без учета межфазного массообмена. Безразмерная частота возмущений, согласно [2], имеет вид ${{\Omega }_{{3,1}}} = \omega \tau _{{vd}}^{{(3,1)}}$, где $\tau _{{vd}}^{{(3,1)}}$ – время релаксации скорости для среднего радиуса капель воды $r_{d}^{{(3,1)}} = \sqrt {{{\left\langle {r_{d}^{3}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {r_{d}^{3}} \right\rangle } {\left\langle {r_{d}^{1}} \right\rangle }}} \right. \kern-0em} {\left\langle {r_{d}^{1}} \right\rangle }}} $. Зависимости рассчитаны по (25) при следующих значениях параметров смеси: ${{p}_{0}} = 0.1$ МПа, ${{T}_{0}} = 327$ К, ${{k}_{v}} = 0.1$. Кривые построены с учетом значений массовых содержаний капель воды ${{m}_{d}} = 0.1$, частиц песка ${{m}_{b}} = 0.1$ и алюминия ${{m}_{c}} = 0.1$. Радиус включений изменялся в диапазоне: для капель воды ${{r}_{d}} \in \left[ {{{{10}}^{{ - 4}}},\;{{{10}}^{{ - 3}}}} \right]$ м, частиц песка ${{r}_{b}} \in \left[ {5 \times {{{10}}^{{ - 5}}},\;{{{10}}^{{ - 4}}}} \right]$ м и алюминия ${{r}_{c}} \in \left[ {{{{10}}^{{ - 7}}},\;{{{10}}^{{ - 6}}}} \right]$ м. Функции распределения включений по размерам имеют вид $N_{0}^{j}({{r}_{j}}) = r_{j}^{{ - 3}}$, $j = d,b,c$.

Рис. 1.

Зависимости относительной скорости звука (а) и декремента затухания на длине волны σ (б) от безразмерной частоты возмущения: 1 – с учетом, 2 – без учета влияния межфазного массообмена.

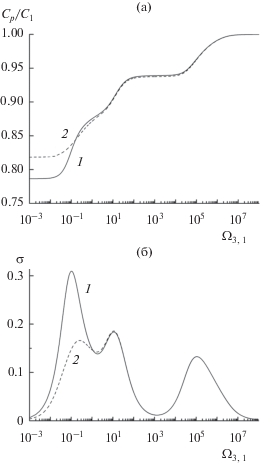
Учет межфазного массообмена приводит к уменьшению относительной скорости только при низких частотах ${{\Omega }_{{3,1}}} < {{10}^{{ - 1}}}$, а при ${{\Omega }_{{3,1}}} > {{10}^{{ - 1}}}$ не оказывает существенного влияния (рис. 1а). Также учет межфазного массообмена приводит к увеличению декремента затухания на длине волны при ${{\Omega }_{{5,3}}} < {{10}^{1}}$ и не оказывает влияния при частотах ${{\Omega }_{{5,3}}} > {{10}^{1}}$ (рис. 1б). Как и следовало ожидать, кривая, описывающая распространение акустической волны, терпит три характерных перегиба. У кривой, описывающей затухание акустической волны, появляются три ярко выраженных максимума. Подобные эффекты связаны с различными теплофизическими свойствами и различными радиусами включений каждой фракции [15]. Выбор данных массовых содержаний и размеров включений каждой фракции обусловлен тем, что при заданных параметрах смеси ярко проявляются подобные эффекты. Если диапазоны изменения параметров включений каждой фракций одного порядка, то подобные эффекты ярко не проявляются. Отметим, что увеличение массовых содержаний каждой фракции приведет к более сильному затуханию волн и снижению относительной скорости звука.

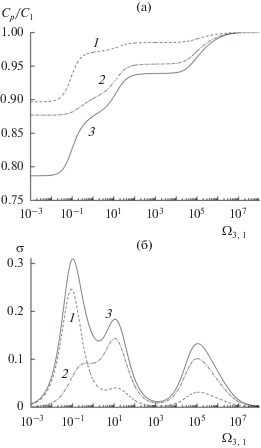
На рис. 2 приведены зависимости относительной скорости ${{{{С}_{p}}} \mathord{\left/ {\vphantom {{{{С}_{p}}} {{{C}_{1}}}}} \right. \kern-0em} {{{C}_{1}}}}$ звука и декремента затухания на длине волны $\sigma $ от безразмерной частоты возмущений ${{\Omega }_{{3,1}}}$ для смеси с такими же параметрами, как на рис. 1. Влияние межфазного тепломассообмена на распространение акустической волны превышает влияние межфазного трения во всем диапазоне рассматриваемых частот (рис. 2а). Основной вклад межфазного тепломассообмена в затухание волны (рис. 2б) проявляется при частоте ${{\Omega }_{{3,1}}} \approx m$, а при частотах ${{\Omega }_{{3,1}}} < 10$ и ${{\Omega }_{{3,1}}} < {{10}^{5}}$ затухание волны в основном связано с эффектами межфазного трения.

Рис. 2.

Зависимости относительной скорости звука (а) и декремента затухания на длине волны σ (б) от безразмерной частоты возмущения с учетом: 1 – индивидуального вклада тепломассообмена между каплями воды и несущей средой и теплообмена между твердыми частицами и несущей средой, 2 – индивидуального вклада межфазного трения, 3 – совместного вклада.

ЗАКЛЮЧЕНИЕ

Изучено распространение акустических волн в многофракционной полидисперсной парогазокапельной смеси газа с твердыми частицами. Представлена замкнутая система интегродифференциальных уравнений движения смеси газа с паром, каплями и твердыми частицами. Выведено дисперсионное соотношение, и рассчитаны дисперсионные кривые. Проанализировано влияние межфазного массообмена на распространение и затухание акустических волн. Установлено, что при моделировании с учетом межфазного массообмена затухание волн больше, а скорость распространения звука в рассматриваемой смеси меньше при низких частотах. Показано влияние учета многофракционности смеси на распространение и затухание акустических волн в воздушном тумане с примесями частиц разных сортов.

Исследование выполнено за счет гранта Российского научного фонда (проект № 20-11-20070).

Список литературы

  1. Нигматуллин Р.И. Динамика многофазных сред. М.: Наука, 1987. 464 с.

  2. Губайдуллин Д.А. Динамика двухфазных парогазокапельных сред. Казань: Изд-во Казанск. матем. об-ва, 1998. 153 с.

  3. Temkin S. Suspension Acoustics: An Introduction to the Physics of Suspension. N.Y.: Cambridge University Press, 2005. 398 p.

  4. Вараксин А.Ю. Обтекание тел дисперсными газовыми потоками // ТВТ. 2018. Т. 56. № 2. С. 282.

  5. Вараксин А.Ю. Столкновения частиц и капель в турбулентных двухфазных потоках // ТВТ. 2019. Т. 57. № 4. С. 588.

  6. Marble F.E. Dynamics of Dusty Gases // Annu. Rev. Fluid Mech. 1970. V. 2. P. 397.

  7. Cole J.E., Dobbims R.A. Measurements of Attenuation and Dispersion of Sound by a Warm Air Fog // J. Atmos. Sci. 1971. V. 28. № 2. P. 202.

  8. Davidson G.A. Sound Propagation in Fog // J. Atmos. Sci. 1975. V. 38. № 2. P. 1106.

  9. Губайдуллин Д.А., Ивандаев А.И. Влияние фазовых превращений на распространение звука в туманах. Сопоставление теории с экспериментом // ПМТФ. 1990. № 6. С. 27.

  10. Шагапов В.Ш. О распространении малых возмущений в парогазокапельной среде // ТВТ. 1987. Т. 25. № 6. С. 1148.

  11. Ивандаев А.И., Нигматуллин Р.И. Особенности распространения слабых возмущений в двухфазных средах с фазовыми переходами // ЖПМиТФ. 1970. № 5. С. 73.

  12. Губайдуллин Д.А., Федоров Ю.В. Сферические и цилиндрические волны в парогазовых смесях с полидисперсными частицами и каплями // ТВТ. 2012. Т. 50. № 5. С. 659.

  13. Гумеров Н.А. Ивандаев А.И. Распространение звука в полидисперсных газовзвесях // ПМТФ. 1988. № 5. С. 115.

  14. Губайдуллин Д.А., Терегулова Е.А., Губайдуллина Д.Д. Распространение акустических волн в многофракционных газовзвесях // ТВТ. 2018. Т. 56. № 5. С. 789.

  15. Губайдуллин Д.А., Зарипов Р.Р. Акустические волны в многофракционных газовзвесях с полидисперсными включениями // ТВТ. 2019. Т. 57. № 3. С. 475.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал