Теплофизика высоких температур, 2021, T. 59, № 1, стр. 140-147
Определение коэффициента теплоотдачи и температуры газового потока по измерениям температуры материала
В. Г. Зверев 1, *, А. А. Светашков 2, А. В. Теплоухов 3
1 Томский государственный университет
г. Томск, Россия
2 Томский политехнический университет
г. Томск, Россия
3 АО “Корпорация "Московский институт теплотехники”
Москва, Россия
* E-mail: zverev@niipmm.tsu.ru
Поступила в редакцию 08.07.2019
После доработки 07.02.2020
Принята к публикации 18.06.2020
Аннотация
На основе решения граничной обратной задачи теплопроводности предложена методика расчета коэффициента теплоотдачи и температуры стационарного газового потока по измерению температуры материала теплоизолированной пластины. В методике не используется сглаживание и численное дифференцирование экспериментальных данных. Дан анализ коэффициентов чувствительности решения к изменению параметров конвективного теплообмена. Определен временнóй диапазон, внутри которого регистрация экспериментальных данных оказывается наиболее информативной для определения искомых параметров с наименьшим влиянием погрешности измерений. Применение методики не требует выбора режима нагрева материала и позволяет повысить точность определения параметров конвективного теплообмена.
ВВЕДЕНИЕ
Решение задач теплового проектирования конструкций при воздействии высокоэнтальпийных газовых потоков на теплозащитные материалы требует знания основных параметров конвективного теплообмена – коэффициента теплоотдачи αe и температуры потока Te [1]. Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой и представляет собой коэффициент пропорциональности в законе Ньютона–Рихмана для конвективного теплового потока [2]. Он играет важную роль в инженерных приложениях и позволяет описание сопряженных процессов переноса тепла в обтекаемом газе и твердом теле разделить на решение двух самостоятельных отдельных задач [3]. На основе знания коэффициента теплоотдачи в граничном условии третьего рода для уравнения теплопроводности в твердом теле осуществляется расчет теплового состояния конструкции [2].
В отличие от температуры, являющейся термодинамической величиной, коэффициент теплоотдачи напрямую нельзя измерить инструментальными методами. Он сложным образом зависит от большого количества параметров, поэтому отсутствуют строгие аналитические зависимости для его расчета на основе уравнений конвективного теплопереноса. На практике коэффициент теплоотдачи обычно определяется из критериальных уравнений, полученных преобразованием определяющих дифференциальных уравнений методами теории подобия. С их помощью обобщаются многочисленные экспериментальные данные для ряда канонических ситуаций по обтекаемому твердому телу и теплоносителю. Такого рода зависимости приводятся в справочной литературе по теплообмену [3].
Однако использование известных критериальных зависимостей для чисел Нуссельта, на основе которых рассчитывается коэффициент теплоотдачи, зачастую приводит к значительным погрешностям, так как реальные ситуации тепловых воздействий на материалы и конструкции, как правило, далеки от канонических. Поэтому с целью более достоверного определения тепловых потоков проводятся экспериментальные исследования в лабораторных, стендовых или реальных условиях эксплуатации, основанные на измерениях температурных полей в материале и их последующей обработке для определения локальных или средних коэффициентов теплоотдачи.
Следует иметь в виду, что любые экспериментальные измерения содержат погрешность, поэтому при их обработке нежелательно использование операции численного дифференцирования из-за ее неустойчивости к возмущению исходных данных. Предварительное сглаживание также приводит к их искажению и вносит дополнительную погрешность в решение.
В этой связи актуальным является вопрос определения параметров конвективного теплообмена по температурным измерениям на основе решения граничных обратных задач теплопроводности (ОЗТ) [4–6]. Необходимость применения ОЗТ обусловлена широким кругом приложений в различных областях науки и техники, и в ряде случаев они являются единственным средством получения информации. Обзор исследований по проблемам и методам решения ОЗТ, а также их различным приложениям можно найти в работах [4–13].
Численная методика решения нелинейной граничной обратной задачи теплопроводности в экстремальной постановке развита в работе [14]. В ней в рамках общего одномерного подхода к описанию задачи численным образом рассмотрено определение нестационарного коэффициента теплоотдачи при смачивании нагретых поверхностей.
В [15] для диагностики стационарных газовых потоков предложена методика определения параметров конвективного теплообмена на основе решения граничной ОЗТ в приближении полубесконечного тела. Это накладывает определенные ограничения на время теплового воздействия и необходимую толщину образца, так как тепловая волна не должна достигать его тыльной поверхности. Учет толщины образца в тепловом процессе позволяет снять ограничения и расширить возможности эксперимента по диагностике воздействия высокоэнтальпийного газового потока на теплозащитные материалы.
Цель данной работы – дальнейшее развитие методики расчета параметров конвективного теплообмена [15] для повышения точности их определения по измерениям температуры материала теплоизолированной пластины на основе решения граничной ОЗТ.
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
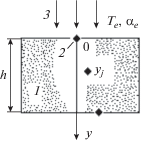
Рассмотрим конвективный нагрев термически инертного образца в виде неограниченной пластины толщиной h стационарным потоком газа с температурой Te и коэффициентом теплоотдачи αe (рис. 1). Тыльная сторона пластины является теплоизолированной, теплофизические свойства материала постоянны. Математическая постановка задачи нагрева образца для рассматриваемого случая имеет вид [2, 16]
(1)
$\frac{{\partial T}}{{\partial t}} = a\frac{{{{\partial }^{2}}T}}{{\partial {{y}^{2}}}},\,\,\,\,a = \frac{\lambda }{{\rho c}},\,\,\,\,t > 0,\,\,\,\,0 < y < h,$(3)
$y = 0{\kern 1pt} :\,\,\,\, - {\kern 1pt} \lambda \frac{{\partial T}}{{\partial y}} = {{\alpha }_{e}}({{T}_{e}} - T),$Рис. 1.
Схема нагрева образца потоком газа: 1 – образец, 2 – датчики температуры на глубине yj, 3 – стационарный поток газа с температурой Te и коэффициентом теплоотдачи αe, h – толщина пластины.
Уравнение (1) описывает тепловое состояние инертного материала с начальным условием (2), краевым условием на наружной (3) и тыльной (4) поверхностях пластины. Здесь T – температура, t – время, y – координата, направленная в глубь образца, ρ – плотность, c – теплоемкость, λ – коэффициент теплопроводности материала; индексы: e – набегающий поток, 0 – начальные условия.
Определение температурной зависимости T(y, t) на основе решения уравнения (1) при известных параметрах конвективного теплообмена Te, αe представляет собой прямую задачу теплопроводности.
Пусть в результате проведения теплофизического эксперимента получены значения температуры Y(yj, ti,j) в различные моменты времени ti,j, 1 ≤ ≤ i ≤ Nj, 1 ≤ j ≤ M, где Nj – число точек измерений по времени для j датчика с координатой yj, M – число датчиков. Восстановление параметров {αe, Te} по известным экспериментальным значениям температуры Y(yj, ti,j) составляет суть граничной обратной задачи теплопроводности [4–6].
Краевая задача (1)–(4) имеет аналитическое решение [2, 16], которое записывается в виде
(5)
$\begin{gathered} \theta (\eta ,{\text{Fo}},{\text{Bi}}) = \frac{{T(y,\,t) - {{T}_{0}}}}{{{{T}_{e}} - {{T}_{0}}}} = \\ = 1 - \sum\limits_{n = 1}^\infty {{{{( - 1)}}^{{n + 1}}}{{A}_{n}}\cos [{{\mu }_{n}}(1 - \eta )]} \exp ( - \mu _{n}^{2}{\text{Fo),}} \\ \end{gathered} $(6)
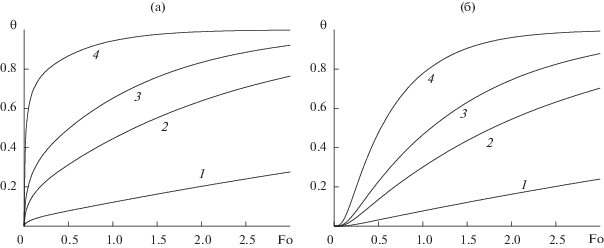
$\begin{gathered} {\text{ctg(}}{{\mu }_{n}}) = \frac{1}{{{\text{Bi}}}}{{\mu }_{n}}, \\ {\text{Fo}} = \frac{{at}}{{{{h}^{2}}}},\,\,\,\,{\text{Bi}} = \frac{{{{\alpha }_{e}}h}}{\lambda },\,\,\,\,\eta = \frac{y}{h}, \\ {{A}_{n}} = \frac{{2{\text{Bi}}\sqrt {\mu _{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} }}{{{{\mu }_{n}}(\mu _{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}})}}. \\ \end{gathered} $Здесь θ, η – безразмерные температура и координата; Fo – число Фурье (безразмерное время); Bi – критерий Био; An – амплитудный множитель; μn – корни характеристического уравнения (6). Для выполнения практических инженерных расчетов номограммы зависимости температуры θ(η, Fo, Bi) для наружной (η = 0) и тыльной поверхностей (η = 1) пластины достаточно подробно представлены в литературе [2, 17]. Графики зависимости θ(0, Fo, Bi) и θ(1, Fo, Bi) для указанных поверхностей пластины при различных значениях Bi в диапазоне 0.1 < Bi < 5 показаны на рис. 2. Видно, что для тыльной поверхности имеет место сдвиг температурных кривых по числу Fo, обусловленный требуемым временем прохождения температурной волны по толщине пластины.
Рис. 2.
Безразмерная температура наружной θ(0, Fo, Bi) (а) и тыльной θ(1, Fo, Bi) (б) поверхностей пластины в зависимости от времени Fo при различных значениях параметра Bi: 1 – Bi = 0.1, 2 – 0.5, 3 – 1, 4 – 5.
Корни μn характеристического уравнения (6) являются положительными и строго возрастающими, поэтому с ростом времени при Fo > 0.55 [2] все члены ряда (5) становятся малыми по сравнению с первым. В этом случае решение (5) упрощается и принимает вид
Данная стадия нагрева соответствует наступлению регулярного теплового режима, при котором зависимость между (Te – T) и временем t в любой точке пластины описывается простой экспонентой, а зависимость ln(Te – T) от времени t имеет вид прямой. Такой характер поведения локального решения послужил основой для разработки приближенных методов расчета коэффициента теплоотдачи αe [18] и успешно применяется на практике в настоящее время.
Однако следует заметить, что c увеличением числа Fo возрастает и влияние тепловых потерь на результаты измерений, которые трудно избежать в теплофизическом эксперименте. Поэтому при его постановке предпочтительны малые времена измерений, где для правильного расчета температуры требуется применение общего вида решения (5).
Несмотря на довольно сложную структуру (5) и необходимость решения трансцендентного уравнения (6), выражение (5) является точным, а не приближенным. Причем это преимущество имеет место и по отношению к численным методам решения прямой задачи (1)−(4) ввиду наличия в них ошибок аппроксимации. Следовательно, прямое использование (5) при решении ОЗТ позволяет повысить точность обработки результатов теплофизического эксперимента без выделения стадии нагрева (начальной, переходной, регулярной) и необходимого диапазона чисел Фурье (Fo).
КОЭФФИЦИЕНТЫ ЧУВСТВИТЕЛЬНОСТИ И ИХ АНАЛИЗ
Для планирования эксперимента необходимо знать оптимальное время, при котором экспериментальные данные содержат максимум информации об искомых параметрах, а влияние погрешности измерений на значения минимально. Математически это соответствует координате максимума производной от решения по искомому параметру.
Рассмотрим безразмерные коэффициенты чувствительности ZTe, ZBi решения (5) к изменению параметров Te и Bi (коэффициента теплоотдачи αe) [4, 6]. Взяв соответствующие производные по этим параметрам, получим
Графики зависимостей ZBi, ZTe от числа Fo для наружной (η = 0) и тыльной (η = 1) поверхности пластины при различных значениях Bi приведены на рис. 3. Чем выше значения этих коэффициентов, тем точнее при данном уровне погрешности измерений можно определить искомый параметр. И наоборот, малая величина этих коэффициентов означает слабый отклик решения на изменение данных параметров и, следовательно, практическую трудность и высокую погрешность их определения из граничной обратной задачи теплообмена.
Рис. 3.
Коэффициенты чувствительности ZTe и ZBi в зависимости от времени Fo для наружной (а) и тыльной (б) поверхности пластины при различных значениях параметра Bi: (а) – η = 0, (б) – η = 1; 1–3 – ZTe, 1 '–3 ' – ZBi для Bi = 0.5, 1, 5.
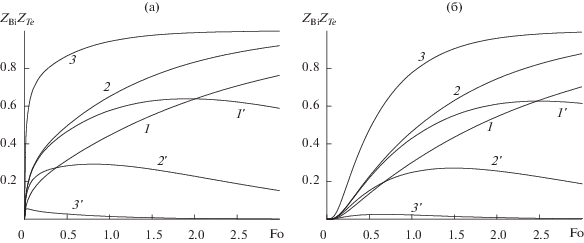
Из рисунка видно, что коэффициент чувствительности ZTe увеличивается с ростом числа Fo, поэтому для определения температуры газового потока Te предпочтительны большие времена. В противоположность этому зависимость ZBi имеет немонотонный характер с наличием максимума, положение и уровень которого зависит от числа Bi. Он находится из условия ${{\partial {{Z}_{{{\text{Bi}}}}}} \mathord{\left/ {\vphantom {{\partial {{Z}_{{{\text{Bi}}}}}} {\partial {\text{Fo}}}}} \right. \kern-0em} {\partial {\text{Fo}}}} = {\text{0}}$, либо графически. Соответствующие значения ZBi(Fomax), θ(Fomax) для различных чисел Bi приведены в табл. 1. Из нее видно, что при Bi > 1 резко падает уровень коэффициента чувствительности ZBi, что осложняет решение граничной ОЗТ. Поэтому при постановке теплофизического эксперимента по определению коэффициента теплоотдачи αe предпочтение следует отдавать случаям с Bi < 1.
Таблица 1.
Координата Fomax максимума коэффициента чувствительности ZBi(Fomax) для наружной (η = 0) и тыльной (η = 1) поверхностей пластины при различных значениях Bi
| Bi | η = 0 | η = 1 | ||||
|---|---|---|---|---|---|---|
| Fomax | ZBi(Fomax) | θ(Fomax) | Fomax | ZBi(Fomax) | θ(Fomax) | |
| 0.5 | 1.91 | 0.64 | 0.62 | 2.49 | 0.63 | 0.63 |
| 1 | 0.81 | 0.29 | 0.60 | 1.49 | 0.27 | 0.63 |
| 3 | 0.08 | 0.09 | 0.53 | 0.80 | 0.06 | 0.61 |
| 5 | 0.03 | 0.06 | 0.52 | 0.65 | 0.03 | 0.60 |
Значение безразмерной температуры θ(Fomax) в точке максимума коэффициента чувствительности ZBi(Fomax) при различных Bi согласно табл. 1 меняется довольно слабо. Для наружной поверхности (η = 0) пластины оно находится в диапазоне от 0.52 до 0.63, для тыльной поверхности – от 0.6 до 0.63 при изменении Bi в широких пределах 0.5 < Bi < 5. Полученные данные дают представление о времени и точках на температурной кривой, которые несут в себе максимум информации о коэффициенте теплоотдачи. Влияние погрешности измерений здесь также будет минимальным. Таким образом, экспериментальная информация для восстановления αe представляет наибольший практический интерес в окрестности точки максимума зависимости ZBi.
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
Рассмотрим общий случай определения αe, Te по экспериментальным значениям температуры Y(yj, ti,j) в моменты времени ti,j для M датчиков с координатами yj (1 ≤ j ≤ M). Математически граничная обратная задача сводится к минимизации суммы квадратов отклонений экспериментальных значений Y(yj, ti,j) от расчетных T(yj, ti,j) в измеренных точках по времени для всех датчиков:
(9)
$\begin{gathered} J({\text{Bi}},{{T}_{e}}) = \\ = \sum\limits_{j = 1}^M {\sum\limits_{i = 1}^{{{N}_{j}}} {{{{\left\{ {Y({{y}_{j}},{{t}_{{i,j}}}) - ({{T}_{e}} - {{T}_{0}})\theta ({{\eta }_{j}},{\text{F}}{{{\text{o}}}_{{i,j}}},{\text{Bi}})} \right\}}}^{2}}} } \to \\ \to \min {\kern 1pt} . \\ \end{gathered} $Используя условие минимума функционала (9), получим систему нормальных нелинейных уравнений метода наименьших квадратов [6, 19] для определения неизвестных {Bi, Te}(так как αe входит множителем в Bi):
(10)
$\left\{ \begin{gathered} \frac{{\partial J}}{{\partial {\text{Bi}}}} = - 2\sum\limits_{j = 1}^M {\sum\limits_{i = 1}^{{{N}_{j}}} {\left\{ {Y({{y}_{j}},{{t}_{{i,j}}})} \right. - } } \hfill \\ \left. { - \,\,({{T}_{e}} - {{T}_{0}})\theta ({{\eta }_{j}},{\text{F}}{{{\text{o}}}_{{i,j}}},{\text{Bi}})} \right\}{{\left( {\frac{{\partial T}}{{\partial {\text{Bi}}}}} \right)}_{{i,j}}} = 0, \hfill \\ \frac{{\partial J}}{{\partial {{T}_{e}}}} = - 2\sum\limits_{j = 1}^M {\sum\limits_{i = 1}^{{{N}_{j}}} {\left\{ {Y({{y}_{j}},{{t}_{{i,j}}}) - } \right.} } \hfill \\ \left. { - \,\,({{T}_{e}} - {{T}_{0}})\theta ({{\eta }_{j}},{\text{F}}{{{\text{o}}}_{{i,j}}},{\text{Bi}})} \right\}{{\left( {\frac{{\partial T}}{{\partial {{T}_{e}}}}} \right)}_{{i,j}}} = 0. \hfill \\ \end{gathered} \right.$Входящие в (10) сомножители в круглых скобках представляют собой рассмотренные выше коэффициенты чувствительности (7), (8) решения в соответствующих точках по времени. Они играют роль весовых множителей при невязке между экспериментальными и расчетными значениями. В частном случае, когда температура потока Te является известной, в (10) остается одно уравнение для определения Bi. Решение системы уравнений (10) осуществлялось численным образом. Следует отметить, что в предложенной методике используются только дискретные измерения температуры и ни на одном из ее этапов не применяется численное дифференцирование и сглаживание экспериментальной зависимости Y(yj, ti,j), влияющее на результат решения ОЗТ.
ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДИКИ
Рассмотрим конвективный нагрев инертного материала с начальной температурой T0 = 0°C. Пусть параметры стационарного газового потока составляют Te = 1000°C, αe = 100 Вт/(м2 K); теплофизические характеристики материала: ρ = = 100 кг/м3, λ = 0.1 Вт/(м K), c = 1000 Дж/(кг K) [15], толщина пластины h = 5 мм. При данных теплофизических характеристиках материала пластины коэффициент температуропроводности составляет a = 10–6 м2/c, критерий Biexact = 5, число Fo = t/25, где t – время в с. Приведенный выше анализ показывает, что при указанном значении Bi коэффициент чувствительности ZBi имеет низкий уровень и пример является достаточно трудным для решения граничной ОЗТ.
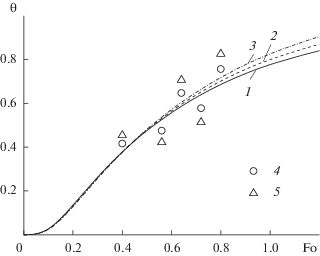
Рассмотрим показания одиночного датчика на поверхности тела (рис. 4). Возьмем несколько произвольных значений времени измерений ti = = {0.2, 0.6, 0.8, 1.0, 1.2} с, что в безразмерном виде соответствует числам Foi = {0.008, 0.024, 0.032, 0.04, 0.048}. В качестве “экспериментальных” значений Yi(yj, ti) здесь и ниже будем использовать возмущенные значения точного решения Texact(yj, ti) с относительной погрешностью ε, вычисленные по формуле Yi,j(yj, ti) = Texact(yj, ti)(1 ± ε). Учитывалась несимметричная ошибка в исходных данных. На рис. 4 кривой 1 показано точное решение, дискретные экспериментальные значения температуры с различной погрешностью от текущих значений указаны значками. Так как коэффициент теплоотдачи αe входит в критерий Bi, то при решении ОЗТ восстанавливалось его значение.
Рис. 4.
Температура наружной поверхности пластины (одиночный датчик): 1 – точные; 2, 3 – восстановленные значения температуры при ε = 0.1 и 0.2; 4, 5 – экспериментальные данные с относительной погрешностью ε = 0.1 и 0.2.
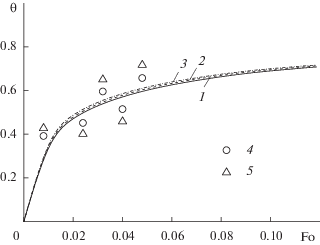
Результаты решения ОЗТ на основе численной реализации системы (10) отнесены к своим точным значениям (Te)exact, Biexact и приведены в табл. 2. В последнем столбце рассмотрен случай определения Bi при известной температуре потока Te на основе решения одного уравнения в (10). Видно, что при отсутствии погрешности в исходных данных (ε = 0) параметры Bi, Te восстанавливаются точно. Наличие ошибки в измерениях, в том числе достаточно высокой в 10% (ε = 0.1) и 20% (ε = 0.2) не увеличивает погрешность решения граничной ОЗТ. Из таблицы видно, что один искомый параметр Bi восстанавливается с большей точностью, чем два {Bi, Te}. Близость кривых 2, 3 на рис. 4 к точному решению 1 с использованием восстановленных значений {Bi, Te} при ε = 0.1 и 0.2 (см. табл. 2) показывает хорошую точность и устойчивость методики к погрешности исходных данных.
Таблица 2.
Решение граничной ОЗТ: датчик на наружной поверхности пластины (η = 0)
| ε | {Te/(Te)exact, Bi/Biexact} | Bi/Biexact |
|---|---|---|
| 0 | {1.0, 1.0} | 1.0 |
| 0.05 | {0.997, 1.02} | 1.01 |
| 0.10 | {0.994, 1.04} | 1.03 |
| 0.20 | {0.983, 1.10} | 1.06 |
Для датчиков, размещенных внутри (η = 0.4) и на тыльной поверхности (η = 1) пластины, использовались более поздние времена измерений ti = {6, 10, 12, 14, 16} с и ti = {10, 14, 16, 18, 20} с, которые по числу Fo составляют значения Foi = = {0.24, 0.4, 0.48, 0.56, 0.64} и Foi = {0.4, 0.56, 0.64, 0.72, 0.8} соответственно. Результаты решения ОЗТ представлены в табл. 3 и 4, а для тыльной поверхности пластины показаны на рис. 5. Из таблиц (последний столбец) следует, что точность восстановления параметра Bi для заглубленных датчиков по сравнению с наружной поверхностью (табл. 2) заметно снижается. То же самое относится и к случаю одновременного определения двух параметров {Bi, Te}. Необходимо отметить, что погрешность исходных данных в 20% (ε = 0.2) все-таки является избыточной, так как реальная ошибка измерений в экспериментах находится на уровне 5–10% (ε ≈ 0.05–0.1). Тем не менее методика позволяет получать приемлемые результаты даже в этом случае, что подтверждается ходом кривых 2, 3 температуры на рис. 5 с использованием восстановленных значений параметров {Bi, Te} из табл. 4. Во всех случаях точность определения температуры среды Te выше, чем параметра Bi (коэффициента теплоотдачи), что находится в полном соответствии с анализом коэффициентов чувствительности.
Таблица 3.
Решение ОЗТ: датчик внутри пластины на глубине (η = 0.4)
| ε | {Te/(Te)exact, Bi/Biexact} | Bi/Biexact |
|---|---|---|
| 0 | {1.0, 1.0} | 1.0 |
| 0.05 | {1.01, 0.98} | 1.04 |
| 0.10 | {1.03, 0.96} | 1.08 |
| 0.20 | {1.05, 0.92} | 1.17 |
Таблица 4.
Решение ОЗТ: датчик на тыльной поверхности пластины (η = 1)
| ε | {Te/(Te)exact, Bi/Biexact} | Bi/Biexact |
|---|---|---|
| 0 | {1.0, 1.0} | 1.0 |
| 0.05 | {1.03, 0.92} | 1.04 |
| 0.10 | {1.06, 0.83} | 1.08 |
| 0.20 | {1.14, 0.68} | 1.16 |
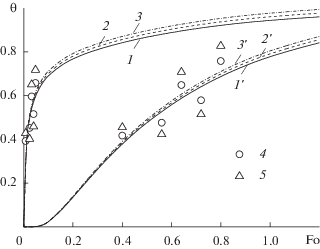
Представляет интерес совместное использование показаний датчиков для рассмотренных выше случаев при решении граничной ОЗТ, так как это увеличивает количество независимых точек измерений в различные моменты времени. Результаты расчетов приведены в табл. 5–7, а в случае размещения двух датчиков на наружной и тыльной поверхностях показаны на рис. 6. Кривые 2, 3 и 2 ', 3 ' на рис. 6, полученные с использованием восстановленных значений {Bi, Te} (табл. 6), воспроизводят точное решение 1 и 1 ', что говорит о хорошей точности их определения. Практически важно, что вполне приемлемый результат достигается и при использовании датчиков на внутренней и тыльной поверхностях (табл. 7). Таким образом, совместное использование показаний нескольких датчиков в различные моменты времени стабилизирует ошибки измерений, повышает информативность и точность идентификации параметров {Bi, Te} конвективного теплообмена.
Таблица 5.
Результаты расчетов: датчики на наружной поверхности (η = 0) и внутри (η = 0.4) пластины
| ε | {Te/(Te)exact, Bi/Biexact} | Bi/Biexact |
|---|---|---|
| 0 | {1.0, 1.0} | 1.0 |
| 0.05 | {1.01, 0.998} | 1.02 |
| 0.10 | {1.02, 0.996} | 1.04 |
| 0.20 | {1.03, 0.992} | 1.08 |
Таблица 6.
Результаты расчетов: датчики на наружной (η = 0) и тыльной (η = 1) поверхностях пластины
| ε | {Te/(Te)exact, Bi/Biexact} | Bi/Biexact |
|---|---|---|
| 0 | {1.0, 1.0} | 1.0 |
| 0.05 | {1.01, 0.997} | 1.02 |
| 0.10 | {1.02, 0.993} | 1.04 |
| 0.20 | {1.04, 0.987} | 1.08 |
ЗАКЛЮЧЕНИЕ
Предложена методика определения коэффициента теплоотдачи αe и температуры Te стационарного газового потока по дискретным измерениям температуры материала теплоизолированной пластины, не содержащая операций численного дифференцирования и сглаживания экспериментальных данных.
На основе анализа коэффициентов чувствительности решения к изменению искомых параметров определен наиболее информативный временнóй диапазон, внутри которого влияние погрешности измерений на значения параметров минимально, что очень важно для планирования и постановки теплофизического эксперимента.
Предложенная методика обработки данных проиллюстрирована на примерах возмущенных показаний датчиков, размещенных на наружной, внутренней и тыльной поверхностях пластины. Полученные результаты показывают, что методика устойчива к погрешности исходных данных, не требует их сглаживания, выбора диапазона измерений по числу Фурье и позволяет повысить точность решения граничной обратной задачи теплопроводности по определению параметров конвективного теплообмена.
Список литературы
Полежаев Ю.В., Юревич Ф.Б. Тепловая защита. М.: Энергия, 1976. 392 с.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Лыков А.В. Тепломассообмен. Спр. М.: Энергия, 1978. 480 с.
Алифанов О.М. Обратные задачи теплообмена. М.: Машиностроение, 1988. 280 с.
Алифанов О.М., Артюхин Е.А., Румянцев С.В. Экстремальные методы решения некорректных задач и их приложение к обратным задачам теплообмена. М.: Наука, 1988. 288 с.
Beck J.V., Blackwell B., St. Clair C.R. Inverse Heat Conduction. Ill-posed Problems. N.Y.: J. Wiley and Sons Publ., 1985. 308 p.
Кабанихин С.И. Обратные и некорректные задачи. Новосибирск: Сиб. науч. изд-во, 2009. 458 с.
Коздоба Л.А., Круковский П.Г. Методы решения обратных задач теплопереноса. Киев: Наукова думка, 1982. 359 с.
Alifanov O.M. Inverse Problems in Identification and Modeling of Thermal Processes: Russian Contributions // Int. J. Numer. Methods Heat Fluid Flow. 2017. V. 27. № 3. P. 711.
Давлетшин И.А., Михеев Н.И. Структура течения и теплообмен при отрыве пульсирующего потока // ТВТ. 2012. Т. 50. № 3. С. 442.
Linda M., Hromasova M. Model Analysis of Temperature Sensors // Engineering for Rural Development. 2016. Jan. P. 566.
Дилигенская А.Н. Метод минимаксной оптимизации в двумерной граничной обратной задаче теплопроводности // ТВТ. 2019. Т. 57. № 2. С. 226.
Туголуков Е.Н., Карпук В.А., Рухов А.В. Решение обратных задач теплопроводности для многослойных тел канонической формы // Вестн. Тамбовск. гос. техн. ун-та. 2013. Т. 19. № 3. С. 577.
Артюхин Е.А., Баранов В.В., Ганчев Б.Г., Ненарокомов А.В. Исследование нестационарного теплообмена при смачивании нагретых поверхностей // ТВТ. 1987. Т. 25. № 5. С. 975.
Зверев В.Г., Назаренко В.А., Панько С.В., Теплоухов А.В. Определение параметров конвективного теплообмена по измерениям температуры материала // ТВТ. 2010. Т. 48. № 5. С. 779.
Carslaw H.S., Jaeger J.C. Conduction of Heat in Solids. N.Y.: Oxford Univ., 1959.
Пехович А.И., Жидких В.М. Расчеты теплового режима твердых тел. Л.: Энергия, 1976.
Кондратьев Г.М. Регулярный тепловой режим. М.: Гостехиздат, 1954.
Kahaner D., Moler C., Nash S. Numerical Methods and Software. N.Y.: Prentice Hall, 1988.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур