Теплофизика высоких температур, 2021, T. 59, № 1, стр. 3-11

ВВЕДЕНИЕ

Прошло уже более 50 лет, как в нашей стране и за рубежом были развернуты исследования различных свойств неидеальной плазмы в широком диапазоне параметров. С результатами этих исследований можно ознакомиться в [1]. Они имели как прикладной, так и общефизический аспект, а их начало совпало с развертыванием в СССР работ по ряду энергетических проектов. Это в первую очередь работы по созданию газофазного ядерного реактора [2] и мощных МГД-генераторов. В области теории определенное стимулирующее значение имел обзор Нормана, Старостина [3], в котором выдвигалась гипотеза о возможном существовании плазменного фазового перехода. Одним из главных методов расчета уравнения состояния, равновесного состава и на их основе кинетических коэффициентов стал метод смеси и построенные с его применением химические, многокомпонентные газоплазменные модели.

Разнообразие моделей и их достаточная сложность были обусловлены тем, что авторы стремились создать модели широкодиапазонные, охватывающие максимально широкий диапазон плотностей (от твердотельных до газовых) и температур (от тысяч до миллионов градусов). Особенно высокая потребность в таких моделях возникала в астрофизике для описания внутреннего состояния звезд и планет, а также в физике высоких плотностей энергии для описания превращений вещества при ударном сжатии. Естественным образом возникала необходимость учета эффектов неидеальности при отсутствии малых параметров и при наличии химических реакций, что приводило к построению сложных интерполяционных соотношений [4–10]. Следует отметить, что определенные проблемы возникали и в связи с теоретическим предсказанием возможности существования плазменного фазового перехода в плотной плазме, представленным в [3]. Авторы моделей, которые верили в его существование, включали такую возможность в разрабатываемую модель. И наоборот. Отметим для примера достаточно известные в литературе химические модели для водорода и инертных газов [4–8, 10], паров металлов [7–9] и т.д. Некоторые из них содержат плазменный фазовый переход, а некоторые не содержат. Все упомянутые модели являются достаточно сложными, и их можно назвать “авторскими”, поскольку повторить их практически невозможно и тем более использовать в экспресс-расчетах, не прибегая к помощи авторов.

В данной работе предлагается химическая модель неидеальной плазмы, как говорят, “для пользователей”, т.е. простая и надежная. Из всего разнообразия плазменных состояний рассматривается неидеальная плазма, которая представляет собой смесь электронов, ионов и атомов – атомарную плазму. Электронная компонента считется невырожденной, классической. Такая плазма охватывает достаточно большую область фазовой диаграммы вещества: по температуре – от нескольких тысяч до десятков тысяч градусов (где начинается вторая ионизация), по плотности – от разреженной и вплоть до критических плотностей, где возникает дефицит малых параметров. Сознательно упрощая номенклатуру частиц (до трех), сосредоточим внимание на проблемах учета эффектов неидеальности в химически реагирующей плазме, по которым, несмотря на 50 лет исследований, ясности нет до сих пор, даже для плазмы атомарной.

Формальными, но легко устранимыми ограничениями области применимости предлагаемой модели являются многократная ионизация, появление молекул и эффекты вырождения электронного газа. Учет этих эффектов для различных химических плазменных моделей несложен и достаточно единообразен.

ОБЩИЕ СООТНОШЕНИЯ

В многочисленных химических моделях, предложенных к настоящему времени, учитываются десятки, а иногда и сотни компонент. В качестве примера можно привести уникальный математический код “SAHA-S”, созданный для учета тонких плазменных эффектов, протекающих на Солнце с учетом многочисленных примесных добавок, в котором учтены около сотни компонент [11]. Это, конечно, штучный, авторский продукт, для создания которого нужны уникальный опыт и много времени.

Большинство различий между моделями обусловлены выбором межчастичных потенциалов и способом расчета поправок на взаимодействие “свободных” частиц как нейтральных, так и заряженных в газоплазменной смеси с реакциями. Отсутствие единого мнения в этом вопросе до настоящего времени связано с одной причиной – недостаточной теоретической обоснованностью самого метода смеси для систем с реакциями.

В настоящей работе ограничимся небольшим числом компонент, чтобы порекомендовать наиболее надежные с точки зрения авторов способы расчета поправок на неидеальность.

Рассмотрим неидеальную смесь атомов ${{N}_{a}},$ ионов ${{N}_{i}}$ и электронов ${{N}_{e}}.$ Система занимает объем $V$ и находится при температуре $kT = {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }{\text{.}}$ Свободную энергию смеси $F$ можно представить в виде идеально-газового слагаемого ${{F}^{0}}$ и добавки $\Delta F,$ описывающей эффекты взаимодействия между частицами:

В (1) e – основание натурального логарифма, ${{\lambda }_{l}} = \sqrt {{{2\pi {{\hbar }^{2}}\beta } \mathord{\left/ {\vphantom {{2\pi {{\hbar }^{2}}\beta } {{{m}_{l}}}}} \right. \kern-0em} {{{m}_{l}}}}} $ – тепловая длина волны Де-Бройля частицы сорта l, ${{Q}_{l}}$ – внутренняя статистическая сумма частицы сорта $l.$ Слагаемые в правой части (2) соответствуют поправкам на неидеальность за счет взаимодействий заряд–заряд, заряд–атом и атом–атом.

В общем виде статистическую сумму частицы сорта $l$ можно представить как:

где ${{g}_{l}},$ ${{E}_{l}}$ – статистический вес и энергия связи частицы сорта l. Подробное описание методики расчета этих величин можно найти во многих монографиях, посвященных физике низкотемпературной плазмы [1, 12].

Для удобства в табл. 1 представлены расчетные формулы для настоящей модели. Необходимые для расчета константы можно найти в общедоступных справочниках; ${{g}_{{ik}}}$ – статистические веса ионов (если есть низколежащие уровни); $\Delta {{E}_{1}}$ – энергия возбуждения первого ионного уровня (для ионов инертных газов, см., например, [13]); ${{g}_{{ak}}},$ ${{E}_{{ak}}}$ – статистические веса и энергия связи электрона в атоме соответственно. Проблеме ограничения формально расходящейся статистической суммы атома посвящены десятки и даже сотни работ. Практика показала, что для расчетов можно использовать практически любой сходящийся вариант: от статсуммы в приближении Планка–Ларкина до статсуммы в приближении ближайшего соседа (ПБС). Не годится к использованию единственная статистическая сумма из ранее предлагавшихся – это статистическая сумма по уровням, рассчитанным в дебаевском потенциале. Заметим сразу, что главным источником неустойчивостей в термодинамике является не статсумма, а снижение потенциала ионизации, вызванное кулоновским взаимодействием свободных зарядов, и поправка к давлению.

В дальнейшем понадобятся химические потенциалы частиц $\beta {{\mu }_{l}} = {{\partial \beta F} \mathord{\left/ {\vphantom {{\partial \beta F} {\partial {{N}_{l}}}}} \right. \kern-0em} {\partial {{N}_{l}}}}.$

Для определения трех неизвестных величин ${{N}_{a}},~{{N}_{i}},~{{N}_{e}}$ имеем три уравнения:

уравнение для полного числа ядер

уравнение электронейтральности

уравнение ионизационного равновесия

Для химического потенциала в температурных единицах запишем

Подставляя химические потенциалы (4) в (3) и вводя степень ионизации $\alpha = {{{{N}_{e}}} \mathord{\left/ {\vphantom {{{{N}_{e}}} N}} \right. \kern-0em} N},$ получим уравнение ионизационного равновесия – формулу Саха: Решением нелинейного уравнения (5) является функция $\alpha \left( {\beta ,n} \right),$ из которой можно вычислить состав плазмы и уравнение состояния. Здесь и в дальнейшем ${{n}_{l}} = {{{{N}_{l}}} \mathord{\left/ {\vphantom {{{{N}_{l}}} V}} \right. \kern-0em} V}$ – соответствующие концентрации частиц.

ВИРИАЛЬНОЕ ПРИБЛИЖЕНИЕ

Первая поправка к свободной энергии, вызванная взаимодействием частиц с потенциалом $V\left( r \right),$ определяется вторым вириальным коэффициентом ${{B}_{{i,j}}}\left( T \right).$ Для различных частиц имеем

а для одинаковых добавляется множитель ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$

Для расчета второго вириального коэффициента существуют два соотношения:

классическое

и квантовое (формула Бета–Уленбека) Здесь ${{g}_{k}},~{{\varepsilon }_{k}},~{{\delta }_{l}}$ – статистические веса, энергии связи и фазы рассеяния парных состояний. Судьба этих соотношений сложилась по-разному, особенно применительно к моделям смеси. Сразу отметим, что формулы (6) и (7) весьма различные. Формула (6) содержит интегрирование по всем расстояниям пары взаимодействующих частиц без разделения состояний на связанные и свободные. Формула (7), наоборот, не содержит интегрирования по расстояниям и состоит из двух слагаемых: первое слагаемое соответствует вкладу связанных состояний, а второе – вкладу свободных или состояниям рассеяния. Казалось бы, именно соотношение (7) следовало бы использовать в системе с реакциями образования парных связанных состояний. Но здесь подстерегают проблемы. Первое слагаемое в (7), как правило, значительно больше второго, и использование непосредственно выражения (7) ведет к абсурду (в каноническом ансамбле). Успешным оказалось его использование в большом каноническом ансамбле (БКА). Для атомарной плазмы в [13] рассчитан квантовый второй вириальной коэффициент и получено уравнение состояния в этом приближении. В работе Семенова А.М. [14] предложен метод исходных атомов и получены уравнения состояния высокой точности для атомарно-молекулярных паров щелочных металлов на основе квантового второго вириального коэффициента (7). Применительно к газоплазменным моделям с одновременным учетом молекул и заметной ионизацией строгих результатов не существует. Видимо, по этой причине химические модели неидеальных, химически реагирующих смесей столь разнообразны. Большинство исследователей, но не все, приняло такую точку зрения: первое слагаемое в (7) необходимо учитывать в виде вклада отдельной компоненты, а второе – как поправку на взаимодействие в непрерывном спектре. Будем исходить из этой концепции.

ВЗАИМОДЕЙСТВИЕ ЗАРЯД–ЗАРЯД ΔF_ch–ch

Это слагаемое породило интенсивную, многолетнюю дискуссию, которая не окончилась и поныне. Обстоятельный обзор основных достижений теории к концу 1960-х гг. и формулировка нерешенных проблем даны в известном обзоре Нормана и Старостина [3]. С последними достижениями можно ознакомиться в [1]. Остановимся на тех из них, которые сохранили свою актуальность в расчетных моделях и в настоящее время. Прежде всего это классическая теория Дебая для электролитов, которая позволила вычислить добавку к свободной энергии в системе заряженных шаров с диаметром D:

где $q$ – заряд шара, а ${{R}_{{\text{D}}}} = {1 \mathord{\left/ {\vphantom {1 {\sqrt {4\pi \beta {{q}^{2}}\left( {{{n}_{e}} + {{n}_{i}}} \right)} }}} \right. \kern-0em} {\sqrt {4\pi \beta {{q}^{2}}\left( {{{n}_{e}} + {{n}_{i}}} \right)} }}$ – дебаевский радиус. Для плазменных моделей было принято $D = 0,$ при этом молчаливо обходился вопрос о сходимости других членов вириального ряда. Для заряженных шаров они конечны, а для точечных зарядов все расходятся, кроме последовательности кольцевых диаграмм. Именно она и приводит к конечному результату (8) с $D = 0.$ Химические модели с его использованием в дальнейшем будем называть дебаевской моделью. Естественно, эти результаты справедливы там, где применимо представление о коллективном самосогласованном характере экранирования заряда (существование функциональной связи плотности частиц и плотности заряда в уравнении Пуассона–Больцмана – приближение сплошной среды). Это требование подразумевает выполнение очевидного неравенства где ${{R}_{i}}$ – радиус ионной ячейки Вигнера–Зейца Как правило, неравенство (9) игнорируется и выражение (8) с $D = 0$ используется в расчетах далеко за границами его применимости. Из неравенства (9) следует, что в сфере с радиусом ${{R}_{{\text{D}}}}$ должно находиться много (больше единицы) частиц. Введем дебаевский параметр кулоновской неидеальности

В литературе также используется параметр неидеальности, иногда называемый маделунговским:

Неравенство (9) будет тогда выглядеть как $\Gamma \leqslant \gamma .$ Используя связь между параметрами $6{{\gamma }^{3}} = {{{{\Gamma }}}^{2}},$ приходим к весьма важному неравенству, определяющему границы применимости дебаевской теории и связанному с коллективным характером экранировки (приближение сплошной среды):

Неравенство (12) очень жесткое и ведет к неожиданному выводу: для учета эффектов неидеальности в низкотемпературной плазме дебаевская теория вообще не нужна, поскольку в области ее применимости (12) эффекты неидеальности малы и, следовательно, их можно не учитывать.

Сторонники плазменного фазового перехода, как правило, игнорируют это неравенство. Во всех теориях, его предсказывающих, используется в том или ином виде дебаевский результат (8) с $D = 0,$ при этом получаемые критические точки перехода лежат в области ${{\Gamma }} = 4{\kern 1pt} --{\kern 1pt} 16,$ т.е. вне границ применимости дебаевского приближения (12). Это обстоятельство, на взгляд авторов, и разделило исследователей на две группы.

Многочисленные эксперименты подтвердили весьма ограниченную область применимости дебаевской теории в плазме. Использование дебаевской поправки в чистом виде давало наихудшее согласие с экспериментальными данными и не обнаруживало существования плазменного фазового перехода в области, предсказанной в [3]. Сторонниками плазменного фазового перехода были предложены различного рода интерполяционные соотношения, среди которых наиболее известна Pade-аппроксимация [15, 16], в которой используется дебаевский результат (8) в комбинации с результатами Маделунга и Гелл-Мана–Брюкнера [17]. Соотношения, предложенные в [15], достаточно сложны, но веских оснований для их применения нет. Рекомендуем для этой поправки простейшее соотношение, основанное на приближении ближайшего соседа. Это приближение использует представление о максимальной величине энергии кулоновского притяжения в ионизованной компоненте плазмы. В плазме низкотемпературной, в отличие от высокотемпературной, свободный электрон всегда находится рядом с ионом и экранирует его (срабатывает больцмановская экспонента). Энергия их взаимодействия и является основным вкладом в полную энергию взаимодействия электрона с плазмой:

Регулярный вывод соотношения (13) для плазмы отсутствует, поэтому свободу выбора константы $c$ оставляем авторам химических моделей. Очевидно, что ее величина близка к единице, у Маделунга $c = 0.895$. В [18] $c = {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4},$ что приводит к простейшему выражению для снижения потенциала ионизации. Возможен и иной выбор. Выражением (13) формально можно пользоваться и в разреженной плазме, поскольку обе поправки (10) и (11) в этом случае малы. Главное, что при ${{\Gamma }} > {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}$ выражение (13) дает значительно меньшую энергию, нежели ${{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {{{R}_{{\text{D}}}}}}} \right. \kern-0em} {{{R}_{{\text{D}}}}}}.$ В табл. 2 приведены соответствующие поправки к давлению, внутренней энергии и снижению потенциала ионизации на основе (13).

В [19, 20] предпринята попытка учесть эффект ограничения фазового пространства для “свободных” частиц, взаимодействующих с кулоновским потенциалом. Показано, что вклад взаимодействия свободных заряженных частиц в термодинамические функции плазмы еще меньше, чем (13).

Отметим завоевавшее популярность приближение Ликальтера [21] или дебаевское приближение в БКА, иногда называемое “большой Дебай”. Это приближение изложено и в оригинальной статье [21], и в монографиях [1, 22]. Приближение Ликальтера возникло как альтернатива дебаевскому приближению и в дальнейшем широко использовалось и используется в плазменных моделях. Оно дает результаты, близкие к ПБС, и тоже может быть рекомендовано для экспресс-расчетов как весьма удачная экстраполяция, хотя теоретически оно слабо обосновано. Приведем основные соотношения этого приближения.

Введем понятие активности ${{z}_{{e,i}}}$ – эффективной плотности электронов и ионов, по которым идет разложение в БКА. Возникает плазменный параметр $\alpha = \beta {{e}^{2}}\sqrt {4\pi \beta {{e}^{2}}\left( {{{z}_{e}} + {{z}_{i}}} \right)} ,$ который связан с параметром ${{\Gamma }}$ в уравнении Ликальтера

Решением этого уравнения является функция $\alpha \left( {{\Gamma }} \right)$, которая позволяет рассчитать все поправки на кулоновскую неидеальность. Например, поправку к давлению и снижение потенциала ионизации:

Приближение Ликальтера завоевало заметную популярность своей простотой, связью, пусть и формальной, с дебаевским приближением в условиях отсутствия строгих результатов. Плазменного фазового перехода приближение Ликальтера не содержит.

ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОН–АТОМ ΔF_e–a

В химических моделях для учета этого вида взаимодействия используется как классический вириальный коэффициент (6), так и квантовый (7) [23]. Для взаимодействия электрон–атом в случае, если существует стабильный отрицательный ион, рекомендуем использовать член с нулевым моментом второго слагаемого (7).

Для расчета фазы рассеяния с нулевым моментом можно, не конкретизируя вид потенциала взаимодействия электрон–атом, воспользоваться приближением Вигнера для описания резонансного рассеяния электронов с импульсом $p$ на атомной системе, с которой он образует слабосвязанное состояние с энергией связи ${{E}_{A}}$ [24]:

После несложных преобразований получим

где ${{\Phi }}\left( x \right)$ – функция ошибок. При низких температурах ($\beta {{E}_{A}} \gg 1$) формула (14) переходит в известное выражение для вириального коэффициента $B_{{ea}}^{{\text{H}}}\left( T \right) = \lambda _{e}^{2}L$ через длину рассеяния, которая в данном случае определяется соотношением $L = {{a}_{0}}\sqrt {{{{\text{Ry}}} \mathord{\left/ {\vphantom {{{\text{Ry}}} {{{E}_{A}}}}} \right. \kern-0em} {{{E}_{A}}}}} $ (где Ry – энергетическая постоянная Ридберга). В результате

ВЗАИМОДЕЙСТВИЕ ИОН–АТОМ ΔF_i–a И АТОМ–АТОМ ΔF_a–a

Вклад состояний непрерывного спектра в квантовый второй вириальный коэффициент подробно рассмотрен Хиллом в монографии [25]. Им показано, что для взаимодействия тяжелых частиц следует использовать его квазиклассическое представление, которое для двух частиц, взаимодействующих с потенциалом $V(r),$ имеет вид (индекс H означает по Хиллу [25]):

где ${{\Gamma }}\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}{\kern 1pt} ,x} \right)$ – неполная гамма-функция. Кажущаяся сложность выражения (15) сделала его малопопулярным в практических химических моделях. Их разработчики часто обращались к более простому, классическому выражению (6), но использовали при этом для расчета тот или иной псевдопотенциал или разного рода процедуры обрезания [8]. Однако применение исходного потенциала, например, для учета взаимодействия между свободными атомами в смеси с молекулами приводит к абсурду и оправдано лишь в случае атомов инертных газов, молекул не образующих.

В работе [26] подробно рассмотрены вириальные коэффициенты для атом-атомных и ион-атомных взаимодействий с использованием квазиклассического второго вириального коэффициента (7) для потенциалов Леннард-Джонса. Здесь приведем точные и приближенные формулы для расчета вторых вириальных коэффициентов.

Определим параметры потенциала Леннард-Джонса, описывающие взаимодействие ион–атом и атом–атом:

В табл. 3 приведены необходимые для конкретных расчетов величины, где ${{C}_{{VdW}}}$ – константа Ван-дер-Ваальса, ${{\alpha }_{D}}$ – поляризуемость атома в атомных единицах (${{a}_{0}}$ – боровский радиус). Для водорода, например, они равны $6.5$ и $4.5$ соответственно. Вводя безразмерную переменную $x = {r \mathord{\left/ {\vphantom {r \sigma }} \right. \kern-0em} \sigma },$ получим

Для функций ${{F}^{{\text{H}}}}\left( \varepsilon \right)$ Муленко И.А. [27] были предложены весьма точные аппроксимации, которые для $a{\kern 1pt} - {\kern 1pt} a$ (12–6) и $i{\kern 1pt} - {\kern 1pt} a$ (12–4) взаимодействий имеют вид

Окончательные выражения для квазиклассических вириальных поправок неожиданно оказываются существенно проще, чем соответствующие выражения даже для расчета по классической формуле (6). Для полноты они внесены в табл. 3. Итоговая поправка к свободной энергии за счет эффектов неидеальности химической модели “для пользователей” имеет вид

ПРИМЕРЫ РАСЧЕТОВ. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Прежде всего, обсудим некоторые особенности учета кулоновской неидеальности, самой дискутируемой в литературе по неидеальной плазме. Конечно, это будет авторская позиция, тем более что дискуссия по данному вопросу продолжается.

Рассмотрим относительное поведение поправок на кулоновскую неидеальность в различных моделях. В качестве переменной выберем параметр ${{\Gamma }}~$ (10), определяемый через исходные плотности заряженных частиц. На рис. 1 представлены графики зависимостей “параметров неидеальности”, рассчитанных в различных приближениях.

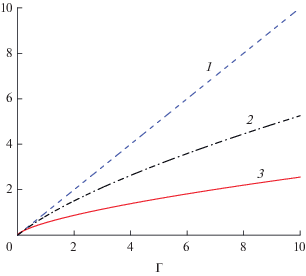
Область применимости дебаевской теории (${{\Gamma }} \leqslant {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}$) в выбранном масштабе даже не просматривается. Видна область и величина завышенных значений энергии, определяемых дебаевской теорией в сравнении с ПБС и даже с приближением Ликальтера.

Обращаем внимание на то, что в дебаевском приближении (кривая 1) плазменный фазовый переход существует, а уже в приближении Ликальтера и тем более в ПБС его нет, а ведь разница между ними не столь велика. Причина, по мнению авторов, очевидна – завышенное притяжение, предполагаемое дебаевской теорией.

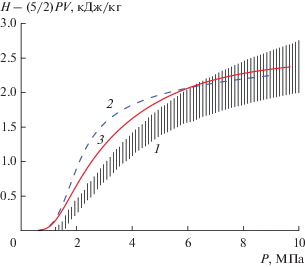
На рис. 2 нанесены уникальные экспериментальные данные [28], полученные на подогреваемой ударной трубе, обработанные специальной методикой для выделения экспериментальной полосы, соответствующей изохоре паров цезия с удельным объемом V = 200 см³/г. Там же нанесены результаты расчетов с использованием дебаевской теории и ПБС. Снова видим различие между этими расчетами и близость к эксперименту результатов ПБС.

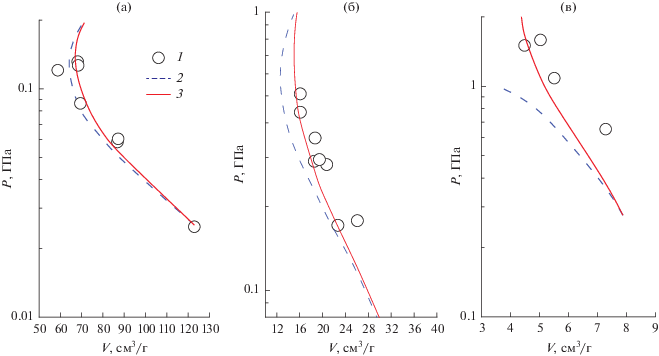
На последующих рисунках приведены зависимости давления от удельного объема на ударных адиабатах Гюгонио и данные ранних экспериментов [29, 30]. На рис. 3 представлены адиабаты аргона, отличающиеся начальным давлением. Хорошо видно появление эффектов неидеальности. Рис. 3б иллюстрирует утверждение о завышенном притяжении в дебаевской модели. На рис. 3в при больших сжатиях (малый удельный объем V < 4) дебаевская модель приводит к потере устойчивости, что является предвестником плазменного фазового перехода. Параметр ${{\Gamma }}$ в этих экспериментах достигает величин 2–4.

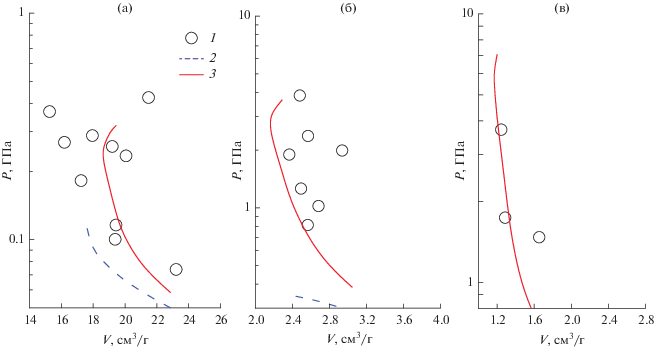
На рис. 4 нанесены аналогичные данные для ксенона. Общая картина приблизительно та же, но достигнутый уровень параметров неидеальности выше и достигает пяти. На рис. 4в все расчеты в области рассмотренных удельных объемов по дебаевской модели не приводят к разумным результатам и дают отрицательные значения давления. Расчеты по ПБС показывают стабильные, устойчивые результаты, близкие к эксперименту во всей области. Следует отметить, что при высоких давлениях на адиабатах ксенона достигаются высокие температуры и заметную роль начинают играть эффекты, связанные со второй ионизацией, чего предлагаемая модель не учитывает.

Рекомендованные формулы для учета электрон-атомного, ион-атомного и атом-атомного взаимодействия широко использовались авторами ранее в серии химических моделей для плазмы паров металлов [31] и отдельно рассмотрены в [26].

Необходимые для конкретных расчетов константы ($I,~$ ${{E}_{A}},$ ${{\alpha }_{D}},$ ${{C}_{{VdW}}}\left( {{{C}_{6}}} \right),$ ${{D}_{{ia}}},$ ${{D}_{{aa}}}$) можно найти в справочнике [32].

ЗАКЛЮЧЕНИЕ

Для построения достаточно простого и надежного варианта трехкомпонентной химической модели плазмы рассмотрены некоторые аспекты учета взаимодействий в химически реагирующей атомарной плазме. Основное внимание уделено кулоновской неидеальности, породившей самые многочисленные дискуссии. В результате предложен простой, но достаточно обоснованный вариант химической модели неидеальной атомарной плазмы, приемлемый “для пользователей”.