Теплофизика высоких температур, 2021, T. 59, № 1, стр. 12-21
Разработка кинетической модели плазмы СВЧ-разряда в режиме электронно-циклотронного резонанса с учетом временнóй эволюции функции распределения электронов
Д. С. Степанов 1, *, Э. Я. Школьников 1
1 Национальный исследовательский ядерный университет
“Московский инженерно-физический институт”
Москва, Россия
* E-mail: DSStepanov@mephi.ru
Поступила в редакцию 26.03.2020
После доработки 18.06.2020
Принята к публикации 18.06.2020
Аннотация
Разработана программа моделирования кинетики газового разряда с учетом временнóй эволюции функции распределения электронов по энергиям на примере СВЧ-разряда в режиме электронно-циклотронного резонанса в молекулярном дейтерии. Модель включает в себя усредненное нагревающее действие СВЧ-поля при циклотронном резонансе, упругие соударения электронов с электронами и тяжелыми компонентами разряда, а также неупругие реакции возбуждения и превращения. Программа учитывает временнýю эволюцию функции распределения электронов под действием указанных процессов, для чего разработан алгоритм, изменяющий границы расчетного диапазона функции распределения в зависимости от ее текущих значений, что позволяет рассматривать ее изменения в широком энергетическом диапазоне. Выработаны условия, определяющие точность работы данного алгоритма, и приведена динамика погрешности счета при вариации параметров этих условий. Показана адекватность и достоверность получаемых в модели результатов, оцененная как по величинам вносимых погрешностей, так и при сравнении со сторонними моделями.
ВВЕДЕНИЕ
Определение динамики протекания кинетических процессов в плазме газового разряда является действенным инструментом при разработке различных плазменных приборов, таких как газоразрядные лазеры, ионные источники и пр. Для этого могут использоваться математические модели различной степени сложности, включающие в себя те или иные приближения, выбор между которыми зависит от условий каждой конкретной задачи. Самый простой метод анализа кинетики газового разряда заключается в рассмотрении системы дифференциальных уравнений относительно концентрации плазменных компонент в приближении локального термодинамического равновесия и при постоянных температурах этих компонент [1]. Такая модель дает возможность оценить скорость развития разряда, его состав, а также значения кинетических коэффициентов, но ее применимость серьезно ограничена первоначальными приближениями. Следующим шагом на пути усложнения расчета газоразрядной кинетики является учет заселенности энергетических уровней рабочего газа [2–4]. Такие модели используются при разработке газовых лазеров, интерпретации спектроскопических исследований и пр. Основное ограничение в применении этих моделей связано с использованием постоянных значений концентрации или температуры электронной компоненты плазмы, иными словами, в квазистационарном приближении. Встречаются также и более сложные варианты моделирования заселенности энергетических уровней, учитывающие функцию распределения (ФР) электронов по энергиям. Тем не менее уравнение Больцмана в них решается также в условии стационара [5, 6]. Нестационарное решение уравнения Больцмана встречается в работах [7–10], где оно используется для исследования заселенности энергетических уровней газа, а также для рассмотрения процесса релаксации плазмы после окончания разряда. Данные модели применяются в областях, посвященных газовым лазерам, медицинским генераторам плазмы, системам поджига и пр. Однако оставление за рамками моделей процессов нагрева заряженных частиц электромагнитными полями, передачи энергии между компонентами плазмы, а также их превращений все еще не позволяет в полной мере исследовать переходные процессы в плазме газового разряда.
Создание математической модели, способной учитывать перечисленные выше процессы вместе с решением той или иной кинетической схемы, расширит возможности теоретического исследования различных газовых разрядов. Несмотря на общий характер поставленной задачи, она посвящена вполне конкретной проблеме описания развития СВЧ-разряда, зажигаемого в дейтерии в режиме электронно-циклотронного резонанса (ЭЦР) [11, 12], что сводит общий механизм взаимодействия электрического поля с компонентами плазмы к вполне конкретному, описанному там же. Таким образом, представленная авторами разработка программы математического моделирования кинетики плазмы газового разряда с учетом временнóй эволюции ФР электронов по энергиям будет проводиться на примере СВЧ-разряда в дейтериевом газе в режиме ЭЦР. По этой же причине здесь пока не требуется рассмотрение заселенности различных энергетических уровней атомов и молекул разряда.
ФИЗИЧЕСКАЯ МОДЕЛЬ
В общем случае для описания динамики развития газового разряда необходимо совместно решить систему кинетических уравнений, составленных для каждой из его компонент i = 1, 2, …, k [13]:
(1)
$\begin{gathered} \frac{{\delta {{f}_{i}}(t,{\mathbf{r}},{\mathbf{p}})}}{{\delta t}} + \frac{\delta }{{\delta {{x}_{\alpha }}}}\left( {{{{v}}_{\alpha }}{{f}_{i}}(t,{\mathbf{r}},{\mathbf{p}})} \right) + {\mathbf{F}}\frac{{\delta {{f}_{i}}(t,{\mathbf{r}},{\mathbf{p}})}}{{\delta {\mathbf{p}}}} = \\ = St{{f}_{i}}(t,{\mathbf{r}},{\mathbf{p}}), \\ \end{gathered} $Однако решение подобной системы является весьма нетривиальной задачей, к тому же получаемая при этом информация зачастую избыточна. В этом случае следует переходить от общей ФР к зависимости только от обобщенного импульса, заменяя усредненную часть макроскопическими уравнениями относительно концентрации, в результате чего система (1) преобразуется следующим образом:
(2)
$\begin{gathered} \frac{{\delta {{f}_{i}}(t,{\mathbf{p}})}}{{\delta t}} + {\mathbf{F}}\frac{{\delta {{f}_{i}}(t,{\mathbf{p}})}}{{\delta {\mathbf{p}}}} = St{{f}_{i}}(t,{\mathbf{rp}}), \\ \frac{{\delta {{n}_{i}}(t,{\mathbf{r}})}}{{\delta t}} + {\text{div}}\left( {{{n}_{i}}(t,{\mathbf{r}}){{{\mathbf{v}}}_{i}}({\mathbf{r}})} \right) = {{N}_{i}}(t,{\mathbf{r}}), \\ \end{gathered} $При использовании системы уравнений (2) для описания динамики плазмы избыточным можно считать и представление ее тяжелых компонент в форме ФР. Дело в том, что электроны в разряде являются наиболее активной составляющей, которая интенсивнее взаимодействует как с электромагнитными полями, так и с тяжелыми частицами, и именно электроны преимущественно определяют эволюцию состояний плазмы. Таким образом, при ее описании целесообразно оставлять уравнение относительно ФР по обобщенным импульсам только для электронной компоненты, а для тяжелых компонент – преобразовывать относительно величины средней энергии (температуры):
(3)
$\begin{gathered} \frac{{\delta {{f}_{e}}(t,{\mathbf{p}})}}{{\delta t}} + {\mathbf{F}}\frac{{\delta {{f}_{e}}(t,{\mathbf{p}})}}{{\delta {\mathbf{p}}}} = St{{f}_{e}}(t,{\mathbf{rp}}),\, \\ \frac{{\delta {{n}_{e}}(t,{\mathbf{r}})}}{{\delta t}} + \,\,{\text{div}}\left( {{{n}_{e}}(t,{\mathbf{r}}){{{\mathbf{v}}}_{e}}({\mathbf{r}})} \right) = {{N}_{e}}(t,{\mathbf{r}}), \\ \frac{{\delta {{w}_{i}}(t)}}{{\delta t}} = {{W}_{i}}(t), \\ \frac{{\delta {{n}_{i}}(t,{\mathbf{r}})}}{{\delta t}} + {\text{div}}\left( {{{n}_{i}}(t,{\mathbf{r}}){{{\mathbf{v}}}_{i}}({\mathbf{r}})} \right) = {{N}_{i}}(t,{\mathbf{r}}), \\ \end{gathered} $Переходя к рассматриваемому в данной работе СВЧ-разряду c ЭЦР, приходится использовать нульмерную геометрию, что обусловлено ограничением доступных вычислительных мощностей и заключается в переходе от ФР электронов по компонентам обобщенного импульса к распределению по энергии, а также к исключению пространственной зависимости для концентрации и средней энергии компонент разряда. Далее необходимо определить вид фигурирующих в (3) функций Ste f(t, E), Ni(t), Wi(t) и $F\frac{{\delta {{f}_{e}}\left( {t,p} \right)}}{{\delta p}}.$
Интеграл столкновений Ste f(t, E) складывается из трех слагаемых, отвечающих соответственно упругим соударениям между электронами, упругим соударениям электронов с тяжелыми частицами, а также неупругим взаимодействиям. В [13] дано общее выражение для интеграла столкновений, подразумевающее описание обеих взаимодействующих компонент через их функции распределения. Так как в текущей задаче этому условию удовлетворяют только упругие соударения электронов между собой, то соответствующий вид имеет лишь это слагаемое:
(4)
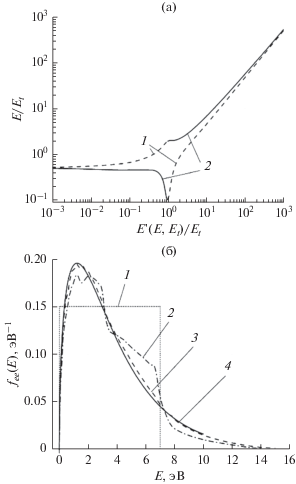
$\begin{gathered} S{{t}_{{ee}}}{{f}_{e}}\left( {t,E} \right) = \int {\left[ {{{f}_{e}}\left( {E{\kern 1pt} '\left( {E,{{E}_{t}}} \right)} \right){{f}_{e}}\left( {{{E}_{t}}} \right) - } \right.} \\ \left. { - \,\,{{f}_{e}}\left( E \right){{f}_{e}}\left( {{{E}_{t}}} \right)} \right]{{{v}}_{{ee}}}{{\sigma }_{{ee}}}\left( {{{E}_{{ee}}}} \right){{n}_{e}}d{{E}_{t}}. \\ \end{gathered} $Здесь E – энергия налетающего электрона; Et – энергия электрона-мишени; E '(E, Et) – энергия, которой должен обладать налетающий электрон, чтобы при его столкновении с электроном-мишенью получился электрон с энергией E; vee – относительная скорость сталкивающихся электронов; Eee – соответствующая этому энергия; σee(Eee) – сечение упругого рассеяния (в данном случае – кулоновское). Функция E '(E, Et) определяется на основе законов сохранения импульса и энергии. В силу положенного ранее отсутствия в задаче каких-либо пространственных измерений, решение должно быть сведено к скалярным величинам кинетической энергии частиц, что осуществимо посредством усреднения по всем возможным начальным углам, а также углам рассеяния. Получаемая таким образом зависимость не включает в себя рассеянные частицы с относительной энергией E/Et, меньшей 0.3, что делает множество этих энергий ограниченным снизу и, как следствие, не дает ФР термализоваться. Недостающие здесь значения определяются множеством углов, на которые частицы могли быть рассеяны, но в используемом приближении эти углы сняты, а значит, упомянутая неточность обязана появляться. В этой связи необходимо выбирать функцию E '(E, Et) исходя из ее способности термализовать любую начальную ФР. На рис. 1 показана удовлетворяющая указанному условию функция E '(E, Et) и результат ее воздействия на ступенчатую в интервале от 0 до 7 эВ ФР. Время релаксации ФР обозначено как τee.
Рис. 1.
Описание упругих соударений электронов: (а) – перераспределение суммарной энергии между двумя рассеянными частицами (1 и 2), (б) – этапы релаксации ступенчатой ФР: 1 – начальная ФР, 2 – спустя τee, 3 – спустя 3τee, 4 – ФР Максвелла.
Следующее слагаемое в интеграле столкновений отвечает упругим соударениям электрона с тяжелыми частицами, ФР которых принята в виде δ-функции относительно их средней энергии (температуры). Взятие интеграла в (4) по такой ФР приводит к следующему виду второго слагаемого интеграла столкновений:
(5)
$\begin{gathered} S{{t}_{{ei{\text{ el}}}}}{{f}_{e}}\left( {t,E} \right) = \\ = \sum\limits_{j = 1}^4 {\left[ {{{f}_{e}}\left( {E_{{ej}}^{'}\left( {E,{{w}_{j}}} \right)} \right) - {{f}_{e}}\left( E \right)} \right]{{{v}}_{{ej}}}{{\sigma }_{{ej}}}\left( {{{E}_{{ej}}}} \right){{n}_{j}}} . \\ \end{gathered} $Здесь j = 1–4 отвечает атому, молекуле, атомарному иону и молекулярному иону дейтерия соответственно; функция $E_{{ej}}^{'}\left( {E,{{w}_{j}}} \right)$ = E + Eej me/Mj, знак “+” в которой обусловлен тем обстоятельством, что энергия электронов принята большей энергии тяжелой компоненты. Последнее слагаемое интеграла столкновений учитывает неупругие взаимодействия электронов с остальными частицами разряда и в целом имеет вид, аналогичный (5). Его особенность заключается в том, что наряду с реакциями, приводящими к потере электронами энергии (запись которых целиком повторяет (5)), существуют реакции, при которых образуются новые электроны, что требует введения в (5) нового члена. Таким образом, выражение для интеграла неупругих столкновений принимает следующий вид:
(6)
$\begin{gathered} S{{t}_{{ei{\text{ inel}}}}}{{f}_{e}}\left( {t,E} \right) = \sum\limits_{j = 1}^M {\left[ {{{f}_{e}}\left( {E + E_{j}^{'}} \right) - {{f}_{e}}\left( E \right)} \right]} \times \\ \times \,\,{{\nu }_{{ej}}}{{\sigma }_{j}}\left( {{{E}_{{ej}}}} \right){{n}_{j}} + \sum\limits_{j = 1}^L {\left[ {{{f}_{e}}\left( {E_{{j1}}^{'}\left( E \right)} \right) + } \right.} \\ \left. { + \,\,{{f}_{e}}\left( {E_{{j2}}^{'}\left( E \right)} \right) - {{f}_{e}}\left( E \right)} \right]{{\nu }_{{ej}}}{{\sigma }_{j}}\left( {{{E}_{{ej}}}} \right){{n}_{j}}, \\ \end{gathered} $Здесь E2 – энергия образовавшегося электрона; B(E1) − слабо меняющаяся функция, равная, например, для дейтерия ≈8.3 эВ в рассматриваемом диапазоне энергий; χ – равномерно распределенная случайная величина в диапазоне от 0 до 1. В обратном случае, при энергии первичного электрона более 200 эВ ионизацию можно рассматривать как рассеяние на свободном электроне, в результате чего потеря энергии первичного электрона рассчитывается посредством решения уравнения относительно доли этой энергии η [16, 17]:
Выражение для изменения концентрации компонента разряда Ni(t) следует из уравнения (6), которое определяет количество актов соответствующего взаимодействия, приходящееся на единичный электрон с энергией E. Таким образом, для получения скорости изменения концентрации реагентов или продуктов реакции необходимо проинтегрировать соответствующие слагаемые из (6) по энергии электрона E, после чего умножить полученные интегралы на концентрацию электронов ne и сложить их:
(7)
${{N}_{i}}\left( t \right) = \sum\limits_{j = 1}^{{{G}_{i}}} {\int {{{f}_{e}}\left( E \right)} {{{v}}_{{ej}}}{{\sigma }_{j}}\left( {{{E}_{{ej}}}} \right){{n}_{j}}{{n}_{e}}dE} ,$Аналогичным образом величина Wi(t) определяется из (5). Для этого необходимо перейти от выраженной в (5) частоты взаимодействия единичного электрона с ансамблем тяжелых частиц, к частоте взаимодействия единичной тяжелой частицы с ансамблем электронов, что происходит заменой nj на ne и обусловлено представлением тяжелой компоненты через среднюю энергию. Последующее умножение полученной частоты на передаваемую при упругом соударении энергию и интегрирование по всей ФР электронов даст скорость изменения энергии тяжелой компоненты:
(8)
${{W}_{i}}\left( t \right) = \int {{{f}_{e}}\left( E \right)} {{{v}}_{{ej}}}{{\sigma }_{j}}\left( {{{E}_{{ej}}}} \right){{E}_{{ej}}}\left( {{{{{m}_{e}}} \mathord{\left/ {\vphantom {{{{m}_{e}}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}} \right){{n}_{e}}dE.$Последней неописанной составляющей системы уравнений (3) является взаимодействие электронов с электромагнитным полем. В общем случае и на языке ФР оно выглядело бы следующим образом. Под действием переменного электрического поля ФР электронов испытывает осцилляции в соответствии с частотой поля и амплитудой, отвечающей его напряженности. В присутствии внешнего магнитного поля амплитуда этих осцилляций может значительно возрастать, что регулируется близостью частоты поля к циклотронному резонансу, а вращение электронов в магнитном поле отражается в ФР как перераспределение ее значений между различными пространственными компонентами. Происходящие при этом упругие соударения электронов с тяжелыми частицами переводят энергию направленного движения вдоль электрического поля к хаотическому тепловому движению. В результате эволюция ФР электронов выглядит как ее общее движение по направлению роста энергии, на которое накладываются высокочастотные осцилляции и периодическое перераспределение энергии между пространственными компонентами. Рассматриваемый здесь ЭЦР осуществляется при частоте электромагнитного СВЧ-поля 2.45 ГГц, что определяет период упомянутых выше осцилляций как 0.4 нс, откуда вытекает необходимость использования временнóй дискретизации не выше 10–3 нс. Принимая во внимание характерное время развития разряда ~105 нc реализация подобного механизма взаимодействия электромагнитного поля с ФР электронов оказывается неосуществимой в силу ограниченных возможностей вычислительной техники. В этой связи необходимо использовать упрощенную модель этого взаимодействия, например модель из [11]. В ней описывается колебательное движение электрона в скрещенных переменном электрическом и постоянном магнитном полях и сопровождающая это хаотизация кинетической энергии направленного движения электронов вследствие упругих соударений с тяжелыми компонентами плазмы, посредством которой электроны плазмы и поглощают энергию поля. В итоге получается скалярное выражение для силы, действие которой с точки зрения передачи энергии электронам в среднем эквивалентно полному действию электромагнитной волны в присутствии внешнего магнитного поля:
(9)
$\begin{gathered} F = \frac{{eE_{0}^{2}\nu }}{{2{{m}_{e}}\left( {{{\omega }^{2}} + {{\nu }^{2}}} \right)}}\gamma \left( {\omega ,{{\omega }_{L}},\nu } \right), \\ \gamma \left( {\omega ,{{\omega }_{L}},\nu } \right) = \frac{{\left( {1 + {{\omega _{L}^{2}} \mathord{\left/ {\vphantom {{\omega _{L}^{2}} {{{\omega }^{2}} + {{{{\nu }^{2}}} \mathord{\left/ {\vphantom {{{{\nu }^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}}}} \right. \kern-0em} {{{\omega }^{2}} + {{{{\nu }^{2}}} \mathord{\left/ {\vphantom {{{{\nu }^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}}}} \right)\left( {1 + {{{{\nu }^{2}}} \mathord{\left/ {\vphantom {{{{\nu }^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}} \right)}}{{\left( {1 - {{\omega _{L}^{2}} \mathord{\left/ {\vphantom {{\omega _{L}^{2}} {{{\omega }^{2}} - {{{{\nu }^{2}}} \mathord{\left/ {\vphantom {{{{\nu }^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}}}} \right. \kern-0em} {{{\omega }^{2}} - {{{{\nu }^{2}}} \mathord{\left/ {\vphantom {{{{\nu }^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}}}} \right) + {{4{{\nu }^{2}}} \mathord{\left/ {\vphantom {{4{{\nu }^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}}}, \\ \end{gathered} $(10)
$\begin{gathered} F\frac{{\delta {{f}_{e}}\left( {t,p} \right)}}{{\delta p}} = \\ = - \frac{{eE_{0}^{2}\nu }}{{2{{m}_{e}}\left( {{{\omega }^{2}} + {{\nu }^{2}}} \right)}}\gamma \left( {\omega ,{{\omega }_{L}},\nu } \right)\frac{{\delta {{f}_{e}}}}{{\delta E}} = S{{t}_{{{\text{heat}}}}}. \\ \end{gathered} $Объединяя вместе все выражения (3)–(10), получим финальную систему уравнений, которую необходимо решить для моделирования кинетики плазмы газового разряда с учетом временнóй эволюции ФР электронов по энергии на примере СВЧ-разряда в дейтериевом газе и в присутствии ЭЦР (i = 1, 2, 3, 4):
(11)
$\begin{gathered} \frac{{\delta {{f}_{e}}\left( {t,E} \right)}}{{\delta t}} = \frac{{eE_{0}^{2}\nu }}{{2{{m}_{e}}\left( {{{\omega }^{2}} + {{\nu }^{2}}} \right)}}\gamma \left( {\omega ,{{\omega }_{L}},\nu } \right)\frac{{\delta {{f}_{e}}}}{{\delta E}} + \\ + \,\,\int {\left[ {{{f}_{e}}\left( {E{\kern 1pt} '\left( {E,{{E}_{t}}} \right)} \right){{f}_{e}}\left( {{{E}_{t}}} \right) - {{f}_{e}}\left( E \right){{f}_{e}}\left( {{{E}_{t}}} \right)} \right]} \times \\ \times \,\,{{\nu }_{{ee}}}{{\sigma }_{{ee}}}\left( {{{E}_{{ee}}}} \right){{n}_{e}}d{{E}_{t}} + \sum\limits_{j = 1}^4 {\left[ {{{f}_{e}}\left( {E_{{ej}}^{'}\left( {E,{{w}_{j}}} \right)} \right) - {{f}_{e}}\left( E \right)} \right]} \times \\ \times \,\,{{\nu }_{{ej}}}{{\sigma }_{{ej}}}\left( {{{E}_{{ej}}}} \right){{n}_{j}} + \sum\limits_{j = 1}^M {\left[ {{{f}_{e}}\left( {E + E_{j}^{'}} \right) - {{f}_{e}}\left( E \right)} \right]} \times \\ \times \,\,{{\nu }_{{ej}}}{{\sigma }_{{ej}}}\left( {{{E}_{{ej}}}} \right){{n}_{j}} + \\ + \,\,\sum\limits_{j = 1}^L {\left[ {{{f}_{e}}\left( {E_{{j1}}^{'}\left( E \right)} \right) + \left. {{{f}_{e}}\left( {E_{{j2}}^{'}\left( E \right)} \right) - {{f}_{e}}\left( E \right)} \right]} \right.} \times \\ \times \,\,{{\nu }_{{ej}}}{{\sigma }_{{ej}}}\left( {{{E}_{{ej}}}} \right){{n}_{j}}, \\ \frac{{\delta {{n}_{e}}\left( t \right)}}{{\delta t}} = \sum\limits_{j = 1}^{{{G}_{e}}} {\int {{{f}_{e}}\left( E \right){{\nu }_{{ej}}}{{\sigma }_{j}}\left( {{{E}_{{ej}}}} \right){{n}_{j}}{{n}_{e}}dE,} } \\ \frac{{\delta {{w}_{i}}\left( t \right)}}{{\delta t}} = \int {{{f}_{e}}\left( E \right){{\nu }_{{ei}}}{{\sigma }_{j}}\left( {{{E}_{{ei}}}} \right){{E}_{{ei}}}\left( {{{{{m}_{e}}} \mathord{\left/ {\vphantom {{{{m}_{e}}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}} \right){{n}_{e}}dE,} \\ \frac{{\delta {{n}_{i}}\left( t \right)}}{{\delta t}} = \sum\limits_{j = 1}^{Gi} {\int {{{f}_{e}}\left( E \right){{\nu }_{{ei}}}{{\sigma }_{j}}\left( {{{E}_{{ei}}}} \right){{n}_{i}}{{n}_{e}}dE,} } \\ \end{gathered} $АЛГОРИТМ
Численное решение системы уравнений (11) осуществляется неявным методом Адамса–Мултона с переменным шагом и порядком интегрирования [18], реализованным в коде Fortran с использованием параллельных вычислений посредством OpenMP. Интегрированию подвергается система из NF + NC + NC – 1 уравнений, где NF – число точек, на которые разбита ФР, NC – число компонент разряда (уравнений для их концентраций), а NC – 1 – число уравнений для средних энергий тяжелых компонент. Для рассматриваемого разряда NC = 5. Дифференциальные уравнения обыкновенно решаются на фиксированной области определения искомой функции, в то время как присутствие в задаче нагрева электронов и их упругих соударений между собой приводит к изменению размеров этой области, что можно наблюдать на примере релаксации ступенчатой ФР на рис. 1б. Таким образом, должны быть сформулированы условия, в соответствии с которыми алгоритм интегрирования будет изменять границы области определения, что при неизменной величине NF означает управление начальным значением энергии E0 и шагом между точками, в которых рассчитывается ФР. При ее расширении значения в новых точках вычисляются с помощью экстраполяции. Эти новые значения существенно влияют на шаг интегрирования, так как он определяется своим минимумом среди всех уравнений системы. Чем больше различие между значениями внутри массивов значений функций fe(E) и Stfe(E), тем сильнее шаг интегрирования по времени не соответствует большей части решаемых уравнений, а общая скорость решения задачи уменьшается. Отсюда следует, что управляющее областью определения ФР условие должно удовлетворять заданной кратности отношения максимального к минимальному значению функций fe(E) и Stfe(E) соответственно Kf и KSt. Эти величины определяют полноту рассмотрения эволюции ФР, и от них зависит как точность решения кинетического уравнения, так и затрачиваемое на это время, а вместе с ним и возможность осуществления решения как такового.
Управление областью определения ФР подразумевает не только ее расширение при превышении значения fe(Emax) или Stfe(Emax) над величинами femax/Kf или Stmaxfe/KSt соответственно, но и сжатие этой области в обратной ситуации, которая возникает на левой границе ФР при ее нагреве (перемещении вправо). В этом случае значение величины E0 становится отличным от нуля и образуется диапазон энергии между 0 и E0, в котором ФР положена равной нулю. При этом соударения электронов могут приводить к ее обратному распространению на эту область, причем необязательно вблизи E0, что обусловлено неупругим взаимодействием. В этой связи необходимо вычислять значения Stfe(E) за пределами области определения ФР и на каждом шаге интегрирования проводить проверку посредством KSt на предмет расширения. Количество точек, на которых это происходит, является параметром решения задачи и равняется NF0 для левой границы области определения и NFmax – для правой.
Удаление значений функций fe(E) и Stfe(E) вносит погрешности в решение уравнения Больцмана, которые должны быть малы и несущественны. В этой связи за их количественным выражением необходимо следить, равно как и за степенью выполнения законов сохранения массы и энергии. Удовлетворяющей обоим этим положениям мерой могут послужить интегралы величин fe(E) и Stfe(E), а также fe(E)E и Stfe(E)E по соответствующим областям определений и их прямые отношения. Так, например, оценка погрешности, вносимой устранением недостаточно высоких значений Stfe(E), осуществляется с помощью следующих выражений:
Таким же образом оцениваются δf и δfE − погрешности функции fe(E), с той лишь разницей, что у нее нет значений за пределами области определения. Однако после каждого шага интегрирования они могут изменяться таким образом, что часть их должна быть удалена или добавлена, а сама fe(E) переопределена на новые границы.
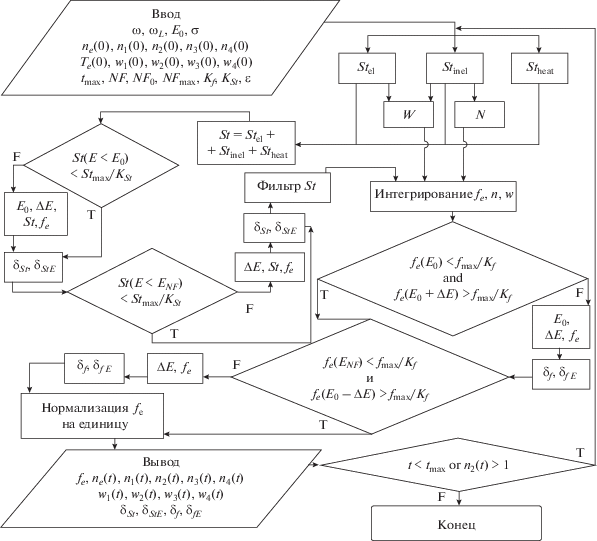
Алгоритм решения кинетического уравнения Больцмана представлен в форме блок-схемы на рис. 2. В первую очередь вводятся необходимые начальные данные, такие как параметры СВЧ-поля, сечения рассматриваемых процессов, стартовые значения для концентраций компонентов разряда, их средних энергий и температуры первичной ФР электронов, а также численные параметры решения, среди которых не обозначены еще два: tmax – максимальное время моделирования и ε – точность интегрирования. Далее вычисляются части интеграла столкновений Stfe(E), отвечающие нагреву, упругим и неупругим соударениям. Из них определяется передаваемая тяжелым компонентам разряда энергия W, а также скорость изменения концентраций N этих компонент и электронов. Полученные здесь величины поступают в блок интегрирования, где вычисляются ФР, концентрации и средние энергии частиц плазмы в следующий момент времени. При этом интеграл столкновений проходит проверку на отсутствие достаточно больших значений за пределами области определения fe(E). Отрицательный исход этой проверки запускает механизм переопределения параметров энергетического разбиения ФР E0, ΔE, а вместе с ним и самих функций Stfe(E) и fe(E). В любом случае не вошедшие в решение значения интеграла столкновений записываются в погрешность δSt и δStE. Непосредственно перед интегрированием осуществляется фильтрование значений Stfe(E) от численных шумов (см. рис. 1б). После интегрирования проверяется выполнение условия нахождения крайних точек новой ФР точно на границе заданного диапазона между значениями fmax и fmax/Kf. В случае невыполнения производится перерасчет fe на энергетическое распределение с новыми параметрами, при которых требуемое условие выполняется. При этом удаленные или добавленные значения ФР приписываются величинам соответствующих погрешностей δf и δfE. Обе ветви указанной проверки завершаются нормировкой новой ФР на единицу. Наконец, новые значения функции распределения электронов fe, концентраций n, средних энергий тяжелых компонент w в текущий момент времени t, а также погрешности δ выводятся вовне. После этого и в случае недостижимости максимального времени счета tmax или превышения концентрации молекулярного дейтерия n2(t) значения 1 см–3 цикл повторяется. В противном случае программа завершает свою работу.
РЕЗУЛЬТАТЫ
Оценка работы алгоритма происходила при следующих параметрах СВЧ-разряда в режиме ЭЦР: ω = 15.4 × 109 с–1, ωL = 14.3 × 109 с–1 (чему соответствуют γ = 100 и B = 815 Гс [11, 12]), E0 = = 2 × 104 В/м, ne(0) = 105 см–3, n1(0) = 2 × 1012 см–3, n2(0) = 8 × 1012 см–3, n3(0) = 2 × 104 см–3, n4(0) = 8 × × 104 см–3, Te(0) = 1 эВ, wi(0) = 0.026 эВ (i = 1, 2, 3, 4). Численные параметры модели принимали следующие значения: tmax = 1 с; NF = NF0 = NFmax = 101, 201, 401; Kf = KSt = 10, 20, 30; ε = 10–8. Для расчетов использовался процессор Intel Core i7 8700K с частотой 3.7 ГГц на 10 потоках. На рис. 3а представлена эволюция ФР электронов по энергии в течение небольшого промежутка времени, что демонстрирует успешное выполнение заложенных в программу механизмов регулирования области определения ФР. Корректность решения кинетической схемы разряда подтверждается динамикой концентрации его компонент, представленной на рис. 3б, которая качественно совпадает с результатами использования более простых моделей из [3, 11], а также демонстрирует количественное сходство между полученными временами развития разряда, которые исчисляются десятками микросекунд.
Первым численным параметром модели является количество точек, на которое разбивается область определения ФР. На рис. 4а представлена динамика погрешностей функций fe(E) и Stfe(E) с течением времени для различных значений NF = NF0 = NFmax и фиксированного Kf = KSt = 20. Сплошными линиями представлена сумма величин δSt и δStE, измеряющих ошибку в законах сохранения вещества и энергии при удалении недостаточно больших значений интеграла столкновений, а штриховыми линиями − сумма величин δf и δfE, выполняющая аналогичную роль для ФР. Несмотря на то что погрешности интеграла столкновений и ФР неразрывно связаны, их рассмотрение отдельно друг от друга удобно для разделения их источников, что проявится позднее. Пока же из рис. 4а следует, что погрешность моделирования эволюции ФР не превышает единиц процентов при использовании от 200 точек и выше. Кроме того, полученные результаты по концентрациям и средним энергиям плазменных компонент отличаются друг от друга не более чем на 0.4%. Отмечая также, что время моделирования для рассматриваемых параметров N составляло 18, 26 и 188 ч соответственно, можно судить в целом о возможности осуществления адекватного моделирования физических процессов посредством разработанного алгоритма за приемлемые сроки, а также о конкретных значениях NF, NF0 и NFmax, которые следует использовать в текущей задаче.
Рис. 3.
Результаты расчетов: (а) – эволюция ФР электронов по энергии в течение времени: 1 – 0 мкс, 2 – 0.1, 3 – 0.5, 4 – 1; (б) – динамика концентраций компонент разряда.
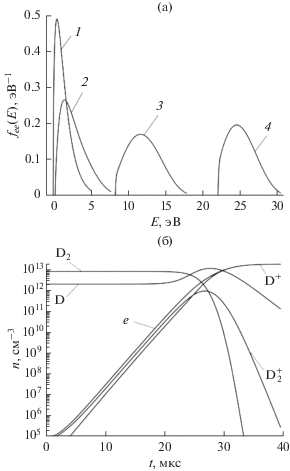
Рис. 4.
Зависимость погрешности решения кинетического уравнения от численных параметров модели: (а) – точности разбиения области определения: 1 – NF = 101, 2 – 201, 3 – 401; (б) – диапазоны учитываемых значений функций fe(E) и Stfe(E): 1 – K = 10, 2 – 20, 3 – 30.
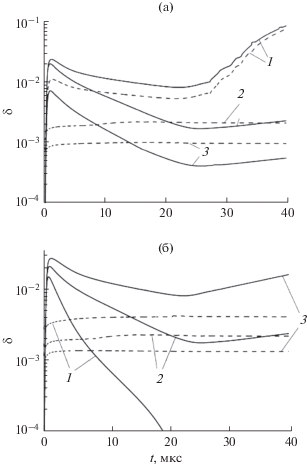
Точность решения кинетического уравнения также определяется параметрами Kf и KSt, чье влияние оценивалось при фиксированных значениях NF = NF0 = NFmax = 201. Динамика погрешностей при вариации этих параметров представлена на рис. 4б.
Погрешность ФР изменяется относительно параметров Kf и KSt – уменьшается при их возрастании. Противоположным образом ведет себя погрешность интеграла столкновений, что обусловлено следующим. Оценка неучтенных значений ФР и интеграла столкновений происходит на конечном диапазоне энергий, определяемом параметрами NF0 и NFmax. И если в случае рассмотрения погрешности ФР, которая монотонно уменьшается при удалении от своего максимального значения, величина оцениваемых значений также стремится к нулю и погрешность уменьшается, то при рассмотрении интеграла столкновений, который вследствие наличия неупругих процессов указанного свойства лишен, оцениваемая погрешность может и возрастать при увеличении диапазона учитываемых значений. Например, для представленных на рис. 4б случаев Kf и KSt, равных 10 и 30 в момент времени 20 мкс, область определения ФР находится в пределах от 429.3 до 429.9 эВ и от 423.8 до 430.4 эВ соответственно. Таким образом, размер области, в которой оценивается погрешность, возрастает с 1.8 до 6.6 эВ, а вместе с ним возрастает и сама погрешность. Тем не менее различия в полученных результатах концентрации и температуры плазменных компонент не превосходят 0.7%. Хотя используемая оценка погрешности решения кинетического уравнения Больцмана является, по сути, оценкой снизу, затухающий характер ее роста, представленный на рис. 4б, позволяет оценивать ее на уровне нескольких процентов, что является приемлемым для практического использования разрабатываемого алгоритма.
ЗАКЛЮЧЕНИЕ
Разработана программа математического моделирования кинетики плазмы газового разряда с учетом временнóй эволюции функции распределения электронов по энергии. Программа учитывает поступление в разряд энергии извне, упругие соударения электронов с электронами и с тяжелыми частицами, а также неупругие реакции возбуждения (без учета заселенности различных энергетических уровней) и превращения атомов и молекул. Вводя данные о начальной ФР электронов, средней энергии тяжелых компонент, их концентрации, сечениях требуемых реакций, а также описывая механизм поступления энергии извне, можно следить за развитием газового разряда с течением времени, получая данные о текущем виде ФР электронов, средней энергии и концентрации всех компонент разряда. Указанная возможность продемонстрирована на примере СВЧ-разряда в режиме электронно-циклотронного резонанса в молекулярном дейтерии. Полученные при таком тестировании результаты качественно и количественно соответствуют результатам других моделей при схожих начальных данных [3, 11]. Экспериментальные данные по ФР электронов в СВЧ-разряде с электронно-циклотронным резонансом в водороде при схожих давлениях (~1 Па) приводятся, например, в [19, 20]. Сложная геометрия представленного в этих работах источника ионов и отсутствие распределения напряженности электрического поля делают явное сравнение результатов затруднительным. Тем не менее полученные ФР электронов обладают сходством с представленными результатами. Таким образом, описанную в настоящей работе программу можно будет использовать для моделирования кинетических процессов в различных газовых разрядах и с учетом эволюции ФР, в частности при исследовании кинетики СВЧ-разряда в режиме электронно-циклотронного резонанса в молекулярном дейтерии.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований в рамках научного проекта № 19-32-90 033.
Список литературы
Shakhatov V.A., Lebedev Y.A., Lacoste A., Bechu S. The Role of Secondary Processes in Kinetics of Triplet States of a Hydrogen Molecule in an ECR Discharge // J. Phys.: Conf. Ser. 2017. V. 927. 012052.
Сторожев Д.А. Кинетические процессы в плазме тлеющего разряда // Физико-химическая кинетика в газовой динамике. 2013. Т. 14. С. 417.
Сторожев Д.А. Численное моделирование кинетики ионизации и диссоциации водорода в плазме разряда Пеннинга в приближении ЛТР // Физико-химическая кинетика в газовой динамике. 2014. Т. 15. С. 229.
Шахатов В.А., Гордеев О.А. Исследование плазмы тлеющего и контрагированного разряда в азоте методами спектроскопии КАРС, оптической интерферометрии и численного моделирования // ЖТФ. 2005. Т. 75. № 12. С. 56.
Федосеев А.В., Сухинин Г.И. Пространственно-временнáя эволюция функции распределения электронов в знакопеременном электрическом поле // Теплофизика и аэромеханика. 2005. Т. 75. С. 609.
Capitelli M., Hassouni K. Coupling of Plasma Chemistry, Vibrational Kinetics, Collisional-Radiative Models and Electron Energy Distribution Functions under Non-Equilibrium Conditions // Plasma Processes Polym. 2017. V. 14. 1 600 109.
Capitelli M., Colonna G., Pietanza L.D., D’Ammando G. Coupling of Radiation, Excited States and Electron Energy Distribution Function in Non-equilibrium Hydrogen Plasmas // Spectrochim. Acta. Part B: Atomic Spectroscopy. 2013. V. 83–84. P. 1.
Dyatko A.N., Kochetov V.I., Napartovich P.A. Non-thermal Plasma Instabilities Induced by Deformation of the Electron Energy Distribution Function // Plasma Sources Sci. Technol. 2014. V. 23. 043001.
Шахатов В.А., Лебедев Ю.А., Lacoste A., Bechu S. Кинетика электронных состояний молекул водорода в неравновесных разрядах. Синглетные состояния // ТВТ. 2016. Т. 54. № 1. С. 120.
Шахатов В.А., Лебедев Ю.А., Lacoste A., Bechu S. Кинетика электронных состояний молекул водорода в неравновесных разрядах. Основное электронное состояние // ТВТ. 2015. Т. 53. № 4. С. 601.
Степанов Д.С., Чеботарев А.В., Школьников Э.Я. Кинетика дейтериевой газоразрядной плазмы в резонаторе нейтронного генератора в режиме электронно-циклотронного резонанса // ТВТ. 2018. Т. 56. № 6. С. 865.
Степанов Д.С., Чеботарев А.В., Школьников Э.Я. Анализ режимов работы СВЧ-источника ионов в режиме электронно-циклотронного резонанса для портативного нейтронного генератора // ТВТ. 2019. Т. 57. № 3. С. 347.
Ландау Л.Д. Физическая кинетика. М.: Физматлит, 2007. 535 с.
Opal C.B., Peterson W.K., Beaty E.C. Measurements of Secondary-Electron Spectra Produced by Electron Impact Ionization of a Number of Simple Gases // J. Chem. Phys. 1971. V. 55. P. 4100.
Vahedi V., Surendra M. A Monte Carlo Collision Model for PIC Method: Applications to Argon and Oxygen Discharges // Comp. Phys. Comm. 1995. V. 87. P. 179.
Аккерман А.Ф., Никитушев Ю.М., Ботвин В.А. Решение методом Монте-Карло задач переноса быстрых электронов в веществе. Алма-Ата: Наука, 1972. 165 с.
Zerby C.D., Keller F.L. Electron Transport Theory, Calculations, and Experiments // Nucl. Sci. Eng. 1967. V. 27. P. 190.
Griffiths D., Higham D. Numerical Methods for Ordinary Differential Equations. Springer, 2010. 274 p.
Svarnas P., Annaratone B.M., Bechu S., Pelletier J., Bacal M. Study of Hydrogen Plasma in the Negative-ion Extraction Region // Plasma Sources Sci. Technol. 2009. V. 18. 045010.
Bechu S., Soum-Glaude A., Bes A., Lacoste A., Svarnas P., Aleiferis S., Ivanov A.A. Jr., Bacal M. Multi-dipolar Microwave Plasmas and Their Application to Negative Ion Production // Phys. Plasmas. 2013. V. 20. 101 601.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур