1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 59, № 2, 2021

Теплофизика высоких температур, 2021, T. 59, № 2, стр. 212-220

Аналитические решения моделей локально-неравновесного теплопереноса

Э. М. Карташов *

Российский технологический университет – МИРЭА (Институт тонких химических технологий им. М.В. Ломоносова)
Москва, Россия

* E-mail: kartashov@mitht.ru

Поступила в редакцию 04.05.2020
После доработки 06.07.2020
Принята к публикации 14.10.2020

Полный текст (PDF)

Аннотация

Рассмотрена серия краевых задач локально-неравновесного теплопереноса в терминах теории нестационарной теплопроводности для уравнений гиперболического типа (волновых уравнений). Изучены математические модели для обобщенного уравнения одновременно в декартовой, цилиндрической (радиальный поток теплоты) и сферической (центральная симметрия) системах координат. Развита методика нахождения аналитических решений обширного класса практически важных задач нестационарной теплопроводности для тел канонической формы (пластина, сплошной цилиндр, сплошной шар) и для частично ограниченных тел (полупространство, ограниченное плоской поверхностью; пространство с внутренней цилиндрической полостью и внутренней сферической полостью). Полученные точные аналитические решения серии модельных задач представляют собой принципиально новые результаты аналитической теплофизики.

ВВЕДЕНИЕ

Классические феноменологические теории процессов переноса в области $\bar {\Omega } = \{ M(x,y,z) \in \bar {D}$ = = $D + S,t \geqslant 0\} $ объединяют такие разнообразные явления, как перенос теплоты Фурье, массы Нернста, электричества Ома, напряжений Ньютона и Гука, фильтрации Дарси, поглощение звуковых волн и т.д. Эти теории имеют градиентное выражение ${\mathbf{q}}(M,t)$ = $ - A{\text{qrad}}U(M,t)$ в виде обобщенного закона переноса (A – коэффициент переноса, q – вектор плотности потока, U – потенциал), базируются на принципе локального термодинамического равновесия и гипотезе сплошной среды. Полученные на этой основе с использованием уравнений баланса дифференциальные уравнения для соответствующих физических величин являются локальными, т.е. в них не учитывается локальная неравновесность процессов. Последнее означает, что при выводе уравнений влияние конечной скорости переноса внутренней энергии пренебрежимо мало и в базовых уравнениях закладывается бесконечная скорость распространения возмущений. Можно сказать, что классические теории переноса справедливы, если скорость протекания процессов много меньше скорости распространения возмущений в рассматриваемой среде. Так, для исторически наиболее распространенной на практике модели теплопроводности, основанной на законе Фурье ${\mathbf{q}}(M,t) = - \lambda {\text{qrad}}T(M,t),$ $t > 0,$ уравнение энергии

$\begin{gathered} {{с\rho \partial T(M,t)} \mathord{\left/ {\vphantom {{с\rho \partial T(M,t)} {\partial t}}} \right. \kern-0em} {\partial t}} = - {\text{div}}{\mathbf{q}}(M,t) + F(M,t), \\ M \in D,\,\,\,\,t > 0, \\ \end{gathered} $
приводит к уравнению параболического типа нестационарного теплопереноса вида [1]
(1)
$\begin{gathered} \frac{{\partial T(M,t)}}{{\partial t}} = a\Delta T(M,t) + \frac{1}{{c\rho }}F(M,t), \\ M \in D,\,\,\,\,t > 0, \\ \end{gathered} $
и соответствующим для (1) краевым задачам с начальными и граничными условиями
(2)
${{\left. {T(M,t)} \right|}_{{t{\kern 1pt} = {\kern 1pt} 0}}} = {{\Phi }_{0}}(M),\,\,\,\,M \in \bar {D},$
(3)
$\begin{gathered} {{\beta }_{1}}\frac{{\partial T(M,t)}}{{\partial n}} + {{\beta }_{2}}T(M,t) = {{\beta }_{3}}\varphi (M,t), \\ M \in S,\,\,\,\,t > 0. \\ \end{gathered} $
Несмотря на некоторые парадоксы при использовании модельных представлений (1)–(3) [2–4], последние не ограничивают область применения краевых задач (1)–(3) как предмет практически необозримого числа исследований в различных областях науки и техники. В то же время следует заметить, что скорости распространения потенциалов любых физических полей не могут принимать бесконечных значений. В реальном теле процесс их изменения происходит с некоторым запаздыванием во времени согласно релаксационным свойствам материалов, учитываемыми коэффициентами релаксации. На уровне элементарных актов (т.е. на микроуровне) происходит задержка во времени процесса передачи кванта энергии относительно момента его получения от элементарного объема тела к соседним элементам. В течение этой задержки ${{\tau }_{r}}$ (время тепловой релаксации) происходит уменьшение потока тепловой энергии ${\mathbf{q}} = - \lambda {\text{qrad}}T$ на величину ${{{{\tau }_{r}}\partial {\mathbf{q}}} \mathord{\left/ {\vphantom {{{{\tau }_{r}}\partial {\mathbf{q}}} {\partial t}}} \right. \kern-0em} {\partial t}}.$ Поэтому ${{\tau }_{r}}$ является мерой инерции теплового потока и связано со скоростью распространения теплоты соотношением ${{{v}}_{р}} = \sqrt {{a \mathord{\left/ {\vphantom {a {{{\tau }_{r}}}}} \right. \kern-0em} {{{\tau }_{r}}}}} .$ Учет локальной неравновесности закладывается в соотношение
(4)
${\mathbf{q}}(M,t) = - \lambda {\text{qrad}}T(M,t) - {{\tau }_{r}}\frac{{\partial {\mathbf{q}}(M,t)}}{{\partial t}},$
учитывающее конечную скорость распространения теплоты. На необходимость учета влияния ограниченности скорости переноса теплоты (массы) указывали А.В. Лыков при исследовании тепло- и влагопереноса в капиллярно-пористых телах [5], в теории теплопроводности Каттанео [6] и Вернотт [7], в теории газодинамики Дж. Максвелл [8]. К более ранним исследованиям, связанным с изучением распространения теплоты в жидкостях, газах и твердых телах с конечной скоростью относятся исследования Л. Тисса [9], Л. Ландау [10] – жидкий гелий; В. Пешкова [11] – кристаллы; Г. Уарда и Г. Уилкса [12] – кристаллы, металлы; Р. Дингла [13] – диэлектрики, сверхпроводники, ферромагнетики; Ф. Лондона [14] – металлы, стекла; С. Аккермана, В. Бертмана, Н. Фейербенка, Р. Гюйе [15] – кристаллический гелий. Большинство авторов использовали в своих экспериментах метод распространения тепловых импульсов. В то же время так называемый второй звук (ВЗ) – конечная скорость – изучался также и теоретически в системах различных квазичастиц: фононный ВЗ – в полупроводниках [16], электронный ВЗ – в металлах [17], спиновые волны – в ферродиэлектрике [18], в газе магнонов [19]. М. Честер [20] рассмотрел указанную проблему с макроскопической точки зрения; С. Калиски [21] предложил ввести в принцип Онзагера характеристику скорости изменения теплового потока – тепловую инерцию. Соотношение (4) получило название гипотеза Максвелла–Каттанео–Лыкова–Вернотта и было проверено экспериментально. Результаты исследования термически переходных процессов в рамках гипотезы (4) в работах Н. Хервига и К. Беккерта [22] по зарегистрированному К. Митра с сотрудниками [23] термическому переходному процессу в ряде тел подтвердили реальность явления тепловой релаксации, и было рассчитано время ${{\tau }_{r}} = 15.5$ с. Кирсанов Ю. и др. [24] измерили время тепловой релаксации ПММА: ${{\tau }_{r}} = 2.4$ с (позже в [25] величина ${{\tau }_{r}}$ была уточнена: ${{\tau }_{r}} = 1.48 \pm 0.15$ c). Уравнение энергии ${{c\rho \partial T(M,t)} \mathord{\left/ {\vphantom {{c\rho \partial T(M,t)} {\partial t}}} \right. \kern-0em} {\partial t}}$ = $ - {\text{div}}{\mathbf{q}}(M,t)$ и соотношение (4) приводят к уравнению переноса гиперболического типа
(5)
$\begin{gathered} \frac{{\partial T(M,t)}}{{\partial t}} = a\Delta T(M,t) - {{\tau }_{r}}\frac{{{{\partial }^{2}}T(M,t)}}{{\partial {{t}^{2}}}}, \\ M \in D,\,\,\,\,t > 0, \\ \end{gathered} $
и соответствующим краевым задачам теплопроводности обобщенного типа. Не останавливаясь подробно на теплофизических процессах, связанных с уравнением (5), заметим, что к их числу относятся прежде всего процессы при высоких скоростях нагрева (охлаждения) границ тела, например: нагрев металлов короткими лазерными импульсами (длительностью от нано- до фемтосекунд), нагрев при трении с высокой скоростью, при тепловых ударах (высокоинтенсивный нагрев или охлаждение) и др. процессы. В [26] автором рассмотрен вопрос корректности постановки математических моделей для уравнения (5) с начальными условиями
(6)
$\begin{gathered} {{\left. {T(M,t)} \right|}_{{t = 0}}} = {{\Phi }_{0}}(M), \\ {{\left. {\frac{{\partial T(M,t)}}{{\partial t}}} \right|}_{{t = 0}}} = {{\Phi }_{1}}(M),\,\,\,\,M \in \bar {D} \\ \end{gathered} $
и граничными условиями
(7)
$\begin{gathered} {{\left. {{{\beta }_{1}}\frac{1}{{{{\tau }_{r}}}}\int\limits_0^t {\frac{{\partial T(M,\tau )}}{{\partial n}}} } \right|}_{{M \in S}}}\exp \left( { - \frac{{t - \tau }}{{{{\tau }_{r}}}}} \right)d\tau + \\ + \,\,{{\beta }_{2}}h\left[ {{{{\left. {T(M,t)} \right|}}_{{M \in S}}} - {{\varphi }_{1}}(t)} \right] = - {{\beta }_{3}}\frac{1}{\lambda }{{\varphi }_{2}}(t),\,\,\,\,t > 0, \\ \end{gathered} $
где ${{\beta }_{1}} = 0,$ ${{\beta }_{2}} = 1,$ ${{\beta }_{3}} = 0$ – граничные условия первого рода; ${{\beta }_{1}} = 1,$ ${{\beta }_{2}} = 0,$ ${{\beta }_{3}} = 1$ – граничные условия второго рода; ${{\beta }_{1}} = 1,$ ${{\beta }_{2}} = 1,$ ${{\beta }_{3}} = 0$ – граничные условия третьего рода. Здесь $S$ – кусочно-гладкая поверхность, ограничивающая область D; n – вектор внешней нормали к $S$ (непрерывный в точках S). Математические модели (5)–(7) значительно отличаются от классических (1)–(3) по сложности их решения. Специфика задач (5)–(7) заключается в относительной простоте исходных математических моделей и трудностях получения их аналитических решений [27–29]. Для областей канонического типа (бесконечная пластина, цилиндр сплошной или полый, шар сплошной или полый) точные аналитические решения гиперболических моделей переноса не получены до сих пор, и данная проблема по существу остается открытой. Для частично ограниченных областей ситуация более удовлетворительная. Здесь основным методом решения задач (5)–(7) является операционный, основы которого применительно к обобщенным задачам разработаны автором в [30] по соотношениям Карслоу и Егера [31]. Однако и для частично ограниченных областей возникают трудности вычислительного характера, что будет показано ниже.

Цель настоящей публикации – предложить новые аналитические решения для математических моделей локально-неравновесного теплопереноса как для ограниченных областей в декартовой, цилиндрической (радиальный поток), сферической (центральная симметрия) системах координат, так и для частично ограниченных областей.

АНАЛИТИЧЕСКИЕ РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ МОДЕЛЕЙ ПЕРЕНОСА ДЛЯ ТЕЛ КАНОНИЧЕСКОЙ ФОРМЫ

Особенностью рассматриваемых ниже аналитических решений является их новая функциональная конструкция, неизвестная ранее в аналитической теплофизике. Излагаемый основной подход нахождения искомых решений покажем вначале для обобщенного волнового уравнения, включающего (как отмечалось) три основные системы координат.

Пусть $T(x,t)$ есть решение задачи вида

(8)
$\begin{gathered} \frac{{\partial T}}{{\partial t}} = a\left( {\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + \frac{{2m + 1}}{x}\frac{{\partial T}}{{\partial x}}} \right) - {{\tau }_{r}}\frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}}, \\ 0 \leqslant x < l\,\,\,\,(m = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}), \\ 0 < x < l\,\,\,\,(m = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}),\,\,\,\,t > 0; \\ \end{gathered} $
(9)
${{\left. {T(x,t)} \right|}_{{t = 0}}} = {{T}_{0}},\,\,\,\,{{\left. {\frac{{\partial T(x,t)}}{{\partial t}}} \right|}_{{t = 0}}} = 0,\,\,\,\,0 \leqslant x \leqslant l;$
(10)
${{\left. {\frac{{\partial T(x,t)}}{{\partial x}}} \right|}_{{x = 0}}} = 0,\,\,\,\,{{\left. {T(x,t)} \right|}_{{x = l}}} = {{T}_{c}},\,\,\,\,t > 0.$
При $m = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}$ рассматривается бесконечная пластина в декартовых координатах, при $m = 0$ – сплошной (неограниченный) цилиндр в цилиндрических координатах (радиальный тепловой поток), при $m = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ – сплошной шар в сферических координатах (центральная симметрия). Поскольку для $m = 0,\,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ должно выполняться условие ${{({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0em} {\partial x}})}_{{x = 0}}} = 0,$ $t > 0,$ то присоединим к этим условиям и случай $m = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2},$ с тем чтобы охватить теорией все три системы координат в (8) одновременно. Впрочем, как будет следовать из развиваемого ниже подхода, последнее ограничение для случая $m = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}$ может быть снято.

В безразмерных переменных

(11)
$\begin{gathered} \xi = \frac{x}{{\sqrt {a{{\tau }_{r}}} }},\,\,\,\,\tau = \frac{t}{{{{\tau }_{r}}}},\,\,\,\,{{l}_{0}} = \frac{l}{{\sqrt {a{{\tau }_{r}}} }}, \\ W(\xi ,\tau ) = \frac{{T(x,t) - {{T}_{0}}}}{{{{T}_{c}} - {{T}_{0}}}} \\ \end{gathered} $
исходная задача принимает вид
(12)
$\begin{gathered} \frac{{\partial W}}{{\partial \tau }} = \frac{{{{\partial }^{2}}W}}{{\partial {{\xi }^{2}}}} + \frac{{2m + 1}}{\xi }\frac{{\partial W}}{{\partial \xi }} - \frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}}, \\ 0 \leqslant \xi < {{l}_{0}}\,\,\,(m = 0,\,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}), \\ 0 < \xi < {{l}_{0}}\,\,\,\,(m = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}),\,\,\,\,\tau > 0; \\ \end{gathered} $
(13)
${{\left. W \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = {{\left. {\frac{{\partial W}}{{\partial \tau }}} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,0 \leqslant \xi \leqslant {{l}_{0}};$
(14)
${{\left. {\frac{{\partial W}}{{\partial \xi }}} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,{{\left. W \right|}_{{\xi {\kern 1pt} = {\kern 1pt} {{l}_{0}}}}} = 1,\,\,\,\,\tau > 0.$
В пространстве изображений по Лапласу $\bar {W}(\xi ,p)$ = $\int_0^\infty {\exp ( - p\tau )W(\xi ,\tau )d\tau } $ решение задачи (12)–(14) имеет вид
(15)
$\bar {W}(\xi ,p) = {{({{{{l}_{0}}} \mathord{\left/ {\vphantom {{{{l}_{0}}} \xi }} \right. \kern-0em} \xi })}^{m}}\frac{{{{I}_{m}}(\bar {\gamma }\xi )}}{{{{I}_{m}}(\bar {\gamma }{{l}_{0}})}},\,\,\,\,\bar {\gamma } = \sqrt {p(p + 1)} ,$
где ${{I}_{m}}(z)$ – модифицированная функция Бесселя.

Для нахождения оригинала (15) используем обобщенную теорему разложения Ващенко–Захарченко [1]: если $\bar {f}(p) = \frac{{\overline {{{f}_{1}}} (p)}}{{p\overline {{{f}_{2}}} (p)}}$ и $p = 0,$ ${{p}_{n}} > 0$ $(n \geqslant 0)$ – простые корни знаменателя, то

(16)
$f(\tau ) = \frac{{{{f}_{1}}(0)}}{{{{f}_{2}}(0)}} + \sum\limits_{n = 1}^\infty {\frac{{\overline {{{f}_{1}}} ({{p}_{n}})}}{{{{p}_{n}}\left[ {\overline {{{f}_{2}}} (p)} \right]_{{p = {{p}_{n}}}}^{'}}}\exp ({{p}_{n}}\tau )} .$
Находим ${{I}_{m}}(\bar {\gamma }{{l}_{0}})$ = ${{i}^{{ - m}}}{{J}_{m}}(i\bar {\gamma }{{l}_{0}}) = 0,$ откуда $\bar {\gamma }{{l}_{0}} = - i{{\mu }_{n}},$ где ${{\mu }_{n}} > 0$ $(n > 0)$ – положительные корни уравнения ${{J}_{m}}(\mu ) = 0,$ расположенные в порядке возрастания. Так как ${{\gamma }_{n}} = \sqrt {{{p}_{n}}({{p}_{n}} + 1)} $ = = $ - i({{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}}),$ то $p_{n}^{2} + {{p}_{n}}$ + ${{({{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}^{2}} = 0,$ откуда имеем два семейства корней
(17)
$p_{n}^{{(1,2)}} = \frac{{ - 1 \pm i{{\omega }_{n}}}}{2},\,\,\,\,{{\omega }_{n}} = \sqrt {{{{\left( {\frac{{2{{\mu }_{n}}}}{{{{l}_{0}}}}} \right)}}^{2}} - 1} .$
Далее в (16) суммируем по корням $p_{n}^{{(1)}}$ и $p_{n}^{{(2)}}{\text{:}}$

(18)
$\begin{gathered} W(\xi ,\tau ) = 1 + {{\left( {\frac{{{{l}_{0}}}}{\xi }} \right)}^{m}}\sum\limits_{n = 1}^\infty {\frac{{{{I}_{m}}({{\gamma }_{n}}\xi )}}{{p_{n}^{{(1)}}\left[ {{{I}_{m}}({{\gamma }_{n}}{{l}_{0}})} \right]_{{p = p_{n}^{{(1)}}}}^{'}}}\exp \left( {p_{n}^{{(1)}}\tau } \right) + } \\ + \,\,{{\left( {\frac{{{{l}_{0}}}}{\xi }} \right)}^{m}}\sum\limits_{n = 1}^\infty {\frac{{{{I}_{m}}({{\gamma }_{n}}\xi )}}{{p_{n}^{{(2)}}\left[ {{{I}_{m}}({{\gamma }_{n}}{{l}_{0}})} \right]_{{p = p_{n}^{{(2)}}}}^{'}}}\exp \left( {p_{n}^{{(2)}}\tau } \right).} \\ \end{gathered} $

Используя далее в (18) следующие соотношения для функций Бесселя:

$z\frac{d}{{dz}}{{I}_{m}}(z) = m{{I}_{m}}(z) + z{{I}_{{m + 1}}}(z),\,\,\,\,{{I}_{{{\nu }}}}( - iz) = {{i}^{{ - {{\nu }}}}}{{J}_{{{\nu }}}}(z),$
после длительных преобразований приходим к искомому оригиналу
(19)
$\begin{gathered} W(\xi ,\tau ) = 1 + 2{{\left( {\frac{{{{l}_{0}}}}{\xi }} \right)}^{m}}\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}) \times \\ \times \,\,\sum\limits_{n{\kern 1pt} = {\kern 1pt} 1}^\infty {\frac{{{{J}_{m}}\left( {\frac{{{{\mu }_{n}}\xi }}{{{{l}_{0}}}}} \right)\left( {\sin \frac{{{{\omega }_{n}}\tau }}{2} + {{\omega }_{n}}\cos \frac{{{{\omega }_{n}}\tau }}{2}} \right)}}{{{{\mu }_{n}}{{\omega }_{n}}{{J}_{{m{\kern 1pt} + {\kern 1pt} 1}}}({{\mu }_{n}})}}} , \\ \end{gathered} $
(20)
${{\omega }_{n}} = \sqrt {{{{\left( {\frac{{2{{\mu }_{n}}}}{{{{l}_{0}}}}} \right)}}^{2}} - 1} ,$
где ${{\mu }_{n}} > 0$ – корни уравнения ${{J}_{m}}(\mu ) = 0.$ Теперь необходимо исследовать область суммирования ряда (19) по корням ${{\mu }_{n}}.$ С одной стороны, ${{\mu }_{n}} > 0,$ с другой стороны, согласно (20), должно быть ${{\mu }_{n}} > {{{{l}_{0}}} \mathord{\left/ {\vphantom {{{{l}_{0}}} 2}} \right. \kern-0em} 2}.$ Таким образом, область суммирования по корням $0 < {{\mu }_{n}} < \infty ,$ где $1 \leqslant n < \infty ,$ распадается на два множества $1 \leqslant n < k{\text{ }}({{\mu }_{k}} < {{{{l}_{0}}} \mathord{\left/ {\vphantom {{{{l}_{0}}} 2}} \right. \kern-0em} 2})$ и k + 1 < $ < n < \infty {\text{ }}({{\mu }_{{k{\kern 1pt} + {\kern 1pt} 1}}} > {{{{l}_{0}}} \mathord{\left/ {\vphantom {{{{l}_{0}}} 2}} \right. \kern-0em} 2}),$ в каждом из которых в (19) будет своя функциональная конструкция. Находим окончательно
(21)
$\begin{gathered} W(\xi ,\tau ) = 1 - 2{{\left( {\frac{{{{l}_{0}}}}{\xi }} \right)}^{m}}\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}) \times \\ \times \,\,\left[ {\sum\limits_{n{\kern 1pt} = {\kern 1pt} 1}^k {\frac{{{{J}_{m}}\left( {\frac{{{{\mu }_{n}}\xi }}{{{{l}_{0}}}}} \right)\left( {{\text{sh}}\frac{{\omega _{n}^{*}\tau }}{2} + \omega _{n}^{*}{\text{ch}}\frac{{\omega _{n}^{*}\tau }}{2}} \right)}}{{{{\mu }_{n}}\omega _{n}^{*}{{J}_{{m{\kern 1pt} + {\kern 1pt} 1}}}({{\mu }_{n}})}} + } } \right. \\ \left. { + \,\,\sum\limits_{n = k{\kern 1pt} + {\kern 1pt} 1}^\infty {\frac{{{{J}_{m}}\left( {\frac{{{{\mu }_{n}}\xi }}{{{{l}_{0}}}}} \right)\left( {\sin \frac{{{{\omega }_{n}}\tau }}{2} + {{\omega }_{n}}\cos \frac{{{{\omega }_{n}}\tau }}{2}} \right)}}{{{{\mu }_{n}}{{\omega }_{n}}{{J}_{{m{\kern 1pt} + {\kern 1pt} 1}}}({{\mu }_{n}})}}} } \right], \\ \end{gathered} $
где

(22)
$\begin{gathered} {{\omega }_{n}} = \sqrt {{{{\left( {\frac{{2{{\mu }_{n}}}}{{{{l}_{0}}}}} \right)}}^{2}} - 1} = i\sqrt {1 - {{{\left( {\frac{{2{{\mu }_{n}}}}{{{{l}_{0}}}}} \right)}}^{2}}} = i\omega _{n}^{*}, \\ 1 \leqslant n < k\,\,\,\,({{\mu }_{k}} < {{{{l}_{0}}} \mathord{\left/ {\vphantom {{{{l}_{0}}} 2}} \right. \kern-0em} 2}), \\ k + 1 < n < \infty \,\,\,\,({{\mu }_{{k{\kern 1pt} + {\kern 1pt} 1}}} > {{{{l}_{0}}} \mathord{\left/ {\vphantom {{{{l}_{0}}} 2}} \right. \kern-0em} 2}). \\ \end{gathered} $

Заметим, что решение (21) в литературе по теории теплопроводности отсутствует.

Рассмотрим далее в общем решении (21) ряд частных случаев для тел канонической формы, а именно бесконечный цилиндр $0 \leqslant \xi \leqslant {{l}_{0}}$ и бесконечную пластину $0 \leqslant \xi \leqslant {{l}_{0}}{\text{ }}(\tau > 0).$ В первом случае решение тепловой задачи

$\begin{gathered} \frac{{\partial W}}{{\partial \tau }} = \frac{{{{\partial }^{2}}W}}{{\partial {{\xi }^{2}}}} + \frac{1}{\xi }\frac{{\partial W}}{{\partial \xi }} - \frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}},\,\,\,\,0 \leqslant \xi < {{l}_{0}},\,\,\,\,\tau > 0, \\ {{\left. {W(\xi ,\tau )} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = {{\left. {\frac{{\partial W(\xi ,\tau )}}{{\partial \tau }}} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}},\,\,\,\,0 \leqslant \xi \leqslant {{l}_{0}}, \\ {{\left. {\frac{{\partial W(\xi ,\tau )}}{{\partial \xi }}} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,{{\left. {W(\xi ,\tau )} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} {{l}_{0}}}}} = 1,\,\,\,\,\tau > 0 \\ \end{gathered} $
имеет вид
(23)
$\begin{gathered} W(\xi ,\tau ) = 1 - 2\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}) \times \\ \times \,\,\left[ {\sum\limits_{n{\kern 1pt} = {\kern 1pt} 1}^k {\frac{{{{J}_{0}}\left( {\frac{{{{\mu }_{n}}\xi }}{{{{l}_{0}}}}} \right)\left( {{\text{sh}}\frac{{\omega _{n}^{*}\tau }}{2} + \omega _{n}^{*}{\text{ch}}\frac{{\omega _{n}^{*}\tau }}{2}} \right)}}{{{{\mu }_{n}}\omega _{n}^{*}{{J}_{1}}({{\mu }_{n}})}} + } } \right. \\ \left. \begin{gathered} \hfill \\ + \,\,\sum\limits_{n{\kern 1pt} = {\kern 1pt} k{\kern 1pt} + {\kern 1pt} 1}^\infty {\frac{{{{J}_{0}}\left( {\frac{{{{\mu }_{n}}\xi }}{{{{l}_{0}}}}} \right)\left( {\sin \frac{{{{\omega }_{n}}\tau }}{2} + {{\omega }_{n}}\cos \frac{{{{\omega }_{n}}\tau }}{2}} \right)}}{{{{\mu }_{n}}{{\omega }_{n}}{{J}_{1}}({{\mu }_{n}})}}} \hfill \\ \end{gathered} \right], \\ \end{gathered} $
где ${{\mu }_{n}} > 0$ корни уравнения ${{J}_{0}}({{\mu }_{n}}) = 0,$ $1 \leqslant n < k$ $({{\mu }_{k}} < {{{{l}_{0}}} \mathord{\left/ {\vphantom {{{{l}_{0}}} 2}} \right. \kern-0em} 2}),$ $k + 1 < n < \infty $ $({{\mu }_{{k + 1}}} > {{{{l}_{0}}} \mathord{\left/ {\vphantom {{{{l}_{0}}} 2}} \right. \kern-0em} 2}),$

(24)
${{\omega }_{n}} = \sqrt {{{{\left( {\frac{{2{{\mu }_{n}}}}{{{{l}_{0}}}}} \right)}}^{2}} - 1} = i\sqrt {1 - {{{\left( {\frac{{2{{\mu }_{n}}}}{{{{l}_{0}}}}} \right)}}^{2}}} = i\omega _{n}^{*}.$

Рассмотрим теперь в (12)–(14) для бесконечной пластины задачу

$\begin{gathered} \frac{{\partial W}}{{\partial \tau }} = \frac{{{{\partial }^{2}}W}}{{\partial {{\xi }^{2}}}} - \frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}},\,\,\,\,0 < \xi < {{l}_{0}},\,\,\,\,\tau > 0; \\ {{\left. {W(\xi ,\tau )} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = {{\left. {\frac{{\partial W(\xi ,\tau )}}{{\partial \tau }}} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,0 \leqslant \xi \leqslant {{l}_{0}}; \\ {{\left. {\frac{{\partial W(\xi ,\tau )}}{{\partial \xi }}} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,{{\left. {W(\xi ,\tau )} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} 1}}} = 1,\,\,\,\,\tau > 0. \\ \end{gathered} $

Операционное (по Лапласу) ее решение имеет вид

(25)
$\bar {W}(\xi ,p) = \frac{1}{p}\frac{{{\text{ch}}\bar {\gamma }\xi }}{{{\text{ch}}\bar {\gamma }{{l}_{0}}}},\,\,\,\,\bar {\gamma } = \sqrt {p(p + 1).} $

Повторим кратко приведенные выше рассуждения:

(26)
$\begin{gathered} {\text{ch}}\bar {\gamma }{{l}_{0}} = \cos ( - i\bar {\gamma }{{l}_{0}}) = 0,\,\,\,\,{{\gamma }_{n}} = i\frac{{(2n + 1)\pi }}{{2{{l}_{0}}}}\,\,\,\,(n \geqslant 0), \\ p_{n}^{{(1,2)}} = \frac{{ - 1 \pm i{{\omega }_{n}}}}{2},\,\,\,\,{{\omega }_{n}} = \sqrt {{{{\left[ {\frac{{(2n + 1)\pi }}{{{{l}_{0}}}}} \right]}}^{2}} - 1} . \\ \end{gathered} $

Применяя далее соотношение (16), находим

(27)
$\begin{gathered} W(\xi ,\tau ) = 1 - \frac{4}{\pi }\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}) \times \\ \times \,\,\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{{{{( - 1)}}^{n}}\cos \frac{{(2n + 1)\pi \xi }}{{2{{l}_{0}}}}\left( {\sin \frac{{{{\omega }_{n}}\tau }}{2} + {{\omega }_{n}}\cos \frac{{{{\omega }_{n}}\tau }}{2}} \right)}}{{(2n + 1){{\omega }_{n}}}},} \\ \end{gathered} $
где

(28)
${{\omega }_{n}} = \sqrt {{{{\left[ {\frac{{(2n + 1)\pi }}{{{{l}_{0}}}}} \right]}}^{2}} - 1} .$

Но решение задачи на этом не заканчивается. Из (28) следует, что $n > {{({{l}_{0}} - \pi )} \mathord{\left/ {\vphantom {{({{l}_{0}} - \pi )} {2\pi }}} \right. \kern-0em} {2\pi }}.$ Рассмотрим два случая. Пусть в первом из них ${{l}_{0}} < \pi ,$ т.е. $n > {{(\pi - {{l}_{0}})} \mathord{\left/ {\vphantom {{(\pi - {{l}_{0}})} {2\pi }}} \right. \kern-0em} {2\pi }}.$ С другой стороны, согласно (26), $n \geqslant 0$ и общим решением этой системы является неравенство $n \geqslant 0.$ Последнее означает, что при ${{l}_{0}} < \pi $ решение задачи имеет вид (27). Пусть теперь ${{l}_{0}} > \pi .$ Тогда область суммирования в (27) $0 \leqslant n < \infty $ распадается на две части: $0 \leqslant n < \left[ {{{({{l}_{0}} - \pi )} \mathord{\left/ {\vphantom {{({{l}_{0}} - \pi )} {2\pi }}} \right. \kern-0em} {2\pi }}} \right] = k$ и $k + 1 < n < \infty ,$ где $\left[ {{{({{l}_{0}} - \pi )} \mathord{\left/ {\vphantom {{({{l}_{0}} - \pi )} {2\pi }}} \right. \kern-0em} {2\pi }}} \right]$ – целая часть числа. Соответственно этому при ${{l}_{0}} > \pi $ решение задачи принимает вид

(29)
$\begin{gathered} W(\xi ,\tau ) = 1 - \frac{4}{\pi }\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}) \times \frac{{{{\partial }^{2}}\Omega }}{{\partial {{u}^{2}}}} \\ \times \,\,\left[ {\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^k {\frac{{{{{( - 1)}}^{n}}\cos \frac{{(2n + 1)\pi \xi }}{{2{{l}_{0}}}}\left( {{\text{sh}}\frac{{\omega _{n}^{*}\tau }}{2} + \omega _{n}^{*}{\text{ch}}\frac{{\omega _{n}^{*}\tau }}{2}} \right)}}{{(2n + 1)\omega _{n}^{*}}} + } } \right. \\ \\ \left. { + \,\,\sum\limits_{n{\kern 1pt} = {\kern 1pt} k{\kern 1pt} + {\kern 1pt} 1}^\infty {\frac{{{{{( - 1)}}^{n}}\cos \frac{{(2n + 1)\pi \xi }}{{2{{l}_{0}}}}\left( {\sin \frac{{{{\omega }_{n}}\tau }}{2} + {{\omega }_{n}}\cos \frac{{{{\omega }_{n}}\tau }}{2}} \right)}}{{(2n + 1){{\omega }_{n}}}}} } \right], \\ \end{gathered} $
где
(30)
$\begin{gathered} {{\omega }_{n}} = \sqrt {{{{\left[ {\frac{{(2n + 1)\pi }}{{{{l}_{0}}}}} \right]}}^{2}} - 1} = \hfill \\ = i\sqrt {1 - {{{\left[ {\frac{{(2n + 1)\pi }}{{{{l}_{0}}}}} \right]}}^{2}}} = i\omega _{n}^{*}. \hfill \\ \end{gathered} $
Соотношение (27) в принципе можно получить из общего решения (19) при $m = ({{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}),$ ${{J}_{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}(z) = \sqrt {{2 \mathord{\left/ {\vphantom {2 {\pi z}}} \right. \kern-0em} {\pi z}}} \cos z,$ ${{J}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(z) = \sqrt {{2 \mathord{\left/ {\vphantom {2 {\pi z}}} \right. \kern-0em} {\pi z}}} \sin z.$

Пусть для бесконечной пластины при заданных выше начальных условиях граничные условия имеют вид

${{\left. {W(\xi ,\tau )} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}} = 1,\,\,\,\,{{\left. {\frac{{\partial W(\xi ,\tau )}}{{\partial \xi }}} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} {{l}_{0}}}}} = 0,\,\,\,\,\tau > 0.$

Находим операционное решение

(31)
$\bar {W}(\xi ,p) = \frac{{{\text{ch}}({{l}_{0}} - \xi )\bar {\gamma }}}{{p{\text{ch}}{{l}_{0}}\overline \gamma }},\,\,\,\,\bar {\gamma } = \sqrt {p(p + 1)} $
и далее по разработанной выше методике получим искомый оригинал:

при ${{l}_{0}} < \pi $

(32)
$\begin{gathered} W(\xi ,\tau ) = 1 - \frac{4}{\pi }\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}) \times \\ \times \,\,\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{\sin \frac{{(2n + 1)\pi \xi }}{{2{{l}_{0}}}}\left( {\sin \frac{{{{\omega }_{n}}\tau }}{2} + {{\omega }_{n}}\cos \frac{{{{\omega }_{n}}\tau }}{2}} \right)}}{{(2n + 1){{\omega }_{n}}}}} ; \\ \end{gathered} $

при ${{l}_{0}} > \pi $

(33)
$\begin{gathered} W(\xi ,\tau ) = 1 - \frac{4}{\pi }\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}) \times \\ \times \,\,\left[ {\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^k {\frac{{\sin \frac{{(2n + 1)\pi \xi }}{{2{{l}_{0}}}}\left( {{\text{sh}}\frac{{\omega _{n}^{*}\tau }}{2} + \omega _{n}^{*}{\text{ch}}\frac{{\omega _{n}^{*}\tau }}{2}} \right)}}{{(2n + 1)\omega _{n}^{*}}} + } } \right. \\ \\ \left. { + \,\,\sum\limits_{n{\kern 1pt} = {\kern 1pt} k{\kern 1pt} + {\kern 1pt} 1}^\infty {\frac{{\sin \frac{{(2n + 1)\pi \xi }}{{2{{l}_{0}}}}\left( {\sin \frac{{{{\omega }_{n}}\tau }}{2} + {{\omega }_{n}}\cos \frac{{{{\omega }_{n}}\tau }}{2}} \right)}}{{(2n + 1){{\omega }_{n}}}}} } \right], \\ \end{gathered} $
где
$\begin{gathered} {{\omega }_{n}} = \sqrt {{{{\left[ {\frac{{(2n + 1)\pi }}{{{{l}_{0}}}}} \right]}}^{2}} - 1} = i\sqrt {1 - {{{\left[ {\frac{{(2n + 1)\pi }}{{{{l}_{0}}}}} \right]}}^{2}}} = i\omega _{n}^{*}, \\ k = \left[ {{{({{l}_{0}} - \pi )} \mathord{\left/ {\vphantom {{({{l}_{0}} - \pi )} {2\pi }}} \right. \kern-0em} {2\pi }}} \right]. \\ \end{gathered} $
Рассмотрим теперь более сложный случай, также не описанный в литературе по теплообмену. Пусть $T(x,t)$ есть решение задачи

(34)
$\frac{{\partial T}}{{\partial t}} = a\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} - {{\tau }_{r}}\frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}},\,\,\,\,0 < x < l,\,\,\,\,t > 0;$
(35)
${{\left. {T(x,t)} \right|}_{{t = 0}}} = {{T}_{0}},\,\,\,\,{{\left. {\frac{{\partial T(x,t)}}{{\partial t}}} \right|}_{{t = 0}}} = 0,\,\,\,\,0 \leqslant x \leqslant l;$
(36)
${{\left. {\frac{1}{{{{\tau }_{r}}}}\int\limits_0^t {\frac{{\partial T(x,\tau )}}{{\partial x}}} } \right|}_{{x = 0}}}\exp \left( { - \frac{{t - \tau }}{{{{\tau }_{r}}}}} \right)d\tau = - \frac{1}{\lambda }{{q}_{0}},\,\,\,\,t > 0;$
(37)
${{\left. {T(x,t)} \right|}_{{x = l}}} = 0,\,\,\,\,t > 0.$

В безразмерных переменных ($\xi ,\tau $)

$\xi = \frac{x}{{\sqrt {a{{\tau }_{r}}} }},\,\,\,\,\tau = \frac{t}{{{{\tau }_{r}}}},\,\,\,\,{{l}_{0}} = \frac{l}{{\sqrt {a{{\tau }_{r}}} }},\,\,\,\,\Theta (\xi ,\tau ) = \frac{{T(x,t) - {{T}_{0}}}}{{{{{{q}_{0}}\sqrt {a{{\tau }_{r}}} } \mathord{\left/ {\vphantom {{{{q}_{0}}\sqrt {a{{\tau }_{r}}} } \lambda }} \right. \kern-0em} \lambda }}}$
задача будет иметь вид

(38)
$\frac{{\partial \Theta }}{{\partial \tau }} = \frac{{{{\partial }^{2}}\Theta }}{{\partial {{\xi }^{2}}}} - \frac{{{{\partial }^{2}}\Theta }}{{\partial {{\tau }^{2}}}},\,\,\,\,0 < \xi < {{l}_{0}},\,\,\,\,\tau > 0;$
(39)
${{\left. {\Theta (\xi ,\tau )} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = {{\left. {\frac{{\partial \Theta }}{{\partial \tau }}} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,0 \leqslant \xi \leqslant {{l}_{0}};$
(40)
$\int\limits_0^\tau {{{{\left. {\frac{{\partial \Theta (\xi ,\tau {\kern 1pt} ')}}{{\partial \xi }}} \right|}}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}}\exp \left[ { - (\tau - \tau {\kern 1pt} ')} \right]d\tau {\kern 1pt} '} = - 1,\,\,\,\,\tau > 0;$
(41)
${{\left. {\Theta (\xi ,\tau )} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} {{l}_{0}}}}} = 0,\,\,\,\,\tau > 0.$

Для решения этой задачи может быть предложен следующий подход. В пространстве изображений (по Лапласу) решение задачи (38)–(41) имеет вид

(42)
$\bar {\Theta }(\xi ,p) = \frac{{p + 1}}{{p\bar {\gamma }}}\frac{{{\text{sh}}({{l}_{0}} - \xi )\bar {\gamma }}}{{{\text{ch}}{{l}_{0}}\bar {\gamma }}},\,\,\,\,\bar {\gamma } = \sqrt {p(p + 1)} .$

Для нахождения оригинала (42) используем изображение (31) и далее оригинал (32), (33). Выражения (31) и (42) дают следующие соотношения:

(43)
$\begin{gathered} \bar {\Theta }(\xi ,p) = \frac{{p + 1}}{p}\int\limits_\xi ^{{{l}_{0}}} {\frac{{{\text{ch}}({{l}_{0}} - \xi {\kern 1pt} ')\bar {\gamma }}}{{{\text{ch}}{{l}_{0}}\bar {\gamma }}}} d\xi {\kern 1pt} ' = \\ = \int\limits_\xi ^{{{l}_{0}}} {\frac{{{\text{ch}}({{l}_{0}} - \xi {\kern 1pt} ')\bar {\gamma }}}{{p{\text{ch}}{{l}_{0}}\bar {\gamma }}}} d\xi {\kern 1pt} '\,\, + \int\limits_\xi ^{{{l}_{0}}} {\frac{{{\text{ch}}({{l}_{0}} - \xi {\kern 1pt} ')\bar {\gamma }}}{{{\text{ch}}{{l}_{0}}\bar {\gamma }}}} d\xi {\kern 1pt} '. \\ \end{gathered} $

Находим оригинал искомого решения

(44)
$\Theta (\xi ,\tau ) = \int\limits_\xi ^{{{l}_{0}}} {W(\xi {\kern 1pt} ',\tau )d\xi {\kern 1pt} '} + \int\limits_\xi ^{{{l}_{0}}} {\frac{{\partial W(\xi {\kern 1pt} ',\tau )}}{{\partial \tau }}} d\xi {\kern 1pt} ',$
где $W(\xi ,\tau )$ имеет вид (32), (33). Вычисление интегралов в (44) не представляет трудностей.

Аналогичным образом рассмотрим уравнение (38) с начальными условиями (39) и граничными условиями

(45)
${{\left. {\Theta (\xi ,\tau )} \right|}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}},\,\,\,\,\tau > 0;$
(46)
$\int\limits_0^\tau {{{{\left. {\frac{{\partial \Theta (\xi ,\tau {\kern 1pt} ')}}{{\partial \xi }}} \right|}}_{{\xi {\kern 1pt} = {\kern 1pt} {{l}_{0}}}}}\exp \left[ { - (\tau - \tau {\kern 1pt} ')} \right]d\tau {\kern 1pt} '} = 1,\,\,\,\,\tau > 0.$

Операционное решение этой задачи имеет вид

(47)
$\bar {\Theta }(\xi ,p) = \frac{{p + 1}}{{p\bar {\gamma }}}\frac{{{\text{sh}}\xi \bar {\gamma }}}{{{\text{ch}}{{l}_{0}}\bar {\gamma }}},\,\,\,\,\bar {\gamma } = \sqrt {p(p + 1).} $

Чтобы определить оригинал (47), воспользуемся изображением (25) с найденным оригиналом. Запишем

$\begin{gathered} \frac{{p + 1}}{{p\bar {\gamma }}}\frac{{{\text{sh}}\xi \bar {\gamma }}}{{{\text{ch}}{{l}_{0}}\bar {\gamma }}} = \frac{{p + 1}}{p}\int\limits_0^\xi {\frac{{{\text{ch}}\xi {\kern 1pt} '\bar {\gamma }}}{{{\text{ch}}{{l}_{0}}\bar {\gamma }}}} d\xi {\kern 1pt} ' = \\ = \int\limits_0^\xi {\frac{{{\text{ch}}\xi {\kern 1pt} '\bar {\gamma }}}{{p{\text{ch}}{{l}_{0}}\bar {\gamma }}}} d\xi {\kern 1pt} '\, + \int\limits_0^\xi {\frac{{{\text{ch}}\xi {\kern 1pt} '\bar {\gamma }}}{{{\text{ch}}{{l}_{0}}\bar {\gamma }}}} d\xi {\kern 1pt} '. \\ \end{gathered} $

Переходя к оригиналам, находим искомое решение задачи (38), (39), (45), (46):

(48)
$\Theta (\xi ,\tau ) = \int\limits_0^\xi {W(\xi {\kern 1pt} ',\tau )d\xi {\kern 1pt} '} + \int\limits_0^\xi {\frac{{\partial W(\xi {\kern 1pt} ',\tau )}}{{\partial \tau }}} d\xi {\kern 1pt} ',$
где $W(\xi ,\tau )$ – оригиналы (27)–(30).

Представляет интерес рассмотреть также обобщенное уравнение (12) с начальными условиями (13) и граничными условиями

(49)
${{\left. {\frac{{\partial W(\xi ,\tau )}}{{\partial \xi }}} \right|}_{{\xi = 0}}} = 0,\,\,\,\,\tau > 0;$
(50)
$\int\limits_0^\tau {{{{\left. {\frac{{\partial W(\xi ,\tau {\kern 1pt} ')}}{{\partial \xi }}} \right|}}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}}\exp \left[ { - (\tau - \tau {\kern 1pt} ')} \right]d\tau {\kern 1pt} '} = 1,\,\,\,\,\tau > 0.$

Операционное решение этой задачи имеет вид

(51)
$\begin{gathered} \bar {W}(\xi ,p) = \frac{{(p + 1){{{({\xi \mathord{\left/ {\vphantom {\xi {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}}^{{ - m}}}}}{{p\bar {\gamma }}}\frac{{{{I}_{m}}(\xi \bar {\gamma })}}{{{{I}_{{m + 1}}}({{l}_{0}}\bar {\gamma })}},\,\,\, \\ \bar {\gamma } = \sqrt {p(p + 1)} . \\ \end{gathered} $

Находим далее

(52)
$\frac{{d\bar {W}(\xi ,p)}}{{d\xi }} = \frac{{p + 1}}{p}\frac{{{{{({\xi \mathord{\left/ {\vphantom {\xi {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}}^{{ - m}}}{{I}_{{m{\kern 1pt} + {\kern 1pt} 1}}}(\xi \bar {\gamma })}}{{{{I}_{{m{\kern 1pt} + {\kern 1pt} 1}}}({{l}_{0}}\bar {\gamma })}}.$

Дальнейшие вычисления связаны с определением оригинала функции

(53)
$\bar {\Psi }(\xi ,p) = \frac{{{{I}_{{m{\kern 1pt} + {\kern 1pt} 1}}}(\xi \bar {\gamma })}}{{p{{I}_{{m{\kern 1pt} + {\kern 1pt} 1}}}({{l}_{0}}\bar {\gamma })}}.$

Применяя рассмотренную выше методику, находим

(54)
$\begin{gathered} \Psi (\xi ,\tau ) = 1 - \frac{{2{{{({\xi \mathord{\left/ {\vphantom {\xi {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}}^{{ - m}}}\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2})}}{{m + 1}} \times \\ \times \,\,\sum\limits_{n{\kern 1pt} = {\kern 1pt} 1}^\infty {\frac{{{{J}_{{m{\kern 1pt} + {\kern 1pt} 1}}}\left( {\frac{{{{\mu }_{n}}\xi }}{{{{l}_{0}}}}} \right)\left( {\sin \frac{{{{\omega }_{n}}\tau }}{2} + {{\omega }_{n}}\cos \frac{{{{\omega }_{n}}\tau }}{2}} \right)}}{{{{\omega }_{n}}{{J}_{m}}({{\mu }_{n}})}},} \\ \end{gathered} $
где ${{\mu }_{n}} > 0$ – корни уравнения ${{J}_{{m + 1}}}(\mu ) = 0,$ ${{\omega }_{n}} = \sqrt {{{{\left( {\frac{{2{{\mu }_{n}}}}{{{{l}_{0}}}}} \right)}}^{2}} - 1} .$

Искомый оригинал – решение задачи (12), (13), (49), (50) – получим из (52), (53):

(55)
$W(\xi ,\tau ) = \int\limits_0^\xi {\Psi (\xi {\kern 1pt} ',\tau )d\xi {\kern 1pt} '\,\,} + \int\limits_0^\xi {\frac{{\partial \Psi (\xi {\kern 1pt} ',\tau )}}{{\partial \tau }}d\xi {\kern 1pt} '} .$

До вычисления интегралов в (55) ряд в (54) следует предварительно привести к соответствующим областям суммирования по изложенной выше методике. Далее можно использовать интегральное соотношение

(56)
$\int\limits_{{{z}_{0}}}^z {{{y}^{{ - \nu }}}{{J}_{{\nu {\kern 1pt} + {\kern 1pt} 1}}}(y)dy} = - \left[ {{{y}^{{ - {{\nu }}}}}{{J}_{{{\nu }}}}(y)} \right]_{{{{z}_{0}}}}^{z}$
и асимптотическую формулу

(57)
${{J}_{\nu }}(z) \cong \frac{{{{z}^{\nu }}}}{{{{2}^{\nu }}\Gamma (1 + \nu )}},\,\,\,\,z \to 0.$

Следует заметить, что изучение обобщенныx уравнений (12) имеет неоспоримую ценность, так как позволяет фактически описать конструкцию аналитических решений в любой из трех систем координат (для пластины, цилиндра и шара), фиксируя последовательно в общем решении индекс функции Бесселя.

АНАЛИТИЧЕСКИЕ РЕШЕНИЯ ДЛЯ ЧАСТИЧНО ОГРАНИЧЕННЫХ ОБЛАСТЕЙ

К числу новых случаев относится задача нестационарной теплопроводности для частично ограниченной области $x > l,$ $t > 0.$ В координатах $(\xi ,\tau )$ задача имеет вид

(58)
$\frac{{\partial W}}{{\partial \tau }} = \frac{{{{\partial }^{2}}W}}{{\partial {{\xi }^{2}}}} + \frac{{2m + 1}}{\xi }\frac{{\partial W}}{{\partial \xi }} - \frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}},\,\,\,\,\xi > {{l}_{0}},\,\,\,\,\tau > 0;$
(59)
${{\left. W \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = {{\left. {\frac{{\partial W}}{{\partial \tau }}} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,\xi \geqslant {{l}_{0}};$
(60)
${{\left. W \right|}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}} = 1,\,\,\,\,\tau > 0;$
(61)
$\left| {W(\xi ,\tau )} \right| < \infty ,\,\,\,\,\xi \geqslant {{l}_{0}},\,\,\,\,\tau \geqslant 0.$

Ее операционное решение записывается как

(62)
$\bar {W}(\xi ,p) = \frac{{{{{({\xi \mathord{\left/ {\vphantom {\xi {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}}^{{ - m}}}{{K}_{m}}(\bar {\gamma }\xi )}}{{p{{K}_{m}}(\bar {\gamma }{{l}_{0}})}},\,\,\,\,\bar {\gamma } = \sqrt {p(p + 1)} .$

Оригинал изображения (62) установим позже. Трудность в его записи заключается в возможном появлении ступенчатой функции Хевисайда, что совершенно не очевидно, если искать оригинал принятым методом операционного исчисления через интеграл Римана–Меллина. Поэтому исследуем вначале асимптотическое представление изображения (62):

(63)
$\begin{gathered} \bar {W}{\text{*}}(\xi ,p) = {{({\xi \mathord{\left/ {\vphantom {\xi {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}^{{ - (m + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}}\frac{1}{p}\,\, \times \\ \times \,\,\exp \left[ { - (\xi - {{l}_{0}})\sqrt {p(p + 1)} } \right]. \\ \end{gathered} $

Но вначале изучим интеграл Римана–Меллина вида

(64)
$\Psi (\xi ,\tau ) = \frac{1}{{2\pi i}}\int\limits_{\beta {\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} + {\kern 1pt} i\infty } {\frac{1}{{\bar {\gamma }(p)}}\exp \left[ {p\tau - \xi {\text{*}}\bar {\gamma }(p)} \right]dp} ,$
где для удобства введены обозначения
(65)
$\begin{gathered} \bar {\gamma }(p) = \sqrt {p(p + 1)} ,\,\,\,\,\xi * = (\xi - {{l}_{0}})(\xi * > 0) \\ (p = \sigma + i\omega ). \\ \end{gathered} $
Для этого предварительно получим представление функции Бесселя мнимого аргумента ${{I}_{\nu }}(z)$ через интеграл Римана–Меллина (которое отсутствует в известных справочниках по специальным функциям). Вывод необходимого соотношения начнем с рассмотрения интегрального соотношения Ханкеля для функции ${{\Gamma }^{{ - 1}}}(k + \nu + 1),$ где $\Gamma (z)$ – гамма-функция. При $\nu > - 1$ можно от контура интегрирования, состоящего из окружности, обходящей начало координат, и далее верхнего и нижнего берегов разреза вдоль отрицательной полуоси, перейти к эквивалентному контуру Бромвича [32] и записать
$\frac{1}{{\Gamma (k + \nu + 1)}} = \frac{1}{{2\pi i}}\int\limits_{\beta {\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} + {\kern 1pt} i\infty } {{{u}^{{ - (k + \nu + 1)}}}\exp (u)du} .$
Функция Бесселя ${{J}_{\nu }}(z)$ есть ряд вида [32]

${{J}_{\nu }}(z) = \sum\limits_{k{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{{{{( - 1)}}^{k}}{{{({z \mathord{\left/ {\vphantom {z 2}} \right. \kern-0em} 2})}}^{{\nu {\kern 1pt} + {\kern 1pt} 2k}}}}}{{\Gamma (k + 1)\Gamma (k + \nu + 1)}}} .$

Далее, используя (66), находим

(67)
$\begin{gathered} {{J}_{\nu }}(z) = \sum\limits_{k{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{{{{( - 1)}}^{k}}{{{({z \mathord{\left/ {\vphantom {z 2}} \right. \kern-0em} 2})}}^{{\nu {\kern 1pt} + {\kern 1pt} 2k}}}}}{{\Gamma (k + 1)}}\frac{1}{{2\pi i}}} \int\limits_{\beta {\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} + {\kern 1pt} i\infty } {{{u}^{{ - (k{\kern 1pt} + {\kern 1pt} \nu {\kern 1pt} + {\kern 1pt} 1)}}}\exp (u)du} = \\ = {{\left( {\frac{z}{2}} \right)}^{\nu }}{\kern 1pt} \frac{1}{{2\pi i}}\int\limits_{\beta {\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} + {\kern 1pt} i\infty } {{{u}^{{ - (\nu {\kern 1pt} + {\kern 1pt} 1)}}}{\kern 1pt} \exp (u)} \sum\limits_{k{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{{{{( - 1)}}^{k}}{{{\left( {\frac{{{{z}^{2}}}}{{4u}}} \right)}}^{k}}}}{{\Gamma (k + 1)}}{\kern 1pt} du} = \\ = {{\left( {\frac{z}{2}} \right)}^{\nu }}\frac{1}{{2\pi i}}\int\limits_{\beta {\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} + {\kern 1pt} i\infty } {{{u}^{{ - (\nu {\kern 1pt} + {\kern 1pt} 1)}}}\exp \left( {u - \frac{{{{z}^{2}}}}{{4u}}} \right)du} . \\ \end{gathered} $
Заменяя в (67) $z$ на $iz$ и учитывая, что ${{i}^{{ - \nu }}}{{J}_{\nu }}(iz) = {{I}_{\nu }}(z),$ находим

(68)
${{\left( {\frac{2}{z}} \right)}^{n}}{{I}_{n}}(z) = \frac{1}{{2\pi i}}\int\limits_{\beta {\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} + {\kern 1pt} i\infty } {\frac{1}{{{{u}^{{n{\kern 1pt} + {\kern 1pt} 1}}}}}\exp \left( {u + \frac{{{{z}^{2}}}}{{4u}}} \right)du} .$

Приведем (64) к виду, сходному с (68). Для этого положим [30]

(69)
${{(p + 1)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {{p}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{y}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{(p + 1)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {{p}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{y}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$
откуда находим
(70)
$\begin{gathered} p = \frac{1}{4}\left( {y + \frac{1}{y} - 2} \right),\,\,\,\, \\ \bar {\gamma }(p) = \frac{1}{4}\left( {y - \frac{1}{y}} \right),\,\,\,\,\frac{{dy}}{y} = \frac{{dp}}{{\bar {\gamma }(p)}}. \\ \end{gathered} $
Преобразуем интеграл (64) путем замены переменной (70). При этом прямая $(\beta - i\infty ,\,\,\beta + i\infty )$ в плоскости $p$ преобразуется в некоторую линию в плоскости $y.$ Эта линия не будет прямой, но по теореме Коши [32] она может быть трансформирована в линию ($\beta {\kern 1pt} '\,\, - i\infty ,\,\,\beta {\kern 1pt} '\,\, + i\infty $). Теперь интеграл (64) примет вид
(71)
$\begin{gathered} \Psi (\xi ,\tau ) = \frac{1}{{2\pi i}}\int\limits_{\beta {\kern 1pt} '{\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} '{\kern 1pt} + {\kern 1pt} i\infty } {\frac{{dy}}{y}} {\kern 1pt} \,\, \times \\ \times \,\,\exp \left[ { - \frac{1}{2}\tau + \frac{1}{4}y(\tau - \xi *) + \frac{1}{{4y}}(\tau + \xi *)} \right]. \\ \end{gathered} $
Если $\tau > \xi *,$ то, полагая $({y \mathord{\left/ {\vphantom {y 4}} \right. \kern-0em} 4})(\tau - \xi *) = u$ в (71), находим, используя (68), при $n = 0{\text{:}}$
(72)
$\Psi (\xi ,\tau ) = \exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}){{I}_{0}}\left( {\frac{1}{2}\sqrt {{{\tau }^{2}} - {{\xi }^{{*2}}}} } \right),\,\,\,\,\tau > \xi {\text{*}}.$
Если $\tau < \xi *,$ то рассмотрим интеграл (71), взятый по замкнутому контуру, изображенному на рис. 1. Этот контур состоит из линии $(\beta {\kern 1pt} '\, - i\infty ,\,\,\beta {\kern 1pt} '\, + i\infty )$ и дуги радиуса $R$ с центром вначале координат. Подынтегральная функция в (71) регулярна внутри контура и на границе. Эта функция внутри контура не содержит ни одного полюса. Тогда по теореме Коши интеграл вдоль указанного контура равен нулю. Можно показать, что при $R \to \infty $ интеграл вдоль дуги окружности обращается в нуль. Таким образом, приходим к результату $\Psi (\xi ,\tau ) = 0,$ $\tau < \xi *,$ т.е.
(73)
$\begin{gathered} \Psi (\xi ,\tau ) = \frac{1}{{2\pi i}}\int\limits_{\beta {\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} + {\kern 1pt} i\infty } {\frac{1}{{\bar {\gamma }(p)}}\exp \left[ {p\tau - \xi {\text{*}}\bar {\gamma }(p)} \right]dp} = \\ = \exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}){{I}_{0}}\left( {\frac{1}{2}\sqrt {{{\tau }^{2}} - {{\xi }^{{*2}}}} } \right)\eta (\tau - \xi *). \\ \end{gathered} $
Теперь продифференцируем обе части (73) по $\xi {\text{*}}$ и затем проинтегрируем по $\tau $ от нуля до $\tau $ (предполагая, что эти операции допустимы). В результате оригинал асимптотического выражения (63) будет иметь вид функциональной конструкции, содержащей ступенчатую функцию Хевисайда:

(74)
$\begin{gathered} \frac{{W{\text{*}}(\xi ,\tau )}}{{{{{({\xi \mathord{\left/ {\vphantom {\xi {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}}^{{ - (m{\kern 1pt} + {\kern 1pt} {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}}}} = \left[ {\exp ({{ - \xi {\text{*}}} \mathord{\left/ {\vphantom {{ - \xi {\text{*}}} 2}} \right. \kern-0em} 2}){{ + }^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}}}} \right. \\ \left. { + \,\,\frac{{\xi {\text{*}}}}{2}\int\limits_{\xi *}^\tau {\exp ({{ - \tau {\kern 1pt} '} \mathord{\left/ {\vphantom {{ - \tau {\kern 1pt} '} 2}} \right. \kern-0em} 2})\frac{{{{I}_{1}}\left( {\frac{1}{2}\sqrt {{{\tau }^{{'2}}} - {{\xi }^{{*2}}}} } \right)}}{{\sqrt {{{\tau }^{{'2}}} - {{\xi }^{{*2}}}} }}d\tau {\kern 1pt} '} } \right]\eta (\tau - \xi *). \\ \end{gathered} $
Рис. 1.

Контур при вычислении интеграла (71).

Разумеется, выявленная особенность оригинала (74) имеет место и для оригинала изображения (62). Находим указанный оригинал с помощью интеграла Римана–Меллина

(75)
$\frac{{W(\xi ,\tau )}}{{{{{({\xi \mathord{\left/ {\vphantom {\xi {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}}^{{ - m}}}}} = \frac{1}{{2\pi i}}\int\limits_{\beta {\kern 1pt} - {\kern 1pt} i\infty }^{\beta {\kern 1pt} + {\kern 1pt} i\infty } {\frac{{{{K}_{m}}(\xi \sqrt {p(p + 1)} )}}{{p{{K}_{m}}({{l}_{0}}\sqrt {p(p + 1)} )}}\exp (p\tau )dp.} $

Подынтегральная функция в (75) имеет две точки ветвления. Применяя для этого случая принятый подход в операционном исчислении и формулу

${{K}_{m}}( \pm iz) = ({{\pi i} \mathord{\left/ {\vphantom {{\pi i} 2}} \right. \kern-0em} 2})\exp \left( { \mp \frac{{im\pi }}{2}} \right)\left[ { \mp {{J}_{m}}(z) + i{{Y}_{m}}(z)} \right],$
находим после длительных преобразований искомое аналитическое решение задачи (58)–(61):
(76)
$\begin{gathered} W(\xi ,\tau ) = \left\{ {1 + \frac{{{{{({\xi \mathord{\left/ {\vphantom {\xi {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}})}}^{{ - m}}}}}{\pi }} \right.\int\limits_0^1 {\left. {\frac{{\left[ {{{J}_{m}}(\xi \sqrt {\rho (1 - \rho )} ){{Y}_{m}}({{l}_{0}}\sqrt {\rho (1 - \rho )} ) - {{Y}_{m}}(\xi \sqrt {\rho (1 - \rho )} ){{J}_{m}}({{l}_{0}}\sqrt {\rho (1 - \rho )} )} \right]}}{{\rho \left[ {J_{m}^{2}\left( {{{l}_{0}}\sqrt {\rho (1 - \rho )} ) + Y_{m}^{2}({{l}_{0}}\sqrt {\rho (1 - \rho )} } \right)} \right]}}\exp ( - \rho \tau {\kern 1pt} ')d\tau {\kern 1pt} '} \right\}} \times \\ \times \,\,\eta \left[ {\tau - \left( {\xi - {{l}_{0}}} \right)} \right]. \\ \end{gathered} $
Можно рассмотреть интересный частный случай найденных выражений (74) и (76) при $m = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2},$ т.е. записать аналитическое решение задачи:

$\begin{gathered} \frac{{\partial W}}{{\partial \tau }} = \frac{{{{\partial }^{2}}W}}{{\partial {{\xi }^{2}}}} - \frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}},\,\,\,\,\xi > 0,\,\,\,\,\tau > 0; \\ {{\left. W \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = {{\left. {\frac{{\partial W}}{{\partial \tau }}} \right|}_{{\tau {\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,\xi \geqslant 0; \\ {{\left. W \right|}_{{\xi {\kern 1pt} = {\kern 1pt} 0}}} = 1,\,\,\,\,\tau > 0,\,\,\,\,\left| {W(\xi ,\tau )} \right| < \infty ,\,\,\,\,\xi \geqslant 0,\,\,\,\,\tau \geqslant 0. \\ \end{gathered} $

Такое решение имеет две различные функциональные формы, тождественные между собой. Первую форму находим из (74)

(77)
$\begin{gathered} W(\xi ,\tau ) = \left[ {\exp ({{ - \xi } \mathord{\left/ {\vphantom {{ - \xi } 2}} \right. \kern-0em} 2}) + ({\xi \mathord{\left/ {\vphantom {\xi 2}} \right. \kern-0em} 2}){{ \times }^{{^{{^{{^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ \left. { \times \,\,\int\limits_\xi ^\tau {\exp ({{ - \tau {\kern 1pt} '} \mathord{\left/ {\vphantom {{ - \tau {\kern 1pt} '} 2}} \right. \kern-0em} 2})\frac{{{{I}_{1}}\left( {\frac{1}{2}\sqrt {{{\tau }^{{'2}}} - {{\xi }^{2}}} } \right)}}{{\sqrt {{{\tau }^{{'2}}} - {{\xi }^{2}}} }}d\tau {\kern 1pt} '} } \right]\eta (\tau - \xi ). \\ \end{gathered} $

Из (76) следует вторая аналитическая форма

(78)
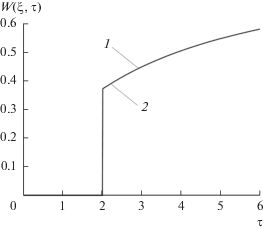
$\begin{gathered} W(\xi ,\tau ) = \left[ {1 - \frac{1}{\pi }\int\limits_0^1 {\exp ( - \rho \tau )\frac{{\sin \xi \sqrt {\rho (1 - \rho )} }}{\rho }d\rho } } \right] \times \\ \times \,\,\eta (\tau - \xi ). \\ \end{gathered} $

Равенство этих выражений установлено автором в [26]. На рис. 2 приведен график кривых $W(\xi ,\tau )$ в сечении $\xi = 2.$ Обе кривые, вычисленные по формулам (77) и (78), практически совпали.

Рис. 2.

Результаты вычисления функции W(ξ, τ) в сечении $\xi = 2{\text{:}}$ 1 – по (77), 2 – (78).

Таким образом, как показывают приведенные рассуждения, даже для частично ограниченной области нахождение аналитических решений волновых уравнений в задачах нестационарной теплопроводности представляет собой достаточно трудоемкую вычислительную проблему аналитической теплофизики.

ЗАКЛЮЧЕНИЕ

Изложены принципиально новые результаты аналитической теплофизики, относящиеся к локально-неравновесному теплообмену в терминах краевых задач нестационарной теплопроводности для уравнений гиперболического типа. Развита методика нахождения точных аналитических решений указанного вида задач теплопереноса для областей канонического типа на основе обобщенных уравнений нестационарной теплопроводности, охватывающих одновременно три системы координат: декартовую, цилиндрическую и сферическую. Рассмотрена серия практических задач нестационарного теплопереноса для частично ограниченных областей.

Список литературы

  1. Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М.: Высшая школа, 2001. 550 с.

  2. Карташов Э.М., Кудинов В.А. Аналитические методы теории теплопроводности и ее приложения. М.: URSS, 2018. 1080 с.

  3. Зарубин В.С. Инженерные методы решения задач теплопроводности. М.: Энергоатомиздат, 1983. 328 с.

  4. Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.

  5. Лыков А.В. Теплопроводность и диффузия. М.: Гизлегпром, 1941. 196 с.

  6. Cattaneo C. Sulla Conduzione de Calore // Atti del Seminaro Matematiko c Fisico dell. Universita di Modena. 1948. V. 3. P. 83.

  7. Vernotte P. Les paradoxes de la theorie continue de I'equation de la chaleur // Compte Rendus. Acad. Sci. Paris. 1958. V. 246. № 22. P. 3154.

  8. Maxwell J.C. On the Dynamical Theory of Gases // Phil. Trans. Royal Soc. London. 1967. V. 157. Part. 1. P. 49.

  9. Tissa L. Transport Phenomena in Helium-2 // Nature. 1938. V. 141. № 3577. P. 913.

  10. Ландау Л.Д. Теория сверхтекучести гелия 2 // ЖЭТФ. 1941. Т. 2. № 6. С. 592.

  11. Пешков В.П. Определение скорости распространения второго звука в гелии // ЖЭТФ. 1946. Т. 16. № 8. С. 744.

  12. Ward J.C., Wilks J. Second Sound and the Thermo-mechanical Effect at Very Low Temperatures // Philos. Mag. 1952. V. 43. № 336. P. 48.

  13. Dinqle R.B. The Velocity of Second Sound in Various Media // Proc. Phys. Soc. 1952. V. 65. № 396A. P. 1040.

  14. London F. Superfluids 2. N.Y.: John Wiley and Sons Inc., 1954. P. 101.

  15. Ackermann C.C., Guyer R.A., Bertman B., Fairbank H.A. Second Sound in Solid Helium // Phys. Rev. Lett. 1966. V. 16. № 18. P. 789.

  16. Гуревич В.Л., Шкловский Р.П. К теории второго звука в полупроводниках // ФТТ. 1966. Т. 8. № 10. С. 3050.

  17. Гуржи Р.Н., Конторович В.М. Электронный звук в металлах // ЖЭТФ. 1968. Т. 55. № 3. С. 1105.

  18. Гуржи Р.Н. О втором звуке в твердых телах // ФТТ. 1965. Т. 7. № 12. С. 3515.

  19. Кащеев В.Н. Распространение второго звука в газе магнонов // Изв. АН Латв. ССР. Cер. физ.-техн. наук. 1969. № 2. С. 36.

  20. Chester M. Second Sound in Solids // Phys. Rev. 1963. V. 131. № 5. P. 2013.

  21. Kaliski S. Wave Equations in Thermoelastisity // Bull. Acad. Polon. Sci. Techn. 1965. V. 13. № 5. P. 409.

  22. Herwiq H., Beckert K. Experimental Evidence about Controversy Concerning Fourier or Non-fourier Heat Conduction in Materials with Non-homogeneous Inner Structure // Heat Mass Transfer. 2000. V. 36. P. 387.

  23. Mitra K., Kumar S., Vedavars A., Mjallemi M.K. Experimental Evidence of Hyperbolic Heat Conduction in Processed Meat // Heat Transfer. Trans. ASME. V. 117. № 3. P. 568.

  24. Кирсанов Ю.А., Кирсанов А.Ю. Об измерении времени тепловой релаксации твердого тела // Изв. РАН. Энергетика. 2015. № 1. С. 113.

  25. Кирсанов Ю.А. Влияние тепловой релаксации и термического демпфирования на переходные процессы при циклических граничных условиях // ТВТ. 2017. Т. 55. № 4. С. 549.

  26. Карташов Э.М. Аналитические решения гиперболических моделей теплопроводности // ИФЖ. 2014. Т. 87. № 5. С. 1072.

  27. Формалев В.Ф. Теплопроводность анизотропных тел. Аналитические методы решения задач. М.: Физматлит, 2014. 310 с.

  28. Формалев В.Ф., Колесник С.А. О тепловых солитонах при волновом теплопереносе в ограниченных областях // ТВТ. 2019. Т. 57. № 4. С. 543.

  29. Формалев В.Ф., Колесник С.А., Кузнецова Е.Л. Влияние компонентов тензора теплопроводности теплозащитного материала на величину тепловых потоков от газодинамического пограничного слоя // ТВТ. 2019. Т. 57. № 1. С. 66.

  30. Карташов Э.М. Оригиналы операционных изображений для обобщенных задач нестационарной теплопроводности // Тонкие хим. технологии. 2019. Т. 14. № 4. С. 77.

  31. Карслоу Г., Егер Д. Операционные методы в прикладной математике. М.: Изд-во иностр. лит., 1948. 294 с.

  32. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1965. 716 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал