1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 59, № 4, 2021

Теплофизика высоких температур, 2021, T. 59, № 4, стр. 514-519

МОДЕЛЬ КОЭФФИЦИЕНТА ГРЮНАЙЗЕНА ДЛЯ ШИРОКОГО ДИАПАЗОНА ПЛОТНОСТЕЙ НА ПРИМЕРЕ МЕДИ

Р. К. Бельхеева *, **

Новосибирский государственный университет (НГУ),
Новосибирск, Россия

* E-mail: rumia@post.nsu.ru
** E-mail: rimbel@academ.org

Поступила в редакцию 05.05.2020
После доработки 28.02.2021
Принята к публикации 19.05.2021

Полный текст (PDF)

Аннотация

Предложен способ описания коэффициента Грюнайзена, позволяющий единым образом описывать как сплошные материалы, для которых ударные адиабаты ведут себя нормальным образом, так и материалы с высокой пористостью, ударные адиабаты которых имеют аномальный ход. Пористый материал рассматривается как простая термодинамически равновесная смесь, для которой выполняется гипотеза аддитивности объемов ее компонентов. Равновесное состояние определяется условиями равенства давлений, температур и скоростей составляющих смеси. При описании смеси используется модель взаимопроникающих и взаимодействующих континуумов. В модели учитывается наличие газа в порах. Выполнены численные расчеты ударно-волнового нагружения и изоэнтропического расширения образцов меди различной пористости. Сравнением расчетных и экспериментальных ударных адиабат и изоэнтроп разрежения показано, что предложенная модель коэффициента Грюнайзена достаточно точно описывает поведение сплошных материалов и материалов с малой и высокой пористостью.

ВВЕДЕНИЕ

Развитие разделов физики и механики, связанных с изучением явлений, происходящих при интенсивных ударно-волновых нагружениях конденсированных сред, вызвано широким использованием методов ударного обжатия при получении новых материалов с заданными свойствами. При описании возникающих гидродинамических процессов необходимо знать термодинамические свойства вещества. Теоретическое описание термодинамических свойств конденсированных тел при высоких давлениях и температурах, возникающих при мощных импульсных нагрузках, представляет собой сложную задачу. Поэтому применяются эмпирические модели, адекватность которых верифицируется сравнением с экспериментальными данными. Уравнение состояния играет важную роль в моделировании процессов, происходящих при высокоскоростных нагружениях. Оно несет информацию о свойствах материала и “индивидуализирует” его. Одним из методов определения уравнения состояния твердых тел является метод ударно-волновых обжатий среды, в результате применения которого определяется ударная адиабата материала, а дополнительные теоретические соображения позволяют вычислить параметры уравнения состояния и зависимость коэффициента Грюнайзена от плотности материала. Современные требования к уравнениям состояния, теоретические и экспериментальные методы исследования термодинамических свойств вещества описаны в [1–3].

При ударно-волновом нагружении пористых материалов возрастает роль теплового давления. Изучение ударного сжатия одного и того же материала при различных начальных пористостях дает более полную картину о свойствах материала и зависимости коэффициента Грюнайзена от термодинамических переменных при высоких давлениях. Большое нагревание при ударном сжатии материалов с высокой пористостью приводит к аномальному поведению ударной адиабаты, заключающемуся в том, что объем среды с возрастанием давления не уменьшается как у конденсированных сред, а увеличивается. Для того чтобы при моделировании отражалось это различие в ходе ударных адиабат для сплошных материалов и материалов с малыми пористостями от аномального хода ударных адиабат для материалов с большими пористостями, необходимо учесть этот фактор при описании коэффициента Грюнайзена.

При амплитудах нагружения до нескольких сотен ГПа зависимость давления от плотности материала и температуры в форме уравнения Ми–Грюнайзена задается формулой

$P = {{P}_{X}} + {{P}_{T}},$
где ${{P}_{X}} = A\left[ {{{{\left( {\frac{\rho }{{{{\rho }_{0}}}}} \right)}}^{n}} - 1} \right]$ – упругая составляющая давления, описываемая уравнением типа уравнения Тета; PT = γρET – тепловая составляющая давления; ρ – плотность среды; ρ0 – параметр уравнения состояния (в случае конденсированного вещества это его плотность при нормальных условиях); A, n – константы, характеризующие вещество; γ – коэффициент Грюнайзена; ET – тепловая энергия. Параметр A вычисляется по формуле
$A = \frac{{c_{0}^{2}{{\rho }_{0}}}}{n},$
где c0 – объемная скорость звука при нормальных условиях.

Внутренняя энергия также представляется в виде суммы двух составляющих:

$E = {{E}_{X}} + {{E}_{T}}.$

Здесь упругая часть энергии сжатия EX связана с упругой составляющей давления зависимостью ${{E}_{X}} = \int_{{{{{\rho }}}_{{\text{0}}}}}^{{\rho }} {\frac{{{{P}_{x}}}}{{{{\rho }^{2}}}}d\rho } ,$ тепловая часть внутренней энергии задается соотношением ET = ${{c}_{v}}(T - {{T}_{0}})$, где ${{c}_{v}}$ – удельная теплоемкость, T – температура, T0 – начальная температура.

Анализ данных, приведенных в литературе, показывает, что с ростом интенсивности ударно-волновых нагрузок коэффициент Грюнайзена уменьшается. Такое поведение коэффициента Грюнайзена закладывалось, например, в модели уравнений состояния в работах [4–9]. При небольших пористостях при нормальном ходе ударных адиабат зависимость γ = ${{\gamma }_{0}}{{\left( {\frac{{{{\rho }_{0}}}}{\rho }} \right)}^{l}}$ при l > 0 описывает именно такое изменение коэффициента Грюнайзена, так как отношение $\frac{{{{\rho }_{0}}}}{\rho }$ < 1 во всем диапазоне изменения давления. Но при высоких пористостях образец в ударной волне сжимается до плотности тем меньшей, чем выше давление, и тогда отношение $\frac{{{{\rho }_{0}}}}{\rho }$ > 1. Если в этом диапазоне пористостей и давлений коэффициент Грюнайзена описывать данным соотношением, то он будет увеличиваться по сравнению с нормальным значением γ0.

В данной работе зависимость коэффициента Грюнайзена от плотности предлагается описывать соотношением

$\gamma = {{\gamma }_{0}}{{\left( {\frac{{{{\rho }_{0}}}}{\rho }} \right)}^{{\ln \frac{\rho }{{{{\rho }_{0}}}}}}}.$

Использование функции $\ln \frac{\rho }{{{{\rho }_{0}}}}$ в показателе обобщает модель коэффициента Грюнайзена, приведенную в [10], поскольку знак логарифма зависит от величины аргумента. Кроме того, показатель степени изменяется с изменением плотности.

ОПИСАНИЕ МОДЕЛИ

В [10] приведены соотношения, выражающие параметры уравнения состояния смеси через соответствующие параметры и массовые доли составляющих. В данной работе способом, описанным в [10], получены формулы, связывающие параметр смеси γ0 и параметры компонентов γi0:

${{\gamma }_{0}} = \frac{n}{{{{c}_{v}}}}{{({{\rho }_{0}}{{B}_{1}})}^{{\ln ({{\rho }_{0}}{{B}_{1}})}}}{{B}_{2}},$
где

$\begin{gathered} {{B}_{1}} = \sum\limits_{i = 1}^N {\frac{{{{x}_{i}}}}{{{{\rho }_{{ii0}}}}}} {{\left( {\frac{{{{A}_{i}}}}{{P + k{{A}_{N}}}}} \right)}^{{1{\text{/}}{{n}_{i}}}}}, \\ {{B}_{2}} = \sum\limits_{i = 1}^N {\frac{{{{x}_{i}}{{\gamma }_{{i0}}}{{c}_{{vi}}}}}{{{{n}_{i}}}}} {{\left( {\frac{{P + k{{A}_{N}}}}{{{{A}_{i}}}}} \right)}^{{\frac{1}{{n_{i}^{2}}}\ln \frac{{{{A}_{i}}}}{{P + k{{A}_{N}}}}}}}. \\ \end{gathered} $

Здесь N – число компонентов в смеси, величины с индексом i относятся к составляющим. В [10] показано, что значение k = 2 гарантирует выполнение условия сходимости. Остальные параметры смеси используются в виде, приведенном в [10].

В [11] для описания коэффициента Грюнайзена предложено выражение, зависящее только от температуры. В нем использованы три внешних параметра, которые выбираются из условия соответствия расчетных ударных адиабат известным экспериментальным результатам для каждого материала. В [12] приведено уравнение состояния, которое не содержит внутренней энергии, и в нем три внешних параметра определяются таким образом, чтобы коэффициент Грюнайзена принимал некоторые заданные значения, причем еще три параметра используются для описания удельной теплоемкости. В [13] учетом зависимости от сжатия модернизируется коэффициент Грюнайзена из [11], при этом применяются пять внешних параметров. В данной работе для описания коэффициента Грюнайзена используется только один внешний параметр γ0.

Из основного уравнения термодинамики

$dS = dE{\text{/}}T + Pdv{\text{/}}T,$
где S – энтропия, $v$ – удельный объем, получим уравнение изоэнтропы разгрузки

$\ln \left( {\frac{{{{c}_{v}}(T - {{T}_{0}})}}{{{{c}_{{{{v}_{{{\text{in}}}}}}}}({{T}_{{{\text{in}}}}} - {{T}_{0}})}}} \right) = - \int\limits_{{{v}_{{{\text{in}}}}}}^v {\frac{{\gamma (v)}}{v}dv.} $

Индекс in относится к исходному состоянию, в котором энтропия S = Sin. Считая, что удельная теплоемкость постоянна ${{c}_{v}}$ = ${{c}_{{{{{v}}_{{{\text{in}}}}}}}},$ получаем следующее выражение, связывающее температуру и плотность на изоэнтропе:

$\begin{gathered} \frac{{T - {{T}_{0}}}}{{{{T}_{{{\text{in}}}}} - {{T}_{0}}}} = \exp \left( { - {{\gamma }_{0}}\left( {\sum\limits_{n = 0}^\infty {{{{( - 1)}}^{n}}} } \right.} \right.\frac{1}{{n!(2n + 1)}} \times \\ \times \,\,\left. {\left. {\left[ {{{{\left( {\ln \frac{\rho }{{{{\rho }_{0}}}}} \right)}}^{{2n + 1}}} - {{{\left( {\ln \frac{{{{\rho }_{0}}}}{{{{\rho }_{{{\text{in}}}}}}}} \right)}}^{{2n + 1}}}} \right]} \right)} \right). \\ \end{gathered} $

Для вычисления скорости звука получаем выражение

${{c}^{2}} = \frac{1}{\rho }\left[ {n\left( {{{P}_{X}} + A} \right) + \left( {\gamma + 1 + 2\ln \frac{{{{\rho }_{0}}}}{\rho }} \right){{P}_{T}}} \right].$

Увеличение массовой скорости в волне разрежения на участке от некоторой точки на адиабате Гюгонио до точки, в которой давление равно нулю, определяется интегралом Римана вдоль изоэнтропы

${{u}_{r}} = {{\int\limits_{v({{P}_{H}})}^{v(P = 0)} {\left[ { - {{{\left( {\frac{{\partial P}}{{\partial v}}} \right)}}_{S}}} \right]} }^{{1{\text{/}}2}}}dv,$
где $v({{P}_{H}}),\,\,v(P = 0)$ – соответственно удельные объемы на адиабате Гюгонио при давлении P = PH и на изоэнтропе разгрузки при давлении P = 0. Скорость свободной поверхности описывается соотношением ufs = u + ur.

Изучить область применимости уравнения состояния, коэффициент Грюнайзена в которой задан логарифмической зависимостью отношения плотностей, можно путем сравнения расчетных и экспериментальных ударных адиабат и изоэнтроп разгрузки для образцов меди различной пористости.

Для проведения расчетов одни и те же параметры уравнения состояния, приведенные в таб-лице, используются для всех значений пористости.

Параметры уравнений состояния воздуха и меди

Вещество ρii0, кг/м3 Ai, Па ni ${{c}_{{vi}}},$
кДж/(кг К) 		γi li
Воздух 1.3 0.695 × 10–3 2.20 0.718 0.16 0.1
Медь 8.93 × 103 329.5 × 108 4.25 0.382 2.00     1.08

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

На графиках, приведенных ниже, цифрами 1 и 1' обозначены кривые, рассчитанные с помощью уравнения состояния, опубликованного в [10] (модель I), а цифрами 2 и 2' – с использованием предлагаемой модели (модель II).

На рис. 1 представлены расчетные ударные адиабаты для сплошной меди в координатах u–(D – u). Сплошные кривые 1, 2 – результаты расчетов настоящей работы, данные для прерывистой кривой 3 любезно предоставлены авторами [14]. В работе [14] ударная адиабата определяется уравнением (40) (в [14]). Данная ударная адиабата получена путем обобщения многочисленных экспериментальных точек и результатов квантовостатистических расчетов авторов [14]. Символами 5–7 обозначены данные экспериментов [16–18] в интерпретации оригинальных работ [16–18], символами 8–10 обозначены данные [16–18] в интерпретации [14]. Кривые 1 и 3 до массовых скоростей 8 км/с сливаются, но с увеличением интенсивности нагрузки кривая 3 отклоняется от 1 и приближается к кривой 2, при массовых скоростях, близких к 16 км/с, кривые 2 и 3 практически сливаются.

Рис. 1.

Ударные адиабаты для сплошных образцов меди в координатах u–(D – u): 3 – данные [14]; 4– экспериментальные данные [15]; 5 – [16]; 6 – [17]; 7 – [18]; 8–10 – данные [16–18] в интерпретации [14].

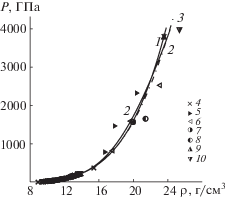
На рис. 2 приведены ударные адиабаты для сплошных образцов меди в ρ–P-координатах. Обозначения те же, что на рис. 1. Поведение кривых аналогично рис. 1.

Рис. 2.

Ударные адиабаты для сплошных образцов меди в координатах плотность–давление: 3 – данные [14]; 4 – экспериментальные данные [15]; 5 – [16]; 6 – [17]; 7 – [18]; 8–10 – данные [16–18] в интерпретации [14].

На рис. 3 приведены расчетные ударные адиабаты (сплошные кривые) и изоэнтропы разгрузки (прерывистые кривые) для сплошных образцов меди в координатах u–P, экспериментальные данные взяты из работы [19]. Хорошее соответствие расчетных кривых и экспериментальных данных для сплошных образцов меди показывает, что параметры уравнения состояния, приведенные в таблице, адекватно описывают материал. Для сплошных образцов меди ударные адиабаты, рассчитанные по обеим моделям, практически сливаются. Отличия начинают проявляться только при очень высоких давлениях. Скорости звука в нагруженных образцах различаются заметнее, и это отражается на различии изоэнтроп разгрузки.

Рис. 3.

Ударные адиабаты и изоэнтропы разгрузки для сплошных образцов меди в координатах u–P и экспериментальные данные [19] (3).

На рис. 4 приведены зависимости скорости звука от давления за фронтом ударной волны в нагруженных образцах сплошной меди. Экспериментальные данные, обозначенные значками 3–6, приведены соответственно в работах [15], [21–23].

Рис. 4.

Зависимости скорости звука от давления за фронтом ударной волны в нагруженных образцах сплошной меди; экспериментальные данные: 3 – [20], 4 – [21], 5 – [22], 6 – [23].

На рис. 5 приведены кривые, построенные по моделям I и II и данным, приведенным в [20, 24, 25] для коэффициента Грюнайзена для сплошных образцов меди. В [20, 24, 25] значения коэффициента Грюнайзена получены путем пересчета измеряемых в экспериментах данных. Однако этих данных недостаточно, чтобы провести сравнение коэффициента Грюнайзена для сплошных образцов меди в широком диапазоне нагрузок. При малых нагрузках данные (приведенные экспериментальные) лучше согласуются с кривой, задаваемой моделью I, но для нагрузок такого уровня коэффициент Грюнайзена можно считать постоянным. Однако с увеличением интенсивности ударной волны данные [20, 24, 25] отклоняются от кривой 1 и приближаются к кривой 2. При интенсивных нагрузках кривые 1 и 2 сближаются. Тенденция в поведении кривых одинаковая, но при малых нагрузках медленнее убывают значения коэффициента Грюнайзена, полученные с использованием модели II. Сравнение кривых, полученных с использованием двух моделей, и кривой, построенной по данным работ [20, 24, 25], показывает допустимость применения модели II для вычисления коэффициента Грюнайзена.

Рис. 5.

Графики зависимостей коэффициента Грюнайзена сплошных образцов меди от плотности в нагруженном образце; экспериментальные данные: 3 – [20], 4 – [24], 5 – [25].

На рис. 6 и рис. 7 приведены ударные адиабаты пористых образцов меди в координатах массовая скорость за фронтом ударной волны–скорость ударной волны и плотность среды–давление за фронтом ударной волны соответственно.

Рис. 6.

Ударные адиабаты для пористых образцов меди в координатах u–D; экспериментальные данные: 3 – [15], 4 – [26], 5 – [27], 6 – [27], 7 – [28], 8 – [28].

Рис. 7.

Ударные адиабаты для пористых образцов меди в координатах ρ–P; экспериментальные данные: 3 – [15], 4 – [26], 5 – [27], 6 – [27], 7 – [28], 8 – [28].

Над каждой кривой указана соответствующая пористость образца. Для наглядности на рис. 6 ударные адиабаты смещены вдоль оси u, а на рис. 7 ударные адиабаты смещены вдоль оси ρ на указанные над кривыми величины. Экспериментальные данные 3–8 взяты соответственно из работ [15], [26–28]. На рис. 6 u–D-адиабаты, рассчитанные по разным моделям, практически не отличаются при малых нагрузках для всех пористостей. С увеличением интенсивности ударно-волнового нагружения кривые, рассчитанные по разным моделям, немного расходятся, но это расхождение менее 7%, что сравнимо с уровнем разброса экспериментальных данных для пористых материалов. Оба семейства кривых с одинаковой степенью точности согласуются с экспериментальными данными. Наибольшее расхождение расчетных кривых отмечается для значений пористости 3 и 5.4. На рис. 7 расхождение ρ–P-адиабат более заметно, чем на рис. 6 u–D, но при больших давлениях кривые, рассчитанные по модели II, расположены ближе к экспериментальным данным. Аналогично на рис. 1 и 2 для сплошных материалов расхождение адиабат более заметно при высоких давлениях и адиабаты в ρ–P-координатах отличаются сильнее, чем в координатах u–D.

На рис. 7 так же, как на рис. 6, наибольшее расхождение расчетных кривых отмечается для значений пористости 3 и 5.4.

Как уже говорилось, в экспериментах измеряются массовая скорость за фронтом ударной волны и скорость ударной волны, а остальные величины чаще всего получаются пересчетом, поэтому более надежным является сравнение в координатах массовая скорость за фронтом ударной волны–скорость ударной волны.

Рис. 6, 7 показывают, что обе модели с одинаковой точностью описывают ударные адиабаты материалов с малыми пористостями, а в ρ–P-координатах кривые, полученные с использованием модели II при пористостях более 5.4, проходят ближе к экспериментальным данным.

ЗАКЛЮЧЕНИЕ

Предложенная в данной работе логарифмическая зависимость коэффициента Грюнайзена от плотности позволяет описать поведение коэффициента Грюнайзена единой формулой как для сплошных материалов, так и для материалов с низкой (менее 3) и высокой (более 5.4) пористостью, при которой проявляется аномальный ход ударных адиабат, когда образцы в ударной волне сжимаются до плотностей тем меньших, чем выше давление. В обоих случаях данная зависимость задает уменьшение коэффициента Грюнайзена с увеличением интенсивности нагружения.

Хорошее соответствие кривых, рассчитанных по модели II, и экспериментальных данных для сплошных образцов меди и образцов меди различной пористости показывает удовлетворительное описание предложенной простой логарифмической зависимостью коэффициента Грюнайзена поведение ударных адиабат как сплошных, так и пористых материалов.

Список литературы

  1. Ломоносов И.В., Фортова С.В. Широкодиапазонные полуэмпирические уравнения состояния вещества для численного моделирования высокоэнергетических процессов // ТВТ. 2017. Т. 55. № 4. С. 596.

  2. Khishchenko K.V. Equation of State for Niobium at High Pressures // Mathematica Montisnigri. 2020. V. 47. P. 119.

  3. Гилев С.Д. Малопараметрическое уравнение состояния алюминия // ТВТ. 2020. Т. 58. № 2. С. 179.

  4. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука, 1966. 632 с.

  5. Трунин Р.Ф., Симаков Г.В., Медведев А.Б. Сжатие титана в ударных волнах // ТВТ. 1999. Т. 37. № 6. С. 881.

  6. Бушман А.В., Ломоносов И.В., Фортов В.Е., Хищенко К.В. Уравнения состояния полимерных материалов при высоких давлениях // Хим. физика. 1994. Т. 13. № 1. С. 64.

  7. Ломоносов И.В., Фортов В.Е., Хищенко К.В. Модель широкодиапазонных уравнений состояния полимеров при высоких плотностях энергии // Хим. физика. 1995. Т. 14. № 1. С. 47.

  8. Хищенко К.В. Температура и теплоемкость полиметилметакрилата за фронтом сильных ударных волн // ТВТ. 1997. Т. 35. № 6. С. 1002.

  9. Хищенко К.В. Уравнение состояния магния в области высоких давлений // Письма в ЖТФ. 2004. Т. 30. № 19. С. 65.

  10. Бельхеева Р.К. Уравнение состояния сильнопористого вещества // ТВТ. 2015. Т. 53. № 3. С. 367.

  11. Кинеловский С.А., Маевский К.К. Моделирование ударно-волнового нагружения многокомпонентных материалов, включающих висмут // ТВТ. 2016. Т. 54. № 5. С. 716.

  12. Кинеловский С.А., Маевский К.К. Численное моделирование термодинамических параметров высокопористой меди // ЖТФ. 2019. Т. 89. № 8. С. 1158.

  13. Гилев С.Д. Малопараметрическое уравнение состояния меди // ФГВ. 2018. Т. 54. № 4. С. 107.

  14. Kadatskiy M.A., Khishchenko K.V. Theoretical Investigation of the Shock Compressibility of Copper in the Average-atom Approximation // Phys. Plasmas. 2018. V. 25. P. 112701.

  15. Levashov P.R., Khishchenko K.V., Lomonosov I.V., Fortov V.E. Database on Shock-wave Experiments and Equations of State Available via Internet // AIP Conf. Proc. 2004. V. 706. P. 87.

  16. Mitchell A.C., Nellis W.J., Moriarty J.A., Heinle R.A., Holmes N.C., Tipton R.E., Repp G.W. Equation of State of Al, Cu, Mo, and Pb at Shock Pressures up to 2.4 TPa (24 Mbar) // J. Appl. Phys. 1991. V. 69. P. 2981.

  17. Трунин Р.Ф., Подурец М.А., Моисеев Б.Н., Симаков Г.В., Попов Л.В. Сравнительная сжимаемость меди, кадмия и свинца при высоких давлениях // ЖЭТФ. 1969. Т. 56. С. 1172.

  18. Трунин Р.Ф., Подурец М.А., Симаков Г.В., Попов Л.В., Моисеев Б.Н. Экспериментальная проверка модели Томаса–Ферми для металлов при высоких давлениях // ЖЭТФ. 1972. Т. 62. С. 1043.

  19. Жерноклетов М.В., Зубарев В.Н., Сутулов Ю.Н. Адиабаты пористых образцов и изэнтропы расширения сплошной меди // ПМТФ. 1984. № 1. С. 119.

  20. Баум Ф.А., Орленко Л.П., Станюкович К.П. и др. Физика взрыва. М.: Наука, 1975. С. 704.

  21. McCoy C.A., Knudson M.D., Root S. Absolute Measurement of the Hugoniot and Sound Velocity of Liquid Copper at Multimegabar Pressures // Phys. Rev. B. 2017. V. 96. P. 174109. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.96.174109

  22. Альтшулер Л.В., Кормер С.Б., Бражник М.И., Сперанская М.П., Фунтиков А.И. Изоэнтропическая сжимаемость алюминия, меди, свинца и железа при высоких давлениях // ЖЭТФ. 1960. Т. 38. Вып. 4. С. 1061.

  23. Hayes D., Hixson R.S., McQueen R.G. High Pressure Elastic Properties, Solid-Liquid Phase Boundary and Liquid Equation of State from Release Wave Measurements in Shock-loaded Copper. In: Shock Compression of Condensed Matter / Eds. M.D. Furnish, L.C. Chhabildas, R.S. Hixson. N.Y.: AIP, 2000. P. 483.

  24. Альтшулер Л.В., Кормер С.Б., Баканова А.А., Трунин Р.Ф. Уравнение состояния алюминия, меди и свинца в области высоких давлений // ЖЭТФ. 1960. Т. 38. Вып. 3. С. 790.

  25. Кормер С.Б., Фунтиков А.И., Урлин В.Д., Колесникова А.Н. Динамическое сжатие пористых металлов и уравнение состояния с переменной теплоемкостью при высоких температурах // ЖЭТФ. 1962. Т. 42. Вып. 3. С. 686.

  26. LASL Shock Hugoniot Data / Ed. S.P. Marsh. Berkeley: Univ. California Press, 1980.

  27. Трунин Р.Ф., Симаков Г.В., Сутулов Ю.Н. и др. Сжимаемость пористых металлов в ударных волнах // ЖЭТФ. 1989. Т. 95. Вып. 3. С. 1024.

  28. Грязнов Б.К., Жерноклетов М.В., Иосилевский И.Л. и др. Ударно-волновое сжатие сильнонеидеальной плазмы металлов и ее термодинамика // ЖЭТФ. 1998. Т. 114. Вып. 4(10). С. 1242.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал